Abstract
Background
Type 1 diabetes (T1D) is a chronic endocrine disorder characterized by high blood glucose levels, impacting millions of people globally. Its management requires intensive insulin therapy, frequent blood glucose monitoring, and lifestyle adjustments. The accurate prediction of the short-term course of glucose levels in the subcutaneous space in T1D people, as measured by a continuous glucose monitoring (CGM) system, is essential for improving glucose control by avoiding harmful hypoglycaemic and hyperglycaemic glucose swings, facilitating precise insulin management and individualized care and, in turn, minimizing long-term vascular complications.
Methods
In this study, we propose an ensemble univariate short-term predictive model of the subcutaneous glucose concentration in T1D targeting at improving its error in the hypoglycaemic region. As such, the underlying basis functions are selected to minimize the percentage of erroneous predictions (EP) in the hypoglycaemic region, with EP being evaluated with continuous glucose error grid analysis (CG-EGA). The dataset comprises 29 individuals with T1D, who were monitored for 2 to 4 weeks during the GlucoseML prospective observational clinical study.
Results
Among six different basis models (i.e., linear regression (LR), automatic relevance determination (ARD), support vector regression (SVR), Gaussian process regression (GPR), eXtreme gradient boosting (XGBoost), and long short-term memory (LSTM)), XGBoost and SVR showed a dominant performance in the hypoglycaemic region and were selected as the constituent basis models of the ensemble model. The results indicate that the ensemble model significantly reduces the percentage of EP in the hypoglycaemic region for a 30 min prediction horizon to 19% as compared with its individual basis models (i.e., XGBoost and SVR), whilst its errors over the entire glucose range (hypoglycaemia, euglycaemia, and hyperglycaemia) are similar to those of the basis models.
Conclusions
The consideration of the performance of the basis functions in the hypoglycaemic region during the construction of the ensemble model contributes to enhancing their joint performance in that specific area. This could lead to more precise insulin management and a reduced risk of short-term hypoglycaemic fluctuations.
Supplementary Information
The online version contains supplementary material available at 10.1186/s12911-025-02867-2.
Keywords: Type 1 diabetes, Continuous glucose monitoring, Glucose prediction, Machine learning
Background
Diabetes mellitus, is a group of chronic metabolic disorders characterized by consistently elevated levels of blood glucose [1]. The main types of diabetes are type 1 diabetes (T1D), formerly known as insulin-dependent or juvenile diabetes, which is characterized by the autoimmune destruction of pancreatic ß-cells, leading to insulin deficiency, and type 2 diabetes, which involves insulin resistance and pancreatic ß-cell dysfunction. Both types are associated with the development of long-term complications, including damage to blood vessels and nerves. Strict control of blood glucose levels has been shown to reduce microvascular complications affecting small blood vessels of peripheral nerves, the retina, and kidneys, as well as macrovascular complications such as atherosclerosis [2]. According to the International Diabetes Federation Type 1 Diabetes Index, as of 2022, 8.75 million individuals are living with T1D globally, with 1.52 million of them being under the age of 20. In the same year, 530,000 new cases of T1D were diagnosed across all age groups, resulting in 182,000 deaths annually attributable to T1D. Notably, an estimated 35,000 deaths related to T1D in 2022 occurred in undiagnosed individuals under 25 years of age, who died within a year of symptomatic onset [3]. A lack of regular access to treatment poses serious and potentially life-threatening health risks for those with this condition. The management of T1D necessitates daily insulin treatment, frequent blood glucose self-monitoring, regular physical activity, and a healthy diet to mitigate complications and premature mortality. Although advancements in medical care and technology have facilitated the survival into adulthood of millions diagnosed with T1D during childhood, optimal control of the disease remains challenging at a worldwide level [4]. Prediction of short-term glucose levels is crucial for T1D patients, allowing more effective day-to-day self-management of the disease and tighter glucose control, thus contributing to the reduction of both dangerous short-term blood glucose fluctuations and the risk of severe long-term complications. For instance, advanced diabetes-technology treatment systems, such as continuous glucose monitoring (CGM) and insulin pumps, integrate prediction models to automate insulin delivery and produce real-time alerts of hyper- or hypo-glycaemic events [5].
Univariate glucose predictive modelling approaches in T1D are based on deep neural network algorithms, with the incorporation of time-domain features emerging as a promising approach, showcasing significantly improved performance with a root mean squared error (RMSE) of 6.31 mgdL−1 over a 30-minute prediction horizon [6]. Deep-ensemble models, including linear regression (LR), vanilla long short-term memory (LSTM), and bidirectional LSTM, which are enhanced with novel meta-learning approaches, significantly outperform traditional nonensemble models in glucose prediction, demonstrating their superior accuracy and effectiveness for T1D management [7]. Additionally, systems that predict glucose levels up to one hour in advance without requiring feature engineering or extensive data preprocessing are crucial for effective T1D management [8].
Research on glucose predictive modelling in T1D underscores the importance of comprehensive models that integrate various factors, such as food carbohydrate intake, insulin doses, and physical activity [9]. Prendin et al. [10] evaluated stochastic models considering contextual factors beyond meal size, i.e., mealtime and insulin dosing. Jaloli and Cescon [11] developed a convolutional neural network (CNN) and LSTM, (CNN-LSTM)-based deep neural network, which improved long-term (90 min) glucose prediction by integrating multiple data sources. Li et al. [12] employed convolutional recurrent neural networks (RNN) to enhance prediction accuracy. Several studies have focused on real-time blood glucose prediction using CGM systems to improve diabetes management. A significant contribution by Zhu T et al. [13] introduces a population-specific glucose prediction model based on the temporal fusion Transformer, personalized with demographic data and integrated into a low-power, wearable device. The temporal fusion Transformer model outperformed several baseline methods in prediction accuracy, highlighting its potential for improving diabetes management. Butt et al. [14] proposed transforming event-based data into discriminative continuous features using a multilayered LSTM-based RNN to predict glucose levels in T1D patients. Hybrid and advanced techniques have also shown significant potential: (i) Isfahani et al. [15] used a hybrid dynamic wavelet-based modelling method, (ii) Hidalgo et al. [16] combined Markov chain-based data enrichment with random grammatical evolution and bagging, and (iii) Rabby et al. [17] implemented a stacked LSTM-based deep RNN with Kalman smoothing. However, deep learning models often require large datasets for accurate personalized glucose predictions. Daniels et al. [18] demonstrated that multitask learning outperforms sequential transfer learning and subject-specific models with neural networks and support vector regression (SVR), achieving at least 93% clinically acceptable predictions using the Clarke Error Grid (EGA) across various prediction horizons (30, 45, 60, 90, and 120 min). This shows that multitask learning enables effective personalized models with less subject-specific data. Clustering and seasonal stochastic methods have demonstrated good accuracy for long prediction horizons. Montaser et al. [19] proposes a framework based on CGM data that partitions variable-length subseries and incorporates indices for detecting abnormal glucose behavior, effectively addressing intra-patient variability and enhancing model performance in supervision and control applications. Furthermore, several challenges hinder the clinical implementation of deep learning algorithms, such as unclear prediction confidence and limited training data for new T1D subjects. To address these issues, Zhu et al. [20] proposed the fast-adaptive and confident neural network (FCNN), which employs an attention-based RNN and model-agnostic meta-learning to provide personalized glucose predictions with confidence and enable fast adaptation for new patients. These studies demonstrated the benefits of integrating diverse biological and behavioural factors into glucose prediction models, leading to improved performance compared with univariate approaches. Some studies have incorporated mechanistic models of carbohydrate and insulin absorption, although these techniques often rely on several assumptions that limit their widespread use [21, 22]. Comparative studies have shown similar short-term prediction results (up to 60 min) between linear and nonlinear models [23–26]. This observation may be attributed to the linear dynamics of short-term glucose regulation or the presence of unaccounted factors in the models.
In this study, we investigate the ability of an ensemble univariate short-term subcutaneous glucose predictive model, which consists of basis models that individually optimize the performance in the hypoglycaemic region, to further improve the error in that region while retaining high accuracy in the hyperglycaemic and euglycaemic regions. As basis functions, we examine models of four different classes: (i) one linear function, i.e., LR, (ii) three kernel-based functions, i.e., automatic relevance determination (ARD), SVR, and Gaussian process regression (GPR), (iii) one tree-based function, i.e., eXtreme gradient boosting (XGBoost), and (iv) a deep learning model, i.e., an LSTM neural network. Subsequently, we construct an ensemble model that factors in the outputs of the two top performing basis models (i.e., SVR and XGBoost) with respect to their hypoglycaemic predictions, as assessed by the continuous glucose error grid analysis (CG-EGA). The utilized dataset was generated within the framework of the GlucoseML clinical study; 29 adults with T1D were followed-up for a period of 2 to 4 weeks under real-life conditions. The glucose concentration in the subcutaneous space was measured via a CGM sensor featuring a sampling period of 1 min. All the models were trained and tested individually by carefully employing cross validation over the training set of each patient. In this context, the ensemble model showed a consistently better performance, in terms of the CG-EGA, over all the examined prediction horizons of 15-, 30- and 60-minutes. Herein, we focused on the development of a univariate glucose predictive model aiming at examining the linear or nonlinear autoregressive capacity of the glucose time series itself with respect to short-term hypoglycaemia prediction, which, in parallel, comprises the simplest input case reducing the need for extensive data collection. This study’s technical novelty lies in the incorporation of the CG-EGA outputs in the hypoglycaemic region in the selection of basis functions of the univariate ensemble model, whereas its clinical impact lies in the verification of the examined hypothesis, i.e., the improvement of the model’s capability in the hypoglycaemic region. Focusing on hypoglycaemia is crucial due to the immediate risks it poses, such as seizures, coma, and even death. Accurate prediction of hypoglycaemia is essential for ensuring patients’ safety and effective glucose management.
Methods
Study population
The dataset analysed in the present study was generated by the GlucoseML-Phase I prospective study, which aimed to collect real-world data systematically from T1D people monitored for a period of 2–4 weeks. The patients used the GlucoMen Day CGM Menarini®1 system featuring a sampling frequency of 1 min. The study enrolled 32 patients, with 26 individuals (82%) completing the entire 4-week monitoring period, 3 patients (9%) completing a 2-week monitoring period, and 3 patients (9%) discontinuing their participation. Informed consent was obtained from all participants prior to their enrollment in the study. As shown in Table 1, the study population consisted of 62% males and 38% females, with an average age of 38 years. 66% of the study patients were on multiple daily insulin injections (MDI), whereas 34% were on a continuous subcutaneous insulin infusion (CSII) regimen. The average baseline HbA1c level across individuals was 7.5%, with a history of severe hypoglycaemia reported by 59% of the patients.
Table 1.
Descriptive characteristics of the GlucoseML-Phase I study cohort
| Feature | Distribution of values | |
|---|---|---|
| Demographics | Gender |
Male: 62% (18) Female: 38% (11) |
| Age | 38 ± 12 years | |
| Anthropometrics | BMI |
Normal weight: 24% (7 kg/m2) Overweight: 41% (12 kg/m2) Obese: 34% (10 kg/m2) |
| Waist circumference |
Female: 86 (71-124 cm) Male: 96 (71-126 cm) |
|
| T1D management | Years since diagnosis |
0-12 years: 38% (11) 12-24 years: 35% (10) 24-36 years: 17% (5) 36-48 years: 10% (3) |
| Type of insulin treatment |
MDI: 66% (19) CSII: 34% (10) |
|
| History of severe hypoglycaemia | 59% (17) | |
| Baseline HbA1c | 7.5 ± 1% | |
| Chronic Complications of T1D |
Albuminuria: 10% (3) Retinopathy: 10% (3) Neuropathy: 3% (1) |
|
| Other metabolic comorbidities | Dyslipidaemia | 52% (15) |
| Central obesity | 31% (9) | |
| Thyroid disease | 24% (7) | |
| Hypertension | 10% (3) | |
| Lifestyle | Smoking | 52% (15) |
| Alcohol | 7% (2) |
Ensemble framework
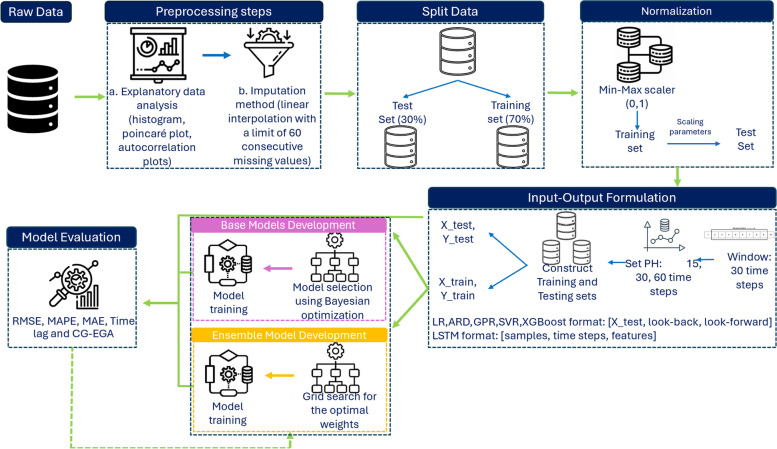
Figure 1 illustrates the methodological approach adopted in this study. First, the subcutaneous glucose concentration time series of each participant , represented by a vector , is visually inspected via a comprehensive exploratory data analysis including analysis of the distribution of data (histogram and Poincaré plot) and autocorrelation plots (autocorrelation function and partial autocorrelation function plot). Missing data in are imputed prior to dataset splitting into training and test sets by employing linear interpolation [27]. In particular, we set the maximum length of the missing data interval to 60 min (i.e., 60 consecutive values) to balance the introduction of the error in the raw data. Subsequently, the subcutaneous glucose concentration time series of each participant, , is split into the training time series () and test time series () using a 70:30 ratio retaining the temporal order of the data in . The training time series is normalized using the min-max scaler within the range [0,1], and the learnt scaling properties () are applied to the normalised test time series [28]:
Fig. 1.
Machine Learning Pipeline of the proposed glucose prediction model
| 1 |
Accordingly, the training vectors and the test vectors , constituting the training set and the test set , are formulated by iterating, for each time point , over the glucose time series and , respectively, using a history window (or “look-back” window) of 30 min (i.e., the previous 30 time points) and a prediction horizon (or “look-forward” window) of 15, 30 and 60 min.
The basis functions of the ensemble model are selected among the LR, ARD, SVR, GPR, XGBoost, and LSTM models. All the models are first finetuned with respect to their hyperparameters by employing the Bayesian optimization algorithm [29] wrapped into a cross-validation scheme over the training set ; the hyperparameters optimizing the cross-validation performance are selected. We employ time series 5-fold cross-validation to systematically tune hyperpatameters and minimize the risk of overfitting, where in each iteration the validation set is ahead of the training set to retain the temporal order of glucose data. Table 2 presents the examined hyperparameter space. Subsequently, each model is trained and evaluated on the training and test sets, respectively. As described in Sect. 2.3, CG-EGA enables the assessment of one model’s performance in each glycaemic region (i.e., hypoglycaemia, euglycaemia, hyperglycaemia), separately. Considering the clinical importance of reducing the error of hypoglycaemic predictions, we selected the two models minimizing the percentage of erroneous predictions (EP) in the hypoglycaemic region according to the CG-EGA analysis of their predictions over the training set. More specifically, SVR and XGBoost exhibit the best behaviour with respect to the prediction of hypoglycaemic values, without compromising their performance in the hyperglycaemic and euglycaemic regions.
Table 2.
Hyperparameter space based on Bayesian optimization for each model
| Model | Hyper-parameters | Range |
|---|---|---|
| Automatic Relevance Determination (ARD) Regression | alpha_1 | 10-10– 10-6* |
| alpha_2 | 10-10– 10-6* | |
| lambda_1 | 10-10 – 10-6* | |
| lambda_2 | 10-10 – 10-6* | |
| Support Vector Regression (SVR) | C | 10-4 – 10-1* |
| Kernel | Linear, rbf, poly, sigmoid | |
| Gaussian Process Regression (GPR) | length scale | 0.01- 10 |
| Linear Regression (LR) | alpha | 0.001 - 10.0* |
| eXtreme Gradient Boosting (XGBoost) | Learning rate | 10-4 – 10-1* |
| n estimators | 50 - 200 | |
| Max depth | 3 - 10 | |
| Min child weight | 1 - 5 | |
| Subsample | 0.5 - 1.0 | |
| Colsample bytree | 0.5 - 1.0 | |
| gamma | 0 - 1.0 | |
| Long-Short Term Memory (LSTM) | Batch size | 8, 16, 24, 32, 64 |
| Learning rate | 10-4 – 10-1* | |
| Num units | 1- 10 | |
| Dropout rate | 0.0 -0.5 | |
| Activation function | tanh, relu | |
| Number of layers | 1 - 5 | |
| Optimiser | adam, rmsprop |
RBF Radial Basis Function, POLY polynomial, RMSPROP Root Mean Square Propagation, *using log-uniform distribution
The ensemble model comprises a linear combination (weighted average) of the SVR and XGBoost basis functions. The optimal weights are likewise selected to optimise the time series 5-cross-validated negative mean squared error (MSE) via grid search over the training set. Grid search is a hyperparameter optimization technique that systematically explores a predefined set of parameter values. This method ensures that the best combination of hyperparameters is identified, enhancing model performance [30]. The search space of the weights is set to [0.0, 0.5, 1.0]. Τhe weight optimisation is followed by the fitting of the ensemble model to the training data.
SVR Method
SVR is a supervised learning algorithm for regression, based on a support vector machine (SVM). Given a set of training samples , where represents the univariate input feature and represents the corresponding glucose value, SVR seeks to find a function that minimizes errors within an -insensitive margin. The prediction function for SVR is given by:
| 2 |
where is the weight and is the bias term. SVR utilizes an insensitive loss function to define acceptable deviations, while balancing the model complexity and the tolerance for deviations:
| 3 |
where and are slack variables that allow deviations outside the -insensitive margin and is a regularization parameter controlling the trade-off between model complexity and error tolerance [31, 32].
XGBoost Method
XGBoost iteratively builds an ensemble of decision trees by -correcting- prior errors to improve training and prediction at each iteration. The predicted glucose value for a given observation is the sum of predictions from all trees:
| 4 |
Each tree contributes an additive prediction, which is refined iteratively to minimize a specified objective function. The objective function combines a loss function measuring prediction error and a regularization term controlling model complexity:
| 5 |
where represents the actual glucose value, denotes the predicted glucose value, is the squared error loss function for regression, and is the regularization term for the -th term [33, 34].
Model evaluation
The performance of the glucose predictive model is assessed individually for each patient using: (i) three pure error metrics, i.e., the RMSE, the mean absolute percentage error (MAPE) and the mean absolute error (MAE), (ii) the Time Lag, which expresses the temporal delay between the actual ( and the predicted () subcutaneous glucose concentrations, and (iii) the CG-EGA, which evaluates the potential clinical impact of the errors given the glycaemic range in which the actual glucose concentration value lies. Equations (6), (7) and (8) provide the formulas for the RMSE, the MAPE and the MAE, respectively:
| 6 |
| 7 |
| 8 |
where denotes the actual subcutaneous glucose concentration value observed at time , denotes the respective predicted value, and is the length of and . The Time Lag, also known as the prediction delay, is defined as the maximizing the cross correlation between and :
| 9 |
In addition to the above performance metrics, we employ the CG-EGA aiming at gaining insight into one model’s performance across the glycaemic regions of hypoglycaemia, euglycaemia and hyperglycaemia. The CG-EGA is composed of: (i) point-error grid analysis (P-EGA), which assesses the glucose prediction errors, and (ii) rate-error grid analysis (R-EGA), which evaluates the rate of change of as compared with that of . The grid is divided into zones on a scatter plot, where the x-axis represents the reference glucose values, and the y-axis represents the predicted glucose values. This plot is divided into different zones, each reflecting varying degrees of clinical significance. Zone A is characterized by minimal prediction errors that have little to no impact on clinical decisions. Zone B indicates errors that could have minor clinical implications, suggesting a need for caution but not immediate intervention. In contrast, Zones C and D reflect errors with moderate to severe clinical consequences, which could result in inappropriate treatment changes or mismanagement of glucose levels. Factoring in both the P-EGA and R-EGA results, the overall CG-EGA classifies errors within each glycaemic region as follows: (i) accurate predictions (AP), where the predicted glucose values are very close to the actual reference glucose values, meaning that these predictions are reliable for clinical decisions, (ii) benign errors (BE), which involve predictions that slightly deviate from actual values but are minor enough not to have significant clinical impact, and (iii) EP, where the predicted values differ substantially from the actual reference values, leading to significant inaccuracies and potential clinical risks or implications [35].
Results
The glycaemic profile of the GlucoseML-Phase I study patients is presented in Fig. 2; Table 3. Figure 2 illustrates the box plots of the percentage of time patients spent in the 5 glycaemic zones, according to the Ambulatory Glucose Profile (AGP) report [36]. This was calculated using the individual subcutaneous glucose concentration time series collected over the monitoring period.
Fig. 2.
The Time in Ranges based on AGP report
Table 3.
The glucose statistics based on AGP report across all patients using CGM data
| AGP Report Variables | Mean ± Standard Deviation |
|---|---|
| Average Glucose (mgdL-1) | 159.9 ± 26.2% |
| Glucose Management Indicator (%) | 7.1 ± 0.6% |
| Glucose Variability (%) | 39.5 ± 6.3% |
Data are presented in the form mean ± standard deviation
In particular, the distribution of the percentage of time spent within the 5 zones (represented by the median (25th percentile, 75th percentile)) is as follows: (i) 1.4 (0.3, 3.1) in Time Below Range–Very Low: (< 54 mgdL−1), (ii) 3.8 (1.4, 5.2) in Time Below Range–Low: (< 70 mgdL−1), (iii) 61.6 (57, 70.1) in Time in Range: (70–180 mgdL−1), (iv) 22.1 (18.3, 25.4) Time Above Range – High: (> 180 mgdL−1), and (v) 7.7 (4.6, 12.1) Time Above Range – Very High: (> 250 mgdL−1). For clearer insights, we have added Additional File 1: Table S1, which presents the same information in a tabular format. In addition, Table 3 presents the average values of the complementary subcutaneous glucose statistics in the AGP report.
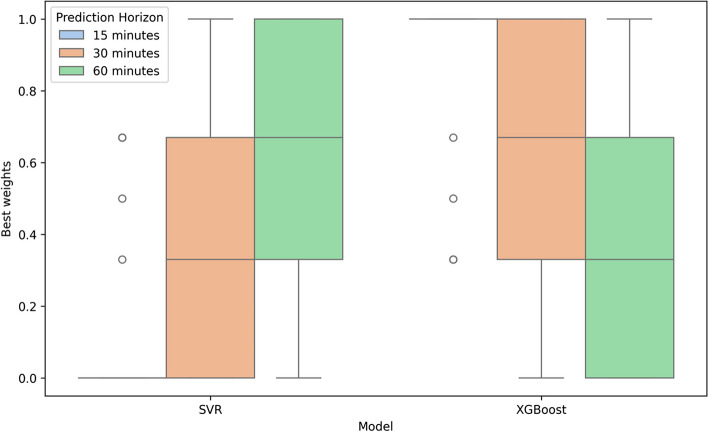
Figure 3 illustrates the optimal weights assigned to the ensemble model following its fitting to the training data. These weights are determined based on the optimization algorithm and hyperparameter space detailed in Sect. 2.2. Table 4 shows the distributions of the RMSE, MAPE, MAE and Time Lag associated with the predictions of the subcutaneous glucose concentration by the ensemble model and the individual basis models for prediction horizons of 15, 30, and 60 min. We observe that LR, ARD and GPR show a comparable performance with respect to the error metrics and the Time Lag for all the prediction horizons, with the average MAPE being close to 13.5% for 30-min predictions and the respective average Time Lag close to 22 min. The LSTM, SVR and XGBoost yield greater errors and, hence, time delays, with the average MAPE associated with 30-min predictions becoming ~16 −17% and the respective average Time Lag ranging from ~24 to ~27 min. The behavior of the ensemble model resembles that of its constituent basis models (SVR and XGBoost) retaining the average RMSE and Time Lag of 30-min predictions equal to ~15.5% and ~25.2%, respectively. As described in Sect. 2.2, we used a 30-minute history window for model predictions. To evaluate the impact of longer history window, we compared the performance of a 60-minute history window across RMSE, MAPE, MAE, and Time Lag metrics, as presented in Additional File 1: Table S2. The differences between the two history windows were minor, suggesting that extending the history window beyond 30 min does not offer significant advantages. Studies have shown that extending the input window beyond 30 min does not necessarily lead to significant improvements in predictive accuracy but can increase computational burden [37]. In clinical settings, where real-time predictions are crucial for timely interventions, a longer history window could introduce processing delays, limiting the utility of predictions for immediate decision-making. Therefore, limiting the input window to 30 min ensures a balance between prediction accuracy and the need for real-time applicability [38]. Based on these findings, our model focuses on 30-minute history window. Figure 4 compares the RMSE values, which are the most commonly used metric across research studies, for ARD, SVR, LSTM, XGBoost, and the proposed ensemble model overprediction horizons of 15, 30, and 60 min. The ensemble model demonstrates competitive RMSE values with relatively tight distributions and a moderate number of outliers, indicating consistent performance across all prediction horizons. However, ARD regression achieves the lowest RMSE values, as shown in Table 4, while the median RMSE for the Ensemble model is slightly higher compared to other methods, as depicted in Fig. 4.
Fig. 3.
The best weights for all patients in the ensemble model
Fig. 4.
A box plot diagram of RMSE results for each model across all prediction horizons
Table 4.
Prediction errors over the test set achieved by the models
| RMSE (mgdL-1) | MAPE (%) | MAE (mgdL-1) | Time Lag | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 15 min | 30 min | 60 min | 15 min | 30 min | 60 min | 15 min | 30 min | 60 min | 15 min | 30 min | 60 min | |
| Linear Regression (LR) | 16.52 ± 4.45 | 26.71 ± 6.58 | 40.71 ± 9.69 | 7.76 ± 2.05 | 13.48 ± 3.57 | 21.84 ± 6.01 | 11.18 ± 2.85 | 19.22 ± 4.66 | 30.47 ± 7.24 | 9.21 ± 3.54 | 22.41 ± 6.25 | 50.03 ± 9.32 |
| Automatic Relevance Determination (ARD) Regression | 16.5 ± 4.42 | 26.67 ± 6.56 | 40.68 ± 9.66 | 7.73 ± 2.04 | 13.45 ± 3.57 | 21.83 ± 6.01 | 11.14 ± 2.84 | 19.17 ± 4.64 | 30.44 ± 7.23 | 9.24 ± 3.54 | 22.34± 6.22 | 50 ± 9.46 |
| Gaussian Process Regression (GPR) | 16.55 ± 4.55 | 27.32 ± 8.68 | 41.48 ± 11.86 | 7.85 ± 2.14 | 13.67 ± 3.8 | 21.91 ± 5.93 | 11.33 ± 3.03 | 19.68 ± 5.66 | 30.97 ± 8.37 | 9.21 ± 3.49 | 22.21 ± 6.93 | 49.9 ± 10.1 |
| Long-Short Term Memory (LSTM) | 21.24 ± 6.93 | 31.85 ± 9.96 | 43.93 ± 11.63 | 10.82 ± 3.59 | 17.01 ± 8.1 | 23.65 ± 5.99 | 15.57 ± 4.72 | 24.01 ± 7.94 | 33.54 ± 8.48 | 13.52 ± 6.14 | 25.38 ± 9.33 | 55.62 ± 13.25 |
| Support Vector Regression (SVR) | 21.92 ± 9.13 | 29.72 ± 9.8 | 42.95 ± 12.11 | 11.37 ± 4.13 | 15.74 ± 4.95 | 22.91 ± 6.23 | 15.63 ± 5.34 | 21.97 ± 6.49 | 32.45 ± 8.75 | 11.55 ± 4.01 | 23.76 ± 6.65 | 51.28 ± 10.99 |
| eXtreme Gradient Boosting (XGBoost) | 20.34 ± 6.33 | 29.39 ± 7.98 | 42.43 ± 10.94 | 10.3 ± 3.38 | 15.57 ± 4.62 | 23.3 ± 6.55 | 14.76 ± 4.56 | 22.01 ± 5.97 | 32.47 ± 8.43 | 13.31 ± 3.68 | 26.79± 6.25 | 53.55 ± 10.92 |
| Ensemble | 20.43 ± 6.34 | 29.32 ± 8.15 | 42.51 ± 11.18 | 10.33 ± 3.41 | 15.48 ± 4.64 | 22.95 ± 6.36 | 14.74 ± 4.53 | 21.8 ± 5.98 | 32.29 ± 8.5 | 12.76 ± 3.97 | 25.28 ± 6.89 | 52.17 ± 11.07 |
Data are presented in the form mean ± standard deviation
Bold values indicate the best model based on the specified metric and prediction horizon
To evaluate the statistical significance of the results, we first assessed the data distribution using the Shapiro-Wilk test. The results, as shown in Additional File 1: Figure S1indicate that some metrics follow a normal distribution, while others do not. Consequently, we applied, the non-parametric statistical test, Mann-Whitney U test [39] to compute p-values across all evaluation metrics RMSE, MAPE, MAE, and Time Lag comparing the performance of all models against the ensemble model for each prediction horizon across all patients. Figure 5 presents the Mann-Whitney U test p-values that compare the RMSE, MAPE, MAE, and Time Lag of all the models with those of the ensemble model for each prediction horizon across all the patients. These p-values indicate the statistical significance of the performance metric differences between the ensemble model and other models, thereby enabling an assessment of the relative effectiveness of the ensemble model in diverse prediction scenarios. Notably, the differences in the means of the RMSE distribution associated with ARD, LR, or GPR and the proposed model, are statistically significant at the 15-minute horizon across all metrics. Furthermore, based on the Time Lag results, ARD, LR, or GPR show statistically significant differences at all prediction horizons. Moreover, LSTM exhibits statistical significance at the 60-minute horizon. The results reveal that as the prediction horizon increases to 30 and 60 min, fewer comparisons show statistically significant differences, indicating that the performance differences between methods become less pronounced at longer horizons.
Fig. 5.
Mann-Whitney U test results (p-values) comparing the ensemble model with the examined basis functions
Table 5 presents the CG-EGA of the predictions derived by the examined models. On the one hand, we observe that the LR, ARD and GPR have mediocre performance in the hypoglycaemic region, reaching 50% of their 30-min predictions in hypoglycaemia to be characterized as erroneous. On the other hand, LSTM, SVR and XGBoost, although associated with greater errors and delays over the entire glycaemic range as compared to the LR, ARD and GPR, they eventually improve the predictions’ accuracy in the hypoglycaemic region for all prediction horizons. More specifically, SVR and XGBoost outperform the LSTM, resulting in 30% erroneous 30-min predictions in hypoglycaemia. The ensemble model: (i) perfectly balances the outputs of its basis models for 15-min predictions in the hypoglycaemic region, (ii) significantly reduces the EP in hypoglycaemia to 19% for a 30-min horizon, and (iii) cannot resolve the mediocre performance of SVR in the hypoglycaemic region for 60-min predictions (SVR: 53%), which leads to an increase in the EP to 42% compared with its best performing underlying function (XGBoost: 22%). In the hyperglycaemic region, the SVR model performs equally well to its best performing underlying basis model for all prediction horizons (15 min: 7%, 30 min: 9%, 60 min: 12%) and, in parallel, outperforms LR, ARD, GPR, and LSTM.
Table 5.
The classification of the prediction errors according to the CG-EGA
| 15 min | 30 min | 60 min | |||||
|---|---|---|---|---|---|---|---|
| Hypo | Hyper | Hypo | Hyper | Hypo | Hyper | ||
| Linear Regression (LR) | AP | 0.54±0.21 | 0.60±0.09 | 0.42±0.22 | 0.58±0.08 | 0.27±0.24 | 0.55±0.09 |
| BE | 0.1±0.04 | 0.26±0.07 | 0.09±0.05 | 0.27±0.07 | 0.08±0.08 | 0.28±0.07 | |
| EP | 0.36±0.21 | 0.14±0.05 | 0.49±0.23 | 0.14±0.05 | 0.65±0.27 | 0.16±0.06 | |
| Automatic Relevance Determination (ARD) Regression | AP | 0.53±0.21 | 0.59±0.09 | 0.41±0.21 | 0.57±0.08 | 0.26±0.23 | 0.55±0.08 |
| BE | 0.1±0.04 | 0.26±0.07 | 0.09±0.05 | 0.28±0.07 | 0.08±0.07 | 0.29±0.06 | |
| EP | 0.37±0.22 | 0.15±0.05 | 0.5±0.23 | 0.15±0.05 | 0.66±0.26 | 0.17±0.06 | |
| Gaussian Process Regression (GPR) | AP | 0.55±0.21 | 0.61±0.09 | 0.41±0.25 | 0.6±0.08 | 0.25±0.26 | 0.58±0.08 |
| BE | 0.1±0.04 | 0.28±0.06 | 0.09±0.06 | 0.3±0.06 | 0.05±0.06 | 0.3±0.06 | |
| EP | 0.35±0.22 | 0.11±0.04 | 0.5±0.25 | 0.11±0.04 | 0.7±0.28 | 0.12±0.05 | |
| Long-Short Term Memory (LSTM) | AP | 0.64 ± 0.21 | 0.7 ± 0.13 | 0.53 ± 0.19 | 0.68 ± 0.12 | 0.54 ± 0.26 | 0.68 ± 0.15 |
| BE | 0.1 ± 0.1 | 0.2 ± 0.08 | 0.08 ± 0.11 | 0.22 ± 0.1 | 0.06 ± 0.09 | 0.21 ± 0.11 | |
| EP | 0.26 ± 0.2 | 0.1 ± 0.06 | 0.38 ± 0.18 | 0.1 ± 0.05 | 0.4 ± 0.25 | 0.11 ± 0.07 | |
| Support Vector Regression (SVR) | AP | 0.67±0.3 | 0.72±0.1 | 0.62±0.3 | 0.68±0.1 | 0.41±0.35 | 0.64±0.11 |
| BE | 0.19±0.25 | 0.18±0.06 | 0.09±0.08 | 0.2±0.06 | 0.05±0.07 | 0.22±0.06 | |
| EP | 0.14±0.25 | 0.1±0.05 | 0.29±0.29 | 0.12±0.06 | 0.53±0.35 | 0.14±0.07 | |
| eXtreme Gradient Boosting (XGBoost) | AP | 0.77±0.15 | 0.73±0.09 | 0.66±0.29 | 0.71±0.09 | 0.73±0.05 | 0.68±0.08 |
| BE | 0.06±0.05 | 0.21±0.06 | 0.04±0.04 | 0.22±0.06 | 0.04±0.03 | 0.23±0.05 | |
| EP | 0.17±0.12 | 0.07±0.04 | 0.29±0.29 | 0.07±0.03 | 0.22±0.07 | 0.09±0.05 | |
| Ensemble | AP | 0.75 ± 0.17 | 0.73±0.09 | 0.75±0.19 | 0.71±0.08 | 0.55±0.34 | 0.67±0.09 |
| BE | 0.1±0.11 | 0.2±0.06 | 0.06±0.05 | 0.21±0.06 | 0.02±0.02 | 0.22±0.05 | |
| EP | 0.15±0.1 | 0.07±0.04 | 0.19±0.15 | 0.09±0.04 | 0.42±0.34 | 0.12±0.06 | |
Data are presented in the form mean ± standard deviation
AP Accurate Predictions, BE Benign Errors, EP Erroneous Predictions
Bold values indicate the best model based on the specified glycaemic region and prediction horizon
Figure 6 illustrates the best and worst outputs of the ensemble model with respect to the CG-EGA for 30-min predictions. The CG-EGA results from the plots in Fig. 6a reveal how strong the performance across different glucose states is for the patient with the best results. In the hypoglycaemia region, the system achieved a high accuracy rate of 90%, with only 8% of the predictions being erroneous and 2% being classified as benign predictions. For euglycaemia, the accuracy is also high at 84%, with 6% EP and 10% benign predictions. In the hyperglycaemia region, the accuracy is good at 71%, with 12% EP and 16% benign predictions. Overall, the system demonstrates excellent accuracy and reliability, particularly under hypoglycaemic and euglycaemic conditions, with the potential for slight improvement in hyperglycaemic predictions. In contrast, the CG-EGA results from the plots in Fig. 6b reflect the patient with the worst performance. In the hypoglycaemia region, the accuracy is moderate at 50%, with 42% of the predictions being erroneous. For euglycaemia, the accuracy is lower at 65%, with 15% EP. In the hyperglycaemia region, the accuracy is 59%, with 16% of the predictions being erroneous.
Fig. 6.
Example of the CG-EGA plots regarding the ensemble model for a 30-min PH. a the best patient case and b the worst patient case
For comparison purposes, we further evaluated the accuracy of the models across different glycaemic ranges, we computed the RMSE, MAE, and MAPE for the following ranges: CGM < 70 mg/dL, 70 < CGM < 180 mg/dL, and CGM > 180 mg/dL. These results, presented in Additional File 1: Table S3, provide a comparison of model performance across the specified glycaemic ranges. In the analysis of these results, we should consider that the RMSE, MAE, and MAPE evaluate the magnitude of prediction errors, ignoring particualrly the sign of the errors and the location of both the actual and predicted glucose values. On the other hand, CG-EGA categorizes errors into clinically meaningful zones considering: (i) both the magnitude and sign of the errors in tandem with the location (hypoglycaemia, euglycaemia, hyperglycaemia) of the actual/predicted glucose values (via the point-error grid analysis), and (ii) the direction and rate of change of predicted vs. the actual time series (via the rate-error grid analysis).
Discussion
In this study, we developed an individualized ensemble glucose predictive model, comprising those basis functions (i.e., SVR and XGBoost) that achieved the best performance in the hypoglycaemic region while retaining low errors across the hyperglycaemic and euglycaemic regions. The utilized dataset comprised CGM time series of 29 T1D patients monitored for a period of 2–4 weeks. The proposed model was trained and tested separately for each patient, with the hyperparameters of both individual basis functions and the weights of the ensemble model being tuned via time series 5-fold cross-validation over the training dataset. The high-frequency sampling rate of CGM data, equal to 1 min−1, provides a detailed profile of glucose fluctuations and, in particular, more accurate observations of rapid glucose changes than CGM data of a 5 min−1 or 15 min−1 sampling rate [40], which might benefit the prediction of hypoglycaemic values. The proposed study introduces a significant innovation through the application of the CG-EGA for both model selection and performance evaluation, emphasizing the clinical implications of prediction errors. By integrating SVR and XGBoost within an ensemble framework, we successfully bridged the gap between numerical accuracy and clinical relevance. On the one hand, SVR, as a kernel-based method, features a high generalization ability in learning nonlinear functions. On the other hand, XGBoost, as a boosting approach, yields, iteratively, to error correction. Ensemble modelling effectively mitigates the inherent limitations of individual models by leveraging their complementary attributes. To this end, the ensemble modeling approach reduces overfitting by leveraging the diversity of individual model predictions.
Our analysis indicates that the ensemble model significantly enhances 30-minute predictions in the hypoglycaemic region, yielding a percentage of EP equal to 19% compared with its individual basis functions, while maintaining similar performance to the less erroneous basis model in the hyperglycaemic range across all prediction horizons (15 min: 7%, 30 min: 9%, 60 min: 12%). The ARD model outperforms all other examined models in terms of numerical error metrics (RMSE, MAPE, MAE); however, its clinical effectiveness, as assessed by the CG-EGA, is considered to be moderate. This aligns with our perspective that CG-EGA, by evaluating the clinical impact of errors rather than solely their numerical magnitude, presents a more comprehensive metric for optimizing and evaluating the performance of a glucose predictive model [41]. To address differences in data availability between patients with 2 weeks and those with 4 weeks of CGM data, we conducted a comparative evaluation of the model performance across these two groups, as presented in Additional File 1: Table S4 and Additional File 1: Table S5. The observed differences in model performance (RMSE, MAPE, and MAE) across all prediction horizons between patients with 2-week and 4-week CGM data underscore the importance of monitoring duration in training predictive models. This is further verified by the results presented in Additional File 1: Table S5, where the 4-week CGM data outperformed the 2-week in the hypoglycaemic region across all prediction horizons. However, the models’ robustness, even with shorter datasets, demonstrates their applicability to real-world scenarios where data availability may be limited. This is particularly relevant in situations where obtaining extended CGM data is impractical, making the models valuable for diverse clinical applications. Furthermore, Additional File 1: Table S4 compares the predictive performance of the models for MDI and CSII groups, highlighting differences in overall error metrics such as RMSE, MAPE, MAE and Time Lag. Additional File 1: Table S5 also presents the results from the CG-EGA. While the CSII group generally showed slightly lower prediction errors across RMSE and MAE, the MDI group exhibited the best performance in the hypoglycaemic zone across all prediction horizons according to the CG- EGA. Additionally, Additional File 1: Table S4 compares the predictive performance of the models for patients with a target baseline HbA1c of 7.0% or lower versus those with HbA1c above 7.0%, as well as between patients who have experienced at least one severe hypoglycaemic event and those who have never experienced such an event. Since our models are personalized, subgroup analyses were performed based on these factors. We observe that patients with a target HbA1c of 7.0% or lower outperformed those with higher HbA1c values across all error metrics and prediction horizons. Additionally, patients with history of severe hypoglycaemic events demonstrated better performance in RMSE and MAE compared to those without such a history. These results are further supported by the CG-EGA, particularly for the 15- and 30-minute prediction horizons, as shown in Additional File 1: Table S5. In Table 6, we present the evaluation of the proposed model on the Ohio dataset (2018) and its direct comparison with three state-of-the-art studies, utilizing the RMSE as the common metric found in all the literature studies. Our observations reveal that the proposed model yields a higher RMSE of approximately 5 mg/dL, which could be clinically significant in the hypoglycaemic region. Nevertheless, we are unable to contrast their performance in the hypoglycaemic region as the studies reported in Table 6 do not provide the CG-EGA figures. To adapt the ensemble model to the OhioT1DM dataset, we did not performed specific adjustments to our model. We applied our pipeline and trained the ensemble model on the OhioT1DM dataset without any modifications. While the ensemble model showed slightly higher RMSE at the 60-minute prediction horizon, this metric does not fully reflect the clinical relevance of predictions. Our primary focus was on CG-EGA, which assesses the clinical accuracy and safety of glucose predictions. CG-EGA results indicate that the ensemble model performs reliably in clinically critical areas, such as hypoglycaemia prediction, even if its RMSE values are slightly higher.
Table 6.
Comparison of the state-of-the-art model’s performance versus our ensemble model in the OhioT1DM dataset
| Model | No. of patients | RMSE (mg/dL) | ||
|---|---|---|---|---|
| Prediction Horizon (min) | ||||
| 15 | 30 | 60 | ||
| Fast adaptive and Confident Neural Network (FCNN) model [20] | 12 | - | 18.64 ± 2.60 | 31.07 ±3.62 |
| Ensemble Models (Stacking VLSTM, BiLSTM, and Linear models) [7] | 12 | - | 19.63 | - |
| Recurrent neural network (RNN) model [8] | 6 | - | 18.87 ± 1.79 | 31.4 ± 2.08 |
| Proposed ensemble model (SVR and XGBoost) | 6 | 17.11 ± 2.48 | 23.37 ± 3.41 | 35.02 ± 3.69 |
| Proposed ensemble model (SVR and XGBoost) | 12 | 17.54 ± 3.12 | 24.07 ± 4.01 | 35.94 ± 5.19 |
The OhioT1DM dataset is described in [42].
The clinical relevance of this study lies in its ability to enhance the prediction of hypoglycaemia, a critical condition for individuals with T1D. By integrating SVR and XGBoost in an ensemble framework and leveraging the CG-EGA for both model selection and evaluation, the proposed model improves the prediction accuracy in the hypoglycaemic region. This improvement in predictive performance is paramount for ensuring patients’ safety and improving their quality of life.
The study presented herein focused exclusively on subcutaneous glucose data, without incorporating other pertinent physiological parameters in the model that may influence glucose levels. Additional variables, such as insulin administration, meal intake or physical activity, could improve the predictive accuracy and personalization of the models. Furthermore, the integration of genetic data and exploration of hypoglycaemia-related genetic polymorphisms could yield further insights into personalized diabetes management and enhance prediction outcomes. Accurate prediction of hypoglycaemia, particularly during the nocturnal and postprandial periods, is of paramount importance for patient safety, as underscored by previous research [43–45]. As a result, our focus will be on predicting glucose levels during these specific times of the day. We also acknowledge that compression lows can introduce noise into CGM data, mimicking hypoglycaemia and potentially confounding model predictions. However, addressing compression lows in preprocessing is challenging due to the lack of reliable markers to distinguish them from true hypoglycaemia [46]. In our study, we used CGM glucose data was without extensive preprocessing to address potential artifacts such as compression lows. This approach was chosen to preserve the temporal integrity of the data and evaluate model performance under realistic conditions. Preprocessing to remove compression lows often relies on assumptions that may exclude true hypoglycaemic events or reduce generalizability. While addressing these artifacts might improve prediction accuracy, existing methods for identifying compression lows are often unreliable and may inadvertently exclude true hypoglycaemic episodes. Therefore, we chose to use CGM data without extensive preprocessing, as supported by prior research [47]. Additionally, while individualized models frequently outperform population-based models in glucose prediction, both approaches possess distinct advantages contingent on the application [13, 48]. It has been proposed that using error weighting [49] or employing the glucose-specific mean squared error (gMSE) [50] as a cost function during the model training could improve clinical performance; however, this approach was not tested for predicting hypoglycaemia in the present study. The gMSE metric adapts the traditional MSE by incorporating a penalty function based on the Clark error grid, which is similar with the CG-EGA, as both aim to evaluate the clinical accuracy of glucose predictions, particularly in relation to hypoglycaemic and hyperglycaemic events We should emphasize that the proposed approach entails individualized prediction models, trained and tested separately for each patient using continuous glucose data collected over several days. In time-series modeling, the volume of temporal data points is crucial as models learn patterns from sequential glucose readings. To prevent overfitting, we used cross-validation for time-series data and early stopping during training. While our model performs well on this dataset, further validation on larger, multi-center datasets would enhance its generalizability. Herein, we examined the generalizability of the proposed model’s results using the OhioDataset, which is a widely accepted benchmark in glucose prediction. Advanced modeling techniques such as transfer learning, imputation methods, and data augmentation will be also explored to enhance model performance in scenarios with constrained data availability. Additionally, integrating population-level trends with personalized modeling approached may further improve the accuracy and generalizability of the predictions. Future research will explore therapy-specific adjustments to optimize model performance. Also, to address the elevated hypoglycaemia risk in MDI users, future research will explore increasing sensitivity to hypoglycaemia by incorporating a cost-sensitive learning framework or optimizing hyperparameters to prioritize low glucose predictions. Our analysis of subgroups based on HbA1c levels and history of severe hypoglycaemic events suggests that these are important factors for glucose prediction. We will explore incorporating these factors into our glucose prediction models in future work. Consequently, we plan to undertake a comparative analysis of the performance of population-based and individualized models in our future work.
Conclusions
This study demonstrated the effectiveness of combining SVR and XGBoost in an ensemble model for short-term glucose prediction in individuals with T1D, with a particular focus on the prediction of hypoglycaemic value. The high frequency of the CGM data and the tailored models for each patient contributed to improved prediction accuracy, with the ensemble model outperforming individual models, especially in clinically critical hypoglycaemic regions. While numerical metrics such as the RMSE and MAPE are useful for assessing model performance, the CG-EGA is more valuable for evaluating the clinical impact of prediction errors [51]. This approach highlights the importance of balancing numerical accuracy with clinical relevance in real-world diabetes management. Although our models provide significant advancements in glucose prediction, future research should integrate broader physiological and genetic data to further enhance the personalization and accuracy of glucose forecasting models. We are currently incorporating physiological parameters from medical devices and data from the GlucoseML study, such as blood pressure, to investigate whether this improves the errors in the critical zones of hypoglycaemia and hyperglycaemia.
Supplementary Information
Acknowledgements
Not applicable.
Abbreviations
- AGP
Ambulatory glucose profile
- AP
Accurate predictions
- ARD
Automatic relevance determination
- BE
Benign errors
- CG-EGA
Continuous glucose error grid analysis
- CGM
Continuous glucose monitoring
- CNN
Convolutional neural network
- CSII
Continuous subcutaneous insulin infusion
- EGA
Clarke error grid
- EP
Erroneous predictions
- FCNN
Fast-adaptive and confident neural network
- GMSE
Glucose-specific mean squared error
- GPR
Gaussian process regression
- LR
Linear regression
- LSTM
Long short-term memory
- MAE
Mean absolute error
- MDI
Multiple daily insulin injections
- MSE
Mean squared error
- P-EGA
Point-error grid analysis
- R-EGA
Rate-error grid analysis
- RMSE
Root mean squared error
- RNN
Recurrent neural network
- SVM
Support vector machine
- SVR
Support vector regression
- T1D
Type 1 diabetes
- XGBoost
eXtreme gradient boosting
Authors’ contributions
DNK, EIG, CP and DIF developed the study concept and the models’ design. DNK developed the machine learning pipeline. DNK, EIG and CP analysed and interpreted the results. MAC, PAC, ST and DNK performed the clinical study and collected the data. DNK and EIG were major contributors in writing the manuscript. EIG, CP and DIF supervised the manuscript. All authors were involved in the revision of the manuscript. All authors have read and approved the final manuscript.
Funding
This research has been co-financed by the European Regional Development Fund of the European Union and Greek national funds through the Operational Program Competitiveness, Entrepreneurship, and Innovation, under the call RESEARCH – CREATE – INNOVATE (project code: T1EDK-03990).
Data availability
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
Declarations
Ethics approval and consent to participate
The study was conducted in accordance with the Declaration of Helsinki and approved by the Ethics Committee of University Hospital of Ioannina, Greece (Institutional Review Board approval number 247/2020). Clinical trial number: not applicable.
Consent for publication
Informed consent was obtained from all the subjects involved in the study.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.World Health Organization. Diabetes. https://www.who.int/health-topics/diabetes (2023). Accessed 14 October 2024.
- 2.Quattrin T, Mastrandrea LD, Walker LSK. Type 1 diabetes. Lancet. 2023;401(10394):2149–62. [DOI] [PubMed] [Google Scholar]
- 3.International Diabetes Federation. IDF Diabetes Atlas. http://diabetesatlas.org/atlas-reports/ (2022). Accessed 14 October 2024.
- 4.Prigge R, McKnight JA, Wild SH, Haynes A, Jones TW, et al. International comparison of glycaemic control in people with type 1 diabetes: an update and extension. Diabet Medicine: J Br Diabet Association. 2022;39(5):14766. [DOI] [PubMed] [Google Scholar]
- 5.American Diabetes Association Professional Practice Committee. 2. Diagnosis and Classification of Diabetes: Standards of Care in Diabetes—2024. Diabetes Care. 2024;47(Supplement 1):20–42.
- 6.Alfian G, Syafrudin M, Anshari M, Benes F, Atmaji FTD, Fahrurrozi I, et al. Blood glucose prediction model for type 1 diabetes based on artificial neural network with time-domain features. Biocybernetics Biomedical Eng. 2020;40(4):1586–99. [Google Scholar]
- 7.Nemat Η, Khadem Η, Eissa MR, Elliott J, Benaissa M. Blood glucose level prediction: Advanced Deep-Ensemble Learning Approach. IEEE J Biomed Health Inf. 2022;26(6):2758–69. [DOI] [PubMed] [Google Scholar]
- 8.Martinsson J, Schliep A, Eliasson B, Mogren O. Blood glucose prediction with Variance Estimation using recurrent neural networks. J Healthc Inf Res. 2019;4(1):1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tsichlaki S, Koumakis L, Tsiknakis M. Type 1 diabetes hypoglycemia prediction algorithms: systematic review. JMIR Diabetes. 2022;7(3):34699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Prendin F, Díez JL, Del Favero S, Sparacino G, Facchinetti A, et al. Assessment of Seasonal Stochastic local models for glucose prediction without meal size information under free-living conditions. Sens (Basel). 2022;22(22):8682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jaloli M, Cescon M. Long-term prediction of blood glucose levels in type 1 diabetes using a CNN-LSTM-Based deep neural network. J Diabetes Sci Technol. 2023;17(6):1590–601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Li K, Daniels J, Liu C, Herrero P, Georgiou P. Convolutional recurrent neural networks for glucose prediction. IEEE J Biomed Health Inf. 2020;24(2):603–13. [DOI] [PubMed] [Google Scholar]
- 13.Zhu T, Kuang L, Piao C, Zeng J, Li K, Georgiou P. Population-Specific glucose prediction in Diabetes Care with Transformer-based deep learning on the Edge. IEEE Trans Biomed Circuits Syst. 2024;18(2):236–46. [DOI] [PubMed] [Google Scholar]
- 14.Butt H, Khosa I, Iftikhar MA. Feature Transformation for efficient blood glucose prediction in type 1 diabetes Mellitus patients. Diagnostics (Basel). 2023;13(3):340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Isfahani MK, Zekri M, Marateb HR, Faghihimani E. A hybrid dynamic wavelet-based modeling method for blood glucose concentration prediction in type 1 diabetes. J Med Signals Sens. 2020;10(3):174–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hidalgo JI, Botella M, Velasco JM, Garnica O, Cervigón C, Martínez R, et al. Glucose forecasting combining Markov chain based enrichment of data, random grammatical evolution and bagging. Appl Soft Comput. 2020;88:105923. [Google Scholar]
- 17.Rabby MF, Tu Y, Hossen MI, Lee I, Maida AS, Hei X. Stacked LSTM based deep recurrent neural network with kalman smoothing for blood glucose prediction. BMC Med Inf Decis Mak. 2021;21(1):101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Daniels J, Herrero P, Georgiou P. A Multitask Learning Approach to Personalized Blood glucose prediction. IEEE J Biomed Health Inf. 2022;26(1):436–45. [DOI] [PubMed] [Google Scholar]
- 19.Montaser E, Díez JL, Bondia J. Glucose prediction under variable-length time-stamped daily events: a Seasonal Stochastic Local modeling Framework. Sens (Basel). 2021;21(9):3188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhu T, Li K, Herrero P, Georgiou P. Personalized blood glucose prediction for type 1 diabetes using Evidential Deep Learning and Meta-Learning. IEEE Trans Biomed Eng. 2023;70(1):193–204. [DOI] [PubMed] [Google Scholar]
- 21.Muñoz-Organero M, Queipo-Álvarez P, García Gutiérrez B. Learning Carbohydrate Digestion and Insulin Absorption Curves using blood glucose Level Prediction and Deep Learning models. Sens (Basel). 2021;21(14):4926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Saiti K, Macaš M, Lhotská L, Štechová K, Pithová P. Ensemble methods in combination with compartment models for blood glucose level prediction in type 1 diabetes mellitus. Comput Methods Programs Biomed. 2020;196:105628. [DOI] [PubMed] [Google Scholar]
- 23.Yang T, Yu X, Ma N, Wu R, Li H. An autonomous channel deep learning framework for blood glucose prediction. Appl Soft Comput. 2022;120:108636. [Google Scholar]
- 24.Zhu T, Uduku C, Li K, Herrero P, Oliver N, Georgiou P. Enhancing self-management in type 1 diabetes with wearables and deep learning. NPJ Digit Med. 2022;5(1):78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Li K, Liu C, Zhu T, Herrero P, Georgiou P. GluNet: a Deep Learning Framework for Accurate glucose forecasting. IEEE J Biomed Health Inf. 2020;24(2):414–23. [DOI] [PubMed] [Google Scholar]
- 26.Xie J, Wang Q. Benchmarking Machine Learning Algorithms on blood glucose prediction for type I diabetes in comparison with classical time-series models. IEEE Trans Biomed Eng. 2020;67(11):3101–24. [DOI] [PubMed] [Google Scholar]
- 27.Lepot M, Aubin J-B, Clemens FHLR. Interpolation in Time Series: an introductive overview of existing methods, their performance criteria and uncertainty Assessment. Water. 2017;9(10):796. [Google Scholar]
- 28.Han J, Kamber M, Pei J. Data Mining: concepts and techniques. 3rd ed. Morgan Kaufmann; 2011. [Google Scholar]
- 29.Frazier P. A tutorial on bayesian optimization. ArXiv Preprint. 2018. arXiv:1807.02811.
- 30.Jiang X, Xu C. Deep Learning and Machine Learning with Grid search to predict later occurrence of breast Cancer metastasis using Clinical Data. J Clin Med. 2022;11(19):5772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Smola AJ, Schölkopf B. A tutorial on support vector regression. Stat Comput. 2004;14(3):199–222. [Google Scholar]
- 32.Xiong L, Zhong H, Wan S, Yu J. Single-point curved fiber optic pulse sensor for physiological signal prediction based on the genetic algorithm-support vector regression model. Opt Fiber Technol. 2024;82:103583. [Google Scholar]
- 33.Friedman JH. Greedy function approximation: a gradient boosting machine. Ann Statist. 2001;29(5):1189–232. [Google Scholar]
- 34.Wang Q, Zou X, Chen Y, Zhu Z, Yan C, et al. XGBoost algorithm assisted multi-component quantitative analysis with Raman spectroscopy. Spectrochim Acta Mol Biomol Spectrosc. 2024;323:124917. [DOI] [PubMed] [Google Scholar]
- 35.Kovatchev BP, Gonder-Frederick LA, Cox DJ, Clarke WL. Evaluating the accuracy of continuous glucose-monitoring sensors: continuous glucose–error grid analysis illustrated by TheraSense Freestyle Navigator data. Diabetes Care. 2004;27(8):1922–8. [DOI] [PubMed] [Google Scholar]
- 36.Czupryniak L, Dzida G, Fichna P, Jarosz-Chobot P, Gumprecht J, et al. Ambulatory glucose Profile (AGP) report in Daily Care of patients with diabetes: practical Tips and recommendations. Diabetes Ther. 2022;13(4):811–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Xue Y, Guan S, Jia W. BGformer: an improved informer model to enhance blood glucose prediction. J Biomed Inf. 2024;157:104715. [DOI] [PubMed] [Google Scholar]
- 38.Dudukcu HV, Taskiran M, Yildirim T. Blood glucose prediction with deep neural networks using weighted decision level fusion. Biocybernetics Biomedical Eng. 2021;41(3):1208–23. 10.1016/j.bbe.2021.08.007. [Google Scholar]
- 39.Wang J, Lv B, Chen X, et al. An early model to predict the risk of gestational diabetes mellitus in the absence of blood examination indexes: application in primary health care centres. BMC Pregnancy Childbirth. 2021;21(1):814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.American Diabetes Association Professional Practice Committee. 7. Diabetes Technology: Standards of Care in Diabetes—2024. Diabetes Care. 2024;47(Supplement 1):126–144.
- 41.De Bois M, Yacoubi MAE, Ammi M. GLYFE: review and benchmark of personalized glucose predictive models in type 1 diabetes. Med Biol Eng Comput. 2022;60(1):1–17. [DOI] [PubMed] [Google Scholar]
- 42.Marling C, Bunescu RC. The ohiot1dm dataset for blood glucose level prediction. In: KHD@ IJCAI; 2018. pp. 60–3. [PMC free article] [PubMed] [Google Scholar]
- 43.Bertachi A, Viñals C, Biagi L, Contreras I, Vehí J, Conget I et al. Prediction of nocturnal hypoglycemia in adults with type 1 diabetes under multiple daily injections using continuous glucose monitoring and physical activity monitor. Sens (Basel). 2020;20(6). [DOI] [PMC free article] [PubMed]
- 44.Vehí J, Contreras I, Oviedo S, Biagi L, Bertachi A. Prediction and prevention of hypoglycaemic events in type-1 diabetic patients using machine learning. Health Inf J. 2020;26(1):703–18. [DOI] [PubMed] [Google Scholar]
- 45.Zhang L, Yang L, Zhou Z. Data-based modeling for hypoglycemia prediction: importance, trends, and implications for clinical practice. Front Public Health. 2023;11:1044059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Camerlingo N, Siviero I, Vettoretti M, Sparacino G, Del Favero S, Facchinetti A. Bayesian denoising algorithm dealing with colored, non-stationary noise in continuous glucose monitoring timeseries. Front Bioeng Biotechnol. 2023;11:1280233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Aliberti A, Pupillo I, Terna S, et al. A Multi-patient Data-Driven Approach to blood glucose prediction. IEEE Access. 2019;7:69311–25. [Google Scholar]
- 48.Afsaneh E, Sharifdini A, Ghazzaghi H, Ghobadi MZ. Recent applications of machine learning and deep learning models in the prediction, diagnosis, and management of diabetes: a comprehensive review. Diabetol Metab Syndr. 2022;14(1):196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Cichosz SL, Kronborg Τ, Jensen MH, Hejlesen O. Penalty weighted glucose prediction models could lead to better clinically usage. Comput Biol Med. 2021;138:104865. [DOI] [PubMed] [Google Scholar]
- 50.Del Favero S, Facchinetti A, Cobelli C. A glucose-specific metric to assess predictors and identify models. IEEE Trans Biomed Eng. 2012;59(5):1281–90. [DOI] [PubMed] [Google Scholar]
- 51.De Bois Μ, El-Yacoubi ΜΑ, Ammi Μ. Integration of clinical criteria into the training of deep models: application to glucose prediction for diabetic people. Smart Health. 2021;21:100193. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.