Adaptation shapes the representational geometry in mouse V1 to efficiently encode the environment

Abstract

Sensory adaptation dynamically changes neural responses as a function of previous stimuli, profoundly impacting perception. The response changes induced by adaptation have been characterized in detail in individual neurons and at the population level after averaging across trials. However, it is not clear how adaptation modifies the aspects of the representations that relate more directly to the ability to perceive stimuli, such as their geometry and the noise structure in individual trials. To address this question, we recorded from a population of neurons in the mouse visual cortex and presented one stimulus (an oriented grating) more frequently than the others. We then analyzed these data in terms of representational geometry and studied the ability of a linear decoder to discriminate between similar visual stimuli based on the single-trial population responses. Surprisingly, the discriminability of stimuli near the adaptor increased, even though the responses of individual neurons to these stimuli decreased. Similar changes were observed in artificial neural networks trained to reconstruct the visual stimulus under metabolic constraints. We conclude that the paradoxical effects of adaptation are consistent with the efficient coding framework, allowing the brain to improve the representation of frequent stimuli while limiting the associated metabolic cost.

Introduction

Visual perception is profoundly affected by adaptation to previous stimuli, which can induce changes in our ability to detect and discriminate stimuli^1,2, as well as generate visual illusions such as the tilt aftereffect³. Adaptation-induced changes in perception have been connected to changes in visual responses⁴ and have been observed in different species^5–7, sensory systems^6,8, and at different stages of sensory processing^5,6,9,10. Despite these studies providing a link between changes in perception and visual responses, the crucial question of whether adaptation makes certain stimuli more discriminable and whether it does so to a specific set of stimuli has only partial answers.

A connection between adaptation-induced changes in perception and visual responses was obtained in studies of tuning curves in single neurons¹¹ or neural populations¹². These studies showed that adaptation can increase discriminability between stimuli¹¹ and decorrelate tuning curves¹². However, it is not clear how all these observed changes affect the ability of a downstream population to discriminate stimuli. In particular, any realistic readout of a population of neurons should generate a response for each stimulus every time it is presented (in a single trial). Noise correlations across different neurons might play an important role, and the average response properties of individual neurons, like their tuning curve, can only partially predict the discrimination performance. The tuning curve is typically estimated by looking at multiple trials, and hence, it is an average property of the neuronal response that cannot be read out in a single trial^13,14. Moreover, the typical tuning curves of individual neurons are affected in multiple ways by adaptation (e.g. by the stimulus presented in the present and by the activity of neurons driven in the past, see¹²), and it is often difficult to capture all these changes using a simple model of the responses of individual neurons. Moreover, it is not clear how these multiple changes affect discriminability.

A more interpretable description of the activity of a neuronal population can be obtained by considering its representational geometry, i.e. the arrangement of all the points in the neural space corresponding to the different experimental conditions¹⁵. This description of the data is interpretable in terms of perception and discriminability because it directly relates to the ability of a linear readout to discriminate between similar stimuli. Moreover, unlike with tuning curves, this description of the data can be applied to single trials. It might, therefore, reveal how adaptation-induced changes in representational geometry interact with other forms of modulation, such as those induced by running. Running strongly affects the visual responses^16,17 and their geometry¹⁸, and reflects changes in behavioral state that might, in turn, affect adaptation¹⁹. Overall, only a few studies have focused on adaptation-induced changes at the population level, and they lacked trial-to-trial resolution^20–22, single-unit resolution¹², or an analysis of population geometry²³. Applying a geometrical approach at the single trial level can reveal how adaptation depends on orientation similarity and whether adaptation-induced and running-induced changes interact in the neural code.

Furthermore, describing adaptation-induced changes from a geometrical perspective could shed light on the computational advantages of adaptation. Computational theories^4,24 have proposed that adaptation can efficiently represent stimuli through population homeostasis maintenance¹², optimization of information transmission²⁵, decorrelation²⁶, response-product homeostasis²⁷, and the trade-off between precision of the representation and metabolic cost^28,29.

For all these reasons, we investigated how adaptation modifies the geometry of representations and how it affects the ability of a linear readout to discriminate between similar stimuli on single trials. We presented to awake mice sequences of visual stimuli in the form of oriented gratings characterized by two distributions: uniform and biased¹². As a first step towards answering which orientations become more discriminable, we first found that in the uniform environment, vertical orientations lead to the lowest discriminability, in contrast with cat³⁰ and primate³¹ V1 neurophysiology, where visual acuity is lowest for oblique orientations. Then, we found that in the biased environment, discriminability increases for stimuli near the adaptor, consistent with human psychophysics studies^2,32, while responses near the adaptor decreased. This scenario is consistent with earlier phenomenological theories of adaptation³³. We observed that running expanded the geometry of representations. Running had a stronger effect in magnitude than adaptation on the geometry of neural representations. However, the increase in discriminability and decrease in responses around the adapted orientation was observed across different locomotion states.

Finally, we leveraged these data to constrain a theoretical model that predicts changes in discriminability in single trials, and that reveals a computational role for the response changes induced by adaptation. Following an efficient coding approach^34,35, we trained an artificial neural network to reconstruct stimuli presented in environments with the same distributions as those used in our experiments (uniform and biased). The network minimized a stimulus reconstruction cost and a metabolic cost to represent the stimuli efficiently. Consistent with our experimental data, we observed an increase in discriminability and a decrease in responses around the adaptor. Our model thus suggests that population responses to stimuli efficiently adapt to the environment statistics.

Results

We presented sequences of static gratings interleaved by blank stimuli to awake head-fixed mice that were free to run on an air-suspended ball (Fig. 1a). The orientation of the gratings was sampled from a uniform distribution (Fig. 1b). We simultaneously recorded hundreds of neurons using two-photon imaging in layers 2/3 of V1 in these mice (Fig. 1c)¹⁶.

Figure 1. Relation between tuning curves and geometry in V1.

a) Two-photon recordings of V1 neurons in head-fixed mice freely moving on a ball while viewing static gratings of different orientations. b) Example segment of oriented grating sequences drawn from a uniform distribution. c) Average normalized activity of all neurons recorded in an example session sorted by their preferred orientation. Orientation at 0 deg is vertical, while at 90 deg is horizontal. d) Distribution of preferred orientations across neurons for individual recording sessions (gray) and averaged across sessions (black). e) Orientation tuning sharpness (concentration parameter of fitted von Mises functions) as a function of the preferred orientation of the neurons for individual recording sessions (gray) and for averaged across recording sessions (black). f) The first two Principal Components (PCs) of the population responses in (c), showing responses in each repeat (small dots) and their averages for each stimulus (large circles). g) Covariance across trials of the population responses. For each stimulus orientation, the ellipse is centered on the average responses, and its axes are proportional to the square root of eigenvalues of the stimulus-conditioned covariance matrix of the trial responses in PC space. h) The first three PCs of the population responses, with lines indicating the main axis of the ellipsoid in (g) in three dimensions. i) Discrimination accuracy of any pair of stimuli, defined as discrimination accuracy of a linear classifier, averaged across all recording sessions. j) Discrimination accuracy for pairs of orientations differing by 15 deg (squares outlined in green in (i)) for each recording session (light green) and averaged across all sessions (dark green).

As a first characterization of how oriented gratings are encoded in the neural population, we studied the neurons’ tuning curves. We estimated the distribution of preferred orientations in the population of recorded neurons when orientations were sampled from a uniform distribution (Fig. 1d). Consistent with previous reports in mammals^30,31,36, we found an overrepresentation of neurons with a preference for the horizontal (90 deg) or vertical (0 deg) orientations (no significant difference in fraction of neurons with a preference for horizontal or vertical orientations across experiments: p = 0.09, Wilcoxon signed-ranked test). A larger number of neurons with a preference for 90 or 0 deg suggests a higher signal-to-noise ratio for these orientations, which appear consistent with a reduced discrimination threshold at horizontal and vertical orientations in human psychophysics experiments^1,30,37. We also characterized the tuning width of the neurons by fitting von Mises functions to the responses of neurons to estimate the concentration parameters (high concentration corresponds to sharper tuning curves) (Fig. 1e). We found sharper tuning curves in neurons preferring horizontal orientations but wider tuning curves in neurons preferring vertical orientations. In conclusion, different tuning curves’ features (distribution of preferred orientations and tuning sharpness) suggest different patterns of orientation-dependent discriminability in the neural population.

To have a full picture, instead of considering single-tuning curves separately, we next focused on the full-dimensional neural activity space (i.e. the space in which the coordinate axes represent the activities of the different neurons). We projected the population responses into low-dimensional space and quantified distances in the full-dimensional activity space. The representations of the stimuli in the activity space reflected the circular symmetry of the visual stimuli (Fig. 1f), but as expected from the inhomogeneities in the tuning curve distribution and properties (Fig. 1d,e), they were not spaced uniformly around a circle. Instead, the distance in the activity space between stimuli with a horizontal orientation or similar was larger than for stimuli with a vertical orientation or similar. This can be seen in visualizations of the geometrical structure of the representations (Fig. 1f,g,h), which we created by using PCA to reduce the dimensionality of the activity space. The same results are also observed in the original full-dimensional activity space by comparing the Euclidean distance between stimuli near the horizontal orientation with the distance between those near the vertical orientation (p < 10⁻⁵, Wilcoxon signed-ranked test; Fig. S1a,b).

To characterize the geometry of the neural representations in a way that directly reflects the information that can be read out by a downstream population, we then measured the ability of linear decoders to discriminate pairs of stimuli (Fig. 1i,j), starting from the case in which all the orientations are presented with equal probability (uniform distribution) The performance of these decoders depends on the representations in the original full-dimensional activity space and, importantly, on the noise’s strength and structure. In general, we observed a simple relation between discriminability and Euclidean distances: the larger the distances, the more discriminable the stimuli (Fig. S1c), When considering pairs of stimuli 15 deg apart, we consistently observed a peak in discrimination accuracy around the horizontal orientation, while the lowest decoding performance was seen for the vertical orientations. These observations suggest that discriminability is primarily modulated by the distances between orientations, rather than by the size or the structure of the noise. Indeed, the noise level of horizontal stimuli was not clearly distinguished from the noise level of vertical stimuli (p = 0.21, Wilcoxon signed-ranked test; Fig. S1a,b). Moreover, the position of the discrimination peak did not depend on the noise structure, as removing correlations modestly increased the discrimination accuracy but not the peak position (Fig. S1d–f). Shorter Euclidean distances at vertical orientations are consistent with wider tuning curves at those orientations (Fig. 1e).

To understand the contribution not only of the tuning width but also of the distribution of preferred orientations to the orientation-dependent discriminability, we considered a lower-dimensional phenomenological model constructed from the average tuning curves of neurons in each of the 12 bins of preferred orientation. We fitted a von Mises function to each of these average tuning curves and then multiplied the fitted curves by the probability density of the associated preferred orientation (Fig. S2c). Alternatively, we only considered the preferred orientation distribution (Fig. S2a) or only the tuning width (Fig. S2b). We then considered the Euclidean distance between pairs of stimuli in the lower dimensional space of 12 superneurons (one superneuron’s tuning curve is the average tuning curve of neurons that approximately prefer one specific orientation out of the 12 possible ones considered in this study) with responses determined by these average tuning curves (Fig. S2d–f). When considering nearby stimuli (Fig. S2g–i), we could observe the decoding peak at the horizontal orientation only when taking into account the tuning width. However, the distribution of preferred orientations was also informative when considering the relation between discriminability and distances across all pairs of orientations (Fig. S2j–l). Hence, we concluded that both the tuning width and the response magnitudes contribute to the peak of discriminability at the horizontal orientation.

Adaptation decreases responses of neurons tuned to the adaptor orientation while increasing discriminability around the adaptor.

To understand how adaptation changes the individual neural responses and the geometry of neural representations, we presented sequences of oriented gratings with different statistics (Fig. 2a): stimulus orientation was sampled from either a uniform or a biased sequence¹², defining two environments that are characterized by different stimulus distributions. In the case of a biased sequence, one orientation was presented 50% of the time, which produced strong adaptation effects around that orientation. When projecting the activity in a space with reduced dimensionality, we observed that adaptation changes the representational geometry in a structured way (Fig. 2b). This geometry in the reduced activity space indicates that the discriminability might actually increase around the adaptor.

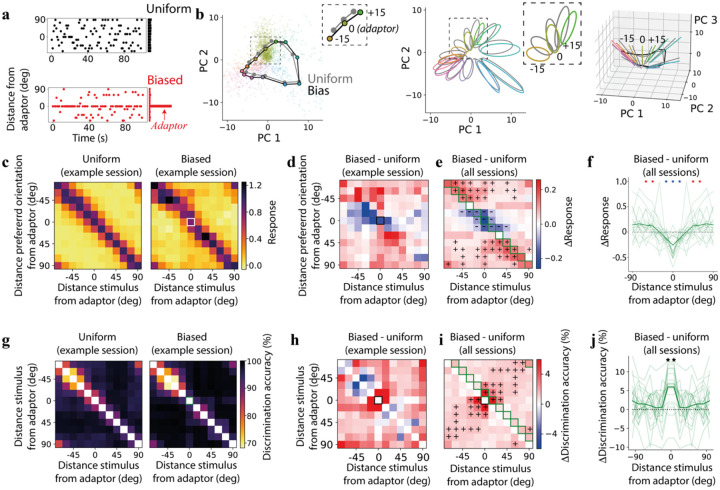
Figure 2. Adaptation increases discriminability around the adaptor while reducing neural responses.

a) Example segment of oriented grating sequences drawn from a uniform (black, same as in Fig. 1b) or biased distribution (red). b) Projection of neural activity in PC space, similar to Fig. 1f, but in a biased environment (colored dots, black lines), gray lines and dots correspond to the uniform environment; insets in the left and center panels focus on the adaptor orientations and orientations that are 15 deg distant from it. c) Average responses of tuned neurons in a single recording session (same as in panel b) whose preferred orientation has a given distance from the adaptor orientation (y-axis) to stimuli with a given distance from the adaptor orientation (x-axis); left: uniform environment; right: biased environment; white square: response to the adaptor stimulus of neurons tuned to the adapter. d) Difference in normalized responses between biased and uniform environments in (c). e) Same as in (d) but across recording sessions; pluses (resp. minuses) correspond to a significant increase (resp. decrease) in responses (p < 0.05, 1-sample t-test); green squares correspond to average values in (f); f) change in average responses between biased and uniform environments at the preferred orientation of each group of neurons (light green: single recording sessions; dark green: average across sessions; red asterisks: significant increase in responses as in (e); blue asterisks: significant decrease in responses as in (e)). g) Discrimination accuracy for any pair of stimuli in a uniform environment for one example session; right: same as the left panel but in a biased environment; green square corresponds to adapter orientation; h) Difference in population discrimination accuracy in an example recording between the biased and the uniform environment in (g). i) Similar to the example session in (h) but averaged across sessions; green squares correspond to average values in (j); pluses correspond to a significant increase in discrimination (p < 0.05, 1-sample t-test). j) Change in discrimination accuracy between biased and uniform environments for stimuli 15 deg apart as a function of the distance of the stimuli from the adapter; light green: individual recording sessions, dark green: average across all sessions; asterisks are a significant increase in discrimination accuracy (p < 10⁻⁴, 1-sample t-test).

We started by investigating how the tuning properties of neurons change in a biased environment. Consistent with previous reports¹², when averaging across recording sessions, we observed that adaptation induced a response decrease in neurons tuned to stimuli near the adaptor orientation (Fig. 2c–f, S3a,b, S4a). We also observed a response increase in neurons whose orientation preference was farther from the adaptor. In the original full-dimensional space, the Euclidean distance between the response to a given orientation and one 15 degrees away had the highest increase for the adaptor orientation (Fig. S3c,d).

We then compared the discrimination accuracy in a uniform environment to that in a biased environment. After estimating the accuracy in the two environments in the full-dimensional neural space (Fig. 2g), we computed the difference between the two environments (Fig. 2h,i, S4b). When considering pairs of similar stimuli that were 15 deg apart, we observed increased discrimination accuracy around the adaptor (Fig. 2j; p < 10⁻⁴, 1-sample t-test). This result was consistent across different adaptor orientations (adaptor at 0 deg: p < 10⁻⁴, 1-sample t-test; adaptor at 45 deg: p = 0.026, 1-sample t-test; Fig. S3e) as well as with increased cosine distance around the adaptor (Fig. S3f). Overall, changes in discriminability were qualitatively similar to observations in human psychophysics experiments^2,32 (but see also³⁸). These results did not depend strongly on the noise structure as they were qualitatively similar when correlations were removed by shuffling the activity of each neuron independently across trials for a given stimulus condition (shuffling, see^13,14,39, Fig. S3g,h). The fact that the noise structure did not play a major role in adaptation-induced changes is consistent with previous reports¹² (but see:²³).

In the previous analysis, the decoder was aware of changes in environments⁴⁰. We then asked whether a decoder unaware of changes in environments can deal with the changes in representational geometry⁴⁰. We trained linear decoders in a uniform environment and tested them in a biased environment or vice versa (Fig. S5a). The discrimination accuracy for pairs of approximately opposite stimuli relative to the adaptor orientation typically increased, including those near the adaptor (Fig. S5a). In other words, it would increase for pairs of stimuli whose orientation was approximately $\pm \theta$ from that of the adaptor. Although the structure of the changes was not exactly the same compared to when a decoder was trained and tested in the same environment, there was a common result: near the adaptor, discriminability increased in biased environments, which was an even more surprising result when the decoder was unaware of a change in context. We also trained a regression model in a uniform environment to estimate the orientation of the stimulus presented (Fig. S5b). We confirmed a classical result showing, for stimuli near the adaptor, a repulsion of the estimated orientations away from the adaptor orientation⁶ when tested in a biased environment.

Representations might change over time for reasons independent of the specific task we are considering (‘representational drift’^41,42). As the biased sequence followed the uniform one, one might wonder whether this geometric change could be explained simply by the temporal separation of the two environments. We thus asked if we could discriminate the same orientation in two blocks of time. The two time blocks could have the same statistics (uniform) or different statistics (uniform and biased). Discriminating two blocks of time with uniform statistics was larger than chance (Fig. S5c,d). However, the discrimination accuracy was greater when discriminating two blocks of time with different statistics. This difference in discrimination accuracy indicated that the passage of time alone was insufficient to explain changes in geometry (Fig. S5c,d).

We generalized the previous analysis by training and testing linear decoders in environments separated by different periods of time. Training and testing could be in the same (uniform) or different (uniform vs. biased) environments but always separated by varying time blocks. As expected, based on the potential presence of representational drifts or recording drift, the discrimination accuracy decreased with time (Fig. S5e).

Running expands the representational geometry along directions different from those encoding stimulus orientation.

Running is one of the main drivers of visual response modulation in the mouse brain^16,17,43. Running increased the distance between stimuli (p < 10⁻¹¹, Wilcoxon signed-ranked test; Fig. 3a). In the activity space, this expansion appears to be along directions that are approximately orthogonal to the dimensions spanned by all the visual stimuli (Fig. 3a), which is consistent with previous reports^18,36. This change in geometry enables the encoding of whether the animal is running or not without interfering with a linear readout of the orientation of the stimulus.

Figure 3. Running expands the geometry of representations.

a) Same format as in Fig. 1f–h, comparing average stimulus responses measured when the mouse was running (squares, solid lines) vs. stationary (diamonds, dashed lines). Dots represent individual trials and are shown only during running. b) Discrimination accuracy between pairs of orientations for a model that has been trained and tested during stationary (left) or running (right) periods; c) Euclidean distance of population responses between any pair of stimuli (averaged across recording sessions). d) Cartoon illustrating the measurement of cross-condition generalization performance (CCGP); left: a model was trained (black contour and black line) to discriminate two orientations (more opaque colors) during the running condition (squares) and then tested (blue contours) to discriminate the same orientation during the stationary condition (diamonds); for illustration purposes, we also plotted the hyperplane separating the points trained in the other condition (blue dotted line); right: same as before but model was trained in the stationary condition and tested in the running condition. e) Discrimination accuracy between pairs of orientations during running for a model that has been trained during stationary periods (left) or vice versa (right).

Running strongly modulated the neural activity, and the locomotion state accounted for more variability than the identity of the visual stimulus. We observed a general increase in Euclidean distances during running (Fig. S6a). We then computed the angle between the coding direction of running (i.e., the vector linking responses during the stationary condition to those during the running condition) and the main direction of variability (as measured by PCA) (Fig. S6b). We then compared this angle with the angle between the main direction of variability and the coding directions of different stimuli (the vector linking average responses to two orientations 15 deg apart, same locomotion condition). We found that the main direction of variability was more aligned with the running direction than the stimulus directions (Fig. S6c).

We compared the discrimination accuracy between any pair of stimuli for stationary and running conditions separately in a uniform environment. We observed a general increase in discrimination accuracy in the running condition (Fig. 3b,c) consistent with an increase in Euclidean distances (Fig. S6a). We then asked if the neural code for orientation is preserved across locomotion conditions. More specifically, we tested if coding directions for different orientations were approximately the same for running and stationary states. We computed the cross-condition generalization performance (CCGP)^15,44: we trained a linear model to discriminate any two angles in one locomotion condition (stationary or running) and test it in the other condition (Fig. 3d). The CCGP (Fig. 3e) was similar to the performance achieved when we trained and tested the decoder using the same locomotion condition (Fig. 3b), supporting the notion that locomotion and stimulus representation in V1 are disentangled (or mostly disentangled¹⁸).

We then asked whether the coding direction of running was preserved across stimulus orientations. We performed another CCGP analysis by estimating the ability to discriminate between stationary and running trials, training the decoder on one stimulus orientation, and testing on another orientation (Fig. S6d). We found that it was possible to decode locomotion, and we did not find a large difference across angles. We also found that destroying correlations increased the discrimination accuracy of the previous analysis (Fig. S6e,f), which is consistent with the main axis of co-variability being aligned with running (Fig. S6b,c). These analyses indicate that there is a subspace in which the locomotion state of the animal is approximately invariant with respect to the stimulus identity.

From the reduced dimensionality representations (Fig. 3a), it seems that the transformation of the geometry from stationary to running can be described as an expansion accompanied by a shift. It is then natural to ask whether this transformation can be explained by a simple scaling model in which all responses in the stationary case are simply multiplied by the same factor. We fit a scaling geometrical model (see Methods for more details), which can be described as a truncated cone, to the neural data. This model accounts only partially (averaged normalized error: 37%) for the change in responses by running (Fig. S6g). In conclusion, while our results on the scaling model indicate that the geometry is more complex than a truncated cone, the results on CCGP show that the expansion of the geometry by running does not interfere substantially with the encoding of the stimulus orientation.

Adaptation increases discriminability across locomotion conditions.

Locomotion mostly preserved adaptation-induced changes. The analysis of the activity space with reduced dimensionality suggests that the changes in representations are approximately similar in different locomotion conditions (Fig. 4a,b). We then studied in which directions of the original full-dimensional neural space the locomotion-induced and adaptation-induced changes happen across orientations. For each orientation, we define the direction of adaptation as the vector between the points in the activity space that represent the responses in uniform and biased environments. We then estimated the angle between the coding direction of stationary/running and the direction of adaptation (Fig. S7a. This angle tended to be negative, although not significantly so. We also estimated the angle between the direction of maximum variability and the direction of adaptation (Fig. S7b). In this case, the angle was significantly negative, indicating that adaptation is oriented toward a decrease of this vector, which typically represents the average activity.

Figure 4. Interaction between adaptation and running.

a) Projection of neural activity in PC space, similar to Fig. 2b, but for the stationary condition only. Colored dots and black lines correspond to a biased environment, while gray lines and dots correspond to a uniform environment. b) Similar to (a) but for the running condition. c) Difference in normalized responses between biased and uniform environments averaged across experiments similar to Fig. 2e, but only for the stationary condition. d) Similar to (c) but for the running condition. e) Difference in population discrimination accuracy between the biased and the uniform environment averaged across recording sessions similar to Fig. 2i but only for the stationary conditions; f) Similar to (e) but for the running condition.

The coding directions for adaptation were preserved when the locomotion state changed. We computed the CCGP for adaptation by training the model to discriminate responses to the adaptor between the uniform and biased environment. We either trained the model in the stationary condition and tested it in the running condition or vice versa (Fig. S7c). We compared the CCGP with the one obtained by discriminating two different uniform blocks so that the only difference would be the passage of time. We found it easier to discriminate between biased and uniform environments than between two uniform environments (Fig. S7d). This shows that adaptation shifted the manifold in a direction not perfectly aligned with the locomotion axis. It would have been more difficult to discriminate between the two conditions if they had been perfectly aligned. When performing a similar operation—discriminating between stationary and running by training linear decoders in a uniform environment and testing them in a biased environment (Fig. S7e)—we did not observe a significant difference in the case of training and testing models in different uniform environments (Fig. S7f).

Finally, we tested how locomotion changes neural responses and discrimination accuracy. We observed decreased responses (Fig. 4c,d; S7g,h) and increased discrimination accuracy (Fig. 4e,f) around the adaptor during running and stationary periods. Thus, even though running had a stronger effect in magnitude on the geometry of representations than adaptation, we observed in either locomotion condition changes similar to those reported without separating locomotion conditions (Fig. 2e,i).

An artificial neural network reproduces the changes in discriminability and population tuning observed in mouse V1.

Since theoretical work has shown that adaptation can increase the efficiency of neural representations, we next asked if our findings could be explained by efficient coding³⁵. We trained 6,000 autoencoder models with metabolic constraints (L1 norm in the hidden layer; Fig. 5a) and different hyperparameters (e.g. noise level, number of neurons, metabolic coefficient) to reconstruct the stimuli. We trained the autoencoder separately on the uniform and biased statistics (Fig. 5b). In the biased environment, because of biased statistics, the autoencoder would be penalized more when misclassifying the adaptor’s orientation as the adaptor is presented more often. The biased statistics also force the autoencoder to represent the adaptor in a more-efficient manner than other orientations.

Figure 5. A normative model reproduces the changes in discriminability and tuning observed in mouse V1.

a) Training set of the model matching the distribution of stimuli in the data. b) Autoencoder trained to minimize a multi-objective function composed of a reconstruction error in the output layer and energy cost (L1-norm sparsity) in the hidden layer; c) PCA on responses in the hidden layer (compare with Fig. 2b and 6l) for one typical model; note the decrease in responses (purple arrow) and increase in distances (green arrows) near the adaptor. d) Difference in average responses between biased and uniform environment computed as in Fig. S3a but for the model. e) Change in average responses between biased and uniform environments at the preferred orientation of each group of neurons, computed as in Fig. S3b but for the example model in (c). f) Difference in discrimination accuracy in an example recording between the biased and the uniform environment, computed similarly to Fig. 2h but for the example model in (c). g) Change in discrimination accuracy between biased and uniform environments for stimuli 15 deg apart as a function of the distance of the stimuli from the adapter, computed similarly to Fig. 2i but for the example model in (c).

Despite the simplicity of the model and the minimal number of assumptions, adaptation changed the population geometry in most models in a way that is similar to the data (Fig. 5c). Within a broad hyperparameter region (Figure S8e), we observed a decrease in responses around the adaptor for neurons tuned to the adaptor (Fig. 5d,e) and an increase in discrimination accuracy around the adaptor (Fig. 5f,g) consistent with our experimental observations (Fig. 2e,f,i,j).

Among the different hyperparameters of the model, we focused on the metabolic penalty and its impact on the metabolic cost, discrimination accuracy, and response magnitude (Fig. S8a–f). We observed that a decreased metabolic penalty increased response magnitudes (Fig. S8b) and discriminability (Fig. S8c) when averaged across all orientations or pairs of orientations. Furthermore, a decrease in metabolic penalty leads to a weaker (and negative) change in response magnitude (Fig. S8e) and an increase in change in discrimination accuracy (Fig. S8f) around the adaptor. These results can be visualized in reduced dimensions as an expansion of the geometry (Fig. S8g) and suggest that the running-induced changes could be interpreted as a decrease in metabolic penalty.

Relation between changes in responses and discriminability induced by the adaptor.

The decrease of responses by adaptation in neurons tuned to the adaptor orientation in the data (Fig. 2e) and the normative model (Fig. 5d) may appear at odds with increased discriminability around the adaptor observed in our data (Fig. 2i) and in the normative model (Fig. 5f). We now show that what we observed in the data reflects an interesting computational strategy that allows the system to better discriminate more frequent stimuli without increasing the metabolic cost. We will compare this strategy with two other scenarios: one where the adaptor discriminability increases but also the metabolic cost, and another where the energy consumption is reduced but also the discriminability of the adaptor decreases.

We started by considering a hypothetical adaptation of tuning curves where the peak responses of the neurons tuned to the adaptor were either depressed (Fig. 6a, S9a) or facilitated (Fig. 6b, S9b). We also considered another hypothetical adaptation of tuning curves (Fig. 6c) consistent with changes observed in the data (Fig 2h) but applied to homogeneous tuning curves. In this way, we would abstract our results away from the inhomogeneities we observed in a uniform environment (Fig. 1) and focus on the changes in a few response properties.

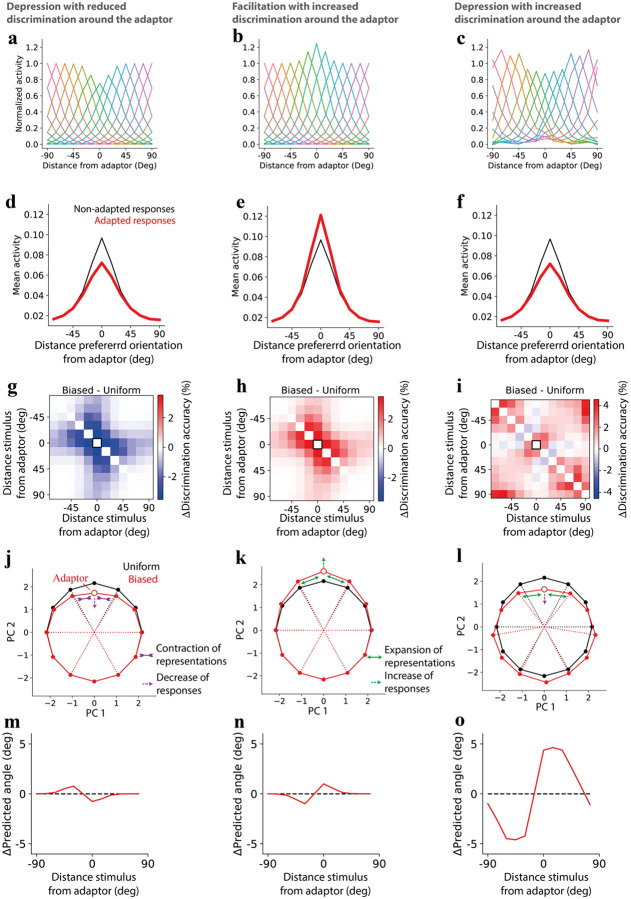
Figure 6. Relationship between changes in responses and discriminability.

a) Normalized population-average responses to different orientations. Each curve corresponds to the average responses of neurons tuned to a specific orientation in a hypothetical, biased environment where the adaptor decreases responses in neurons tuned to the adaptor at the adaptor location. b) Similar to (a) but the adaptor increases responses in neurons tuned to the adaptor at the adaptor location. c) Similar to (a) and (b) but the increase and decrease in responses reflects that observed in the data (see Methods). d-f) hypothetical average firing rate of neurons if their responses were not adapted but the distribution of orientation was biased (black) and firing rate of neurons when their responses are adapted as in (a-c) consistently with a biased distribution of orientations (red). g-i) difference in discrimination accuracy (here, computed based on population discriminability between any pair of stimuli) between a homogenous population (representing biased condition) and the same population after applying the perturbation in tuning curves in (a-c). Black squares correspond to adapter orientation; j) Projected neural activity in PCA space before and after changes in (a) decreases responses (purple dashed arrow toward the center) and reduces distances and discrimination accuracy near the adaptor (purple inward arrows). k) Same as in (j), but changes in (b) are applied, which increase responses (green dashed arrow farther from the center) and enhance distances between stimuli near the adaptor (green outward arrows) as well as discrimination accuracy. l) Despite the response decrease (purple dashed line), the changes in (c) enhance distances and discrimination accuracy near the adaptor (green outward arrows). m-o) Angle prediction in the biased environments of (a-c) after training a model in a uniform environment. The angle is calculated from a linear regression of $\text{cos}\theta$ and $\text{sin}\theta$, where $\theta$ is the stimulus orientation, followed by computing $\text{arctan}(\text{sin}\theta /\text{cos}\theta )$.

What is the advantage of a simple response depression (Fig. 6a)? We measured the metabolic cost as the average firing rate over time based on the biased environment in the experiments. Assuming this biased environment, we compared the metabolic cost if the responses were uniform (non-adapted) or depressed (Fig. 6d). As expected, a response depression around the adaptor led to a decrease in metabolic cost compared to the non-adapted responses. We then estimated discrimination accuracy to different pairs of stimuli, assuming independent and identically distributed noise when responses were depressed compared to when were non-adapted. As expected, because of a decrease in signal-to-noise ratio, discrimination accuracy decreased around the adaptor, thus to the most frequent stimuli. Thus, response depression has the advantage of decreasing metabolic cost but the disadvantage of decreasing discriminability. The reverse emerges when considering response facilitation (Fig. 6b): facilitation has the advantage of increasing discrimination accuracy around the adaptor (Fig. 6h) but the disadvantage of increasing metabolic cost (Fig. 6e).

Finally, we estimated the metabolic cost and discrimination accuracy as the average firing rate based on the biased distribution used in the experiments. What are the consequences of these tuning curve changes in a biased environment? The changes in responses observed in the data and applied to a homogenous population present two advantages: they decrease the metabolic cost (Fig. 6f) and, at the same time, increase discrimination accuracy around the adaptor (Fig. 6f).

To find an intuitive explanation for how these two seemingly incompatible changes can happen simultaneously, we inspected the representations projected in a reduced dimensionality activity space (Fig. 6l). We observed that while responses near the adaptor got closer to the center, as expected from a decrease in responses, the stimuli near the adaptor got farther away from it, leading to a local increase in discrimination accuracy. These results can be compatible with a combination of changes in gain and warping of tuning curves⁴⁵ and they can be contrasted to the cases of simple depression (Fig. 6j) or facilitation (Fig. 6k), in which there was an increase or a decrease in both responses and discrimination accuracy.

The adaptation-induced changes observed in the data and reproduced by the model have two benefits: reduction in metabolic cost and increase in overall discriminability. Is there any cost? Let us assume that the visual system decodes the stimulus orientation by estimating the angle from the neural population vector. Let us also assume that the decoder is unaware of changes in representational geometry⁴⁰ (Fig. S5a,b). This means that a decoder trained in a default environment (e.g. a uniform environment) could be tested in another environment (e.g. one specific biased environment) differently from a decoder trained and tested in the same environment (Fig. 2). Then, for the unaware decoder, there is a strong repulsion of the estimated angle near the adapted orientation (Fig. 6l,o), i.e. the estimated angle is farther from the adaptor than it really is, creating a bias. This repulsion is what we observed in the data (Fig. S5b) and is consistent with a stronger reduction of tuning curves at the flank near the adaptor¹².

Repulsion of orientations near adaptation is consistent with the tilt aftereffect^33,46,47, where a long exposure to a stimulus (e.g., vertical) can produce the illusion that a different but similar stimulus (e.g., slightly oblique) will be perceived more different than what it is (e.g., more oblique). This issue would be less prominent in the other hypothetical adaptation-induced changes in geometry (Fig. 6j,k,m,n), suggesting that having an unbiased representation of the orientation may be, to some degree, less important than a robust discriminability between two angles and a metabolic cost under control. In other words, adaptation-induced changes may improve the ability to tell apart two stimuli (focusing on their relative difference of orientations) while decreasing the ability to identify the absolute orientation of those stimuli.

Discussion

We investigated how the representational geometry in mouse V1 is shaped by adaptation under environments with different stimulus statistics. More specifically, we presented oriented gratings sampled from uniform and biased distributions. Consistently with previous studies in cat V1¹², we observed that adaptation decreases the neurons’ responses to the adaptor orientation. However, we also observed increased discriminability around the adaptor. A normative model could explain these results, suggesting that the observed changes in the representational geometry emerge from a trade-off between improving the representation of frequent stimuli and reducing the metabolic cost of responding to these more frequent stimuli.

The analysis of the geometry in the uniform case is not fully consistent with human psychophysics studies. In humans, visual acuity is higher for both horizontal and vertical orientations and lower for oblique stimuli^1,48, a phenomenon known as “oblique effect”³⁷, which is consistent with several neurophysiology studies in cat³⁰ and primate V1³¹. However, we found that vertical orientations were less discriminable than oblique orientations when reading out from the neural populations we recorded. The reason for this discrepancy is not clear. One possible explanation is that in the natural scene observed by mice, especially those observed while running, vertical shapes are less frequent or important.

The geometric analysis in the biased case revealed that despite the decrease in responses, discriminability increases between the stimuli around the adaptor, consistent with human psychophysics studies^2,32 and theoretical models^32,49. A reduced dimensionality analysis shows intuitively how the decrease in responses and increase in discriminability can coexist through a non-uniform transformation of the circle representing the uniform environment. The geometry in the low-dimensional space is consistent with earlier phenomenological theories of adaptation³³ but was not until now shown in neural population data. In previous studies in primate V1¹¹ only an analysis at the level of single neurons was performed, except for a study on neuron pairs²³, which focused only on local discrimination and thus did not on the full population geometry. Furthermore, the results on pairwise noise correlations in primate V1 in²³ were different from those in cat V1¹². It remains to be understood whether our population analysis of mouse V1 would match that of primates and cats.

Running strongly affects visual responses^16,17,43, and adaptation effects can depend on the animal’s behavioral state¹⁹. We observed that, while running expands the stimulus representations, the increase in the discriminability of an adapted stimulus and the decrease in its responses are present during both stationary and running periods.

To understand how orientation, adaptation, and running information are formatted in V1, we performed several CCGP analyses^15,44,50. We found that the discriminability of a pair of stimuli depended on the test locomotion condition (higher during running). However, the coding directions for pairs of stimuli in the two locomotion conditions were approximately the same, enabling a decoder trained on stationary stimuli to work also in the running condition (and vice versa). The same geometry supported a higher-than-chance discriminability of stationary vs. running conditions when training a decoder in one orientation and testing it in another one, suggesting that the coding direction of running was approximately preserved across stimulus orientations. Another CCGP analysis suggested that it was also preserved across environments, and thus, adaptation did not affect the running direction. Finally, a different CCGP analysis showed that adaptation shifts the manifold in a direction not perfectly aligned with the locomotion axis.

All these results indicate that the locomotion state is encoded, and despite that it is not strongly interfering with the readout of the stimulus orientation. In other words, stimulus orientation and locomotion states are two approximately disentangled variables, enabling a simple linear readout to generalize across multiple situations without any need for retraining. This indicates that the geometry is dominated by a relatively low-dimensional structure^18,51, which is not trivial to observe in activity spaces whose ambient dimensionality is elevated (i.e. when considering a large number of neurons). This structure has been observed in multiple brain areas across different species^{15,44,50,52,53}.

Normative theories of adaptation have been based on different frameworks, not necessarily mutually exclusive, including redundancy reduction, predictive coding, surprise salience, inference, and efficient coding²⁴. Following an efficient coding approach^35,54, we trained an artificial neural network³⁴ to represent stimuli in different environments under energy constraints. Variations of an efficient coding approach have considered different objective functions, such as the maximization of mutual information⁵⁵. Here, similarly to previous work, we considered a tradeoff between representation fidelity and metabolic cost^28,34,56. Differently from previous studies, we not only considered its effect on changes in tuning curves and perceptual effects but also on the full population geometry. After comparing networks trained under biased or uniform statistics, we observed an increase in discriminability and a decrease in responses around the adaptor, consistently with our experimental data. It would be interesting to understand how our theory would apply to different forms of adaptation, such as contrast adaptation^20,22 or even affecting other sensory modalities, such as the auditory one⁵⁷, and compare it to other related normative theories^58,59.

In conclusion, our model suggests that the stimuli representation is efficiently encoded in a way that considers the stimulus statistics. Several open questions stem from our study. The first question is to understand the detailed neural mechanisms underlying the observed phenomena in the data. The second question is whether the mouse perception reflects the finding in the neural population. Answering this question will require the animal to perform a discrimination task.

Methods

All experimental procedures were conducted in accordance with the UK Animals (Scientific Procedures Act) 1986. Experiments were performed at University College London under personal and project licenses released by the Home Office following appropriate ethics review.

Mice

We recorded neural activity from 12 transgenic animals (5 males, 7 females) in which specific cell types were labeled by a functional or structural indicator. In this study, we focused on all neurons recorded, independently of cell type. Experiments in which an interneuron class was labeled with tdTomato and recorded together with other cells were conducted in double-transgenic mice obtained by crossing Gt(ROSA)26Sor < tm14(CAG-tdTomato)Hze > reporters with appropriate drivers: Pvalb<tm1(cre)Arbr > (1 male, 1 female), Vip<tm1(cre)Zjh > (1 female), Sst<tm2.1(cre)Zjh > (3 males, 1 female), and GAD-nls-mCherry (1 male, 2 females). Experiments in which indicator was expressed uniquely in one neuron class were conducted in single transgenic mice: Scnn1a-Cre (1 female). Mice were used for experiments at adult postnatal ages (P59–214).

Animal preparation and virus injection

The surgeries were performed in adult mice in a stereotaxic frame and under isoflurane anesthesia (5% for induction, 0.5%–3% during the surgery). During the surgery, we implanted a head-plate for later head fixation, made a craniotomy with a cranial window implant for optical access, and, on relevant experiments, performed virus injections, all during the same surgical procedure. In experiments where an interneuron class was recorded with other cells, mice were injected with an unconditional GCaMP6m virus, AAV1.Syn.GCaMP6m.WPRE.SV40 (#100841; concentration 2.23 10¹²). In experiments where a cell type (excitatory L4 neurons) was labeled by unique expression, mice were injected with AAV-Flex-hSyn-GCaMP6m (#100845; concentration 2.23 10¹²). In a subset of mice crossed with GAD-nls-mCherry (n = 2 females), a sparse set of unspecified neurons (most of them excitatory) were labeled, and the following viruses were injected: pAAV-FLEX-tdTomato (#28306-AAV1; concentration 2.5 10¹²); pENN.AAV.CamKII 0.4.Cre.SV40 (#105558; concentration 4 10⁸). All viruses were acquired from University of Pennsylvania Viral Vector Core. Viruses were injected with a beveled micropipette using a Nanoject II injector (Drummond Scientific Company, Broomall, PA 1) attached to a stereotaxic micromanipulator. Six to seven boli of 100–200 nL virus were slowly (23 nl/min) injected unilaterally into monocular V1, 2.1–3.3 mm laterally and 3.5–4.0mm posteriorly from Bregma and at a depth of L2/3 (200–400 mm).

Visual stimuli

Stimuli were horizontal static two-dimensional Gabor functions presented in a location adjusted to match the center of GCaMP expression on one of two screens that spanned 45 to +135 of the horizontal visual field and ± 42.5 of the vertical visual field. During the gray screen presentation (duration 0.5 s), the screens were set to a steady gray level equal to the background of all the stimuli presented for visual response protocols. Gabor functions were presented for 0.5 s, with a spatial frequency of 0.1 cycles/deg and a width of 13 Deg.

Stimulus environments

The static gratings presented in the sequences were sampled from either uniform or biased distributions. In the biased distribution, one orientation (45 deg, n=12 recordings; 0 deg, n=7 recordings) was presented 50% of the time. The other stimuli were sampled from a uniform distribution in the remaining trials. In n=6 recordings, the contrast of 7% of the repeats was set to 0, otherwise the contrast was always at 100% at the center of the Gabor stimuli. The number of trials in each sequence was approximately either 1,000 (n=1 recording), 2,000 (n=12 recordings) or 2,500 (n=6 recordings). We always presented first a uniform environment, then a biased environment and lastly another uniform environment.

Imaging

Experiments were performed at least two weeks after the virus injection. We used a commercial two-photon microscope with a resonant-galvo scanhead (B-scope, ThorLabs, Ely UK) controlled by ScanImage⁶⁰, with an acquisition frame rate of about 30Hz (at 512 by 512 pixels, corresponding to a rate of 4.28–7.5 Hz per plane), which was later interpolated to a frequency of 20 Hz, common to all planes. Recordings were performed in the area where expression was strongest. In most recordings (n = 16) this location was in the monocular zone (MZ, horizontal visual field preference > 30 deg)⁶¹. Other recordings (n = 11) were performed in the callosal binocular zone (CBZ, n = 4, 0–15 deg)⁶² and others (n = 7) in the acallosal binocular zone (ABZ, 15–30 deg).

Data analysis

Data processing

We analyzed raw calcium movies using Suite2p, which performs several processing stages⁶³. First, Suite2p registers the movies to account for brain motion, then clusters neighboring pixels with similar time courses into regions of interest (ROIs). Based on their morphology, we manually curated ROIs in the Suite2p GUI to distinguish somata from dendritic processes. For spike deconvolution from the calcium traces, we used the default method in Suite2p⁶³. The outcome of spike deconvolution was the inferred spike probability up to an unknown multiplicative constant independent for each neuron. We later normalized all neural responses at the end of the preprocessing stage, and thus, the unknown multiplicative constant was not influential.

Retinotopic mapping

We initially mapped the retinotopy before the adaptation experiments to determine where to place a stimulus in a given recording. To do this mapping, we used sparse noise stimuli, consisting of black or white squares with a width of 6 deg visual angle on a grey background, which were presented to the mouse for 30 min. Squares appeared randomly at fixed positions in a 15 by 45 grid spanning the retinotopic range of the computer screens. At any one time, 2% of the squares were shown.

Normalization of neural responses

For each neuron $i$, trial $t$, and environment $l$, spontaneous activity $x_{s,i,l}\left(t\right)$ was computed as the average inferred spike probability over 250 ms before the stimulus onset while evoked activity $x_{e,i,l}\left(t\right)$ was computed as the average inferred spike probability for the whole stimulus duration of 500 ms.

We then detrended the activity in the way described in this paragraph. We considered the average spontaneous activity, averaged across neurons ${\bar{x}}_{s,l}\left(t\right)\equiv {⟨x_{s,i,l}\left(t\right)⟩}_i$, for each of the three environments (uniform #1, biased, uniform #2). We then separated the values of ${\bar{x}}_{s,l}\left(t\right)$ for each trial depending on the running speed (stationary: v < 1cm/s; low speed: 1 cm/s < v < 15 cm/s; high speed: v > 15 cm/s). In each environment, we considered the locomotion condition out of these three (stationary, low speed, high speed) with the largest number of trials. We finally fit an exponential $f_l\left(t\right)=a{e}^{-bt}+c$ on the values ${\bar{x}}_{s,l}\left(t\right)$ of this condition. We then divided $f_l\left(t\right)$ to all neurons from spontaneous $x_{s,i,l}\left(t\right)$ and evoked $x_{e,i,l}\left(t\right)$ by that in the given environment $l$, giving the new values $r_{s,i,l}\left(t\right)=x_{s,i,l}\left(t\right)/f_l$ and $r_{e,i,l}\left(t\right)=x_{e,i,l}\left(t\right)/f_l$ for spontaneous and evoked activity.

Finally, we z-scored the evoked activity as follows. For each neuron $i$ and environment $l$, we computed the average spontaneous activity, averaged across environments ${\bar{r}}_{s,i}={⟨r_{s,i}\left(t\right)⟩}_{t,l}$ and the standard deviation averaged across environments ${\sigma }_{r,s,i}={⟨\sigma {\left[r_{s,i,l}\left(t\right)\right]}_t⟩}_l$. When then computed for each neuron $z_{i,l}\left(t\right)=\left[r_{e,i,l}\left(t\right)-{\bar{r}}_{s,i}\right]/{\sigma }_{r,s,i}$.

Tuning parameters

For each neuron $i$ and environment $l$, we computed the preferred orientation by first considering the average response of a neuron across repeats of the same stimuli in a uniform environment $z_{i,l}(\theta )={⟨z_{i,l}\left(t\right)⟩}_{t\in \theta }$ to an orientation $\theta$. We then computed ${\tilde{z}}_{i,l}(\theta )=z_{i,l}(\theta )-\underset{\theta }{\text{min}}{z}_{i,l}(\theta )$. Then, the preferred orientation corresponded to the circular mean ${\phi }_i=\text{atan}2\left(\frac{1}{n_s}{\sum }_{\theta }{\tilde{z}}_{i,l}\left(\theta \right)\text{cos}\theta ,\frac{1}{n_s}{\sum }_{\theta }{\tilde{z}}_{i,l}\left(\theta \right)\text{sin}\theta \right)$, where $n_s=12$ is the number of stimuli.

To estimate average tuning curves based on preferred orientations (also known as super-neurons), we grouped each neuron into one of $n_s$ groups based on the closer discrete orientation. We then took the average responses across neurons without normalizing their responses (other than the normalization already described in a previous session), giving rise to $z_{e,l}(\theta ,\phi )$, where $\phi$ it the assigned preferred orientation of a super-neuron.

To compute a phenomenological model of the Euclidean distances between average tuning curves we proceeded as follows: we first fitted these average tuning curves to von Mises function and estimated the amplitude ${\mathrm{a}}_{\phi }$ and concentration parameter ${\kappa }_{\phi }:m(\theta ,\phi )={\mathrm{a}}_{\phi }\text{exp}\left[{\kappa }_{\phi }(\theta -\phi )\right]$ (we dropped the environment index $l$ as this analysis was done only in the uniform environment). Then, we computed an average concentration parameter ${\bar{\kappa }}_{\phi }$, together with an average amplitude ${\overline{\mathrm{a}}}_{\phi }$, by fitting a single von Mises function $\bar{m}\left(\theta ,\phi \right)={\mathrm{a}}_{\phi }\text{exp}\left[{\kappa }_{\phi }(\theta -\phi )\right]$ after averaging all individual responses, which were circularly shifted based on their preferred orientation. After this, we considered two cases: (i) fixed concentration but variable amplitudes or (ii) fixed amplitude but variable width.

Discriminability

We decoded the orientation of the static gratings presented to the mice using the population activity from V1 neurons. Let us consider environments with different stimulus statistics, i.e. different probability of stimulus presentation with a given orientation. For each environment, we computed the discrimination accuracy between any pair of stimuli. When considering the same environment, we equalized the number of trials for each recording session in the following way: we computed the minimum number of repeats for a given orientation across all 12 orientations. Then, we used 2/3 of these repeats for training the model and 1/3 for testing the model. We used a Linear Support Vector Classification as a model trained on all neurons recorded for a particular session with a regularization parameter equal to 0.1. We then tested the discrimination accuracy of the model on the test data.

In other analyses, training and testing data were from different environments (e.g., training in a uniform condition and testing in a biased condition). We still computed the minimum number of repeats per stimulus in the training and testing environment separately in those cases. We did not need to take only a fraction of this minimum number.

Cross-condition generalization performance

To compute the cross-condition generalization performance (CCGP)^15,44, we typically considered two different variables, for example, stimulus orientation $\theta$ and locomotion condition (stationary and running). We then trained, for example, a linear decoder to discriminate between two angles, ${\theta }_1$ and ${\theta }_2$, during the stationary condition and tested the decoder to discriminate the same angles in the running condition. We sampled the number of trials to balance them across classes separately in the training and test set.

Normative Model

Model training

We trained an autoencoder model with three different layers: an input layer $\mathit{x}$ with $n_x=121$ units (corresponding to a vectorized 11×11 image), a hidden layer $\mathit{r}$ with $n_r$ units, an output layer $\mathit{y}$ with $n_y=n_x$ units. We used sigmoid activation functions. The goal of the autoencoder was to minimize a cost function $E=E_1+\lambda E_2$ where $E_1=\frac{1}{n_x{n}_t}\sum _{i,t}\left(x_{i,t}-\right.{\left.y_{i,t}\right)}^2$ and $E_2=\frac{1}{n_x{n}_t}\sum _{i,t}{r}_{i,t}$, which, since $r_{i,t}>0$, represents an L1 sparsity constraint (metabolic cost). We added Gaussian noise with strengths ${\epsilon }_x$ and ${\epsilon }_r=1.0$ in the input and hidden layers. We trained the autoencoder using Pytorch using a batch size of 500 and a max number of epochs of 3,000 if convergence was not reached. We set the convergence error to $0.05\cdot {\epsilon }_x^2$. We implemented gradient descent with the Adam algorithm with a learning rate of 10⁻⁴.

We scanned through three different hyperparameters: the penalty factor on the metabolic cost $\lambda \in \{0.,0.1,0.25,0.5,1.\}$, the noise in the input ${\epsilon }_x\in \{0.25,0.5,1.,2.\}$, the number of hidden units $n_r\in \{500,1,000,2,000,3,000,5,000\}$ for a total of 100 of different sets of hyperparameters. We repeated 30 trainings with random initializations for each of these parameters.

Stimuli presented to the model

Similarly to the experiments, we presented sequences of oriented gratings plus blank stimuli with zero contrast to the model. Both uniform and biased environments had 2,000 blank stimuli. Then, 120 trials were added with 10 repeats of one orientation for each of the 12 considered orientations. In addition, 1,000 other stimuli were drawn from a von Mises distribution with a concentration parameter of 0 in the uniform environment and a concentration parameter of 150 in the biased environment. Stimuli had a size of 11×11 pixels and corresponded to a Gabor function with a spatial scale of 10 pixels and spatial frequency of 1.5 pixels.

Decoding of model responses

We computed discrimination accuracy using the same method used for the neural data but we only used a subset $n_d=50$ of the artificial neurons to decode the direction of motion from the population activity. In contrast to the training procedure, for the decoder we used the trained models as forward models but changed the level of noise in the input to ${\epsilon }_x^{\left(d\right)}=0.3$ and, similarly, in the hidden layer to ${\epsilon }_r^{\left(d\right)}=0.2$. The values of $n_d,{\epsilon }_x^{\left(d\right)}$, and ${\epsilon }_r^{\left(d\right)}$, where chosen to ensure compatibility on the experimental results on discrimination accuracy.