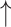Abstract
Image-to-image translation can create large impact in medical imaging, as images can be synthetically transformed to other modalities, sequence types, higher resolutions or lower noise levels. To ensure patient safety, these methods should be validated by human readers, which requires a considerable amount of time and costs. Quantitative metrics can effectively complement such studies and provide reproducible and objective assessment of synthetic images. If a reference is available, the similarity of MR images is frequently evaluated by SSIM and PSNR metrics, even though these metrics are not or too sensitive regarding specific distortions. When reference images to compare with are not available, non-reference quality metrics can reliably detect specific distortions, such as blurriness. To provide an overview on distortion sensitivity, we quantitatively analyze 11 similarity (reference) and 12 quality (non-reference) metrics for assessing synthetic images. We additionally include a metric on a downstream segmentation task. We investigate the sensitivity regarding 11 kinds of distortions and typical MR artifacts, and analyze the influence of different normalization methods on each metric and distortion. Finally, we derive recommendations for effective usage of the analyzed similarity and quality metrics for evaluation of image-to-image translation models.
Keywords: Metrics, Image synthesis, MRI, Similarity, Image quality
Subject terms: Computer science, Magnetic resonance imaging
Introduction
Image synthesis
Recent advances in generative artificial intelligence (AI) within the natural image domain have demonstrated a remarkable capability to produce synthetic images with high fidelity, capturing nuances such as lighting variations, textures, and object placements1,2. The implications of these advancements are far-reaching, with applications spanning various domains such as computer vision, graphics, augmented and virtual reality, or creative arts. Still, many challenges remain, including potential biases in generated images, the need for enhanced diversity and controllability in generation, and ethical considerations surrounding the use of AI-generated content.
The adaptation of generative modeling concepts such as Generative Adversarial Networks (GANs)3 or diffusion models4,5 to the medical imaging domain is being explored with continuously growing interest and many relevant use cases have already been identified, such as data augmentation6 or image conversion and enhancement by image-to-image translation7. For training deep neural networks, typically very large and diverse data sets are needed, but these are rarely available for medical imaging tasks. Generative networks can amend available data with synthetic samples and thereby improve the performance of other image analysis tasks6.
Image-to-image translation
Another line of research develops conditional generative models for image-to-image translation, which aims to translate a given source image to a synthetic target image, showing the same content (e.g. patient, organ or biological sample) as the source but with a different appearance (e.g. contrasting structures differently, changing texture or resolution). Source and target typically belong to different image domains. Depending on the availability of source and target pairs of the same patient or structure in the training data, image-to-image translation can be performed in a paired2 or unpaired8 manner, also referred to as supervised or unsupervised. Image-to-image translation models are trained to transfer characteristics from the target domain to a specific image from the source domain without changing the represented image content.
Medical image synthesis tasks
These tasks are specifically interesting in medical applications7, because they allow to translate a medical image from one domain to another. Source and target domain may differ by imaging modality or acquisition parameters, such that image-to-image translation allows translation, e.g., from computed tomography (CT) to magnetic resonance (MR) imaging9 or vice-versa10, from T1-weighted MR to T2-weighted MR11, CT to positron emission tomography (PET)12, PET to CT13, or from native MR to contrast-enhanced MR14,15. There is a significant patient benefit, when the source image can be acquired with less harm, more quickly or at a lower cost, compared to the the target image, which might be preferred for diagnosis. Low-quality or low-resolution images can be restored, improved, or the resolution increased16. For radiation therapy, which is planned on the basis of CT images, MR to CT synthesis has been investigated10. MR to CT synthesis is also used to facilitate registration between both modalities17. The translation between different MR sequences (T1-weighted, T2-weighted, T2-FLAIR) can complete missing series for improved diagnosis18–21. For reducing patient burden with contrast agents, researchers work on the translation of native or low-dose MR images to synthetic high contrast-enhanced images22.
Validation metrics for image synthesis
However, validation of these approaches is not straightforward. If a reference image, representing the desired synthesis result, is available for each generated image, a group of metrics called reference metrics can assess the similarity between predicted and reference images (see Fig. 1A). These reference images are often already leveraged for training synthesis models in a paired or supervised manner. Reference metrics are sometimes called full-reference metric to distinguish from weak-reference metrics, that only use partial information or features of the reference image. The term similarity metric is also synonymously used for reference metric.
Fig. 1.
Overview of image-to-image translation and types of evaluation metrics. (1) A source image from a source domain is transformed to a prediction in the target domain by an image-to-image translation model. If a reference image is given, this also belongs to the target domain. Then there are multiple possibilities to apply metrics. (A) Reference metrics directly compare prediction and reference image. (B) Non-reference metrics can be applied to the prediction alone, but also—if available—to a reference image. Then both non-reference metric scores can be compared. As an additional option (C), the reference and the prediction can be further processed in a downstream task, i.e. a segmentation task as a second (2) step. The performance of both downstream task results is then assessed with a downstream task metric, i.e. a segmentation metric.
However, not always paired reference images are available. In this case, non-reference metrics, also called quality metrics, can be applied (see Fig. 1B). As quality requirements may vary between tasks and image domains, metrics for different aspects have been developed, e.g. for measuring blurriness23, contrast24, noisiness25 or other features inspired by human perception26. Depending on the application of synthesized images, the evaluation of the images in a downstream task is more appropriate, than the evaluation of the images themselves27. Downstream task metrics operate on further processed results and not on the predicted or reference image (see Fig. 1C). For GANs, so-called distribution based metrics are very popular28. These assess the distributions of extracted image features of a larger set of generated images. For example, the Inception score29 assesses how distinct and evenly distributed classes are predicted by an Inception architecture based classifier trained on ImageNet (InceptionNet30). And the Frêchet Inception Distance31 assesses how well Gaussian modeled activation layer distributions of the InceptionNet match between generated and reference image sets. As these metrics do not assess single images, these metrics are not in the scope of this study.
In the domain of natural images, reference metrics have been extensively tested on synthetically distorted images. The Tampere Image Database32 and the LIVE Image Quality Assessment Database33,34 contain 25-29 reference images and differently distorted versions thereof, additionally annotated with a human quality score. Metric scores for various full-reference metrics were correlated with human scores to identify the best performing metrics.
Specifically for image synthesis, a study35 assessed metrics on outputs of image synthesis results. However, these results cannot be fully transferred to medical image synthesis. Even though similar studies for medical images36,37 exist, the included distortions, such as JPEG compression artifacts and white noise are less relevant for medical image synthesis. Instead, MR imaging, including acquisition and reconstruction, exhibits very specific artifacts, such as bias field, ghosting or stripe artifacts. Additionally, certain synthesis models may introduce other kinds of distortions, e.g. the insertion of artificial structures or registration artifacts that arise from misaligned source and target images. In this study, we create a similar benchmark dataset for the medical images domain consisting of 100 MR reference images and 11 mostly MR specific distortions. Applying the distortions in an isolated manner in five defined strengths results in well defined distortions. This allows us to compare different metrics regarding their sensitivity towards each kind of distortion separately, instead of averaging over a fixed group of distortions. This is crucial, because the effect of distortions on image quality may be rated differently for different medical applications.
Validation in the medical domain
Analysis, processing and generation of medical images can have severe impact on patient outcome and patient safety. Therefore, the Food and Drug Administration (FDA) in the United States requires technical and clinical evaluation for every software as a medical device to be approved38. Technical validation provides objective evidence, that the software correctly and reliably processes input data and generates output data with the appropriate level of accuracy and reproducibility. Clinical validation measures the ability of a software to yield a clinically meaningful output in the target health care situation. For evaluating medical algorithms based on artificial intelligence, guidelines about trial protocol designs39 have been agreed on by an expert consortium. However, systemic reviews of published papers on AI-based algorithms in the medical domain have revealed, that only a small fraction of studies adheres to such guidelines, i.e. external validation40,41. Often, details of clinical validation studies, such as test population statistics, are not published, not even for FDA-approved software42. Another review found that the median number of health-care professionals engaged in clinical validation was only four43, which limits the reliability and generizability of such studies. Recent validation studies of FDA approved image-to-image translation software rely strongly on technical assessment of phantom measurements by similarity metrics44,45. While the number of FDA approved medical devices based on AI software is still increasing by 14% (2022), the increase has been slowing down compared to 2020 (39%)46.
The lack of adequate trials for clinical validation is certainly only one part of the problem. Appropriate technical validation is crucial at an even earlier stage of development. Metrics for biomedical image analysis and segmentation have been extensively described47,48, and can be leveraged to indirectly assess synthetic images via downstream tasks49. Even though a huge amount of metrics has been used for the evaluation of synthetic medical images3,50, to our knowledge guidelines for the selection of appropriate similarity and quality metrics are not available. Loss functions for medical image registration, if used to compare a synthetic image with its reference image, are also leveraged for measuring image similarity, and overlap strongly with the selected reference metrics in this study51. For validating synthetic MR images, especially structural similarity index measure (SSIM), and peak signal-to-noise ratio (PSNR) are used extensively. A review on image-to-image translation with generative adversarial networks (GANs) or convolutional neural networks (CNNs) in the medical domain52 reported the use of SSIM in 84% studies and PSNR in 61% of studies, that synthesize MR images. A further review on synthetic contrast-enhancement of MR images53 reports evaluation by SSIM and PSNR in 75% of the studies. This is in opposition to known crucial weak points of SSIM and PSNR, such as underestimated blurriness54, bad correlation to human perception55–57 and difficulties with float-valued images58,59. Therefore, a systematic analysis of appropriate metrics for MR image synthesis validation is needed.
Contribution
In this paper, we provide a comprehensive analysis of the sensitivity of 11 reference and 12 non-reference metrics to 11 different distortions, that are relevant for MR image synthesis and of which some have not been assessed with the selected metrics before. Furthermore, we investigate the influence of five normalization methods before metric assessment. After analyzing metric sensitivity in detail, and discussing specific shortcomings or advantages of the investigated metrics, we recommend how to select and best apply metrics for validating image-to-image translation methods specifically for MR image synthesis.
Methods
In this section, we give an overview of reference and non-reference metrics for assessing the quality of images. Since most reference and non-reference metrics strongly depend on the intensity value ranges of the images they assess, the examination of metrics must be combined with the examination of normalization methods, that adjust the intensity value ranges. Therefore, we first introduce normalization methods that are frequently used to bring MR images to a common intensity value scale or as prerequisite for certain metrics.
Intensity ranges and data formats
For two reasons, normalization of medical images is needed prior to similarity or quality assessment. First, image intensities of non-quantitative image modalities are not comparable between two images, due to missing standardization. For example, in MR imaging, the same tissue may be represented by different values depending on scanner, software version or surrounding tissue. In this case, normalization must be applied in order to achieve comparability between two or more images. Normalization or standardization is not only needed as a prerequisite for metric assessment but is usually already performed as a preprocessing step for image-to-image translation models. For deep-learning based methods, a reasonable and standardized scale such as  or [0, 1] is recommended60. By modality specific normalization, deep-learning based models may even improve generalizability in case of heterogeneous input data sources61,62.
or [0, 1] is recommended60. By modality specific normalization, deep-learning based models may even improve generalizability in case of heterogeneous input data sources61,62.
Second, most metrics were designed and developed for 8-bit unsigned integer data format. In many cases, medical images are acquired in a larger 16-bit integer or 32-bit float value range and need to be normalized into the [0, 255] range. Alternatively, an additional data range parameter is introduced to adapt to other intensity ranges. For 8-bit images, the data range parameter L is then set to 255, assuming an intensity value range between 0 and 255. For float valued images, the intensity value range is generally infinite, but L should be set to a finite value spanning the range of at least all observed intensity values. Therefore, L is typically set to the difference of maximum and minimum value of an image I ( ), or the difference of the joint maximum and minimum of two images I and R (
), or the difference of the joint maximum and minimum of two images I and R ( ), or of a set of images
), or of a set of images  (
( ). If
). If  , then
, then  . It is argued58, that using
. It is argued58, that using  results in SSIM values, that do not vary with individual image minimum and maximum values. At least
results in SSIM values, that do not vary with individual image minimum and maximum values. At least  should be used for reference metrics on two images I and R instead of
should be used for reference metrics on two images I and R instead of  or
or  , because possibly
, because possibly 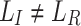 , and then the reference metric would yield different results when interchanging I and R.
, and then the reference metric would yield different results when interchanging I and R.
Normalization methods
Several normalization methods62,63, such as Zscore, Minmax or Quantile normalization have been used for MR images. These normalization methods ensure, that intensity values are near  or strictly between [0, 1], before model training14,64. Other variants of Minmax utilize percentiles or quantiles for scaling and/or additional clipping, or estimate percentiles based on a region-of-interest (ROI) contained in the image. For example, the WhiteStripe normalization65 determines reference ranges in a white matter region of the brain. Afterwards, these parameters are used to shift and scale the intensity values.
or strictly between [0, 1], before model training14,64. Other variants of Minmax utilize percentiles or quantiles for scaling and/or additional clipping, or estimate percentiles based on a region-of-interest (ROI) contained in the image. For example, the WhiteStripe normalization65 determines reference ranges in a white matter region of the brain. Afterwards, these parameters are used to shift and scale the intensity values.
In addition, normalization methods have been developed specifically for MR (piece-wise linear histogram matching66) or even specifically for brain MR images (cf. WhiteStripe65) in order to obtain quantitative comparable intensities for the same brain or body structures.
In a similar fashion, other normalization types besides Zscore can be adapted. For instance, for deep learning based MRI liver tumor segmentation67, a Minmax normalization was applied by using the 2% and 98% percentiles 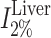 and
and 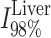 of the local intensity distribution within a region of interest in the liver for rescaling. In order to match histogram modes and minimum and maximum percentiles of an MR dataset showing the same body region, a piece-wise linear standardization procedure66 has been proposed. The authors argue that MR images exhibit an unimodal or bimodal histogram for most body regions, where the foreground concentrates around the first or second mode.
of the local intensity distribution within a region of interest in the liver for rescaling. In order to match histogram modes and minimum and maximum percentiles of an MR dataset showing the same body region, a piece-wise linear standardization procedure66 has been proposed. The authors argue that MR images exhibit an unimodal or bimodal histogram for most body regions, where the foreground concentrates around the first or second mode.
However, we assume, that different MRI sequences may generally display different histogram shapes and a different distribution of contrasted tissue types. Therefore, each MRI sequence should be normalized separately. Possibly, detecting and excluding the background could be beneficially done simultaneously for multi-modal MR images. Binning can be regarded as a normalization method to convert float values to 8-bit integer values. In this case 256 bins are used. It also removes information, because close but different intensities are mapped to the same bin value. By additionally copying the binned gray value to three color channels, images can further be converted to RGB images. Binning is needed for some metrics, because they require a finite number of intensity values (see “Statistical dependency metrics: NMI and PCC” section), or it is used to easily apply a method for 8-bit images to a binned float valued image. The normalization methods investigated within this study are defined in detail in Supplementary Sect. A.2, an overview is shown in Table 1.
Table 1.
Overview of normalization methods.
| Method | Description | Parameters | References |
|---|---|---|---|
| Minmax | Shifts and scales image intensity values to a range with given minimum and maximum value | Result range: 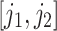
|
62 |
| cMinmax | Clips at lower and upper percentiles before Minmax. More robust to high and low outliers | Result range: 
|
|
| ZScore | Shifts the intensity values to a mean 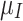 of 0 and scales to unit standard deviation of 0 and scales to unit standard deviation 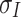
|
 |
62 |
| Quantile | Shifts the intensity values to a median of 0 and scales to a unit inter-quartile range (IQR =  ) ) |
median(I) = 0, IQR = 1 | 62 |
| Binning | Binning: All intensity values are mapped to B (=256) equidistant bins | Discrete result range: 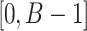
|
|
| PL | Piecewise-Linear: The histogram is scaled linearly in two pieces to match three landmarks 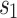 , , 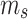 , and , and  of a standard histogram derived from a set of reference images of a standard histogram derived from a set of reference images |
Result range:  , mode: , mode: 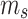 , depends on a training dataset , depends on a training dataset |
66 |
The target intensity range 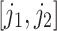 can be chosen arbitrarily, but is typically set to [0, 1] or
can be chosen arbitrarily, but is typically set to [0, 1] or 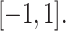
Reference metrics
Reference metrics are based on comparing a reference image R with another image I. Both images are assumed to have the same spatial dimensions. An overview of the reference metrics analyzed in this study is given in Table 2. If the image I was not acquired with the same modality or the same time point as image R, spatial alignment has to be ensured before applying a reference metric. Typically, this is achieved by image registration techniques.
Table 2.
Overview of reference (similarity) and non-reference (quality) metrics.
| Group | Abbreviation | Description | Similarity 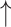 [min, max] |
Implementation | References | |
|---|---|---|---|---|---|---|
| Reference (Similarity) Metrics | SSIM | SSIM | Structural Similarity Index Measure: combination of structure, luminance and contrast |
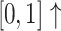
|
tm, ski | 73 |
| MS-SSIM | Multi-Scale SSIM: SSIM on original and 4 downscaled image resolutions |

|
tm | 74 | ||
| CW-SSIM | Complex Wavelet SSIM: ignores phase shifts in the wavelet domain, ignores small rotations and spatial translations |

|
gh75 | 76 | ||
| PSNR | PSNR | Peak Signal-to-Noise-Ratio: relation of data range to MSE |
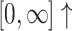
|
tm, ski | 77 | |
| Error Metrics | NMSE | Normalized Mean Squared Error |
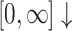
|
|||
| MSE | Mean Squared Error |

|
skl | |||
| MAE | Mean Absolute Error |

|
skl | |||
| Learned Metrics | LPIPS | Learned Perceptual Image Patch Similarity |
|
pypi78, tm | 79 | |
| DISTS | Deep Image Structure and Texture Similarity Metric |
|
gh75,80 | 81 | ||
| Statist. Depend. | NMI | Normalized Mutual Information: MI with fixed range |

|
ski | ||
| PCC | Pearson Correlation Coefficient |
|
skl | |||
| Down-stream | DSC | Dice Similarity Coefficient: segmentation metric, evaluating overlap |
|
itk | ||
Quality 
|
||||||
| Non-Reference (Quality) Metrics | Blurriness | BE | Blur Effect: difference of gradients when additionally blurred |
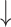
|
ski | 23 |
| BR | Blur Ratio: ratio of blurred pixels to edge pixels |

|
– | 82 | ||
| MB | Mean Blur: sum of inverse blurriness divided by number of blurred pixels |
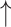
|
– | 82 | ||
| VL | Variance of Laplacian |

|
ski+np | 83 | ||
| BEW | Blurred Edge Widths |
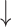
|
– | 84 | ||
| JNB | Just Noticeable Blur |
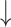
|
gh(C++)85 | 86 | ||
| CPBD | Cumulative Probability of Blur Detection |
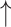
|
gh87 | 88 | ||
| MR Quality | MLC | Mean Line Correlation (also average structural noise): mean correlation between neighbored rows and columns |
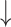
|
– | 89 | |
| MSLC | Mean Shifted Line Correlation (also average nyquist ghosting): mean correlation between rows and columns, that are with half image distance apart |

|
– | 89 | ||
| Learned Quality | BRISQUE | Blind/Referenceless Image Spatial Quality Evaluator |
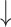
|
pypi90 | 91 | |
| NIQE | Natural Image Quality Evaluator |

|
gh92 | 93 | ||
| Noisiness | MTV | Mean Total Variation: Mean L2-normed gradient in x- and y- direction |

|
– | 25 | |
Slight spatial misalignment between paired images has been identified as a problem when evaluating with reference metrics, such that specialized methods have been investigated for this purpose. By assessing similarity in the complex-wavelet domain, complex-wavelet SSIM (CW-SSIM) is able to ignore small translations, scaling and rotations76. A score derived from features of the Segment Anything Model (SAM), mainly compares semantic features and therefore better ignores different style and small deformations94. The learned Deep Image Structure and Texture Similarity (DISTS) metric gives more weight to texture similarity, ignoring fine-grained misalignment of these textures81.
For natural images, a large set of reference metrics has been benchmarked on the Tampere Image Dataset32 or the LIVE Image Quality Assessment Database34. Many of the standard metrics from natural imaging have been frequently applied to medical images. However, some careful modifications are necessary for images with a data type other than 8-bit unsigned integer. In the following, we introduce the investigated reference metrics with some more detail and background and highlight important adaptions. A full list of metrics and their calculation is found in Supplementary Sect. A.3.
Structural similarity index measure
The structural similarity index measure (SSIM) combines image structure, luminance, and contrast, which are calculated locally for each pixel73. Several variants of SSIM exist. Multi-scale SSIM (MS-SSIM)74 calculates local luminance, contrast and structure additionally for four downscaled versions of the images and combines them in a weighted fashion. MS-SSIM is more sensitive towards large-scale differences between the images to be compared. This puts less impact on high resolution details. The complex-wavelet SSIM (CW-SSIM)76 was specifically designed to compensate for small rotations and spatial translations. For this metric, only the coefficients of the complex-wavelet transformed images I and R are used, such that small phase shifts between both images are ignored. This additional freedom may allow unnatural results, when CW-SSIM is used for model optimization35. As an adaption of SSIM to float valued images, the data range parameter L (see “Intensity ranges and data formats” section) is used to scale the internal constants 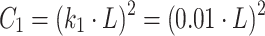 and
and 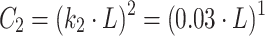 (and
(and  ), which are used to make computations numerically stable (see supplement Sect. A.3, Eq. (41)). It can be derived from the SSIM calculation, that a high data range parameter L and thereby high values for
), which are used to make computations numerically stable (see supplement Sect. A.3, Eq. (41)). It can be derived from the SSIM calculation, that a high data range parameter L and thereby high values for  , lead to SSIM values near 1, because the constants
, lead to SSIM values near 1, because the constants  dominate the calculation compared to the observed intensity values. In these cases, SSIM is not very informative. This has been experimentally observed before59, and a default normalization of float value ranged images to the range [0, 1] and a modification of constants
dominate the calculation compared to the observed intensity values. In these cases, SSIM is not very informative. This has been experimentally observed before59, and a default normalization of float value ranged images to the range [0, 1] and a modification of constants  to
to 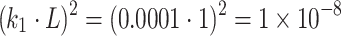 was proposed. Common implementations also define different default values for L. As the skimage71 package generally assumes float valued images to be in the range
was proposed. Common implementations also define different default values for L. As the skimage71 package generally assumes float valued images to be in the range  , its implementation of SSIM defines
, its implementation of SSIM defines 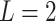 as default. The torchmetrics72 implementation of SSIM sets
as default. The torchmetrics72 implementation of SSIM sets  as default for images I and R.
as default for images I and R.
The choice for the data range parameter
L is directly related to normalization techniques that rescale image intensities: If images I and R are scaled by factor a to 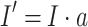 and
and  , then calculating SSIM on
, then calculating SSIM on  and
and 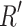 with
with  will be the same as calculating SSIM on I and R with L. However, if image intensities are additionally shifted by an additive value b, the luminance term will increase with b and yield different SSIM values. If this shift b is negative, as it typically is with Zscore normalization (see Supplementary Sect. A.2, Eq. (3)), this can lead to negative SSIM values58.
will be the same as calculating SSIM on I and R with L. However, if image intensities are additionally shifted by an additive value b, the luminance term will increase with b and yield different SSIM values. If this shift b is negative, as it typically is with Zscore normalization (see Supplementary Sect. A.2, Eq. (3)), this can lead to negative SSIM values58.
Peak signal-to-noise ratio
Peak signal-to-noise ratio (PSNR) was developed to measure the reconstruction quality of a lossy compressed image compared to the uncompressed reference image77. However, it is frequently used as a metric for assessing image similarity. The PSNR is infinite for identical images and decreases monotonically as the differences between image I and reference R increase. The data range parameter L is incorporated in the PSNR as the peak signal. The noise in the PSNR is calculated as the mean squared error (MSE, see “Error metrics” section). For natural images, improved variants of PSNR called PSNR-HVS and PSNR-HVS-M have been developed, that seem to correlate closer to the human visual system32. Adapted implementations for variable intensity ranges and experiments with medical images are not available at this time. A deeper exploration of these metrics remains important future work.
Error metrics
This group of metrics, including mean absolute error (MAE), mean square error (MSE), root mean square error (RMSE) and normalized mean square error (NMSE), directly depends on the absolute difference of intensity values at equal pixel locations. The metrics MSE, RMSE, and NMSE are based on the squared difference and due to convex shape of the quadratic function, these metrics give more weight to large differences than MAE, which is based on the unsquared absolute difference. By normalization with the standard deviation of the reference image, NMSE assigns a higher similarity to images with a higher standard deviation, i. e. with high variation and a large range of intensity values. On the contrary, the same intensity differences lead to a lower similarity, if the reference image has a very low standard deviation, i. e. it appears very homogeneous. However, the scale and range of all these metrics strongly depend on the intensity value ranges and, thereby, also on the normalization method.
Learned metrics: LPIPS and DISTS
Learned perceptual image patch similarity (LPIPS) relies on image feature maps from a trained image classification model. For the LPIPS metric, an Alex-Net or VGG-architecture backbone exist79. The VGG version of LPIPS was recommended for usage as a traditional perceptual loss, while the Alex-Net version should be preferred as a forward metric. The latter one is also faster at inference due to the smaller network, so we analyzed LPIPS with Alex-Net in “Experiments” section. Even though the networks were trained on RGB images, the trained networks expect an input range of  , e.g. by previous Minmax normalization. LPIPS has shown great correlation with human perception and outperforms many other similarity metrics on natural images while the type of employed architecture has only minor influence79. It has occasionally been used for validation of medical image synthesis95, and is commonly applied as perceptual loss for training medical image-to-image translation models3.
, e.g. by previous Minmax normalization. LPIPS has shown great correlation with human perception and outperforms many other similarity metrics on natural images while the type of employed architecture has only minor influence79. It has occasionally been used for validation of medical image synthesis95, and is commonly applied as perceptual loss for training medical image-to-image translation models3.
The Deep Image Structure and Texture Similarity (DISTS) metric is an adaption of LPIPS giving more focus on texture81.
Statistical dependency metrics: NMI and PCC
Mutual information (MI) estimates the amount of information of an image R, that can be predicted from image I. MI is widely used as an optimization criterion for multi-modal image registration96. It has been used sporadically as a metric for validation of image synthesis52,63. The NMI has a fixed value range of [1, 2], which is preferable for comparing absolute metric scores and interpretability. The Pearson correlation coefficient (PCC), is a statistical dependency metric which measures the degree of linear dependency between the intensities in I and R at each pixel location. As PCC is defined by correlation and NMI and MI both operate on normalized binned images, previous normalization that purely scales and shifts, such as Minmax, Zscore or Quantile normalization, does not have any effect on the resulting scores. The reference metrics investigated within this study are defined in detail in Supplementary Sect. A.3, an overview is shown in Table 2.
Indirect evaluation with downstream tasks
Another option for validation is to consider which tasks are going to be performed downstream from a synthesized image. Whenever one of these tasks is performed, the quality of synthetic images can also be assessed by measuring the performance of the specific task on the image compared to the performance of the reference image. In medical image-to-image translation, which aims for improved medical diagnosis or treatment, assessing the performance of medical diagnosis or treatment directly derived from digital images is very desirable. In this context, synthetic images must be processed in the same way as the reference image and should have equal outcomes in the downstream task. However, deviations between synthetic images and reference images can be accepted, when they have no impact on the downstream task. As an example, if a synthetic MR image is generated for detecting a brain tumor, it is to some extent irrelevant if healthy brain tissue in the synthetic image appears slightly different than in the true reference image, as long as it is clearly identified as the same type of healthy tissue. If a synthetic histology image is rated with the same grade of cancer as the reference image, the exact cell-wise correspondence might not be important. Many downstream tasks on medical images can be nowadays performed automatically, including:
Detection or segmentation of organs, cells and lesions, e.g. the Segmentation of brain tumors from T1-weighted native, T1-weighted contrast enhanced, T2-weighted, and fluid attenuation inversion recovery (FLAIR) MR images49 [Related downstream task metrics: DSC, Intersection over Union (IoU)].
Classification of images or image segments, e.g. the synthesis of clinical skin images with 26 types of conditions, verified by classification scores of dermatologists97 [Related downstream task metrics: Accuracy, Precision, Recall, F1-Score].
Transfer learning and data augmentation, e.g. the synthesis of chest X-ray for data augmentation and evaluation of classification model on real data with and without synthetic training data98 [Related downstream task metrics: e.g. Sensitivity, Specificity, Area Under the Receiver-Operator-Characteristic curve (AUROC)].
Multi-modal registration, e.g. the registration of synthesized MR image from CT image to MRI atlas instead of registration of CT image to MRI atlas99 [Related downstream task metrics: MSE, MI].
Dose calculation in radiation therapy planning, e.g. the synthesis of a planning CT from MRI for use in a radiation planning tool100 [Related downstream task metrics: relative difference of planned radiation dose].
Detection, segmentation and classification metrics for the biomedical domain have been well documented and discussed47,48. Also, a study of a segmentation metric systematically analyzed the sensitivity to relevant simulated distortions101. Therefore, the performance of such tasks with synthetic images can be well compared to the performance with reference images to validate the use of synthetic images for a specific task. The concept of downstream task evaluation metrics recognizes that the final goal of image synthesis in the medical domain is to generate useful and correct images rather than images, that are visually appealing102. However, if image synthesis was optimized regarding a certain downstream task, the resulting images might not be optimal for other non-related tasks. Specifically, they might have a fake appearance, that does not interfere with the downstream task, but would be misleading for direct review of medical practitioners. Furthermore, the evaluation of downstream tasks can substantially depend on the performance of the downstream task method. If a segmentation model fails on a large set of reference images, the comparison to segmentations on synthetic images is obsolete. The amount and variety of downstream tasks and corresponding metrics are almost unlimited, but to discuss and analyze the value of downstream tasks, we include the evaluation of a downstream segmentation model with a popular segmentation metric, namely the Dice Similarity Coefficient (DSC)47,103.
Non-reference quality metrics
Non-reference metrics, often also called quality metrics or blind metrics, try to assess the quality of a distorted image without knowing the undistorted reference. As a reference might not be available, these metrics can be applied in many evaluation settings. However, there is a huge amount of such metrics and most of them assume a certain kind of distortion to be detected. The correlation of many of these metrics with human perception has been investigated26. But also deviations between these scores and diagnostic quality perceived by radiologists have been observed104. Blurriness metrics were quite successful in detecting images with reduced quality as perceived by humans in different image domains.
In this paper, we select and present a set of quality metrics (see Table 2) that could complement reference metrics and detect especially those distortions, which reference metrics can miss. It has often been discussed5,105, that error metrics are not sensitive to blurring, which can be problematic because synthesis models may create blurry results. That is why we evaluated a set of blurriness metrics, that do not need a reference. Similar to the learned similarity metrics, also learned quality metrics have shown to provide useful quality scores for natural images91,93. Last, we assessed metrics, that detect MR acquisition artifacts89 or noise25.
Blurriness metrics
A large set of metrics has been developed to measure the sharpness or, inversely, the blurriness of images to filter out low-quality images. Methods assessing image blur operate either on the spatial domain, the spectral domain, e.g. through wavelet or fast Fourier transform. In addition, there are learned blur detection methods as well as combinations106. Blur assessment methods in the spatial domain, such as the Blur-Effect23 or the variance of the Laplacian (VL)83, can exploit local image gradients. Others rely on binary edge detection, with the drawback, that thresholds are needed to decide which pixel belongs to an edge and which one does not. Hence, thresholds need to be adapted for varying intensity value ranges. In general, spectral domain transforms are computationally more costly, so methods on the spatial domain tend to perform faster.
The mean blur (MB) and blur ratio (BR) metrics were jointly82 designed to assess blurriness and edges based on a ratio called inverse blurriness. A set of blurriness metrics has been derived from the concept of measuring blurred edge widths (BEW)84. This idea was extended with a notion of just noticeable blur (JNB)86, and evaluates the image in smaller blocks. A further blurriness metric measures the cumulative probability of blur detection (CPBD)88 extending the approach of JNB.
The incorporated just noticeable blur width is based on experiments with 8-bit integer valued images. Similarly the MB and BR metrics were designed for 8-bit integer valued images. Therefore, our implementation uses a data range parameter for adapting to larger intensity ranges. Further details of the implementations can be found in our published repository at www.github.com/bayer-group/mr-image-metrics.
MR quality metrics
In MR images, specific artifacts may appear, which are related to image acquisition and reconstruction. These artifacts may not only appear on real images, but could be reproduced in synthetic images, which is undesirable. Therefore, the use of MR specific quality metrics could efficiently improve validation of MR synthesis models. In order to select the preferred image from a repeated set of image acquisitions of the same patient, Schuppert et al.89, evaluated a set of image quality metrics. Mean line correlation (MLC, in89 denoted as “average structural noise”) and mean shifted line correlation (MSLC, in89 denoted as “average nyquist ghosting”) were revealed to be among the best metrics to predict which image was preferred among repeated acquisitions. Possibly, these metrics are able to detect common MR acquisition artifacts, such as ghosting or motion artifacts, that would lead to repeated acquisitions. The MLC metric is defined as the mean correlation between neighboring lines of pixels in an image. The MSLC metric is defined as the mean correlation between image lines, that are separated by half of the image width or height respectively.
Learned quality metrics
Similar to learned reference metrics, also non-reference metrics have been developed from learned image features. The blind/ reference-less image spatial quality evaluator BRISQUE91 leverages 18 spatial image features extracted from distorted training images of the LIVE database34 annotated with a quality score. A simple support vector machine regression model was trained to predict the annotated quality scores from the extracted set of features.
The natural image quality evaluator (NIQE)93 does not rely on training with annotated images. Instead, a multi-variate Gaussian model is parameterized from the same set of 18 spatial features, but extracted from two scales. A reference model was parameterized from features from a training set of undistorted images to obtain the multivariate Gaussian model. Images were selected from copyright free Flickr data and from the Berkeley image segmentation database107. The NIQE metric assesses the distance of fitted test image parameters to the parameters of the reference model. Due to the characteristics of the training set and assumed differences to MR images regarding intensity value distributions, the NIQE metric may not be directly transferable to MR images.
Noise metrics
For denoising of images, total variation25 has been used as a criterion for noisiness. Therefore, mean total variation seems promising as a measure of undesired noise.
Because noise can be reduced by blurring, blurriness metrics might act as inverse noisiness metrics. In other words, an increasing degree of blurriness may correlate with decreasing noise. Inversely, adding noise may disguise blurriness and therefore impair blurriness metrics for image quality assessment.
The non-reference metrics investigated within this study are defined in detail in Supplementary Sect. A.3, an overview is shown in Table 2.
Experiments
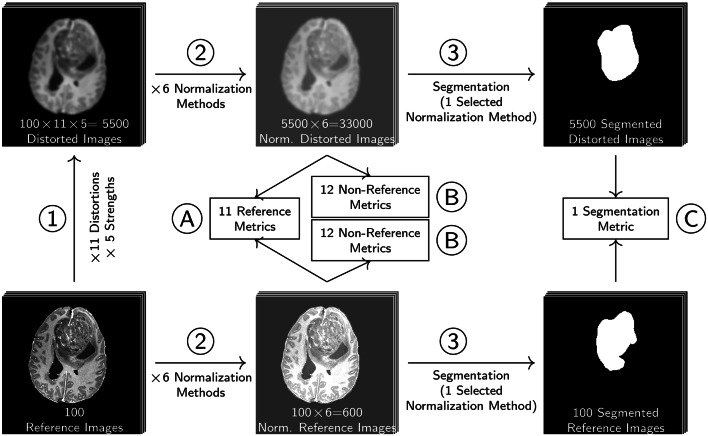
In order to systematically investigate reference and non-reference metrics, we distorted 100 T1-weighted contrast enhanced MR images with 11 different types of distortions in five strengths. For the reference metrics (see “Reference metrics” section), the similarity between each distorted image and its undistorted reference was calculated. For the non-reference metrics (see “Non-reference quality metrics” section), the metric scores for all distorted and undistorted images were assessed. For the segmentation metric (see “Indirect evaluation with downstream tasks” section), we trained a model and predicted segmentations for all distorted and undistorted images. The segmentation metric assessed the agreement between segmentations derived from distorted images and segmentations derived from the respective undistorted reference image. In addition, images individually normalized with one of six different normalization methods, including no normalization, leaving the images with raw intensity values. The workflow of the experiments is illustrated in Fig. 2. In image-to-image tasks, MR source or target images are typically normalized for model training and the synthesized images are generated in this normalized space. Validation of synthesized images can either be performed in this normalized space, such that the normalized target image is used as reference and the synthesized image is assumed to already be normalized appropriately. Another possibility is to invert the previously performed normalization method on the synthesized image to the original intensity range. Then the synthesized image can be compared to the target image in the original intensity range. In our experiments, we test the metrics in the original and a normalized intensity range. As some distortions slightly or more drastically extend or reduce the intensity range of the reference image, different normalization methods result in different alignment of histograms of the reference and the distorted images. The LPIPS metric requires an input range of [− 1 and 1], therefore we decided to apply Minmax and cMinmax normalization to the required target range of 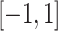 . The DISTS metric requires an input range of [0, 1]. Even though all normalization methods besides Minmax and cMinmax do not satisfy the required input ranges, we did evaluate the metrics after these normalization methods to investigate deviations to the recommended type of normalization.
. The DISTS metric requires an input range of [0, 1]. Even though all normalization methods besides Minmax and cMinmax do not satisfy the required input ranges, we did evaluate the metrics after these normalization methods to investigate deviations to the recommended type of normalization.
Fig. 2.
Workflow of experiments. (1) 100 reference images were distorted with one of 11 distortions (see “Distortions” section) with one of five strengths. (2) The distorted images and the reference images were individually normalized with one of six normalization methods (see “Normalization methods” section), including no normalization and omitting piece-wise linear (PL) normalization, which depends on a reference dataset. (A) Reference and (B) non-Reference metric scores were obtained from normalized distorted images and normalized reference images. (3) The segmentation model was applied to one normalization method only, because the fully automatic segmentation setup integrated all preprocessing steps, including Zscore normalization.
This experimental setup allows to qualitatively derive the sensitivity of each analyzed metrics to each of the tested distortion types. Assuming that different distortions applied with the same strength should receive the same similarity or quality score, deviations of metric scores between different distortions of the same strengths can be interpreted as strong or weak sensitivity to certain distortions.
Data
We selected the first 100 cases of the Brain Synthesis (BraSyn) 2023 Challenge, available at www.synapse.org/brats2023108–110. We further selected only T1-weighted contrast-enhanced (T1c) images. The images all show human brains with glioma tumors. The provided data has already been preprocessed including skull-stripping (removal of the skull), background voxel intensities are set to 0, resampling to a unit mm voxel spacing, registration to a centered brain atlas. For better visualization and reduced computation time, we extracted the centered 2D slice of each 3D volume with a size of 240 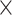 240 pixels.
240 pixels.
Segmentation model for downstream task
We trained an automatically configuring U-Net based segmentation network111 on the T1c images of the BraSyn dataset train split. The prediction of three classes (1: whole tumor, 2: tumor core, 3: enhancing tumor) was optimized for 300 epochs, using 1 fold and with a DICE cross entropy loss and deep supervision. The model was selected by the best validation score at epoch 323. The architecture of the U-Net included five residual blocks, with downsampling factors 1, 2, 2, 4 and 4, initially 32 features and one output channel activated by a sigmoid function per class, resulting in approx. 29 million parameters. The model was trained to segment all three annotated tumor classes. As a preprocessing step for training and inference, Zscore normalization was applied to the input images. Therefore, no other normalization methods were tested. For evaluation of the DSC metric (see Supplementary Sect. A.3, Eq. (18)), we infered the model on all reference and all distorted images.
Distortions
We selected a wide range of distortions, which we expect to appear with MR image synthesis. The parameters of all distortions were scaled to five increasing strengths, where a strength of one should be a minimal distortion, which is not immediately visible and five a strongly visible distortion, which clearly impedes any diagnosis. We initially scaled the distortion parameters to comparable strengths by a reader study with six experienced researchers (see Supplementary Sect. A5). The final parameters for each distortion are listed in Supplementary Sect. A.4. Examples for minimum (strength = 1) and maximum (strength = 5) distortions are shown in Fig. 3.
Fig. 3.
Examples of distorted images for lowest strength  , up to the maximal distortion strength
, up to the maximal distortion strength 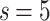 . For
. For 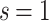 , the distortions are hardly visible and therefore the images appear all the same. All distorted images are displayed with the same intensity range as the reference image, i.e. the range was clipped in case of higher or lower values. The change in the image distorted by ghosting is highlighted by a green arrow. Further examples of distorted images are provided in the Supplementary Figs. S.2–S.7.
, the distortions are hardly visible and therefore the images appear all the same. All distorted images are displayed with the same intensity range as the reference image, i.e. the range was clipped in case of higher or lower values. The change in the image distorted by ghosting is highlighted by a green arrow. Further examples of distorted images are provided in the Supplementary Figs. S.2–S.7.
Among the selected distortions, Translation and Elastic Deformation were applied as spatial transforms, that are commonly found, when the reference is not well aligned to the image to be tested. This is frequently the case in image-to-image translation, when the input image was acquired with a different modality or at a different time point. Usually, the patient has moved in between and registration was possibly not sufficient. Translation was modeled as an equal shift of all pixels along the x and y-axis and parameterized with a fraction of the image width and height. Elastic deformation was modeled by placing a grid with a given number of points on the image, randomly displacing grid points, and linearly interpolating between the new point positions. The displacements were sampled from a normal distribution with increasing parameter 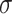 and the number of points was reduced for higher distortion strengths.
and the number of points was reduced for higher distortion strengths.
Intensity distortions, that shift, stretch or compress the histogram, such as gamma transforms or an intensity shift, can appear between different scanning parameters, because MR does not guarantee a fixed intensity scale. For gamma transforms, images are first normalized by Minmax to range [0, 1]. This ensures, that the intensity value range is unchanged under gamma transformation, which is simply potentiating with a parameter 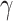 . Then, the intensities are scaled back to the original intensity range. We call gamma transforms for
. Then, the intensities are scaled back to the original intensity range. We call gamma transforms for 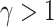 denominated Gamma High, while those with
denominated Gamma High, while those with 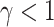 are named Gamma Low. Both types of distortions are parameterized with increasing or decreasing values of
are named Gamma Low. Both types of distortions are parameterized with increasing or decreasing values of  respectively for increasing distortion strengths. Intensity shifts are modeled by adding a fraction of the maximum intensity range to the intensity value of all pixels.
respectively for increasing distortion strengths. Intensity shifts are modeled by adding a fraction of the maximum intensity range to the intensity value of all pixels.
Further distortions, that represent typical acquisition artifacts of MR images are ghosting, stripe and bias field artifacts. Ghosting artifacts appear as shifted copies of the image, arising from erroneous sampling in the frequency space. Scaling a single pixel with an intensity parameter in the frequency space causes artificial Stripe Artifacts. Bias fields appear as low frequency background signals, that we model by multiplying with an exponential of a polynomial function of degree three (see Supplementary Sect. A.4 Eq. (45)). All of these MR acquisition distortions may moderately expand the intensity range of the distorted image compared to the reference image.
Gaussian noise or Gaussian blurring are not restricted to MR acquisition but, as in most imaging modalities, they are frequently observed and were also analyzed in our study. Gaussian noise adds intensity values randomly sampled from a normal distribution with 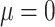 and increasing
and increasing  to each pixel intensity. Gaussian blur convolves the reference image with a Gaussian filter with increasing
to each pixel intensity. Gaussian blur convolves the reference image with a Gaussian filter with increasing 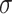 .
.
Last, we investigate the effect of Replace Artifacts, where parts of the image content are replaced, in this case by mirrored regions. In the BraSyn data set, in most cases, there is a tumor in exactly one hemisphere of the brain. By mirroring one hemisphere onto the other one, a second tumor is inserted into, or a tumor is removed from the second hemisphere. We scaled this distortion by mirroring an increasing fraction of the hemisphere. Replacing brain structures in one hemisphere by structure in the other one, simulates the generation of synthetic structures, that were not in the input image. This is a known problem of some synthesis models, e. g. of cycleGAN architectures112. The detection of such synthetically inserted structures is highly desired for image-to-image translation model validation.
Results
Reference metrics
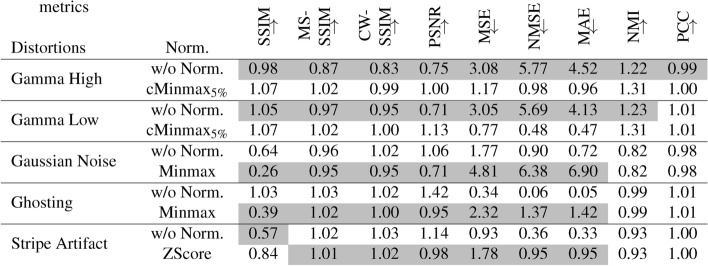
The complete results for all reference metrics, all distortion strengths and all normalization methods are contained in the Supplementary Figs. S.8–S.10. There, for each metric and normalization method, the trends of all distortions for increasing strengths are shown. The selected and compressed results in Table 3, contain the median metric values over all strengths and images for one selected and recommended normalization method. For LPIPS and DISTS, images we show results for Minmax normalization to range 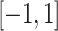 and [0, 1] respectively as recommended by the authors of the used implementations. For DSC, Zscore normalization was part of the segmentation process. For all other metrics, we show results without normalization as these seem representative and we were not aware of any recommended normalization method. Table 3 only contains the DSC on the foreground (union of all three tumor classes), as the DSC segmentation scores for all three classes are very similar (see Supplementary Fig. S.15). In the performed experiments, dependencies between distortions of different strengths and metric scores can be observed. The majority of metrics indicate decreasing similarity or decreasing quality for increasing distortion strengths. This can be described as sensitivity of a metric to a distortion or an effect of a distortion to a metric. Specifically, stronger changes of metrics scores observed for one distortion, compared to other distortions can be interpreted as a higher sensitivity of the metric or a stronger effect of the distortion to this metric. The results are described in the following, ordered by distortions.
and [0, 1] respectively as recommended by the authors of the used implementations. For DSC, Zscore normalization was part of the segmentation process. For all other metrics, we show results without normalization as these seem representative and we were not aware of any recommended normalization method. Table 3 only contains the DSC on the foreground (union of all three tumor classes), as the DSC segmentation scores for all three classes are very similar (see Supplementary Fig. S.15). In the performed experiments, dependencies between distortions of different strengths and metric scores can be observed. The majority of metrics indicate decreasing similarity or decreasing quality for increasing distortion strengths. This can be described as sensitivity of a metric to a distortion or an effect of a distortion to a metric. Specifically, stronger changes of metrics scores observed for one distortion, compared to other distortions can be interpreted as a higher sensitivity of the metric or a stronger effect of the distortion to this metric. The results are described in the following, ordered by distortions.
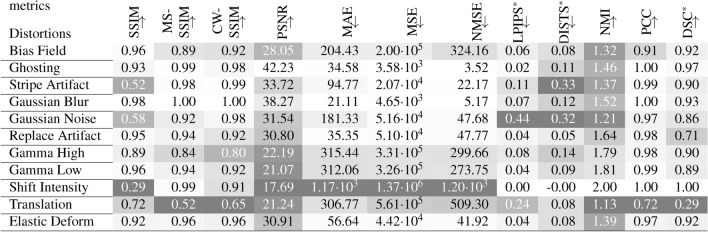
Table 3.
Median reference metric values for each distortion evaluated on 100 images and all distortions strength.All reference metric scores shown here were assessed on images without normalization, except LPIPS*, DISTS* and DSC*. The darker the background the higher the sensitivity of the metric to the respective distortion compared to all other distortions. The arrows indicate, if the metric increases (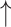 ) or decreases (
) or decreases ( ) with higher similarity.
) with higher similarity. 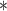 : For LPIPS Minmax normalization to [− 1, 1] was used, for DISTS Minmax normalization to [0, 1] was applied and DSC was assessed after Zscore normalization and segmentation. Results for all normalization methods can be found in Supplementary Figs. S.8–S.15.
: For LPIPS Minmax normalization to [− 1, 1] was used, for DISTS Minmax normalization to [0, 1] was applied and DSC was assessed after Zscore normalization and segmentation. Results for all normalization methods can be found in Supplementary Figs. S.8–S.15.
Bias Field has a moderate effect on most metrics. MS-SSIM is much more sensitive to simulated bias field artifacts than simple SSIM or CW-SSIM. The error metrics show clearly increased (dissimilarity) scores, while the LPIPS score is hardly effected. Compared to other distortions, PCC drops noticeably with bias field distortions. Ghosting generally has a weak effect on most metrics, except on NMI and DISTS. Stripe Artifacts strongly influence a subset of metrics, including SSIM, LPIPS, DISTS and NMI, while most other metrics are not sensitive to this type of distortion. Blurring is hardly accounted for by most metrics, the strongest changes can be observed by the DISTS and NMI metrics. Regarding Gaussian Noise, SSIM is very sensitive, while MS-SSIM and CW-SSIM are not. The effect on error metrics is limited, while both learned metrics and NMI clearly indicate dissimilarity. Replace Artifacts are hardly detected by most metrics. Besides DSC, which aligns well with the distortion strength, PSNR and NMI are most sensitive. Gamma transforms with an increasing 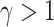 (Gamma High) or a decreasing
(Gamma High) or a decreasing  (Gamma Low) similarly influence all metrics. All of them, except PSNR, assess the distortions with
(Gamma Low) similarly influence all metrics. All of them, except PSNR, assess the distortions with 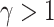 as stronger. Regarding constant Intensity Shifts, NMI and PCC are invariant. Their scores reflect perfect similarity. The same holds, when the images are normalized by any of the five normalization methods (see Supplementary Figs. S.8–S.15). Particularly for LPIPS and DISTS, Minmax normalization is recommended as standard. For all other metrics, except MS-SSIM and CW-SSIM, intensity shifts substantially decrease similarity. Translation strongly reduces the assessed similarity for all metrics besides DISTS. Even very small translations of strength
as stronger. Regarding constant Intensity Shifts, NMI and PCC are invariant. Their scores reflect perfect similarity. The same holds, when the images are normalized by any of the five normalization methods (see Supplementary Figs. S.8–S.15). Particularly for LPIPS and DISTS, Minmax normalization is recommended as standard. For all other metrics, except MS-SSIM and CW-SSIM, intensity shifts substantially decrease similarity. Translation strongly reduces the assessed similarity for all metrics besides DISTS. Even very small translations of strength  , which corresponds to a 1% shift (2.4 pixels in our experiments), are clearly noticeable, as shown in Supplementary Sect. B.1. Only CW-SSIM is quite insensitive with respect to small translations, but is still very sensitive, when translation is strong. Compared to translation, Elastic Deforms only influence similarity metrics decently. Even stronger deformations have less impact on the metric scores, than the weakest translation does.
, which corresponds to a 1% shift (2.4 pixels in our experiments), are clearly noticeable, as shown in Supplementary Sect. B.1. Only CW-SSIM is quite insensitive with respect to small translations, but is still very sensitive, when translation is strong. Compared to translation, Elastic Deforms only influence similarity metrics decently. Even stronger deformations have less impact on the metric scores, than the weakest translation does.
There are some coherent observations regarding the normalization method and certain types of distortions. Selected results are shown in Table 4. 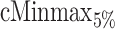 normalization reduces gamma transforms, such that most metrics are less sensitive to gamma transforms after
normalization reduces gamma transforms, such that most metrics are less sensitive to gamma transforms after 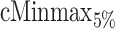 normalization, compared to their standard normalization method. Minmax normalization amplifies Gaussian noise, Zscore normalization amplifies stripe artifacts.
normalization, compared to their standard normalization method. Minmax normalization amplifies Gaussian noise, Zscore normalization amplifies stripe artifacts.
Table 4.
Comparison of relative metric scores for selected distortions for comparison of normalization methods. As a relative metric score, the median of one selected distortion is divided by the median metric score of all distortions. The gray background indicates higher sensitivity in the comparison of two normalization methods. LPIPS, DISTS and DSC metric are not shown, due to fixed recommendations regarding the normalization method. Normalization methods and distortions were selected, where the similarity uniformly changed for between two normalization methods within one type of distortion and for all reference metrics. The arrows indicate, if the metrics metric increases ( ) or decreases (
) or decreases ( ) with increasing similarity.
) with increasing similarity.
Gaussian noise and stripe artifacts most strongly decrease the DSC. Translated segmentations have decreasing overlap and thereby very low DSC. Tumors, which were inserted or removed by the Replace Reflect distortion are well indicated by decreasing DSC.
Non-reference metrics
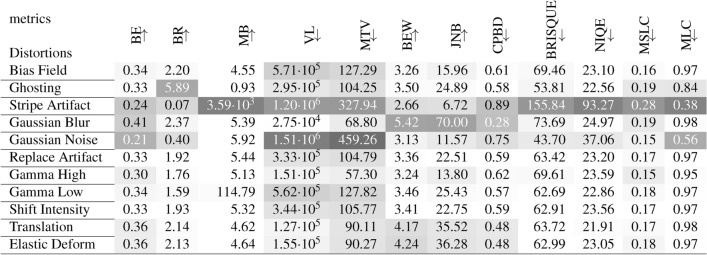
The results for all non-reference metrics, all distortion strengths and all normalization methods are given in Supplementary Figs. S.11–S.14. The median metric scores are summarized in Table 5 for images, that were normalized by Binning, as most of the metrics were designed for 8-bit images. This assures, that the metrics are most likely used as intended and sensitivity to a type of distortion is expected to be more consistent. Large differences between normalization methods are found for MB, BR and NIQE. We describe the results ordered by quality metric groups.
Table 5.
Median non-reference metric values for each distortion over 100 images. All non-reference metrics were assessed with binning normalization, which best resembles the intended use on 8-bit integer valued images for which most of these metrics were developed. Results for all normalization methods can be found in Supplementary Figs. S.11–S.14. The darker the background the higher the difference to the median metric value of the reference images. The arrows indicate, if the metric increases ( ) or decreases (
) or decreases ( with image quality.
with image quality.
All Blurriness and Noisiness Metrics, except MB, can distinguish well between different strengths of blurring. At the same time, the blurriness scores diverge in the opposite direction for increasing strengths of stripe artifacts and Gaussian noise. Only BEW scores are not influenced much by these distortions. All blurriness and noisiness metrics show coherent deviations for images with spatial Translation (see also Supplementary Figs. S.12–S.13). MR Quality Metrics, i.e. MLC and MSLC, clearly identify stripe artifacts. MLC is very sensitive to noise, but generally hardly reflects the distortion level. MSLC can identify ghosting, best with  normalization (see also Supplementary Fig. S.13). The Learned Quality Metrics BRISQUE and NIQE clearly attest low quality to images with stripe artifacts. However, the BRISQUE score indicates higher quality for very weak stripe artifacts and for images with Gaussian noise or ghosting (see also Supplementary Fig. S.14). The NIQE score indicates lower quality for Gaussian noise.
normalization (see also Supplementary Fig. S.13). The Learned Quality Metrics BRISQUE and NIQE clearly attest low quality to images with stripe artifacts. However, the BRISQUE score indicates higher quality for very weak stripe artifacts and for images with Gaussian noise or ghosting (see also Supplementary Fig. S.14). The NIQE score indicates lower quality for Gaussian noise.
Discussion
The experiments demonstrate specific weaknesses of the popular SSIM and PSNR metrics. They are strongly decreased by constant intensity shifts if no normalization is applied. PSNR is very dependent on the kind of normalization, which complicates its use as a comprehensive metric for comparing studies of different authors. This has been pointed out before63, but the normalization parameters are still not reported in many papers about medical synthesis models58. SSIM and PSNR underestimate blurring and thereby favor blurred images over differently distorted images. This is inline with reported findings of previous studies57,113. SSIM and PSNR are both very sensitive to spatial translation, which is a frequently occurring issue in paired image-to-image translation. The source image and the reference image may not acquired by the same hardware or not immediately at the same time points and therefore the patient may not have the same location in both images. The proper use of the data range parameter of SSIM for medical images and potential biases have been investigated58, suggesting to use the dataset minimum and maximum values. In existing implementations of SSIM or PSNR, the default data range parameter might not be appropriate. For SSIM, although commonly applied on Zscore normalized MR images, a bias was demonstrated58 with negative values, which we did not specifically investigate. Even though the generation of synthetic structures is an issue in image-to-image translation112, highly relevant replace artifacts are not sufficiently assessed by SSIM and PSNR. Unexpected behaviour of SSIM and PSNR as mentioned above was illustrated by examples114.
So how can these weaknesses be overcome? CW-SSIM is able to ignore small translations, due to calculation in the complex-wavelet domain. The DISTS metric also successfully focuses more on texture than spatial alignment. Precise registration would also strongly improve similarity assessment. However, interpolation may introduce blurring as shown by coherent variations of assessed quality by all non-reference quality metrics on spatially translated images. Our experiments also suggest, that a few strong local elastic deformations have a lot less impact on similarity metrics than rigid translations. At the same time, rigid registration is easier to solve via optimization than elastic registration, because only a few parameters need to be determined.
Replace artifacts remain underestimated by most similarity metrics. For those artifacts, that resemble structures of diagnostic interest, the evaluation of segmentations with a specific segmentation model is useful. In our evaluation, we use a segmentation model, that was trained to detect different tumor regions. It successfully detects replace artifacts, where the tumor is doubled or removed. In this study, we did not perform further stability tests of the segmentation model. The DSC scores evaluated on the segmented images generally very well represent the expected differences between the reference and its distorted versions and manual inspection of selected segmentations did not uncover any obvious segmentation failures.
The non-reference quality metrics can give valuable additional information about the quality of synthesized images. Blurring is easily and reliably detected by all blurriness metrics. For most metrics, assessed blurriness also decreases with other distortions, such as Gaussian noise, ghosting or gamma transforms, when these increase image contrast.
For assessing ghosting, the MR quality metrics MLC and MSLC were evaluated. The MLC metric represents the line-wise correlation between neighboring lines. The reference value in our experiments lies at 96%, which is probably caused by high anatomical consistency in the present pixel spacing. It strongly decreases for stripe artifacts, which fits to the fact, that the stripes change relations between local image intensities and are not oriented along the x- or y-axis. Random Gaussian noise reduces statistical correlation and thereby also MLC. Ghosting also reduces MLC, as it additionally distorts image intensities locally. The MSLC metric only slightly increases with ghosting, a bit more using cMinmax normalization. One reason could be the relative weak scaling of the ghost intensity in our experiments. In contrast, stripe artifacts significantly increased the MSLC metrics. Compared to MLC, by coincidence, stripes seem to be in the same phase at the half-image width distance and thereby drastically increase line-wise correlation.
Although the result tables for reference metrics (Table 3) and for non-reference metrics (Table 5) show absolute metric scores with and without normalization, both are representative for all results. In our experiments, reference images and distorted images had similar intensity ranges. Of course, MSE, MAE and NMSE yield much larger values without normalization, but by filling the background of the result tables with different shades of gray we emphasize the relative sensitivity of the metrics, and we found that the relative sensitivity is very similar between all normalizations for all metrics, with three exceptions: (1) Intensity shift is fully removed by any normalization leading to perfect similarity or equal quality to the reference. (2) BR, MB and NIQE display large differences between normalization methods and do not seem to measure blurriness or quality as intended when applied on non-8-bit integer valued images, which could be a problem of the adapted implementation, but also a problem of metric design. For all other non-reference metrics, the relative sensitivity does not seem to change with normalization. (3) We highlighted all uniform effects of normalization methods to reference metrics in Table 4, where we observe that certain normalization methods amplify or mitigate certain distortions. Gaussian noise and Ghosting, which extend the intensity value range compared to the reference image, are amplified by Minmax normalization, because the extended intensity value range is more strongly compressed. Stripe artifacts shift image mean values and therefore Zscore normalization creates shifts between originally corresponding intensity values. Gamma transforms, that compress intensity values at very high and low values are mitigated by cMinMax normalization, as this stretches intensities apart again. Therefore, normalization methods can be used to improve similarity or quality of images. Further distortions could be reduced by other methods, e.g. Bias field correction115, which was designed to remove bias field artifacts.
Our experiments were performed on T1-weighted contrast-enhanced MR images of the human brain and are therefore restricted to the BraSyn dataset. Future work should include a much broader set of MR images with other sequences and body regions to make sure, that the results are valid more generally. However, we assume, that the results are transferable to most MR sequences, because the characteristics, that are critical for metric assessment, are equally present (large value range, non-quantitative measurement, types of artifacts). The background in the BraSyn dataset takes up a large fraction of the image and was specifically preprocessed and set to 0. These factors largely influence some of the metrics, especially SSIM, PSNR and the error based metrics and therefore other data could yield different experimental results. We expect that using masks with these metrics will change absolute metric scores, but relative observations probably persist. However, the application of masks with metrics, that do not assess similarity or quality on a per-pixel basis, but require a neighborhood, is still to be implemented as future work. For the segmentation related DSC, taking different sub-regions into account, is already being explored101. Furthermore, we did not investigate differences between a slice-wise 2D and a 3D application of the selected metrics. This should be considered specifically for MR images, and has already been reported to have significant impact58.
The distortions analyzed in this study are to different degrees realistic. Ghosting116, Stripe artifacts117 and Bias field118 were performed by simulation methods based on MR physics. Other distortions are perhaps less realistic, but account for important problems when acquiring and processing MR images. While other studies35,37 collected real image outputs of image synthesis models, we applied well-defined distortions in an isolated manner. This allows to better distinguish sensitivity of metrics between different distortions and to better understand specific metric properties.
In comparison to other metric benchmarks32,34, we do not compare the metric scores to human quality assessment. For each type of distortion, we tried to select five comparable strengths. As shown in Fig. 3, the lowest and highest strengths were scaled to appear almost not visible or to decrease quality to an equally poor level. Even though distortion parameters might not be scaled perfectly to human perception, we assume, that the overall qualitative observations about which metrics are most sensitive towards which kind of distortions and the following conclusions are still valid.
We are aware, that absolute values of different metrics cannot be directly compared, because most metrics relate non-linearly to human perception32,34. Therefore, rank correlation is often utilized to compare different metrics. However, we provide absolute scores, which better display how far apart they are for single distortions. At the same time, we consider the ranking of different distortion types for each metric to derive the sensitivity. For the observation of different dynamics with distortion strengths we refer the reader to the Supplementary Figs. S.8–S.15.
After LPIPS, a huge amount of deep-learning based reference and non-reference methods, among them PieApp119, MetaIQA120, P2P-BM121, HyperIQA122 and AHIQ123, has been proposed in the recent years, which were able to further improve performance on quality benchmark datasets such as LIVE and TID2013. The number of methods is increasing incredibly fast, and not all methods could be included in this study. This also holds true for a further number of more established metrics, such as FSIM124, VIF125 and IW-SSIM126, that were not included. We especially focused on methods that have been applied to the medical domain more frequently52. The investigation of further methods and their applicability to the medical domain remains further work.
Conclusions
For the validation of medical image-to-image translation, we gave a broad overview of possible metrics. For 11 reference, 12 non-reference metrics and a segmentation metric, we presented a detailed study of their sensitivity to 11 types of distortions, which are specific for MR images. As a conclusion, we give a few recommendations for the selection and application of appropriate validation metrics.
There is no optimal metric. Depending on the application, sensitivity to specific distortions is desired or not. Usually, a combination of metrics should be chosen, considering all expected distortions of the application. As reference metrics, the combination of SSIM, LPIPS, MSE and NMI is able to detect a large set of undesired distortions. MS-SSIM, PCC, DISTS, NMSE, and MAE do not give much additional information. MSE is the most frequently used error metric and therefore best suited for comparison to previous studies. In general, the use of PSNR should not be recommended. CW-SSIM is appropriate in addition to ignore slight misalignments to reference images.
MB, BR and NIQE do not yield consistent quality scores for increasing distortion strengths and dramatically deviate for different intensity value ranges. They cannot be recommended for medical images.
For detecting blurriness, BE and BEW and CPBD perform very robustly. When images are noisy or show stripe artifacts, BEW is hardly influenced. MB, BR and NIQE do not yield consistent quality scores for increasing distortion strengths and dramatically differ for different normalization methods. They cannot be recommended.
Of all tested non-reference metrics, MLC and MSLC are best able to indicate ghosting artifacts.
If normalization was used before metric assessment, the method and all relevant parameters must be reported in detail. These parameters must be considered, when comparing scores across studies, because normalization parameters can have a significant effect on absolute metric values.
The data range parameter L is commonly used to adapt metrics, that were originally designed for a fixed 8-bit value range, to float valued images with potentially infinite intensity value ranges. However, scaling or binning to the range (0, 255) is often more consistent with the original design due to internal constants (e.g. SSIM) and thresholds (e.g. JNB). For reference metrics, the data range should be derived at least from both images if not from the whole dataset.
For NMI and PCC, a data range parameter L is not needed and normalization can be omitted, if similar intensity values represent similar tissue types. Otherwise, an appropriate normalization method should aim for mapping similar tissue types to similar intensity values.
If source images and target images are not spatially aligned, they must be registered with highest possible precision before evaluating with reference metrics. Rigid translation reduces assessed similarity more substantially than small local elastic deformations. CW-SSIM is robust against small translations. The type of interpolation used for registration may additionally blur the images. For LPIPS and DISTS, Minmax normalization to [0, 1] and [− 1,1] is recommended. For non-quantitative image modalities such as MR, any kind of normalization is always recommended.”
A segmentation downstream task is extremely useful for evaluation, because small but relevant structures are assessed. The performance of the segmentation model must be verified before using the segmentations for similarity assessment.
In summary, the metrics for evaluation of image-to-image MR synthesis models must be selected carefully. Frequently used SSIM and PSNR cover a large range of distortions, but have specific weaknesses, that must be covered by other metrics. Specifically PSNR does not seem appropriate for the evaluation of synthetic images. We suggest to always select metrics, that are able to detect undesired distortions specific and typical for the desired application and that are insensitive towards admitted and expected distortions. Which metrics are most appropriate can be directly derived from our experimental relative metric scores. As metrics are also often used as loss functions for model training35 or validation metrics for model selection, the choice of appropriate metrics can directly improve image synthesis models before clinical validation by human readers and thereby reduce development time and costs.
Supplementary Information
Acknowledgements
The authors like to thank the Bayer team of the AI Innovation Platform for providing compute infrastructure and technical support.
Author contributions
M.D. and M.L. designed the study, M.D. performed the experiments, and analysed the results. All authors reviewed and contributed to the manuscript.
Data availability
The BraSyn 2023 dataset is available at www.synapse.org/brats2023. The code for all metrics and distortions is available at www.github.com/bayer-group/mr-image-metrics.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-025-87358-0.
References
- 1.Saharia, C. et al. Palette: Image-to-image diffusion models. In ACM SIGGRAPH 2022 Conference Proceedings, SIGGRAPH’22 (Association for Computing Machinery, 2022). 10.1145/3528233.3530757.
- 2.Isola, P., Zhu, J.-Y., Zhou, T. & Efros, A. A. Image-to-image translation with conditional adversarial networks. In 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 5967–5976 (2017). 10.1109/CVPR.2017.632.
- 3.Yi, X., Walia, E. & Babyn, P. Generative adversarial network in medical imaging: A review. Med. Image Anal.58, 101552. 10.1016/j.media.2019.101552 (2019). [DOI] [PubMed] [Google Scholar]
- 4.Ho, J., Jain, A. & Abbeel, P. Denoising diffusion probabilistic models. In Advances in Neural Information Processing Systems Vol. 33 (eds Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M. & Lin, H.), 6840–6851 (Curran Associates, Inc., 2020).
- 5.Müller-Franzes, G. et al. A multimodal comparison of latent denoising diffusion probabilistic models and generative adversarial networks for medical image synthesis. Sci. Rep.13, 12098 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kebaili, A., Lapuyade-Lahorgue, J. & Ruan, S. Deep learning approaches for data augmentation in medical imaging: A review. J. Imaging9, 81. 10.3390/jimaging9040081 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kaji, S. & Kida, S. Overview of image-to-image translation by use of deep neural networks: Denoising, super-resolution, modality conversion, and reconstruction in medical imaging. Radiol. Phys. Technol.12, 235–248 (2019). [DOI] [PubMed] [Google Scholar]
- 8.Zhu, J.-Y., Park, T., Isola, P. & Efros, A. A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In 2017 IEEE International Conference on Computer Vision (ICCV) 2242–2251 (2017). 10.1109/ICCV.2017.244.
- 9.Hong, K.-T. et al. Lumbar spine computed tomography to magnetic resonance imaging synthesis using generative adversarial network: Visual Turing test. Diagnostics12(2), 530 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bahrami, A., Karimian, A. & Arabi, H. Comparison of different deep learning architectures for synthetic CT generation from MR images. Phys. Medica90, 99–107. 10.1016/j.ejmp.2021.09.006 (2021). [DOI] [PubMed] [Google Scholar]
- 11.Zhu, L. et al. Make-a-volume: Leveraging latent diffusion models for cross-modality 3d brain MRI synthesis. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2023 (eds Greenspan, H. et al.) 592–601 (Springer, 2023).
- 12.Ben-Cohen, A., Klang, E., Raskin, S. P., Amitai, M. M. & Greenspan, H. Virtual pet images from CT data using deep convolutional networks: Initial results. In Simulation and Synthesis in Medical Imaging (eds Tsaftaris, S. A., Gooya, A., Frangi, A. F. & Prince, J. L.) 49–57 (Springer, 2017).
- 13.Li, Q. et al. Eliminating CT radiation for clinical pet examination using deep learning. Eur. J. Radiol.154, 110422 (2022). [DOI] [PubMed] [Google Scholar]
- 14.Ammari, S. et al. Can deep learning replace gadolinium in neuro-oncology?: A reader study. Investig. Radiol.57, 99–107 (2022). [DOI] [PubMed] [Google Scholar]
- 15.Baltruschat, I. M., Kreis, F., Hoelscher, A., Dohmen, M. & Lenga, M. fRegGAN with k-space loss regularization for medical image translation (2023). https://arxiv.org/abs/2303.15938.
- 16.Weigert, M. et al. Content-aware image restoration: Pushing the limits of fluorescence microscopy. Nat. Methods15, 1090–1097 (2018). [DOI] [PubMed] [Google Scholar]
- 17.Lu, J., Öfverstedt, J., Lindblad, J. & Sladoje, N. Is image-to-image translation the panacea for multimodal image registration? A comparative study. PLoS ONE17, 1–33. 10.1371/journal.pone.0276196 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Raut, P., Baldini, G., Schöneck, M. & Caldeira, L. Using a generative adversarial network to generate synthetic MRI images for multi-class automatic segmentation of brain tumors. Front. Radiol.3, 1336902. 10.3389/fradi.2023.1336902 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sharma, A. & Hamarneh, G. Missing MRI pulse sequence synthesis using multi-modal generative adversarial network. IEEE Trans. Med. Imaging39, 1170–1183. 10.1109/TMI.2019.2945521 (2020). [DOI] [PubMed] [Google Scholar]
- 20.Zhan, B., Li, D., Wu, X., Zhou, J. & Wang, Y. Multi-modal MRI image synthesis via GAN with multi-scale gate mergence. IEEE J. Biomed. Health Inform.26, 17–26. 10.1109/JBHI.2021.3088866 (2022). [DOI] [PubMed] [Google Scholar]
- 21.Yurt, M. et al. mustGAN: Multi-stream generative adversarial networks for MR image synthesis. Med. Image Anal.70, 101944. 10.1016/j.media.2020.101944 (2021). [DOI] [PubMed] [Google Scholar]
- 22.Mallio, C. A. et al. Artificial intelligence to reduce or eliminate the need for gadolinium-based contrast agents in brain and cardiac MRI: A literature review. Investig. Radiol.58, 746 (2023). [DOI] [PubMed] [Google Scholar]
- 23.Crété-Roffet, F., Dolmiere, T., Ladret, P. & Nicolas, M. The Blur Effect: Perception and estimation with a new no-reference perceptual blur metric. In SPIE Electronic Imaging Symposium Conference on Human Vision and Electronic Imaging Vol. XII, EI 6492–16 (San Jose, 2007).
- 24.Shurcliff, W. A. Studies in optics: A.A. Michelson, University of Chicago Press, 1927, republished in 1962 as phoenix science series no. 514 paperback, 176 pp. illustrated, \$1.75. J. Phys. Chem. Solids24, 498–499 (1963). [Google Scholar]
- 25.Rudin, L. I., Osher, S. & Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom.60, 259–268. 10.1016/0167-2789(92)90242-F (1992). [Google Scholar]
- 26.Pianykh, O. S., Pospelova, K. & Kamboj, N. H. Modeling human perception of image quality. J. Digit. Imaging31, 768–775 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Xing, X., Nan, Y., Felder, F., Walsh, S. & Yang, G. The beauty or the beast: Which aspect of synthetic medical images deserves our focus? In 2023 IEEE 36th International Symposium on Computer-Based Medical Systems (CBMS) 523–528 (IEEE Computer Society, 2023). 10.1109/CBMS58004.2023.00273.
- 28.Borji, A. Pros and cons of GAN evaluation measures: New developments. Comput. Vis. Image Underst.215, 103329. 10.1016/j.cviu.2021.103329 (2022). [Google Scholar]
- 29.Salimans, T. et al. Improved techniques for training GANs. CoRR abs/1606.03498 (2016). arXiv:1606.03498.
- 30.Szegedy, C. et al. Going deeper with convolutions. In 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 1–9 (2015). 10.1109/CVPR.2015.7298594.
- 31.Heusel, M., Ramsauer, H., Unterthiner, T., Nessler, B. & Hochreiter, S. GANs trained by a two time-scale update rule converge to a local nash equilibrium. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17 6629–6640 (Curran Associates Inc., 2017).
- 32.Ponomarenko, N. et al. A new color image database tid2013: Innovations and results. In Advanced Concepts for Intelligent Vision Systems (eds Blanc-Talon, J., Kasinski, A., Philips, W., Popescu, D. & Scheunders, P.) 402–413 (Springer, 2013).
- 33.Sheikh, H., Sabir, M. & Bovik, A. A statistical evaluation of recent full reference image quality assessment algorithms. IEEE Trans. Image Process.15, 3440–3451. 10.1109/TIP.2006.881959 (2006). [DOI] [PubMed] [Google Scholar]
- 34.Sheikh, H., Wang, Z., Cormack, L. & Bovik, A. Live image quality assessment database release 2. http://live.ece.utexas.edu/research/quality.
- 35.Ding, K., Ma, K., Wang, S. & Simoncelli, E. P. Comparison of image quality models for optimization of image processing systems. CoRR abs/2005.01338 (2020). [DOI] [PMC free article] [PubMed]
- 36.Chow, L. S., Rajagopal, H. & Paramesran, R. Correlation between subjective and objective assessment of magnetic resonance (MR) images. Magn. Resonance Imaging34, 820–831. 10.1016/j.mri.2016.03.006 (2016). [DOI] [PubMed] [Google Scholar]
- 37.Kastryulin, S., Zakirov, J., Pezzotti, N. & Dylov, D. V. Image quality assessment for magnetic resonance imaging. IEEE Access11, 14154–14168. 10.1109/ACCESS.2023.3243466 (2023). [Google Scholar]
- 38.International Medical Device Regulators Forum. Software as a medical device (SAMD): Clinical evaluation—Guidance for industry and food and drug administration staff (2017). https://www.fda.gov/regulatory-information/search-fda-guidance-documents/software-medical-device-samd-clinical-evaluation.
- 39.Cruz Rivera, S. et al. Guidelines for clinical trial protocols for interventions involving artificial intelligence: The spirit-AI extension. Lancet Digit. Health2, e549–e560 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kim, D. W., Jang, H. Y., Kim, K. W., Shin, Y. & Park, S. H. Design characteristics of studies reporting the performance of artificial intelligence algorithms for diagnostic analysis of medical images: Results from recently published papers. Korean J. Radiol.20, 405–410 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Liu, X. et al. A comparison of deep learning performance against health-care professionals in detecting diseases from medical imaging: A systematic review and meta-analysis. Lancet Digit. Health1, e271–e297. 10.1016/S2589-7500(19)30123-2 (2019). [DOI] [PubMed] [Google Scholar]
- 42.Khunte, M. et al. Trends in clinical validation and usage of US food and drug administration-cleared artificial intelligence algorithms for medical imaging. Clin. Radiol.78, 123–129. 10.1016/j.crad.2022.09.122 (2023) (Special Issue Section: Artificial Intelligence and Machine Learning). [DOI] [PubMed] [Google Scholar]
- 43.Nagendran, M. et al. Artificial intelligence versus clinicians: Systematic review of design, reporting standards, and claims of deep learning studies. BMJ368, m689. 10.1136/bmj.m689 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yasui, K. et al. Validation of deep learning-based CT image reconstruction for treatment planning. Sci. Rep.13, 15413 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bonardel, G. et al. Clinical and phantom validation of a deep learning based denoising algorithm for F-18-FDG pet images from lower detection counting in comparison with the standard acquisition. EJNMMI Phys.9, 36 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Food and Drug Administration (FDA). Artificial intelligence and machine learning (AI/ML)-enabled medical devices, accessed 14 March 2024; https://www.fda.gov/medical-devices/software-medical-device-samd/artificial-intelligence-and-machine-learning-aiml-enabled-medical-devices.
- 47.Reinke, A. et al. Understanding metric-related pitfalls in image analysis validation. Nat. Methods21, 82–194 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Maier-Hein, L. et al. Metrics reloaded: Recommendations for image analysis validation. Nat. Methods21, 195–212 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Baltruschat, I. M., Janbakhshi, P. & Lenga, M. Brasyn 2023 challenge: Missing MRI synthesis and the effect of different learning objectives (2024). arXiv:2403.07800.
- 50.Nečasová, T., Burgos, N. & Svoboda, D. Validation and evaluation metrics for medical and biomedical image synthesis. In Biomedical Image Synthesis and Simulation (eds Burgos, N. & Svoboda, D.) 573–600. The MICCAI Society Book Series, chap. 25 (Academic Press, 2022).
- 51.Chen, J. et al. A survey on deep learning in medical image registration: New technologies, uncertainty, evaluation metrics, and beyond. Med. Image Anal.100, 103385. 10.1016/j.media.2024.103385 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.McNaughton, J. et al. Machine learning for medical image translation: A systematic review. Bioengineering10, 1078 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Haase, R. et al. Artificial contrast: Deep learning for reducing gadolinium-based contrast agents in neuroradiology. Investig. Radiol.58, 539–547 (2023). [DOI] [PubMed] [Google Scholar]
- 54.Mudeng, V., Kim, M. & Choe, S.-W. Prospects of structural similarity index for medical image analysis. Appl. Sci.12, 3754 (2022). [Google Scholar]
- 55.Huynh-Thu, Q. & Ghanbari, M. Scope of validity of PSNR in image/video quality assessment. Electron. Lett.44, 800–801 (2008). [Google Scholar]
- 56.Korhonen, J. & You, J. Peak signal-to-noise ratio revisited: Is simple beautiful? In 2012 Fourth International Workshop on Quality of Multimedia Experience, 37–38 (2012). 10.1109/QoMEX.2012.6263880.
- 57.Wang, Z. & Bovik, A. C. Mean squared error: Love it or leave it? a new look at signal fidelity measures. IEEE Signal Process. Mag.26, 98–117. 10.1109/MSP.2008.930649 (2009). [Google Scholar]
- 58.Gourdeau, D., Duchesne, S. & Archambault, L. On the proper use of structural similarity for the robust evaluation of medical image synthesis models. Med. Phys.49, 2462–2474. 10.1002/mp.15514 (2022). [DOI] [PubMed] [Google Scholar]
- 59.Baker, A. H., Pinard, A. & Hammerling, D. M. On a structural similarity index approach for floating-point data. IEEE Trans. Vis. Comput. Gr.30, 1–13. 10.1109/TVCG.2023.3332843 (2023). [DOI] [PubMed] [Google Scholar]
- 60.Goodfellow, I., Bengio, Y. & Courville, A. Deep Learning, chap. 12.2.1 Preprocessing, 448 (MIT Press, 2016). http://www.deeplearningbook.org.
- 61.Tellez, D. et al. Quantifying the effects of data augmentation and stain color normalization in convolutional neural networks for computational pathology. Med. Image Anal.58, 101544. 10.1016/j.media.2019.101544 (2019). [DOI] [PubMed] [Google Scholar]
- 62.Onofrey, J. A. et al. Generalizable multi-site training and testing of deep neural networks using image normalization. Proceedings. IEEE International Symposium on Biomedical Imaging 348–351 (2019). [DOI] [PMC free article] [PubMed]
- 63.Reinhold, J. C., Dewey, B. E., Carass, A. & Prince, J. L. Evaluating the impact of intensity normalization on MR image synthesis. In Medical Imaging 2019: Image Processing vol. 10949 (eds Angelini, E. D. & Landman, B. A.) 109493H (International Society for Optics and Photonics SPIE, 2019). 10.1117/12.2513089. [DOI] [PMC free article] [PubMed]
- 64.Haase, R. et al. Reduction of gadolinium-based contrast agents in MRI using convolutional neural networks and different input protocols: Limited interchangeability of synthesized sequences with original full-dose images despite excellent quantitative performance. Investig. Radiol.58, 420 (2023). [DOI] [PubMed] [Google Scholar]
- 65.Shinohara, R. T. et al. Statistical normalization techniques for magnetic resonance imaging. NeuroImage Clin.6, 9–19 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Nyúl, L. G. & Udupa, J. K. On standardizing the MR image intensity scale. Magn. Resonance Med.42, 1072–1081 (1999). [DOI] [PubMed] [Google Scholar]
- 67.Hänsch, A., Chlebus, G. & Meine, H. Improving automatic liver tumor segmentation in late-phase MRI using multi-model training and 3d convolutional neural networks. Sci. Rep.12, 12262. 10.1038/s41598-022-16388-9 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.McCormick, M., Liu, X., Ibanez, L., Jomier, J. & Marion, C. ITK: Enabling reproducible research and open science. Front. Neuroinform.8, 13. 10.3389/fninf.2014.00013 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Numpy Developers. The fundamental package for scientific computing with python. https://numpy.org/.
- 70.Pedregosa, F. et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res.12, 2825–2830 (2011). [Google Scholar]
- 71.van der Walt, S. et al. Scikit-image: Image processing in Python. PeerJ2, e453. 10.7717/peerj.453 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Torchmetrics—Measuring reproducibility in Pytorch (2022). 10.21105/joss.04101.
- 73.Wang, Z., Bovik, A. C., Sheikh, H. R. & Simoncelli, E. P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process.13, 600–12 (2004). [DOI] [PubMed] [Google Scholar]
- 74.Wang, Z., Simoncelli, E. & Bovik, A. Multiscale structural similarity for image quality assessment. In The Thirty-Seventh Asilomar Conference on Signals, Systems and Computers, 2003, vol. 2, 1398–1402 (2003). 10.1109/ACSSC.2003.1292216.
- 75.Ding, K. IQA optimization (2020). https://github.com/dingkeyan93/IQA-optimization/.
- 76.Sampat, M. P., Wang, Z., Gupta, S., Bovik, A. C. & Markey, M. K. Complex wavelet structural similarity: A new image similarity index. IEEE Trans. Image Process.18, 2385–2401. 10.1109/TIP.2009.2025923 (2009). [DOI] [PubMed] [Google Scholar]
- 77.Huynh-Thu, Q. & Ghanbari, M. Scope of validity of PSNR in image/video quality assessment. Electron. Lett.44, 800–801 (2008). [Google Scholar]
- 78.Perceptual similarity metric and dataset. https://pypi.org/project/lpips/.
- 79.Zhang, R., Isola, P., Efros, A. A., Shechtman, E. & Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. CoRR ayn/1801.03924 (2018). arXiv:1801.03924.
- 80.Ding, K. https://github.com/dingkeyan93/DISTS.
- 81.Ding, K., Ma, K., Wang, S. & Simoncelli, E. P. Image quality assessment: Unifying structure and texture similarity. IEEE Trans. Pattern Anal. Mach. Intell.44, 2567–2581. 10.1109/TPAMI.2020.3045810 (2022). [DOI] [PubMed] [Google Scholar]
- 82.Choi, M. G., Jung, J. H. & Jeon, J. W. No-reference image quality assessment using blur and noise. Int. J. Electr. Comput. Eng.3, 184–188 (2009). [Google Scholar]
- 83.Pech-Pacheco, J., Cristobal, G., Chamorro-Martinez, J. & Fernandez-Valdivia, J. Diatom autofocusing in brightfield microscopy: A comparative study. In Proceedings 15th International Conference on Pattern Recognition. ICPR-2000, Vol. 3, 314–317 (2000). 10.1109/ICPR.2000.903548.
- 84.Marziliano, P., Dufaux, F., Winkler, S. & Ebrahimi, T. A no-reference perceptual blur metric. In Proceedings. International Conference on Image Processing, vol. 3, III–III (2002). 10.1109/ICIP.2002.1038902.
- 85.Roberts, D. https://github.com/davidatroberts/No-Reference-Sharpness-Metric.
- 86.Ferzli, R. & Karam, L. J. A no-reference objective image sharpness metric based on the notion of just noticeable blur (JNB). IEEE Trans. Image Process.18, 717–728. 10.1109/TIP.2008.2011760 (2009). [DOI] [PubMed] [Google Scholar]
- 87.Karam, L. & Narvekar, N. https://github.com/0x64746b/python-cpbd.
- 88.Narvekar, N. D. & Karam, L. J. A no-reference image blur metric based on the cumulative probability of blur detection (CPBD). IEEE Trans. Image Process.20, 2678–2683. 10.1109/TIP.2011.2131660 (2011). [DOI] [PubMed] [Google Scholar]
- 89.Schuppert, C. et al. Whole-body magnetic resonance imaging in the large population-based German national cohort study: Predictive capability of automated image quality assessment for protocol repetitions. Investig. Radiol.57, 478 (2022). [DOI] [PubMed] [Google Scholar]
- 90.Guha, R. https://pypi.org/project/brisque.
- 91.Mittal, A., Moorthy, A. K. & Bovik, A. C. No-reference image quality assessment in the spatial domain. IEEE Trans. Image Process.21, 4695–4708. 10.1109/TIP.2012.2214050 (2012). [DOI] [PubMed] [Google Scholar]
- 92.Gupta, P. https://github.com/guptapraful/niqe.
- 93.Mittal, A., Soundararajan, R. & Bovik, A. C. Making a “completely blind’’ image quality analyzer. IEEE Signal Process. Lett.20, 209–212. 10.1109/LSP.2012.2227726 (2013). [Google Scholar]
- 94.Li, Y. et al. Samscore: A semantic structural similarity metric for image translation evaluation (2023). arXiv:2305.15367.
- 95.Liu, J. et al. One model to synthesize them all: Multi-contrast multi-scale transformer for missing data imputation. IEEE Trans. Med. Imaging42, 2577–2591. 10.1109/TMI.2023.3261707 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Maes, F., Collignon, A., Vandermeulen, D., Marchal, G. & Suetens, P. Multimodality image registration by maximization of mutual information. IEEE Trans. Med. Imaging16, 187–198. 10.1109/42.563664 (1997). [DOI] [PubMed] [Google Scholar]
- 97.Ghorbani, A., Natarajan, V., Coz, D. & Liu, Y. DermGAN: Synthetic generation of clinical skin images with pathology. In Proceedings of the Machine Learning for Health NeurIPS Workshop (eds Dalca, A. V. et al.), vol. 116 of Proceedings of Machine Learning Research 155–170 (PMLR, 2020).
- 98.Jang, M. et al. Image Turing test and its applications on synthetic chest radiographs by using the progressive growing generative adversarial network. Sci. Rep.13, 2356 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.McNaughton, J. et al. Synthetic MRI generation from CT scans for stroke patients. BioMedInformatics3, 791–816. 10.3390/biomedinformatics3030050 (2023). [Google Scholar]
- 100.Zimmermann, L. et al. An MRI sequence independent convolutional neural network for synthetic head CT generation in proton therapy. Z. Med. Phys.32, 218–227 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Andrews, S. & Hamarneh, G. Multi-region probabilistic dice similarity coefficient using the aitchison distance and bipartite graph matching (2015). arXiv:1509.07244.
- 102.Xing, X., Nan, Y., Felder, F., Walsh, S. & Yang, G. The beauty or the beast: Which aspect of synthetic medical images deserves our focus? In 2023 IEEE 36th International Symposium on Computer-Based Medical Systems (CBMS) 523–528 (IEEE Computer Society, 2023). 10.1109/CBMS58004.2023.00273.
- 103.Dice, L. R. Measures of the amount of ecologic association between species. Ecology26, 297–302. 10.2307/1932409 (1945). [Google Scholar]
- 104.Mason, A. et al. Comparison of objective image quality metrics to expert radiologists’ scoring of diagnostic quality of MR images. IEEE Trans. Med. Imaging39, 1064–1072. 10.1109/TMI.2019.2930338 (2020). [DOI] [PubMed] [Google Scholar]
- 105.Jayachandran Preetha, C. et al. Deep-learning-based synthesis of post-contrast t1-weighted MRI for tumour response assessment in neuro-oncology: A multicentre, retrospective cohort study. Lancet Digit. Health3, e784–e794. 10.1016/S2589-7500(21)00205-3 (2021). [DOI] [PubMed] [Google Scholar]
- 106.Zhu, M., Yu, L., Wang, Z., Ke, Z. & Zhi, C. Review: A survey on objective evaluation of image sharpness. Appl. Sci.13, 2652. 10.3390/app13042652 (2023). [Google Scholar]
- 107.Martin, D., Fowlkes, C., Tal, D. & Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings Eighth IEEE International Conference on Computer Vision. ICCV 2001, vol. 2 416–423 (2001). 10.1109/ICCV.2001.937655.
- 108.Baid, U. et. al. The RSNA-ASNR-MICCAI brats 2021 benchmark on brain tumor segmentation and radiogenomic classification (2021). arXiv:2107.02314.
- 109.Menze, B. H. et al. The multimodal brain tumor image segmentation benchmark (BRATS). IEEE Trans. Med. Imaging34, 1993. 10.1109/TMI.2014.2377694 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Bakas, S. et al. Advancing the cancer genome atlas glioma MRI collections with expert segmentation labels and radiomic features. Nat. Sci. Data4, 170117. 10.1038/sdata.2017.117 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Consortium, M. MONAI: Medical open network for AI (2023). https://docs.monai.io/en/stable/auto3dseg.html.
- 112.Cohen, J. P., Luck, M. & Honari, S. Distribution matching losses can hallucinate features in medical image translation. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2018 (eds Frangi, A. F., Schnabel, J. A., Davatzikos, C., Alberola-López, C. & Fichtinger, G.) 529–536 (Springer, 2018).
- 113.Liu, J. et al. Dyefreenet: Deep virtual contrast CT synthesis. In Simulation and Synthesis in Medical Imaging (eds Burgos, N., Svoboda, D., Wolterink, J. M. & Zhao, C.) 80–89 (Springer, 2020).
- 114.Dohmen, M., Truong, T., Baltruschat, I. M. & Lenga, M. Five pitfalls when assessing synthetic medical images with reference metrics (2024), accepted at Deep Generative Models workshop at MICCAI 2024; arXiv:2408.06075.
- 115.Tustison, N. J. et al. N4ITK: Improved N3 bias correction. IEEE Trans. Med. Imaging29, 1310–20 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Axel, L., Summers, R. M., Kressel, H. Y. & Charles, C. Respiratory effects in two-dimensional Fourier transform MR imaging. Radiology160, 795–801 (1986). [DOI] [PubMed] [Google Scholar]
- 117.Stadler, A., Schima, W., Ba’ssalamah, A., Kettenbach, J. & Eisenhuber, E. Artifacts in body MR imaging: Their appearance and how to eliminate them. Eur. Radiol.17, 1242–55. 10.1007/s00330-006-0470-4 (2007). [DOI] [PubMed] [Google Scholar]
- 118.Van Leemput, K., Maes, F., Vandermeulen, D. & Suetens, P. Automated model-based bias field correction of MR images of the brain. IEEE Trans. Med. Imaging18, 885–896. 10.1109/42.811268 (1999). [DOI] [PubMed] [Google Scholar]
- 119.Prashnani, E., Cai, H., Mostofi, Y. & Sen, P. PieAPP: Perceptual image-error assessment through pairwise preference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2018).
- 120.Zhu, H., Li, L., Wu, J., Dong, W. & Shi, G. MetaIQA: Deep meta-learning for no-reference image quality assessment. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 14131–14140 (2020). 10.1109/CVPR42600.2020.01415.
- 121.Ying, Z. et al. From patches to pictures (PaQ-2-PiQ): Mapping the perceptual space of picture quality. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 3572–3582 (2020). 10.1109/CVPR42600.2020.00363.
- 122.Su, S. et al. Blindly assess image quality in the wild guided by a self-adaptive hyper network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2020).
- 123.Lao, S. et al. Attentions help CNNs see better: Attention-based hybrid image quality assessment network. In 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW) 1139–1148 (2022). 10.1109/CVPRW56347.2022.00123.
- 124.Zhang, L., Zhang, L., Mou, X. & Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process.20, 2378–2386. 10.1109/TIP.2011.2109730 (2011). [DOI] [PubMed] [Google Scholar]
- 125.Sheikh, H. & Bovik, A. Image information and visual quality. IEEE Trans. Image Process.15, 430–444. 10.1109/TIP.2005.859378 (2006). [DOI] [PubMed] [Google Scholar]
- 126.Wang, Z. & Li, Q. Information content weighting for perceptual image quality assessment. IEEE Trans. Image Process.20, 1185–1198. 10.1109/TIP.2010.2092435 (2011). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The BraSyn 2023 dataset is available at www.synapse.org/brats2023. The code for all metrics and distortions is available at www.github.com/bayer-group/mr-image-metrics.