Emergence of collective oscillations in massive human crowds

Abstract

Dense crowds form some of the most dangerous environments in modern society¹. Dangers arise from uncontrolled collective motions, leading to compression against walls, suffocation and fatalities^2–4. Our current understanding of crowd dynamics primarily relies on heuristic collision models, which effectively capture the behaviour observed in small groups of people^5,6. However, the emergent dynamics of dense crowds, composed of thousands of individuals, remains a formidable many-body problem lacking quantitative experimental characterization and explanations rooted in first principles. Here we analyse the dynamics of thousands of densely packed individuals at the San Fermín festival (Spain) and infer a physical theory of dense crowds in confinement. Our measurements reveal that dense crowds can self-organize into macroscopic chiral oscillators, coordinating the orbital motion of hundreds of individuals without external guidance. Guided by these measurements and symmetry principles, we construct a mechanical model of dense-crowd motion. Our model demonstrates that emergent odd frictional forces drive a non-reciprocal phase transition⁷ towards collective chiral oscillations, capturing all our experimental observations. To test the robustness of our findings, we show that similar chiral dynamics emerged at the onset of the 2010 Love Parade disaster and propose a protocol that could help anticipate these previously unpredictable dynamics.

Analysis of the confined crowds at the San Fermín festival in Spain shows that dense crowds can self-organize into macroscopic chiral oscillators, coordinating the orbital motion of hundreds of individuals without external guidance.

Main

Stir your morning tea or coffee and watch. To explain the formation of a vortex in your hot beverage, physicists, engineers and mathematicians treat fluids as continua and ignore the complex dynamics at the molecular scales: they use the basic laws of fluid mechanics. Beyond fluids, descriptions of living matter as continua have been instrumental in understanding the large-scale flows of the cytoskeleton, cell tissues and animal groups, where the interactions between the elementary units remain largely unknown^8–11. In stark contrast, active-matter hydrodynamics has made limited strides in explaining crowd dynamics^5,12.

Most reproducible experiments and observations of pedestrian dynamics are indeed based on small groups of individuals whose motion cannot be accurately captured by continuum descriptions^5,6. Consequently, the dominant approach is based on heuristic models of two-body interactions^5,6,13–16. Introduced nearly 30 years ago, these models accurately predict the trajectories of individuals within small groups of pedestrians^5,17, and are used worldwide for safety evacuation models. However, determining which behavioural models are best suited to capture and explain the flows that emerge in massive crowds remains an open question^{3,5,12,18–20}. The intrinsic unpredictability and hazards of mass gatherings have been major impediments to characterizing the uncontrolled dynamics of dense crowds through safe and reproducible measurements. When confined, dense crowds create one of the most dangerous environments, where hundreds of individuals can move en masse over metres, press others against walls, and lead to suffocation and fatalities². But, understanding how individuals interact with their neighbours in crowded environments is not a prerequisite to explain and predict the macroscopic dynamics of dense crowds—just as models of molecular interactions are not required to account for macroscopic fluid flows.

Here we study confined crowds composed of thousands of close-packed individuals whose dynamics can be analysed safely and repeatedly. We compare their motion with crowd quakes observed at the onset of the Love Parade disaster in 2010^4,21 and reveal that, past a critical density, confined crowds can undergo spontaneous oscillations that involve the synchronous orbital motion of hundreds of individuals in the absence of external cues or control mechanisms. Combining insights gained from our consistent measurements with symmetry principles, we construct a mechanical theory of dense crowds from first principles, without resorting to behavioural hypothesis. We show that dense crowds realize an unanticipated form of odd frictional matter, and explain how odd friction and confinement conspire to induce a transition towards collective chiral oscillations. To help prevent accidents, we provide a strategy to monitor the motion of dense crowds in real time, and anticipate their uncontrolled collective dynamics.

Collective motion emerges in dense crowds

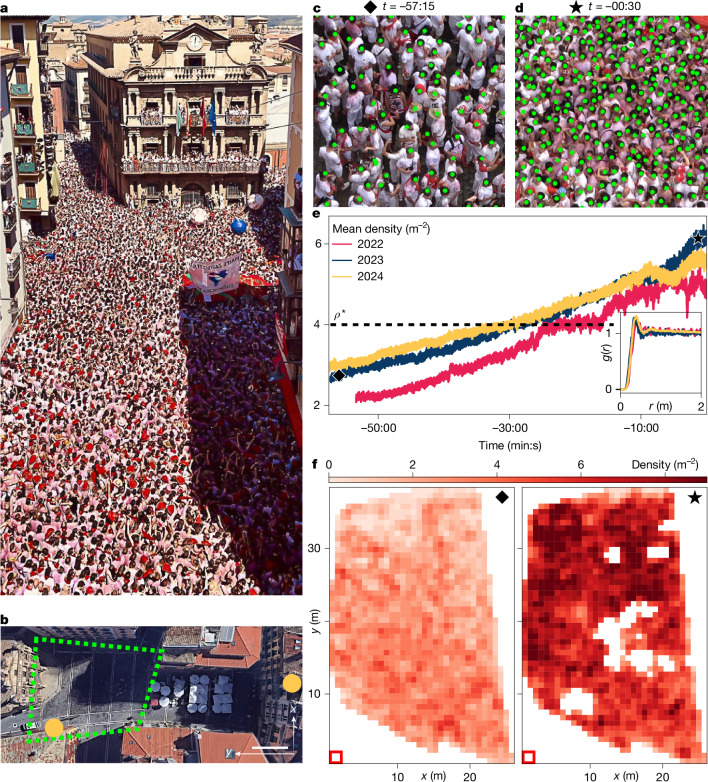
The opening ceremony of the San Fermín festival, the Chupinazo, allows us to perform repeated series of measurements on safe yet densely packed crowds. This event gathers more than 5,000 participants every year, on 6 July, at the exact same hour, on the Plaza Consistorial in the city of Pamplona, Spain (Fig. 1a). This plaza is about 50-m long and 20-m wide, and the surrounding buildings offer clear observation spots to take hours of high-resolution footage (Fig. 1b). We have repeated our observations in four different years (2019, 2022, 2023 and 2024) before and after the 2020 COVID-19 pandemic, and under different weather conditions (Methods). Owing to sub-optimal imaging in 2019, some measurements are performed on only the 2022, 2023 and 2024 datasets.

Fig. 1. Gathering of a massive crowd in Pamplona, Spain.

a, Picture of the crowd at the opening ceremony of the San Fermín festival (2019). b, Aerial view of the Plaza Consistorial. We analyse the crowd dynamics in the region delimited by the dashed polygon. The orange dots are the observation spots. Scale bar, 10 m. c, Close-up view on the crowd 57 minutes and 15 seconds before the opening of the festival. The green dots show the position of the head of the festival attendees (Methods). d, Close-up view on the crowd 30 seconds before the opening of the festival. The crowd density has markedly increased. e, Plot of the mean number density of the crowd as a function of the time to the festival opening. Diamond, t = −57:15 (see c); star, t = −00:30 (see d). The crowd density increases slowly and monotonically. The dashed line indicates the value of ρ*. The measurement error is smaller than the statistical variations that define the width of the plots. Inset: radial distribution function g(r) computed from the position of individuals and averaged over about 7 minutes before the festival opening (see Methods for details). f, Snapshots of two local-density maps for t = −57 min 15 s (left) and t = −30 s (right). The white areas correspond to regions where the field of view is obstructed by buildings, flags and balloons (see a and Methods).

To gain some intuition about the type of crowd we study, we invite the reader to watch Supplementary Videos 1–4 first. They summarize the evolution of the crowd dynamics before the opening of the festival (we also show typical snapshots in Extended Data Fig. 1). From 10:00 to 12:00 (Fig. 1c), a joyful mass of people dressed in white clothes progressively gathers on the plaza, where they dance, sing, drink and celebrate, until the crowd becomes closely packed, thereby preventing the participants from moving freely (Fig. 1d). A few seconds before the opening of the festival, all participants concomitantly stop their motion and raise a red handkerchief. Orchestras then exit the city hall, perform and depart from the square leading to the dispersion of the massive crowd in the streets of Pamplona. In this article, if not specified otherwise, we focus on the time interval that precedes the opening of the festival, during which no external drive or signal dictates the dynamics of the participants. We report measurements performed in the polygon shown in Fig. 1b.

Extended Data Fig. 1. Top views of the Chupinazo crowd.

The crowd first gathers and fills the plaza Consistorial. When the average density of people exceeds ~ 4 m⁻² the crowd undergoes spontaneous oscillations. In our article we investigate solely these two regimes. Then, at noon, the festival starts and all attendees raise red handkerchiefs. Finally, several orchestras surrounded by the police force performs in the crowd, and exit the plaza Consistorial followed by the festival attendees.

We view the crowd as an active continuum and therefore quantify its dynamical states by measuring two fields: the number density ρ(r, t), and the local velocity v(r, t) where r and t are the position and time, respectively. We measure ρ owing to the automated detection of the head of each participant as detailed in Methods. In Fig. 1e, we show that the average density ρ(t) = ⟨ρ(r, t)⟩_r increases linearly over time, reaching a value close to six people per square metre when the festival starts (t = 00:00). However, this average value does not capture the density heterogeneities seen in Fig. 1f. Locally, ρ(r, t) can reach values as high as nine people per square metre (think of nine persons packed in a shower cabin). These heterogeneities are, however, poorly correlated in space, as seen in the pair correlation functions plotted in the inset of Fig. 1e.

Together with their extreme density, the large velocity fluctuations are the most striking visual features of the Chupinazo crowd. As seen in Supplementary Video 5, when ρ becomes large enough, groups of hundreds of individuals undergo uncontrolled correlated motion. Our central goal is to quantify, predict and elucidate this dynamics.

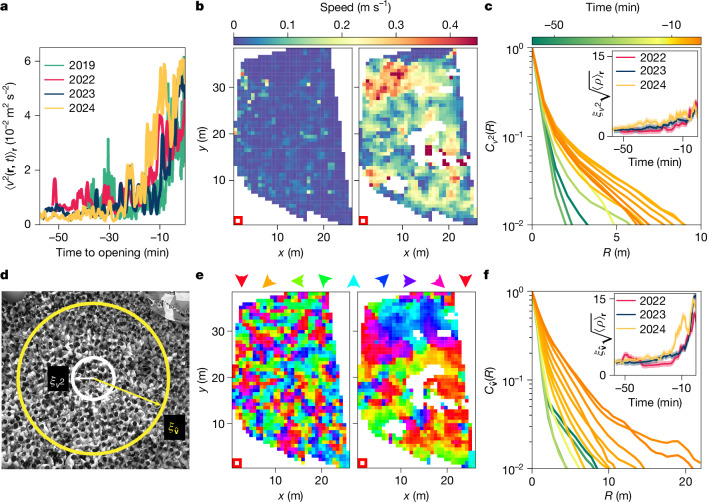
To measure the local flow field, we use conventional particle image velocimetry. In Methods, we detail how we compute v(r, t), in the regions of space where the flags and balloons visible in Fig. 1a do not obstruct our observations. Unlike the crowd density, the velocity fluctuations ⟨v²(r, t)⟩_r do not increase steadily with time (Fig. 2a). Instead, at early times, when the crowd gathers, the velocity fluctuations are small and stationary. However, about 30 minutes before the festival opening, when the density reaches a critical value of ρ* = (4.0 ± 0.5) m⁻², the crowd dynamics undergoes a sharp transition captured by a linear increase of ⟨v²(r, t)⟩_r augmented by activity bursts (Fig. 2a). These bursts are localized not only in time but also in space. The two snapshots of the speed field v(r, t) = ∣v(r, t)∣ in Fig. 2b contrast the quiet and homogeneous dynamics in the dilute regime (left) with the unsteady and heterogeneous motion that emerges in denser crowds (right) (see also Supplementary Videos 6 and 7). Computing the speed-field correlations and the associated correlation length ${\xi }_{v^2}$ (Fig. 2c), we find that the hotspots where the crowd flows at high speed extend at most over a few metres regardless of the crowd density (Fig. 2c,d). Furthermore, plotting the local speed of the crowd against its local density in Supplementary Fig. 1, we find that the two quantities do not correlate. In the crowd-modelling language, the concept of fundamental diagram does not apply to our dense crowds⁵.

Fig. 2. Emergence of spatially correlated motion in dense crowds.

a, Spatially averaged velocity fluctuations plotted versus time. The fluctuations increase about 30 minutes before the opening of the festival. The measurement error is smaller than the thickness of the solid lines given the integration over all the local velocities, and the running average over a 1-min interval. b, Heat maps of the local crowd speed at t = −57:15 and t = −00:30 (2023 data). The flows of dense crowds are heterogeneous. c, Spatial correlation function of the squared speed, $C_{v^2}$, plotted versus the distance R for different times (2023). Inset: associated correlation lengths measured in 2022, 2023 and 2024, and normalized by the typical distance between two attendees. The thickness of the lines represents the combined errors on ξ and ρ. The error on ξ is estimated on the spatial resolution of the spatial correlations and the error on ρ is estimated on the typical fluctuations of the mean density against time. d, Illustrations of the extent of the orientation and speed correlations at t = −00:30. The correlations of $\hat{\mathbf{v}}$ reflect the directed motion of hundreds of individuals. e, Maps of the local orientation of the spontaneous flows in the crowd (same times as in b). In dense crowds, the orientation of the emergent flows correlates over more than 10 m. f, Spatial correlation function of the orientation field, $C_{\widehat{\mathbf{v}}}$, plotted versus the distance R for different times (2023). Inset: associated correlation lengths measured in 2022, 2023 and 2024, and normalized by the typical distance between two attendees. The thickness of the lines represents the combined errors on ξ and ρ.

The local orientation of the spontaneous flows $\hat{\mathbf{v}}(\mathbf{r},t)$ reveals a richer behaviour (Fig. 2e,f). In Fig. 2f, we can see that the orientational correlation length ${\xi }_{\widehat{\mathbf{v}}}$ increases sharply when macroscopic velocity fluctuations emerge (when ρ(t) > ρ*). These measurements quantify the most striking feature seen in Supplementary Video 5: in densely packed crowds, groups of hundreds of individuals spontaneously move along the same direction without relying on any external guidance (Fig. 2d).

The temporal order of dense-crowd dynamics

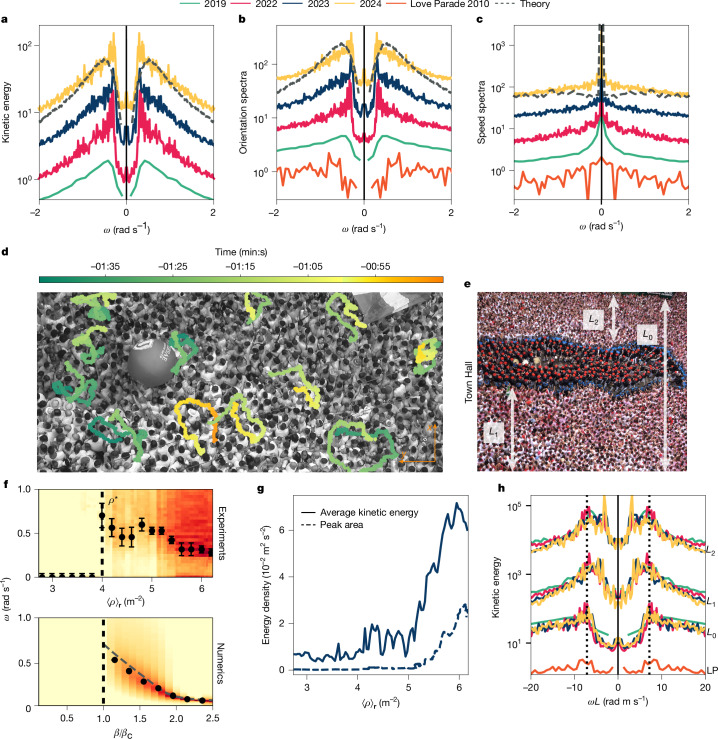
To gain a deeper insight into the crowd flows, we characterize their spectral properties and reveal their temporal order. In Fig. 3a, we plot the power spectrum of the kinetic energy in the dense regime $S_{\mathbf{v}}\left(\omega \right)={⟨\mid \mathbf{v}\left(\mathbf{r},\omega \right){\mid }^2⟩}_{\mathbf{r}}$, where v(r, ω) is the Fourier transform of v(r, t) in the time domain. At high density, the velocity spectra consistently peak at a finite frequency ±ω₀, where ω₀ = (0.35 ± 0.05) rad s⁻¹. This pivotal observation implies that the dynamics of the dense crowds is not chaotic but periodic in time: they feature underdamped oscillations with a period of about 18 s. We stress that this period is: (1) not set by any mechanical, visual or acoustic stimulus; (2) much longer than all timescales associated with human body motion; and (3) not observed in the dilute regime (Extended Data Fig. 2). We can unambiguously conclude that the emergence of oscillations in dense crowds is a collective phenomenon.

Fig. 3. Dense crowds oscillate spontaneously.

For model details, see equations (1) and (2) and Methods. See Methods for simulation parameters. a, Power spectra of v (that is, the kinetic energy) measured in 2019, 2022, 2023 and 2024 along with predictions from our mechanical model. The spectra are shifted for increased readability. b,c, Normalized power spectra of $\widehat{\mathbf{v}}$ (b) and v² (c) measured in 2019, 2022, 2023 and 2024, as well as in the Love Parade 2010, and compared with predictions from our mechanical model. The spectra are shifted for increased readability. d, Raw trajectories tracked in the 2023 crowd. We do not observe sequences of back-and-forth motion. e, Illustrations of the different confinement lengths used in the rescaled spectra shown in h. It is noted that L₀ and L₁ extend up to the wall located at the bottom of the image, which is not visible in the current view. f, Heat maps in logarithmic scale showing the variations of the kinetic energy spectrum with the spatially averaged density (experiments), and with the windsock parameter β/β_c of our numeric simulations. The black dots indicate the value of ω₀ and the vertical dashed line represents ρ* and β = β_c. The dashed grey line in the bottom panel represents the theoretical evolution of ω₀ with β/β_c. For β < β_c, the spectra are flat, so we set ω₀ = 0. The experimental error bars were estimated manually. g, Variations of the total kinetic energy and of the area below the peak of the power spectrum (ω ∈ [0.25, 0.40] rad s⁻¹) with the mean crowd density (2023). Oscillatory dynamics dominate the kinetic energy of the crowd. h, Normalized power spectra of v plotted against rescaled pulsation ωL, where L is the confinement length. The spectra measured with the confinement length L₀ correspond to those shown in a. The spectra measured with the confinement length L₁ and L₂ correspond to the crowd dynamics during the orchestra performance (see e). The measured widths are L₀ = 23.1 m, L₁ = 10.0 m, L₂ = 9.1 m (Chupinazo) and LP = 11 m (Love Parade 2010). The dotted black lines represent the rescaled pulsation ω₀L.

Extended Data Fig. 2. Evolution of the kinetic energy spectra with the crowd density.

Kinetic energy spectra S_v(ω) measured at three different times (time window: 3 mins). For each spectrum we indicate the mean value of the crowd density. a, d and g, At low density the spectra peak at zero: the crowd does not oscillate. b, e and h, When the mean density exceeds ~ 4 people per square meter, the kinetic energy spectra feature two peaks at finite frequency. The crowd oscillates. c, f and i, When the crowd density further increases, the peaks become narrower thereby indicating a longer persistence of the oscillations.

To grasp the nature and origin of this collective dynamics, we plot the spectra of the orientation and speed fields in Fig. 3b,c. We find that the peak in the kinetic energy spectrum solely stems from orientational oscillations. By contrast, the magnitude of the flow does not oscillate in time and undergoes aperiodic fluctuations; its spectrum remains peaked around ω = 0 at all densities. These spectral properties tell us that the crowd oscillations do not stem from back-and-forth motions, but from orbital trajectories followed by the individuals packed in the crowds. This conclusion is further confirmed by the tracking of their Lagrangian trajectories, shown in Fig. 3d.

To confirm that our findings apply more broadly, and do not rely on any prior information gathered by the attendees of the San Fermín festival, we analyse the publicly available recordings of the Duisburg Love Parade disaster⁴ (https://www.youtube.com/watch?v=QpzISdBE3dA). Although the crowd dynamics at the onset of the 2010 stampede have been consistently referred to as ‘turbulent’⁴, ref. ²¹ reported periodic velocity oscillations. Running our data analysis on raw videos, we find that when the crowd density was as high as 8 ± 1 m⁻², the Duisburg crowd featured the exact same oscillations as the Chupinazo crowd: they do not reflect linear swaying motion²¹, but the emergence of chiral orientational oscillations characterized in Fig. 3b,c. Crowd quakes are not turbulent but periodic.

To better understand how the state of the crowd evolves as the mean density increases, we perform a time–frequency analysis of the flows measured in the Chupinazo crowds in Fig. 3f. We plot the variations of the instantaneous kinetic energy spectrum S_v(ω; t) = ⟨∣v(r, ω; t)∣²⟩_r, and indicate the values ω₀(t) of the pulsation at the maxima of the kinetic energy (v(r, ω; t) represents the Fourier transform of the velocity field within 3-min-long time intervals). The evolution of ω₀ with ρ shows that the transition from noisy to coherent oscillatory flows is very sharp and occurs at ρ* = (4.0 ± 0.5) m⁻², when the velocity fluctuations start increasing with crowd density (Fig. 2a). ω₀ then decreases slowly (Fig. 3f), whereas the temporal coherence of the oscillations increases with ρ (Extended Data Fig. 3). The comparison between the variations of S_v(ω₀; t) and the total speed fluctuations in Fig. 3g confirms that the kinetic energy of the crowd is chiefly determined by its emergent oscillatory motion.

Extended Data Fig. 3. In dense crowds, spontaneous oscillations dominate the speed fluctuations of the crowd flow. The oscillations become increasingly coherent as the density increases.

a, d and g, Magnitude of the spatially averaged velocity fluctuations plotted versus time. b, e and h, Time-frequency plots of the kinetic energy spectra (time window: 3 mins). Black dots: maxima of the energy spectra, i.e., oscillation frequency of the crowd flow. Same plot as in Fig. 3f of the text and comparison with the 2022 and 2024 data which show the same trends. c, f and i, Evolution of the relaxation time τ(t) of the spontaneous oscillations measured as the full width at half maximum of the instantaneous kinetic energy spectra. We illustrate the definition of τ in Extended Data Fig. 2.

We stress that this dynamics is qualitatively different from the stop-and-go waves observed when dense polarized crowds move unidirectionally^3,14,22. The stop-and-go waves are by definition associated with speed oscillations of unidirectional flows. The chiral oscillations we have uncovered are also markedly different from the mosh-pit tradition of heavy-metal concerts¹⁸. In this setting, the crowds are organized into long-lived vortices, which we have never observed in ‘crowd quakes’.

At this stage, it is worth discussing the practical implications of our main findings. When the crowd density reaches its maximal value, groups of several hundreds of confined people can undergo self-sustained oscillations over metres. The mass of these macroscopic groups, represented by the yellow circle in Fig. 2d, can exceed 10 tons. We hence conclude that monitoring the evolution of ω₀(t) in real time, on raw images, can provide a very effective strategy to anticipate dangerous mass motion in dense crowds. As a matter of fact, the transition to oscillatory motion is very sharp, and is unambiguously detectable while the amplitude of the displacements remains smaller than the people size (Fig. 3f and Extended Data Fig. 3). Furthermore, detecting spontaneous oscillations does not rely on any advanced detection and tracking algorithms. Our spectral analysis should provide a readily applicable tool to anticipate the uncontrolled and self-sustained motions that can emerge in dense crowds.

Dense crowds are odd frictional matter

Beyond its practical significance, the discovery of collective chiral oscillations requires a theoretical explanation rooted in fundamental physics principles. To construct this theory, we first identify the role of confinement, and quantify the emergent chirality of the crowd dynamics. These two results will prove to be instrumental to our mathematical model.

To address the role of confinement, we perform an additional series of measurements after the festival opening, when a security team splits the crowd into two halves (Fig. 3e and Supplementary Video 4). We find that the two decoupled crowds still oscillate but at a higher frequency. We measure the shortest dimension of the crowds before and after the festival opening, and the extent of the region of space where the 2010 Love Parade crowd featured chiral oscillations (Methods). Figure 3h shows that the velocity spectra of these markedly different crowds peak at the same value when rescaling the frequency ω by the inverse of the confinement length L. This result strongly suggests that the period of the emergent oscillations depends on confinement, and is not an intrinsic ‘material’ property.

We now focus on the chirality of the crowd dynamics. The oscillations of the flow field, and the resulting orbits of the Lagrangian trajectories, are chiral. In principle, the parity of the dynamics could be either spontaneously broken, or imprinted in the intrinsic handedness of the human bodies or in chiral behavioural factors previously reported in pedestrian groups^18,23. To distinguish between these scenarios, we measure the local handedness of the oscillations as follows. By applying a band-pass filter to the velocity field, we focus on the oscillatory dynamics at ω₀ and filter out the additional random motion of the crowd (Methods). We then define a spin field ϵ(r, t) which takes the value ±1 when the filtered velocity rotates in a clockwise or anticlockwise direction. Figure 4a illustrates the temporal evolution of ϵ(r, t) in a dense crowd (see also Supplementary Video 8). The spin field is not homogeneous in space and fluctuates in time: the handedness of the chiral oscillations is not a priori determined. In addition, the distribution of the local and instantaneous spin values is perfectly symmetric (Fig. 4b). These observations readily imply that the chirality of the oscillatory motion stems from spontaneous symmetry breaking. In Fig. 4c, we show the evolution of the correlation length of the spin field ξ_ϵ (Methods). It shows that groups oscillating with the same handedness extend across system-spanning scales.

Fig. 4. Dense crowds support chiral oscillations with non-prescribed handedness.

a, The colours indicate the local handedness ϵ(r, t) of the oscillatory displacements in a crowd where ⟨ρ(r, t)⟩_r ≈ 6 m⁻² (2023). We compute ϵ(r, t) for the oscillatory component of the dynamics by applying a band-pass filter ω ∈ [0.25, 0.40] rad s⁻¹ to v(r, t) (Methods). b, Probability P(ϵ) of the spin variable in an approximately 7-min-long interval before the opening of the festival (2022, 2023 and 2024). In agreement with our theory, the parity of the dynamics is not explicitly broken (see equation (2) and Methods for the numerical parameters). The error bars are estimates based on the jackknife method (Methods). c, The correlation length ξ_ϵ of ϵ(r, t) measures the size of the regions where the crowd oscillations have a uniform handedness (Methods). The thickness of the lines represents the measurement error.

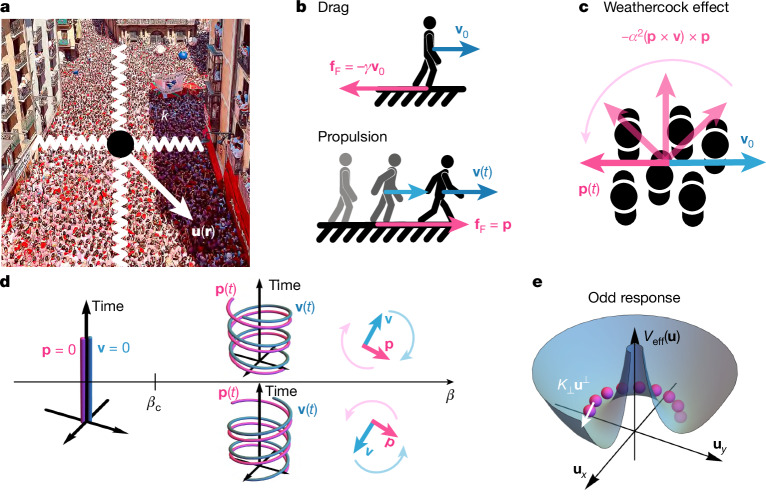
With these last observations, we are now equipped to answer the question of how dense crowds self-organize into coherent chiral oscillators. Regardless of the microscopic mechanisms that power the motion of people, and dictate their interactions, the macroscopic dynamics of the crowd obeys a fundamental law: linear-momentum conservation. As we focus on the temporal dynamics, we perform a mean-field approximation and disregard the spatial heterogeneities of the crowd. Momentum equation then reduces to Newton’s second law: ∂_tv = f/ρ, where f is the total body force density experienced by the crowd and v is the velocity of its centre of mass. Here f = f_C + f_F models the interactions with the confining walls f_C and the friction with the ground f_F (ref. ¹²). Our theory consists of determining the constitutive relations that define f_C and f_F without resorting to any behavioural conjecture.

The confining force hinders the displacement of the crowd u (v = ∂_tu). We therefore posit that f_C derives from a potential V: f_C = −∇V(u). It is indeed clear that in closely packed crowds, f_C chiefly originates from the contact interactions between the (soft) individuals, and with the rigid walls. In this regime, it derives from a confining potential V (Fig. 5a). The friction force is more subtle. We decompose it as the sum of two terms sketched in Fig. 5b: a standard passive drag −γρv relaxes velocity fluctuations, and a propulsive-friction term ρp reflects the conversion of body deformations into motion. The crowd dynamics then takes the compact form

$${\partial }_t\mathbf{v}=-\gamma \mathbf{v}+\mathbf{p}-k\mathbf{u},$$ 1

where we performed a harmonic approximation to write $V\left(\mathbf{u}\right)=\frac{1}{2}k\rho u^2$, where k is the stiffness of the confining potential. However, we cannot approximate p by a constant vector, as it would merely induce a finite directed displacement of the crowd. We therefore need to account for the dynamics of p, an internal degree of freedom that embodies both physical and cognitive aspects of the interactions between the crowd and the ground. This constitutive relation takes the generic form:

$${\partial }_t\mathbf{p}=-{\gamma }_{\mathbf{p}}\mathbf{p}+{\gamma }_{\mathbf{p}}\beta \mathbf{v}-{\alpha }^2\left(\mathbf{p}\times \mathbf{v}\right)\times \mathbf{p}.$$ 2

where γ_p and γ_pβ are in principle nonlinear functions of v², p² and p ⋅ v (Methods and Supplementary Information). To write equation (2), we have used three symmetry considerations. First, it must be rotationally invariant given the isotropic velocity correlations seen in Extended Data Fig. 4. Second, it must be parity invariant as the chirality of the circular trajectories is not a priori prescribed. Lastly, we model homogeneous crowds. Therefore, equation (2) must be translationally invariant and hence cannot depend on u.

Fig. 5. Emergent odd mechanics in crowd motion.

a, When packed, the crowd is a soft medium confined by the walls of the Plaza Consistorial. Within a harmonic approximation, the resulting confining potential V(u) can be modelled by a spring stiffness k (third term in equation (1)). b, Illustration of the two contribution to the friction force in equation (1). Top: when the crowd moves at a velocity v₀, it experiences a passive drag in the opposite direction −γv₀. Bottom: the crowd is an active medium. It can propel owing to the propulsive component p of the friction force. It is noted that in our mean-field theory, these forces are not defined at the single-individual scale, but at macroscopic scales of the order of ${\xi }_{\widehat{\mathbf{v}}}$. c, Illustration of the weathercock term in equation (2). As the crowd propels with a velocity v, the α² term rotates the orientation of the propulsive force p in the direction opposite to v. d, The pink and blue lines represent the world lines of the p and v variables, respectively. When β < β_c, the crowd is in a quiescent state, the velocity and the propulsive force vanish. When β = β_c, a non-reciprocal phase transition results in a spontaneous chiral-symmetry breaking. The crowd oscillates along limit cycles of opposite handedness. The oscillations are sustained as v chases p, while p moves away from v (weathercock effect). e, When integrating out the fast degrees of freedom (p(t)), we are left with an effective theory where the centre of mass of the crowd evolves along the ridge of an effective ‘Mexican hat’ potential under the action of an ‘odd spring’ of stiffness K_⊥. The odd stiffness arises from the active friction on the ground.

Extended Data Fig. 4. Velocity correlations in dense crowds.

a, The heatmap represents the values of the spatial autocorrelation of the velocity field measured in 2022 in the dense regime. The dashed line marks where the correlation value reaches 0.1. b, Same plot for the 2023 experiments. c, Same plot for the 2024 experiments.

Given these symmetries, equation (2) is the most general first-order constitutive equation we can write, and it has a clear physical meaning. The first term damps the fluctuations of p at a rate γ_p and favours crowds in a force-free state. The second term aligns p with the flow, amplifies the propulsive force as the crowd moves, and therefore destabilizes the quiescent state. It is a ‘windsock’ term typical of dry active matter^24,25. The third term illustrated in Fig. 5c is nonlinear and accounts for the reaction of the crowd against directed flows. It is generically non-zero in dry active matter as well^26–28. It models a ‘weathercock’ effect: α² rotates p in the direction opposite to the flow, while keeping its magnitude constant. In Supplementary Information, we thoroughly discuss the role of all nonlinearities and inertia, and demonstrate that orientational oscillations at constant speed require α² to be finite and positive.

To test the predictive power of our theory, we focus here on its overdamped limit and show that it provides an accurate description of all our experimental findings. Neglecting inertia, equation (1) defines a four-dimensional dynamical system whose steady states reflect the two dynamics observed in our crowds (Methods). When confinement and friction are strong enough to stabilize the dynamics against the ‘windsock’ effect, there exists only one stable fixed point where p = v = 0. It corresponds to the quiescent state of the dilute crowds (ρ < ρ*). Conversely when β is large enough, the parity symmetry of the dynamics is spontaneously broken. The quiescent crowd undergoes a non-reciprocal transition⁷ towards a chiral state where both v and p rotate spontaneously, while keeping their norm constant (Fig. 3b,c). This dynamics captures the collective oscillations of our dense crowds.

To go beyond this qualitative comparison, we study numerically how v and p responds to Langevin noise sources and compute the power spectra of the crowd flows. Our numerical simulations correctly account for all our experimental findings. First, we find that the kinetic energy spectrum shows a clear peak at a finite frequency ω₀(β) past the bifurcation threshold β_c; it is nearly flat with no finite-frequency feature below β_c (Fig. 3f). Remarkably, our analytical theory and simulations accurately capture: (1) the chiral oscillations of the flow orientation and the incoherent fluctuations of its magnitude (Fig. 3a–c and Extended Data Fig. 5d); (2) the discontinuous jump followed by a slow decrease of ω₀ past the onset of spontaneous oscillations (Fig. 3f); (3) the fat tails of the kinetic energy spectrum (Fig. 3a–c); and (4) the equal probability of clockwise and anticlockwise chiral motion (Fig. 4b). Lastly, we show in Methods that equations (1) and (2) predict that the frequency of the chiral oscillations should decrease with the system size in agreement with the ω₀ ∝ 1/L scaling law shown in Fig. 3h.

Extended Data Fig. 5. Determination of the constitutive relation p({u}, {v}) for the active friction.

To determine how the active friction force depends on the local state of the crowd we compute the spectra S_v, $S_{v^2}$, the distribution of the spin variable ϵ(t), the amplitude of velocity fluctuations v_⋆ (radius of the limit cycles when they exist) and the angular frequency of oscillation Ω_⋆. The different models are detailed in the SI. Only the overdamped model with a spontaneous parity breaking (d) is able to reproduce the salient features observed in our experiments. Simulation parameters are γ = 1, α = 1, γ_p = 18, k = 0.027, η = 0.45, σ = 0, σ_p = 2 and β_c = γ + k/γ_p (d) and γ = 1, α = 1, γ_p = 50, σ = 0, σ_p = 5 and β_c = γ (e).

We have built a predictive theory of dense crowds rooted in basic physics principles. However, the origin of periodic motion, that is, the existence of stable limit cycles, is not readily apparent from inspecting equations (1) and (2). To gain a deeper intuition, it is worth considering the asymptotic limit where the propulsive force relaxes faster than the flow (γ_p ≫ k/γ). This allows us to see that dense crowds provide a prototypical example of odd frictional matter. Integrating out the propulsive friction in equations (1) and (2), the dynamics in the chiral phase reduces to the equations of a particle living in a ‘Mexican hat’ potential V_eff, and coupled to an odd-elastic spring²⁹ of stiffness ±K_⊥ that applies a force transverse to the displacement u (Methods and Supplementary Information):

$$\gamma {\partial }_t\mathbf{u}=-\mathbf{\nabla }{V}_{\mathrm{eff}}\left(\mathbf{u}\right)\pm K_{\perp }{\mathbf{u}}^{\perp },$$ 3

where ${\mathbf{u}}^{\perp }=\widehat{\mathbf{z}}\times \mathbf{u}$ ($\hat{\mathbf{z}}$ is the unit vector in the vertical direction). Equation (3) hence provides a straightforward explanation for the emergence of spontaneous oscillations. As sketched in Fig. 5e, V_eff sets the amplitude of the chiral orbits and odd elasticity sustains a uniform orbital dynamics along the circular ridge of the potential. Another useful analogy arises when taking a time derivative of equation (3). In steady states, it reduces to ∂_tv = ±(K_⊥/γ)v^⊥ and corresponds to the dynamics of a charged particle in a magnetic field. The transverse force is analogous to the Lorentz force, and the periodic oscillations of dense crowds can be thought of as cyclotron orbits powered by odd frictional forces. However unlike in magnetic systems, and in typical realizations of odd matter, the handedness of the chiral trajectories is undetermined and results from a spontaneous symmetry breaking.

Conclusion

Through a combination of experimental measurements and theory, our findings show how collective chiral oscillations can spontaneously animate dense crowds in the absence of external stimuli. By repeatedly analysing the motion of dense crowds composed of thousands of individuals in a reproducible and safe environment, we revealed that their flows are not chaotic but periodic in time and locally chiral. Guided by these symmetry-breaking phenomena, we have constructed a general theory of dense-crowd motion that captures all our experimental observations. We show that collective oscillations in dense crowds arise from a non-reciprocal phase transition towards a chiral oscillatory state. Not only does this description remain consistent across four occurrences of the San Fermín festival but also it holds for the 2010 Love Parade disaster. Therefore our findings provide a practical strategy to anticipate dangerous crowd behaviour in confined environments. From a fundamental perspective, our study establishes a robust mechanical framework for understanding the dynamics of crowds and animal groups, and more broadly, offers a perspective on emergent chirality in non-equilibrium matter.

Methods

Image acquisition, density and velocity measurements in the Chupinazo crowd

In this section, we explain how we film the dense crowds and how we convert raw images into quantitative data.

The Chupinazo crowd

The crowds we film in Pamplona are composed of the attendees of the San Fermín festival. Most of them are locals who are well aware of how the event unfolds: they know the dress code and when to raise their red handkerchiefs, and they eagerly await the orchestra after the festival opening speech and fireworks. Many foreign tourists are also present, and the crowd consists mostly of young adults of all genders. As the Chupinazo is broadcast on the Spanish national networks and popularized internationally, we can assume that most of the participants are aware of the high crowd density that they will be confronted with before gathering. As a result, participants of the Chupinazo come in a festive mood, with evident signs of alcohol consumption. When the crowd is sparse, small groups of people can be seen singing, clapping and lightly pushing each other without creating significant movement. However, when the crowd density exceeds ρ*, we observe high-amplitude motions, referred to as crowd quakes in a different context²¹. Unlike, for instance, at heavy-metal concerts, there are no signs of individuals actively pushing others when the crowd is dense; instead, people try protecting themselves from the crowd. Lastly, those unable to enter the square at the entrances keep on accessing the Plaza Consistorial and pushing inwards. Two entrances are blocked by police forces until just a few minutes before noon. Here, hundreds of people (mostly locals) try gathering in the already crowded square. The number of people on the Plaza Consistorial peaks at noon and can be as large as about 6,000 people.

We filmed four Chupinazo events, in 2019, 2022, 2023 and 2024. The 2020 and 2021 editions were cancelled because of COVID-19 restrictions. The weather was sunny in 2019 and 2023. It was cloudy and rainy in 2022 and 2024. We were not informed of and did not observe any change in the organization of the ceremony.

Image acquisition

We recorded videos from the two observation spots indicated in Fig. 1b. In 2022, 2023 and 2024, we used Sony FDR-AX33 and Sony FDR-AX43A camcorders on both spots. The frame rate was 25 frames per second and the resolution was 3,840 × 2,160 pixels (4K videos). In 2019, we used telephoto lenses (Sigma 150–600 mm F5-6.3 DG OS HSM ∣ S) mounted on Nikon D500 cameras with a frame rate of 30 fps and a resolution of 3,840 × 2,160 pixels. We illustrate the observation set-up in Extended Data Fig. 6. The cameras were mounted on standard tripods on the balcony of the leftmost building (fifth floor of the tourism office of Pamplona, 2023 and 2024), and on custom mounts on the rightmost observation point (private balcony on the fourth floor of the highest building surrounding the Plaza Consistorial, 2019, 2022, 2023 and 2024).

Extended Data Fig. 6. Observation setup.

a, Aerial view of the plaza Consistorial and location of the two observation spots. The dashed lines show two typical pictures taken in 2022 (red) and 2023 (orange). b, Image taken from the leftmost spot at t = −00: 30. c, d, Pictures of our custom camera mounts fixed on a building balcony. e, Image taken from the rightmost spot at t = −00: 30.

Image correction protocol

We used the same protocol as in ref. ¹² to correct for the perspective distortions. In short, we mapped the pixel coordinates (u, v) of every frame to a coordinate in the square frame (x, y, z). The goal was to generate images with fixed pixel dimensions in metres. This was done using planar homography, assuming pinhole cameras and neglecting the height of the z axis³⁰. To do so, we first selected a reference image of the plaza (Extended Data Fig. 7a) when clear of pedestrians. We chose a set of four points distributed over the square and matched them on a satellite view from Google Earth Pro (Extended Data Fig. 7b). We then computed the planar homography matrix using these four points from the two views and rescaled all the images accordingly. Finally, by measuring the distances on the satellite view in metres and in pixels, we determined the size of the pixels in metres. In the rescaled images, all the pixels have the same dimensions (Extended Data Fig. 7c). In Extended Data Fig. 7, we show the set of points used in 2023, on the raw image, the satellite view and the resulting rescaled image. The pixels on the corrected images are almost squares and their dimensions respectively in the x, y directions correspond to 0.028 × 0.029 m, 0.046 × 0.045 m, 0.012 × 0.012 m and 0.013 × 0.012 m in 2019, 2022, 2023 and 2024, respectively.

Extended Data Fig. 7. Planar homography and dynamical masking of the perturbations to the field of view.

a, Raw image (2023) of the plaza Consistorial. We identify four distinctive features on the ground and label their positions (green dots). b, Location of the four same spots on a satellite view (Google Earth Pro). c, Same image as in a after the planar homography correction (2023). d, Raw image showing balloons and flags held by the festival attendees (2022). e, Flags and balloons automatically detected by the YOLOv8 neural network and highlighted with bright colors. f, Velocity field measured on the corrected images around the flags and balloons only.

To estimate the relative error caused by the planar homography protocol, we compared the distances between the original reference points with the distances measured in our corrected images. We found the following relative errors respectively in the x, y directions: 1% × 12%, 1% × 1%, 1% × 3% and 1% × 3% in 2019, 2022, 2023 and 2024, respectively.

As in ref. ¹², we also corrected for the zero-height approximation. Previously, we assumed that all visible pixels in the images lie on the same plane as the ground. However, we observed the heads of pedestrians that are not on the ground. Here we recall the formula and give the values measured for the zero-height approximation correction. More details can be found in ref. ¹². Let Δx′ represent the distance measured between two heads in images corrected for perspective distortion. Owing to the height of pedestrians, that distance is overestimated. Let Δx denote the distance between the feet of the same pedestrians in the same image. These distances are related by the following equation

$$\mathrm{\Delta }x=\mathrm{\Delta }{x}^{\prime }\frac{H-h}{H},$$ 4

where H is the height of the observation spot and h is the typical height of pedestrians. This relationship is valid in all direction and is independent of the position in the image. We set h = 1.73 m based on the average height of Spanish people and we estimated H = 16 ± 1 m by using a picture of the buildings with pedestrians serving as a length reference³¹.

Finally, in 2019, the weather was sunny and the shadow cast by the buildings introduced artefacts in our particle image velocimetry (PIV) measurements (Fig. 1a). To address this issue, we performed an additional image processing step. We used a Python script available on GitHub to homogenize the brightness of the image^32,33. This procedure removed all the PIV artefacts that arise at the edge of the building shadows.

Time interval of unguided crowds

Each year, we focus on an approximately 1-h time interval. We defined the origin of time as when the festival attendees raise their red handkerchief to signal the opening of the festival and change their behaviour according to the Chupinazo tradition. This happens around noon, and before the festival officially starts no external guidance dictates the dynamics of the crowd. No acoustic, visual or mechanical signal coordinates the motion of the crowd.

Spatial delimitation of our measurements

Before the opening of the festival, part of the celebration consists of holding large flags and playing with big balloons on the square (Extended Data Fig. 7d). When we measured the density and velocity fields, we needed to make sure to consider only the regions of space devoid of these objects that obstruct our field of view.

To do so, we used a standard machine learning tool, YOLOv8³⁴. It is designed to detect specified objects on images. We trained it on 15 images from 2019 and 2022 by manually annotating the polygons enclosing the balloons and flags on our pictures. In practice, we annotated the images using the labelstudio software on the raw images. The area and position of the detected objects were then corrected using the planar homography parameters and converted into dynamical masks applied to every frame (Extended Data Fig. 7e). Both the density and the velocity fields were computed on the masked images (Extended Data Fig. 7f).

Detection of the attendees and density measurement

To detect the position of the head of the people in the crowds, we took advantage of the machine learning algorithm P2PNet³⁵. It is designed to estimate the number of people in a picture based on a convolutional neural network pretrained on 300 images with dense crowds (ShanghaiTech dataset³⁶). We further trained the neural network on 4 manually annotated images taken from our 2019, 2022 and 2023 footage. To annotate the images, we used a homemade Python script and trained P2PNet for 3,500 epochs of 4 batches. The discrepancy between the automated and manual counting procedures in the full field of view of a picture is smaller than 5%. We detected the heads on the raw images (Fig. 1c,d).

We aimed to clean the data before computing the density by minimizing the impact of false positives and missed detections. Given that pedestrians continuously appear in the frames, they are more likely to be correctly detected compared with the occurrence of false positives or misses. We predicted that detection errors manifest as high-frequency ‘flashes’. To counteract this, we converted the detection data into a density field by applying a Gaussian convolution over the detected points where 3σ approximately equals the size of a head, σ being the typical width of the two-dimensional Gaussian. This density field was then averaged over 0.4 s, and a 33% threshold was applied to retain only points of high occurrence. A maxima-finding algorithm was subsequently employed to obtain the cleaned detection data.

To define the density field, we used the same windows (dimensions and locations) as the velocity field (Supplementary Table 1). In each window, approximately 1.5 × 1.5 m² in size, we counted the number of people and divided this value by the window area. Given the quality of our images, we were able to detect the individuals and define the local density field in the region shown in Fig. 1b only for our 2022, 2023 and 2024 images.

We used trackpy³⁷ to measure the trajectories shown in Fig. 3d.

Measurement of the velocity field

We describe Chupinazo crowds as continua. As frequently used in fluid mechanics, we measured the Eulerian velocity field in the crowd using conventional PIV¹². We used a typical window size of about 1.5 m and a typical time step of about 0.5 s. The precise different values to characterize the observed dynamics are summarized in Supplementary Table 1. The measurement error of the two components of the velocity field in a single PIV box is of 0.1 m s⁻¹ in 2019 and 2022, 0.05 m s⁻¹ in 2023 and 2024.

Image acquisition, density and velocity measurements in the 2010 Love Parade

In this section, we explain the origin of the data and the process of converting raw images into quantitative data.

The Love Parade 2010

The Love Parade 2010 was a music festival held in July in Duisburg, Germany⁴. During the event, 21 people died and more than 500 were injured at the main entry of the festival area (Extended Data Fig. 8). This traumatic event has been the subject of numerous scientific studies, also because a number of videos showing the convergence towards the catastrophe have been publicly released⁴.

Extended Data Fig. 8. Emergence of collective oscillations during the Love Parade 2010, Duisburg, Germany.

a, Satellite view of the main entry to the Love Parade 2010 festival (Google Earth). The dotted squares indicate the fields of view of the two publicly available video clips we analysed (see Methods). Clip 1: green polygon; Clip 2: orange rectangle. b, Power spectra of the velocity field v, velocity orientation $\widehat{\mathbf{v}}$, and squared norm v² corresponding to clip 1 (see Methods). c, Same power spectra computed from clip 2 (see Methods).

Videos

Numerous recordings from mobile phones and cameras are available on the internet. The organizer released some camera footage of the main entry where the catastrophes occurred, before they happened (https://www.youtube.com/watch?v=QpzISdBE3dA). We selected two clips (clip 1 from 14:04 to 15:46 and clip 2 from 19:24 to 19:49) where we observed high-amplitude motion of the crowd.

Image correction protocol

We were unable to perform any image correction on the Love Parade 2010 data.

Density measurement

We were unable to measure the density in clip 1 owing to the low resolution, which hindered detection and manual annotation. In clip 2, we annotated one image. We estimated the area covered by the field of view by measuring the shoulder-to-shoulder width of festival attendees in pixels and then converting it to metres. Our estimate of the crowd density is ρ = 8 ± 1 m⁻².

Measurement of the velocity field

We used the same methodology for the Chupinazo and the Love Parade crowds. We measured the Eulerian velocity field in the crowd using conventional PIV¹². As not enough reference points are visible on the images to perform perspective correction, we used the raw images to measure the approximated velocity field. We summarize the values of the different parameters chosen to characterize the observed dynamics in Supplementary Table 1.

Power spectra

We use the same methodology as for the Chupinazo crowds.

Characterization tools

We developed all our numerical tools using mostly the numpy package of the Python numerical language.

Radial pair correlation function

We used data from the detection of the attendees (see above) and the function static.pair_correlation_2d from trackpy³⁷, which takes into account non-periodic boundary conditions. The radial pair correlation function is computed in a rectangle devoid of flags and balloons and averaged over a period of about 7 minutes in the densest crowds (see below).

Power spectra

To compute the power spectra of the velocity v(r, t), velocity orientation $\hat{\mathbf{v}}(\mathbf{r},t)$, and squared speed v²(r, t) fields of Fig. 3a–c, we first computed the discrete-time Fourier transform for each position r using the numpy.fft.fft function. For the sake of consistency, we normalized these values by the total duration of the signal. A perfect cosine signal with pulsation ω₀ would have a discrete-time Fourier transform showing peaks of amplitude 1/2 at ±ω₀. The local spectra are given by the squared norm of each discrete-time Fourier transform signal. Finally, we performed spatial averages of the local spectra to compute S_v(ω), $S_{\widehat{\mathbf{v}}}\left(\omega \right)$ and $S_{v^2}\left(\omega \right)$. These spectra were computed using signals of duration 6 min 30 s for the 2023 data, 7 min 30 s for the 2022 data and 30 s for the 2019 data. In 2019, the safety system of our cameras reset them approximately every 30 s owing to overheating. We therefore computed our spectra over shorter time intervals, but averaged them over all our 30-s-long acquisitions.

To accurately compare the 2019, 2022 and 2023 spectra, we divided the spectra by their mean value between ω = −2 rad s⁻¹ and ω = 2 rad s⁻¹ and the final spectra were obtained after a final smoothing over 5 subsequent data points.

Time–frequency characterization

To perform the time–frequency analysis of Fig. 3f, we applied the above method to compute the power spectra on time intervals [t, t + Δt] with Δt = 3 min and repeated the same operation for increasing values of t with a step of 1 s.

Correlation lengths

To compute the radial correlation functions of the velocity, orientation and speed fields, we first computed their two-dimensional spatial correlation functions. The value of the correlation C_f(R) of a vector function f(r, t) is given by

$$C_{\mathbf{f}}\left(\mathbf{R}\right)=\frac{{⟨\delta \mathbf{f}\left(\mathbf{r},t\right)\cdot \delta \mathbf{f}\left(\mathbf{r}+\mathbf{R},t\right)⟩}_{\mathbf{r},t}}{{⟨\delta {\mathbf{f}}^2\left(\mathbf{r},t\right)⟩}_{\mathbf{r},t}},$$ 5

where δf(r, t) = f(r, t) − ⟨f(r, t)⟩_r,t and with ⟨⋅⟩_r,t standing for an average over positions r and time t. In practice, we compute the value of δf at the point r + R using numpy.roll to shift the data that form the vector δf(r). We then use numpy.nanmean to compute the averages. We parallelized this computation using multiprocessing.Pool. To compute the radial correlation function, we created bins corresponding to radial displacements. For a bin ranging from r₀ to r₀ + δr, we averaged all the values of the two-dimensional correlation function C(R) for r₀ ≤ ∣R∣ < r₀ + δr. We defined the instantaneous correlations by performing the time average over 3-min-long intervals. We defined the correlation lengths as the distances at which the radial correlation functions reach the value 0.1.

Chirality of the local dynamics

Here we focus on the oscillatory component of the crowd motion. We first applied a temporal band-pass filter to the velocity field. The filter width was set to the full-width at three-quarter maximum height of the power spectra shown in Fig. 3a. In practice, we performed a time Fourier transform on the velocity field, we applied the band-pass filter and performed an inverse Fourier transform.

We defined the local spin field ϵ(r, t) as the sign of the instantaneous increment of the angle θ made by the velocity with the x axis. For each position in space, we computed the orientation of the filtered velocity field $\theta \in [\mathrm{-\pi },\mathrm{\pi }]$. We healed the discontinuities of θ(r, t) so that $\theta \in [-\infty ,\infty ]$. We performed a moving average of time window T₀/2, with T₀ = 2π/ω₀ and ω₀ the pulsation of the maximum of the power spectrum. At each position r and time t, we measure the sign ϵ(r, t) of the time variations of θ(r, t), which defines the spin field ϵ(r, t) = ±1. We illustrate this protocol in Extended Data Fig. 9 and show the resulting spin fields for the 2022 event, which reveal the same phenomenology as in Fig. 4. We estimated the error bars of the spin field distribution using the jackknife method over 10,000 samples³⁸. For the correlation length of the spin field, we ran the band-pass filter on time windows of 3 min and computed the correlation length as detailed above.

Extended Data Fig. 9. Chiral dynamics of dense crowds and construction of the spin field.

a, Time variations of the angle θ(r, t) made by the filtered velocity field with the x − axis for one position r (2023 data). The band-pass filter applied to v is a rectangular window for ω ∈ [0.25, 0.40] rad/s. b, Same time series as in a after unwinding the angular variable and smoothing it over a time window of width π/ω₀, where ω₀ = 0.32 rad/s is the oscillation frequency. Note that the angular frequency of v(r, t) is strongly persistent but changes in time. The handedness of the dynamics is an emergent dynamical property. c, Corresponding spin field measured at t = −02: 30 in 2023.

Phenomenological inference of the active friction laws

In this section, we show that confinement and odd frictional forces conspire to yield spontaneous chiral oscillations at an incoherent speed in dense crowds.

Odd friction and spontaneous symmetry breaking

Our starting point is the mean-field description of the crowd mechanics, which takes the form of Newton’s second law ∂_tv = f/ρ, where ρ is the mass density and f is the sum of all the body forces originating from the interactions between the pedestrians and the ground or between the pedestrians and the confining walls. We decompose it into four terms: f(t) = −ργv(t) + ρp(t) − ρku + ρσζ(t), where the first drag term classically models the damping of the velocity fluctuations via the momentum exchange with the ground. In the spirit of a Landau expansion, we retain the lowest-order term in v and consider a linear drag force. The second term is what we refer to as an active friction with the ground. It is a vector that models the conversion of the body deformations into propulsive forces. The third term stems from the confinement of the crowd by walls. Again, in the spirit of a Landau expansion, we retain the lowest-order term in the displacement variable u (with v = ∂_tu). The last term in the force definition is a Langevin noise source that classically accounts for the coupling to all the fast degrees of freedom ignored within our mean-field picture. ζ(t) is a Gaussian random noise of zero mean and covariance $⟨\mathbf{\zeta }\left(t\right)\mathbf{\zeta }\left(t^{\prime }\right)⟩=\delta \left(t-t^{\prime }\right)\mathbb{I}$.

In Supplementary Information, we show that the constitutive relation that defines the propulsive force p cannot take the form p(t) = f(v(t), u(t)) (see also Extended Data Fig. 5a–c). In others words, we must take into account the proper dynamics of p. Because the crowd is globally isotropic (Extended Data Fig. 4) and has no reference position in space, the constitutive equation must be independent of u and invariant upon rotations. Furthermore, our experimental observations show that the parity symmetry of the crowd is not explicitly broken. We thus proceed to a systematic Landau expansion to find the most general constitutive equation. Restricting ourselves to first-order derivatives in time and keeping only the leading-order nonlinearities, corresponding to the six third-order terms, we find

$$\begin{array}{c}{\partial }_t\mathbf{p}=-{\gamma }_{\mathbf{p}}\left(1+{\eta }_1{\mathbf{p}}^2+{\eta }_2{\mathbf{v}}^2\right)\mathbf{p}+{\gamma }_{\mathbf{p}}\beta \left(1-{\eta }_3{\mathbf{p}}^2-{\eta }_4{\mathbf{v}}^2-{\eta }_5\mathbf{v}\cdot \mathbf{p}\right)\mathbf{v}\hfill \\ -{\alpha }^2\left(\mathbf{p}\times \mathbf{v}\right)\times \mathbf{p}+{\sigma }_{\mathbf{p}}{\mathbf{\zeta }}_{\mathbf{p}}.\hfill \end{array}$$ 6

where ηs are material parameters and ζ_p(t) is another Gaussian random noise of zero mean, covariance $⟨{\mathbf{\zeta }}_{\mathbf{p}}\left(t\right){\mathbf{\zeta }}_{\mathbf{p}}\left(t^{\prime }\right)⟩=\delta \left(t-t^{\prime }\right)\mathbb{I}$ and uncorrelated from ζ(t). We discuss in Supplementary Information the effect of all terms and all nonlinearities in Newton’s second law and equation (6). We study them one at a time to single out their impact on the crowd dynamics. The conclusion of this thorough investigation is that our experimental findings are nicely captured by a minimal model where inertia plays a negligible role and where only two nonlinearities rule the dynamics of the p variable. The α² term which we refer to as a ‘weathercock’ term in the main text is essential to yield chiral orientational oscillation. However a second nonlinearity is required to stabilize the oscillatory dynamics against fluctuations. More accurately, we show that the dynamics is unstable when all the η_i vanish. However, stable chiral states can emerge when η₁ ≠ 0, η₃ ≠ 0 or η₅ ≠ 0. As the stability domain of the chiral states is much larger when stabilized by a nonlinear windsock effect (η₃ and η₅), we therefore focus on a minimal model where we disregard inertia and retain only the α² and η₃ nonlinearities.

The mechanics of dense crowds is then captured by a minimal set of two equations:

$$\left\{\begin{array}{c}{\partial }_t\mathbf{u}=-\frac{k}{\gamma }\mathbf{u}+\frac{1}{\gamma }\mathbf{p}+\frac{\sigma }{\gamma }\mathbf{\zeta },\hfill \\ {\partial }_t\mathbf{p}=-{\gamma }_{\mathbf{p}}\mathbf{p}+\beta {\gamma }_{\mathbf{p}}\left(1-\frac{\eta }{{\gamma }_{\mathbf{p}}}{\mathbf{p}}^2\right){\partial }_t\mathbf{u}-{\alpha }^2\left(\mathbf{p}\times {\partial }_t\mathbf{u}\right)\times \mathbf{p}+{\sigma }_{\mathbf{p}}{\mathbf{\zeta }}_{\mathbf{p}},\hfill \end{array}\right)$$ 7

where we have set all η_i to zero, except η₃ ≡ η/γ_p. The first equation corresponds to Newton’s second law and the second equation is the constitutive equation of the crowds. We provide a physical interpretation of this constitutive relation in the main text. The nonlinear η term implies that the amplitude of the windsock effect decreases as the amplitude of the propulsive force increases. We also note that this equation is strikingly similar to the mechanical description of active solid metamaterials derived in ref. ²⁷ from a microscopic model. Only the sign in front of the double cross-product is different.

Although equation (7) has a clear physical meaning, it is unpractical to investigate the fixed points, the limit cycles and the stability of the dynamics. To characterise the deterministic dynamics of our nonlinear system (σ = σ_p = 0), we write $\mathbf{u}=v\widehat{\mathbf{u}}$, with u the norm of u and $\widehat{\mathbf{u}}$ its orientation. We then inject this form into equation (7), and express the dynamics in terms of the three variables u (the displacement magnitude), v = ∂_tu (the ‘speed’) and ${\Omega }^2={\left({\partial }_t\widehat{\mathbf{u}}\right)}^2$ (the square of the angular velocity of $\widehat{\mathbf{u}}$). We then find

$$\left\{\begin{array}{c}{\partial }_{t}u=v,\hfill \\ {\partial }_{t}v=u{\Omega }^2\left(1+k{\alpha }^2{u}^2\right)+\frac{{\gamma }_{\mathbf{p}}}{\gamma }\left\{\beta -{\beta }_{\mathrm{c}}-\frac{\beta \eta }{{\gamma }_{\mathbf{p}}}\left[{\left(\gamma v+ku\right)}^2+{\gamma }^2{u}^2{\Omega }^2\right]\right\}v-\frac{k{\gamma }_{\mathbf{p}}}{\gamma }u,\hfill \\ \frac{u}{2}{\partial }_t{\Omega }^2=-2v{\Omega }^2+\frac{{\gamma }_{\mathbf{p}}}{\gamma }\left\{\beta -{\beta }_{\mathrm{c}}-\frac{\beta \eta }{{\gamma }_{\mathbf{p}}}\left[{\left(\gamma v+ku\right)}^2+{\gamma }^2{u}^2{\Omega }^2\right]\right\}u{\Omega }^2-k{\alpha }^2{u}^2\left(v+\frac{k}{\gamma }u\right){\Omega }^2,\hfill \end{array}\right)$$ 8

with β_c = γ + k/γ_p. We stress here that the dynamical variable Ω² does not prescribe the direction of rotation of u but only its rate of change.

Fixed points and limit cycles

We now look for the fixed points of the dynamics (u_⋆, v_⋆, ${\Omega }_{\star }^2$) by setting the partial derivatives to zero in equation (8). The first fixed point is trivial and corresponds to quiescent crowds where u_⋆ = 0 and v_⋆ = 0, whereas ${\Omega }_{\star }^2$ is ill defined as the displacement vanishes (u_⋆ = 0). There also exists a second pair of non-trivial fixed points for β > β_c characterized by v_⋆ = 0

$$\begin{array}{c}{u}_{\star }^2=\frac{{\gamma }_{\mathbf{p}}}{2k^2{\alpha }^2\left(1+\frac{\beta \eta }{{\alpha }^2}\right)}\left\{\beta -{\beta }_{\mathrm{c}}-\frac{k}{{\gamma }_{\mathbf{p}}}\left(1+\frac{\beta \eta }{{\alpha }^2}\right)-\frac{\beta \eta \gamma }{{\alpha }^2}\right)\hfill \\ \left(+\sqrt{{\left[\beta -\gamma +\frac{\beta k\eta }{{\gamma }_{\mathbf{p}}{\alpha }^2}-\frac{\beta \eta \gamma }{{\alpha }^2}\right]}^2+\frac{4k\beta \eta \gamma }{{\gamma }_{\mathbf{p}}{\alpha }^2}\left(1+\frac{\beta \eta }{{\alpha }^2}\right)}\right\}\hfill \end{array}$$ 9

and

$${\Omega }_{\star }^2=\frac{k{\gamma }_{\mathbf{p}}}{\gamma \left(1+k{\alpha }^2{u}_{\star }^2\right)}.$$ 10

This second pair of fixed point corresponds to two circular limit cycles for u (and v). The radius of the limit cycles is u_⋆ for u (and u_⋆∣Ω_⋆∣ for v), and they are swept at opposite angular frequencies ±Ω_⋆. To make sure that these two limit cycles explain the oscillatory dynamics of our crowds, we must first show that they are stable to small perturbations.

Linear stability of the fixed points and limit cycles

We now study the linear stability of the two fixed points. For the trivial fixed point, we linearize equation (7) in the noiseless limit around (u_⋆ = 0, p_⋆ = 0), and find

$${\partial }_t\left(\begin{array}{c}\hfill \mathbf{u}\hfill \\ \hfill \mathbf{p}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill -k/\gamma \hfill & \hfill 1/\gamma \hfill \\ \hfill -k\beta {\gamma }_{\mathbf{p}}/\gamma \hfill & \hfill {\gamma }_{\mathbf{p}}\left(\beta -\gamma \right)/\gamma \hfill \end{array}\right)\left(\begin{array}{c}\hfill \mathbf{u}\hfill \\ \hfill \mathbf{p}\hfill \end{array}\right).$$ 11

The trace of the matrix is γ_p(β − β_c)/γ. It changes sign when β = β_c. The determinant is given by kγ_p/γ and always remains positive. We thus conclude that the trivial fixed point is stable if β < β_c, as the matrix has two eigenvalues with a negative real part. Instead, the matrix has two eigenvalues of positive real part when β > β_c and the quiescent fixed point hence becomes unstable. This criterion coincides with the emergence of the limit cycles.

We now address the stability of the two limit cycles. We set u = u_⋆ + δu, v = δv and ${\Omega }^2={\Omega }_{\star }^2+\delta {\Omega }^2$ and linearize the above equations with respect to δu, δv and δΩ². We find

$$\begin{array}{c}{\partial }_t\left(\begin{array}{c}\hfill \delta u\hfill \\ \hfill \delta v\hfill \\ \hfill \delta {\Omega }^2\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 2k{\alpha }^2{u}_{\star }^2{\Omega }_{\star }^2\hfill & \hfill k^2{\alpha }^2{u}_{\star }^2/\gamma \hfill & \hfill u_{\star }\left(1+k{\alpha }^2{u}_{\star }^2\right)\hfill \\ \hfill -4{\gamma }_{\mathbf{p}}{\Omega }_{\star }^2\left(\beta -{\beta }_{\mathrm{c}}\right)/\left(\gamma u_{\star }\right)\hfill & \hfill -2{\Omega }_{\star }^2\left[2+k{\alpha }^2{u}_{\star }^2\left(1+2\beta \eta /{\alpha }^2\right)\right]/u_{\star }\hfill & \hfill -2\beta \eta \gamma u_{\star }^2{\Omega }_{\star }^2\hfill \end{array}\right)\hfill \\ \times \left(\begin{array}{c}\hfill \delta u\hfill \\ \hfill \delta v\hfill \\ \hfill \delta {\Omega }^2\hfill \end{array}\right).\hfill \end{array}$$ 12

The eigenvalues μ of the Jacobian matrix are solutions of the cubic equation −μ³ + τμ² + νμ + Δ = 0, with τ the trace and Δ the determinant. The three coefficients of the characteristic polynomial depend on β and read

$$\left\{\begin{array}{c}\tau =\frac{k{\alpha }^2{u}_{\star }^2}{\gamma }\left[k-\frac{2\beta \eta \gamma {\gamma }_{\mathbf{p}}}{{\alpha }^2\left(1+k{\alpha }^2{u}_{\star }^2\right)}\right],\hfill \\ \Delta =-\frac{4k{\gamma }_{\mathbf{p}}^2}{{\gamma }^2}\left[\beta -{\beta }_{\mathrm{c}}-\frac{\beta \eta \gamma }{{\alpha }^2}\left(\frac{k{\alpha }^2{u}_{\star }^2}{1+k{\alpha }^2{u}_{\star }^2}\right)\right],\hfill \\ \nu =-\frac{2k{\gamma }_{\mathbf{p}}}{\gamma }\left[\left(1+\beta \eta k{u}_{\star }^2\right)\left(2-\frac{k{\alpha }^2{u}_{\star }^2}{1+k{\alpha }^2{u}_{\star }^2}\right)+k{\alpha }^2{u}_{\star }^2\right].\hfill \end{array}\right)$$ 13

The limit cycles are stable if the three eigenvalues have a negative real part. This is equivalent to imposing that τ < 0, Δ < 0 and ν + Δ/τ < 0. In Supplementary Information, we analyse extensively the conditions under which these three inequalities are verified. We show that there are ranges of parameters for which the limit cycles are stable for all values of β, leading to stable chiral states above β_c. Instead, there are some other ranges of parameters for which the limit cycles can destabilize for some values of β. Our results are summarized in the stability diagram = (γγ_p/k, γη/α²) shown in Extended Data Fig. 10.

Extended Data Fig. 10. Phase diagram representing the stability of the limit cycles of the overdamped model with an additional non-linearity.

(term η₃, see Methods and SI for further details). The region in pink corresponds to the range of parameters for which the limit cycles are stable for all values of the windsock parameter β. In the blue region, there are values of β for which the limit cycles are unstable. Because we do not observe chaotic motion of the crowd, the hydrodynamic coefficients characterizing the Chupinazo crowd in the overdamped regime lie in the pink region.

We have therefore shown that our mechanical model of confined dense crowds evolves according to a dynamics that cannot be captured by a steepest descent in an effective potential. This so-called non-reciprocal and nonlinear dynamics is here characterized by a mean-field phase transition (a bifurcation) from a trivial state to a chiral state where v chases p while p runs away from v along circular trajectories swept at constant rate. This stationary chiral dynamics can operate along two possible directions selected by initial conditions. The parity symmetry of the dynamics is spontaneously broken.

Crowds as frictional odd matter

Our stability analysis shows that the propulsive force must relax faster than the displacement field to observe spontaneous oscillations: γ_p > k/γ. This finding a posteriori justifies the relevance of the asymptotic analysis γ_p ≫ k/γ discussed in the main text, which we now detail (see also Supplementary Information). In this limit, we can ignore the time variations of the fast variable p, which is instantly slaved to u (in the absence of noise). We can then generically decompose p as p = (−K_∥ + k)u + K_⊥u^⊥, and solve for K_∥ and K_⊥ by using this form in the algebraic equation satisfied by p:

$$\mathbf{p}=\frac{\beta }{\gamma }\left(1-\frac{\eta }{{\gamma }_{\mathbf{p}}}{\mathbf{p}}^2\right)\left(-k\mathbf{u}+\mathbf{p}\right)-\frac{{\alpha }^2}{\gamma {\gamma }_{\mathbf{p}}}\left[\mathbf{p}\times \left(-k\mathbf{u}+\mathbf{p}\right)\right]\times \mathbf{p}.$$ 14

where we have used Newton’s second law to express v = ∂_tu, as a function of u and p. We are then left with a single equation for the degree of freedom u that takes the form ∂_tu = −∇V_eff(u) ± (K_⊥/γ)u^⊥, where ∇V_eff(u) = K_∥u. The dynamics of the crowd is akin to that of a particle falling in an effective potential V_eff and couples to a nonlinear odd spring K_⊥. Again the sign of K_⊥ is not a priori specified and can take both values with equal probability. We sketch the dynamics of the particle in Fig. 5e. Deep in the chiral phase (β ≫ β_c), V_eff has the shape of a ‘Mexican hat’. Once the particle reaches the minimum of the potential, u takes a finite value. In turn, the particle dynamics orbits at constant speed along the ground-state circle under the action of of the odd spring force either in the clockwise or anticlockwise direction depending of the sign of K_⊥. This minimal model nicely captures the chiral dynamics of the dense crowds and provides an intuitive explanation for its nonlinear dynamics.

Numerical methods

Numerical integration schemes

We solve equation (7) using a fourth order Runge–Kutta scheme³⁹, with a time step δt (see below). We compute the velocity, orientation and speed spectra for n_run different realizations of the random noise forces and random initial conditions. All spectra are measured in a steady-state regime after n_st preliminary integration steps specified below.

The definition of the spin ϵ(t) requires filtering the velocity field. To do so, we computed the mean velocity spectrum S_v over the n_run runs and performed a moving average of size n_w = 10. We then defined our band-pass filter by considering only the angular frequencies ω for which the value of the smoothed spectra satisfies ${\max }_{{\omega }^{\prime }}{S}_{\mathbf{v}}\left({\omega }^{\prime }\right)-S_{\mathbf{v}}\left(\omega \right)\le \left[{\max }_{{\omega }^{\prime }}{S}_{\mathbf{v}}\left({\omega }^{\prime }\right)-S_{\mathbf{v}}\left(0\right)\right]/4$ (quarter-difference between the maximum and the value of the spectrum at zero angular frequency). We finally used inverse fast Fourier transform to compute the filtered signals ${\tilde{v}}_x$ and ${\tilde{v}}_y$. From these filtered signals, we then determined the angle that the filtered velocity field makes with the x axis: $\theta =\arctan \left({\tilde{v}}_y/{\tilde{v}}_x\right)$. The resulting discontinuous time series was defined on the unit circle. We then unwound this time series to define the orientation angle over $\mathbb{R}$. Finally, we defined the spin ϵ(t) as the sign of the difference between two consecutive values of the orientation angle.

We estimated the error bars associated with the power spectra and histograms of ϵ using the jackknife method over n_run measurements³⁸.

Simulation parameters

Without loss of generality, we can set γ = 1 and α = 1, which amounts to defining our units of length and time. The model has then six control parameters, which are β, γ_p, k, η, σ and σ_p. To integrate the equations of motion, we set δt = 0.001, so that the damping coefficients in equations (1) and (2) verify k/γ ≳ 20δt and 1/γ_p ≳ 100δt for the typical values of γ_p and k that we consider. This value of δt also ensures that the angular frequency Ω_⋆ always remains in our simulation window. The number of steps n is set so that the system explores exhaustively its phase space. Finally, the number of steps n_st = 1.5 × 10⁵ is set so that the system reaches the limit cycle when β > β_c.

The n_run = 100 simulations are initialized on one of the limit cycles in the absence of noise when β > β_c, namely, $\mathbf{u}=u_{\star }(\cos \phi \widehat{\mathbf{x}}+$ $\sin \phi \widehat{\mathbf{y}})$ with φ drawn uniformly in the range $[\mathrm{-\pi },\mathrm{\pi }]$, and $\mathbf{p}=u_{\star }\sqrt{k^2+{\gamma }^2{\Omega }_{\star }^2}[\cos \left(\phi +{\varphi }_{\star }\right)\widehat{\mathbf{x}}+$ $\sin \left(\phi +{\varphi }_{\star }\right)\widehat{\mathbf{y}}]$, where $\tan {\varphi }_{\star }=\gamma {\Omega }_{\star }/k$ with equal probability for the sign of Ω_⋆. Otherwise, the simulations are initialized from u = 0 and p = 0.

For Fig. 3a–c, we used k = 0.027, γ = 1.00, γ_p = 18.00, β/β_c = 1.10, η = 0.45, σ = 0.00 and σ_p = 2.00. For Fig. 3f, we used γ = 1.00, γ_p = 18.00, η = 0.45, σ = 2.00 and σ_p = 2.00.

Online content

Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at 10.1038/s41586-024-08514-6.

Author contributions

D.B. and I.Z. designed the research. N.B., I.Z. and D.B. designed the experiments. F.G., B.G., N.B., I.Z. and D.B. built the experimental set-up and recorded the crowd dynamics. F.G., B.G. and D.B. analysed the data. B.G. and D.B. worked on the theory. All authors discussed the results. F.G., B.G. and D.B. wrote the paper. F.G. and B.G. contributed equally to this work.

Peer review

Peer review information

Nature thanks Antoine Tordeux and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.

Data availability

The data that support the plots within this paper are available on Zenodo at 10.5281/zenodo.14050598 (ref. ⁴⁰).

Code availability

All the simulation codes that support this study are available on Zenodo at 10.5281/zenodo.14050598 (ref. ⁴⁰).

Competing interests

The authors declare no competing interests.

Extended data

is available for this paper at 10.1038/s41586-024-08514-6.

Supplementary information

The online version contains supplementary material available at 10.1038/s41586-024-08514-6.