Abstract
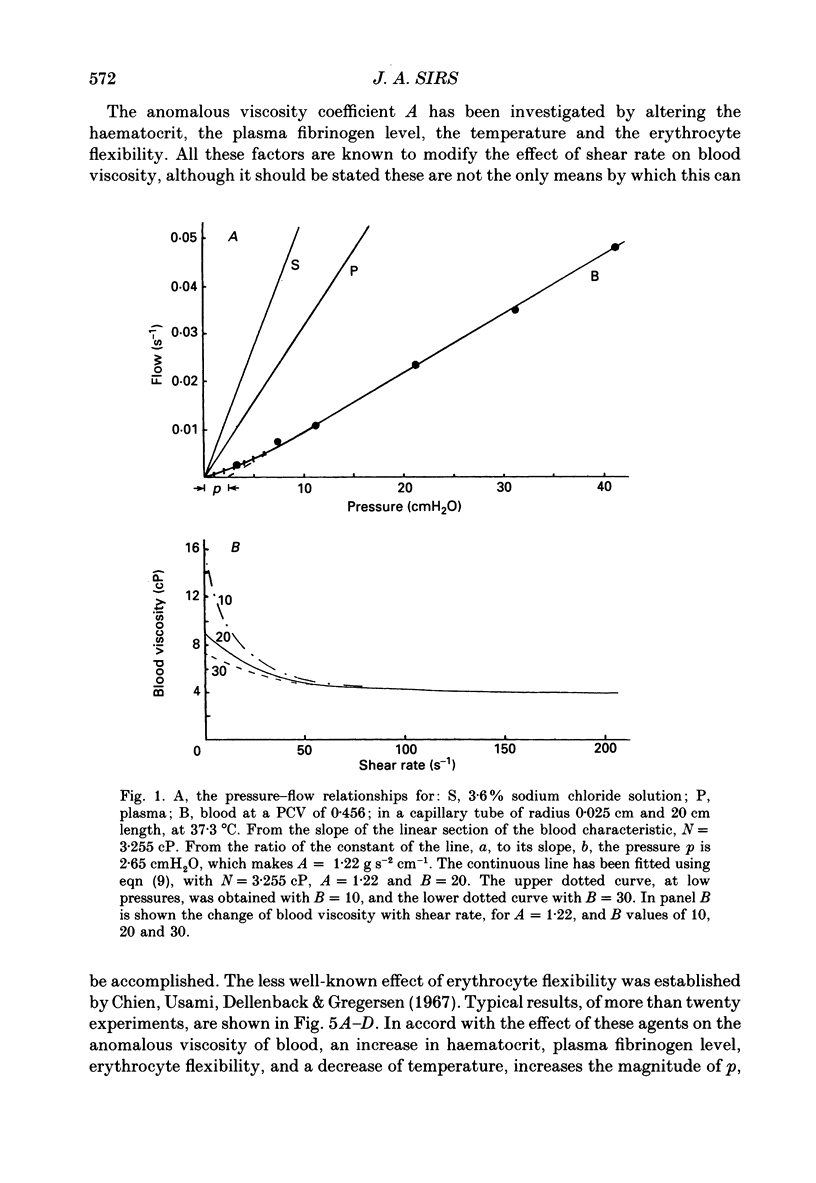
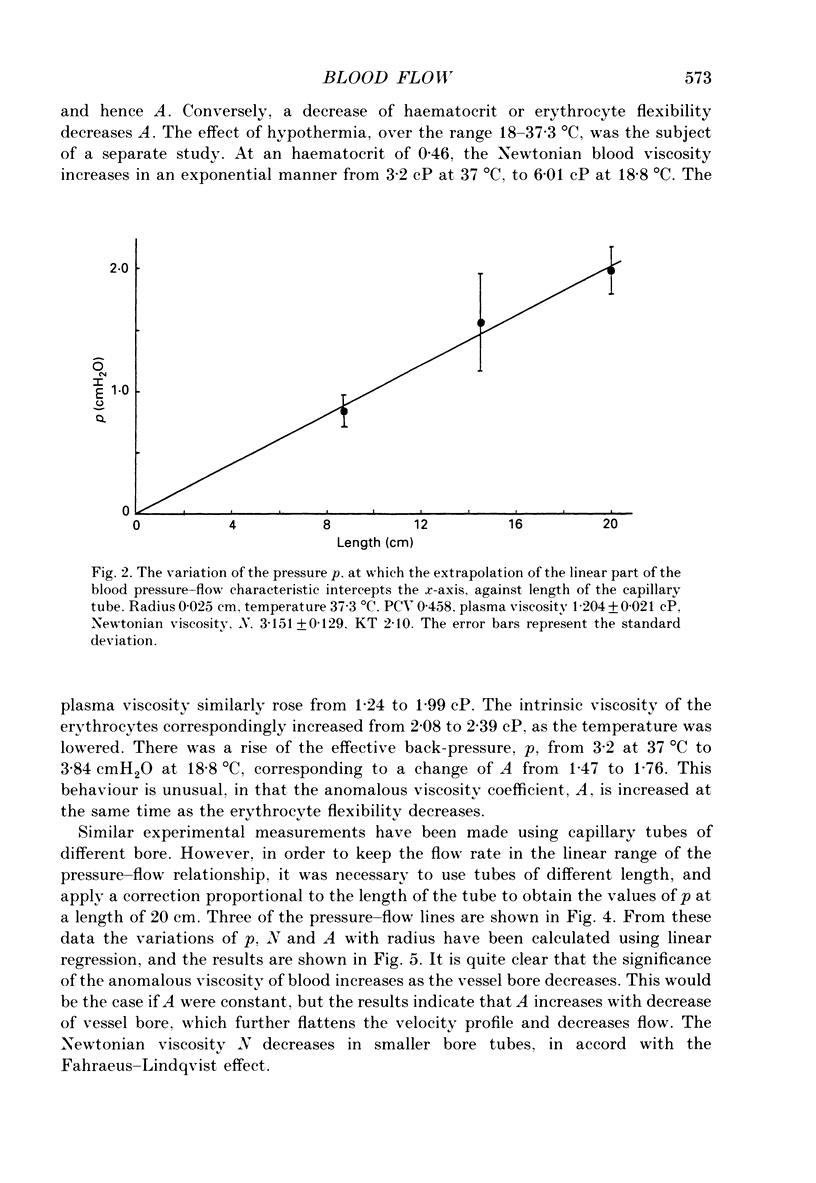
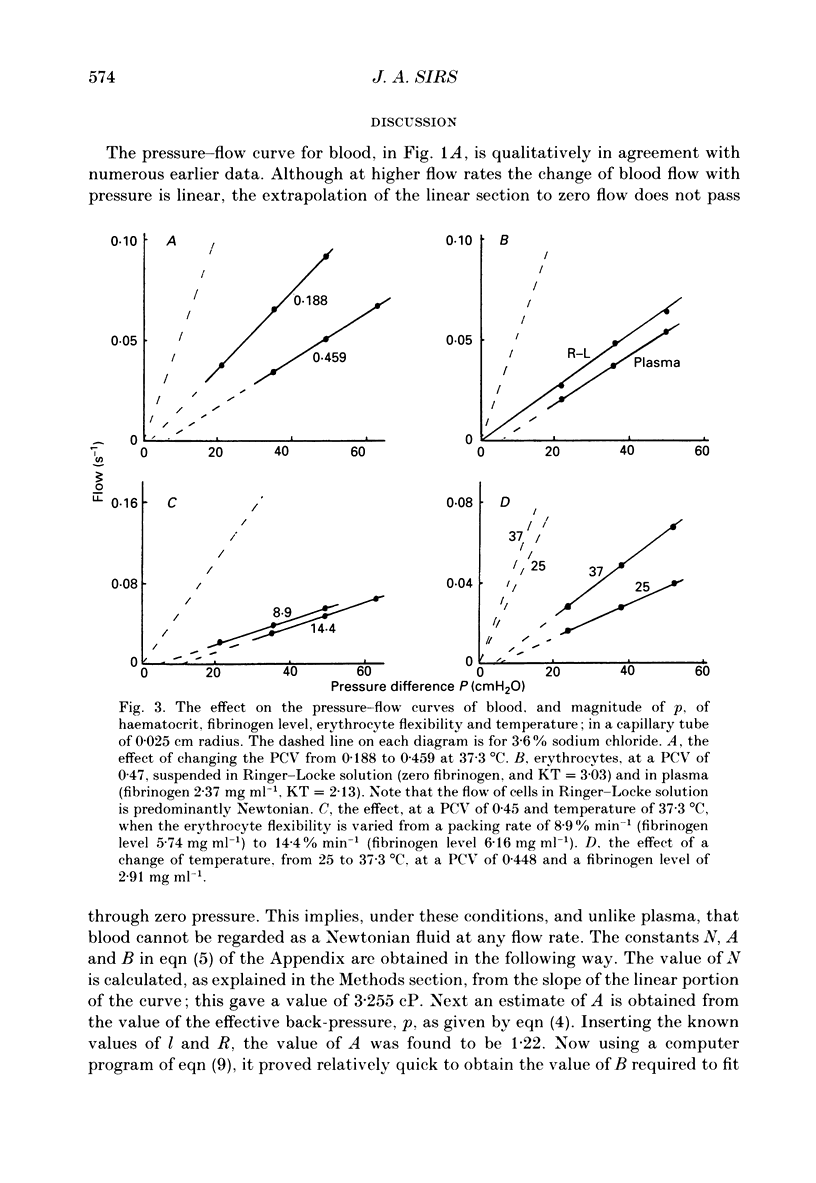
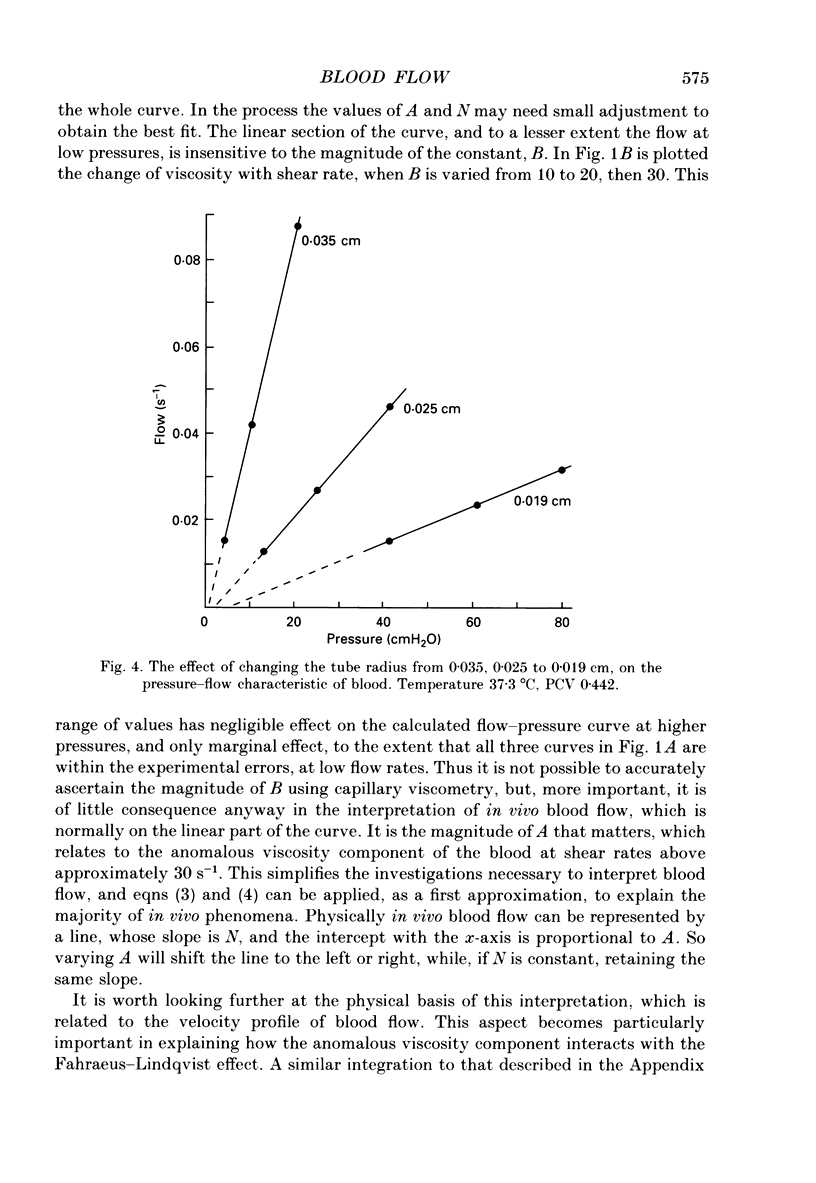
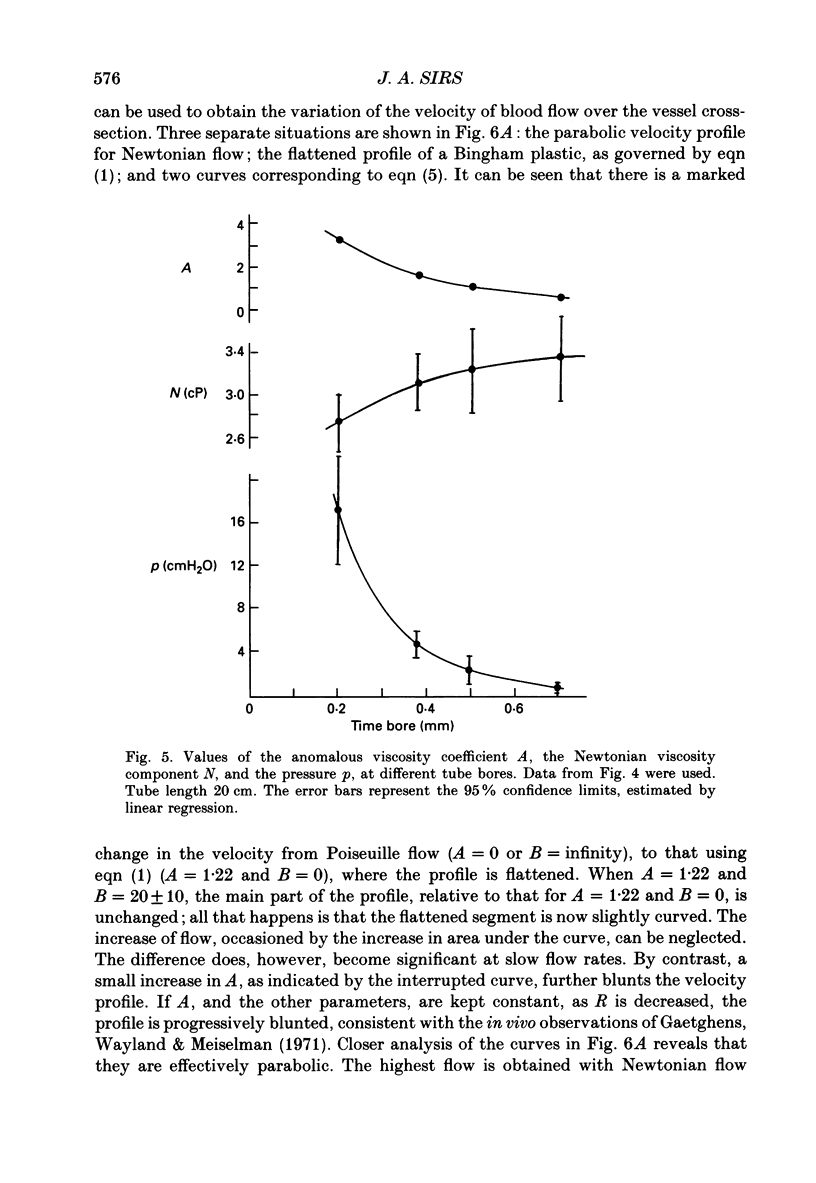
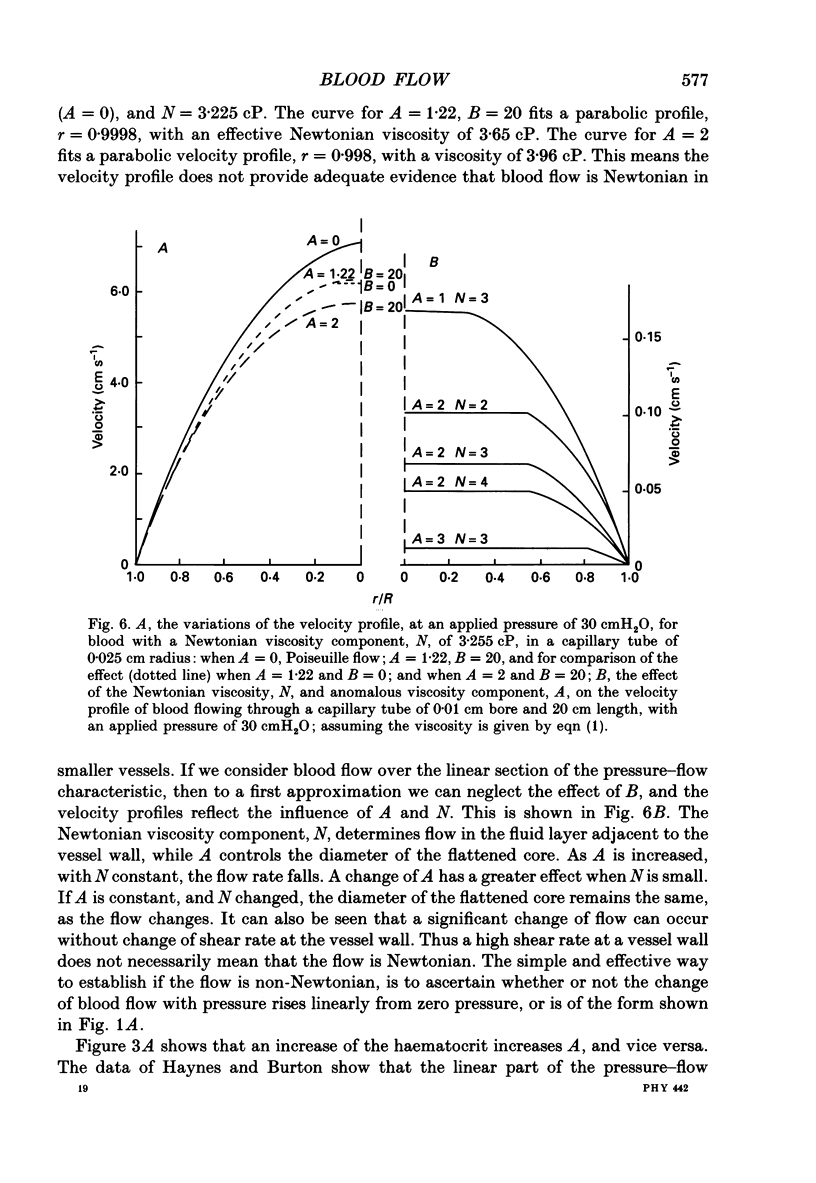
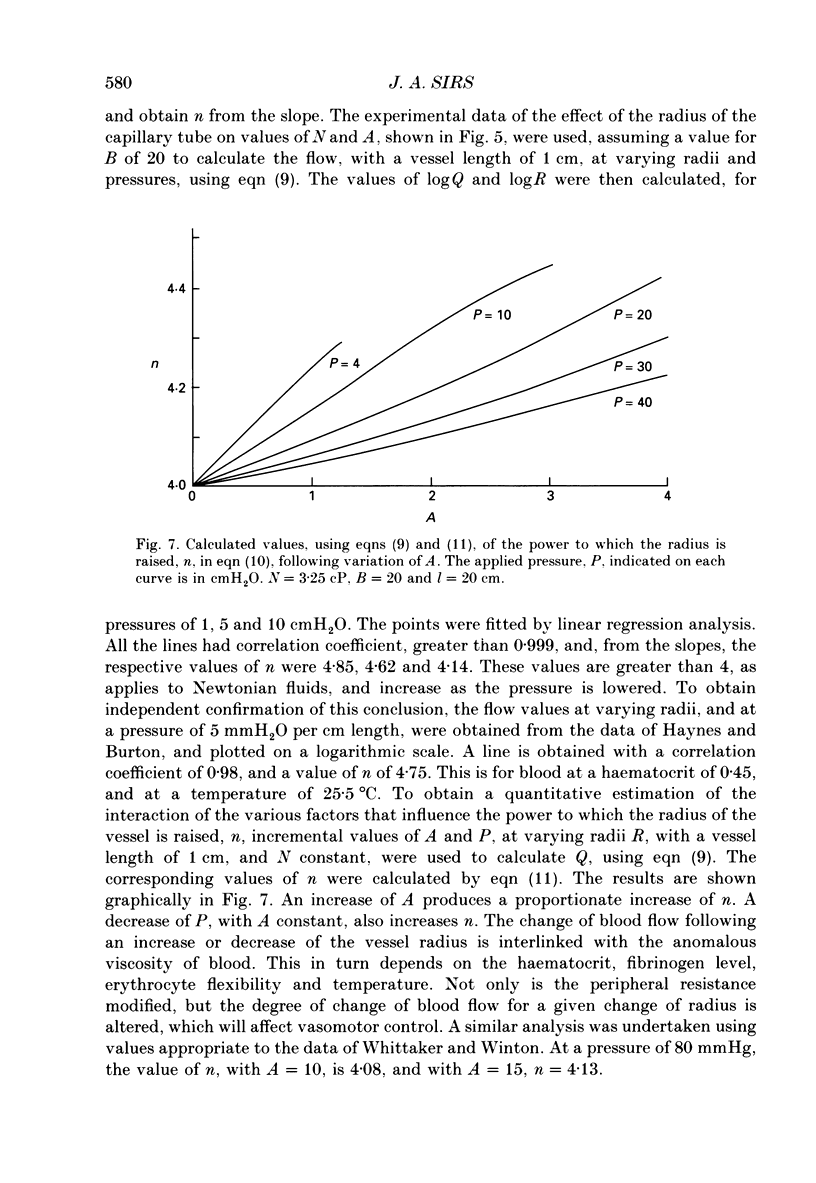
1. The current interpretation of in vivo blood flow is mainly based on the Hagen-Poiseuille equation, although blood is not a Newtonian fluid. In this paper, experimental pressure-flow curves of blood are explained on the basis that the viscosity of the blood is the sum of two components, a Newtonian viscosity term, N, and an anomalous viscosity term equal to A/(B + D), where A and B are constants, and D the shear rate. 2. To a first approximation, blood flow in capillary tubes, comparable to that in vivo, can be deduced if the applied pressure in Poiseuille's equation is reduced by an effective back-pressure, p, equal to 8Al/3R, where l is the length of the capillary tube, and R its radius. 3. The theory explains the progressive change, from a parabolic velocity profile in large vessels, to a flattened profile in small vessels, as observed in vivo. 4. Experimental evidence is given that p is proportional to the length, and increases with decrease of R. The effect of the anomalous viscosity coefficient A was studied by varying the haematocrit, fibrinogen level, erythrocyte flexibility and temperature. 5. As the tube bore is decreased, the Fahraeus-Lindqvist effect decreases N, but this is offset by an increase of the anomalous component, A. This results, at lower pressures, in an increase of the effective blood viscosity in small vessels and of the peripheral resistance, and, at higher pressures, in a decrease of the effective blood viscosity. 5. Blood flow is proportional to the radius to the power n, where n is a variable that increases with increase of A and decrease of the applied pressure.
Full text
PDF







Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Amin T. M., Sirs J. A. The blood rheology of man and various animal species. Q J Exp Physiol. 1985 Jan;70(1):37–49. doi: 10.1113/expphysiol.1985.sp002895. [DOI] [PubMed] [Google Scholar]
- Chien S., Usami S., Dellenback R. J., Gregersen M. I. Blood viscosity: influence of erythrocyte deformation. Science. 1967 Aug 18;157(3790):827–829. doi: 10.1126/science.157.3790.827. [DOI] [PubMed] [Google Scholar]
- Gregersen M. I., Bryant C. A., Hammerle W. E., Usami S., Chien S. Flow Characteristics of Human Erythrocytes through Polycarbonate Sieves. Science. 1967 Aug 18;157(3790):825–827. doi: 10.1126/science.157.3790.825. [DOI] [PubMed] [Google Scholar]
- HAYNES R. H., BURTON A. C. Role of the non-Newtonian behavior of blood in hemodynamics. Am J Physiol. 1959 Nov;197:943–950. doi: 10.1152/ajplegacy.1959.197.5.943. [DOI] [PubMed] [Google Scholar]
- Kemble J. V., Hickman J. A. Postoperative changes in blood viscosity and the influence of haematocrit and plasma-fibrinogen. Br J Surg. 1972 Aug;59(8):629–632. doi: 10.1002/bjs.1800590813. [DOI] [PubMed] [Google Scholar]
- PROTHERO J. W., BURTON A. C. The physics of blood flood in capillaries. II. The capillary resistance to flow. Biophys J. 1962 Mar;2:199–212. doi: 10.1016/s0006-3495(62)86849-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rampling M. W., Gaffney P. J. The sulphite precipitation method for fibrinogen measurement; its use on small samples in the presence of fibrinogen degradation products. Clin Chim Acta. 1976 Feb 16;67(1):43–52. doi: 10.1016/0009-8981(76)90215-1. [DOI] [PubMed] [Google Scholar]
- Sirs J. A. Automatic recording of the rate of packing of erythrocytes in blood by a centrifuge. Phys Med Biol. 1970 Jan;15(1):9–14. doi: 10.1088/0031-9155/15/1/302. [DOI] [PubMed] [Google Scholar]
- Whittaker S. R., Winton F. R. The apparent viscosity of blood flowing in the isolated hindlimb of the dog, and its variation with corpuscular concentration. J Physiol. 1933 Jul 10;78(4):339–369. doi: 10.1113/jphysiol.1933.sp003009. [DOI] [PMC free article] [PubMed] [Google Scholar]


