Use of Multivariate Linkage Analysis for Dissection of a Complex Cognitive Trait

Abstract

Replication of linkage results for complex traits has been exceedingly difficult, owing in part to the inability to measure the precise underlying phenotype, small sample sizes, genetic heterogeneity, and statistical methods employed in analysis. Often, in any particular study, multiple correlated traits have been collected, yet these have been analyzed independently or, at most, in bivariate analyses. Theoretical arguments suggest that full multivariate analysis of all available traits should offer more power to detect linkage; however, this has not yet been evaluated on a genomewide scale. Here, we conduct multivariate genomewide analyses of quantitative-trait loci that influence reading- and language-related measures in families affected with developmental dyslexia. The results of these analyses are substantially clearer than those of previous univariate analyses of the same data set, helping to resolve a number of key issues. These outcomes highlight the relevance of multivariate analysis for complex disorders for dissection of linkage results in correlated traits. The approach employed here may aid positional cloning of susceptibility genes in a wide spectrum of complex traits.

Introduction

Investigation of the genetic etiology underlying susceptibility to a common disorder often depends on the use of a number of related indices of severity for genetic mapping, since no single measure fully reflects the complex phenotype. This is the case for such common traits as asthma/atopy (Cookson 2002), late-onset diabetes (Wiltshire et al. 2002), osteoporosis/bone density (Peacock et al. 2002), and cardiovascular disorders (Mitchell et al. 1996), as well as for such major childhood learning disorders as developmental dyslexia (Fisher and DeFries 2002), specific language impairment (SLI Consortium 2002), and attention-deficit/hyperactivity disorder (Fisher et al. 2002b). The question of how to appropriately treat such correlated measures in genetic analyses is an acute issue for many complex traits. In the vast majority of previous studies involving multiple correlated measures, each measure has been analyzed independently (Cookson 2002; Fisher and DeFries 2002; Peacock et al. 2002; SLI Consortium 2002; Wiltshire et al. 2002). However, univariate approaches have a number of major drawbacks. First, there are unresolved issues regarding how best to adjust for the multiple testing of correlated measures, for which Bonferroni corrections are overconservative. Second, there is a potential loss in power when not analyzing all of the data simultaneously (Boomsma and Dolan 1998). Third, critical questions arise when attempting to interpret and integrate data from univariate linkage analysis of different measures (see Fisher and DeFries 2002). For example, if a study finds strong evidence for linkage—but only with a single measure—does that indicate that the genetic effect is somehow specific to that particular aspect of the phenotype? Further complications arise when comparing data from different data sets. If investigation of one sample reveals significant linkage to one measure whereas studies of a second sample identify linkage to the same region but with a different (yet related) measure, can this be considered to be a “replication”?

Multivariate genetic linkage analysis has the potential to resolve the above issues. The approach has long been described (Schork 1992, 1993; Amos 1994; Blangero and Almasy 1997) but to the best of our knowledge has not yet been applied beyond specific bivariate applications and analysis of candidate genes (Amos et al. 1990; Williams et al. 1999; Duggirala et al. 2001; Soria et al. 2002). In the present study, we demonstrate the utility of a full multivariate approach by applying it to developmental dyslexia, a frequent childhood disorder that involves reading difficulties that cannot be explained by lack of educational opportunity, general cognitive impairment, or gross sensorineural problems (Fisher and DeFries 2002). The reading problems associated with dyslexia are only one aspect of a complex syndrome, with a constitutional basis (Habib 2000), that is likely to involve multiple genetic risk factors (Fisher and DeFries 2002). Despite intensive studies in a variety of disciplines, the etiologic basis of dyslexia remains obscure, with contrasting theories placing different emphasis on alternative aspects of the phenotypic profile (Habib 2000).

The specific gene variants that influence dyslexia have yet to be identified, but linkage studies have mapped potential risk loci to a number of chromosomes, including 2, 3, 6, 15, and 18 (Smith et al. 1983; Cardon et al. 1994, 1995; Grigorenko et al. 1997; Schulte-Körne et al. 1998; Fagerheim et al. 1999; Fisher et al. 1999, 2002a; Gayán et al. 1999; Nopola-Hemmi et al. 2001; Fisher and DeFries 2002). Some of these studies have investigated what could be referred to as a “global” phenotype, involving either qualitative analysis of a dichotomous definition of overall affection status (Smith et al. 1983; Schulte-Körne et al. 1998; Fagerheim et al. 1999; Nopola-Hemmi et al. 2001) or quantitative analysis of a continuously distributed composite index of severity (Cardon et al. 1994, 1995). However, given the observed phenotypic complexity and the lack of consensus regarding “core” deficits, there is currently much interest in the use of hypothetical components that appear to tap distinct but related features of the cognitive profile of a dyslexic individual. This requires genetic analysis of multiple correlated measures of language- and reading-related abilities, which has previously been achieved by performing separate univariate analyses for each quantitative measure or phenotypic classification (Grigorenko et al. 1997; Fisher et al. 1999, 2002a; Gayán et al. 1999). As mentioned above, interpretation of these univariate results has raised many problems, the resolution of which represents a key challenge facing researchers in this field (Fisher and DeFries 2002). For example, some investigators have proposed, on the basis of the comparison of magnitudes of the linkage test statistic, that different components of the dyslexia phenotype might map to distinct genetic loci and that this could reflect simple one-to-one relationships between genes and separable cognitive processes (Grigorenko et al. 1997). However, it has been argued that levels of linkage may vary owing to factors that are unconnected to the size of the underlying genetic effect, including the sensitivity of the psychometric test, the age distribution of the sample, or stochastic influences resulting from small sample size (Fisher et al. 1999, 2002a).

In earlier work, using a univariate variance-components approach (Fisher et al. 1999, 2002a), we investigated genomewide linkage to multiple reading- and language-related measures in U.K. families with dyslexia. We identified a number of regions that might harbor genes influencing dyslexia, but results tended to be inconsistent for different measures, highlighting the aforementioned limitations of univariate analyses. Two observations were of particular interest, the first of which was a replication of linkage to 6p21.3 (Cardon et al. 1994, 1995) and the second of which was a highly significant novel finding on 18p11.2. For 6p21.3, there was evidence of linkage to tests of phoneme awareness (PA), phonological decoding (PD), orthographic coding (OC-irreg), and single-word reading (read), but with some variability in levels of significance. For 18p11.2, the discrepancy between the measures was even more marked, with strong linkage evidence for single-word reading, exceeding genomewide significance (P=.00001). The remaining measures showed only weak support for linkage to 18p11.2 (all P values >.01). When a univariate framework is used, it is not possible to evaluate the relationships between these correlated measures with regard to any specific QTL. Here, we employ a multivariate linkage approach in an attempt to overcome many of the drawbacks associated with previous attempts, for the dissection of this complex cognitive trait.

Sample and Methods

The Sample

The families were identified through a dyslexia clinic at the Royal Berkshire Hospital (Reading, United Kingdom). Children were ascertained as probands if their single-word reading was >2 SDs below that predicted by tests of verbal or nonverbal reasoning. The family of a proband was then included in the study if there was evidence of reading disability in one or more siblings, on the basis of either parental reports or school history (Fisher et al. 1999). Eighty-nine nuclear families, comprising 224 siblings (135 independent or 195 total sibling pairs), were ascertained to form the initial set of families in this study. A second set of families were also collected, composed of 84 families (112 independent or 143 total sibling pairs).

All the children in both samples were administered a battery of standardized psychometric tests. These included tests of single-word reading, spelling, a series of reading-related measures devised to tap either the phonological or orthographic processes involved in reading, as well as measures of intelligence quotient (IQ). The reading (read) and spelling (spell) tests were taken from the British Ability Scales (BAS) (Elliot et al. 1983). The phonological measures included a nonword reading test (Castles and Coltheart 1993) to assess PD, as well as a measure of PA, which involves the oral manipulation of phonemes to form spoonerisms (Gallagher and Frederickson 1995). The orthographic measures included a test of irregular-word reading (OC-irreg) (Castles and Coltheart 1993) and a forced-choice task to identify the correct spelling of a word compared with a phonologically identical nonword (OC-choice) (Gayán and Olson 2001). Two subtests of verbal and nonverbal reasoning were taken from the BAS, to assess an individual’s IQ. The ascertainment criteria and descriptive statistics of the phenotypic measures for these families have been reported in detail elsewhere (Marlow et al. 2001). In the present study, all the reading-related measures were shown to have moderate-to-high phenotypic correlations with one another (range 0.38–0.80), with the majority of the measures correlated >0.50. As the phenotyped sample was composed only of siblings, genetic and shared environmental effects were confounded. Estimates of the proportion of phenotypic variance attributable to these combined familial effects are termed “familialities.” Assessment of the degree of familiality indicated substantial familial variation in all the measures (range 0.37–0.80) and were very similar to previous estimates obtained from this sample (Marlow et al. 2001). Any differences are likely to be due to the removal of two individuals from the present study, because a maximum of four siblings per family were accommodated in the current analysis. We imposed a restriction of four siblings per family in these analyses for computational efficiency; it is not a practical restriction of the Mx computer package (Neale 1995; for the Mx script, see the WTCHG Bioinformatics Website) or of the underlying statistical theory, which can be generalized to larger families. Familial correlations between each of the measures in the current data set are high (range 0.47–0.94), indicating a high degree of genetic similarity between the majority of the measures. This suggests that the measurements should be amenable to multivariate linkage analysis. Furthermore, twin studies support the presence of genetic effects influencing the covariance between multiple reading- and language-related measures, as well as those influencing independent trait variance (Gayán and Olson 2001).

A complete genome scan was performed on the first set of families by using 401 polymorphic markers (Fisher et al. 2002a). Data were also included from 16 markers genotyped for targeted studies of 6p21.3 (Fisher et al. 1999). The second set of families were analyzed for replication and were genotyped only for five markers on 18p11 (Fisher et al. 2002a). Univariate analyses across the entire genome have been described elsewhere (Fisher et al. 2002a).

Statistical Analysis

The present study employed a Cholesky decomposition framework for covariance modeling (Neale and Cardon 1992; Eaves et al. 1996), in which the expected covariance matrix is decomposed into the product of a saturated lower triangular matrix and its transpose. This factorial representation ensures that estimates of the covariance matrix are positive definite. For N traits and S_i siblings in family i, the Cholesky model for siblings includes an N×N triangular matrix of additive genetic (A) effects that also contain the shared sibling environmental effects plus a matrix of nonshared environmental effects (E):

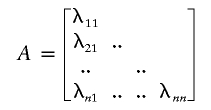and

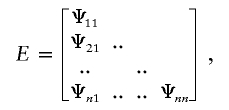where n=6 for the present study and where λ_kl and ψ_kl represent the factor loadings of the kth trait on the lth factor (k=1,…,n; l=1,…,k).

For each family, the sibling covariance matrix, Σ, is a square matrix of dimensions NS_i×NS_i. For example, for two siblings,

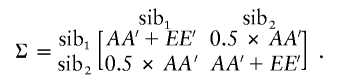In the absence of shared environmental and nonadditive genetic effects, the product matrices AA′ and EE′ are the expected covariance matrices owing to additive genetic and nonshared environmental effects, respectively. For the present data set, families with as many as four siblings were included, and, for each sibling, six variables were measured. All the variables were Z-transformed across all individuals prior to analysis. For QTL estimation, the addition of estimates of the identity-by-descent (IBD)–sharing probability extends the expected sibling-pair covariance matrix to be

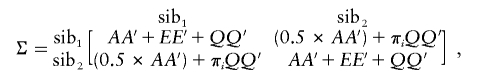where 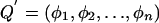, so that the QTL variance for the kth trait is φ²_k and the QTL covariance between traits k and j is φ_kφ_j, and where π_i is the proportion of alleles shared IBD by the ith sibling pair. In the absence of shared environmental and nonadditive genetic effects, the matrices AA′ and EE′ are as before, and the additional matrix QQ′ represents the contribution of the QTL at each location. GH2.0 (Pratt et al. 2000) was used to obtain multipoint estimates of sharing probabilities between each sibling pair at equally spaced intervals along the genome. When the observed covariances are influenced by shared environmental effects, the cross-sibling scalar factor of 0.5 may be insufficient to account for the additional familiality. In the present results, the testing of different scalar values revealed no appreciable biases in the likelihood-ratio tests (data not shown).

A weighted maximum-likelihood approach was used to estimate the polygenic, nonshared environmental, and QTL effects on the basis of the covariance structure of the sibling pairs conditional on their sharing probabilities at each position in the genome. The likelihood of the vector of phenotypes (X) in each family (i), X_i, was

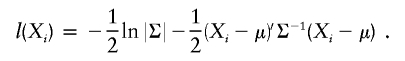Minimization of this function and all model comparisons were performed in Mx (Neale 1995; for the Mx script, see the WTCHG Bioinformatics Website).

The overall evidence for a QTL at each position in the genome was tested by allowing A and E to be full rank with maximum-likelihood values estimated with and without all parameters in Q in the model. The difference between these two nested models is distributed asymptotically as χ². In univariate variance-components models, this χ² is drawn from a 50:50 mixture of χ² distributions having 1 df and point mass 0 (Self and Liang 1987); however, the underlying χ² distribution for multivariate models has not been described. We conducted 25,000 simulations of the same environmental and background polygenic covariances observed in our data, combined with a null model of no QTL effects on any trait. Surprisingly, modeling these effects by use of the same models as were applied to the reading data yielded a χ² distribution that resembled a standard χ² distribution with 6 df—that is, one with degrees of freedom equal to the difference in numbers of parameters estimated in the full model and the model of no QTL effects (χ² mean 6.05; variance 11.878). The .05 and .01 significance levels also resembled those of a 6-df χ² distribution (χ² [.05] observed 12.46 vs. expected 12.59; χ² [.01] observed 16.76 vs. expected 16.80), although they were slightly conservative. The simulations suggest that the degrees of freedom in multivariate applications may be more complicated than in the univariate case (we conducted univariate simulations by using the same computer programs, the results of which closely matched the 50:50 mixture, as expected [Amos et al. 2001]). Because this issue warrants further detailed attention, we used the conservative convention of degrees of freedom equal to the difference in nested-model parameters for all analyses.

Within this likelihood framework, the contribution that each variable makes to the evidence of linkage can be estimated by comparing the likelihood of the model with and without the parameter. If the fit is not significantly decreased by removing the parameter, then it can be dropped from the model; however, if the fit is significantly worse, then the parameter should remain in the model, since it is contributing to the multivariate evidence for linkage.

This variance-components approach assumes multivariate normality and is known to be sensitive to departures from that assumption (e.g., see Allison et al. 1999). Although these samples were initially ascertained for dyslexia, the selection scheme did not induce substantial deviations from normality for the quantitative traits examined here (Marlow et al. 2001). Each variable has been assessed for univariate normality, and none showed a significant deviation. Also, the significance levels of the univariate variance-components results have been assessed empirically through simulation. The PA measure behaved as predicted by theory, and the other variables showed a slightly inflated level of significance (Fisher et al. 2002a).

Results

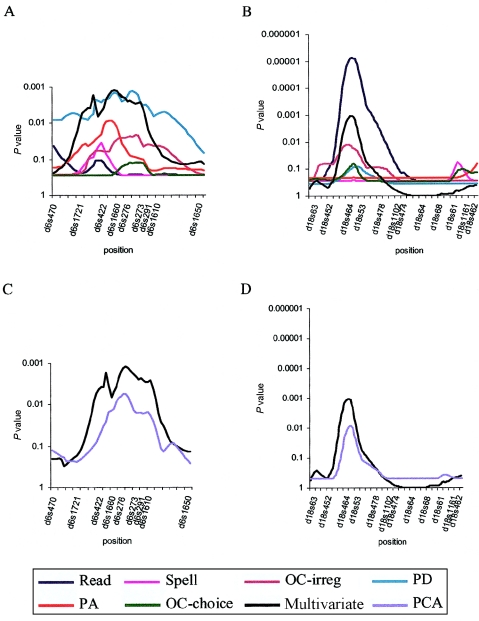
We evaluated the putative QTLs on chromosomes 6 and 18 by using the U.K. data set (Fisher et al. 1999, 2002a). For chromosome 6 (fig. 1A), the multivariate analysis outperformed all the univariate analyses (P = .0012, with 6 df, vs. most significant univariate measure [PD]: P=.0014, with 1 df). In contrast, for chromosome 18 (fig. 1B), the multivariate result is not as significant (P=.0011) as the univariate result for the highest single measure (read, P=.00001). These results point to an increase in power on chromosome 6 but a different pattern on chromosome 18. With regard to chromosome 18, it is likely that the significance level of the multivariate linkage is conservative owing to the estimation of all parameters—that is, it may be possible to reduce the degrees of freedom if some of the parameters are statistically equal. In addition, the results suggest that the univariate result for single-word reading on chromosome 18 may be inflated owing to the stochastic effects of sampling a complex trait. That is, a genome scan was conducted, and, in univariate analyses, the maximal evidence came from a single trait even though six were examined. If a QTL on chromosome 18 truly influences multiple aspects of reading disability, then the specific pattern of univariate results could result, in part, from random fluctuations. Therefore, the more modest multivariate result probably better reflects the true effect of the QTL on chromosome 18, and the additional information available through the covariance of each measure allows a more precise estimation in the same sample.

Figure 1.

Multivariate and univariate linkage analysis of the six reading-related measures—on a 54-cM region of chromosome 6p (A) and a 137-cM region spanning the whole of chromosome 18 (B)—and comparison of multivariate linkage and use of the first factor from a PCA approach as the phenotypic measure for linkage analysis, on chromosomes 6p (C) and 18 (D). A subset of the markers are shown on the graphs. The significance of the linkage results are reported in all cases as P values. For univariate measures, the P values are empirically derived as described elsewhere (Fisher et al. 2002a); for multivariate and PCA results, the P values are asymptotic, as described in the text.

We also examined the effect that each of the measures contributed to the multivariate result. Formal assessments of the effect of each trait, considered simultaneously in the context of all other measures (table 1), indicated that all reading- and language-related parameters contributed significantly to the multivariate linkage on chromosomes 6 and 18 at the 5% level. On chromosome 18, even measures that appear unlinked in univariate analyses (e.g., spell and PA) are highly significant in the multivariate analysis, owing to the extent to which the covariance between these measures is linked to this QTL.

Table 1.

Significance of Each Measure with Respect to the Multivariate Linkage on Chromosomes 6 and 18

Model (No. of Parameters)a	−2*LLb	χ2c	dfd	Pe
Chromsome 6:
Full (54)	2,672.130
Drop OC-irreg (53)	2,681.940	9.81	1	.0002
Drop PD (53)	2,691.335	19.205	1	.00001
Drop spell (53)	2,686.122	13.992	1	.0002
Drop read (53)	2,678.557	6.427	1	.01
Drop PA (53)	2,687.246	15.116	1	.0001
Drop OC-choice (53)	2,677.195	5.065	1	.02
Chromosome 18:
Full (54)	2,671.991
Drop OC-irreg (53)	2,691.974	19.983	1	.000007
Drop PD (53)	2,688.087	16.096	1	.00006
Drop spell (53)	2,686.953	14.962	1	.0001
Drop read (53)	2,693.516	21.525	1	.000004
Drop PA (53)	2,679.563	7.572	1	.006
Drop OC-choice (53)	2,687.486	15.495	1	.00008

^aIn the full model, there are 54 parameters; these refer to the 21 parameters for both the polygenic and environmental matrices, the 6 parameters for the QTL matrix, and the 6 means. Each model was tested against the full model.

^bThe −2*log likelihood for each model.

^cThe difference between the two likelihoods (full model vs. model shown).

^dThe difference in the number of parameters between the two models.

^eTaken from standard tables.

The effect that IQ has on the multivariate analysis at these two loci was also tested. IQ is modestly phenotypically correlated with the other psychometric measures in this sample (range 0.22–0.38) (Marlow et al. 2001), and, in univariate variance-components analysis, the IQ measure is nonsignificant for the QTLs on chromosomes 6 and 18 (data not shown). Table 2 shows the results of including the IQ measure for each chromosome. Dropping the IQ parameter from the full model does not result in a significant change in the likelihood; thus, modeling of IQ does not improve the fit of the model for either QTL.

Table 2.

Effect of IQ on Multivariate Linkage to Chromosomes 6 and 18, Assessed Using a Likelihood-Ratio Approach^[Note]

	Chromosome 6	Chromosome 18
−2*LL:
Full model	3,125.461	3,133.159
Drop IQ	3,128.456	3,135.931
χ2 (with 1 df)	2.995	2.772
P value	.08a	.10a

Note.— The variables are as described in table 1.

^aNonsignificant at the 5% level.

As an alternative to a multivariate analysis that includes the genetic relationship between individuals, it is possible to construct a composite phenotype by use of principal-components analysis (PCA), factor analysis, or other grouping schemes (Allison et al. 1998). Linkage analysis can then be performed on this composite measure. For the comparison of these approaches, PCA was performed for the six reading-related measures. The loadings from the first factor (which accounted for 54% of the variance) were used to construct a score that was then used in univariate linkage analyses of chromosomes 6 and 18. In both cases, the full multivariate approach outperformed the use of a PCA score (figs. 1C and 1D). For chromosomes 6 and 18, the use of a PCA score decreased the significance level (on chromosome 6, the PCA P=.006, as compared with the multivariate P=.0012; on chromosome 18, the PCA P=.009, as compared with the multivariate P=.0011). The discrepancy between the two methods is presumably due both to the underlying effect that the QTL has on the variance and covariance of each of the measures and to the extent that this effect differs at the phenotypic and genetic levels. If the pattern is similar at both levels, then little difference would be expected between the methods; if the pattern differs, then so would their performances. How an unknown QTL affects the variance and covariance of multiple measures cannot be known in advance; however, an advantage of the full multivariate approach is that it incorporates all the data, allowing the known genetic relationships and the molecular data to best estimate the genetic and environmental influences on the set of phenotypes.

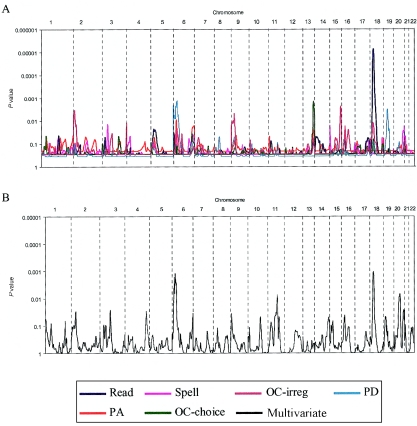
Having compared the PCA approach with the multivariate approach, we subsequently analyzed data from the remainder of the genome in the U.K. families by using the multivariate framework (fig. 2). Although the findings on chromosomes 6 and 18 remained the most significant (with both having similar significance levels when the multivariate models were used), this contrasted with the results of univariate analysis, in which chromosome 18 gave a much higher significance level for the measure of reading. No other loci stand out with the same level of significance as do chromosomes 6 and 18; however, the next two most significant loci are on chromosomes 11 and 20. These two regions were not identified in the multipoint univariate analysis. Currently, these two loci are being followed up in a second set of U.K. families. A number of peaks (chromosomes 2, 3, and 9) appeared in both the univariate and multivariate results, as did discrepancies between the two analyses. These are regions where further modeling will be performed, to investigate which measures are affecting the multivariate linkage.

Figure 2.

Complete genome screen for the U.K. sample with dyslexia. A, Univariate approach, analyzing the six reading-related measures. B, Multivariate approach. The significance of the linkage results is reported in all cases as P values. For univariate measures, the P values are empirically derived as described elsewhere (Fisher et al. 2002a); for multivariate results, the P values are asymptotic. The chromosome numbers along the top indicate the location of the results.

The use of the multivariate approach can assist in the interpretation of putative replication findings. In our previous work, we obtained evidence of linkage to 18p11.2 in a second set of families from the United Kingdom (Fisher et al. 2002a). Univariate analyses revealed that the location of linkage in this second U.K. set was virtually identical to that in the genome-scan families; however, whereas the genome-scan data set had shown strongest linkage to the single-word–reading measure, the most significant findings in the second set were for the PA test. The lack of concordance between measures raised concerns over whether this finding represented a true replication (Fisher et al. 2002a). The multivariate analyses of the U.K. genome-scan sample that we have presented here demonstrate that all the measures significantly contribute to the linkage on chromosome 18 in the initial data set. The replication data set was analyzed using the multivariate approach, and, again, each parameter was tested to see if it significantly contributed to the fit of the model. All the reading-related measures except spelling contributed to the multivariate linkage on chromosome 18 (table 3). These results suggest that a locus (or loci) on 18p11.2 influences multiple measures in each data set and that the independent findings comprise a true replication.

Table 3.

Significance of Each Measure with Respect to the Multivariate Linkage on Chromosome 18 for the Replication Set of Families^[Note]

Model (No. of Parameters)	−2*LL	χ2	df	P
Full (54)	2,766.236
Drop OC-irreg (53)	2,773.117	6.881	1	.009
Drop PD (53)	2,774.062	7.826	1	.005
Drop spell (53)	2,769.052	2.816	1	.09a
Drop read (53)	2,773.260	7.024	1	.008
Drop PA (53)	2,776.654	10.418	1	.001
Drop OC-choice (53)	2,771.202	4.966	1	.03

Note.— The variables are as described in table 1.

^aNonsignificant at the 5% level.

Discussion

Here, we have described the first full multivariate genomewide screen, to our knowledge, for a complex trait, by conducting simultaneous analysis of six correlated reading- and language-related measures in a U.K.-based sample of families with dyslexia. These results provide further support for the proposal that QTLs on 6p21.3 and 18p11.2 influence dyslexia susceptibility. In addition, the present study serves as an example of the multivariate linkage approach's value for the handling of correlated measures. We have illustrated that this method has many advantages over univariate analysis and has great potential for the aiding of future positional-cloning efforts.

One drawback of the present multivariate approach is that the degrees of freedom are increased proportional to the number of traits, possibly making the test overly conservative. However, it may be possible to reduce these through further modeling. Also, there is an inherent assumption of multivariate normality when using a variance-components approach to analyze any number of measures. In the present data, all the traits are normally distributed individually, but their underlying multivariate distribution is unknown. In this case, simulation procedures can be used to estimate the effect that any departure from normality has on the size of the P value.

We have shown here that the use of multivariate analysis can resolve many of the critical issues that arise when multiple correlated measures are analyzed separately. The approach helps to remove the need to correct for multiple testing of phenotypes, and the power of the analysis can be greater owing to the increase in information in the sample that results from including the covariance between measures. It also aids in defining the measures that contribute to the linkage or replication of a region. This may clarify the pattern of QTL influence on the multiple traits, for which univariate results can be counterintuitive. Thus, our findings emphasize that researchers in the field should be cautious about drawing conclusions regarding specificity on the basis of strengths of linkage with individual traits (Fisher and DeFries 2002). Early univariate analyses of the 6p dyslexia-susceptibility locus (Grigorenko et al. 1997) led to suggestions that it was specific to PA, and, in our initial univariate investigations, 18p11.2 appeared primarily to influence single-word reading (Fisher et al. 2002a). Yet, the multivariate analysis, exploiting the additional information from the covariance between the measures, suggests that each locus has an impact on multiple traits. The increase in information also moderated the apparent bias that yielded exceptional evidence for linkage to a single trait on chromosome 18. Furthermore, using the multivariate approach, we obtained clearer evidence for replication than that observed in univariate analyses. Although univariate linkage to chromosome 18 in our replication data set was predominantly seen for a different measure from that in the first data set, multivariate analyses indicated that the QTL significantly influenced both measures in both data sets.

The increase in power gained by using a multivariate approach will vary depending on the specific patterns of the etiologic influences. If the phenotypic traits are uncorrelated both genetically and environmentally, then the multivariate approach will perform poorly in comparison with the univariate analyses, owing to the overfitting of the orthogonal data. If the only source of covariance is from nonshared environmental effects, then this may result in increased power, by reducing the error variance, or it may decrease the apparent linkage signal due to excess degrees of freedom. When background genetic effects influence the sibling covariance, their effects on power depend on the relationship with those of the QTL. Several of these patterns have been discussed in the context of simulated data and theory (Boomsma and Dolan 1998; Evans 2002), although further investigations are needed to fully explore situations in which multivariate analyses either are most appropriate or are less desirable than other strategies.

Finally, the genetic multivariate approach outperformed an alternative approach based on PCA prior to linkage analysis. As well as giving an increase in power over the use of PCA, multivariate analysis is considerably more flexible. It allows the genetic data to determine the best-fitting model to the variance and covariance of the measures and can vary at each locus. The PCA composite score is constructed without regard to the genetic relationship of the measures and is fixed throughout the genome. The multivariate approach adopted here could potentially have a wider appeal to the analysis of other complex traits.