Informative Missingness in Genetic Association Studies: Case-Parent Designs

Abstract

We consider the effect of informative missingness on association tests that use parental genotypes as controls and that allow for missing parental data. Parental data can be informatively missing when the probability of a parent being available for study is related to that parent’s genotype; when this occurs, the distribution of genotypes among observed parents is not representative of the distribution of genotypes among the missing parents. Many previously proposed procedures that allow for missing parental data assume that these distributions are the same. We propose association tests that behave well when parental data are informatively missing, under the assumption that, for a given trio of paternal, maternal, and affected offspring genotypes, the genotypes of the parents and the sex of the missing parents, but not the genotype of the affected offspring, can affect parental missingness. (This same assumption is required for validity of an analysis that ignores incomplete parent-offspring trios.) We use simulations to compare our approach with previously proposed procedures, and we show that if even small amounts of informative missingness are not taken into account, they can have large, deleterious effects on the performance of tests.

Introduction

The use of parental genotypes as controls for diseases with early onset has become the design of choice in genetic association studies because of concerns about spurious association arising from unmeasured population stratification in a traditional case-control study. Standard transmission/disequilibrium tests (TDTs) and other association tests that use parental genotypes as controls require genotype data on case probands as well as on both parents (intact trios). For some diseases, this requirement can cause difficulties, and a variety of approaches have been proposed to allow analysis of samples that include both intact trios and probands for whom genotype data from one parent is missing (Clayton 1999; Sun et al. 1999; Weinberg 1999; Cervino and Hill 2000). Although the subset of intact trios obtained by ignoring those families not having both parents available for genetic analysis can be analyzed with only minimal additional assumptions, methods allowing inclusion of probands with missing parental information have often used strong additional assumptions. In particular, most methods proposed to date assume that the distribution of genotypes of the missing parents (conditionally on genotypes of the offspring and the available parent, if any) are not different from those parents whose genotypes were observed. This assumption allows reconstruction of the missing parents’ genotype, using the parental genotype frequencies estimated among those parents who are observed. We will refer to the situation in which genotype frequencies among missing parents (conditional on offspring and the available parent, if any) is the same as that among observed parents as “missing at random” (MAR) (Little and Rubin 2002).

By contrast, informative missingness occurs when the reason that a parent is missing is related to his or her genotype at the locus of interest. Informative missingness can occur for several reasons. First, alleles at the locus may, in fact, cause or be proximal to a locus that causes the disease of interest, which may lead to differential missingness. For example, in a study of genetic factors in an aggressive form of cancer, parents carrying the disease-predisposing allele may be more likely to be missing. Second, alleles at the locus may cause—or be proximal to a locus causing a different disease that results in—parental missingness. In an era when the same candidate genes are tested for involvement in a variety of conditions, this coincidence cannot be ruled out. Alternatively, in genome scans, use of a large number of closely spaced markers increases the chance that a marker is linked to some locus that may cause parental missingness by association with a disease other than the one under study. Finally, if there is population substructure and if the propensity to be missing is correlated with allele frequency in the subpopulations, then the genotype frequencies in the intact trios will not be representative of those among the missing parents. For example, in a study of the leptin receptor gene, Chagnon et al. (2000) found 192 available parents from 99 white nuclear families but only 88 available parents from 115 African American families. Furthermore, the rarer K109R allele of the leptin receptor gene was twice as frequent in whites as in African Americans. As a result, data for this allele are informatively missing in this study. (It should be noted that Chagnon et al. analyzed white and African American families separately and hence their results are not in question.) The second and third situations described above can affect the null distribution of an association test statistic and can, as a result, lead to invalid inference, whereas the first situation only affects the alternative hypothesis (because, if a marker locus is not associated with a disease-causing locus, it is implausible that the parental missingness is related to the disease of interest) and hence only affects power.

Because there is no genotype information available on the missing parents, it may appear that informative missingness is intractable. However, we show that it is possible, by utilizing natural constraints imposed on the genotype of the missing parent by genotypes of the available parent and the offspring, to fit flexible models that allow for the effect of parental genotype on parental missingness. In the present article, we use this modeling approach to develop tests and related parameter estimates that are valid when parental data are informatively missing. Using simulated data, we compare the power and size of our approach to those of existing approaches when data are MAR, and we show that, when data are informatively missing, the performance of our approach is superior to approaches that assume MAR.

In some studies, the proportion of probands with missing parents will reflect the population proportion. In other studies, the proportion of probands with missing parents may be part of the design, and, in particular, probands with no available parents may be excluded. The methods we propose here remain valid when sampling is conditional on parental availability. We believe the approach we use is generalizable to more complicated missingness situations. In further work, we plan to consider the design in which an unaffected sib is sampled for each proband who has only one available parent. Finally, some currently available methods, such as the reconstruction-combined (RC)–TDT (Knapp 1999) and family-based association tests (FBATs) (Rabinowitz and Laird 1999; Horvath et al. 2001) do not require the MAR assumption. However, these approaches can be substantially underpowered. For example, both the RC-TDT and FBATs ignore data from families with a single affected proband and only one available parent. A recent proposal by Rabinowitz (2002) is an improvement in this regard but still ignores such families unless the lone parent is heterozygous. Furthermore, interest in these approaches is motivated by the idea that reconstruction of parental genotypes inherently introduces bias. Although it is true that use of the information in parental genotypes can introduce bias, it can also lead to increased power. For this reason, we consider here only approaches that are based, to some degree, on successful reconstruction of parental genotypes.

Association Tests with Parental Genotypes as Controls in the Presence of Informative Missingness

We adopt an approach based on likelihoods for data on the genotype G_o of an offspring and a set of parental genotypes G_p={G_f,G_m}, where G_f is the paternal genotype and G_m is the maternal genotype. We will assume a locus with two alleles, one of which may confer elevated risk either directly or by being in linkage disequilibrium with a disease-predisposing locus. Then, G_o will denote the number of copies of the selected allele in the offspring genotype (taking the value 0, 1, or 2), with the same convention for G_f and G_m. Let the missingness pattern R≡(r_f,r_m)=(1,1) if neither parent is missing, R=(0,1) if the father but not the mother is missing, R=(1,0) if the mother but not the father is missing, and R=(0,0) if both parents are missing. For a given missingness pattern R, let G^o_p and G^m_p denote the observed and missing parental genotype information, respectively, so that, for R=(1,0), G^o_p=G_f and G^m_p=G_m. If R=(1,1), then G^m_p is the empty set and G^o_p=G_p. Finally, let D_o denote the offspring phenotype with D_o=1 being affected. Following Weinberg (1999), we will refer to single-parent–single-offspring families as “dyads” and to single offspring with no parents as “monads.”

We first consider a prospective likelihood for data on parental genotypes G_p, offspring genotypes G_o, offspring disease status D_o, and parental missingness R that loosely reflects the temporal sequence of events that generate the data. The joint probability of G_p, G_o, D_o, and R can be written as:

The likelihood in equation (1) applies to the target population and not necessarily to a study population in which sampling was conditional on offspring disease status D_o or, possibly, on missingness R.

We assume that

This is a plausible assumption in many settings, because the offspring genotype can reasonably influence parental missingness only through the offspring phenotype which is included in the conditioning. However, there are situations in which this could be violated—for example, if offspring genotype affected severity of offspring phenotype, which, in turn, affected parental missingness, or if offspring genotype affected age at onset, which, in turn, affects parental missingness.

If we assume that equation (2) holds, it follows that

so that conditional probabilities of transmission are the same in families with missing parents as in intact trios. Note that, without equation (2), naive use of the TDT with data from only those probands whose parents were available would not be valid, since calculation of the null distribution of offspring genotypes conditional on parental genotypes would depend on parental missingness.

When equation (3) holds, we can develop an analysis scheme that reflects the way data are sampled in a genetic association study. By design, only affected probands (D_o=1) are sampled, and, in addition, there may be some control of the number and type of missing data patterns allowed. For example, an investigator may specify the number of intact trios and the number of dyads and may wish to exclude monads. To analyze data from such a study, we consider the distribution of the parental and offspring genotype data (G_o,G_p ) conditional on both the offspring phenotype D_o and parental missingness R, which is denoted as “L_c” and written, using equation (3), as

We will base inference on L_c; the first factor on the right of the second equal sign contains the parameters of interest, whereas the second contains nuisance parameters that must be estimated if probands with missing parental data are included in the study population. It should be noted that inference may be based on L_c, even if the sampling was not conditional on parental missingness R.

In principle, equation (1) would specify P[G_p|D_o,R] in terms of the population genotype frequencies and mating probabilities that specify P[G_p], as well as the transmission parameters in P[G_o|G_p] (e.g., see Clayton 1999). Instead, we treat P[G_p|D_o,R=(1,1)] as a primitive quantity to be estimated. Define

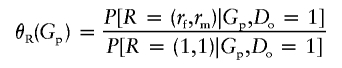and note that

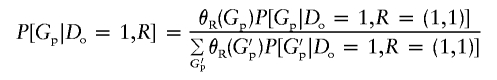(Satten and Kupper 1993; Satten and Carroll 2000). Hence, we may write equation (4) as

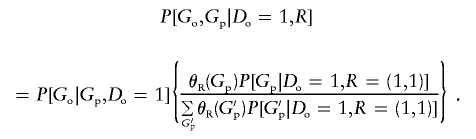To obtain a likelihood that uses only the observed parental data, we sum L_c over the parental genotypes that are missing. Let

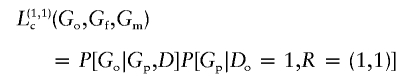and define

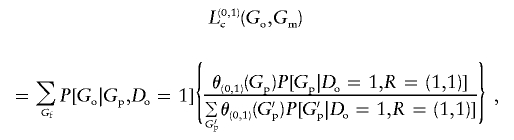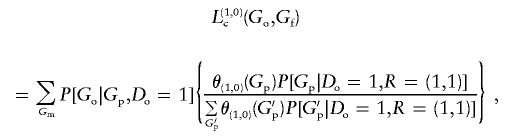and

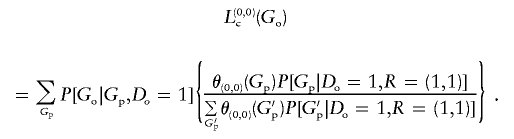Then we may write the likelihood of the proband genotype and whatever parental genotype data is observed as

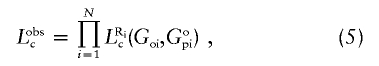where R_i, G_oi, and G^o_pi are the missingness indicator, offspring genotype, and observed parental information for the ith proband, respectively.

We use an unrestricted model for P[G_p|D_o=1,R=(1,1)] that does not assume Hardy-Weinberg equilibrium (HWE) or mating symmetry by allowing eight parameters for the nine parental mating types (the probability of the ninth parental mating type is determined by the requirement that the mating type frequencies add to one). The term P[G_o|G_p,D_o] is as calculated by Schaid and Sommer (1993) and is given in table 1. It can be written in terms of two parameters, β₁=Ln{P[D_o=1|G_o=1]/P[D_o=1|G_o=0]} and β₂=Ln{P[D_o=1|G_o=2]/P[D_o=1|G_o=0]}, or can be expressed in terms of a single parameter β if a multiplicative model (β₂=2β,β₁=β) of genetic action is assumed (for which case the maximization of P[G_o|G_p,D_o=1] for intact trio data closely resembles the TDT). If θ_R(G_p) does not depend on G_p, then P[G_p|D_o=1,R]=P[G_p|D_o=1] and our likelihood reduces to that of Weinberg (1999) (see also Cervino et al. 2000), corresponding to MAR data (Little and Rubin 2002).

Table 1.

Model for Transmission Disequilibrium, after Schaid and Sommer (1993)

Gp={Gf,Gm}	Go	P[Go|Gp,Do=1]
{2,2}	2	1
{1,2} or {2,1}	1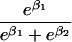
	2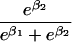
{0,2} or {2,0}	1	1
{1,1}	0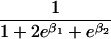
	1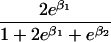
	2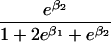
{0,1} or {1,0}	0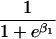
	1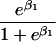
{0,0}	0	1

Because P[G_p|D_o=1,R=(1,1)] describes parental genotypes among intact trios, it is easily estimated. The odds θ_R(G_p) are more difficult to estimate, and it is not possible to fit a nonparametric model for θ_R(G_p), since, in theory, the missing parents can be as different as possible from the observed parents, within the constraint that their genotypes must be consistent with the offspring and observed parental genotype data. However, we take the view that a reasonably simple process should be generating missingness, which we can hope to capture in relatively simple models for θ_R(G_p). For example, missingness of each parent may be determined by their sex and genotype (and not their spouses’ genotype) if missingness is due to morbidity associated with the candidate locus. For loci that affect behavior, a possible model is that missingness may be determined by the total number of parental risk alleles. We propose the following family of models:

and

if the sample also includes monads, we would use

This model allows for different proportions of missing fathers and mothers (through the intercepts γ₀₁ and γ₁₀) and for separate log-linear effects of paternal genotype on paternal missingness (γ_ff), maternal genotype on paternal missingness (γ_fm), maternal genotype on maternal missingness (γ_mm), and maternal genotype on maternal missingness (γ_mf). We have found that the parameters in this model are identifiable in the simulations we have conducted. It should be noted that this model represents a considerable reduction in the potential number of parameters required to specify P[G_p|D_o,R] using an unrestricted model. The parameters in such a model are not identifiable, and even replacing equations (6) and (7) with models that have separate terms I[G_f=1], I[G_f=2], I[G_m=1], and I[G_m=2] resulted in poor convergence in some situations. The parameters γ₀₁ and γ₁₀ (and γ₀₀ if monads are included) drop out of the conditional likelihood and hence do not need to be estimated. If γ_ff=γ_fm and γ_mm=γ_mf, then the model predicts that the total number of risk alleles in the parental generation determines missingness. If γ_ff=γ_mm and γ_fm=γ_mf, then the effect of risk alleles on missingness is the same for males and females. The intercepts γ₀₁ and γ₁₀ governing the main effects of sex can still differ, so this condition corresponds to no gene-sex interaction in missingness. If γ_fm=γ_mf=0, then each parent’s missingness depends only on his or her risk alleles.

Inference about parameters β can be performed using any likelihood-based procedure, including score tests, Wald tests, or likelihood ratio tests. In addition, score and Wald tests can be calculated using robust (or “sandwich”) variances. This is appealing, because both the missingness model or the penetrance model (if β has a single component) can be misspecified, in which case variance estimates based solely on the information matrix can be misleading (Kent 1982; White 1982). In our simulations, we found that the Wald test based on the robust variance performed the best overall, followed by the robust score test of Boos (1992). An alternative approach would be to maximize P[R|G_p,D_o]P[G_o|G_p,D_o]P[G_p|D_o], as suggested (but not implemented) by Weinberg (1999). This approach can be implemented using the expectation-maximization (EM) algorithm (Dempster et al. [1977]) but involves estimating additional nuisance parameters (γ₀₁, γ₁₀, and γ₁₁). In general, conclusions from this approach should be very similar to those presented here, although in some simulations we have found slightly elevated type 1 error rates with this likelihood (results not shown).

When only intact trios are analyzed, it is possible to develop approaches that are impervious to unmeasured population stratification (e.g., the usual TDT and the approach of Schaid and Sommer [1993]). When averaging over parental genotypes, as we do here, there is the possibility of introducing a bias due to unmeasured population substructure. To understand how our approach handles this, consider likelihood L_c|z, which is like L_c but which additionally conditions on subpopulation Z:

Because P[G_o|G_p,D_o] depends only on relative risk parameters β and not absolute risks, we do not need to condition P[G_o|G_p,D_o] on Z, under the assumption that relative risks are constant across subpopulations. When L_c|z is averaged over Z, using the distribution P[Z|D_o,R], it yields:

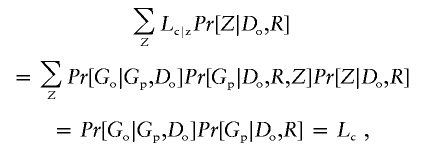which is the likelihood we consider. In other words, the conditional likelihood that is the basis of our inference is also the marginal model that results from averaging over population substructure. Thus, if the model for P[G_p|D_o,R] is saturated, then this likelihood is valid under population stratification. Unfortunately, a fully saturated model for P[G_p|D_o,R] cannot be fit when missingness is informative. Hence, the results of maximizing our conditional likelihood will be valid only to the extent that the model for Pr[G_p|D_o,R] captures the truth. In the “Simulation Examples” section below, we see empirically that our approach does provide a sufficiently rich description of parental genotypes that it remains valid under population stratification.

Finally, there has been increasing interest in parent-of-origin effects and maternal genotype effects. In principle, these can be added to the model for P[G_o|G_p,D_o], according to the methods of Weinberg et al. (1998), Wilcox et al. (1998), and Weinberg (1999). However, it is not clear whether such effects can be estimated in the presence of informative missingness, and these effects are absent in the examples considered in the next section (see the article by Weinberg [1999] for some speculation on this topic). This is an area that deserves further study.

Simulation Examples

To compare our new tests and estimators with previously proposed estimators, we conducted simulation studies with various patterns of missing parental information and varying population substructure. All data were generated using the prospective likelihood equation (1), and rejection sampling was used to achieve sampling goals for the number of trios and dyads. We have conducted a large number of simulations, from which we report the results of four scenarios that are chosen to illustrate important points. The model choices for these scenarios are summarized in table 2. For each scenario, we give results obtained using five models for θ_R, to illustrate the effects of complexity of the missingness model on the size and power of our tests. These models are all versions of equations (6 and 7), constrained as specified in table 3. Table 4 summarizes our simulation results obtained using a 1-df model of genetic action corresponding to a multiplicative increase in disease risk with each additional risk allele, with a nominal 5% size. Table 5 summarizes our simulation results obtained using a 2-df model of genetic action.

Table 2.

Summary of Scenarios Used for Simulations

Scenario,Subpopulation (z)	Pr[rf = 1|Gf = g,z]	Pr[rm = 1|Gm = g,z]	Pr[Do = 1|Go = g,z]	RiskAlleleFrequency	No. ofTrios/Dyads
1, 1	.70−.10I[g > 0]	.90−.10I[g > 0]	.05ψI[g>0]	.15	200/200
1a, 1	.70−.10I[g > 0]	.90−.10I[g > 0]	.05ψI[g>0]	.15	100/100
1b, 1	.70−.10I[g > 0]	.90−.20I[g > 0]	.05ψI[g>0]	.15	200/200
2, 1	.50	.50	.05ψg	.15	200/200
3, 1	.99	.95	(.05 · z)ψI[g > 0]	.27	200/200
3, 2	.25	.51	(.05 · z)ψI[g > 0]	.14	200/200
4, 1	.99	.95	(.05 · z)ψI[g > 0]	.14	200/200
4, 2	.25	.51	(.05 · z)ψI[g > 0]	.27	200/200
4a, 1	.99	.95	(.05 · z)ψI[g = 2]	.14	200/200
4a, 2	.25	.51	(.05 · z)ψI[g = 2]	.27	200/200

Table 3.

Summary of Parameter Constraints in Models for Missingness Odds θ_R

Model,No. of Parametersin Model for θR	Effect of MissingParent’s Genotype	Effect of AvailableParent’s Genotype
1, 1	γff = γmm	γfm = γmf = 0
2, 2	γff≠γmm	γfm = γmf = 0
3, 2	γff = γmm	γfm = γmf
4, 3	γff≠γmm	γfm = γmf
5, 4	γff≠γmm	γfm≠γmf

Table 4.

Size (ψ=1) or Power (ψ>1) of 1-df Association Tests for Various Missing Parental Data Scenarios^[Note]

	Results for Scenario
	1 with ψ =			1a with ψ =	1b with ψ =	2 with ψ =			3 with ψ =			4 with ψ =			4a with ψ =
Analysis	1.0	1.5	2.0	1.0	1.0	1.0	1.5	1.75	1.0	1.5	1.8	1.0	1.5	1.8	4.5
Intact Trios	5.0	38.5	84.1	5.1	5.1	5.1	56.6	85.6	5.0	41.1	70.1	5.1	40.6	70.7	47.2
MAR	13.9	(88.0)	(99.8)	9.2	22.3	4.8	77.4	97.1	13.9	(24.7)	(60.9)	13.7	(89.2)	(98.7)	(90.3)
TRANSMIT	14.9	(88.4)	(99.8)	10.0	25.4	4.5	77.1	97.1	14.9	(23.8)	(60.1)	18.2	(91.0)	(99.0)	(99.9)
1-TDT	8.4	(70.6)	(97.9)	6.6	13.9	4.8	70.5	94.5	5.2	49.5	80.8	5.0	50.9	82.3	66.3
Model:
1	4.4	47.7	90.6	4.7	4.6	4.6	66.9	91.9	5.2	52.1	81.1	8.3	(37.1)	(66.7)	35.3
2	4.3	48.2	90.9	4.7	4.7	4.6	66.6	92.0	5.3	52.1	81.0	8.5	(36.9)	(66.5)	35.4
3	4.5	47.9	90.9	4.7	4.7	4.6	67.2	92.1	5.3	53.1	83.0	4.8	47.1	76.3	56.3
4	4.4	48.4	91.1	4.7	4.7	4.6	66.9	92.2	5.3	52.9	82.9	4.8	46.7	76.0	56.2
5	4.4	48.4	91.1	4.8	4.7	4.7	67.0	92.2	5.2	53.0	82.9	4.8	46.5	76.1	56.1
AIC	6.1	51.9	91.3	6.8	5.4	5.6	73.6	94.6	5.4	52.9	82.9	5.1	47.0	76.5	54.4

Note.— Parentheses indicate the test is invalid because of inflated size.

Table 5.

Size (ψ=1) or Power (ψ>1) of 2-df Association Tests for Various Missing Parental Data Scenarios^[Note]

	Results for Scenario
	1 with ψ =			1b with ψ =	2 with ψ =			3 with ψ =			4 with ψ =			4a with ψ =
Analysis	1.0	1.5	2.0	1.0	1.0	1.5	1.75	1.0	1.5	1.8	1.0	1.5	1.8	4.5
Intact Trios	4.3	34.7	81.0	4.5	4.6	47.5	78.3	5.0	40.1	73.9	5.2	37.2	69.3	78.5
MAR	10.3	(81.5)	(99.6)	17.0	3.8	67.0	93.9	10.1	(32.4)	(73.0)	10.9	(84.4)	(98.5)	(98.7)
Model:
1	4.1	45.7	92.0	4.2	3.9	56.2	85.9	5.0	54.3	86.1	11.9	(54.4)	(86.2)	71.5
2	4.1	46.0	92.2	4.2	3.9	56.0	85.9	5.0	54.3	86.2	11.9	(54.6)	(86.3)	71.0
3	4.0	45.9	92.1	4.1	3.9	56.0	86.2	4.9	53.8	87.2	5.3	51.4	84.7	88.0
4	4.0	46.0	92.3	4.1	3.8	56.1	86.0	4.9	54.0	87.3	5.3	51.6	84.8	87.2
5	4.0	45.9	92.5	4.2	3.8	56.0	86.0	4.9	53.9	87.3	5.3	51.6	84.8	87.5
AIC	5.4	49.6	99.6	4.9	4.3	63.6	90.3	5.0	53.9	87.2	5.6	51.7	84.9	87.9

Note.— Parentheses indicate the test is invalid because of inflated size.

For each simulation, we generated 10,000 data sets, each having an equal number of intact trios and dyads (sample sizes given in table 2). We also give results for three previously proposed methods. The first is the likelihood-based MAR proposal of Weinberg (1999; see also Cervino and Hill [2000]). Here, we modify this proposal to use a Wald test with a robust (sandwich) variance estimate to conform to the statistic we use for our approach; results using the likelihood-ratio statistic originally proposed by Weinberg were generally similar and are not shown. For comparisons with our 1-df test, we also give results for the “robust” version of the 1-TDT of Sun et al. (1999) and the TRANSMIT program of Clayton (1999), which is available on the Internet. The original proposal of Sun et al. (1999) was flawed in that, as sample size increased (while keeping the proportion of intact trios and probands with single parents constant), the statistic increasingly weighted probands with single parents. In consultation with F. Sun, we give a modified version of this statistic in Appendix A. We also include results obtained by ignoring all data from families with only one parent, which is valid, since equation (2) is satisfied for all simulations considered here. Finally, we include the results of a model-selection procedure that automatically selects either one of the five informative missingness models of table 3 or the MAR approach, by minimizing the Akaike information criterion (AIC) (Akaike 1985).

We first show how a small amount of informative missingness can have a large, deleterious effect on the standard association tests that assume MAR; we refer to this situation as scenario 1. We generated data using a dominant disease model with phenocopy, that is, Pr[D_o=1|G_o=0]=0.05 and Pr[D_o=1|G_o>0]=0.05ψ. The risk allele had a 15% frequency in the population, and we generated parental genotypes, using assortative mating and departure from HWE corresponding to a fixation index F=0.05. Finally, each mother had a 90% chance of being genotyped if she carried no copies of the risk allele but had an 80% chance of being genotyped if she carried one or two copies of the risk allele; each father had a 70% chance of being genotyped if he carried no copies of the risk allele but had a 60% chance of being genotyped if he carried one or two copies of the risk allele.

Tables 4 and 5 give the proportion of simulations (expressed as a percent) for which the null hypothesis was rejected, for three values of the relative risk ψ. When ψ=1, the null hypothesis of no association between the locus and a locus that affects disease status holds. Hence, a valid test should reject the null hypothesis in ∼5% of simulations. This is the case for the analysis that uses only intact trios, but the 1-df MAR test rejects the null hypothesis in almost 14% of simulations; TRANSMIT rejects the null hypothesis in almost 15% of simulations. At 7.3%, the size of the 1-TDT was closer to the nominal value but was still inflated. The 2-df MAR test also performed poorly, rejecting the null hypothesis in >10% of simulations. Each of the five informative missingness models rejected the null hypothesis at a rate close to (for 1 df) or slightly below (for 2 df) the nominal rate for this scenario.

As tables 4 and 5 show, when ψ>1, accounting for informative missingness can still result in a gain in power over analysis that uses only intact trios. Interestingly, the gain in power was similar for each of models 1–5, indicating that there is no penalty for fitting a fairly rich model of informative missingness. Results for the MAR, TRANSMIT, and 1-TDT tests are given in parentheses, since they are misleading given the considerable inflation in the size of the test under the null hypothesis. The AIC procedure for 1 df shows a small gain in power over models 1–5 but, when ψ=1, the size of the AIC model-selection procedure was significantly elevated above the nominal 5%. The AIC performed better for the 2-df tests, presumably because these tests were slightly conservative.

The parameters in scenario 1a are identical to those in scenario 1, except that only 100 cases and controls were sampled in each simulation. The inflation in size of the AIC procedure is increased for 1 df (results for 2-df tests are not presented, because the relatively low allele frequency and smaller sample size led to simulated data sets with no offspring with two risk alleles). Parameters in scenario 1b are identical to those in scenario 1, except that the probability of a mother being seen if she carried one or two copies of the risk allele was lowered from 0.8 to 0.7. Here we see that the size of the 1-TDT, MAR, and TRANSMIT tests are all well above the nominal 5%. The 2-df AIC procedure is appropriately sized at 4.9%. All five models in the conditional likelihood approach do not exceed the nominal size for scenarios 1a and 1b. The 1-df and 2-df tests gave comparable power for this scenario.

In scenario 2, we considered a case where data were truly missing at random. For this simulation, parents had a 50% chance of being seen independent of genotype or sex. Data were generated using the disease model Pr[D_o=1|G_o=g]=0.05ψ^g, but all other simulation parameters are the same as in scenario 1. Because the MAR approach is valid for this scenario, all methods have the appropriate size when ψ=1. However, when ψ>1, we see that there is a cost associated with allowing for informative missingness, since the MAR test has greater power than our tests. However, allowing for informative missingness still results in an improvement over the analysis that uses only intact trios. Model selection based on the AIC recovers about half of the power lost by allowing for the possibility of informative missingness. The 2-df tests had notably less power than the 1-df tests for this scenario, because the data were generated using a log-linear disease-risk model (see table 2).

Scenario 3 corresponds to a situation in which informative missingness is the result of population stratification. The parameters for this scenario are motivated by the level of missingness found in the study of Chagnon et al. (2002). Data were generated from an admixture of two subpopulations, indexed by z=1,2, corresponding to whites and African Americans, respectively, but were analyzed assuming we were not able to stratify on ethnicity. We used Pr[z=1]=0.8 and Pr[r_f=1|z=1]=98/99, Pr[r_m=1|z=1]=94/99,Pr[r_f=1|z=2]=29/115, and Pr[r_m=1|z=2]=59/115 based on the proportions of available parents by race and sex reported by Chagnon et al. (2002). Data were generated using the disease model Pr[D_o=1|G_o=g,z]=(0.05*z)ψ^I[g>0], based on Centers for Disease Control data that the prevalence of obesity in African Americans is approximately twice that of whites (see Centers for Disease Control and Prevention Web site). We used the frequency of the R allele at the K109R RFLP in the leptin receptor gene as the risk allele reported by Chagnon et al. (2002), corresponding to frequencies 0.27 and 0.14 in whites and African Americans, respectively. Again, the sizes of the MAR and TRANSMIT tests are greatly elevated, while our approach preserves size. Interestingly, our modification of the 1-TDT performs quite well in this situation, preserving size and having nearly as great power as our approach. Surprisingly, the power of the MAR test is very low, lower even than that achieved by using only intact trios. In this scenario, the 2-df tests have slightly higher power than the 1-df tests

Scenario 4 is identical to scenario 3 except that the allele frequencies in the two subpopulations were interchanged. Here we do see a difference between the four models, with the less-rich models (1 and 2) having inflated size under the null hypothesis and markedly less power (for the 1-df tests) than even the analysis that only uses intact trios under the alternative, while the richer models have a modest gain over intact trios. Note that in this scenario the 1-TDT has moderately greater power than the 1-df conditional approach, although the 2-df approach has slightly higher power than the 1-TDT. The AIC procedure does not result in an increase in power over use of models 3, 4, or 5. Finally, scenario 4a differs from scenario 4 only in that the mode of transmission is recessive rather than dominant (so that results for ψ=1 from scenario 4 apply to scenario 4a as well). Note that a much higher effect (ψ=4.5) is required to achieve comparable power. The 1-TDT has noticeably greater power than the 1-df conditional approach, but the 2-df tests markedly outperform any of the 1-df tests

Although we have presented only four scenarios, some general conclusions can be drawn. First, our simulations show that it is possible to account for informative missingness of parental genotypes and still gain power over an analysis that uses only intact trios. When the MAR assumption is true, allowing for informative missingness can incur a loss in power. However, when missingness is informative, the MAR-based approaches can give misleading results and can even result in lower power than our new procedure. Second, it is important to use a rich enough model of missingness to guarantee appropriate test size. Fortunately, it appears that fitting rich models, such as our models 3–5, does not generally incur a decrease in test power (although we have seen rare cases in which this does, in fact, happen). Finally, the AIC model-selection procedure can result in a modest increase in power when data are MAR, but it has a slightly inflated size for 1-df tests

Comparison of tables 4 and 5 indicates that, when the genetic mechanism is not multiplicative, the 2-df tests give similar (in scenario 1) or superior (in scenarios 3 and 4) performance compared with 1-df tests. This gain in power is especially striking when the mechanism is recessive (scenario 4a). However, when the 1-df test corresponds to the correct mechanism (as in scenario 2) the 2-df test has inferior performance. These conclusions are in concordance with those of Weinberg et al. (1998) and suggest the use of 2-df tests when the mechanism is unknown or is suspected to be not multiplicative, especially if there is a chance that the mode of inheritance is recessive.

Although we have considered only hypothesis testing, our conditional-likelihood approach can also be used to estimate parameters in the relative risk model. Although we have not examined the coverage of CIs for parameter estimates under the alternative hypothesis, our results, in tables 4 and 5, when ψ=1 indicate appropriate coverage of 95% CIs under the null hypothesis (since Wald tests correspond to determining whether the 0 is contained in a CI for β).

Discussion

Genetic association studies that use parental genotypes as controls require genotype data from both parents; when these data are missing, they must be inferred in some way. Previous methods have assumed that the conditional distribution of parental genotypes among the missing parents was the same as that among the parents who were observed. We have shown that this assumption, when violated, may result in tests and estimation procedures that are severely biased. In particular, the chance of rejecting the null hypothesis when it is actually true (the size of the test) can be greatly inflated. We have proposed a conditional-likelihood approach that allows parental missingness to be informative. We have shown, through simulation studies, that the parameters in our model are identifiable and that it performs adequately in situations in which standard procedures fail. Finally, we have shown that use of the AIC to select the missingness model has close-to-appropriate size and increases the power of our procedure.

In the present article, we have considered only nuclear families with a single affected proband. Incorporating information on additional sibs (independent of affection status) can potentially increase the power of our procedure. Unfortunately, sibs may themselves be subject to informative missingness. We plan to consider this, as well as association tests for quantitative traits, in future work. Finally, informative missingness can affect other genetic studies. For example, parametric linkage analyses of pedigree data in which some founders are missing also typically assume that the distribution of genotypes of the missing spouses of founders are the same as for those founders whose genotypes are observed. We plan to consider the effect of informative missingness on linkage analyses as well.

Appendix A : Modified 1-TDT of Sun et al. (1999)

Sun et al. (1999) have proposed tests of transmission disequilibrium that use probands with only one parent (among other situations). These 1-df tests are not likelihood based but are, instead, based on comparing the relative occurrence of probands who have more risk alleles than their one available parent with probands who have fewer risk alleles than their one available parent. Sun et al. propose the following test statistic that combines data from intact trios and probands with only one parent. Let b (c) denote the number of heterozygous parents who transmit (do not transmit) the risk allele to their offspring. Let b_f (c_f) denote the number of probands whose mothers are missing and who have more (fewer) copies of the risk allele than their father. Let b_m (c_m) denote the number of probands whose fathers are missing and who have more (fewer) copies of the risk allele than their mother. Let M(P) denote the number of probands with one parent available when that parent is the mother (father). Sun et al. proposed the test statistic

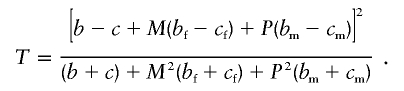This test should not be used, because the contribution from families with one parent has different scaling with sample size than the contribution from families with both parents. As the sample size increases, this statistic will increasingly favor the data from families with only one parent. After consultation with F. Sun (personal communication), we modified the statistic to replace M by M/(M+P) and to replace P by P/(M+P), so that the contribution of families with both parents and that of families with only one parent were the same. The resulting statistic is reported in the simulation results as the 1-TDT.