Estimation and Testing of Parent-of-Origin Effects for Quantitative Traits

Abstract

Recent progress in developing family-based association methods has extended their use to the analysis of quantitative traits in the offspring and to the estimation, for dichotomous traits, of the relative contribution of genetic and environmental mechanisms for parent-of-origin effects. However, many traits of interest are not naturally measured on a binary scale yet are suspected or known to be influenced by imprinted genes, and there is consequent interest in seeking evidence for parent-of-origin effects at these loci. Here we show how simple linear models can be used to estimate these parent-of-origin effects for a broad class of phenotypes; in particular, normally distributed quantitative traits are easily dealt with.

Introduction

The use of family data, particularly child-parent trios, for tests of association and linkage has expanded dramatically in recent years, and such tests have now been developed for a wide range of response and family types (Whittaker and Morris 2001). Here we present some further extensions motivated by current interest in identifying and characterizing genetic variants associated with variation in early life phenotypes, such as parameters of fetal and infantile growth, and in exploring the relationship between genetic variation, early growth, and adult disease phenotypes, such as diabetes and obesity (Hattersley and Tooke 1999). Many of the genes implicated in the regulation of early mammalian growth, such as the insulinlike growth factors and their receptors, are known to be imprinted, and there is consequent interest in seeking evidence for parent-of-origin effects at these loci. However, as noted by Weinberg and colleagues (1998, 1999), parent-of-origin effects observed in the examination of parent-offspring triads do not necessarily reflect differential genetic transmission effects. The maternal genotype, unlike the paternal counterpart, has the opportunity to influence fetal development—and potentially the risk of adult disease—through the mediation of altered uterine environment. Appropriate reparameterization of the transmission/disequilibrium test (TDT) (Spielman and Ewens 1996) allows such genetic and nongenetic parent-of-origin effects to be distinguished (Weinberg et al. 1998; Weinberg 1999), and recent studies of the effect of variation at the insulin/insulinlike growth factor 2 (IGF2) locus on type 2 diabetes (T2D) (Huxtable et al. 2000) and childhood obesity (Le Stunff et al. 2001) suggest that both may contribute to offspring phenotype. However, available methods for these analyses have been restricted to discrete traits wherein triads are ascertained on the basis of an affected proband, and it has not been possible to conduct equivalent analyses on relevant continuous traits in the offspring, such as birth weight. The purpose of the present article is to point out how easily standard linear models, similar to those used in existing methods for the analysis of quantitative traits (Allison 1997; George et al. 1999; Abecasis et al. 2000), can be used to allow the estimation and testing of genetic and nongenetic parent-of-origin effects for quantitative traits. Despite being suggested, in passing, by Allison (1997) and, as argued above, being of key importance in many studies, this does not at present seem to be widely appreciated. However, van den Oord (2000) has suggested the use of finite mixture models to perform such analyses for dialleleic loci.

For clarity, we begin with the simplest possible situation; possible extensions will be sketched later. Consider a dialleleic marker with alleles M and m, and suppose we have a sample of child-parent trios in which a quantitative trait has been measured on the offspring. Let i, j, and k be the number of M alleles in the father, mother, and child, respectively, and write 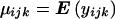for the expected value of the child phenotype in the appropriate marker class, with y_ijk∼N(μ_ijk,σ²_e). The simplest test of association is to test for a difference in means between child marker classes, that is, to test the significance of the γ_k terms in the model μ_ijk=γ_k; but this is, of course, vulnerable to population stratification. To avoid this, we exploit the fact that if the marker is not linked to a QTL (so that marker and QTL alleles are transmitted independently from parent to child), child phenotype is independent of child marker genotype, given the parental marker genotypes. Hence, we produce a test of association and linkage by testing the significance of the γ_k terms in

fitted under the constraint that β^*_ij=β^*_ji (i.e., parental symmetry) and with an appropriate constraint to ensure the parameters are identifiable. This allows for dominance and therefore gives a generalized TDT type test (Schaid 1996). The natural analogue of the original TDT (Spielman and Ewens 1996) omits the dominance term, to give the additive model

Note that, at present, these models allow only for the effect of population structure on μ_ijk. More-complicated models are possible; for example, the error variance σ²_e could also vary across strata. It would be surprising if this sort of effect were strong enough to seriously affect our results, but the standard diagnostics should, as always, be checked, and more-sophisticated or more-robust models should be fitted, as required.

Either of these models may now be extended to allow for maternal effects. The work of Weinberg (1999) would suggest adding effects for the MM and Mm maternal genotypes, to give

where I_{[ ]} is the appropriate indicator variable. However, this assumes that maternal effect is the same for all paternal genotypes. This may not hold; for example, population structure could lead to the maternal effect being more pronounced in certain strata. Thus, it may be safer to instead remove the parental symmetry constraint, to give

Note that, for this model, β_ij and γ_k are completely confounded in families where both parents are homozygous, since the values of i and j completely determine the value of k. Such families are useful in estimating σ², but their omission will generally have only a slight effect on inference for γ_k. For notational convenience, we assume the μ_ijk=β_ij+γ_k model in the remainder of the present article.

Finally, we can add genetic parent-of-origin effects. Here, we shall be concerned with the effect of paternally transmitted alleles, so let x be the number of M alleles transmitted from father to child, giving the model

Here, γ_k represents the change in mean due to inheritance of kM alleles, averaged over the possible parental/sex combinations, and τ is the change in mean due to transmission of a paternal M allele. Maternal-transmission effects can, of course, be added in the same way. It is also possible to add interactions between the transmitted allele and maternal genotype, although there may be little information in the data regarding these interaction terms.

However, when all three individuals are heterozygous, x is unknown: in the absence of other information, we can infer only that x was 1 or 0, with equal prior probability. There are a number of possible solutions to this problem. First, we could do additional typing at one or more tightly linked markers; this will often allow the parental origin of the child alleles to be resolved. Second, we could apply one of the standard statistical techniques for dealing with missing data, for example, the expectation maximization (EM) algorithm (Dempster et al. 1977), which—to express it in approximate terms—averages over the possible values of x, weighting each appropriately. Finally, we could simply replace x by its prior expectation of 0.5: this will often give a very good approximation to the more sophisticated EM-based approach.

We have described the analysis of traits with y_ijk∼N(μ_ijk,σ²_e), but these models extend easily to any exponential family distribution via the usual generalized linear model machinery (McCullagh and Nelder 1989). However, there are situations in which we may be reluctant to make distributional assumptions (e.g., when ascertainment is difficult to model, and a nonparametric test might be preferred). Permutation-based tests are often the method of choice in such situations but are problematic here. For example, we might consider testing for the presence of parent-of-origin or maternal effects by permuting the male/female parental labels or, for an effect of paternally transmitted allele or child genotype, by permuting the paternally transmitted alleles; however, there is no permutation that provides a test of the parent-specific transmission effect while including maternal effect and child-genotype terms. However, close correspondence of these permutation distributions to the closed form expected under H₀ gives reassurance that our model assumptions are reasonable, and it forms a useful supplement to the usual diagnostic tests. Alternatively, we could use methods requiring weaker assumptions, for instance, quasi–likelihood-based (Heyde 1997) or robust regression (Rousseeuw and Leroy 1987) methods.

The models described above also extend automatically to multiple alleles when the appropriate terms are added. However, the number of parameters rises very rapidly as the number of alleles increases, so consideration should be given to fitting more-parsimonious models, for instance, by omitting between-allele–interaction (i.e., dominance) terms. Multiple sibs can also be accommodated; the models described above are still appropriate, but multiple sibs cannot be treated as independent observations, because of shared environment and polygenic contributions. There are two obvious ways of dealing with intersib correlation. Generalized estimating equations may be used; alternatively, a random family effect may be added to the above models. Burton et al. (1998) give a nice introduction to these extensions of the standard linear model. Finally, other covariates may, of course, be added to these models to reflect measured environmental or genetic influences on the trait of interest. However, care must be taken with the addition of interactions between covariates and the genetic variables. For example, if an interaction between covariate and child genotype is included—but the interaction between parental marker class and the covariate is not—the model is no longer robust against population structure.

We now illustrate our approach, using previously unpublished data on the relationship between early growth and the insulin locus. Recent studies have shown that INS variable number of tandem repeats (VNTR)–associated susceptibility to T2D is preferentially transmitted through paternal class III alleles and is, by implication, mediated through imprinted mechanisms active in early life (Huxtable et al. 2000). Evidence for similar imprinting effects modulating the known association between INS-VNTR and early growth (Dunger et al. 1998) would provide further support for a common genetic mechanism. As part of a larger study of genetic influences on early growth (based on the University College London Fetal Growth Study [Hindmarsh et al. 2002]), we have analyzed data generated from 118 trios, ascertained via unselected consecutive births and genotyped for the −23Hph1 variant, which acts as a surrogate for VNTR class, with ambiguities in the parental origin of fetal alleles resolved through additional INS-VNTR class I typing. As our outcome variable, we use body length at age 6 mo, measured as a standard deviation score that is calculated using sex-specific U.K. reference data. We will concentrate on illustration of the methods introduced in the present article rather than on the underlying biology.

Fitting the model μ_ijk=β_ij+γ_k+τx, under the assumption of normally distributed errors, gives the results in table 1. The parameter estimates suggest that maternal inheritance of a class III allele increases length (γ₁,γ₂>0), whereas paternal inheritance of a class III allele reduces length (τ<0). We can investigate the statistical significance of these findings by fitting the following submodels:

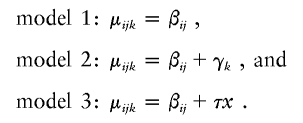The residual sums of squares (RSS), residual degrees of freedom (rdf), and Akaike's information criteria (AIC) (Akaike 1974) for these models are in table 2, together with P values and F statistics for comparisons of models 1, 2, and 3 with the full model and for comparisons of models 2 and 3 with model 1. The results are rather inconclusive. Although adding the paternal-transmission effects to a model containing the child-genotype terms significantly improves fit (P=.038), the full model μ_ijk=β_ij+γ_k+τx is not a significant improvement on model 1 (P=.159), and adding the child-genotype terms to model 3 does not significantly improve fit (P=.654). That is, the paternal-transmission effect is apparent only when the child-genotype terms are included in the model, but these terms are not, in themselves, significant. However, AIC favors model 3, in which paternal-transmission, but not child-genotype, effects are included.

Table 1.

Parameter Estimates, Standard Errors, t Value, and P Value for Full Model

Parametera	Estimate	SE	t	P
Intercept	.4325	.1641	2.64	.01
β0,1	−.1356	.4212	−.322	.748
β0,2	−.7653	.7289	−1.05	.296
β1,0	.0698	.2928	.238	.812
β2,0	.3105	.5323	.58	.561
τ	−1.0526	.5017	−2.10	.038
γ1	.7195	.4258	1.69	.094
γ2	.6548	.6923	.95	.346
β1,1-β0,1-β1,0	.1900	.5110	.372	.710
β2,1-β1,0-β0,2	1.3717	.8382	1.64	.105
β1,2-β0,1-β2,0	−.7044	1.1438	−.62	.539

^aExpressions of β_ij are parental terms, γ_i represents the effects of child genotype, and τ represents the effect of paternal transmission of a class III allele. In each case, the subscripts indicate the number of class III alleles transmitted.

Table 2.

Comparison of Models^[Note]

				Full model		Model 1
Model	RSS	rdf	AIC	F	P	F	P
Full	103.7	107	6.77	…	…	…	…
1	108.8	110	6.46	1.76	.159	…	…
2	108.0	108	9.53	4.40	.038	.426	.654
3	106.6	109	4.49	1.48	.231	2.29	.1329

Note.— Model 1 assumes no effects of child genotype or paternal transmission, model 2 assumes no effects of paternal transmission, and model 3 assumes no effects of child genotype.

The population structure and maternal effects are nowhere significant (P⩾.3), so it could be argued that we should remove them. If this is done, AIC favors a model in which both paternal-transmission and child-genotype effects are included. Again, child-genotype effects are not, in themselves, significant (P=.104), but paternal-transmission effects are significant (P=.008) in the presence of child-genotype effects.

We have assumed normally distributed errors in these analyses. This seems reasonable a priori, and, in each case, the usual diagnostic plots do not suggest any substantial departure from model assumptions. Refitting the models with the use of robust regression—specifically, MM estimation as implemented for the statistical language R in the MASS library (Venables and Ripley 1999)—also gives reassuringly similar results.

It seems that our best model for these data has both child-genotype terms and paternal-transmission effects, but substantial uncertainty remains. A further complication to interpretation is our rather low power to test the hypotheses of interest in these preliminary data. A full-power study for these methods is a substantial undertaking, because of the large parameter space that must be explored makes a full-power study a substantial undertaking, which we do not attempt here. However, we can gain considerable insight by performing a simple simulation study based on this example. Table3 shows power for each of the comparisons in table 2, with a type 1 error rate of 0.05 if we assume that the parameter estimates for the full model given in table 1 are correct and if we base simulations on the distribution of genotypes found in the current study. Sample sizes equal to or double or triple that of the current study are considered, and, in each case, power is based on 10,000 replicates. Reassuringly, we see that, although the preliminary study is rather underpowered, sample sizes to achieve high power are well within reach for effects of the magnitude found in the current study. Note also that the inclusion of paternal-transmission effects has greatly increased our power to detect effects of child genotype: for example, when the sample size is triple that of the original study, the power to detect effects of child genotype is increased from 0.27 when paternal-transmission effects are not included (so a test analogous to a standard quantitative trait TDT is performed) to 0.76 when the paternal-transmission effects are included.

Table 3.

Power for F Tests^[Note]

	Power for Comparison with
Sample Sizeand Model	Full Model	Model 1
Original:
1	.44	…
2	.54	.11
3	.31	.31
Double:
1	.78	…
2	.84	.18
3	.58	.56
Triple:
1	.93	…
2	.94	.27
3	.76	.74

Note.— Comparisons of model 1 (no effects of child genotype or paternal transmission), model 2 (no effects of paternal transmission), and model 3 (no effects of child genotype) with the full model and comparisons of models 2 and 3 with model 1. The fitted model in table 1 is assumed to be true; the significance level is .05; and the sample size is equal, double, or triple the original study size.

To conclude, we have shown how standard linear models can be used to investigate parent-of-origin effects. This is relevant not just to studies of early human phenotypes but to a wide range of traits (in humans, animal models, and domesticated species) in which important continuous traits are thought to be determined by complex interactions between imprinted genes and pre- and postnatal environment.