Affected-Sib-Pair Data Can Be Used to Distinguish Two-Locus Heterogeneity from Two-Locus Epistasis

To the Editor:

I was surprised by the conclusions of Vieland and Huang (2003), who maintain that two-locus heterogeneity cannot be distinguished from two-locus epistasis on the basis of affected-sib-pair (ASP) data. Since a number of previous studies (not cited or discussed by Vieland and Huang [2003]) have, in fact, used ASP data to distinguish between two-locus heterogeneity and two-locus epistasis (see, for example, Cordell et al. 1995, 2000; Farrall 1997), there appears to be some contradiction between the conclusions drawn by Vieland and Huang (2003) and previous work.

An obvious explanation for the contradiction would be that the definitions of heterogeneity and epistasis used by Vieland and Huang (2003) differ from those used in previous studies. There is still some debate in the literature over the precise mathematical definition of epistasis, and, indeed, the term is often used without definition, so that it is difficult to know which definition is being assumed in any given situation (Cordell 2002). Most models are defined in terms of an underlying penetrance matrix for the effects of two diallelic loci,

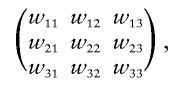where w_ij is the penetrance for genotype i at locus 1 and genotype j at locus 2 (i.e., the probability of disease, given that an individual has i-1 copies of the risk allele at locus 1 and j-1 copies of the risk allele at locus 2). Vieland and Huang appear to only consider the situation in which the underlying penetrance matrix takes one of the following forms,

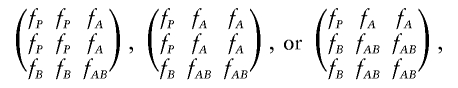which they refer to as RR (recessive-recessive), RD (recessive-dominant), and DD (dominant-dominant), respectively. Given this parameterization, they choose to define two-locus heterogeneity as the parameter restriction

and two-locus epistasis as any penetrance model not satisfying this restriction.

As pointed out by Vieland and Huang (2003), this definition does not coincide with the definition of a heterogeneity model used by Risch (1990), nor does it coincide with his definitions of an additive or a multiplicative model, all of which have, in various situations, been considered to represent a lack of epistasis (Cordell 2002). Thus, we have one immediate explanation for the apparent contradiction between the conclusions of Vieland and Huang (2003) and the results of Cordell et al. (1995, 2000) and Farrall (1997), who used the Risch (1990) definitions of heterogeneity, additivity, and multiplicativity: it is possible that ASP data can be used to distinguish two-locus heterogeneity from two-locus epistasis when these concepts are defined in terms of the Risch (1990) models of heterogeneity, additivity, and multiplicativity, but not when they are defined using the definition proposed by Vieland and Huang (2003).

Details of the methodology for distinguishing between the Risch (1990) two-locus models of heterogeneity, additivity, and multiplicativity using ASP data are described in Cordell et al. (1995, 2000) and Farrall (1997). Briefly, these authors show that the 3 × 3 matrix of (2, 1, 0) identity-by-descent (IBD)–sharing probabilities for ASPs can be written in terms of the prior IBD-sharing probabilities and eight variance-component–ratio parameters: V_A1/K², V_D1/K², V_A2/K², V_D2/K², V_A1A2/K², V_A1D2/K², V_D1A2/K², and V_D1D2/K². Here, K corresponds to the population prevalence of disease; V_Ai and V_Di correspond to the additive and dominance variances due to locus i; and V_A1A2, V_A1D2, V_A2D1, and V_D1D2 to the additive × additive, additive × dominance, dominance × additive, and dominance × dominance variances due to locus 1 and locus 2, respectively (Kempthorne 1957). Although these parameters, together with the underlying penetrances and allele frequencies from which they are derived, are not individually identifiable from the 3 × 3 matrix of IBD sharing, the eight variance-component–ratio parameters are identifiable. The fit of different penetrance models is compared by performing likelihood ratio tests, with the likelihood defined in terms of these eight variance-component–ratio parameters. The general epistatic (saturated) model corresponds to a situation in which the eight parameters are allowed to vary freely; the additive model (which can be shown to be virtually indistinguishable from the heterogeneity model with regard to IBD sharing among ASPs) corresponds to the restriction that  /V_A1A2/K²=V_A1D2/K²=V_D1A2/K²=V_D1D2/K²=0; and the multiplicative model corresponds to the combined restrictions V_A1A2/K²=V_A1/K²×V_A2/K², V_A1D2/K²=V_A1/K²×V_D2/K², V_D1A2/K²=V_D1/K²×V_A2/K², and V_D1D2/K²=V_D1/K²×V_D2/K².

Although the definition of heterogeneity proposed by Vieland and Huang (2003) does not precisely correspond to that used by Risch (1990), these definitions can, in fact, be shown to be equivalent in the special case of a model with no phenocopies (f_P=0). The rationale for the model proposed by Vieland and Huang (2003) appears to come from the desire to express the population prevalence, K, in the form

which is a natural expression for the probability of the union of two independent events. In the Risch heterogeneity model, the penetrances w_ij may be written as x_i+y_j-x_iy_j, and Risch (1990) showed that, with this parameterization, the population prevalence can also be written as

where K₁ and K₂ correspond to contributions of locus 1 and 2, respectively, so that the Risch model also leads to the desired population prevalence structure. Note that the actual definitions of K₁ and K₂ in the Risch formulation differ from the definitions of K_A and K_B in the Vieland and Huang formulation, except when f_P=0. It is not clear whether the Vieland and Huang definition of heterogeneity,

in fact leads to the desired prevalence structure if f_P≠0, since their calculation of the prevalence, K, as

(which does lead to the desired structure when K_A and K_B are defined as q²_Af_A and q²_Bf_B, respectively) in fact only holds when f_P=0. In the RR model of Vieland and Huang (2003), the Risch heterogeneity model can be shown to correspond to the restriction

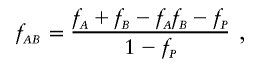which might be considered to be a more general form of heterogeneity than that proposed by Vieland and Huang (2003).

Nevertheless, Vieland and Huang (2003) are correct in stating that, given a set of penetrances satisfying either the Risch (1990) or the Vieland and Huang (2003) definition of heterogeneity, it is possible to find another set of penetrances, equally compatible with the observed IBD sharing, that does not satisfy the respective definition of heterogeneity. This is because for any set of penetrances, w_ij, it can be shown that multiplying each penetrance by a constant, C, leads to an identical set of variance-component ratios and thus to an identical set of IBD-sharing probabilities. For the additive and multiplicative models of Risch (1990), this has no effect on the underlying penetrance structure, since we may write the new penetrance as W_ij=Cw_ij=Cx_i+Cy_j=X_i+Y_j, for the additive model, and 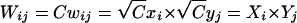, for the multiplicative model. For the heterogeneity model, however, we have W_ij=Cw_ij=Cx_i+Cy_j-Cx_iy_j, which cannot in general be written as X_i+Y_j-X_iY_j. Similarly, one can show that, on the prevalence scale, the additive and multiplicative structures (K=K₁+K₂ and K=K₁K₂, respectively) are unaltered by multiplying the penetrance matrix by a constant, but the heterogeneity structure becomes K=CK₁+CK₂-CK₁K₂ or, equivalently, K/C=K₁+K₂-K₁K₂. Thus, the models fitted by Cordell et al. (1995, 2000) and Farrall (1997) can be thought of as implicitly using this as their definition of heterogeneity on the prevalence scale, for any constant value of C. Although perhaps less satisfactory than the original structure, K=K₁+K₂-K₁K₂, it can nevertheless be seen to correspond to a situation in which the effects of the two loci act in the required form with regard to the scaled prevalence, K/C, rather than with regard to the prevalence itself. Alternatively, because of the close correspondence between the Risch heterogeneity and additive models with regard to IBD sharing among ASPs (Cordell et al. 1995), one can simply consider “heterogeneity” to be defined as corresponding to an additive model for the penetrance and prevalence structures.

The Risch definition of heterogeneity is much more general than the Vieland and Huang formulation, as it does not assume dominance or recessiveness at either locus. It has the advantage of extending to multiallelic systems and does not, as suggested by Vieland and Huang (2003), preclude models with no phenocopies (which can be modeled, for example, by allowing x₁=y₁=0). Moreover, we have seen that a generalization of this formulation leads to models for IBD-sharing probabilities that can be tested using ASP data. For all these reasons, the Risch (1990) definition would seem to be preferable to that proposed by Vieland and Huang (2003). A final question of interest is whether the penetrance models implied by either of the prevalence structures, K=K₁+K₂-K₁K₂ or K/C=K₁+K₂-K₁K₂, do in fact correspond to some biological mechanism of interest. There is still considerable debate within the literature concerning the biological interpretation of mathematical models of epistasis (Cordell 2002). Some would argue that biological models of interest at the micro scale (at the level of biochemical reactions, for example) are indistinguishable when measured at the macro scale of epidemiological studies, since many different underlying models can lead to essentially the same disease risks (Thompson 1991). As mentioned, several authors have considered departure from a multiplicative model as an indication of epistasis, which can be tested on the basis of a positive correlation between IBD-sharing probabilities at the relevant loci (Holmans 2002). This definition leads to natural tests of interaction on the log-odds scale in the standard epidemiological framework, but it is unclear whether there is any advantage to this definition with regard to elucidation of the underlying biological mechanisms. Others have used tests based on different aspects of the correlational structure of genotype data across loci (e.g., Cox et al. 1999). The relationship between these tests and tests based on mathematical models for the penetrance matrix remains to be elucidated.