Evolution of entanglement entropy at SU(N) deconfined quantum critical points

Abstract

Over past two decades, the enigma of the deconfined quantum critical point (DQCP) has attracted broad attention across physics communities, as it offers a new paradigm beyond the Landau-Ginzburg-Wilson framework. However, the nature of DQCP has been controversial based on conflicting numeric results. In our work, we demonstrate that an anomalous logarithmic behavior in the entanglement entropy (EE) persists in a class of models analogous to the DQCP. On the basis of quantum Monte Carlo computation of the EE on SU(N) DQCP spin models, we show that for a series of N smaller than a critical value, the anomalous logarithmic behavior always exists, which implies that previously determined DQCPs in these models do not belong to conformal fixed points. In contrast, when $N\ge N_{\mathrm{c}}$ with an $N_{\mathrm{c}}$ we evaluate to lie between 7 and 8, DQCPs are consistent with conformal fixed points that can be understood within the Abelian Higgs field theory.

Entanglement entropy reveals a critical N_c separating nonconformal fixed points and genuine DQCPs.

INTRODUCTION

Over the past two decades, the perplexing enigma of the deconfined quantum critical point (DQCP) (1–6) has attracted broad attention across the communities of condensed matter, from quantum materials to quantum field theory and high-energy physics. The DQCP offers a new paradigm in theory beyond the Landau-Ginzburg-Wilson framework of symmetry breaking and phase transitions (1, 4–7), which has inspired fascinating theoretical ideas such as the connection to the ‘t Hooft anomaly and higher-dimensional symmetry protected topological states (8), emergent symmetry and fractionalized degrees of freedom (9–13), etc. It has since attracted enormous efforts in numerical simulations (2, 13–18) and experiments (19–25). However, the nature of DQCP has remained highly controversial. Take the square-lattice SU(2) J-Q model (2) as an example: It was initially believed to realize a continuous quantum phase transition between Néel and valence bond solid (VBS) states, but over the years, conflicting results have been reported, such as first-order versus continuous transition (26–31), critical exponents that are found to be incompatible with conformal bootstrap bounds (3, 18, 32, 33), or possible multicritical behavior (34). No consensus has been reached to date.

Similar complications also occur in many more recent DQCP models, such as the fermionic models realizing sequences of transitions from a Dirac semimetal (DSM) through a quantum spin Hall insulator to a superconductor (16, 35), or from a DSM through a VBS to an antiferromagnet (17, 36). Although the fermionic models have several advantages over the J-Q model, e.g., the absence of symmetry-allowed quadruple monopoles and the associated second length scale that corresponds to the breaking of the assumed U(1) symmetry down to ${\mathrm{\mathbb{Z}}}_4$, incompatible critical exponents persist, and the accumulating numerical results also point toward the absence of a conformal field theory (CFT) of these DQCPs (16, 17, 35–39).

One clear sign of the perplexity of the DQCP is the anomalous logarithmic subleading contribution to the perimeter law in the finite-size scaling form of Rényi entanglement entropy (EE). It is known that for a CFT in $2+1$ dimensions, the second Rényi EE scales as (40, 41)

$$S_A^{(2)}(l_A)={\mathit{al}}_A-s\text{ln}{l}_A+c+O(1/l_A)$$ (1)

where $l_A$ is the length of the boundary between the entanglement region A and its complement $\overline{A}$, a is the coefficient of the perimeter law term, s is the coefficient of the logarithmic correction (log correction), c is a constant, and $O(1/l_A)$ denotes the leading finite-size correction. While the value of a is nonuniversal, the universal coefficient s of the log correction depends only on the geometry of the entanglement region A for a given CFT. Crucially, in a CFT when the boundary of A is smooth without any sharp corners, s must vanish. In contrast, if the boundary of A has sharp corners, then in a unitary CFT, s is generally positive and its value depends on the opening angles of the corners (40, 42, 43).

It is the goal of this work to show that the anomalous logarithmic subleading contribution, in particular a nonzero value of s for entanglement regions with smooth boundary, is actually very ubiquitous, in a series of models that can be viewed as SU(N) generalizations of the DQCP. Vanishing of the anomalous log correction determines the critical value $N_c$ of N, above which the EE measurement is consistent with the expectations of CFTs.

Our approach of analyzing DQCP is to systematically investigate the scaling of the second-order Rényi EE upon partitioning into subregions with smooth boundaries and subregions with corners (44). As a proof of concept, we choose the square-lattice SU(N) DQCP spin model (45–48) from $N=2,3$ (the J-Q model) to $N=\mathrm{5,7,8,10,12,15,18,20}$ (the $J_1-J_2$ model); see Fig. 1A. Using the nonequilibrium incremental quantum Monte Carlo (QMC) algorithm to measure the EE (49–52), we show that for $N=\mathrm{2,3,5,7}$, the previously determined DQCPs all show a finite log correction, for subregions with smooth boundaries. These DQCPs are therefore incompatible with CFT descriptions, and are most likely weakly first order. In contrast, when $N\ge 8$, the EE scaling with smooth entanglement boundaries for the DQCPs no longer has an obvious logarithmic subleading correction, and they are compatible with continuous phase transitions. This is further supported by the EE scaling at $N=8,10,\mathrm{...,18,20}$ for regions with corners, which shows a logarithmic correction with $s>0$. We find that our numerically extracted value of s for $N\ge 8$ is reasonably consistent with the expectations from the Abelian Higgs theory in the large-N limit (1, 3, 46, 53), which features unitary conformal fixed points (54–56). Thus, our results suggest the existence of a finite critical $N_{\mathrm{c}}$ above which the DQCP becomes continuous. On the basis of the behavior of EE with smooth boundary, our numerical results suggest that $N_{\mathrm{c}}$ lies between 7 and 8.

Fig. 1. SU($\mathit{N}$) ${\mathit{J}}_{\mathit{1}}\mathit{-}{\mathit{J}}_{\mathit{2}}\mathit{-}\mathit{Q}$ model and its phase diagram.

(A) $J_1-J_2-Q$ model on square lattice with white (black) sites representing sublattice A (B). Solid lines correspond to nearest-neighbor antiferromagnetic exchange $J_1$ and next-nearest-neighbor ferromagnetic exchange $J_2$. Green shaded squares indicate four-spin ring exchange Q. (B) Phase diagram as function of $g=J_2/J_1$, $q=Q/(Q+J_1)$, and N. Colored dots indicate transition points, at which we analyze the finite-size scaling behavior of the EE. When $N\le 4$, the transition is tuned by q between Néel at small Q and VBS at large Q. When $N>4$, the transition is tuned by g between VBS at small $J_2$ and Néel at large $J_2$.

Distinguishing a weakly first-order transition from a truly continuous one is a challenging numerical task when using conventional local observables and their correlation functions. In our work, this difficulty is overcome by studying the EE, which is a nonlocal observable and can reveal subtle structures in quantum many-body wave functions beyond conventional measurements (40, 41, 43, 52, 57, 58). The log coefficient of the EE has to satisfy the $\text{positivity}$ requirement for a unitary CFT (59). Our results support the realization of a true DQCP between Néel and VBS phases at finite but large N and allow us to demonstrate the absence of a conformal fixed point for $N=\mathrm{2,3,5,7}$.

RESULTS

We study the SU(N) spin model defined in a Hilbert space of N local states (colors) at each site of the square lattice (45–48), as shown in Fig. 1A. We assume SU(N) spins in the fundamental representation on sublattice A and in the conjugate representation on sublattice B, i.e., ${\mid \mathrm{\alpha }\rangle }_A\to U_{\mathrm{\alpha },\mathrm{\beta }}{\mid \mathrm{\beta }\rangle }_A$, ${\mid \mathrm{\alpha }\rangle }_B\to U_{\mathrm{\alpha },\mathrm{\beta }}^{*}{\mid \mathrm{\beta }\rangle }_B$, with the state ${\sum }_{\mathrm{\alpha }}{\mid \mathrm{\alpha }\rangle }_A{\mid \mathrm{\alpha }\rangle }_B$ an SU(N) singlet (60, 61). The Hamiltonian reads

$$H=-\frac{J_1}{N}{\displaystyle \sum _{\langle \mathit{ij}\rangle }}{P}_{\mathit{ij}}-\frac{J_2}{N}{\displaystyle \sum _{\langle \langle \mathit{ij}\rangle \rangle }}{\mathrm{\Pi }}_{\mathit{ij}}-\frac{Q}{N^2}{\displaystyle \sum _{\langle i,j\rangle ,\langle k,l\rangle }}{P}_{\mathit{ij}}{P}_{\mathit{kl}}$$ (2)

where the $J_1$ term is the SU(N) generalization of the nearest-neighbor antiferromagnetic interaction, as $P_{\mathit{ij}}$ is defined as the projection operator onto the SU(N) singlet between a pair of spins i and j on different sublattices, and the $J_2$ term is the SU(N) generalization of the next nearest-neighbor ferromagnetic interaction, as ${\mathrm{\Pi }}_{\mathit{ij}}$ is the permutation operator acting between sites having the same representation on the same sublattice, i.e., ${\mathrm{\Pi }}_{\mathit{ij}}\mid \mathrm{\alpha }\mathrm{\beta }\rangle =\mid \mathrm{\beta }\mathrm{\alpha }\rangle$. We also add a four-spin ring exchange term Q for the $N=\mathrm{2,3,4}$ cases, where $\langle i,j\rangle ,\langle k,l\rangle$ are spin pairs located on adjacent corners of a four-site plaquette, see Fig. 1A. This term preserves the translational and rotational symmetries of the square lattice and was found to stabilize a VBS state with ${\mathrm{\mathbb{Z}}}_4$ symmetry breaking at large Q (14, 15, 47).

The phase diagram of Eq. 2, spanned by the axes of $q=\frac{Q}{J_1+Q}$, $g=\frac{J_2}{J_1}$, and N, is shown in Fig. 1B. It is consistent with previous QMC works (14, 15, 45–48, 62). At $N=\mathrm{2,3,4}$, a transition between Néel and VBS state can be induced upon tuning $q=\frac{Q}{J_1+Q}$ for fixed $J_2=0$ (2, 15, 27, 63, 64). For $N\ge 5$, the $J_1$-only model for $J_2=Q=0$ already has a VBS ground state (62, 65–67), and a Néel-VBS transition can be induced by tuning $g=J_2/J_1$ for fixed Q = 0 (14, 47, 62). In the Supplementary Materials, we show that our critical couplings $q_c$ and $g_c$ agree with those in the literature (2, 15, 27, 45–48, 63, 64). We also determine the corresponding critical exponents at a few representative values of N.

Finite-size scaling of EE

The scaling of the EE for a quantum critical point of a 2D lattice model, described by a CFT, is given in Eq. 1. In a CFT, the coefficient s can be written as $s={\sum }_{i}s({\mathrm{\alpha }}_i)$, where ${\mathrm{\alpha }}_i$ is the opening angle of the i-th corner on the boundary of the region A. Here, $s(\mathrm{\alpha })$ is a universal quantity for a CFT (40, 42, 43), satisfying a number of nontrivial constraints. For our purpose, the following two conditions are the most relevant (59, 68, 69):

1) In a CFT, we must have $s(\mathrm{\pi })=0$. This is equivalent to the statement that smooth entanglement cuts should have no log correction.

2) In a unitary CFT $s(\mathrm{\alpha })\ge s(\mathrm{\pi })=0$ for $\mathrm{\alpha }\in (0,\mathrm{\pi }]$.

The corner contribution has previously been numerically and/or analytically computed for different CFTs. For example, it is known that $s(\mathrm{\pi }/2)=0.01496$ for a single (2 + 1)D Dirac fermion CFT (36, 70), $s(\mathrm{\pi }/2)=0.0064$ for a single real free boson (44), and $4s(\mathrm{\pi }/2)=0.081(4)$ for a square region at the $(2+1)$D O(3) transition (51, 52, 71–73). In addition, a spontaneous symmetry breaking (SSB) phase with Goldstone modes is expected to exhibit a scaling form of the EE analogous to Eq. 1, with an additional contribution $s_{\mathrm{G}}=-n_{\mathrm{G}}/2$ to the coefficient s of the log correction, where $n_{\mathrm{G}}$ corresponds to the number of Goldstone modes (74).

EE with smooth boundaries

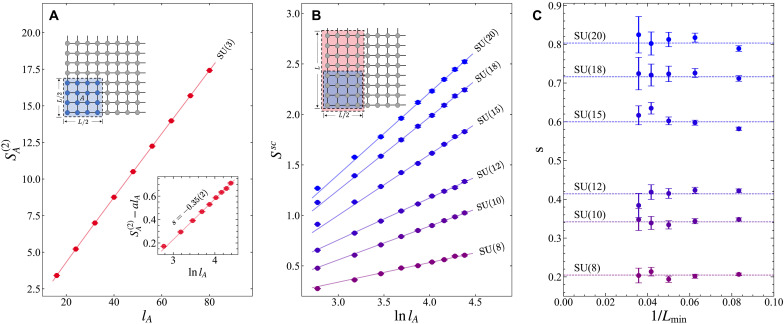
Our QMC-obtained EE for the Hamiltonian in Eq. 2 with smooth bipartition (or equivalently with $\mathrm{\alpha }=\mathrm{\pi }$ corners) are shown in Fig. 2. Since the entanglement region A is of the size $L\times L/2$, the boundary length of A is $l_A=2L$. We plot $S_A^{(2)}(l_A)$ as a function of $l_A$ for each N at its corresponding putative DQCP and fit a functional form according to Eq. 1.

Fig. 2. Second-order Rényi EE and its scaling behavior at the SU($\mathit{N}$) DQCPs with smooth boundaries.

(A) EE $S_A^{(2)}$ as function of boundary length $l_A=2L$ of the entanglement region A with smooth boundaries for different values of N, with the partitioning shown in the inset. The perimeter law behavior $\propto {\mathit{al}}_A$ becomes more prominent for increasing N. (B) EE with perimeter law contribution subtracted, i.e., $S_A^{(2)}-{\mathit{al}}_A-\text{constant}$, as a function of $\text{ln}{l}_A$ for different values of N. The slopes of these curves reflect the coefficient s of the logarithmic term in Eq. 1. For $N\le 7$, there is a finite nonzero $\text{ln}L$ subleading correction to the perimeter law; while as N increases over 8, the slope decreases and eventually vanishes at sufficiently large N. For $N>8$, the subleading correction fits better with the form $1/L$ rather than $\text{ln}L$, as we discuss quantitatively with the ${\mathrm{\chi }}^2/k$ value and the subtracted EE in the Supplementary Materials. For illustration purposes, the fitting in (B) starts from $L_{\text{min}}=16$ at all N values. (C) Finite-size drift of fitted s as a function of $1/L_{\text{min}}$, where $L_{\text{min}}$ corresponds to the smallest retained system size in the fitting process.

As shown in Fig. 2A, the obtained $S_A^{(2)}$ for all N values are dominated by the perimeter law scaling, i.e., when $l_A$ becomes large, a linear term in $S_A^{(2)}$ manifests. However, a clear difference appears once we subtract the perimeter law contribution from the data. In Fig. 2B, we plot $S_A^{(2)}-{\mathit{al}}_A$ versus $\text{ln}{l}_A$. The slope of these curves reveals the values of s for different N. One sees that for the cases of SU(2), SU(3), SU(5), and SU(7), we have a finite log coefficient $s<0$ (revealed by a positive slope in Fig. 2B), violating the equality $s(\mathrm{\pi })=0$. Therefore, our observation of a finite $s(\mathrm{\pi })$ here shows that the putative DQCPs for small N, e.g., $N=\mathrm{2,3,5,7}$, are incompatible with a CFT. Figure 2C demonstrates the finite-size analysis for the fitted s. We can see the s values for SU(3), SU(5), and SU(7) are robust as one increasing the smallest retained system size $L_{\text{min}}$ in the fitting process. Only from SU(8) on, the value of s becomes close to zero $s\approx 0$ as one increases $L_{\text{min}}$.

The N dependence of the EE scaling exhibited in Fig. 2 (B and C) has important implications for the fate of SU(N) DQCPs. As one increases N in the SU(N) model, there is a clear change in the nature of the transition, as indicated by the fitted s shown in Fig. 2C. A comprehensive fitting quality analysis is presented in the Supplementary Materials, by comparing the fitting with $\text{ln}L$ and $1/L$ finite size correction, using the ${\mathrm{\chi }}^2/k$ value, as well as the “subtracted EE” devised in (73). For $N=\mathrm{2,3,5,7}$, s is found to be finite. By contrast, for $N=\mathrm{10,12,15}$, s vanishes in the thermodynamic limit. Therefore, the behavior of EE at these transitions is compatible with CFTs. SU(8) represents a boundary case in which the fitted s of smooth cut becomes indistinguishable from zero within the error bar, and the subleading correction to the perimeter law fits equally well with $\text{ln}L$ and $1/L$ (please refer to the Supplementary Materials). The SU($N\ge 8$) Néel-to-VBS transitions are, therefore, candidates for genuine DQCPs in the original sense, i.e., continuous quantum phase transitions between two different SSB phases, described by CFTs. This suggests the existence of a finite critical value $N_{\mathrm{c}}$, above which the transition becomes continuous. Our numerical data shown in Fig. 2C for smooth boundary, together with the extended analysis shown in figs. S13 and S14, suggest that $N_{\mathrm{c}}$ lies between 7 and 8.

EE with sharp corners

We also analyze the subleading contribution to EE for subregions with corners, especially for $N>N_{\mathrm{c}}$ where continuous transitions are expected and the corner coefficients are expected to be universal.

Figure 3A presents the scaling of Rényi EE for a subregion A with four $\mathrm{\alpha }=\mathrm{\pi }/2$ corners, as depicted in the upper inset, at the SU(3) DQCP as a representative case for $N<N_c$. As shown in the lower inset of Fig. 3A, the EE with four $\mathrm{\alpha }=\mathrm{\pi }/2$ corners of the SU(3) DQCP clearly shows a negative log coefficient, $s=-0.35(2)$. The logarithmic coefficient with four sharp $\mathrm{\pi }/2$ corners is close to those we have obtained with smooth boundaries, $s(\mathrm{\pi })=-0.34(2)$, as depicted in Fig. 2 (B and C). This suggests that the observed log corrections with corners for small N are inherited from the smooth boundary case. Similar behavior has also been observed in the SU(2) J-$Q_2$ and J-$Q_3$ model (51, 73, 75) and fermion DQCP models (35, 36, 51, 76). The corner contribution in these cases is too small to be numerically detectable compared to the large negative $s(\mathrm{\pi })$ of smooth boundaries.

Fig. 3. Second-order Rényi EE and its scaling behavior at the SU($\mathit{N}$) DQCPs with corner cuts.

(A) EE $S_A^{(2)}$ as a function of boundary length $l_A=2L$ of the entanglement region A with corner cuts at SU(3). The upper inset demonstrates the entanglement region A with four $\mathrm{\pi }/2$ corners. The lower inset reflects its negative log correction $s<0$, which we attribute to the contribution from the smooth part of the boundary. (B) Subtracted corner EE $S^{\text{sc}}$ as a function of $\text{ln}{l}_A$ at $N>N_c$. $S^{\text{sc}}$ is defined as the difference between $S_A^{(2)}$ of the smooth (red) and corner (blue) regions that have the same boundary length $l_A=2L$, as shown in the inset. The slope of the linear fitting equals the log coefficient s, which purely comes from four $\mathrm{\pi }/2$ corners and monotonically increases against N. For $N>N_c$, $s>0$ for all cases studied in this work, consistent with the CFT constraint. The linear fitting in (B) starts from L_min = 16 for all N values. (C) demonstrates the change of fitted s against the smallest system sizes retained in the fitting process. Benefiting from the linear scaling of $S^{\text{sc}}$ against $\text{ln}{l}_A$, the fitted s does not drift much as increasing $L_{\text{min}}$. The dashed line denotes the averaged s values among all $L_{\text{min}}$ cases.

At $N\ge N_{\mathrm{c}}$, we observe from Fig. 2 that $s(\mathrm{\pi })$ vanishes as expected from CFT predictions. In this case, the logarithmic correction is caused by four sharp $\mathrm{\pi }/2$ corners. To extract the subleading terms in EE precisely, we use a recently developed algorithm (77) to measure the subtracted corner EE ($S^{\text{sc}}$), defined as the difference between the EEs of subregions with the same boundary length for smooth and cornered boundaries, i.e., red and blue regions, respectively, in the inset of Fig. 3B (see section S2) in one Monte Carlo simulation. With this method, the leading perimeter law contribution is automatically canceled out, and $S^{\text{sc}}$ scales as $S^{\text{sc}}=s\text{ln}{l}_A+c+O(1/l_A)$ according to Eq. 1. Here, s comes entirely from the corner contributions, and a linear fit of $S^{\text{sc}}$ against $\text{ln}{l}_A$ is stable enough to extract subleading logarithmic coefficient.

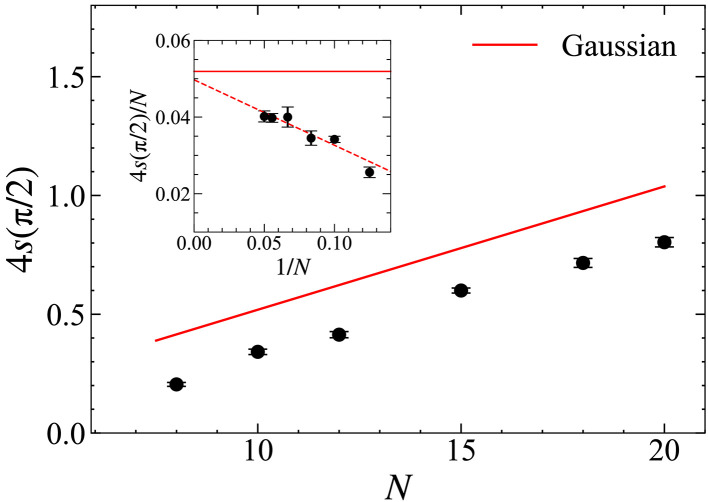
Figure 3B presents the $S^{\text{sc}}$ data for $N\ge N_{\mathrm{c}}$ up to N = 20. The slope of the linear fitting equals the log coefficient from four $\mathrm{\pi }/2$ corners, that is, $4\times s(\mathrm{\pi }/2)$, and its drift against $L_{\text{min}}$ is shown in Fig. 3C. For all $N\ge N_{\mathrm{c}}$ investigated, the $s(\mathrm{\pi }/2)$ values are compatible with the positivity constraint. $s(\mathrm{\pi }/2)$ values are also consistent with the theoretical expectation from N-component Abelian-Higgs and noncompact ${CP}^{N-1}$ field theories at leading order, which have been suggested as continuum descriptions of the SU(N) DQCPs (6, 47, 78): In the large-N limit, these theories are weakly coupled (56). We, therefore, expect the leading contribution to the log coefficient at large N to be given by the corresponding Gaussian theory of the scalar bosons (79). For the Abelian-Higgs model with N complex components, this implies that s is linear against N with slope $0.0064\times 2N$ per $\mathrm{\pi }/2$ corner of subregion A at large N (44). The red line in Fig. 4 illustrates this large-N expectation for four $\mathrm{\pi }/2$ corners, the slope of which agrees with our data at all N values investigated considering numerical uncertainties. Moreover, the fit of $4s(\mathrm{\pi }/2)/N$ as a function of $1/N$, shown in the inset of Fig. 4, gives $4s(\mathrm{\pi }/2)/N=0.050(2)-0.17(2)/N+O(1/N^2)$, in agreement with the large-N expectation ${\text{lim}}_{N\to \infty }4s(\mathrm{\pi }/2)/N=0.0512$.

Fig. 4. Fitted log coefficient from four $\mathbf{\pi }/\mathbf{2}$ corners at large N.

The main panel shows $4s(\mathrm{\pi }/2)$ as a function of N with the red line indicating the corresponding Gaussian value. The black dots are the averaged s values among all $L_{\text{min}}$ in Fig. 3C, with the error bar denoting the SD. The inset shows $4s(\mathrm{\pi }/2)/N$ as a function of $1/N$, together with a linear fit (dashed line), yielding $4s(\mathrm{\pi }/2)/N=0.050(2)-0.17(2)/N+O(1/N^2)$, which agrees with the Gaussian value (solid line) for $N\to \infty$.

The consistency of $s(\mathrm{\pi })$ with a CFT for $N\ge 8$, together with the agreement of the value of $s(\mathrm{\pi }/2)$ for large N with the field theory expectation, serves as evidence that the transition in the SU(N) lattice model for $N\ge N_{\mathrm{c}}$ realizes a genuine DQCP, described by the N-component Abelian-Higgs field theory.

DISCUSSION

We have numerically studied the scaling of EE in a series of SU(N) spin models, realizing direct transitions between SU(N) Néel and VBS phases. By analyzing the subleading logarithmic corrections, we find that for relatively small values of N (including $N=\mathrm{2,3,5,7}$) the transition cannot be described by a CFT, while for larger values $N=8,10,\mathrm{...,18,\; 20}$ the EE scaling is compatible with a CFT description. These observations suggest the existence of a critical value $N_{\mathrm{c}}$ above which the SU(N) DQCP is realized as a true continuous transition. Taking N as a continuous variable, our data suggest that $N_{\mathrm{c}}$ lies between 7 and 8.

A recent preprint (80) studied the second-order Rényi entropy of the SU(2) J-Q model with a different smooth cut from our current work, i.e., instead of a straight smooth cut that is along either the $\widehat{x}$ or $\widehat{y}$ direction, the reference made a “tilted” smooth cut that is along the $\widehat{x}+\widehat{y}$ or $\widehat{x}-\widehat{y}$ direction. Within error bar, it was found that the logarithmic correction to the perimeter law vanishes in this case. However, in an upcoming work, we will show that even with a tilted smooth cut, the subleading logarithmic contribution still exists in the third and fourth Renyi entropy of the SU(2) J-Q model, although the coefficient s is smaller than the one for the straight smooth cut. Hence, we expect that the existence of logarithmic subleading contribution to EE with smooth boundary is indeed ubiquitous for $N<N_{\mathrm{c}}$, regardless of the direction of the cut. However, the direction dependence of the coefficient of the logarithmic term remains as a puzzle which needs to be addressed in future studies.

A candidate field theory for the family of SU(N) DQCPs is the N-component Abelian-Higgs model. Four-loop renormalization group calculations (56) suggest that the theory has a stable and real fixed point for $N\ge N_{\mathrm{c}}=12(4)$, which then collides with a bicritical fixed point for $N\searrow N_{\mathrm{c}}$. This $N_{\mathrm{c}}$ is also compatible with numerical results for a lattice version of the Abelian-Higgs model (81). The value is close to the estimated $N_{\mathrm{c}}$ from the EE measurements. For $N<N_{\mathrm{c}}$, the two fixed points annihilate and disappear into the complex plane, leaving behind a weakly first-order transition governed by “walking behavior” (82). This is illustrated in Fig. 5, which shows the schematic renormalization group flow of the Abelian-Higgs model for different values of N. Here, the renormalization group coupling $\mathrm{\lambda }$ can be understood to parametrize the quartic self-interaction of the complex order-parameter field. The walking behavior for $N<N_{\mathrm{c}}$ is one possible explanation of the observed anomalous logarithmic subleading terms of EE with smooth boundary.

Fig. 5. Illustration of fixed-point collision scenario.

(A) Schematic renormalization group $\mathrm{\beta }$ functions for the coupling $\mathrm{\lambda }$, representing universal field theories that effectively describe the deconfined quantum phase transition for different values of N. An example would be the quartic scalar coupling of the N-component Abelian-Higgs model. Corresponding renormalization group flow trajectories are shown in (B). For $N>N_{\mathrm{c}}$, there are two fixed points, shown as blue dots in (A). The attractive one leads to true critical scaling, as indicated by the blue renormalization group trajectories in (B). Decreasing N shifts the $\mathrm{\beta }$ function down, until the two fixed points collide at some critical $N=N_{\mathrm{c}}$, indicated by the green dashed curves in (A) and (B). Decreasing N further, the fixed points annihilate and disappear into the complex plane, i.e., no true critical behavior can occur anymore. However, for $N\lesssim N_{\mathrm{c}}$, the renormalization group flow remains slow in the vicinity of the now complex fixed points, giving rise to walking behavior and drifting in the exponents, see red curves in (A) and (B).

Another possible mechanism for the observed $s(\mathrm{\pi })<0$ is the Goldstone modes from SSB. In an SSB state with $n_{\mathrm{G}}$ Goldstone modes, the EE indeed has a subleading logarithmic correction with coefficient $s_{\mathrm{G}}=-n_{\mathrm{G}}/2$ when the subregion has a smooth boundary (74). For the SU(2) DQCP in the J-$Q_3$ model, this scenario was recently investigated in (75). By including finite-size corrections in the formula for the scaling of EE in the SSB phase, it was found that the anomalous EE scaling may be captured by a weak SSB of the emergent SO(5) symmetry with four Goldstone modes, giving $s_{\mathrm{G}}=-2$. It is also interesting to notice that our $S^{\text{sc}}$ data are nonlinear against either $\text{ln}L$ or $1/L$ for $N<N_c$ (see fig. S15). For small N, we observe that $S^{\text{sc}}$ scales linearly with L (see fig. S16), implying that the perimeter law coefficients for smooth and corner cuts are different even though both cuts have the same boundary length $l_A=2L$. A possible source for this anomaly may be the unequal critical fluctuations of the remaining VBS moments in different cuttings (80), which also points to a weekly first-order scenario at $N<N_c$. Whether the above phenomena persist at other DQCPs and bipartitions is worth studying in future works.

Last, there is a distinct possibility that the logarithmic correction originates from near-marginal renormalization group flow on the entanglement cut. More precisely, the Rényi entropy can be viewed as the expectation value of a Rényi defect operator. The CFT result $s(\mathrm{\pi })=0$ holds in the deep IR limit of both the bulk and the defect. In other words, it assumes that the defect is conformal. However, for finite-size calculations and when the renormalization group flow on the defect is governed by nearly marginal operators, for a window of system sizes logarithmic behavior can arise. However, it is difficult to explain in this scenario why anomalous logarithmic corrections are observed for several values of $N=\mathrm{2,3,5,7}$, as the scaling dimensions of operators on defects should change with N, and unlikely to remain nearly marginal for these different values of N. Thus, we conclude that the anomalous corrections are unlikely due to defect renormalization group flows, and should be attributed to bulk properties.

MATERIALS AND METHODS

We compute the second-order Rényi EE of the model in Eq. 2 with QMC (83) on lattices with linear sizes $L=8,12,16,\dots ,40$. We keep the inverse temperature $\mathrm{\beta }\equiv 1/T=L$ at N = 2, $\mathrm{\beta }=8L$ for $N=18,20$, and $\mathrm{\beta }=4L$ for other intermediate N values to circumvent thermal pollution (see the Supplementary Materials for detailed analysis).

As reviewed earlier, the subleading corrections to the EE in a CFT need to satisfy nontrivial conditions (40, 42–44). We now turn to the EE measurements of the transitions in the phase diagram of Fig. 1B. To this end, a non-equilibrium incremental QMC algorithm is developed (49–52, 84–86) for the SU(N) spin model. Details of the implementation are given in the Supplementary Materials. Here, we only mention that to compute the second-order Rényi EE $S_A^{(2)}$ for quantum spin systems, there are many previous attempts based on the swap operator and its extensions (41, 87–92) and the data quality is always a serious issue when approaching large system sizes for extracting the subleading universal scaling coefficients. This problem has been greatly relieved by the incremental algorithm, which converts the Rényi EE into the free energy difference between partition functions on two different manifolds, with the help of Jarzynski equality (49, 50, 93) and the incremental trick (51). Controlled EE results, including the log coefficient of the EE inside the Néel phase of the antiferromagnetic Heisenberg model and at its (2 + 1)D O(3) quantum critical points (50–52, 71, 73) and the topological EE inside the Kagome ${\mathrm{\mathbb{Z}}}_2$ quantum spin liquid (52), have been obtained. We note the latest developments, realizing the EE as an exponential observable (94) and simpler incremental approaches without nonequilibrium process have been put forward (36, 94, 95).

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S11

Table S1

References