A material dynamically enhancing both load-bearing and energy dissipation capability under cyclic loading

Abstract

Material properties gradually degrade under cyclic loading, leading to catastrophic failure. It results in large costs for inspection, maintenance, and downtime. Besides, materials require combinations of performance such as load bearing and energy dissipation. However, improving one performance of a material often sacrifices another performance, making it difficult to create materials with optimal performance profiles. Here we report a liquid-infused porous piezoelectric scaffold (LIPPS) that simultaneously enhances its load-bearing and energy dissipation capability under cyclic loading. For example, after 12 million loading cycles, LIPPS increases its modulus by 3600% and hysteresis by 3000%. From a CT study, this behavior is attributed to the self-recoverable mineralization under mechanical loading. Moreover, LIPPS shows a reprogrammable stiffness distribution based on the loading distribution, which enables the material to generate multiple shapes by self-folding. Our findings can contribute toward unprecedented opportunities in soft robotics, vehicles, infrastructure, and tissue engineering and contribute to the new paradigm of material selection with improved resilience and sustainability.

A bone-inspired material improves its performance over time rather than degrades under repeated use.

INTRODUCTION

Similar to the aging process of our body, repeated mechanical loading on structures, devices, and vehicles leads to the generation and propagation of defects in the materials. Over time, these defects accumulate and lead to deterioration of mechanical performance and the premature failure of components (1, 2). As a result, periodic inspection and maintenance are conducted to find defects, make repairs, and estimate the remaining lifetime to prevent catastrophic failure, incurring large costs and downtime. Among many material properties that degrade under cyclic loading, load-bearing and energy dissipation capabilities are crucial properties for the structural performance of materials across various applications, from soft robotics to aircraft (3). The elastic modulus of a material is vital for load-bearing components, as it determines the deformation of a material under a load and the ability to withstand multiple loading cycles, making it a primary material property considered in engineering applications. In addition, hysteresis is essential for energy-dissipating components, as it allows materials to effectively dissipate the loading energy and maintain structural integrity. However, these material properties tend to be mutually exclusive, resulting in trade-offs between improving stiffness and energy dissipation that hinder the creation of materials with optimal combinations of these properties (4). For example, materials with high stiffness do not typically have high damping such as metals, while materials with high damping such as rubbers do not exhibit high stiffness (3, 5, 6). Related current efforts to address this trade-off challenge primarily focus on improving one property, such as the toughness of a material, while minimizing the reduction of other properties, such as stiffness under static loading (5–7). Nevertheless, even if properties are initially optimized, cyclic loading will lead to defects and accumulating degradation of both stiffness and toughness over time, shortening the lifetime of materials. To extend material lifetime, an ideal material would have the ability to improve both stiffness and dissipation properties as well as repair defects and damage that arise over time.

In this regard, there are salient examples in nature that strike a balance between both properties without sacrificing the other, with bones addressing these challenges in an elegant way (8–10). Through a process known as mechanotransduction, bone converts fluid motion from structural deformation into a signal to induce mineralization (8–10). This allows the mechanical properties of bone to be enhanced in response to applied loading by synthesizing reinforcing materials using local resources contained within surrounding body fluids (11). The porous network structure of bone is advantageous in this process as it enables easy storage and transport of body fluids that contain resources for mineral formation (8, 10, 12). These dynamically adaptive behaviors make these natural mechanisms an intriguing source of inspiration for developing transformative synthetic materials that mimic existing solutions in nature.

Recently, there have been seminal works to develop materials that use mechanical cues to enhance their mechanical properties through the formation of stronger bonds and crosslinking (by polymerization) within the material (1, 13–16). However, most of these materials (i) do not simultaneously enhance both load-bearing and energy dissipation capabilities upon cyclic mechanical loading, (ii) have limited load-bearing capability (17), (iii) require additional energy to enhance the material (18), (iv) are difficult to synthesize (18), (v) need to be used in a liquid environment (19), and (vi) are constrained by a specific material system. These limitations restrict the utility of existing mechanically adaptive materials.

In addition to creating materials capable of improving their mechanical properties, the ability to control the stiffness distribution in a structure has been actively studied to make self-folding structures (20, 21). However, stiffness changes are usually imparted through irreversible processes and require multiple materials with varying stiffness combinations. These restrictions limit the range of shape transformations that are possible after fabrication and tend to require multistep fabrication procedures or dedicated equipment. Instead, reversible stiffness distribution control over a single material for reconfiguration into various distinct shapes would be desirable. To address these challenges, we are inspired by the ability of bone to strengthen in response to mechanical loading, its good stiffness and toughness, and its ability to dynamically control the stiffness distribution in response to the location and magnitude of loading. Unlike natural materials like bone, engineering applications often require noncellular materials. We leverage the piezoelectric effect as an alternative of cellular mechanisms of bone, enabling the creation of materials that adapt to external loading without cells. Moreover, while bone operates within a liquid environment, engineering solutions often require a nonliquid environment. We report a liquid-infused material, inspired by Nepenthes pitcher plants that can form a liquid-infused surface in air due to microstructures made of hydrophilic material that can trap water within its structure (22). Built upon our previous study on piezo charge–induced mineralization (19), we report a liquid-infused porous piezoelectric scaffold (LIPPS) that simultaneously enhances both its load-bearing and energy dissipation capabilities in response to cyclic loading (e.g., an increase of 3600% and 3000%, respectively, after 12 million loading cycles) and its application to force-based reprogrammable self-folding materials (see Fig. 1 for overview). Furthermore, the LIPPS can be synthesized with various matrix materials including polydimethylsiloxane (PDMS) and hydrogel, making LIPPS not bound to a specific material system.

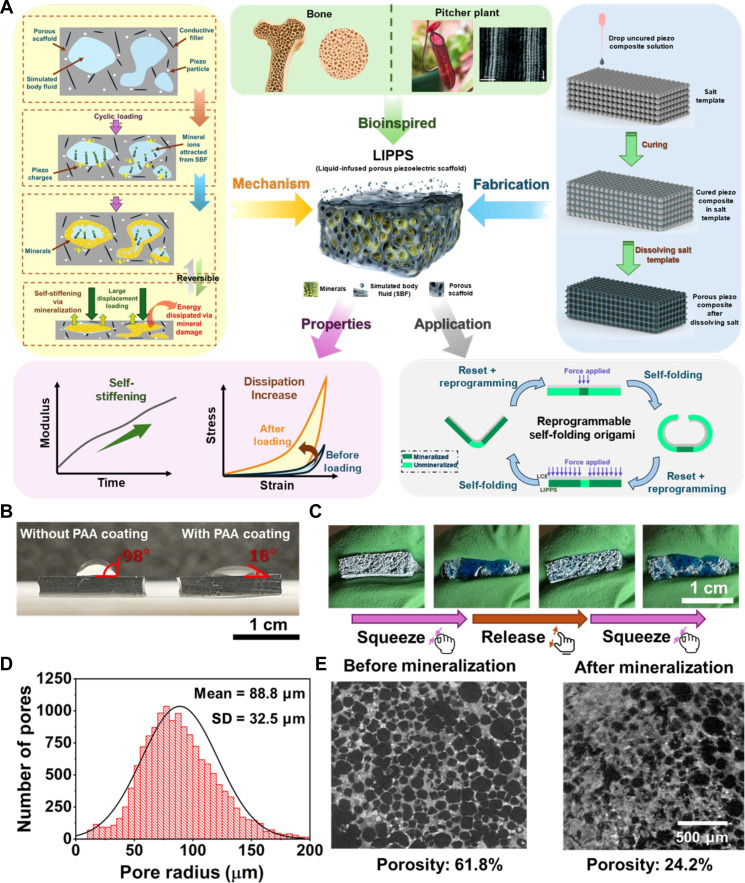
Fig. 1. Overview of LIPPS and characterizations of liquid infusion and pores.

(A) Overview of LIPPS, highlighting the bioinspiration from bone and the pitcher plant, the reversible reinforcement mechanism, the fabrication process to create the porous composite, mechanical property changes showing increasing stiffness and dissipation after cyclic loading, and the reprogrammable self-folding mechanism and example applications. [Pitcher plant morphology image (22): copyright 2004, The National Academy of Sciences] (B) Effects of surface functionalization: initial hydrophobic surface without PAA coating and high contact angle versus hydrophilic surface with PAA coating and decreased contact angle due to PAA coating. (C) Liquid infusion capability of the porous composite scaffold with PAA coating showing the ability to store mineral ion solution within the composite. (D) Pore radius distribution analyzed from micro-CT showing that pore sizes are below the capillary length of water. (E) Mineralization characterization from micro-CT comparing porosity changes after mineralization, with porosity decreasing due to mineral filling of the pore space.

To realize such a material, we derived inspiration from bone and pitcher plants (Fig. 1A, top) and rationalized the synthesis approach based on our previous work on a pitcher plant–inspired slippery liquid-infused porous surfaces (23) as follows: (i) An open-cell porous microstructure is preferred for fluid transport within a material (24, 25), (ii) the pore size should be below the capillary length of the liquid (26), (iii) a smaller pore size is preferred as capillary force is inversely proportional to pore size (26), and (iv) a surface property that promotes spontaneous wicking of a liquid is preferred (27) (also known as hydrophilic for a water-based solution). We aimed to synthesize a porous piezoelectric material where a mineral solution is infused to allow the material system to respond to the cyclic loading by synthesizing minerals within the porous structure.

RESULTS

The LIPPS was synthesized by simply mixing PDMS (the matrix material), carbon nanotubes [CNTs; conductive fillers), and barium titanate BaTiO₃ (BTO); piezoelectric particles] with n-heptane into a sacrificial salt template (see section S1 for details) (25, 28). We also synthesized LIPPS by using an agarose hydrogel as a matrix material (see section S4 for details). After curing the solution, dissolution of the salt template yields an open-cell porous structure as schematically shown in Fig. 1A (right). Subsequently, to increase the hydrophilicity of the composite for liquid infusion, polyacrylic acid (PAA) was coated to the pore surface of the composite (Fig. 1B). This surface treatment enabled LIPPS to infuse simulated body fluids (SBF) that serve as an electrolyte, to continue to supply reinforcing mineral ions even when removed from liquid environments (Fig. 1C).

The resulting material pore structure was characterized using computed tomography (CT), revealing a pore radius distribution with a mean radius of 88.8 μm and a standard deviation of 32.5 μm (see Fig. 1D), which is well below the capillary length of water (~2.7 mm under ambient conditions) (26). Upon external loading, charges generated by piezo particles in LIPPS attracted mineral ions in SBF and facilitated mineralization within the pore (Fig. 1A, left). Micro-CT characterization following mineralization through 6 million cycles of cyclic loading revealed a decrease in LIPPS porosity from 61.8 to 24.2%, indicating that minerals occupied 61% of the pore space (Fig. 1E and section S2).

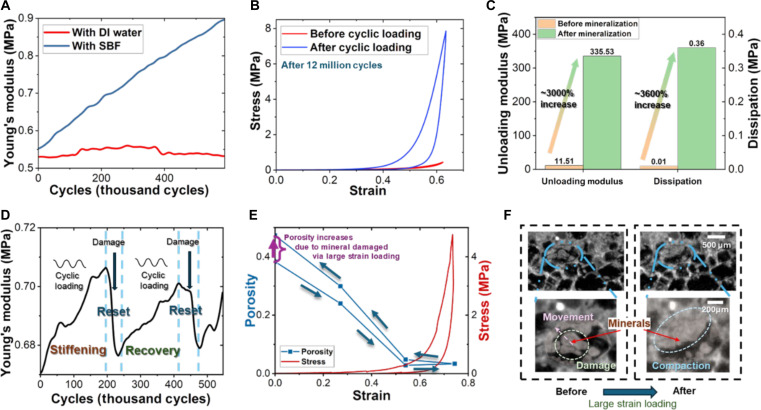
The effects of mineralization and changes in porosity on modulus and energy dissipation were measured under dynamic cyclic loading. Following mineralization in LIPPS through cyclic loading (frequency: 5 Hz, stress amplitude: 100 kPa) with infused SBF, a substantial increase in Young’s modulus and hysteresis was observed compared to a piezo composite subjected to cyclic loading with infused deionized (DI) water [as depicted in Fig. 2 (A to C) and section S3]. Specifically, after 600,000 loading cycles, the Young’s modulus of the composite mineralized with infused SBF increased by more than 60%, while the Young’s modulus of the composite without mineralization (infused with DI water) showed no substantial modulus change (Fig. 2A). Moreover, after 12 million cycles, the load-bearing and the energy dissipation capabilities of LIPPS markedly increased as shown from the comparison of the stress-strain curves (Fig. 2B). The unloading modulus, the tangential modulus for unloading condition, of LIPPS increased by 3000% and dissipation increased by 3600% (Fig. 2C). After the minerals are damaged by applying large strains over 60%, LIPPS recovered its behavior by remineralizing under cyclic loading (Fig. 2D). The characteristics of LIPPS are desirable because (i) it can endure daily loading conditions (also known as low to medium amplitude cyclic loading) by improving both load-bearing and energy dissipation capabilities; (ii) it shows a J-shape strain-stiffening behavior to prevent damage from excessive strain; (iii) it can dissipate large amounts of energy when a large amplitude loading is applied such as an accident or unexpected loading condition; and (iv) it is reusable as it recovers after minerals are damaged from large displacements. These results indicate that LIPPS can simultaneously enhance both load-bearing and energy dissipation capabilities upon cyclic mechanical loading and does not require additional energy inputs to enhance the material. Furthermore, the load-bearing capability can be enhanced substantially and does not require a liquid environment.

Fig. 2. Mechanical behavior of LIPPS under cyclic loading.

(A) Young’s modulus increase of LIPPS with mineral ion solution compared to the control composite with DI water, showing substantial increases in the modulus from mineral reinforcement. (B) Stress-strain curve of LIPPS before and after cyclic loading, showing hysteresis increase from mineralization. (C) Analysis of unloading modulus and dissipation increase of LIPPS after mineralization that indicate simultaneous enhancement of both properties by over an order of magnitude. (D) Characterization of mechanical property change reversibility with recovery of modulus after damage and cyclic loading. (E) Porosity change and stress-strain curve after loading and unloading, showing porosity increase after damage from large strain loading to reset the LIPPS. (F) Micro-CT scan showing mineral structural changes, movement, and breakage, with mineral compaction and movement as potential energy dissipation mechanisms during loading.

To understand the relationship between the microstructure change and material performance, we used a submicrometer resolution CT for in situ characterizations of the LIPPS during loading and unloading (Fig. 2, E and F, and section S2). The micro-CT analysis results showed that the porosity increased after applying large strain loading due to the damage of reinforcing minerals, which dissipates energy during breakage (Fig. 2E). The zoomed-in images of minerals within the pores showed that minerals were damaged, moved, and compacted (Fig. 2F), all of which contribute to energy dissipation from fracture and friction.

Unlike most materials whose mechanical properties degrade under cyclic loading, the LIPPS enhanced its properties upon cyclic loading. This places LIPPS in the previously unoccupied first quadrant (i.e., “white space”) of the Ashby property change chart (Fig. 3A). Moreover, there was no trade-off between stiffness and dissipation increase (Fig. 3, A and B). In addition, LIPPS is not limited to a specific matrix material such as PDMS. LIPPS based on hydrogel also showed a substantial increase in stiffness and dissipation (Fig. 3A and section S4). This indicates that LIPPS has a potential for excellent compatibility with various matrix materials. These unique property changes as well as versatility make the behavior of LIPPS to stand out from existing mechanically adaptive materials.

Fig. 3. Comparisons of the property changes of LIPPS and other materials under cyclic loading.

(A) Ashby plot showing the relative percentage change in dissipation versus the relative percentage change in unloading modulus after cyclic loading, showing that LIPPS performance is in the previously unoccupied quadrant with increases in both modulus and dissipation. The plot includes LIPPS with PDMS and hydrogel matrices, conventional materials, and data from literature references [cortical bone (44) and glass fiber reinforced polymer composite (45)]. (B) Radar charts comparing the best performance of current state-of-the-art mechanically adaptive materials (13, 16, 19) with LIPPS. Left: Maximum reported property ratios after cyclic loading compared to initial values showing substantially higher property change ratios in modulus, dissipated energy density and ratio, toughness, and storage energy density for LIPPS compared to existing mechanically adaptive materials. Right: Absolute value ranges of reported properties before and after cyclic loading, showing the larger modulus and toughness values of LIPPS compared to existing mechanically adaptive materials.

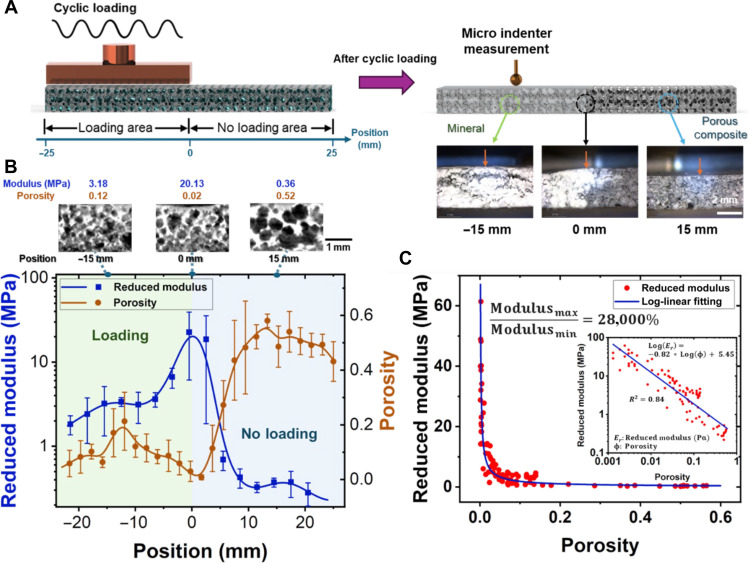
Further analyses of the properties of LIPPS compared with previously reported mechanically adaptive materials showed that LIPPS outperformed the property enhancement ratio by up to two orders of magnitude and was the only material that increased dissipation under cyclic loading. In addition, LIPPS showed much higher values and range in load-bearing, failure resistance, and energy dissipation capabilities (Fig. 3B and section S5). The unique ability of LIPPS to be stiffened upon mechanical loading and to recover after mineral damage can be used for the reversible control of stiffness distribution within a single material to create reprogrammable self-folding structures. Figure 4 (A and B) shows the effects of the position of mechanical loading on the spatial distribution of mineralization, the porosity of the material, and the reduced modulus which is the characterization of local elasticity from microindentation tests. From the results, there was up to 280 times difference in modulus within the sample as shown in Fig. 4C depending on the mechanical loading.

Fig. 4. Programming of stiffness distribution with loading.

(A) Illustration of the microindentation test for LIPPS using a bone-like force-based method to control the distribution of mineralization and resulting stiffness, with cyclic loading leading to an increase in modulus and a decrease in porosity due to mineral formation. (B) Porosity and reduced modulus distribution across different loading areas, showing the decrease in porosity in locations under cyclic loading. (C) Correlation between porosity and reduced modulus with log-linear fitting that indicates a strong relationship between the modulus increase and porosity decrease from mineralization.

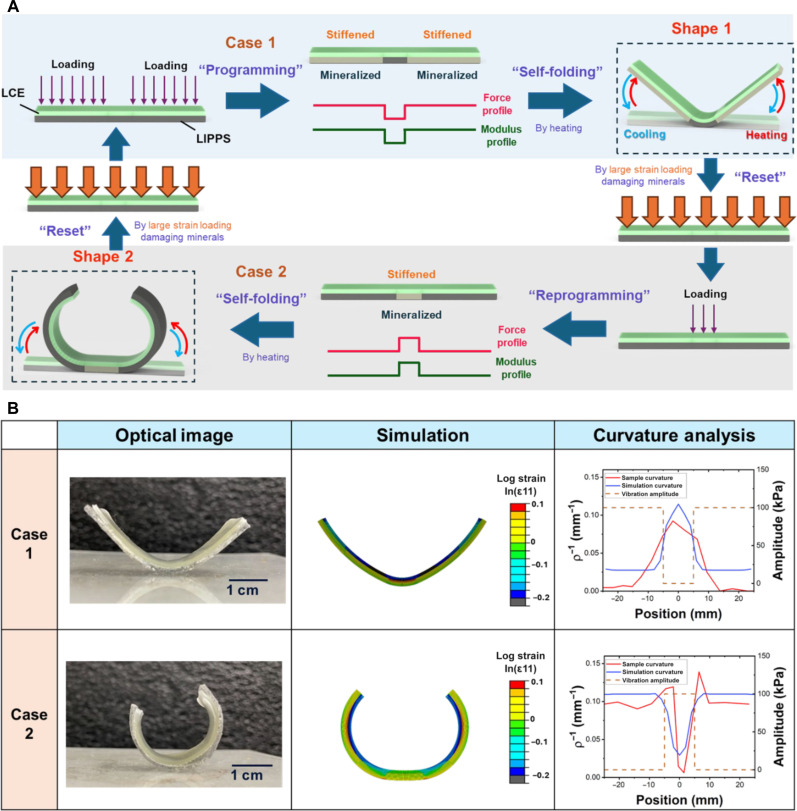
On the basis of the reversible mechanical property and porosity change results, we fabricated a bilayer self-(un)folding material using LIPPS and a liquid crystal elastomer (LCE) (see section S6 for details). The LCE has a characteristic of reversible shrinkage upon heating beyond the nematic-isotropic transition temperature and a recovery of the initial shape upon cooling (29, 30). As schematically shown in Fig. 5A, depending on the location of the mechanical loading, different parts of the bilayer material can be stiffened. As a result, these parts can work as constraints during actuation of the LCE and determine the overall shape of the self-folding behavior during heating. Areas with higher stiffness are harder to curve, while areas with lower stiffness are easier to deform when the LCE undergoes thermal shrinkage. Upon cooling, the bilayer material can reversibly recover the original flat shape. Unlike most other origami structures, which require multiple materials or different structural distributions, our self-folding material consists of a uniform material without structural differences.

Fig. 5. Force-based reprogrammable self-folding material (LCE-LIPPS).

(A) Illustration of reversible stiffness distribution programming and its application for shape transformation through self-folding. Applied loading programs the material by induced mineralization and stiffening depending on the distribution and amplitude of the loading. During heating, the LCE deforms the programmed shape based on the modulus distribution of the material. The material can be reset through large strain loading that damages the reinforcing minerals. The reset material can be reprogrammed with an altered loading pattern and distribution, resulting in a different shape transformation under heating. (B) Characterization of self-folding shape transformation through optical imaging, simulation, and curvature analysis. In case 1, the LIPPS is stiffened across the profile of the material except for an unloaded central section, resulting in deformation concentrated at the center of the material. In case 2, the LIPPS is stiffened only in the center of the material, resulting in a material that is unmineralized outside of this central region and deformation that increases further from the central mineralized section.

Moreover, it has the potential to reversibly reprogram the material’s behaviors by resetting the stiffness distribution through damaging minerals with large strain loading. By applying different loading conditions, the material can also achieve various self-folding behaviors from the same self-folding material. For example, as shown in Fig. 5A, programming the specimen by applying case 1 loading results in a “V” shape formation upon heating. Then, after cooling the specimen and resetting the stiffness distribution via large strain loading, an altered loading condition can be applied to reprogram the specimen such as case 2 to exhibit a “U” shape by self-folding. To further understand the self-folding process, a finite element model is established using Abaqus (Fig. 5B). The color in the figure represents the magnitude of the logarithmic strain, which indicates the amount of bending deformation in the material. In both case 1 and case 2, the deformation happens mostly in the porous PDMS region near the LCE-LIPPS interface (red color), while the mineralized region remains nearly undeformed. The simulation results suggest that the LCE-driven bending deformation of the soft porous PDMS region is the major driving factor of the self-folding behavior. We compared our experimental results with simulations for both the V and U cases. As shown in Fig. 5B, areas subjected to loading resulted in lower curvature, while areas with no or lower loading exhibited higher curvature. This correlation between loading condition and curvature demonstrates good control of the self-folding behavior by our bilayer self-folding material, highlighting its potential for applications such as adaptive and reconfigurable structures.

DISCUSSION

The LIPPS not only has intriguing spatial and temporal behaviors in response to cyclic mechanical loading but also provides opportunities to study unprecedented phenomena that occur from coupling mechanical stress with material synthesis. The LIPPS also validates the bioinspired approach to overcome a previously accepted paradigm of mutual exclusivity in mechanical property trade-offs. While we have used either PDMS or hydrogels as matrix materials and an SBF as a liquid mineral ion electrolyte, one can incorporate combinations of various matrix materials and compositions of electrolytes. For example, for higher load-bearing capability, materials such as an epoxy or a cement can be adopted as a matrix material to increase the initial modulus of the material, while metal-based ionic solutions can be used to compose an electrolyte to allow for stronger materials to further enhance the mechanical properties of the reinforced composite. One can also consider adding additives for controlling crystallinity (31) or various functional particles in an infused liquid to autonomously change, for example, optical, electrical, magnetic, or thermal properties upon mechanical loading. In our example, BTO was used to impart piezoelectric properties, and CNTs were added to improve electrical conductivity, but silver or gold particles could be added to improve thermal conductivity and heat dispersion as well as transparency or reflectivity (32). The liquid electrolyte composition can be also selected or modified on the basis of the operation environment to consider factors such as freezing temperature, boiling temperature, and humidity.

We envision that our findings can provide stepping stones toward unprecedented opportunities in various fields including soft robotics (33–36), vehicles (37), infrastructure (38), and tissue engineering/medical devices (39) and can contribute to changing the paradigm (40) of material selection to create more resilient materials and improve safety and sustainability. For example, in soft robotics, compliance is ideal for increasing flexibility and safety, particularly in situations involving close contact with humans. However, soft materials are exposed to risk from damage that is not easily repairable. A material that can locally adapt its mechanical properties under higher stress environments may be desirable to optimize material integrity. Given the range of achievable modulus, the LIPPS could provide mechanisms to prevent damage without sacrificing flexibility. For vehicles and infrastructures, they undergo varying cyclic loadings which degrade material properties and can result in sudden premature failure. Materials that can adapt to varying loading conditions and improve their properties under cyclic loading can contribute to addressing such challenges with more development of stiffer material systems. Similarly, medical devices implanted into the body such as orthopedic implants not only carry risks of damage and fracture under extended use but also can lead to stress shielding due to mismatches in stiffness with surrounding tissues. A material that could adapt its mechanical properties to match the environment could provide a mechanism to minimize stress shielding. Furthermore, the ability to regenerate the material with minerals similar to bone material could further reduce the failure risk while improving osseointegration, potentially improving patient outcomes.

Overall, the LIPPS shows the ability to increase both load-bearing and energy dissipation capabilities under cyclic loadings due to piezoelectric charge–induced mineralization. This characteristic can help overcome the trade-off between stiffness and hysteresis of current materials. Furthermore, the ability of LIPPS to not only stiffen upon mechanical loading but also recover after mineral damage allows the material to have a mechanism for reversible control over the stiffness distribution within a single material. These characteristics lend the material to be able to create reprogrammable self-folding structures as well as provide utility for environments with load-bearing and energy dissipation demands. Such materials could be notably advantageous in a range of applications including soft robotics where preventing failure without compromising flexibility through localized enhancement is ideal, in vehicular and infrastructure materials to mitigate damage and prevent premature failure under extended loading and in medical devices where the ability to reducing fracture risk while minimizing stiffness mismatches between implants and tissues through the generation of biocompatible mineral structures could improve patient outcomes.

MATERIALS AND METHODS

LIPPS synthesis based on PDMS

To synthesize porous piezoelectric composites, we used PDMS as a matrix material, CNTs as conductive fillers, and BaTiO₃ (BTO) as piezo particles. First, we mixed PDMS, CNT, and BTO together with n-heptane as a diluting solution to help the composite solution to easily permeate into a salt template. Then, we poured the composite solution onto a salt template and cured the composite at 70°C overnight. Next, we dissolved the salt template in DI water overnight to create an unpoled porous piezo composite. After forming the composite, we aligned the dipoles to enhance the piezoelectric properties using a poling procedure (41).

LIPPS fabrication based on hydrogel

To synthesize LIPPS based on hydrogel, we used agarose hydrogel at an 8 wt % concentration. Because of the conductive nature of the hydrogel, we first added agarose to the SBF solution and mixed BaTiO₃ (BTO) with the agarose-dissolved solution. This mixture was stirred and boiled, heating it to 100°C until the agarose was completely dissolved, resulting in a thick concentrated homogeneous solution. Subsequently, 200 wt % salt was added and quickly mixed with the solution. Then, the hot agarose solution was poured into a mold, and the gels were allowed to form by refrigerating the gel solution at 0°C. Last, the sacrificial salt embedded in hydrogel was dissolved in the water, and a porous piezo hydrogel was obtained.

Mechanical testing

For mechanical testing, an Instron ElectroPuls E1000 dynamic testing system was used to apply cyclic loading with a frequency of 5 Hz and an amplitude of 100 kPa and characterize the mechanical behaviors of the materials.

Porosity measurement using micro-CT

For porosity measurement and porous structure characterization, we used the RX Solutions EasyTom 150/160 micro-CT and analyzed the pore space from micro-CT images using ImageJ.

Fabrication of the force-based reprogrammable self-folding material

To fabricate reprogrammable self-folding materials, LIPPS was prepared with a thickness of 1.5 mm using a salt template and subjected to a cyclic loading pattern. Simultaneously, LCE was prepared according to specified procedures from a previous study (42). For monodomain LCEs, they were initially stretched after curing, followed by crosslinking under UV light. PDMS was used as an adhesion layer and cured at a temperature of 50°C. The self-folding behavior was achieved by placing the bilayer material in an oven at a temperature of 135°C. For reprogramming, a large strain loading with strain higher than 70% was applied to the LIPPS, followed by the application of an altered loading pattern, and the steps were repeated.

Modulus mapping

The modulus distribution of the half-loaded LIPPS was measured using microindentation tests. The LIPPS strip (50 mm length by 6 mm width by 3 mm thickness) was adhered to a glass slide and mounted on a Femtotools FT-MTA03 Micromechanical Testing and Assembly System. A polystyrene sphere was attached to the force probe of the microindenter. The spherical indenter was positioned above the LIPPS surface and driven into the material to a specific depth of 10 to 90 μm at a speed of 100 μm/s and then retracted at the same speed. Displacement and contact force were recorded during both loading and retraction, and the Oliver-Pharr model (43) was used to determine the local reduced modulus. Tests were conducted at various locations along the strip’s length to map the modulus distribution. Testing locations were spaced to ensure independent measurements, with two areas tested across the width of the sample at each location and three repetitions per area were performed.

Simulation of self-folding behaviors

The self-folding origami structure was simulated in Abaqus using a finite element model with linear elastic materials and thermal expansion. The Young’s modulus for LIPPS was set to 300 kPa for porous PDMS and 5 MPa for the mineralized region, with a thermal expansion coefficient of 0. For LCE, the Young’s modulus was set to 300 kPa, and the thermal expansion coefficient was set to 1. Both materials had a Poisson’s ratio of 0.49. The two-dimensional plane strain bilayer composite had an LCE top layer (56 mm by 1 mm) and an LIPPS bottom layer (8-mm inner, 48-mm outer, 1.4-mm thick). Two cases were simulated, varying the material distribution in the LIPPS layer. Symmetric boundary conditions and temperature-induced thermal strain were applied, with nonlinear geometry enabled for finite deformation.

Statistical analysis

To analyze the pore structure of the nonmineralized LIPPS, we used a 15 mm–by–15 mm–by–3 mm region of interest from the CT scans. The watershed algorithm was used to segment and identify individual pores within the sample. This segmentation method enabled us to calculate the pore radius for each pore in the dataset. The distribution of pore radii was analyzed using a normal distribution fitting, yielding the mean and SD, which are presented in Fig. 1D. We further explored the relationship between the reduced modulus and porosity, where porosity was determined from both microindentation testing and CT scans. A log-linear fitting model was applied to these datasets to investigate this relationship. The reduced modulus data were obtained from microindentation tests, while the corresponding porosity values were extracted from the CT scan analysis. The fitted relationship between reduced modulus and porosity is discussed in Fig. 4C.

Supplementary Materials

This PDF file includes:

Supplementary Text

Tables S1 to S5

Figs. S1 to S11

References