A Comparison of Bayesian Methods for Haplotype Reconstruction from Population Genotype Data

Abstract

In this report, we compare and contrast three previously published Bayesian methods for inferring haplotypes from genotype data in a population sample. We review the methods, emphasizing the differences between them in terms of both the models (“priors”) they use and the computational strategies they employ. We introduce a new algorithm that combines the modeling strategy of one method with the computational strategies of another. In comparisons using real and simulated data, this new algorithm outperforms all three existing methods. The new algorithm is included in the software package PHASE, version 2.0, available online (http://www.stat.washington.edu/stephens/software.html).

Current high-throughput genotyping technologies, when applied to DNA from a diploid individual, are able to determine which two alleles are present at each locus but not the haplotype information (that is, which combinations of alleles are present on each of the two chromosomes). Knowledge of the haplotypes carried by sampled individuals would be helpful in many settings, including linkage-disequilibrium mapping and inference of population evolutionary history, essentially because genetic inheritance operates through the transmission of chromosomal segments. Experimental methods for haplotype determination exist, but they are currently time-consuming and expensive. Statistical methods for inferring haplotypes are therefore of considerable interest. In some studies, data may be available on related individuals to assist in this endeavor, but in general such data may be either unavailable or only partially informative. We focus here on the problem of statistically inferring haplotypes from unphased genotype data for a sample of (“unrelated”) individuals from a population.

Several approaches to this problem have been proposed, notably Clark’s algorithm (Clark 1990) and the EM algorithm (which produces an estimate of the maximum likelihood of haplotype frequencies) (Excoffier and Slatkin 1995). Stephens et al. (2001a) introduced two Bayesian approaches, one (their Algorithm 2, or “naive Gibbs sampler”) that used a simple Dirichlet prior distribution, and a second, more sophisticated approach (their Algorithm 3), in which the prior approximated the coalescent. Results on simulated SNP and microsatellite data, as well as more limited comparisons using real data (Stephens et al. 2001b), suggested that this second approach, implemented in the software PHASE v1.0, produced consistently more accurate haplotype estimates than previous methods. In addition, Stephens et al. (2001a) point out other advantages of a Bayesian approach to this problem, including the ability to provide accurate measures of uncertainty in statistically estimated haplotypes, which in principle could be used in subsequent analyses (although practical considerations mean that this has seldom been fully exploited in practice).

More recently, two other Bayesian approaches to this problem have been published: Niu et al. (2002) introduced an algorithm that they refer to as “PL,” which was implemented in the software HAPLOTYPER; and Lin et al. (2002) also introduced a Bayesian algorithm, which they generously attribute to us, but which nevertheless differs in substantive ways from the algorithms in Stephens et al. (2001a).

Here we highlight the conceptual differences between these different Bayesian methods, some of which may be unclear from the original papers. We note that the main contribution of Niu et al. (2002)—the introduction of computational strategies to greatly reduce running times—can also be applied to the other algorithms, and we describe a new version of PHASE that exploits these strategies. In our comparisons of data sets considered by Niu et al. (2002) and Lin et al. (2002), we found that this new version of PHASE outperforms the other two methods. Our comparisons also demonstrate that the apparently inferior performance of PHASE compared to HAPLOTYPER in some of the comparisons of Niu et al. (2002) was not, as they suggest, due to the fact that the data sets considered in these comparisons deviated from the implicit (coalescent-based) modeling assumptions underlying PHASE. Rather, it was due to the fact that, to obtain reliable results, PHASE required longer runs than Niu et al. (2002) employed.

Bayesian haplotype reconstruction methods treat the unknown haplotypes as random quantities and combine

• • prior information—beliefs about what sorts of patterns of haplotypes we would expect to observe in population samples—with

• • the likelihood—the information in the observed data—

to calculate the posterior distribution, the conditional distribution of the unobserved haplotypes (or haplotype frequencies) given the observed genotype data. The haplotypes themselves can then be estimated from this posterior distribution: for example, by choosing the most likely haplotype reconstruction for each individual.

In Bayesian approaches to complicated statistical problems, it is helpful, conceptually, to distinguish between the following separate issues:

• 1. The model, or prior distribution (“prior”), for the quantities of interest—in this case, for population haplotype frequencies. For a given data set, different prior assumptions will, in general, lead to different posterior distributions, and hence to different estimates.
• 2. The computational algorithm used. For challenging problems, including this one, the posterior distribution cannot be calculated exactly. Instead, computational methods—typically Markov chain Monte Carlo (MCMC)—are used to approximate it. Different computational tricks or different numbers of iterations will change the quality of approximations produced by Bayesian methods.

The three Bayesian approaches we consider here differ in both the prior and the computational algorithms used, as we now describe.

We consider first the differences in prior distributions. Stephens et al. (2001a) described two algorithms based on two different priors for the haplotype frequencies: the first, the “naive Gibbs sampler,” used a Dirichlet prior distribution; the second, implemented in PHASE v1.0, used a prior approximating the coalescent. In their comparisons, the algorithm based on the approximate coalescent prior substantially outperformed the algorithm based on the Dirichlet prior. The subsequent algorithms of Niu et al. (2002) and Lin et al. (2002) are each based on the Dirichlet prior.

Interestingly, Niu et al. (2002) and Lin et al. (2002) attribute rather different properties to the Dirichlet prior. Niu et al. (2002) state that their method “imposes no assumptions on the population evolutionary history.” In contrast, Lin et al. (2002) attribute the success of their method to the fact that the “neutral coalescent model, which [it] incorporates, is a reasonable approximation of the random collection of human sequences used as test data.” The truth, we suggest, lies somewhere in between. The Dirichlet prior arises naturally in genetics models with so-called parent-independent mutation (Stephens and Donnelly 2000)—that is, when the genetic sequence of a mutant offspring does not depend on the progenitor sequence. This assumption about the mutation process does not apply (even approximately) to DNA sequence data or to data at multiple SNP or microsatellite loci. Thus, the use of a Dirichlet prior can be thought of as making simple but highly unrealistic assumptions about the genetic processes underlying the evolution of the study population. In contrast, the approximate coalescent prior used in Stephens et al. (2001a) is based on the arguably more complex but decidedly more realistic assumption that the genetic sequence of a mutant offspring will differ only slightly from the progenitor sequence (often by a single-base change).

We can informally illustrate an important operational difference between the Dirichlet prior and what we have called an “approximate coalescent prior” as follows. Sometimes an unresolved genotype can be broken up into two haplotypes, one or both of which is already known (or assumed) to be present in the sample. Both priors will put substantial weight on this possibility. In contrast, suppose that an unresolved genotype cannot be broken up in such a way, but that it can be broken up so that both haplotypes are similar to, but not identical to, known haplotypes (where “similar to” here means that one haplotype can be formed from the other by one or a small number of single-base changes). The approximate coalescent prior will put substantial weight on this reconstruction, but the Dirichlet prior will choose randomly between all possible reconstructions, giving no additional weight to the one involving haplotypes similar to those already seen. Analogous problems occur with Clark’s method and the EM algorithm. (Indeed, the maximum likelihood estimate for haplotype frequencies, which the EM algorithm aims to find, corresponds to the mode of the posterior distribution for a particular Dirichlet prior. In this sense, the EM algorithm gives the same answer as a Bayesian procedure with an unrealistic prior.)

Whatever one’s view on the accuracy of the coalescent as a model for real data, it is difficult to imagine any actual population sample where guessing the haplotypes at random will be more accurate than choosing haplotypes that are similar to others in the sample. Indeed, the main innovation in Lin et al. (2002) can be thought of as an ad hoc modification of the Dirichlet prior to avoid this undesirable “guessing-at-random” behavior. Their modification is that, when considering whether an individual’s genotypes can be resolved into haplotypes that match other haplotypes in the sample, they look for matches only at positions where the individual is heterozygous, ignoring the data at positions where the individual is homozygous. As a consequence of this, the algorithm never reaches the situation considered above, where no “matching” haplotypes exist, and it therefore avoids choosing randomly between all possible reconstructions. This modification has certain computational advantages over the approximate coalescent prior—in particular, Lin et al. (2002) exploited a computational trick from the naive Gibbs sampler in Stephens et al. (2001a) to produce an efficient algorithm. However, as our comparisons below demonstrate, the resulting algorithm is less accurate than one based on the approximate coalescent prior. This is because the genotypes at positions where an individual is homozygous carry potentially valuable information about the phase relationships at the other (heterozygous) positions—information that is exploited by the approximate coalescent prior when close-matching haplotypes are sought.

Whether the posterior distribution for one prior will provide better estimates than the posterior distribution for a different prior will depend on which of the priors does a better job of capturing features of the real data. We continue to believe, on the basis of both general population genetics and the evidence of the superior performance of the PHASE algorithm in comparisons here—and in Stephens et al. (2001a, 2001b)—that the use of an approximate coalescent prior will lead to better estimates than the use of a Dirichlet prior (even with the modification made by Lin et al. [2002]).

In addition to these differences in priors, the three Bayesian methods also differ in their computational approaches. Both algorithms in Stephens et al. (2001a), and the algorithm in Lin et al. (2002), used relatively unsophisticated MCMC algorithms based on Gibbs sampling. An important innovation in Niu et al. (2002) is the introduction of two computational tricks—prior annealing and partition ligation—for reducing the computational effort required to obtain a good approximation to the true posterior distribution. These ideas are largely independent of the prior used, and similar ideas can be applied to the approximate coalescent prior used in PHASE (and could be applied to the modified Dirichlet prior of Lin et al. [2002]), as we outline below. Qin et al. (2002) apply similar ideas to make the EM algorithm computationally tractable for large data sets.

Our discussion above may appear to construct a rather concrete divide between models (prior distributions) and computation. This is deliberate: we want to emphasize the distinct role that each of these components can play in the quality of the final solution obtained. However, in practice, there is often a strong interaction between these two components of a Bayesian analysis. Indeed, the algorithm implemented in PHASE was not actually developed in the conventional way of writing down a prior and likelihood and then developing a computational method for sampling from the corresponding posterior (and neither, incidentally, was the algorithm of Lin et al. [2002]). Rather, the posterior is defined implicitly as the stationary distribution of a particular Markov chain, which in turn is defined via a set of (inconsistent) conditional distributions. Although defining posterior distributions in this way is not without its potential pitfalls, the algorithm in Stephens et al. (2001a) was designed to circumvent these (see appendix A). Furthermore, this unconventional approach has the advantage of avoiding some of the computational difficulties of sampling from the posterior corresponding to an exact coalescent prior, while capturing the salient features of such a prior, notably the tendency for haplotypes in a population to be similar to other haplotypes in the population. Although Niu et al. (2002) claim that the “pseudoposterior probabilities” that our “pseudo-Bayesian” algorithm attaches to the constructed haplotypes are difficult to interpret, simulation results show these probabilities to be reasonably well calibrated relative to a coalescent prior, even in the presence of moderate amounts of recombination (Stephens et al. 2001a).

We now outline a modified version of PHASE that continues to make use of an approximate coalescent prior but exploits ideas from Niu et al. (2002) to improve computational efficiency and to increase the size of the problem that can be handled. For convenience, in the following description we use “frequency” to refer to relative frequency.

Similar to Niu et al.'s PL algorithm (2002), our algorithm follows a divide-and-conquer strategy of initially estimating haplotype frequencies within short blocks of consecutive loci (SNPs) before successively combining estimates for adjacent blocks to obtain estimates of haplotypes across the whole region under consideration. Note that we are using the term “block” to refer simply to a set of consecutive loci, with no implication about the patterns of linkage disequilibrium present. Results from Niu et al. (2002) suggest that the way in which the block boundaries are chosen is relatively unimportant: to encourage independence of results from multiple runs of the algorithm, we randomly chose the length of each block to be six, seven, or eight loci, with probabilities 0.3, 0.3, and 0.4, respectively. To each block we applied Algorithm 3 from Stephens et al. (2001a), with the following alterations:

• 1. We updated each individual in turn, in a random order (with a different random order for each sweep).
• 2. When updating an individual, we updated all ambiguous loci in the block under consideration, rather than choosing five at random (we consider a locus to be ambiguous in a particular individual if the individual either is heterozygous or is missing one or both alleles at that locus).
• 3. To improve mixing during burn-in iterations, with probability β (the value of which is specified below) we computed the probability of each haplotype pair as being proportional to the sum, rather than the product, of the appropriate conditional probabilities. This modification makes the algorithm more likely to visit configurations in which only one of the two haplotypes is similar to other haplotypes in the sample, thus improving mixing of the MCMC scheme.

The value of β was decreased linearly from 1.0 to 0.0 over 100 burn-in iterations (where one iteration means updating every individual once) and was then fixed at 0.0 for 100 further iterations. During these 100 further iterations, for each haplotype that could possibly occur in the sample, we obtained a (Rao-Blackwellized) estimate of the posterior mean of its frequency in the sample.

The above procedure results in an estimate of the haplotype frequencies within each short block. We then apply a variant on the idea of progressive ligation from Niu et al. (2002) to iteratively combine consecutive blocks. Niu et al. (2002) suggest taking from each block the B haplotypes with the highest estimated frequencies and forming a list, L, of the B² possible concatenated haplotypes (where B is some integer to be specified; Niu et al. used B in the range 40–50). We follow this suggestion, but rather than taking a fixed value of B (as Niu et al. [2002] seem to suggest), we choose B separately for each block, in such a way as to include all haplotypes whose estimated sample frequency is f/2n or greater, where n is the number of diploid individuals in the sample and f is some constant to be specified. (We used f=0.001: bigger values of f result in shorter lists, and hence faster runs, at the cost of a potential decrease in the accuracy of the approximation to the posterior distribution.) Once we have formed L, we obtain new estimates for the haplotype frequencies within the newly created block by applying the same MCMC algorithm described above (including the burn-in with linearly decreasing β from 1.0 to 0.0) to the new block, allowing each individual to be made up only of pairs of haplotypes in L. We then continue this ligation procedure, each time concatenating the last-formed block with the adjacent small block. When all blocks have been combined (into a single final block containing all loci), we estimate each individual’s pair of haplotypes by its posterior mode obtained from the final 100 iterations.

The algorithm above includes several variables (particularly f, and the number of iterations) whose values will affect both run times and the reliability of the approximation to the posterior distribution. The particular values we used were chosen so that, in preliminary tests on a few of the data sets, multiple runs of the algorithm from different starting points typically gave similar haplotype estimates. To aid in the comparison of results of different runs, we monitored the value of a “pseudo-likelihood” (Besag 1974), defined as

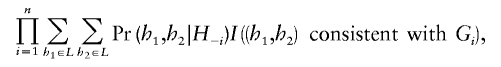where H_-i is the set of all haplotypes in the current MCMC configuration, excluding the individual i, G_i is the genotype of the individual i, and I(·) is the indicator function.

This pseudo-likelihood can be thought of as providing a measure of the goodness of fit of the estimated haplotypes to the underlying model. When different runs give very different values for the goodness of fit, this suggests that the runs may be too short to provide reliable results. Furthermore, among multiple runs on the same data set, we would expect those with the highest values of this pseudo-likelihood (averaged over the final 100 iterations, say) to provide the more accurate results.

Our preliminary tests suggested that, with the parameter values we used, multiple runs of the algorithm did occasionally produce results with rather different values of the pseudo-likelihood, suggesting that the algorithm sometimes converged to a local, rather than global, mode of the posterior distribution. In our first set of comparisons below, to alleviate this problem, we ran the whole algorithm on each data set five times independently and chose the solution corresponding to the run that maximized a pseudo-likelihood averaged over the final 100 iterations. In our second set of comparisons, to reduce computation, we ran the algorithm on each data set only once; we would expect a multiple-run strategy to slightly improve average accuracy.

Our first set of comparisons is based on similar comparisons made by Niu et al. (2002), who ran PHASE and HAPLOTYPER on several data sets, and found that HAPLOTYPER performed more accurately in many cases. We compared

• • Lin et al.'s algorithm (2002) (using code kindly provided by S. Lin), run at its default run-length;

• • HAPLOTYPER, run at its default settings;

• • PHASE v1.0 (which implements Algorithm 3 from Stephens et al. [2001a]), run at its default settings; and

• • the modified version of PHASE described here

on several data sets for which Niu et al. (2002) found PHASE performed poorly.

We used two different criteria for assessing accuracy:

• 1. The error rate, as defined by Niu et al. (2002)—namely, the proportion of individuals whose haplotype estimates are not completely correct.
• 2. A more stringent measure of accuracy, which measures the similarity between the estimated haplotypes and the true haplotypes. Specifically, we counted how many individual nucleotides must be changed in the estimated haplotypes to make them the same as the known haplotypes and divided this by the largest value it could possibly take (given the genotype information) to obtain a number between 0 and 1.

We describe the second measure as “more stringent” because it makes a more detailed comparison between the estimated and true haplotypes, rather than simply determining whether each estimate is correct or incorrect. This measure can thus discriminate between methods even in cases where it is unrealistic to expect a statistical method to completely determine haplotypes at every site, as may be the case for many real data sets, particularly those including low-frequency alleles or sites/loci spread over a large genetic distance.

Table 1 gives, for each type of data and for each method, the mean individual error rate (criterion 1 in the list above). By this measure of accuracy, the modified version of PHASE and HAPLOTYPER perform similarly. PHASE v1.0, run at its default values, performs considerably better than the results reported for PHASE in Niu et al. (2002), but perhaps slightly less well than the modified version. Note, however, that the apparently large difference in error rates for the angiotensin-converting–enzyme (ACE) data (0.18 vs. 0.28) actually corresponds to making an error on just one additional individual. Somewhat surprisingly, the algorithm of Lin et al. (2002) performed consistently less well than the other methods, most notably on the simulated data. Runs 100 times longer than the default settings produced almost identical average performance for these simulated data sets (results not shown). Nevertheless, computational problems may still be (partly) responsible for the poor performance of the algorithm in these data sets, and performance might be improved by the use of a more sophisticated computational scheme.

Table 1.

Mean Individual and Single-Site Error Rates ^[Note]

	Individual Error Rate for Data Set
Algorithm	β2ARa	ACEb	CFTRc	Simulated datad
Lin et al. (2002)	0.18	0.31	0.54	0.40
HAPLOTYPER	0.09	0.19	0.40	0.020
PHASE	0.04	0.28	0.46	0.068
Modified PHASE	0.05	0.18	0.47	0.045
	Single-Site Error Rate for Data Set
Lin et al. (2002)	0.19	0.11	0.43	0.30
HAPLOTYPER	0.11	0.11	0.66	0.031
PHASE	0.03	0.10	0.36	0.047
Modified PHASE	0.03	0.03	0.37	0.028

Note.— Each number in the table is an average over 100 (or, for the last column, 20) data sets. The results for the best-performing method in each column are in boldface/italics.

^aThese data (Drysdale et al. 2000) were used by Niu et al. (2002) to explore sensitivity of methods to deviations from Hardy-Weinberg equilibrium (HWE). We simulated 100 data sets, each containing 15 individuals, by pairing randomly chosen haplotypes according to the “strong heterozygote favoring” model used by Niu and colleagues, as described in their paper (Niu et al. 2002). Each of the 100 data sets contained either zero, one, or two homozygotes, which were the cases where Niu et al. (2002) saw the poorest performance of PHASE compared with HAPLOTYPER. Although Niu et al. (2002) suggest that excess heterozygosity might result from a selective advantage for heterozygotes, selection will not cause deviations from HWE unless the fitness differences are very extreme (e.g., lethal recessives).

^bThese data (Rieder et al. 1999) were used by Niu et al. (2002) to test the stability of algorithms. As in Niu et al. (2002), we ran each algorithm 100 times on the known genotypes, each run using a different initial value for the seed of the random number generator.

^cCystic fibrosis data from Kerem et al. (1989). As in Niu et al. (2002), we randomly permuted the subset of 57 haplotypes with no missing data 100 times, to generate 100 data sets, each containing 28 hypothetical individuals.

^dZ. S. Qin kindly provided 20 data sets, each containing data for 20 individuals at 20 loci, simulated under the bottleneck model used by Niu et al. (2002). We understand (Z. S. Qin, personal communication) that the bottleneck simulations of Niu et al. (2002) made the assumption that in the bottleneck population all loci were in complete linkage equilibrium. This is a nonstandard assumption in this context and seems likely to produce simulated haplotypes that exhibit very different patterns to those expected under what we would consider more plausible assumptions.

Table 1 also summarizes the performance of each algorithm on the more stringent criterion (criterion 2 in the list above), which we call the “single-site error rate.” By this measure of accuracy, the modified version of PHASE consistently and substantially outperforms both HAPLOTYPER and Lin et al.'s algorithm (2002) on these data sets. This indicates that when the methods are unable to reconstruct the haplotypes completely, the PHASE-estimated haplotypes tend to be much more similar to the true haplotypes—presumably because the true haplotypes conform more closely to the assumptions of the approximate coalescent prior than to those of the Dirichlet prior. In particular, it seems that the apparently inferior performance of PHASE in the comparisons of Niu et al. (2002) was not due to its sensitivity to deviations from the assumptions of the coalescent model (as Niu et al. [2002] suggested) but rather to the fact that the 5,000 updates they used (compared with the default of 2,000,000 updates, which we used here) were insufficient for the algorithm to provide a reasonable approximation to the posterior distribution.

For our second set of comparisons, we examine the performance of Lin et al.'s algorithm (2002), HAPLOTYPER, and the modified version of PHASE for the data sets in Lin et al. (2002). (PHASE v1.0 is omitted from these comparisons because of its high computational demands for data sets of this size.) For ease of comparison, we use two measures of accuracy based on those in Lin et al. (2002):

• 1. The error rate, as defined by Stephens et al. (2001a)—namely, the proportion of ambiguous individuals whose haplotype estimates are not completely correct. Note that, although this differs from Niu et al.'s (2002) definition of error rate, which was used above, methods that perform well by one of these criterion will tend also to perform well by the other.
• 2. The switch error, which measures the proportion of heterozygote positions whose phase is wrongly inferred relative to the previous heterozygote position. This differs qualitatively from the single-site error rate used above, in that it does not depend on the accuracy of a method in inferring longer-range phase relationships, and so is perhaps most appropriate where these longer-range phase relationships cannot be accurately inferred by statistical means (which may be the case for some of these data sets). Note that the switch error is 1-theswitchaccuracydefinedbyLinetal. We make this change from an accuracy measure to an error rate, so that, like the other measures we use, small values indicate accurate haplotype estimates.

Because these data sets have some missing genotypes, not all the true haplotypes are completely known, and so, strictly, it is not actually possible to compute either of these criteria. To finesse this problem, Lin et al. (2002) scored phase calls in each individual only at sites where neither allele was missing (S. Lin, personal communication). To allow comparisons with the results of Lin et al. (2002), we take the same approach here. Table 2 shows the performance of each of the methods by both criteria. The modified version of PHASE appreciably outperforms the other two methods, again presumably because of the greater accuracy of the approximate coalescent prior.

Table 2.

Error Rate and Switch Error Rate for the Data Sets Considered by Lin et al. (2002) ^[Note]

	Error Rate for Data Set
Algorithm	GLRA2	MAOA	KCND1	ATR	GLA	TRPC5	BRS3	MECP2
Lin et al. (2002)	.79	.61	.54	.62	.89	.58	.72	.85
HAPLOTYPER	.89	.76	.72	.72	.79	.72	.79	.64
Modified PHASE	.76	.54	.46	.45	.68	.58	.67	.77
	Switch Error Rate for Data Set
Lin et al. (2002)	.14	.10	.22	.29	.22	.13	.14	.23
HAPLOTYPER	.16	.12	.27	.32	.16	.20	.15	.19
Modified PHASE	.10	.07	.13	.18	.11	.13	.10	.15

Note.— The results for HAPLOTYPER and the Lin et al. (2002) algorithm are taken from table 1 in Lin et al. (2002). The results for PHASE were obtained by us on 100 data sets simulated in the same way as those used to produce table 1 in Lin et al. (2002) (i.e., by randomly pairing the 40 X-chromosome haplotypes used by Lin et al. [2002], kindly provided by D. Cutler). Each number in the table is based on results for 100 data sets. For example, the error rates are the total number of mistakes made across all 100 data sets, divided by the total number of ambiguous individuals in all 100 data sets. The results for the best-performing method in each column are in boldface/italics.

Finally, we note that Lin et al. (2002) made additional comparisons between their method, HAPLOTYPER, and the EM algorithm using only the common variants (minor allele frequency >0.2) on the same data sets and found that their algorithm outperformed the others. For these data sets, which naturally contain many fewer SNPs than the full data sets, all three algorithms perform better in absolute terms, and the algorithms of PHASE and Lin et al. (2002) perform more similarly (results not shown).

The estimation of haplotypes from population data for the sizes of data sets currently being generated, as well as those likely in the context of the proposed Haplotype Map Project, is a challenging problem that requires sophisticated computational methods. It appears that Bayesian approaches have much to offer, not only in terms of accuracy of estimation but also in their ability to incorporate, in a natural way, features such as genotyping error, missing data, or additional information (for example, from pedigrees) and to provide a coherent framework in which to account for the uncertainty associated with estimates of haplotypes or haplotype frequencies in later analyses. Among Bayesian approaches, the comparisons reported here and elsewhere suggest that PHASE provides the most accurate reconstructions.

The modified version of PHASE reported here very substantially reduces the computational time involved in running the method. For example, on our desktop machine with an 800-MHz Pentium III processor, the implementation we used for our comparisons took roughly 30 min of central processing unit (CPU) time per data set for the largest gene used in the second set of comparisons (TRPC5), which consisted of 20 diploid individuals typed at 165 SNPs. Shorter runs taking roughly 2 min each produced almost identical average accuracy for this gene, suggesting that in this case our choice of run-length was conservative. Although these times exceed the 10 s that Lin et al. (2002) quote for their algorithm on the same data set and the 35 s it takes HAPLOTYPER (with “Rounds” set to 20) on our machine, it is clear that even much larger problems will remain well within the bounds of practicality. Furthermore, the efficiency of our current implementation could be improved in several ways, if necessary. However, in our view, other aspects of the problem deserve more urgent attention. For example, all three methods considered here ignore the decay of linkage disequilibrium with distance between markers. Furthermore, in most applications, estimating haplotypes or even population haplotype frequencies will not be the ultimate goal. To fully capitalize on Bayesian methods for haplotype reconstruction, it is necessary to integrate the analysis of the haplotypes—be it testing for association with a disease phenotype or estimating recombination rates, for example—with the haplotype estimation procedure, to fully allow for uncertainty in the haplotype estimates. A new version of PHASE developed by M.S. (v2.0, available from M.S.'s Web site) implements both the modified version of PHASE described here and some of these extensions, resulting in still more accurate haplotype estimates (details will be published elsewhere).

Appendix A : Potential Pitfalls of Defining Posterior Distributions Implicitly, and How They Are Avoided

In the text, we note that there are potential pitfalls associated with the fact that the posterior distribution sampled from by PHASE (both the version implementing the algorithm from Stephens et al. [2001a] and the new version described here) is defined implicitly as the stationary distribution of a particular Markov chain, which in turn is defined via a set of inconsistent conditional distributions. Here, “inconsistent” means that there is no joint distribution that has these conditional distributions. The fact that these conditional distributions are inconsistent is potentially problematic, as a Gibbs sampler based on inconsistent conditional distributions is not, in general, guaranteed to converge to a proper probability distribution. However, in this case, convergence to a proper distribution is guaranteed, because the Markov chain has a finite state space (the space of all possible haplotype reconstructions) and is irreducible and aperiodic. (All such Markov chains have a stationary distribution and converge to this stationary distribution; e.g., Theorem 7.4 in Behrends [2000]).

A second potential technical problem with using inconsistent conditional distributions in Gibbs sampling is that, using the standard “fixed scan” approach to Gibbs sampling, where each individual is updated in turn in some fixed order, the stationary distribution could depend on the order used. This seems undesirable, and so, to avoid this, Stephens et al. (2001a) used a “random scan” Gibbs sampler, in which, at each iteration, a random individual is chosen for updating (with each individual being equally likely). In this paper, we used a different, and perhaps slightly preferable, random scan strategy, in which, at each iteration, all individuals are updated in a random order, with a different random order for each iteration. Both schemes clearly ensure that the stationary distribution is independent of the order in which the individuals were input into the algorithm.