Haplotype Block Partition with Limited Resources and Applications to Human Chromosome 21 Haplotype Data

Abstract

Recent studies have shown that the human genome has a haplotype block structure such that it can be decomposed into large blocks with high linkage disequilibrium (LD) and relatively limited haplotype diversity, separated by short regions of low LD. One of the practical implications of this observation is that only a small fraction of all the single-nucleotide polymorphisms (SNPs) (referred as “tag SNPs”) can be chosen for mapping genes responsible for human complex diseases, which can significantly reduce genotyping effort, without much loss of power. Algorithms have been developed to partition haplotypes into blocks with the minimum number of tag SNPs for an entire chromosome. In practice, investigators may have limited resources, and only a certain number of SNPs can be genotyped. In the present article, we first formulate this problem as finding a block partition with a fixed number of tag SNPs that can cover the maximal percentage of the whole genome, and we then develop two dynamic programming algorithms to solve this problem. The algorithms are sufficiently flexible to permit knowledge of functional polymorphisms to be considered. We apply the algorithms to a data set of SNPs on human chromosome 21, combining the information of coding and noncoding regions. We study the density of SNPs in intergenic regions, introns, and exons, and we find that the SNP density in intergenic regions is similar to that in introns and is higher than that in exons, results that are consistent with previous studies. We also calculate the distribution of block break points in intergenic regions, genes, exons, and coding regions and do not find any significant differences.

Introduction

The pattern of linkage disequilibrium (LD) plays a central role in genomewide association studies to identify genetic variation responsible for common human diseases. SNP markers are preferred over microsatellite markers for association studies because of their abundance along the human genome (SNPs with minor allele frequency >0.1 occur in ∼1 of every 600 bp) (Wang et al. 1998), the low mutation rate, and accessibilities to high-throughput genotyping. However, genotyping a large number of individuals for every SNP is still too expensive to be practical when using current technology.

The number of SNPs required for genomewide association studies depends on the LD pattern. Recent studies (Daly et al. 2001; Johnson et al. ²⁰⁰¹; Patil et al. ²⁰⁰¹; Dawson et al. 2002; Gabriel et al. ²⁰⁰²) have shown that the human genome can be partitioned into discrete blocks of high LD separated by shorter regions of low LD, such that only a small fraction of characteristic (“tag”) SNPs are sufficient to capture most of haplotype structure of the human genome in each block. The haplotype block structure with the corresponding tag SNPs can be extremely useful for association studies in which it is not necessary to genotype all SNPs. A recent simulation study (Zhang et al. ^2002a) indicated that the genotyping effort could be significantly reduced without much loss of power for association studies.

In a large-scale study of chromosome 21, Patil et al. (2001) identified, by a rodent-human somatic cell hybrid technique, 20 haplotypes consisting of 24,047 SNPs (with at least 10% minor allele frequency) spanning >32.4 Mb. They developed a greedy algorithm to partition the haplotypes into 4,135 haplotype blocks with 4,563 tag SNPs on the basis of two criteria: (1) in each block, at least 80% of the observed haplotypes are represented more than once; and (2) the total number of tag SNPs for distinguishing at least 80% of haplotypes is as small as possible. For the same data, Zhang et al. (2002b) reduced the number of blocks and tag SNPs to 2,575 and 3,582, respectively, using a dynamic programming algorithm. Both studies tried to minimize the total number of tag SNPs for the entire chromosome. However, when resources are limited, investigators may not be able to genotype all the tag SNPs and, instead, must restrict the number of tag SNPs used in their studies. An objective of the present article is to prioritize SNPs and corresponding chromosomal regions for genotyping in association studies with limited resources. We first give a mathematical formulation for this problem and then develop two dynamic programming algorithms for haplotype block partitioning to maximize the fraction of the genome covered by a fixed number of tag SNPs.

The goal of association studies is to identify genetic variation responsible for human complex diseases and traits. Thus, it is necessary to know the functional SNPs. In addition, to understand the biological implications of haplotype block structure, we must know whether the results, such as the SNPs at the starting points of long blocks, are associated with biological functions. To address these questions, we first apply our algorithms to a data set of SNPs on human chromosome 21 (Patil et al. 2001) to obtain the corresponding haplotype block partitions. We then search the dbSNP database and human genome resources in the National Center for Biotechnology Information (NCBI) database to identify SNPs located in regions of known biological functions, which are, specifically, genes, exons, coding regions, and nonsynonymous SNPs. Finally, we statistically characterize the relationship between the SNPs at the beginning of the haplotype blocks and the SNPs in these regions to assess the biological implications of the haplotype blocks.

Methods

We first formulate the problem of haplotype block partitioning with limited resources, and then we provide algorithmic solutions. We also calculate the distribution of SNPs along coding and noncoding regions.

Haplotype Block Partitioning with Limited Resources

Assume that we are given K haplotype samples consisting of consecutive SNPs: s₁,s₂,…,s_n. For simplicity, the SNPs are referred as 1,2,…,n. Let h₁,h₂,…,h_K be the K haplotype samples. Each haplotype h_k,k=1,2,…,K can be represented as an n-dimensional vector with the ith component h_k(i)=0, 1, or 2 being the allele of the kth haplotype at the ith SNP locus, where 0 indicates missing data, and 1 and 2 are the two alleles.

Here, we follow the definitions of ambiguous and unambiguous haplotypes and the haplotype blocks proposed by Patil et al. (2001) and used by Zhang et al. (2002b). To make the present article self-contained, we summarize the definitions of “ambiguous” and “unambiguous” haplotypes. Consider haplotypes defined by SNPs i and j. Two haplotypes, k and k′, are compatible if the alleles for the two haplotypes are the same at the loci with no missing data, that is, h_k(l)=h_k^′(l) for any l,i⩽l⩽j, and h_k(l)h_k^′(l)≠0. A haplotype in a block is ambiguous if it is compatible with two other haplotypes that are themselves incompatible. For example, consider three haplotypes h₁=(1,0,0,2), h₂=(1,1,2,0), and h₃=(1,1,1,2). Haplotype h₁ is compatible with haplotypes h₂ and h₃, but h₂ is not compatible with h₃, because they differ at the third locus. Thus, h₁ is an ambiguous haplotype, whereas h₂ and h₃ are unambiguous haplotypes. In the remainder of the present article, only unambiguous haplotypes will be included in the analysis. Compatible haplotypes will be treated as identical haplotypes.

A segment of consecutive SNPs can form a block if at least α percent of unambiguous haplotypes are represented more than once in the samples (Patil et al. 2001; Zhang et al. ^2002b). The tag SNPs are selected on the basis of the measure of haplotype quality in each block. Different measures of block quality have been used, depending on the purpose of a study. For example, Patil et al. (2001) defined the tag SNPs as the minimum subset of SNPs that can distinguish at least α percent of the unambiguous haplotypes. Another measure is based on haplotype diversity (Johnson et al. 2001). We can choose tag SNPs that minimize the number of SNPs that can account for at least β percent of overall haplotype diversity. In the present article, we follow the definition of tag SNPs used by Patil et al. (2001).

Given α and the above-mentioned criterion for defining tag SNPs, Zhang et al. (2002b) developed a dynamic programming algorithm for haplotype block partitioning to find a partition with the minimum total number of tag SNPs. For a fixed number of SNPs to be genotyped, we consider haplotype block partitions with some SNPs being excluded. For a set of consecutive SNPs (s_i,s_i+1,…,s_j), we define the following functions:

• block(i,…,j)=1 if at least αM(α<1) unambiguous haplotypes defined by the SNPs s_i,s_i+1,…,s_j are represented more than once, where M⩽K is the total number of unambiguous haplotypes defined by the SNPs s_i,s_i+1,…s_j.

• f(i,…,j): the number of tag SNPs within the block. Given a set of disjointed blocks, B={B₁,B₂,…,B_l} and B₁≺…≺B_l, where B₁≺B₂ indicates that the last SNP of B₁ is located before the first SNP of B₂, (if the last SNP of B₁ and the first SNP of B₂ are not consecutive, the interval between them is excluded from this block partition); the total number of tag SNPs for these blocks is defined by .

• L(i,…,j): the length of the block. We simply define it as the number of SNPs in this block, L(i,…,j)=j-i+1. We can also define it as the actual length of the genome spanning from the ith SNP to the jth SNP. Given a set of disjointed blocks, B={B₁,B₂,…,B_l}, the total length for these blocks is .

With a given number of tag SNPs, our goal is to find the haplotype block partition to maximize the total length of the region included. We formulate the problem as follows:

Block partition with a fixed number of tag SNPs (FTS)

Given K haplotypes consisting of n consecutive SNPs and an integer m, find a set of disjointed blocks B={B₁,B₂,…,B₁} with f(B)⩽m such that L(B) is maximized.

This problem can be converted to an equivalent, “dual” problem as follows:

Block partition with a fixed genome coverage (FGC)

Given a chromosome with length L, K haplotypes consisting of n consecutive SNPs, and β⩽1, find a set of disjoint blocks B={B₁,B₂,…,B_l} with L(B)⩾βL such that f(B) is minimized.

In the following, we propose a two-dimensional (2D) dynamic programming algorithm for the FTS problem and then a parametric dynamic programming algorithm for the FGC problem.

A 2D Dynamic Programming Algorithm

Let S(j,k) be the maximum length of the genome that is covered by, at most, k tag SNPs for the optimal block partition of the first j SNPs, j=1,2,…,n. Set S(0,k)=0 for any k⩾0 and S(0,k)=-∞ for any K<0. Then,

and

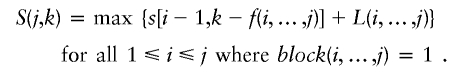Let B={B₁,…,B_J} be the set of disjointed blocks for S(j,k), such that L(B) is maximal with the constraint f(B)⩽k. Then either the last block B_J ends before j, such that S(j,k)=S(j-1,k), or B_J ends exactly at j and starts at some i^*,1⩽i^*⩽j, such that S(j,k)=S[i^*-1,k-f(B)]+L(B_J). Using this recursion, we can design a dynamic programming algorithm to compute S(m,n), the maximum length of genome that is covered by m tag SNPs. The optimal block partition B can be found by backtracking the elements of S that contribute to S(m,n).

The space complexity for this algorithm is O(m·n). If we have precomputed the values of block(·), f(·), and L(·), then the time complexity of this algorithm is O(N·m·n), where N is the number of SNPs contained in the largest block, and N≪n generally. In fact, given a block of k SNPs (i.e., s_i,…,S_i+k−1), the computation time for L(·) is O(1), and the computing time for block(i,…,i+k−1) is O(K²N), because we need to determine whether any two of the K haplotypes are compatible at these k SNPs in the block. In total, there are, at most, O(nN) blocks, which requires O(K²N²n) time for computing all values of block(·). As mentioned elsewhere (Zhang et al. ^2002b), the problem of calculating f(i,…,i+k−1) is NP complete, which means that there are no polynomial time algorithms computing f(·) for any input. Theoretically, the time needed for the enumeration method proposed elsewhere (Zhang et al. ^2002b) is, at most, O(NK), but it is much shorter in practice. Considering the computation of block(·) and f(·), the overall time complexity becomes O(K²N^K+2n+Nmn).

A Parametric Dynamic Programming Algorithm

For a consecutive set of SNPs i,…,j, if block(i,…,j) = 1 and if this block is included in the partition, then f(i,…,j) equals the number of tag SNPs. If these SNPs are excluded in the partition, the penalty for this exclusion is defined as λL(i,…,j), where λ is the parameter for deletion and λ⩾0. λ can be regarded as the penalty for each unit length of the excluded regions. Using this scoring scheme, we can score a block partition by f(B)+λL(E), where B represents the included blocks, and E represents the excluded SNPs. Let the scoring function S(j,λ) be the minimum score for the optimal block partition of the first j SNPs (j=1,2,…,n) with respect to the deletion parameter λ. Let S(j,λ)=0. We can apply the dynamic programming algorithm to obtain S(j,λ) by the following recursion:

and

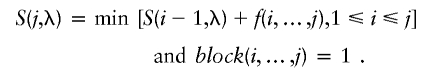For any given λ⩾0, the dynamic programming algorithm that uses the above recursion can compute the minimum score.

For any j, if there exists i* satisfying 1⩽i^*⩽j and S(j,λ)=S(i^*-1,λ)+λL(i^*,…,j), then the block [i^*,…,j] is included in the partition. Otherwise, there must exist i* satisfying 1⩽i*⩽j and S(j,λ)=S(i^*-1,λ)+f(i^*,…,j), such that the interval [i^*,…,j] is excluded from the partition. The penalty for the excluded intervals equals the product of and the total length of these intervals. For any λ⩾0, S(n,λ) equals the sum of the total number of tag SNPs for included blocks and the penalty for excluded intervals. It should be noted that the parametric dynamic programming method is a classical computational tool in sequence alignment, in which the parameters are the weight of matches, mismatches, insertions/deletions, and gaps (Waterman et al. 1992; Gusfield et al. ¹⁹⁹⁴). In the following, we use a method similar to that used by Gusfield et al. (1994) and Waterman et al. (1992), to study the properties of block partitions according to the deletion parameter λ.

Obviously, S(n,0)=0, since all SNPs are excluded from the block partition, and S(n,∞) equals the minimum number of tag SNPs for the entire genome, because all SNPs are included in the block partition. S(n,∞) can be obtained by the dynamic programming algorithm described elsewhere (Zhang et al. (2002b). For any fixed λ>0, the parametric dynamic programming algorithm can compute the optimal solution with included blocks and excluded intervals. Let the length of the included blocks be equal to βL. Then, the number of tag SNPs is S(n,λ)-λ(1-β)L. In fact, S(n,λ)-λ(1-β)L must be equal to the minimum number of tag SNPs that is necessary to include at least βL of the genome length. Otherwise, there must exist a partition that needs only m<S(n,λ)-λ(1-β)L tag SNPs to cover at least βL of the genome, and this partition can reduce the score to m+λ(1-β)L<S(n,λ), which contradicts the assumption that S(n,λ) is the minimum. Using ideas similar to those discussed by Waterman et al. (1992), it can be shown that S(n,λ) has the following properties:

S(n,λ) is an increasing, piecewise-linear, and convex function of λ. The right-most linear segment of S(n,λ) is constant. The intercept and slope for S(n,λ) for each piecewise-linear segment are the total number of tag SNPs and the total length of excluded intervals, respectively.

Waterman et al. (1992) proposed a method to find S(n,λ) for all λ⩾0 efficiently. To make the present article self-contained, a brief description of the idea and a brief sketch of the algorithm are given in this paragraph and the next. Assume that, for an arbitrary λ_i, we obtain S(n,λ_i)=a+λ_ib, where a equals the number of tag SNPs for the included blocks, and b equals the length of the deleted intervals. Define a linear function s(λ)=a+λb by a and b. By definition, S(n,λ) is minimal. Therefore, S(λ)⩽S(n,λ) for any λ⩾0, including λ_i where s(λ_i)=(n,λ_i). Since S(n,λ) is piecewise linear, the point (λ_i,S(n,λ_i)) must be located within some linear segment L_i(λ) of S(n,λ). If (λ_i,S(n,λ_i)) is not located at the end of L_i(λ), s(λ) should be exactly the line defined by L_i(λ), because s(λ)⩾L_i(λ) when λ is ∼λ_i, and, at the same time, s(λ_i)=L_i(λ_i). Repeating this idea, we are able to find all such line segments for S(n,λ).

The algorithm begins with S(n,0), and S(n,∞), S(n,0) = 0, and the slope of the corresponding line L₀ equals the total length of the genome. S(n,∞) equals the minimum number of tag SNPs, and the corresponding line L_∞ is horizontal. Let the intersection point for L_∞ and L₀ be (x,y). If S(n,x)=0, then L₀ and L_∞ together define the entire function of S(n,λ). Otherwise, S(n,x)<y, and the corresponding line L_x for the point [x,S(n,x)] intersects both L₀ and L_∞. We then divide λ into two regions—[0,x] and [x,∞]—and repeat the above procedure for these two regions separately, until all the line segments of S(n,λ) are found.

To find all the intersection points of the piecewise-linear segments of S(n,λ), we need to compute S(n,λ) for any specific λ efficiently. In the above algorithm, the calculation of min_1⩽i⩽j(S(i-1,λ)+f(i,…,j)) depends on the block structure of the haplotypes and is the same as the dynamic programming algorithm (Zhang et al. ^2002b). If we have precomputed the values of block(·), f(·), and L(·), the parametric algorithm takes O(Nn²) time, where N is the number of SNPs contained in the largest block. However, if L(·) is an additive function, we can improve the algorithm to O(Nn) time (Waterman et al. 1992; Waterman ¹⁹⁹⁵). Considering the computation of block(·),f(·), the total time for finding S(n,λ) is O(K²N^K+2n+NSn), where K is the total number of haplotype samples, and S is the number of segments in S(n,λ), which is less than the total number of tag SNPs.

After finding all the line segments of S(n,λ), we know the entire function of S(n,λ). At each intersection point [x,S(n,x)], several block partitions with different numbers of tag SNPs and lengths of excluded intervals may have the same score. We will choose the right-most one with the maximum number of tag SNPs and the minimum length of excluded intervals. For each line segment between two intersection points, both the total number of tag SNPs and the total length of excluded intervals are constant along this segment, and both are equivalent for the low intersection point between this segment and the previous segment. We can sort the number of tag SNPs in ascending order, according to the deletion parameters at the intersection points. The gaps between these numbers give us information as to how the block partition is affected by the deletion parameter λ.

Results

Source of Data

We test our algorithms on a data set of human chromosome 21 reported by Patil et al. (2001). The data set includes 20 haplotypes of 24,047 SNPs (at least 10% minor allele frequency) spanning >32.4 Mb. These SNPs are located in four contigs. Here, we apply our algorithms to the largest contig, NT_002836, which contains 21,840 SNPs. We search the dbSNP database and the human genome resources in the NCBI database to identify SNPs in genes, introns, exons, and coding regions and nonsynonymous SNPs. We distinguish coding regions from exons, because not all exons are translated into proteins. In fact, about a third of all the exons are untranslated. We then apply the algorithms to partition the haplotypes into blocks that include all the SNPs in coding regions.

Haplotype Blocks with Limited Resources

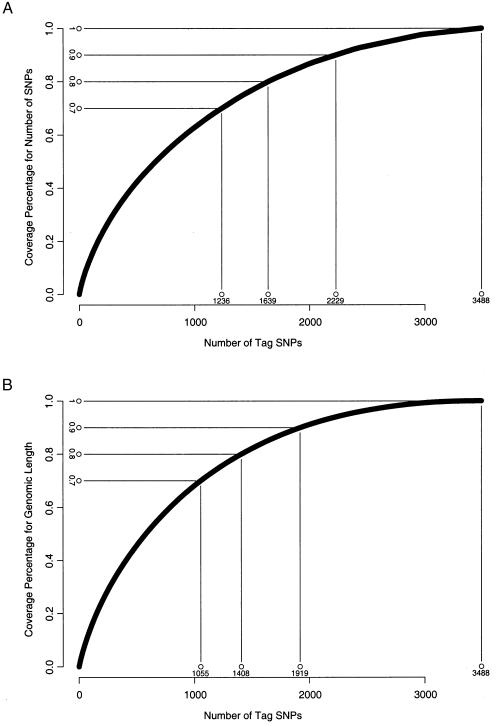
The parameters used in the algorithms are set as follows. The number of tag SNPs for a block, f(·), is defined by the minimum number of SNPs that can distinguish at least α=80% of unambiguous haplotypes, and f(·)=1 when there is one haplotype with ⩾80% frequency. L(i,…,j) is set as either the number of SNPs in included blocks or the genome length of these blocks. Figure 1A shows the relationship between the number of tag SNPs and the ratio of the number of SNPs in included blocks over the total number of SNPs, using the 2D dynamic programming algorithm. The minimum number of tag SNPs that can cover 70%, 80%, 90%, and 100% of all SNPs are also shown in figure 1A. A total of 3,488 tag SNPs can cover 100% of SNPs, and this number becomes 2,229 for coverage of 90% of SNPs and 1,639 for coverage of 80% of SNPs. Figure 1B shows the relationship between the number of tag SNPs and the ratio of the length of the sequence of included blocks over the length of the whole sequence, as well as the minimum number of tag SNPs for covering 70%, 80%, 90%, and 100% of the genome sequence.

Figure 1.

Results of the 2D dynamic programming for block partitioning. A, Relationship between the number of tag SNPs and the percentage of the total number of SNPs being included. B, Relationship between the number of tag SNPs and the percentage of the actual genomic length being included.

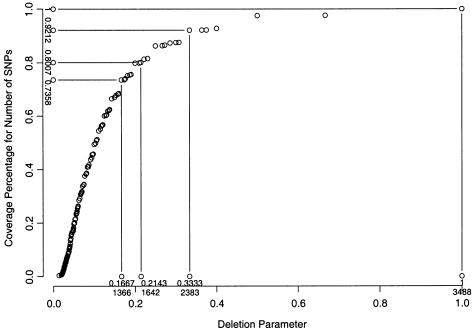
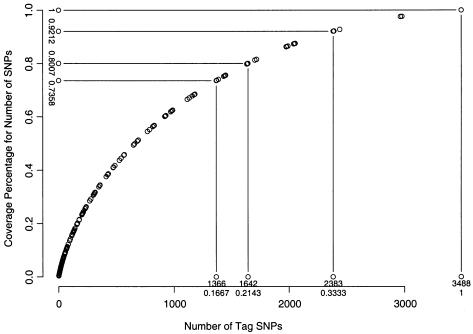
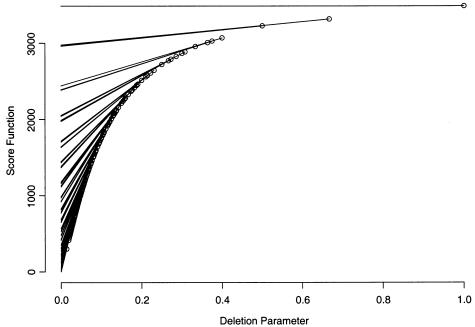
We also implement the parametric dynamic programming algorithm and test it on the same data set. We set L(·) to be the number of SNPs, L(i,…,j)=j-i+1. Figure 2 shows the relationship between the percentages of the total number of SNPs being included and the deletion parameter λ at the intersection points of the piecewise-linear segments. Figure 3 shows the relationship between the percentages of the total number of SNPs being included and the number of tag SNPs required at the intersection points of the piecewise-linear segments. When figure 3 is compared with figure 1, the corresponding numbers of tag SNPs shown in each figure give comparable percentages of the total number of SNPs included. The scoring function with respect to the deletion parameter with the right-most segment of each intersection point is shown in figure 4. The slopes of the lines connecting two adjacent intersection points in figures 3 and 4 are very useful for selecting tag SNPs for genotyping.

Figure 2.

Relationship between the deletion parameter (λ) and the corresponding coverage of the total number of SNPs at the intersection points of piecewise-linear segments of the score function S(n,λ), using the parametric dynamic programming algorithm. The penalty for a set of excluded consecutive SNPs is chosen as the product of the deletion parameter λ and the number of SNPs.

Figure 3.

Relationship between the number of tag SNPs and the corresponding percentage of the total number of SNPs being included at the intersection points of piecewise-linear segments of the score function S(n,λ), using the parametric dynamic programming algorithm. The penalty for a set of excluded consecutive SNPs is chosen as the product of deletion parameter λ and the number of SNPs.

Figure 4.

Scoring function S(n,λ) with respect to the deletion parameter λ. The penalty for a set of excluded consecutive SNPs is chosen as the product of deletion parameter λ and the number of SNPs.

SNPs at Coding and Noncoding Regions

We searched the dbSNP database and the human genome resources of the NCBI database to identify SNPs in genes, introns, exons, coding regions, and nonsynonymous SNPs. We distinguish coding regions from exons because not all exons are translated into proteins.

Instead of using the contig NT_002836, which is not mapped in the human genome at the NCBI database, we use the mapped contig NT_011512, which contains the contig NT_002836, to search the positions of the SNPs. On July 18, 2002, the length of the contig NT_011512 was 28,512,199 bp. There are 380 mapped genes and 38,083 mapped SNPs in the contig NT_011512 in the NCBI database. Among the 380 genes, 357 have both exon information and coding information, and the rest are either pseudogenes or unconfirmed genes. We therefore included only these 357 genes in our analysis. The total lengths of the genes, the exons, and the coding regions are 15,425,073, 486,409, and 315,574 bp, respectively, corresponding to 54.10%, 1.71%, and 1.11%, respectively, of contig NT_011512. Among the 21,840 SNPs used by Patil et al. (2001), 20,503 are mapped to the dbSNP database and the human genome resources of the NCBI database, and 38 have ambiguous map positions (at least two positions in one contig), which were excluded from further analysis.

Table 1 shows the numbers of SNPs in genes, exons, and coding regions, together with the number of nonsynonymous SNPs. Table 2 shows the density of SNPs (expressed as the average number of SNPs per kilobase and its 95% CI) in intergenic regions, genes, introns, exons, and coding regions, based on the data of Patil. et al. (2001). The last row gives the P values of the observed data under the null hypothesis that SNPs are uniformly distributed along the chromosome. Table 2 shows that the densities of SNPs in intergenic regions, genes, introns, and coding regions are similar to the average density along the chromosome. However, the density in exons is somewhat lower than the average (P=.1). This observation is consistent with previous studies on SNPs in coding and noncoding regions. The reason for the relatively high density of SNPs in genes is that most of the gene regions are in introns. However, it is surprising that the density in coding regions is somewhat higher than that in exons. Figure 5 shows histograms for the number of genes with different numbers of SNPs in genes, exons, and coding regions and the number of nonsynonymous SNPs.

Table 1.

Numbers of SNPs in Different Regions of the Genome

	No. of SNPs in
Type of SNPs	NT_002836a	NT_011512b
Mapped	20,503	38,089
Ambiguously mapped	38	117
In genes	11,055	20,814
In introns	10,736	20,041
In exons	319	773
In coding regions	221	476
Nonsynonymous	144	278

^aPatil et al. ²⁰⁰¹.

^bNCBI database.

Table 2 .

Densities of SNPs and Their CIs in Different Regions of the Genome for the Contig NT_002836^[Note]

	Density of SNPs in
	IntergenicRegions	Genes	Introns	Exons	CodingRegions
SNPs/kb	.722	.717	.719	.656	.700
95% CI	(.71–.73)	(.71–.73)	(.71–.73)	(.65–.79)	(.63–.81)
Pa	.60	.60	.93	.10	.69

Note.— Contig NT_002836 is described by Patil et al. (2001).

^aCalculated under the null hypothesis that the SNPs are uniformly distributed along the chromosome.

Figure 5.

The histograms for the number of genes according to the number of SNPs in genes (a), the number of SNPs in exons (b), the number of SNPs in coding regions (c), and the number of non-synonymous SNPs (d).

We partition the haplotypes into blocks, using the dynamic programming algorithm (Zhang et al. ^2002b), and test whether the starting SNPs of the blocks are evenly distributed along the chromosome. The number of tag SNPs in each block, measured by f(·), is defined as the minimum number of SNPs that can distinguish at least 80% of unambiguous haplotypes. We obtain a total of 2,182 blocks. The number of starting SNPs in different regions is given in table 3. We assess the association between the SNPs in the beginning of the haplotype blocks and in regions with known biological functions, such as exons. Differences in distribution of the starting SNPs along the chromsome were not statistically signficant.

Table 3.

The Number of Starting SNPs in Blocks and the Average Number of Starting SNPs per Megabase in Various Regions of the Genome

	No. of SNPs in
	IntergenicRegions	Genes	Exons	CodingRegions
Starting SNPs	1,025	1,157	39	25
Starting SNPs/Mb	78	75	80	79
Pa	.49	.49	.82	.89

^aCalculated under the null hypothesis that the SNPs are uniformly distributed along the chromosome.

To investigate the pattern of LD in the haplotype blocks obtained above, we plot a histogram of the number of blocks with different numbers of distinct haplotypes (fig. 6). We find that most of the blocks contain seven or fewer distinct haplotypes; only 213 blocks (∼10%) contain eight or more distinct haplotypes, and 1,204 (55%) contain four or fewer distinct haplotypes. A small number of haplotypes within a block indicates a strong LD signal.

Figure 6.

Histogram for the number of blocks according to the number of distinct haplotypes in a block. The blocks are obtained on the basis of a data set of human chromosome 21 from Patil et al. ²⁰⁰¹, using the dynamic programming algorithm (Zhang et al. ^2002b). The number of tag SNPs in each block, measured by f(·), is defined as the minimum number of SNPs that can distinguish at least 80% of unambiguous haplotypes.

One of the advantages of the algorithms used in the present study is that functions of SNPs, such as whether they are in coding or noncoding regions, can be incorporated into the algorithms. In an association study, investigators may put more weight on SNPs within coding regions than on those in noncoding regions. One method is to add higher penalty to the SNPs in coding regions. In the parametric dynamic programming algorithm, we define the length of a set of consecutive SNPs i,…,j,L(i,…,j) as follows:

where n_c is the number of SNPs in coding regions and T is a relatively large positive number. We implemented the parametric dynamic programming algorithm, using this definition of L(·), to obtain the corresponding block partitions. We set T=1,000. The number of tag SNPs for a block, f(·), is defined by the minimum number of SNPs that can distinguish at α⩾80% of unambiguous haplotypes. We let f(·)=1 if a single haplotype has a frequency ⩾80%. For example, we obtain 596 blocks with 1,081 tag SNPs representing 14,048 SNPs when the deletion parameter α is set at 0.140. All 221 SNPs in the coding regions are included in this block partition.

Discussion

Several recent studies have suggested that the human genome can be divided into blocks with high LD within each block. Because of this feature, a relatively small fraction of SNPs can capture most of the haplotypes in each block. Previously, Zhang et al. (2002b) developed a dynamic programming algorithm for haplotype block partition to minimize the total number of tag SNPs across the whole genome. However, in a genetic study with limited resources, investigators may wish to genotype only a fixed number of SNPs. The problem then becomes how to choose tag SNPs and the corresponding genomic regions to maximize the genome coverage with the fixed number of tag SNPs. In the present article, we formulate the problem of finding the haplotype blocks by use of a restricted number of tag SNPs. We provide two dynamic program algorithms to solve this problem. One of the advantages of the algorithms is that properties of SNPs, such as whether they are in coding or noncoding regions, can be incorporated into the algorithms, whereas, in an association study, investigators may put more weight on SNPs within coding regions than on those in noncoding regions.

As an initial step to understand the biological implications of haplotype blocks, we characterize the relationship between the starting SNPs of haplotype blocks from the optimal block partition and the SNPs in regions with known biological functions. We find that the starting SNPs of haplotype blocks are evenly distributed in genes, exons, and coding regions.

We apply the algorithms for haplotype block partition with limited resources to a contig of a data set of SNPs on human chromosome 21. In this example, we require that all the SNPs in coding regions be selected. The algorithms developed in the present study are flexible enough to allow investigators to decide the weights for SNPs with different functions. In the present article, we use the fraction of haplotypes represented by the tag SNPs as a quality measure. Other quality measures, such as haplotype diversity (Johnson et al. 2001), can be easily incorporated into the programs. The output from the algorithms can guide investigators to SNPs for genotyping, to maximize the success of association studies.

The algorithms developed in the present article are based on haplotype data. Although laboratory techniques, such as allele-specific long-range PCR (Michlataos-Beloin et al. ¹⁹⁹⁶) or diploid-to-haploid conversion (Douglas et al. 2001), have been used to determine haplotypes in diploid individuals, these approaches are technically difficult, labor intensive, and expensive. Most of the time, it is unrealistic to do a large-scale study across the whole genome, as was done by Patil et al. (2001). For these reasons, multiple sets of large-scale genotype data rather than haplotype data are being generated. Thus, it is important to develop methods to extract haplotype block information from genotype data directly. The dynamic programming algorithms developed in the present study, combined with methods for haplotype inference (e.g., Qin et al. ²⁰⁰²) can be used to achieve this objective.