Abstract
Many linkage studies are performed in inbred populations, either small isolated populations or large populations with a long tradition of marriages between relatives. In such populations, there exist very complex genealogies with unknown loops. Therefore, the true inbreeding coefficient of an individual is often unknown. Good estimators of the inbreeding coefficient (f) are important, since it has been shown that underestimation of f may lead to false linkage conclusions. When an individual is genotyped for markers spanning the whole genome, it should be possible to use this genomic information to estimate that individual's f. To do so, we propose a maximum-likelihood method that takes marker dependencies into account through a hidden Markov model. This methodology also allows us to infer the full probability distribution of the identity-by-descent (IBD) status of the two alleles of an individual at each marker along the genome (posterior IBD probabilities) and provides a variance for the estimates. We simulate a full genome scan mimicking the true autosomal genome for (1) a first-cousin pedigree and (2) a quadruple-second-cousin pedigree. In both cases, we find that our method accurately estimates f for different marker maps. We also find that the proportion of genome IBD in an individual with a given genealogy is very variable. The approach is illustrated with data from a study of demyelinating autosomal recessive Charcot-Marie-Tooth disease.
Introduction
Many linkage studies are performed in small isolated populations and in populations with a long tradition of marriages between relatives. In these populations, the set of relationships between individuals might not be known exhaustively, since genealogies can be very complex with potentially unknown loops. Therefore, no accurate knowledge of each individual’s inbreeding coefficient can be gained from the known genealogy. The inbreeding coefficient (f) is the probability that the two alleles at any locus in an individual are identical by descent (Malécot 1948). In this article, we consider only identity by descent (IBD) within an individual.
In the case of homozygosity mapping for recessive traits (Lander and Botstein 1987), good estimators of f are important for declaring a region as a candidate for harboring a susceptibility locus. Indeed the linkage statistic relies on an increased genome sharing within the affected individuals, compared with what would be expected under random segregation in the genealogies of the individuals. If we do not know the genealogies exhaustively, we may underestimate f. Underestimation of f may artificially increase the statistics and, hence, the rate of false-positive results (Miano et al. 2000).
We are interested in developing a methodology to estimate an individual’s f without requiring any knowledge of the parental relationships. To do so, we need to characterize the IBD process along the individual’s genome and estimate its parameters without using the parental relationships. Stam (1980) was the first to propose a model for the IBD process along the genome of an individual in finite random mating populations. However, he assumed that he could observe continuous IBD data on the genome, whereas only discrete identity-by-state (IBS) data can be observed (marker genotypes). More recently, Abney et al. (2002) used a similar model and estimated its parameters from the individual’s genealogy. Here, we propose to rely on the individual’s marker genotype data to estimate these parameters. To do so, we use a hidden Markov model (HMM) for the IBD process of the individual. The IBD transition probabilities depend on the genetic distance between the markers and two unknown parameters: f, the inbreeding coefficient of the individual, and a, such that af is the instantaneous rate of change per centimorgan from no IBD to IBD.
First, we present the methodology. Then, we show simulation results for (1) a first-cousin pedigree and (2) a quadruple-second-cousin (cyclic sibship exchange) pedigree (Thompson 1988), to evaluate the proposed method and to validate our estimates. Finally, we illustrate the method on data from a study of Charcot-Marie-Tooth (CMT) disease (Charcot and Marie 1886; Tooth 1886).
Methods
Estimation of the Inbreeding Coefficient through Use of HMM
We propose here to estimate f for an individual, from marker data on that individual's entire autosomal genome, by means of the maximum-likelihood method. Latent random variables (the IBD status at the markers) underlie these observed marker data. A marker k has either two alleles IBD (Xk=1) or two alleles non-IBD (Xk=0). We approximate the IBD process X along the genome by a Markov chain. This approximation was shown to give results close to the true ones for genealogies such as first-cousin marriages but also for more complex ones (Thompson 1994). With the Markov approximation, the IBD status at marker k depends only on the IBD status at adjacent loci, and the probability of the IBD statuses along each autosomal chromosome pair can be written as
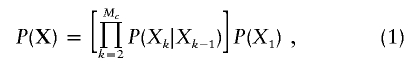 |
where Mc is the number of markers on chromosome c. Therefore, we need only characterize the single-locus IBD probability and the transition IBD probabilities between adjacent loci. The single-locus IBD probability P(Xk) is our parameter of interest: the inbreeding coefficient f. The transition IBD probabilities are as follows:
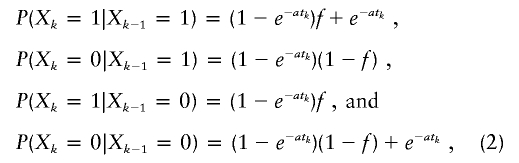 |
where tk is the genetic distance (in cM) between marker k-1 and k. We assume an absence of genetic interference, and the genetic map is assumed to be known without error. In the first line of equation (2) describing the probability of staying IBD, the final term, e-atk, corresponds to no change in the coancestry over a segment of length tk, and the other term, (1-e-atk)f, corresponds to a change in the coancestry, in which case IBD results with equilibrium probability f. Note that our model is similar to that of Stam (1980). Indeed, in his model, he assumes that the lengths of both IBD and non-IBD segments are distributed exponentially, with mean lengths 1/α and 1/λ, respectively. Our model corresponds to his, with α=a(1-f) and λ=af.
From equations (1) and (2), we can compute the likelihood Lx(f,a) for f and a if we observe the IBD status x at the markers. However, only the genotypes Y are observed at the markers. The previous approximation allows us to use an HMM to calculate the probability of the marker genotype data. For genotype data Yc on the autosomal chromosome pair c, we have
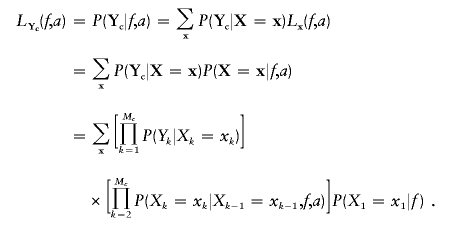 |
This likelihood LYc can then be calculated using the Baum algorithm (Baum 1972; Boehnke and Cox 1997; Epstein et al. 2000), which uses a recurrence relationship (Mc times) on one-dimensional sums to compute this Mc-dimensional sum. The algorithm goes forward along the genome to compute recursively
 |
with R*1(x)=P(X1=x). From R*M (where 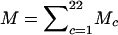 ), we can calculate the probability of Y:
), we can calculate the probability of Y:
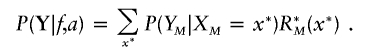 |
The probability of Yk is determined by Xk and is a function of the allele frequencies at marker k (table 1). We have also included a simple model for genotyping errors and mutations similar to the one of Broman and Weber (1999). When the genotype Yk is missing at a marker k, we sum over all possible genotypes, regardless of the IBD status Xk, so P(Yk|Xk=x)=1 for all x. The probability of Xk is determined by Xk-1, as presented in equation (2).
Table 1.
Probabilities of the Genotype Yk Given the IBD Status Xk and the Error Model[Note]
|
Probability when |
||
| Yk | Xk=0 | Xk=1 |
| AiAi | p2i | (1-ε)pi+εp2i |
| AiAj | 2pipj | ε2pipj |
Note.— pi = Frequency of allele Ai; ε = rate of error.
We perform numerical maximization of 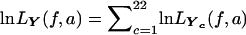 through use of GEMINI (Lalouel 1979) to obtain the maximum-likelihood estimates (MLEs) of f and a, hereafter denoted as
through use of GEMINI (Lalouel 1979) to obtain the maximum-likelihood estimates (MLEs) of f and a, hereafter denoted as 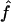 and
and 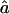 , respectively. To obtain variance estimates for
, respectively. To obtain variance estimates for 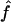 and
and 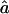 , we need to compute the observed information matrix IY. The variance of
, we need to compute the observed information matrix IY. The variance of 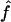 is then
is then 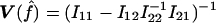 , and the variance of
, and the variance of 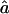 is
is 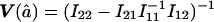 , where Iij is the element from the ith row and jth column of IY. This observed information IY is the negative curvature of the log-likelihood surface lnLY at its maximum. The information IY provided by the observed data Y about the parameters f and a is equal to the information that would be provided by the latent IBD process X (since the distribution of Y given X does not depend on f and a) minus the penalty of observing only Y and not X (Sundberg 1974; Louis 1982):
, where Iij is the element from the ith row and jth column of IY. This observed information IY is the negative curvature of the log-likelihood surface lnLY at its maximum. The information IY provided by the observed data Y about the parameters f and a is equal to the information that would be provided by the latent IBD process X (since the distribution of Y given X does not depend on f and a) minus the penalty of observing only Y and not X (Sundberg 1974; Louis 1982):
When the notation 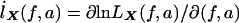 and
and 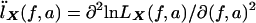 is used, we have IX=
is used, we have IX=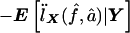 . IX is the expected information from X conditional on the observed genotype data Y. Then, the penalty term in equation (3) for not observing the IBD status at the markers is
. IX is the expected information from X conditional on the observed genotype data Y. Then, the penalty term in equation (3) for not observing the IBD status at the markers is
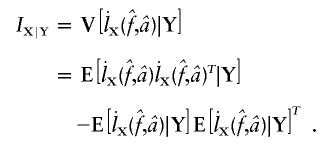 |
Since each term of equation (3) is a conditional expectation, each one can be estimated by a Monte Carlo method sampling X from its joint posterior distribution P(X|Y). We start with XM sampled from P(XM=x|Y). Then, Xk-1 is obtained by sampling from P(Xk-1=x|Xk=x*,Xk+1,…,XM,Y) as we go backward along the genome for k=M…2. These probabilities are easily obtained from the forward-backward Baum algorithm (Baum et al. 1970). Indeed,
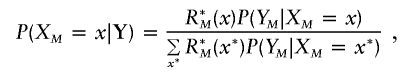 |
and, with the HMM structure, we have
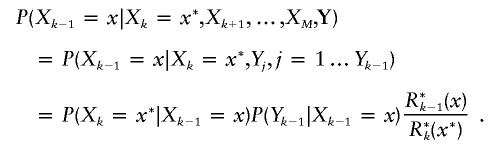 |
Simulation Study
We evaluate our proposed methodology by simulation. First, we want to validate our estimates of f and a. Then, we study their sensitivity to misspecification of marker allele frequencies. We generate, for individuals belonging to two different genealogies, 1,000 replicates of a full-genome scan composed of 22 autosomal chromosome pairs mimicking the true genome and giving a total length of ∼33 morgans (through use of the Genedrop program of MORGAN2.5 [available from the Pangaea Web site]) for three different marker maps. For each marker, the true IBD status can be determined by making use of the founder allele labels.
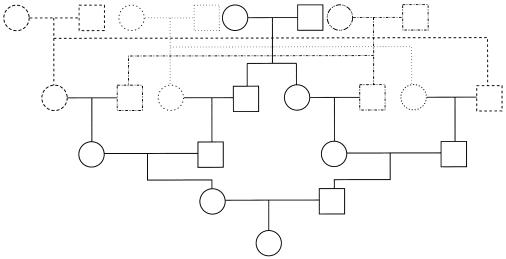
The two genealogies considered are first cousin (hereafter denoted as “1C”) and quadruple second cousin (cyclic type; “4×2C”), as shown in figure 1. These two genealogies (g1 and g2, respectively) have the same expected proportion of genome IBD (fg1=fg2=1/16=0.0625) but different distributions of this IBD along the genome (and, hence, different values of a). For 4×2C, one expects to see smaller IBD blocks than for 1C, because of more remote common ancestors, and also to see more of these blocks, because of the multiple common ancestors. We compute the exact two-locus inbreeding coefficient from the genealogy (through use of the kin program of MORGAN2.5 [available from the Pangaea Web site]) for 1 cM⩽t⩽10 cM and solve 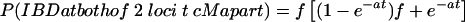 (from eq. [2]) for a, with f=fg1 or f=fg2. The values of a are not sensitive to t, and we get an expected a from the genealogy: ag1≈0.063 for 1C and ag2≈0.084 for 4×2C. This implies that, for 1C, the expected mean IBD block length is [ag1(1-fg1)]-1≈17 cM and, for 4×2C, [ag2(1-fg2)]-1≈13 cM. We chose these two genealogies because they are likely to be found in reality and have the same expected proportion of genome IBD but different a values.
(from eq. [2]) for a, with f=fg1 or f=fg2. The values of a are not sensitive to t, and we get an expected a from the genealogy: ag1≈0.063 for 1C and ag2≈0.084 for 4×2C. This implies that, for 1C, the expected mean IBD block length is [ag1(1-fg1)]-1≈17 cM and, for 4×2C, [ag2(1-fg2)]-1≈13 cM. We chose these two genealogies because they are likely to be found in reality and have the same expected proportion of genome IBD but different a values.
Figure 1.
Quadruple-second-cousin pedigree (cyclic type)
For each replicate, we consider three different marker map scenarios: (S1) SNPs every 1.67 cM, with allele frequencies 0.4/0.6 (1,972 markers); (S2) microsatellites every 5 cM, with five equifrequent alleles (672 markers); and (S3) microsatellites every 10 cM (347 markers). For each marker map scenario, we estimate f and a from the marker genotype data through use of our HMM. We call these estimators 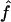 and
and 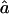 . From the true marker IBD status, we compute the proportion of markers IBD (
. From the true marker IBD status, we compute the proportion of markers IBD (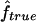 ), the expected value of which is fg1 for 1C and fg2 for 4×2C. Then, we evaluate how estimating marker allele frequencies on a small sample could impact the estimates of f and a. For each replicate, we estimate the allele frequencies at each marker from a sample of 30 control individuals drawn from the population in which patients were studied and the allele frequencies are known. For the SNP map (S1), we sample our controls from a population with allele frequencies 0.4/0.6 for all markers and call the scenario S1′. For the microsatellite maps (S2 and S3), we sample the 30 controls from a population with allele frequencies 0.2/0.2/0.2/0.2/0.2 and call the scenarios S2′ and S3′, respectively. Finally, we look at the impact of having maps in which the markers do not have equifrequent or nearly equifrequent alleles. For each replicate, we still have the same true marker IBD status as we did previously, but now the SNP map has allele frequencies 0.2/0.8 (map scenario Z1) and the microsatellite maps have allele frequencies 0.02/0.08/0.3/0.3/0.3 (map scenarios Z2 and Z3, for the 5-cM and 10-cM spacing, respectively). For these three map scenarios, we look at the sensitivity of
), the expected value of which is fg1 for 1C and fg2 for 4×2C. Then, we evaluate how estimating marker allele frequencies on a small sample could impact the estimates of f and a. For each replicate, we estimate the allele frequencies at each marker from a sample of 30 control individuals drawn from the population in which patients were studied and the allele frequencies are known. For the SNP map (S1), we sample our controls from a population with allele frequencies 0.4/0.6 for all markers and call the scenario S1′. For the microsatellite maps (S2 and S3), we sample the 30 controls from a population with allele frequencies 0.2/0.2/0.2/0.2/0.2 and call the scenarios S2′ and S3′, respectively. Finally, we look at the impact of having maps in which the markers do not have equifrequent or nearly equifrequent alleles. For each replicate, we still have the same true marker IBD status as we did previously, but now the SNP map has allele frequencies 0.2/0.8 (map scenario Z1) and the microsatellite maps have allele frequencies 0.02/0.08/0.3/0.3/0.3 (map scenarios Z2 and Z3, for the 5-cM and 10-cM spacing, respectively). For these three map scenarios, we look at the sensitivity of 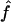 and
and 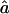 to the estimation of marker allele frequencies from a small control sample of 30 individuals (called Z1′ for the SNP map, Z2′ for the 5-cM microsatellite map, and Z3′ for the 10-cM microsatellite map). Whenever an allele was not observed in the control sample, we gave this allele a frequency of 0.01 and recomputed the other allele frequencies so that the frequencies still added to 1.
to the estimation of marker allele frequencies from a small control sample of 30 individuals (called Z1′ for the SNP map, Z2′ for the 5-cM microsatellite map, and Z3′ for the 10-cM microsatellite map). Whenever an allele was not observed in the control sample, we gave this allele a frequency of 0.01 and recomputed the other allele frequencies so that the frequencies still added to 1.
In all cases, we present the median values over all the replicates, along with the observed 95% CI. We show median values rather than mean ones, because a is a convex monotone function of the transition IBD probabilities. Thus, the mean value of the estimates provides an overestimate of the expected value of 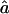 , but the median value of the estimates does not. For f, the median was equal to the mean
, but the median value of the estimates does not. For f, the median was equal to the mean 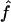 in our simulations. Finally, we also look at the correlation between
in our simulations. Finally, we also look at the correlation between 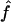 and
and 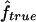 over the simulation replicates for the three map scenarios S1, S2, and S3.
over the simulation replicates for the three map scenarios S1, S2, and S3.
Results
Simulation Results
Table 2 shows the median values of the estimates of f and a under the simulation conditions for the three map scenarios (S1, S2, and S3) and both 1C and 4×2C. For both genealogies, the median values of 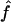 are very close to the proportion of genome IBD expected for these two genealogies, fg1=fg2=0.0625. The median estimates are also very similar among all marker maps. The 95% CI is wider at 10 cM than at 5 cM for the microsatellite marker maps. Indeed, for the same level of polymorphism, less information is provided about the IBD status at one marker by the adjacent marker for looser maps, in comparison with tighter ones. Similarly, for both genealogies and all marker maps, the median values of
are very close to the proportion of genome IBD expected for these two genealogies, fg1=fg2=0.0625. The median estimates are also very similar among all marker maps. The 95% CI is wider at 10 cM than at 5 cM for the microsatellite marker maps. Indeed, for the same level of polymorphism, less information is provided about the IBD status at one marker by the adjacent marker for looser maps, in comparison with tighter ones. Similarly, for both genealogies and all marker maps, the median values of 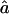 are very close to the expected ag1≈0.063 and ag2≈0.084, for 1C and 4×2C, respectively. The CI for
are very close to the expected ag1≈0.063 and ag2≈0.084, for 1C and 4×2C, respectively. The CI for 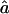 is rather sensitive to marker density, and we observe some estimates >1 at 10 cM. This reflects the fact that, with a 10-cM map, there are too few stretches of IBD markers that can be observed to allow a precise estimate of this parameter.
is rather sensitive to marker density, and we observe some estimates >1 at 10 cM. This reflects the fact that, with a 10-cM map, there are too few stretches of IBD markers that can be observed to allow a precise estimate of this parameter. 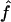 and
and 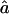 are good estimates of f and a on average, but the variability in the estimates seems quite large.
are good estimates of f and a on average, but the variability in the estimates seems quite large.
Table 2.
Median Estimates of f and a and 95% CIs over All Replicates, from Marker Genotypes under Three Map Scenarios (S1, S2, and S3) for Offspring of First Cousins (1C) and Quadruple Second Cousins (4×2C)
| Simulationa |
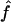 (95% CI) (95% CI) |
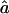 (95% CI) (95% CI) |
| 1C, fg1=.0625, ag1=.063: | ||
| S1 | .066 (.021–.123) | .063 (.022–.165) |
| S2 | .064 (.023–.123) | .063 (.021–.195) |
| S3 | .065 (.012–.133) | .066 (.017–1.182) |
| 4×2C, fg2=.0625, ag2=.084: | ||
| S1 | .063 (.022–.114) | .088 (.037–.226) |
| S2 | .063 (.020–.114) | .086 (.032–.240) |
| S3 | .064 (.006–.127) | .089 (.024–1.278) |
(fg1, ag1) and (fg2, ag2) are the expected (f, a) for 1C and 4×2C, respectively. Each simulation included 1,000 replicates. S1 = SNPs every 1.67 cM, frequency .4/.6; S2 = microsatellites every 5 cM, five alleles, frequency .2/.2/.2/.2/.2; S3 = microsatellites every 10 cM, five alleles, frequency .2/.2/.2/.2/.2.
Since very similar results were obtained for both 1C and 4×2C, only results for 1C are presented hereafter. To evaluate how much of this variability is due to our method, we compare our estimate (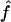 ) to the proportion of markers IBD (
) to the proportion of markers IBD (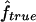 ) rather than to the inbreeding coefficient expected from the genealogy. Table 3 gives
) rather than to the inbreeding coefficient expected from the genealogy. Table 3 gives 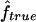 and the estimates obtained from the observed IBS data with the three marker maps (S1, S2, and S3) for 1C. The table shows that, even when the true IBD status is known, there is a large variability in
and the estimates obtained from the observed IBS data with the three marker maps (S1, S2, and S3) for 1C. The table shows that, even when the true IBD status is known, there is a large variability in 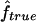 . This means that two individuals with the same genealogy may be characterized by very different values of f. For instance, an offspring of 1C (fg1=0.0625) can have as little as 3% or as much as 12% of his or her genome IBD. In addition, for S1 and S2 maps, both the median and 95% CI for
. This means that two individuals with the same genealogy may be characterized by very different values of f. For instance, an offspring of 1C (fg1=0.0625) can have as little as 3% or as much as 12% of his or her genome IBD. In addition, for S1 and S2 maps, both the median and 95% CI for 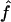 are very similar to the ones for
are very similar to the ones for 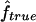 , although the variability of
, although the variability of 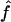 is always slightly larger because the IBD status has to be inferred from the IBS data. For S3, we can see that the variability of the estimate
is always slightly larger because the IBD status has to be inferred from the IBS data. For S3, we can see that the variability of the estimate 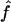 is much larger than that of
is much larger than that of 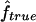 , because marker genotypes every 10 cM do not provide good information on the hidden IBD status at the markers.
, because marker genotypes every 10 cM do not provide good information on the hidden IBD status at the markers.
Table 3.
Median Estimates of f and 95% CI over All Replicates, from IBD Data (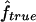 ) and from Marker Genotypes (
) and from Marker Genotypes (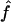 ) under Three Map Scenarios (S1, S2, and S3) for Offspring of First Cousins
) under Three Map Scenarios (S1, S2, and S3) for Offspring of First Cousins
| Simulationa |
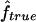 (95% CI) (95% CI) |
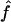 (95% CI) (95% CI) |
| S1 | .061 (.024–.120) | .066 (.021–.123) |
| S2 | .061 (.024–.120) | .064 (.023–.123) |
| S3 | .060 (.023–.118) | .065 (.012–.133) |
Each simulation included 1,000 replicates. S1 = SNPs every 1.67 cM, frequency .4/.6; S2 = microsatellites every 5 cM, five alleles, frequency .2/.2/.2/.2/.2; S3 = microsatellites every 10 cM, five alleles, frequency .2/.2/.2/.2/.2.
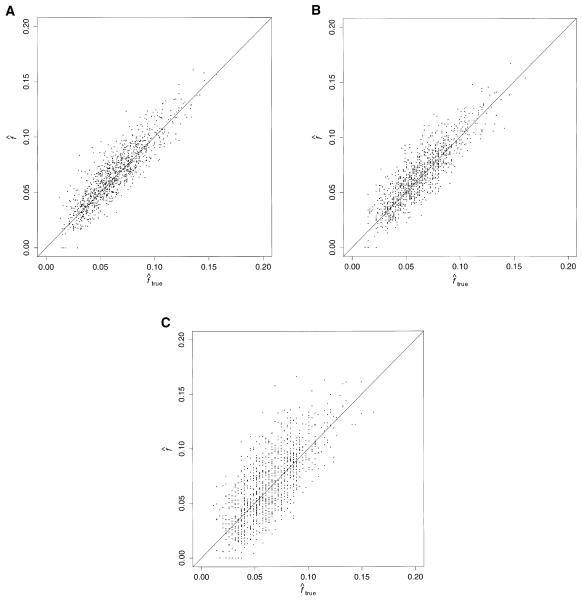
Figure 2 shows the correlation between 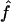 and
and 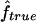 , with each dot corresponding to a simulation replicate for 1C. The correlation between
, with each dot corresponding to a simulation replicate for 1C. The correlation between 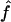 and
and 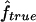 is very high (0.89) when marker map S1 is used. Similar results were also observed for 4×2C, with a correlation of 0.84 for marker map S1. Hence,
is very high (0.89) when marker map S1 is used. Similar results were also observed for 4×2C, with a correlation of 0.84 for marker map S1. Hence, 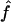 is a good estimate of the proportion of markers IBD, and it also reflects well the high variability of this proportion. Again, we can see that the correlation is not as good for the estimates obtained from markers observed only every 10 cM (map S3).
is a good estimate of the proportion of markers IBD, and it also reflects well the high variability of this proportion. Again, we can see that the correlation is not as good for the estimates obtained from markers observed only every 10 cM (map S3).
Figure 2.
Estimated f (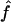 ) versus marker IBD proportion (
) versus marker IBD proportion (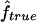 ) for offspring of first cousins under 1.67-cM SNP map with marker allele frequencies 0.4/0.6 (S1) (A), 5-cM microsatellite map with marker allele frequencies 0.2/0.2/0.2/0.2/0.2 (S2) (B), and 10-cM microsatellite map with marker allele frequencies 0.2/0.2/0.2/0.2/0.2 (S3) (C). The solid line represents
) for offspring of first cousins under 1.67-cM SNP map with marker allele frequencies 0.4/0.6 (S1) (A), 5-cM microsatellite map with marker allele frequencies 0.2/0.2/0.2/0.2/0.2 (S2) (B), and 10-cM microsatellite map with marker allele frequencies 0.2/0.2/0.2/0.2/0.2 (S3) (C). The solid line represents 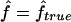 .
.
Table 4 shows the sensitivity of our estimations to marker allele frequency accuracy for 1C, looking at marker map scenarios S1, S2, and S3. For all marker maps, we observe a small upward bias for the estimates of f when the control individuals are drawn from the same population as the patients (S1′, S2′, and S3′). The largest bias is observed for the 10-cM map S3′ but is still within the 95% CI of 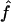 . When the genotype data are simulated with markers having a rare allele (table 5), results are very similar, but the variability is slightly increased (especially for the 10-cM map) because of the decreased informativeness of each marker.
. When the genotype data are simulated with markers having a rare allele (table 5), results are very similar, but the variability is slightly increased (especially for the 10-cM map) because of the decreased informativeness of each marker.
Table 4.
Median Estimates of f and 95% CIs over All Replicates, for Offspring of First Cousins, Using Marker Genotypes
| Simulationa |
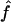 (95% CI) (95% CI) |
| S1 | .066 (.021–.123) |
| S1′ | .068 (.023–.127) |
| S2 | .064 (.023–.123) |
| S2′ | .071 (.027–.130) |
| S3 | .065 (.012–.133) |
| S3′ | .073 (.020–.140) |
Marker allele frequencies are the theoretical ones (S1, S2, and S3) or were estimated on a control sample of 30 individuals (S1′, S2′, and S3′). Each simulation included 1,000 replicates. S1 = SNPs every 1.67 cM, frequency .4/.6; S2 = microsatellites every 5 cM, frequency .2/.2/.2/.2/.2; S3 = microsatellites every 10 cM, frequency .2/.2/.2/.2/.2.
Table 5.
Median Estimates of f and 95% CIs over All Replicates, for Offspring of First Cousins, Using Marker Genotypes
| Simulationa |
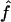 (95% CI) (95% CI) |
| Z1 | .065 (.019–.124) |
| Z1′ | .070 (.022–.128) |
| Z2 | .065 (.020–.127) |
| Z2′ | .071 (.023–.132) |
| Z3 | .066 (.000–.139) |
| Z3′ | .076 (.012–.148) |
Marker allele frequencies are the theoretical ones (Z1, Z2, and Z3) or were estimated on a control sample of 30 individuals (Z1′, Z2′, and Z3′). Each simulation included 1,000 replicates. Z1 = SNPs every 1.67 cM, frequency .2/.8; Z2 = microsatellites every 5 cM, frequency .02/.08/.3/.3/.3; Z3 = microsatellites every 10 cM, frequency .02/.08/.3/.3/.3.
Application to Real Data: Families with CMT Disease
CMT disease is the most frequent inherited neuropathy. On the basis of motor-nerve conduction velocities (MNCVs) at the median nerve, two main types can be distinguished: the axonal type (MNCV >40 m/s) and the demyelinating type (MNCV <35 m/s) (Harding and Thomas 1980; Bouche et al. 1983). For both types, modes of inheritance can be autosomal dominant, autosomal recessive, or X-linked.
We had genome-scan data for 26 unrelated individuals affected with demyelinating CMT and originating from the Mediterranean basin (Northern Africa, France, and Italy). The mode of inheritance seemed likely to be recessive: all parents of the affected individuals were clinically healthy, without neurological signs of peripheral neuropathy. In addition, all patients were tested for the PMP22 duplication on chromosome 17 (the most frequent causative gene for the dominant form of demyelinating CMT) and the results were negative. Finally, parents of an affected individual were always related: most couples were reported as first cousins, two were reported as second cousins, and one was reported as first cousins with paternal grandparents also being first cousins. For six individuals, the parental relationships were not precisely reported. Hence, for these six individuals, the usual LOD-score calculations could not be performed.
The marker map had microsatellite markers spaced at ∼10 cM (for a total of 376 markers) and with an average expected heterozygosity of 0.79. We estimated the marker allele frequencies for the parents of the affected individuals, when available, not taking into account their relatedness. This will potentially increase the frequency of rare alleles at a marker.
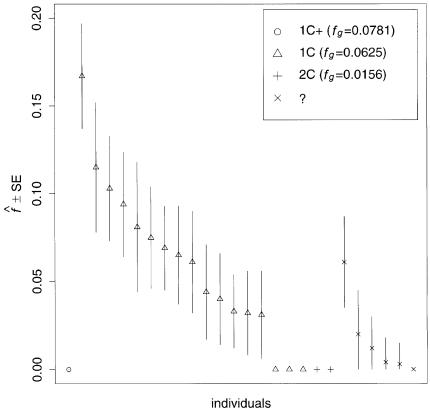
We used our method to study the inbreeding coefficients of all 26 affected individuals. Figure 3 shows the estimates of f we obtained for each individual. The values of the estimates ranged from 0 to 0.167. The six affected individuals with no genealogical information had 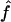 in the lower part of this range, between 0 and 0.061.
in the lower part of this range, between 0 and 0.061.
Figure 3.
Estimated f (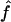 ) for the 26 individuals with CMT disease. Solid lines represent
) for the 26 individuals with CMT disease. Solid lines represent 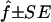 . SEs were obtained from the observed Fisher information matrix with 8,000 Monte Carlo realizations. 1C+ = first-cousin offspring whose paternal grandparents are also first cousins; 1C = first-cousin offspring; 2C = second-cousin offspring; ? = no genealogical information. fg is the proportion of genome IBD expected from the genealogy.
. SEs were obtained from the observed Fisher information matrix with 8,000 Monte Carlo realizations. 1C+ = first-cousin offspring whose paternal grandparents are also first cousins; 1C = first-cousin offspring; 2C = second-cousin offspring; ? = no genealogical information. fg is the proportion of genome IBD expected from the genealogy.
This application illustrates how genomic data can be used to provide estimates of f when no information on the genealogy is available. However, our estimates have to be taken with caution, for two reasons. The marker map has a mean marker spacing of 10 cM, and some marker genotypes are missing. As we have shown by simulation, a denser map is necessary for reliable estimations. In addition, we do not have a good control sample for the marker allele frequency estimation and, as we showed, it may lead to overestimation of 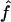 .
.
Discussion
In small isolated populations and in populations with a long tradition of marriages between relatives, there exist very complex genealogies with unknown loops. Therefore, the inbreeding coefficient f of an individual is often unknown. Here, we have presented a method that can reliably estimate the individual’s f from marker data on his or her entire genome, without requiring any knowledge of the genealogy.
We have found by simulations that our estimator is unbiased. There is a very good correlation between our estimator and the true proportion of genome IBD, as long as maps are dense enough. Our estimator also requires good estimates of marker allele frequencies. We have shown that estimating marker allele frequencies from a small sample of control individuals will always tend to slightly overestimate the inbreeding coefficient.
We have also found very different estimates of f for two individuals with the same genealogy. This is not a result of our estimation method but represents the true variability of the proportion of genome IBD. The observed variability is due to the finite length of the human genome, which leads to a small number of independent observations in the individual’s genome. This variability in the proportion of genome IBD around the value expected from the individual’s genealogy had also been pointed out by Stam (1980).
From the estimation of the parameters f and a, one can compute the IBD probabilities at each marker of the genome of the individual (posterior IBD probabilities) via the Baum algorithm (Baum et al. 1970). This can then be used to perform a homozygosity mapping–type analysis even when no genealogical information is available for the affected individuals. For each affected individual, the posterior IBD probability at a marker can be controlled for his or her “genomic” inbreeding coefficient. Accumulation, over independent affected individuals, of excess sharing at a marker will be considered as evidence for the presence of a recessive gene in the neighborhood.
Finally, this method can be generalized to other kinds of linkage analyses in inbred populations. For instance, we have previously shown that the maximum LOD score affected-sib-pair method (Risch 1989) is quite sensitive to an underestimation of the parental relationships (Leutenegger et al. 2002). We are currently extending our method to a pair of individuals for application in affected-sib-pair analyses in inbred populations. In that case, for each sib pair, we are estimating the maternal and paternal inbreeding coefficients, the parental kinship coefficient, and the corresponding a values.
Acknowledgments
We wish to thank Eric LeGuern (INSERM U289) and the French Association Française contre les Myopathies/INSERM research network on the autosomal recessive forms of CMT disease. A.-L.L. was supported by the Fondation pour la Recherche Médicale and by funds to E.A.T. from the Burrough’s Wellcome–funded Program in Mathematics and Molecular Biology.
Electronic-Database Information
The URL for data presented herein is as follows:
- Pangaea, http://www.stat.washington.edu/thompson/Genepi/pangaea.shtml (for the Genedrop and kin programs of the MORGAN2.5 software package)
References
- Abney M, Ober C, McPeek MS (2002) Quantitative-trait homozygosity and association mapping and empirical genomewide significance in large, complex pedigrees: fasting serum-insulin level in the Hutterites. Am J Hum Genet 70:920–934 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baum LE (1972) An inequality and associated maximization technique in statistical estimation for probabilistic functions of Markov processes. Inequalities 3:1–8 [Google Scholar]
- Baum LE, Petrie T, Soules G, Weiss N (1970) A maximization technique occurring in the statistical analysis of probabilistic functions on Markov Chains. Ann Math Stat 41:164–171 [Google Scholar]
- Boehnke M, Cox NJ (1997) Accurate inference of relationships in sib-pair linkage studies. Am J Hum Genet 61:423–429 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouche P, Gherardi R, Cathala HP, Lhermitte F, Castaigne P (1983) Peroneal muscular atrophy. Part 1. Clinical and electrophysiological study. J Neurol Sci 61:389–399 [DOI] [PubMed] [Google Scholar]
- Broman KW, Weber L (1999) Long homozygous segments in reference families from the Centre d’Étude du Polymorphisme Humain. Am J Hum Genet 65:1493–1500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charcot J, Marie P (1886) Sur une forme particulière d’atrophie musculaire progressive, souvent familiale, débutant par les pieds et les jambes et atteignant plus tard les mains. Rev Med 6:97–138 [Google Scholar]
- Epstein M, Duren W, Boehnke M (2000) Improved inference of relationship for pairs of individuals. Am J Hum Genet 67:1219–1231 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harding AE, Thomas PK (1980) Genetic aspects of hereditary motor and sensory neuropathy (types I and II). J Med Genet 17:329–336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lalouel J (1979) GEMINI—a computer program for optimization of general nonlinear functions. Technical Report 14, University of Utah, Department of Medical Biophysics and Computing, Salt Lake City, UT [Google Scholar]
- Lander ES, Botstein D (1987) Homozygosity mapping: a way to map human recessive traits with the DNA of inbred children. Science 236:1567–1570 [DOI] [PubMed] [Google Scholar]
- Leutenegger AL, Génin E, Thompson EA, Clerget-Darpoux F (2002) Impact of parental relationships in maximum lod score affected sib-pair method. Genet Epidemiol 23:413–425 [DOI] [PubMed] [Google Scholar]
- Louis TA (1982) Finding the observed information matrix when using the EM algorithm. J R Stat Soc Ser B 44:226–233 [Google Scholar]
- Malécot G (1948) Les mathématiques de l’hérédité. Masson, Paris [Google Scholar]
- Miano MG, Jacobson SG, Carothers A, Hanson I, Teague P, Lovell J, Cideciyan AV, Haider N, Stone EM, Sheffield VC, Wright AF (2000) Pitfalls in homozygosity mapping. Am J Hum Genet 67:1348–1351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risch N (1989) Genetics of IDDM: evidence for complex inheritance with HLA. Genet Epidemiol 6:143–148 [DOI] [PubMed] [Google Scholar]
- Stam P (1980) The distribution of the fraction of the genome identical by descent in finite random mating populations. Genet Res Camb 35:131–155 [Google Scholar]
- Sundberg R (1974) Maximum likelihood theory for incomplete data from an exponential family. Scand J Statist 1:49–58 [Google Scholar]
- Thompson EA (1988) Two-locus and three-locus gene identity by descent in pedigrees. IMA J Math Appl Med Biol 5:261–279 [DOI] [PubMed] [Google Scholar]
- ——— (1994) Monte Carlo estimation of multilocus autozygosity probabilities. In: Sall J, Lehman A (eds) Proceedings of the 1994 Interface Conference. Interface Foundation of North America, Fairfax Station, VA, pp 498–506 [Google Scholar]
- Tooth H (1886) The peroneal type of progressive muscular atrophy. PhD thesis, Cambridge University, Cambridge, UK [Google Scholar]