Abstract
Association studies are widely seen as the most promising approach for finding polymorphisms that influence genetically complex traits, such as common diseases and responses to their treatment. Considerable interest has therefore recently focused on the development of methods that efficiently screen genomic regions or whole genomes for gene variants associated with complex phenotypes. One key element in this search is the use of linkage disequilibrium to gain maximal information from typing a selected subset of highly informative single-nucleotide polymorphism (SNP) markers, now often called “tagging SNPs” (tSNPs). Probably the most common approach to linkage-disequilibrium gene mapping involves a three-step program: (1) characterization of the haplotype structure in candidate genes or genomic regions of interest, (2) identification of tSNPs sufficient to represent the most common haplotypes, and (3) typing of tSNPs in clinical material. Early definitions of tSNPs focused on the amount of haplotype diversity that they explained. To select tSNPs that would have maximal power in a genetic association study, however, we have developed optimization criteria based on the r2 measure of association and have compared these with other criteria based on the haplotype diversity. To evaluate the full program and to assess how well the selected tags are likely to perform, we have determined the haplotype structure and have assessed tSNPs in the SCN1A gene, an important candidate gene for sporadic epilepsy. We find that as few as four tSNPs are predicted to maintain a consistently high r2 value with all other common SNPs in the gene, indicating that the tags could be used in an association study with only a modest reduction in power relative to direct assays of all common SNPs. This implies that very large case-control studies can be screened for variation in hundreds of candidate genes with manageable experimental effort, once tSNPs are identified. However, our results also show that tSNPs identified in one population may not necessarily perform well in another, indicating that the preliminary study to identify tSNPs and the later case-control study should be performed in the same population. Our results also indicate that tSNPs will not easily identify discrepant SNPs, which lie on importantly discriminating but apparently short genealogical branches. This could significantly complicate tagging approaches for phenotypes influenced by variants that have experienced positive selection.
Introduction
Recent developments have raised expectations that statistically powerful genetic association studies are now feasible. These developments are as follows: increasing knowledge of the human genome (e.g., from the Human Genome Project), providing information about the location and function of genes and allowing the systematic evaluation of appropriate candidate genes for a given disease or drug response; increasing availability of SNPs that can be used as markers within candidate regions; and increasing knowledge about the biology of both common diseases and the actions of drugs used in their treatment. Finally—and most relevant to our purposes here—there is the mounting evidence that the human genome has much greater levels of linkage disequilibrium (LD) than previously predicted on the basis of theoretical models assuming an idealized demography and uniform recombination (Kruglyak 1999). In some cases, there are clear tracks, or “blocks,” of elevated LD in which haplotype diversity is very limited (e.g., see Daly et al. 2001; Goldstein 2001; Jeffreys et al. 2001). Taken together, these developments lead us to suggest that the most promising current approach to statistically powerful genetic association studies (Goldstein 2001; Johnson et al. 2001) would be (a) to select either candidate genes appropriate for the condition of interest or genomic regions that are implicated by linkage analyses; (b) to determine their haplotype structures in control individuals from target populations for these genes or regions; and (c) to select a (presumably small) number of tagging SNPs (tSNPs) for analysis in clinical trials. tSNPs (i.e., SNPs selected on the basis of their LD properties) have also been referred to as “haplotype tagging SNPs” (htSNPs) (Johnson et al. 2001), but this belies the fact that their immediate purpose in association studies is to tag other causal SNPs, not haplotypes per se (Goldstein et al., in press).
Most of the details of how to implement such a program remain to be determined, however, and a number of concerns have been raised concerning its overall prospects. For example, there are concerns about the quality of the SNP databases, their applicability across populations, and such methodological issues as how to recognize LD-block boundaries and define tSNPs within them. More fundamental concerns have also been raised, such as whether many of the gene variants that underlie common disease are themselves common, as postulated in the common-disease/common-variant hypothesis (Chakravarti 1999; Weiss and Clark 2002). Questions have also been raised as to the extent to which LD in the human genome is “blocklike,” the extent to which this requires or results from heterogeneity in recombination rate along the genome, and the extent to which a simple haplotype structure within blocks requires or results from unusual demographic processes (e.g., a recent human population bottleneck) (Zhang et al. 2002). Simulations have also shown that, even when recombination does occur mainly in narrow hotspots, the pattern of LD may or may not be functionally blocklike, depending on the demographic history of the population (Stumpf and Goldstein 2003). Although the idea of finding useful tSNPs does not in itself depend on the existence or quality of LD blocks, the pattern of LD will determine the properties of tags, including the economy afforded by the use of tags and the extent to which the tags will be carried across populations. The detailed structure of recombination in the human genome will affect these characteristics by its effect on LD patterns and on their similarities across populations. Here, we are concerned with evaluating one core aspect of this integrated program for genetic association studies: the resolution of haplotype structure and the identification and population-specificity of appropriate tSNPs. For example, there are no agreed-upon protocols for the determination of haplotype structure nor are there agreed-upon statistical approaches for the selection and evaluation of tSNPs. It remains unclear how much of an experimental savings may be afforded by the use of tSNPs in the analysis of clinical material. Finally, regardless of how tSNPs are identified, it is not clear how well they can be transferred into new populations. Here, we address these questions by determining the haplotype structure of the SCN1A gene, a candidate gene in epilepsy, and by evaluating the expected performance of tSNPs in family samples of Chinese residents of Singapore. These results were compared in a closely related population (Malay residents of Singapore) and a more distantly related population (Europeans).
The SCN1A Gene and Epilepsy
Neuronal hyperexcitability is a cardinal feature of the pathophysiology of epilepsy. Sodium currents play an important role in the generation and propagation of the action potential and, thus, in neuronal excitability, so genes encoding the brain sodium channel (Nav1) are major candidate genes for epilepsy. The sodium channel consists of a principal pore-forming β subunit and two auxiliary β subunits (Catterall 2000). The α subunit exhibits four homologous domains (I–IV), each of which has six transmembrane segments (S1–S6). At least 11 different genes, designated “SCN1A” through “SCN11A,” encode the α subunit, and at least three different genes, designated “SCN1B” through “SCN3B,” encode the β subunit (Plummer and Meisler 1999). Channels encoded by SCN1A, SCN2A, SCN3A, SCN8A, and SCN5A are expressed in the human brain (Donahue et al. 2000; Whitaker et al. 2001). During recent years, mutations associated with monogenic forms of human epilepsy have been identified in SCN1A (Escayg et al. 2000, 2001; Abou-Khalil et al. 2001; Claes et al. 2001; Sugawara et al. 2001; Wallace et al. 2001), SCN2A (Sugawara et al. 2001), and SCN1B (Wallace et al. 1998).
The SCN1A gene is located on chromosome 2q24 and contains 27 exons, spanning ∼139 kb of genomic sequence (Wallace et al. 2001). At least 24 different mutations in various regions of the SCN1A gene have been identified that cause Mendelian forms of epilepsy. Of these, nine are associated with the clinical phenotype known as “generalized epilepsy with febrile seizures plus” (GEFS+ [MIM 604233]) or variants including partial seizures (Escayg et al. 2000, 2001; Abou-Khalil et al. 2001; Sugawara et al. 2001; Wallace et al. 2001). Expression studies of three of the GEFS+ mutations in human cell lines showed defects in channel inactivation, resulting in a persistent inward sodium current during sustained depolarization (Lossin et al. 2002). This defect is likely to cause enhanced neuronal excitability. These findings suggest that a gain of function is responsible for the increased seizure susceptibility in these syndromes.
Fifteen other mutations in SCN1A have been identified in patients with severe myoclonic epilepsy of infancy (Claes et al. 2001; Sugawara 2002). These findings imply that genetic variation at different sites in SCN1A contributes to a wide range of seizure types. Therefore, SCN1A is also considered to be a major candidate gene contributing to common, nonmonogenic epilepsies, which account for the majority of epilepsies. A recent study tested the involvement of SCN1A variants in 165 familial and 61 sporadic cases of generalized idiopathic epilepsy and identified four possible disease-associated variants (Escayg et al. 2001). The interest in this gene lies not only in its possible causal role in epilepsy but also in its potential influence on the efficacy of antiepileptic drug treatment. Many of the major antiepileptic drugs are known to act by use-dependent and voltage-dependent inhibition of sodium currents by binding to critical amino acids located in the S6 segment of domain IV of the sodium channel α subunit (Kuo 1998; Catterall 1999). These findings suggest that variations in SCN1A may also contribute to antiepileptic-drug responsiveness. For these reasons, it is timely to perform systematic screens for common polymorphisms in the sodium-channel genes that may (a) predispose to the common epilepsies and (b) influence the response to the common antiepileptic drugs.
In a recent simulation study, Zhang et al. (2002) have demonstrated that the tagging strategy can be efficient under a simple demographic model and the assumption of uniform recombination. Although the generality of recombination hotspots is unclear, it is now beyond dispute that recombination rates in the human genome are uneven. For a true appreciation of the economy afforded by tags, this economy must therefore be empirically evaluated in the populations of interest. Here, we evaluate the tagging approach empirically, by applying the multistep program to SCN1A, a candidate gene in which there was little prior information concerning its pattern of LD. One reason for our selection of SCN1A is that it is a relatively large gene in terms of genomic sequence, with many exons. For these reasons, it would be difficult to take a direct, resequencing approach to SCN1A in a genetic association study. A panel of 24 SNPs and 1 insertion/deletion polymorphism (indel) within SCN1A—determined both from the public dbSNP database and, de novo, from resequencing efforts—were investigated within 32 Singapore Chinese trios, together with 6 SNPs lying outside the SCN1A gene. The degree of population-specificity of the tagging program was assessed by typing a smaller panel of 15 markers (a subset of the original 25) in 32 Singapore Malay trios and 32 trios of European ancestry. Although LD patterns are known to vary considerably from one region of the genome to another, we chose the SNC1A gene without prior knowledge of patterns of LD, thus ensuring that it was not preselected for desirable LD properties.
Methods
Samples and SNP Detection
DNA was obtained from 32 trios (mother, father, and child) of Chinese descent and 32 trios of Malay descent from the population of Singapore (anonymized legacy collection) and from 32 trios of European descent (CEPH Utah collection). The Singapore Chinese trios were used in the initial phase to find a suitable initial panel of SNPs. All exons known to harbor mutations in patients with epilepsy at the time of our study were sequenced (Escayg et al. 2000, 2001; Claes et al. 2001; Wallace et al. 2001), because we were interested in finding any mutations, even very rare ones, in these important exons. Primers to amplify these exonic sequences were taken from published material (Claes et al. 2001; Wallace et al. 2001). Because of their lower polymorphism levels, however, exonic sequencing is not the most efficient method for finding SNPs in order to describe haplotype structure. We therefore also performed resequencing in an additional 10 amplicons of an approximate length of 500 bp in introns at various sites throughout SCN1A. Primers for these amplicons were designed using the Primer3 program, after filtering the genomic sequence (GenBank accession number AC010127) by use of the RepeatMasker program. Where possible, the primers were designed around SNPs present in the dbSNP database (i.e., where prior evidence existed of polymorphism). In regions where no dbSNPs were available, the amplicons were placed as far as possible between exonic amplicons, taking into account repetitive sequences.
PCR conditions were as follows: initial denaturation at 95°C for 15 min, followed by 35 cycles of denaturation at 94°C, annealing at 57°C–63°C, and extension at 72°C (each for 30 s), plus a final extension phase of 10 min at 72°C. PCR was performed with 5 ng of DNA, 2.5 mM of MgCl2, 0.2 mM of each dNTP, 0.5 μM of each primer, and 0.25 U of Qiagen HotStartTaq polymerase, in a total volume of 10 μl. PCR products were sequenced in both directions with a dideoxy terminator kit and were analyzed with an automated sequencer (ABI 3100).
A total of 27 amplicons (17 exonic and 10 intronic) were sequenced in all 32 Singapore Chinese trios. Because initial results indicated that the entire gene was composed of one block of LD, we subsequently chose additional SNPs in short stretches ∼1.5 Mb, ∼170 kb, ∼100 kb, and ∼50 kb upstream and ∼140 kb, ∼190 kb, and ∼240 kb downstream of exon 1. The following SNPs were chosen from the dbSNP database: 1224648, 948473, 2155878, and 1919854 (upstream); and 1432272, 891819, and 2060167 (downstream). Primer design and PCR conditions were as described above. First, each of these seven amplicons was sequenced in 16–32 samples, to confirm the presence of a polymorphic site, and, if a polymorphic site was present, sequencing was performed in all 64 trios. PCRs for the amplicon that contained dbSNP 1432272 failed, so this amplicon was removed from further consideration.
Error Checking
Of the 25 SNPs found within SCN1A, 6 were randomly chosen for retyping within six randomly selected Singapore Chinese trios, six Singapore Malay trios, and four European trios. Among 264 successfully retyped genotypes, eight discrepancies were found with the original retypings, giving an estimated genotyping error rate of 1.5% if it is assumed that new typings have the same error rate as the original typings. A more conservative estimate of 3.0% is obtained if it is assumed that the new typings are without error (because extra care was taken in producing these data). It is also possible to use observed cases of Mendelian inconsistencies in the trio data to estimate genotyping error. The new typings produced three cases of mother-father-child genotype sets (from 75 full sets) that were inconsistent with Mendelian inheritance. Interestingly, in all three cases, the new typings matched the original typings, suggesting some biochemical reason for consistent mistyping, given that parental status had been confirmed at other loci. By assuming that the occurrence of more than one genotyping error per mother-father-child genotype set is negligible and that genotyping error affects only one allele in the genotype (so homozygotes appear as heterozygotes and heterozygotes appear as either homozygote with equal probability), we calculated that only 28.0% of genotype errors affecting mother-father-child genotype sets would show up as a Mendelian inconsistency. The three observed Mendelian inconsistencies therefore suggested a genotyping error rate of 4.8%. However, since all cases of Mendelian inconsistency in the original data set were resolved either by retyping or by setting as missing data, our calculation also suggested that the frequency of undetected genotyping error that remained in the original data was 3.4%, consistent with the frequency of 3.0% obtained with our earlier method based on retyping. Taking 3.0% as our error rate, we note that, in individuals genotyped for 25 loci (with two haplotypes per individual), we would expect 31.5% of haplotypes to be in error. We also note that, when we applied an expectation-maximization (EM) algorithm to estimate haplotype frequencies from our 25-locus Singapore Chinese data, 31.4% of the estimated gene pool was composed of haplotypes with a frequency <2%, including many apparently recombinant types (see the “Results” section [“Haplotype Structure”]). It is therefore possible that all these estimated low-frequency haplotypes are the result of genotyping error. However, analysis presented later indicates that, in spite of this possibility, the performance of tagging-SNP sets quickly reached a plateau with increasing set size, and that performance was thus affected more by the properties of high LD and SNP redundancy exhibited by the high-frequency haplotypes than by the properties of low-frequency haplotypes.
Haplotype Structure
Despite the use of trios to help in the resolution of phase, we found that only 36 of a possible 128 parental chromosomes could be completely resolved into phased haplotypes for all 25 markers within SCN1A, the failures being due to either triple heterozygotes or missing data at one or more locus. To make more efficient use of the data, we devised an EM estimation algorithm specifically to deal with trio data. The algorithm combines information from resolved and unresolved chromosomes and, in unresolved cases, restricts the set of possible haplotypes to those consistent with known data in both parents and child. Full details will be presented elsewhere. The algorithm is available in the TagIT software package (see the Goldstein Lab Web site).
Selection of tSNPs—Performance Criteria
There is currently no consensus on the criterion that best measures the performance of a set of tSNPs in the capturing of information on haplotype structure within a block. We analyzed and compared our data by using a variety of different criteria, including all those used by Johnson et al. (2001) and elaborated by Clayton (2002) (criteria 4, 5, and 7–9 in table 1). Broadly, these criteria can be split into two types: those based on capturing as much as possible of the original haplotype diversity present in the set of known SNPs K when reduced to the smaller set H of tSNPs; and those based on establishing as high an association as possible between the reduced tSNP set H and the larger set K. The latter type is concerned most directly with the issue of prediction—that is, the ability of the reduced set H to detect unknown SNPs in the set A of all SNPs within the block (where H is a subset of K and K is a subset of A). In particular, this framework allows a statistically natural approach for assessing how well tSNPs are expected to perform in a genetic association study, since one uses the set of known SNPs K to make statistical statements about the performance of the tSNPs H against the universe of all SNPs A (see below).
Table 1.
tSNP Performance Criteria
| Criterion | Symbol | Details |
| Diversity: | ||
| 1. tSNP groups | G | Number of haplotypes, or groups, defined in the data set in question by the tSNP set |
| 2. Haplotype-diversity ratio | h[htSNP]/h | Probability that two randomly chosen chromosomes are in different tSNP-defined groups, given that they are in different K-defined haplotypes; h[htSNP] is the tSNP-defined haplotype diversity in the data set in question (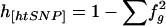 , where fg is the frequency of chromosomes in the gth tSNP-defined group), and h is the haplotype diversity found using the set K of all known SNPs in the data set , where fg is the frequency of chromosomes in the gth tSNP-defined group), and h is the haplotype diversity found using the set K of all known SNPs in the data set |
| 3. Minus largest confounded frequency | -max(fcon) | max(fcon) is the largest frequency of the second most common haplotype (defined using the set K of all known SNPs) nested within any one tSNP-defined group; all K-defined haplotypes with frequency greater than max(fcon) will be in separate tSNP-defined groups |
| 4. Proportion of diversity explained | Pi | Probability that two randomly chosen chromosomes are in different tSNP-defined groups, given that they have different allele types at locus i; 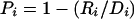 ,where Di=2n2fi(1-fi) and ,where Di=2n2fi(1-fi) and 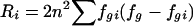 (where n is the total number of chromosomes in the data set [Pi does not depend on n, because the terms cancel], fi is the frequency of chromosomes that have allele 1 at locus i (allele 1 may be arbitrarily assigned to either allele), and fgi is the frequency of chromosomes both in the gth tSNP-defined haplotype and that have allele 1 at locus i) (where n is the total number of chromosomes in the data set [Pi does not depend on n, because the terms cancel], fi is the frequency of chromosomes that have allele 1 at locus i (allele 1 may be arbitrarily assigned to either allele), and fgi is the frequency of chromosomes both in the gth tSNP-defined haplotype and that have allele 1 at locus i) |
| 5. Minus residual diversity | 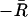 |
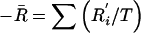 , where , where 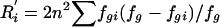 and and 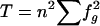 (where T is the total number of pairwise comparisons within groups) (where T is the total number of pairwise comparisons within groups) |
| Association: | ||
| 6. Haplotype r2 | r2[hap]i | Coefficient of determination from an analysis of variance of locus i among the G groups (coding alleles at locus i as “0” or “1”); r2[hap]i=1-R′i/Di, where 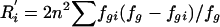
|
| 7. Best-single r2 | r2[sing]i | Maximum of the G coefficients of determination obtained by taking each tSNP-defined haplotype in turn and performing an analysis of variance of locus i among the two groups defined by membership or nonmembership of the gth haplotype |
| 8. Best-clumped r2 | r2[clump]i | Maximum of the 2G-1-1 coefficients of determination obtained by taking each way of clumping G tSNP-defined haplotypes into two nonempty subsets and performing an analysis of variance of locus i among the two groups thus defined |
| 9. Chance-corrected haplotype r2 | r2[CChap]i | Chance-corrected version of r2[hap]i, to account for the amount of explained sum of squares that is expected by chance; r2[CChap]i=(r2[hap]i-C)/(1-C), where 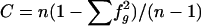
|
Both diversity and association can be measured in different ways. Table 1 is by no means exhaustive but does cover a number of sensible ways of defining these terms. The association-based criteria concentrate on r2, the coefficient of determination (explained sum of squares divided by total sum of squares) from fitting a linear model defined in different ways, depending on the criterion in question (but each based in some way on haplotype information provided by the tSNPs), to the allelic state information at some locus i. Both diversity and association can be expressed in ways that are mathematically very similar. As an illustration of this, note that, in the definition for the proportion of diversity explained in table 1, Di is proportional both to the gene diversity for locus i in the data set in question and to the total sum of squares in an analysis of variance of locus i among the G groups (coding the alleles at locus i as “0” or “1”). Ri is proportional to a weighted-average residual sum of squares in an analysis of variance among the G groups (using weights fg for the residual sum of squares from each group, where fg is the frequency of the gth group). If the unweighted (rather than the weighted) residual diversity is used, r2[hap]i, rather than Pi, is obtained.
Most criteria in table 1 result in a set of K values, one for each of the K loci in the set of known SNPs K. This raises the issue of how to reduce this set of K values to a single number representing the performance of a tagging set H. Two methods were used. The first, “average-locus” method takes a weighted average of all K values, using weights pi(1-pi), where pi is the frequency of the minor allele at locus i. This weighting is intuitively reasonable in that loci with small values of pi (and low weight) have less information on haplotype structure. For r2-based criteria, this weighting can also be motivated as the overall coefficient of determination from a linear regression performed on the data from all loci combined, comparing a model in which each locus can respond differently to tSNP haplotype information with a null model in which tSNP haplotype information does not influence the allele frequency for each locus. This also reflects the idea that low-frequency SNPs will be difficult to tag and thus are down-weighted in the selection criterion. The second, “worst-locus” method takes the minimum from the set of K values. The idea behind this method is to find sets of tSNPs that perform well even for the worst case, as represented by the locus with the lowest value for the criterion.
Results
SNPs Detected
Within SCN1A, 27 amplicons were sequenced (17 exonic and 10 intronic). Of these, 11 contained one or more polymorphic SNPs with a minor allele frequency ⩾10%. Overall, 25 markers (1 exonic SNP, 23 intronic SNPs, and 1 intronic indel) were detected (table 2 and fig. 1). Twelve of these are dbSNPs (four dbSNPs included in our amplicons were not polymorphic in our samples), whereas another SNP, located in exon 16, has been detected previously (Escayg et al. 2001). Thus, 12 of the 25 markers detected within SCN1A are novel. All of these markers are SNPs except for a novel triallelic polymorphism consisting of a 4-bp indel with two forms for the inserted sequence (an A/T polymorphism in the final base). Information on this marker is presented in table 2 as a biallelic polymorphism (indel) only. For tagging purposes, this marker was treated as binary so that all loci could be treated equally, but we note that the A/T polymorphism in the final base was found in very close association with other loci, so little information was lost by dropping it.
Table 2.
Summary Data on 31 Polymorphisms Typed in the Present Study
| Marker Name (dbSNP Namea) | Regionb | Amplicon | Positionc | Allelesd | Minor AlleleFrequencye(%) | HWTestf |
| snp20 (rs1919854) | Upstream | O1 | −1,464 kb | A/G | 16.7 | .788 |
| snp21 (rs2155878) | Upstream | O2 | −168 kb | A/G | 3.2 | .821 |
| snp22 | Upstream | O2 | −168 kb | G/A | 2.9 | .862 |
| snp23 | Upstream | O2 | −168 kb | G/A | 3.1 | .855 |
| snp1 (rs590478) | Intron 1 | I1 | −49,740 | A/G | 34.4 | .048 |
| snp2 (rs573936) | Intron 1 | I1d | −10,204 | A/G | 32.3 | .154 |
| snp3 | Intron 1 | I1d | −10,203 | C/T | 15.3 | .656 |
| snp4 | Intron 1 | I1d | −10,074 | C/T | 13.7 | .211 |
| snp4a (rs2892992) | Intron 3 | A1 | 11,706 | A/T | 37.7 | .205 |
| snp4b (rs1381108) | Intron 3 | A1 | 11,745 | T/C | 28.3 | .248 |
| snp4c (rs1381109) | Intron 3 | A1 | 11,854 | A/C | 40.6 | .034 |
| snp4d | Intron 3 | A1 | 11,982 | T/C | 39.1 | .014 |
| snp4e (rs1461199) | Intron 3 | A1 | 12,099 | T/C | 27.1 | .764 |
| snp4f (rs1461200) | Intron 3 | A1 | 12,122 | A/G | 32.0 | .189 |
| snp5 | Intron 3 | E2 | 15,135 | T/C | 28.1 | .202 |
| snp6 | Intron 5 | E5 | 20,590 | T/G | 12.5 | .253 |
| snp7 | Intron 5 | E5 | 20,605 | A/G | 40.6 | .418 |
| snp8 (rs2126152) | Intron 14 | E14 | 33,971 | G/A | 12.7 | .986 |
| snp9 | Intron 14 | E14 | 34,006 | C/A | 11.9 | .283 |
| snp9a | Intron 14 | A2 | 34,332 | T/C | 20.2 | .682 |
| snp9b (rs1019723) | Intron 14 | A2 | 34,388 | C/T | 33.1 | .308 |
| snp9c (rs1019724) | Intron 14 | A2 | 34,424 | G/A | 12.9 | .243 |
| snp9d (rs1019725) | Intron 14 | A2 | 34,439 | C/T | 26.7 | .403 |
| snp10 | Intron 16 | E16 | 37,068 | T/C | 12.5 | .253 |
| snp11g | Exon 16 | E16 | 37,361 | A/G | 12.5 | .253 |
| indel12 | Intron 17 | I17b | 39,782–39,785 | N/D | 28.6 | .186 |
| snp13 | Intron 17 | I17b | 39,877 | G/A | 10.5 | .374 |
| snp14 | Intron 18 | E18 | 59,651 | T/C | 14.3 | .186 |
| snp15 (rs919198) | Intron 25 | I25 | 78,969 | G/A | 13.3 | .221 |
| snp17 (rs891819) | Downstream | O3 | 187 kb | G/A | 30.3 | .114 |
| snp16 (rs2060167) | Downstream | O4 | 241 kb | C/T | 44.7 | .160 |
If present in the dbSNP database.
As identified by Wallace et al. (2001).
Position (in bp, unless otherwise indicated) according to June 2002 freeze of Human Genome Project physical map, relative to first base of exon 1 as identified by Wallace et al. (2001).
With major allele given first and minor allele given second.
Using Singapore Chinese data, parents only.
Test for Hardy-Weinberg equilibrium (Guo and Thompson 1992), using Singapore Chinese data, parents only. No significant P values were found, after Bonferroni correction.
Reported previously as “exon 16: 3199 (T1067A)” by Escayg et al. (2001).
Figure 1.
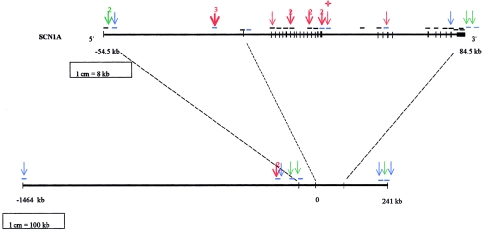
Structure of SCN1A and position of SNPs in and around the gene. Base-pair positions are relative to the first base of SCN1A exon 1. The bottom line represents ∼1.7 Mb of chromosome 2q24. The top line shows SCN1A enlarged, with exons represented by vertical lines and boxes (first exon = exon 1A; last exon = exon 26). Small horizontal lines show approximate location of amplicons (black = published primers; blue = newly designed primers). Arrows show the approximate positions of SNPs, with numbers above arrows if more than one closely spaced SNP was detected (blue arrows = dbSNPs polymorphic in our samples; green arrows = dbSNPs not polymorphic in our samples; red arrows = newly discovered SNPs). The red star indicates a 4-bp deletion in intron 17.
Of the six amplicons designed around SCN1A that successfully amplified, four contained one or more polymorphic SNPs. The amplicons including dbSNPs 1919854, 2060167, and 898919 each contained one SNP as described in the dbSNP database. The amplicon that included dbSNP 2155878 contained the dbSNP plus two additional, previously unidentified SNPs. Therefore, of the six SNPs found outside SNC1A, two were novel.
Positional information and other summary data on all these loci are presented in table 2 and figure 1. There is no significant evidence for a departure from Hardy-Weinberg equilibrium, after Bonferroni corrections are applied to each locus.
Pattern of LD across SCN1A
LD was investigated between all pairs of loci by first estimating pairwise haplotype frequencies through use of the trio-based EM algorithm, then assessing the statistical strength of association via a likelihood-ratio test (comparing EM frequencies with haplotype frequencies estimated assuming no LD) and estimating the strength of association through use of the D′ LD measure. Restricting our attention to the 25 SNPs located within the SCN1A gene, spread over ∼130 kb, we found a significant negative correlation between D′ and physical distance (r=-0.299, and P=.014, using a two-tailed Mantel test with 105 randomizations). However, significant P values could be found even between the most-widely-separated loci, indicating that, although there was evidence for some recombination (and/or gene conversion) throughout the gene, the level of this recombination had not been enough to break down the LD throughout the gene. When we examined LD with the SNPs lying outside the SCN1A gene, we found significant association of many SNPs (including snp1) with snp17, but not with any other outside SNPs. This suggests that a block of high LD extends at least as far as 100 kb downstream of the end of SCN1A, but there is no evidence that it extends as far as 160 kb downstream or 120 kb upstream.
Haplotype Structure
The presence of significant LD throughout the SCN1A gene means that the smallest sufficient tagging-SNP sets will be found by consideration of haplotypes for the gene as a whole. Table 3 presents estimated parental-gene-pool haplotype frequencies for the entire SCN1A gene region (25 SNPs), using data from the 32 Singapore Chinese trios. The table compares estimates obtained using the EM algorithm with those obtained using resolved parental chromosomes only. For individual haplotypes, the two sets of estimates differ most notably in the frequency of haplotype E (9.2% using EM vs. 18.2% using resolved chromosomes). Another important difference between the two sets of estimates is that 18.5% of the EM-estimated gene pool is composed of 172 haplotypes with frequencies <1%, whereas, by definition, the minimum nonzero frequency estimate in a sample of 44 resolved chromosomes is 2.3%. Provided that chromosomes assort randomly and that missing data are not dependent on the underlying allele or genotype, the EM estimates should be more accurate, because they are based on all the available information. However, the fact that inferred haplotype frequencies can be <1/128, even though a sample of 32 trios has only 128 parental chromosomes, underlines that these are only estimates of the true gene-pool frequencies, which introduces an additional source of uncertainty when tSNP performance is assessed.
Table 3.
Haplotype Structure of SCN1A in Singapore Chinese
|
Frequency(%) |
|||
| IDa | Haplotypeb | EMc | ResolvedChromosomesd(n=44) |
| A | 0011101111010111110110111 | 21.6 | 20.5 |
| B | 1111110110111110011111111 | 14.2 | 15.9 |
| C | 1101011001111111111111111 | 10.8 | 15.9 |
| D | 1110011011111111111111100 | 10.8 | 13.6 |
| E | 1111011001111111111111111 | 9.2 | 18.2 |
| F | 1111110110100001001001011 | 5.7 | 6.8 |
| G | 0111110110100001001001011 | 2.5 | 4.5 |
| H | 1101110110111110011111111 | 1.7 | 2.3 |
| I | 1111110110100101001001011 | 1.7 | 2.3 |
| J | 1011101111010111110110111 | 1.7 | … |
| K | 0011110111010111110110111 | 1.7 | … |
Haplotype designation.
Loci are arranged in the order snp1–snp15 (as in table 2). A haplotype is reported if observed in resolved chromosomes or if EM frequency is >1%. 1 = major allele; 0 = minor allele.
Frequencies estimated by the EM algorithm for trio data.
Frequencies estimated from resolved parental chromosomes only.
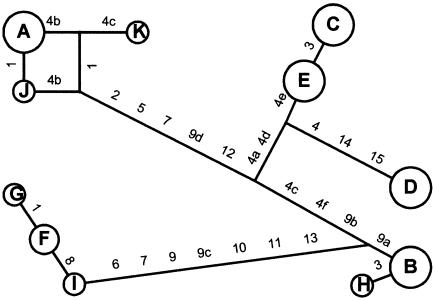
Figure 2 shows a reduced median network for the haplotypes in table 3 and illustrates several points in regard to tagging-SNP efficiency. There is evidence that long branches separate some of the major haplotypes (A–D and F); these branches feature several markers that are in complete LD because they fall on the same branch, and this immediately suggests that some level of tagging should be effective (to reduce redundant typing on these branches). Conversely, one discrepant SNP—that is, a single SNP that, on its own, separates two high-frequency haplotypes—is also evident (see the “tSNPs—Assessment of Sufficiency” subsection, below). In this case, snp3 is the only SNP that separates haplotypes C and E. The figure also reveals some evidence of recombination, gene conversion, and/or typing error, in that some SNPs (specifically, snp1, snp3, snp4c, and snp7) appear in multiple places throughout the network; however, most of these produce only minor haplotypes (e.g., G, H, and K), with the exception of snp7, which separates both A and F from other major haplotypes. Note, however, that a small amount of recombination and/or gene conversion may actually benefit a tagging-SNP strategy. This is because the same SNP may be used to delineate more than one branch, whereas, under an infinite-sites no-recombination model, only one SNP can ever delineate one branch.
Figure 2.
Reduced median haplotype network based on data in table 3. SNPs separating haplotypes are indicated on relevant branches.
tSNPs—Assessment of Sufficiency
The question of sufficiency can be broken into two questions: (1) is the known SNP set K sufficiently large to capture the haplotype structure in the full set A of all possible SNPs? and (2) is the tSNP set H sufficient to capture the haplotype structure in K? There are some issues common to both questions. One issue is that asymptotic performance behavior (as one increases the size of either H or K) provides an indication that it is not worth increasing the size of either set. Another issue is that it may be reasonable to assume that a causative SNP x is drawn from the same distribution of SNPs as those in K (but see below [“Sufficiency of K”]). In this case, dropping each SNP in turn from K and assessing the power of the remaining SNPs to detect the excluded one is a useful method to assess the sufficiency of H or K in the detection of x. A final issue is that the choice of the performance criterion with which to assess sufficiency must be considered. Because we are interested in the assessment of performance in relation to a future test for association with an unknown SNP, we choose to concentrate on association-based, rather than diversity-based, measures of performance. Measures based on r2 have the advantage that they approximately represent the effective units of sample size in a case-control association study (see Pritchard and Przeworski 2001 for the two-allele case and Goldstein et al. 2003 for the case of more than two alleles). We used haplotype r2 as a general measure because it can capture more types of association than best-single or best-clumped r2 measures (haplotype r2 can capture information on different levels of association in different haplotypes, whereas best-single r2 and best-clumped r2 reduce the problem to two groups with the same level of association among haplotypes in the same group, and their values can never exceed the haplotype r2 value). We used the weighted-average version, rather than the worst-locus version, because the former uses information from all loci. When we compared best tSNP sets selected using the different weighted-average performance criteria given in table 1, we found that the weighted-average haplotype r2 values were at least 90% of the maximum possible value, provided that the number of SNPs in the set was greater than three, indicating a high congruence among the different weighted-average performance criteria. In contrast, the worst-locus criteria exhibited much less congruence, with worst-locus haplotype r2 values being in some cases only 3% of the maximum possible value for tSNP sets of size three.
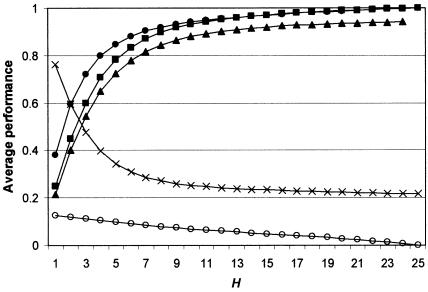
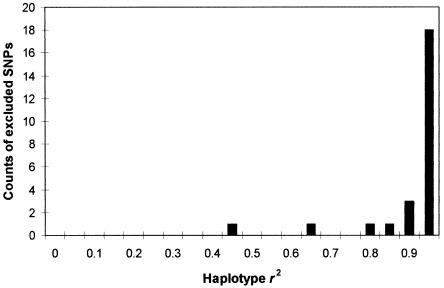
Sufficiency of K.—Figure 3 shows that the average performance of randomly chosen SNP sets displays asymptotic behavior as their size increases. If we can assume that our set K is randomly chosen from all possible sets of size K+1, then we can extrapolate that mean performance will not be greatly altered by the addition of one—or even several—SNPs. We can approximate the ability of K to detect a causative SNP x by examining the ability that tSNPs drawn from a reduced set of size K-1 have to detect the SNP that has been excluded from the set (fig. 4). Figure 4 reveals one SNP (snp3) for which a low r2 value (0.489) is obtained even when all other SNPs are used to construct haplotypes. The reason why snp3 is difficult to tag is that it is the only SNP that marks off a high-frequency haplotype (C) as distinct from haplotype E. Most other high-frequency haplotypes are distinguished from one another by multiple SNPs. Haplotype C, however, is discrepant in having a short branch length to the nearest other haplotype (as measured by number of distinguishing SNPs) and, thus, in appearing to be young yet occurring at a high frequency. For this reason, we call the SNP that marks it off (i.e., snp3) “discrepant.”
Figure 3.
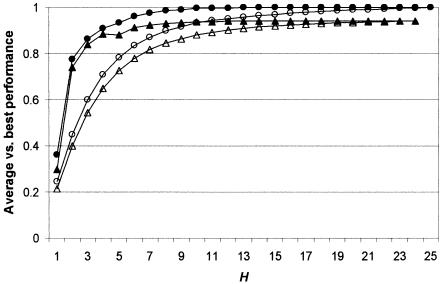
Average performance of randomly chosen SNP sets of size H. Performance indicators are as follows: solid circles = haplotype diversity ratio; squares = weighted-average haplotype r2; triangles = mean haplotype r2 against excluded loci (maximum H=24, because one locus is excluded); crosses = modal haplotype frequency; open circles = largest confounded frequency.
Figure 4.
Histogram of haplotype r2 values between each of 25 excluded loci and the remaining set of 24 SNPs. The lowest value is for snp3.
If discrepant SNPs, such as snp3, are included in the set K, they will not cause a problem, as they will always be selected as tags. But, if K were to be “exhaustively sufficient,” then we would want some assurance that there are no such discrepant SNPs outside K. This would be achieved if no high-frequency haplotypes were defined by K, since undiscovered discrepant SNPs can occur only by breaking up an existing high-frequency haplotype into two subcomponents. In principle, if enough SNPs were sampled, then each individual chromosome would be unique, and no high-frequency haplotypes would exist. In practice, the asymptotic behavior of the curve describing the decrease in modal haplotype frequency with SNP-set size (fig. 3) suggests that K would have to be very large to do this. A less exhaustively sufficient criterion for K would be to assess the probability that an unknown causative SNP, x, is a discrepant SNP. Of the 25 sets of size K-1, the probability that r2<0.8 is 1/25=0.04 (i.e., when snp3 is excluded). The probability that x is a discrepant SNP and associates poorly with K should therefore be no greater than 0.04.
This calculation, however, assumes that whether a SNP is causal has no bearing on whether it is also discrepant. But since causal SNPs have a phenotypic effect, this assumption may not be justified. In fact, under some versions of the common-disease/common-variant hypothesis, variants that cause predisposition to common disease may be positively selected in some populations or in some genetic backgrounds. The variants then have their deleterious effects only after a change in environment or genetic background. Positive selection, however, can increase the frequency of young haplotypes, leading to short discriminating branch lengths for high-frequency haplotypes and, therefore, to discrepant SNPs. To the extent that positive selection has influenced the variants relevant to disease predisposition and/or the genetics of variable drug response, this could present a serious complication to haplotype mapping by use of tSNPs.
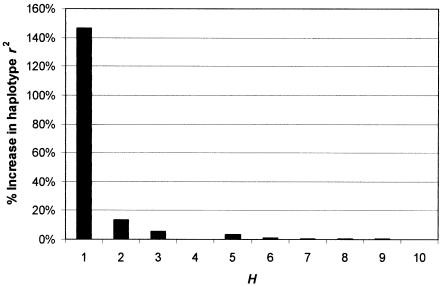
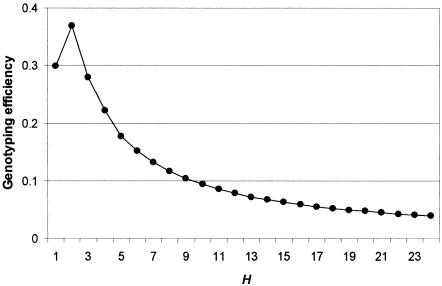
Sufficiency of H.—Figure 5 confirms that carefully selected tSNP sets can outperform randomly selected sets and can more quickly achieve performance levels close to those available if all K SNPs were used. Indeed, it is possible to reduce the tSNP-set size from 25 to 14 (56% of the total) without any loss of performance at all, since the 11 dropped SNPs all associate perfectly with SNPs in the remaining 14. It is clear that there is no benefit to increasing the tSNP-set size beyond H=14. Further reductions in H are possible but would require a cost-benefit assessment weighing the cost of additional genotyping against the benefit of increased power to detect a causative SNP x. The asymptotic behavior between r2 and H indicates a rule of diminishing returns. Figure 6 shows that, once H=6, each additional SNP added to H only marginally increases power. Equivalent power can be achieved by increasing the sample size by ∼1% (using the approximate relationship that r2 represents the effective unit of sample size in a case-control association study [Pritchard and Przeworski 2001]). An optimal value for tSNP-set size H can be found if one is willing to make a quantitative assessment of the cost of additional genotyping against the cost of increasing sample size. In the most extreme case, sample collection incurs no cost; thus, the total cost is proportional to nH, where n is the sample size, since this reflects the amount of genotyping effort. In this case, the optimal size of H is only 2 (fig. 7). This allows us to place the optimal H value between 2 and 14, with a reasonable value occurring in the range 4–9.
Figure 5.
Comparison of the performance of best tSNP sets against the average performance of randomly chosen sets of size H. Solid circles = weighted-average haplotype r2 of best sets; open circles = weighted-average haplotype r2 of randomly chosen sets; solid triangles = mean haplotype r2 of best sets against excluded loci (maximum H=24, because one locus is excluded); open triangles = mean haplotype r2 of randomly chosen sets against excluded loci.
Figure 6.
Percentage increase in mean haplotype r2 of best sets against excluded loci when H is increased to H+1.
Figure 7.
Genotyping efficiency with increasing H. Efficiency = r2/H, where r2 is the mean haplotype r2 of best sets against excluded loci (maximum H=24, because one locus is excluded).
tSNPs—Ability to Detect Low-Frequency SNPs
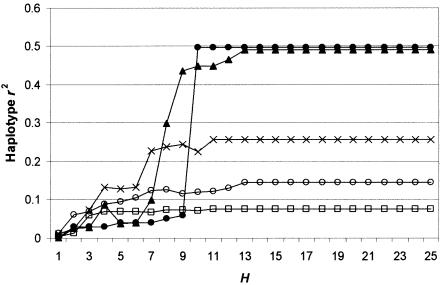
All the 25 SNPs in K have minor allele frequencies >10%. Thus, assessing the performance of tSNP sets by use of K does not address the issue of how well such sets are able to predict the state of low-frequency SNPs. This issue is of concern because it not yet known whether causative mutations are more likely to be common or rare (Chakravarti 1999; Weiss and Clark 2002). Our resequencing efforts in SCN1A uncovered five low-frequency SNPs (with minor allele frequencies of 0.82%, 0.86%, 0.94%, 1.69%, and 2.50%), in addition to the SNPs described so far. We used these SNPs to assess best tSNP sets selected using the Chinese data (fig. 8). We found that the association with these low-frequency SNPs was generally low, although two SNPs displayed a sharp increase in r2 as H increased to 10. In all cases, a plateau in r2 with increasing H was again observed. Thus, regardless of how hard it would be to detect such low-frequency SNPs, the chances of doing so are as good when using a smaller set of tSNP loci as when typing all 25 high-frequency loci, although a larger optimal H than for higher-frequency SNPs is indicated.
Figure 8.
Haplotype r2 between each of five low-frequency (<2.7%) loci and best tSNP sets of size H (chosen to maximize weighted-average haplotype r2 among 25 high-frequency SNPs).
tSNPs—Performance in Other Populations
A subset of 15 of the 25 SNPs in SCN1A were also typed in 32 Singapore Malay trios (anonymized legacy collection) and 32 trios of European ancestry (taken from CEPH Utah pedigrees). Haplotype frequencies were estimated using the trio EM algorithm and were compared with the Singapore Chinese trios (table 4). All three populations were significantly differentiated from each other (exact test on known resolved chromosomes). We assessed the performance, in the other two populations, of the best tSNP sets determined in the Singapore Chinese, using the weighted-average haplotype r2 criterion (figs. 9 and 10). For the Malay data set, all tSNP sets perform within 85% of the possible maximum, and, for H>4, the sets perform within 95% of the maximum. For the European data set, the tSNP sets perform very badly for H<6, in some cases performing no better than a randomly chosen tSNP set. For H⩾6, however, performance is within 93.5% of the possible maximum.
Table 4.
Haplotype Structure in Subset of SNPs in Singapore Chinese, Singapore Malays, and Europeans
|
EM Frequency(%) |
||||
| IDa | Haplotypeb | SingaporeChinese | SingaporeMalays | Europeans |
| 1 | 111111111111111 | 27.1 | 40.5 | 18.7 |
| 2 | 001101011110111 | 25.0 | 12.5 | 8.8 |
| 3 | 110111111111111 | 13.5 | 9.9 | … |
| 4 | 111011111111100 | 11.7 | 1.9 | … |
| 5 | 111110000001011 | 5.8 | 5.6 | 5.6 |
| 6 | 011110000001011 | 3.1 | … | .5 |
| 7 | 001111111111111 | 2.3 | 1.9 | 5.8 |
| 8 | 111110010001011 | 1.7 | 2.8 | 2.0 |
| 9 | 101101011110111 | 1.6 | 2.0 | … |
| 10 | 000101011110111 | .8 | … | … |
| 11 | 010111111111111 | .8 | 6.6 | … |
| 12 | 111011111111111 | .4 | 2.8 | … |
| 13 | 111001011110111 | … | 1.9 | … |
| 14 | 111111111111101 | … | 1.9 | … |
| 15 | 110111111101111 | … | 1.1 | … |
| 16 | 111111111110111 | … | 1.1 | … |
| 17 | 111101011110111 | … | 1.0 | … |
| 18 | 111111100111111 | … | … | 15.0 |
| 19 | 111110011001011 | … | … | 11.6 |
| 20 | 001110011001011 | … | … | 4.4 |
| 21 | 101110011001011 | … | … | 3.3 |
| 22 | 101110000001011 | .9 | … | 2.3 |
| 23 | 001101000110111 | … | … | 1.7 |
| 24 | 011011111111100 | … | … | 1.6 |
| 25 | 011111111111111 | … | 1.0 | 1.4 |
| 26 | 001101010110111 | … | … | 1.2 |
| 27 | 001110000001011 | … | … | 1.1 |
| 28 | 111111110111111 | … | … | .9 |
| 29 | 111111101111111 | .8 | … | .9 |
| 30 | 001100011010111 | … | … | .8 |
Haplotype designation.
Loci are arranged in the order snp1–snp15 (as in table 2), excluding snp4a–snp4f and snp9a–snp9d. Haplotypes are reported if observed in resolved chromosomes or if EM frequency is >1% in at least one population. 1 = major allele; 0 = minor allele.
Figure 9.
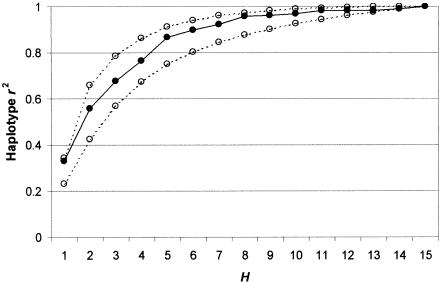
Weighted-average haplotype r2 in the Singapore Malay data set for best tSNP sets of size H that were ascertained in the Singapore Chinese data set (solid line)—compared with the average performance of randomly chosen SNP sets (lower dotted line) and of best tSNP sets ascertained using the Malay data set (upper dotted line).
Figure 10.
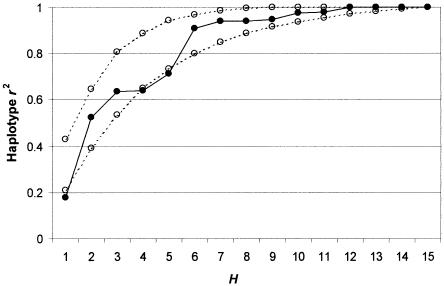
Weighted-average haplotype r2 in the European data set for best tSNP sets of size H that were ascertained in the Singapore Chinese data set (solid line)—compared with the average performance of randomly chosen SNP sets (lower dotted line) and of best tSNP sets ascertained using the European data set (upper dotted line).
Table 4 reveals the reason for this behavior. The Singapore Malays and Singapore Chinese differ in estimated haplotype frequencies, but all the major haplotypes (with frequency >5%) are found in both populations. Thus, tSNP sets designed to distinguish haplotype structure in the Singapore Chinese tend to do well in the Singapore Malays also. In contrast, two major haplotypes in the Singapore Chinese (haplotypes 3 and 4) are completely absent in the European sample, whereas other haplotypes important in the Europeans (haplotypes 18 and 19) are completely absent in the Singapore Chinese. Furthermore, because snp3 is an important discrepant SNP in the Singapore Chinese, it appears in almost all best tSNP sets, yet it is monomorphic in the Europeans so provides no relevant information at all in this data set. These results show that tSNPs determined in one population may not necessarily be good tSNPs in another if the populations are sufficiently differentiated. This problem may be offset by increasing the size of the tSNP set, but only at the cost of including possibly redundant SNPs in the tSNP set. We also note that the set K used to optimize the performance of the tSNP set H was ascertained in the Singapore Chinese only and that separate ascertainment of SNPs in the Singapore Malays and Europeans could have led K to be different in these populations and could further reduce the performance of H.
Discussion
In the present study, we have verified many of the elements of the tagging approach to genetic association studies. Using only a modest amount of resequencing, we have been able to determine the haplotype structure of a genomically large candidate gene, SCN1A. Similar to earlier reports (Daly et al. 2001; Johnson et al. 2001), we have found a large block of LD within which haplotype diversity is low.
We did not characterize the location, width, or LD properties of the boundaries of the high-LD block that we found. However, since we established a minimum size for this block (290 kb, between snp1 and snp16), many, if not all, functional mutations relevant to SCN1A are likely to be within the same high-LD region. We estimate that the set A of all SNPs in this block is likely to contain >500 SNPs with frequency >10% (combining a genomewide nucleotide-diversity estimate of =7.51×10-4 [International SNP Map Working Group 2001] with recent estimates of SNP allele-frequency distributions [see the Allele Frequency/Genotype Project Web site]). Our finding of a large LD region, together with a simple haplotype structure as defined by our high-frequency SNPs, indicated that a multistep approach to functional-variant mapping could be effective for SCN1A. We proceeded to test this through extensive analysis of tSNP sets of various sizes.
Regardless of how tSNP sets were assessed, a plateau in performance with increasing set size was observed. The plateau is a reflection of redundancy in information, with many loci displaying an “all-or-nothing” distribution of allelic state on haplotypic backgrounds defined by other loci. This redundancy means that, although an optimal tSNP size depends on the criteria being used, it is clear that the use of all 25 loci in a subsequent case-control study would be pointless. Indeed, repeated testing of individual loci for association would lead to greater problems of multiple testing and reduced overall power if all 25 loci were typed indiscriminately. Whereas other methods account for the correlation structure of genealogical data (e.g., see Templeton et al. 2000), tSNPs provide the additional advantage of economy in terms of time and cost.
Our analysis confirmed that a small tSNP set could be very effective in predicting the allelic state of an unknown high-frequency causative mutation, given that such mutations are likely to be part of the same haplotype structure as defined by the 25 loci that we typed within SCN1A. The savings relative to an exhaustive search and assessment of all high-frequency loci within the LD block are likely to be considerable. Using an association-based criterion to select the best tSNP sets (best-clumped r2, averaged over loci), we found that only four tSNPs could predict the allelic state of an excluded locus with an average coefficient of determination of 0.89 in the Singapore Chinese data set. We therefore estimate that we can match the power of typing all ∼500 high-frequency SNPs in the SCN1A LD block by typing only four SNPs in a case-control study with just a 13% increase in sample size for the Chinese. This would represent a 110-fold savings in terms of genotyping effort, and this is aside from the additional effort of identifying all of these ∼500 SNPs in the beginning. We also found that SNPs ascertained from the public databases revealed the same haplotypic structure as those found de novo from resequencing. This indicates that further savings could be achieved by basing the pilot set of known SNPs K on the public databases only, provided that marker density is adequate and that appropriate allowance for monomorphism in reported SNPs is made (in the present study, 4 of 16 reported dbSNPs were monomorphic).
Our results suggest that a case-control study to look for functional variants in SCN1A could indeed yield positive results, owing to the high association between the haplotypes defined by a small set of tSNPs and one or more causal variants, but there are a number of caveats. One of these is that, although the average association with excluded loci is high, our data also illustrate that there may be individual cases where association is low. Discrepant SNPs that distinguish apparently young haplotypes will not generally be well tagged. Even in this worst-case scenario, however, the discrepant snp3 has a coefficient of determination of 0.54 in the Chinese data set, indicating that a 1.86-fold increase in sample size would be needed to match the power of a study that typed this SNP directly. Because snp3 is the only discrepant SNP in a set of 25, it does not appear that this form of discrepancy will present a serious obstacle to haplotype mapping by use of tSNPs, unless causal SNPs are more likely to be discrepant than average because of selection; if the latter were the case, it could pose a serious complication, and this possibility requires further investigation. Interestingly, in this regard, snp3 not only is discrepant but also has a sharp allele-frequency difference between Europe (where no copies of the minor allele were found) and Asia, consistent with the possibility that it has been selected in recent times.
Another caveat is whether the causative SNP is at low frequency. Our results suggest that a tSNP approach will be less likely to be successful in identifying such loci. In contrast, low-frequency causative SNPs will cause problems of low power even in exhaustive SNP-hunting association studies, especially if penetrance is low. Such loci will be difficult to identify, whatever method is used. Unfortunately, the relative importance of rare and common SNPs in predisposition to common disease remains poorly known (Pritchard 2001; Reich and Lander 2001). For the case of variable drug response, however, the importance of common variants is much better established (Goldstein 2003).
A final caveat is that our comparisons of the performance of tSNP sets in populations other than the one in which they were ascertained shows that tSNP sets cannot always be ported from one population to another. Instead, the results suggest that tSNP strategies should be applied separately, at least within different geographic areas. In contrast, the fact that tSNPs ascertained in Singaporeans of Chinese ancestry can be applied to Singaporeans of Malay ancestry provides some reassurance that, within the major human ancestral geographic groups, tSNPs are portable among populations. More work will be required in order to verify this as a general rule, however.
A separate issue (aside from the ability of tSNPs to detect a causative SNP) is how easy or difficult it will be to go on to pinpoint the location of the causative SNP. In the most extreme scenario, LD across the entire block could be so high that a causative SNP could lie anywhere in the block on the associated chromosome. In less extreme scenarios, rare recombination events within the LD block could be used to indicate a more local region for the causative SNP. Evidence for such events can be found in our data, in which some low-frequency haplotypes can be explained only by evoking either recombination or recurrent mutation. It remains to be seen, however, the extent to which low-frequency recombinations can aid in localization of causative SNPs within a block, especially in cases of incomplete penetrance, which weakens the association between phenotype and haplotypic background. In many cases, it seems likely that functional assays will be required in order to assess which of many putative causal variants are the important ones.
For the purpose of the identification of tSNP sets that can predict allele states at unknown loci, criteria that measure association are the most appropriate. The best way to apply such criteria, however, is not obvious. This is hardly surprising, given that the best ways to analyze multipoint genetic association studies—incorporating genotypic, rather than haplotypic, data—remain issues open to debate. However, the criteria that we have used are reasonable. Future analytical developments may improve tSNP selection but will leave the performance results presented here as acceptable minimums. As for the choice of optimal tSNP-set size, this will depend on the relative importance of individual sample size n versus genotyping effort n*H. Although an exact solution would be possible only through a formal decision-theoretic approach, solutions for optimal tSNP-set size obtained under these two extremes (n vs. n*H) provide upper and lower limits to what the reasonable set size should be. For our data, we show that, even using the upper limit for tSNP-set size thus obtained, a very substantial savings over the cost of genotyping all SNPs in the SCN1A high-LD block would be obtained, with little or no reduction in average power to detect high-frequency causative SNPs.
Finally, we note that the tSNP-selection criterion that we recommend, haplotype r2 (implemented as criterion 5), relies on a linear model in which the haplotypes formed by the tSNPs are independent predictors. If this criterion is selected, then the performance expected on the basis of the selection criterion will not necessarily be realized, unless a linear model is used on the basis of all the tSNP-defined haplotypes observed in the cases and the controls. It may not be sufficient to individually test either the tSNPs alone or the presence/absence of single haplotypes that they define for frequency differences between cases and controls.
Acknowledgments
This work was supported by the Royal Society/Wolfson Research Merit Award (to D.B.G.) and the Biomedical Research Council of Singapore.
Electronic-Database Information
The accession number and URLs for data presented herein are as follows:
- Allele Frequency/Genotype Project, http://snp.cshl.org/allele_frequency_project/
- dbSNP Home Page, http://www.ncbi.nlm.nih.gov/SNP/
- GenBank, http://www.ncbi.nlm.nih.gov/Genbank/ (for genomic clone containing SCN1A [accession number AC010127])
- Goldstein Web site, http://popgen.biol.ucl.ac.uk/software.html (for the TagIT program)
- Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim/ (for GEFS+) [PubMed]
- Primer3, http://www-genome.wi.mit.edu/cgi-bin/primer/primer3_www.cgi
- RepeatMasker, http://analysis.molbiol.ox.ac.uk/pise_html/RepeatMasker.html
References
- Abou-Khalil B, Ge Q, Desai R, Ryther R, Bazyk A, Bailey R, Haines JL, Sutcliffe JS, George AL Jr (2001) Partial and generalized epilepsy with febrile seizures plus and a novel SCN1A mutation. Neurology 57:2265–2272 [DOI] [PubMed] [Google Scholar]
- Catterall WA (1999) Molecular properties of brain sodium channels: an important target for anticonvulsant drugs. Adv Neurol 79:441–456 [PubMed] [Google Scholar]
- ——— (2000) From ionic currents to molecular mechanisms: the structure and function of voltage-gated sodium channels. Neuron 26:13–25 [DOI] [PubMed] [Google Scholar]
- Chakravarti A (1999) Population genetics—making sense out of sequence. Nat Genet 21:56–60 [DOI] [PubMed] [Google Scholar]
- Claes L, Del-Favero J, Ceulemans B, Lagae L, Van Broeckhoven C, De Jonghe P (2001) De novo mutations in the sodium-channel gene SCN1A cause severe myoclonic epilepsy of infancy. Am J Hum Genet 68:1327–1332 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton D (2002) Choosing a set of haplotype tagging SNPs from a larger set of diallelic loci. http://www-gene.cimr.cam.ac.uk/clayton/software/stata/htSNP/htsnp.pdf (accessed July 17, 2003)
- Daly MJ, Rioux JD, Schaffner SF, Hudson TJ, Lander ES (2001) High-resolution haplotype structure in the human genome. Nat Genet 29:229–232 [DOI] [PubMed] [Google Scholar]
- Donahue LM, Coates PW, Lee VH, Ippensen DC, Arze SE, Poduslo SE (2000) The cardiac sodium channel mRNA is expressed in the developing and adult rat and human brain. Brain Res 887:335–343 [DOI] [PubMed] [Google Scholar]
- Escayg A, Heils A, MacDonald BT, Haug K, Sander T, Meisler MH (2001) A novel SCN1A mutation associated with generalized epilepsy with febrile seizures plus—and prevalence of variants in patients with epilepsy. Am J Hum Genet 68:866–873 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Escayg A, MacDonald BT, Meisler MH, Baulac S, Huberfeld G, An-Gourfinkel I, Brice A, et al (2000), Mutations of SCN1A, encoding a neuronal sodium channel, in two families with GEFS+2. Nat Genet 24:343–345 [DOI] [PubMed] [Google Scholar]
- Goldstein DB (2001) Islands of linkage disequilibrium. Nat Genet 29:109–111 [DOI] [PubMed] [Google Scholar]
- ——— (2003) Pharmacogenetics in the laboratory and the clinic. N Engl J Med 348:553–556 [DOI] [PubMed] [Google Scholar]
- Goldstein DB, Ahmadi KR, Weale ME, Wood NW. Genome scans and candidate gene approaches in the study of common diseases and variable drug responses. Trends Genet (in press) [DOI] [PubMed] [Google Scholar]
- Guo SW, Thompson EA (1992) Performing the exact test of Hardy-Weinberg proportion for multiple alleles. Biometrics 48:361–372 [PubMed] [Google Scholar]
- International SNP Map Working Group (2001) A map of human genome sequence variation containing 1.42 million single nucleotide polymorphisms. Nature 409:928–933 [DOI] [PubMed] [Google Scholar]
- Jeffreys AJ, Kauppi L, Neumann R (2001) Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nat Genet 29:217–222 [DOI] [PubMed] [Google Scholar]
- Johnson GCL, Esposito L, Barratt BJ, Smith AN, Heward J, Di Genova G, Ueda H, et al (2001) Haplotype tagging for the identification of common disease genes. Nat Genet 29:233–237 [DOI] [PubMed] [Google Scholar]
- Kruglyak L (1999) Prospects for whole-genome linkage disequilibrium mapping of common disease genes. Nat Genet 22:139–144 [DOI] [PubMed] [Google Scholar]
- Kuo CC (1998) A common anticonvulsant binding site for phenytoin, carbamazepine, and lamotrigine in neuronal Na+ channels. Mol Pharmacol 54:712–721 [PubMed] [Google Scholar]
- Lossin C, Wang DW, Rhodes TH, Vanoye CG, George AL Jr (2002) Molecular basis of an inherited epilepsy. Neuron 34: 877–884 [DOI] [PubMed] [Google Scholar]
- Plummer NW, Meisler MH (1999) Evolution and diversity of mammalian sodium channel genes. Genomics 57:323–331 [DOI] [PubMed] [Google Scholar]
- Pritchard JK (2001) Are rare variants responsible for susceptibility to complex diseases? Am J Hum Genet 69:124–137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Przeworski M (2001) Linkage disequilibrium in humans: models and data. Am J Hum Genet 69:1–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich DE, Lander ES (2001) On the allelic spectrum of human disease. Trends Genet 17:502–510 [DOI] [PubMed] [Google Scholar]
- Stumpf MPH, Goldstein DB (2003) Demography, recombination hotspot intensity, and the block structure of linkage disequilibrium. Curr Biol 13:1–8 [DOI] [PubMed] [Google Scholar]
- Sugawara T, Mazaki-Miyazaki E, Fukushima K, Shimomura J, Fujiwara T, Hamano S, Inoue Y, Yamakawa K (2002) Frequent mutations of SCN1A in severe myoclonic epilepsy in infancy. Neurology 58:1122–1124 [DOI] [PubMed] [Google Scholar]
- Sugawara T, Mazaki-Miyazaki E, Ito M, Nagafuji H, Fukuma G, Mitsudome A, Wada K, et al (2001) Nav1.1 mutations cause febrile seizures associated with afebrile partial seizures. Neurology 57:703–705 [DOI] [PubMed] [Google Scholar]
- Templeton AR, Weiss KM, Nickerson DA, Boerwinkle E, Sing CF (2000) Cladistic structure within the human lipoprotein lipase gene and its implications for phenotypic association studies. Genetics 156:1259–1275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace RH, Scheffer IE, Barnett S, Richards M, Dibbens L, Desai RR, Lerman-Sagie T, Lev D, Mazarib A, Brand N, Ben-Zeev B, Goikhman I, Singh R, Kremmidiotis G, Gardner A, Sutherland GR, George AL Jr, Mulley JC, Berkovic SF (2001) Neuronal sodium-channel α1-subunit mutations in generalized epilepsy with febrile seizures plus. Am J Hum Genet 68:859–865 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace RH, Wang DW, Singh R, Scheffer IE, George AL Jr, Phillips HA, Saar K, Reis A, Johnson EW, Sutherland GR, Berkovic SF, Mulley JC (1998) Febrile seizures and generalized epilepsy associated with a mutation in the Na+-channel β1 subunit gene SCN1B. Nat Genet 19:366–370 [DOI] [PubMed] [Google Scholar]
- Weiss KM, Clark AG (2002). Linkage disequilibrium and the mapping of complex human traits. Trends Genet 18:19–24 [DOI] [PubMed] [Google Scholar]
- Whitaker WR, Faull RL, Waldvogel HJ, Plumpton CJ, Emson PC, Clare JJ (2001) Comparative distribution of voltage-gated sodium channel proteins in human brain. Brain Res Mol Brain Res 88:37–53 [DOI] [PubMed] [Google Scholar]
- Zhang K, Calabrese P, Nordborg M, Sun F (2002) Haplotype block structure and its applications to association studies: power and study designs. Am J Hum Genet 71:1386–1394 [DOI] [PMC free article] [PubMed] [Google Scholar]