Novel Case-Control Test in a Founder Population Identifies P-Selectin as an Atopy-Susceptibility Locus

Abstract

To avoid problems related to unknown population substructure, association studies may be conducted in founder populations. In such populations, however, the relatedness among individuals may be considerable. Neglecting such correlations among individuals can lead to seriously spurious associations. Here, we propose a method for case-control association studies of binary traits that is suitable for any set of related individuals, provided that their genealogy is known. Although we focus here on large inbred pedigrees, this method may also be used in outbred populations for case-control studies in which some individuals are relatives. We base inference on a quasi-likelihood score (QLS) function and construct a QLS test for allelic association. This approach can be used even when the pedigree structure is far too complex to use an exact-likelihood calculation. We also present an alternative approach to this test, in which we use the known genealogy to derive a correction factor for the case-control association χ² test. We perform analytical power calculations for each of the two tests by deriving their respective noncentrality parameters. The QLS test is more powerful than the corrected χ² test in every situation considered. Indeed, under certain regularity conditions, the QLS test is asymptotically the locally most powerful test in a general class of linear tests that includes the corrected χ² test. The two methods are used to test for associations between three asthma-associated phenotypes and 48 SNPs in 35 candidate genes in the Hutterites. We report a highly significant novel association (P=2.10^-6) between atopy and an amino acid polymorphism in the P-selectin gene, detected with the QLS test and also, but less significantly (P=.0014), with the transmission/disequilibrium test.

Introduction

Association studies are an essential step in the genetic dissection of complex traits. Whereas linkage studies yield relatively broad locations for susceptibility loci, association studies can be used to test the role of particular candidate genes. However, classical case-control tests might detect differences between cases and controls owing to ignored population substructure or improperly accounted relatedness among individuals and not necessarily owing to a true association between a locus and a trait. We focus here on the problem of performing valid association studies for binary traits in samples with related individuals in which the relationships are known. Such a situation may be encountered in outbred populations (Risch and Teng 1998; Slager and Schaid 2001). In isolated populations, the relatedness among individuals may be considerable, with many or all individuals related through multiple lines of descent. Neglecting such correlations among individuals can lead to seriously spurious associations. This has been illustrated by Newman et al. (2001) in a study conducted in a sample of Hutterites from South Dakota. The ∼750 members of their sample are descendants of just 64 founders and are related to each other by a 13-generation, 1,623-member pedigree. Using an association test for quantitative traits developed by Abney et al. (2002) that takes the pedigree structure into account, Newman et al. (2001) illustrated the dramatic effect on false-positive rates of neglecting interindividual correlations.

To overcome this problem, family-based association tests have been widely, if not systematically, used, even though they have some disadvantages. In particular, the need for genotype information on family members, such as parents or sibs, can drastically reduce the number of cases available for a study, a concern that may be particularly relevant for late-onset diseases. Devlin and Roeder (1999) have proposed to use genomic controls to correct association tests for unknown relatedness among individuals. However, when the genealogy of the sample is entirely known, it is preferable to use this information. Slager and Schaid (2001) have derived a correction factor for the Armitage trend test to account for the presence of close relatives (e.g., siblings and cousins) from outbred populations, but this method cannot handle complex inbred pedigrees. Furthermore, little is known about the relative power of these different approaches.

Here, we propose a method for case-control association studies of binary traits, a method suitable for any set of related individuals, provided that their genealogy is known. In particular, it can be used in large inbred pedigrees. The method takes into account interindividual correlations, as well as intraindividual correlations due to inbreeding, by conditioning on the pedigree structure. Because we want the method to be suitable even when the pedigree structure is far too complex to use an exact-likelihood calculation, we base inference on the quasi-likelihood score (QLS) function (also known as the “quasi-score function” [e.g., see McCullagh and Nelder 1989; Heyde 1997]). This quasi-score function has been proposed by Wu et al. (2000) and by M.S.M., X. Wu, and C.O. (unpublished data) for estimation of allele frequencies in large inbred pedigrees. In that case, it results in the best linear unbiased estimator. We extend their approach to construct a QLS test for allelic association. The exact computation of the correlations among alleles requires inbreeding coefficients for all individuals and kinship coefficients for all pairs of individuals included in the analysis.

We also present an alternative approach to this test, in which we derive a correction factor for the case-control association χ² test based on the variance that appropriately accounts for inter- and intraindividual correlations. As for the QLS test, this correction factor is performed conditional on the pedigree structure. The latter strategy is similar to the one used by Slager and Schaid (2001), although they used a variance computed conditional on the identity-by-descent (IBD) information obtained using the marker genotype data rather than an unconditional variance. We note that exact computation of the conditional variance is generally infeasible in complex pedigrees. By deriving the noncentrality parameters of both the QLS and corrected χ² statistics, we obtain analytical results that allow us to compare the power of the two approaches. Furthermore, we show that both tests belong to a general class of linear tests, with the QLS test being asymptotically the locally most powerful test of this class under certain regularity conditions.

In what follows, we shall first describe the QLS test statistic for allelic association and derive the variance correction of the case-control χ² test. We will then study the null distributions of the tests and compare their power in Hutterite samples. Finally we will use these statistics to test, in Hutterite samples, the association between three different asthma-related phenotypes (asthma [MIM 600807], bronchial hyperresponsiveness [BHR], and atopy) and a set of 48 SNPs located in 35 candidate genes that were selected because of their known or suspected role in the inflammatory process.

Methods

The QLS Test for Allelic Association

We develop a test for association between a single marker and a binary trait, based on case-control data from a founder population but also useful in outbred populations with sampled relatives. We first focus on the case of a biallelic marker and then extend the method to the multiallelic case.

Biallelic Case

Consider a group of N subjects sampled from a population of known genealogy. Consider a biallelic marker with alleles labeled “0” and “1.” We start by considering the situation in which the marker has no association with the trait (the null model), and we briefly review the results of Wu et al. (2000) and M.S.M., X. Wu, and C.O. (unpublished data) on allele-frequency estimation for this case. We then present the alternative model and derive the QLS statistic. Let Y=(Y₁,…Y_i…,Y_N)^T be a vector with element Y_i equal to  1/2× (the number of alleles of type 1 in individual i). Y_i=0,  1/2, or 1. Let p be the frequency of allele 1, 0<p<1, and let Σ be the covariance matrix of Y. It can be shown that Σ= 1/2p(1-p)K, where

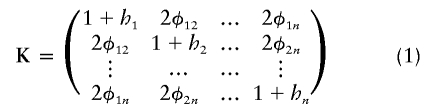with h_i being the inbreeding coefficient of individual i and φ_ij the kinship coefficient between individuals i and j. We note that K will be invertible, provided that each MZ twin pair (if any) is entered as a single individual in the matrix.

Define m=E(Y). By construction, m is a column vector of length N (N-vector) with m=p1, where 1 is an N-vector of 1s. Let D_p= ∂m/∂p=1. Wu et al. (2000) and M.S.M., X. Wu, and C.O. (unpublished data) have proposed to use the quasi-score function U=D^T_pΣ^-1(Y-m) to estimate p by setting 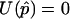(e.g., see McCullagh and Nelder 1989). The solution to this equation is

which M.S.M. and X. Wu (unpublished data) have shown to be the best linear unbiased estimator of p.

We now consider the case in which the marker is associated with the trait (the alternative model). Suppose that N_c subjects among the N are cases and that N_t are controls so that N_c+N_t=N. To test for an allelic association between the marker and the disease, we propose to consider the following model: E(Y)=μ=(μ₁,…μ_i,…μ_N)^T with

Under the null hypothesis of no association, r=0, whereas, under the alternative hypothesis, r≠0. p is now considered a nuisance parameter. We allow the covariance matrix of Y, Ω, to depend on both p and r. However, it turns out that we do not need to specify the exact form of Ω. We simply require that Ω=Σ when r=0 and that Ω be differentiable and invertible. The quasi-score function corresponding to our model is

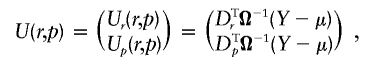where

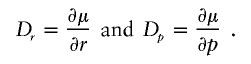D_p and D_r are N-vectors with D_p as previously described and D_r=(d₁…d_N)^T where d_i=1 if i is a case and d_i=0 if i is a control. We propose to use this quasi-score function to build a QLS statistic. The classical score statistic when the null hypothesis is composite (r=r₀ and p is a nuisance parameter), as described by Cox and Hinkley (1974), has the following form

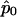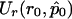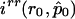where is the maximum likelihood estimate of p when r=r₀. and are, respectively, the derivative over r of the log-likelihood and the (r,r)th entry of the inverse of the information matrix, both computed with 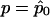and r=r₀. This statistic does not involve the existence of a likelihood function from which the score function is derived by differentiation. It can therefore be generalized to the case of quasi likelihood (Heyde 1997), where the derivative of the log-likelihood is replaced by the quasi-score function U and the information matrix is replaced by E(UU^T). In our case, this substitution results in the statistic

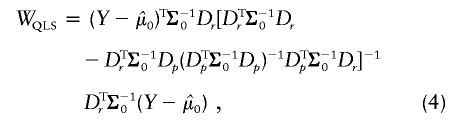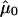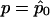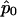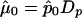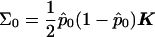where and Σ₀ are, respectively, the expectation and the covariance matrix of Y evaluated at r=0 and , where is the maximum quasi-likelihood estimate of p when r=0. Thus, and with 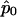calculated using eq. (2). As demonstrated by Heyde (1997), W_QLS should follow a χ² distribution with 1 df under the null hypothesis, provided that 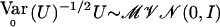under the null. Simulations testing the accuracy of this null distribution will be presented in the “Results” section.

Suppose, now, that the N subjects belong to F independent families sampled in an outbred population. For each family f of size N_f, we define Σ_f and K_f, its covariance and correlation matrices. Σ_f and K_f are N_f×N_f matrices with entries given in eq. (1) for K_f and Σ_f= 1/2p(1-p)K_f. When all the individuals in the sample are outbred, K_f has all its diagonal elements equal to 1. It comes from eq. (2) that

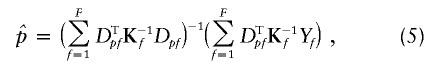where Y_f is the N_f- vector of allele indicators for the N_f members of the fth family and D_pf is an N_f-vector of 1s. Similarly, W_QLS is computed as in eq. (4), with all the terms of the form X^TΣ^-1₀B in this formula (where X and B are N-vectors: either D_p D_r or 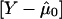), computed as 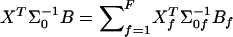, where X_f and B_f are the N_f-subvectors of X and B corresponding to the N_f members of the fth family.

Multiallelic Case

Consider a locus with a different alleles. Let Y=(Y₁,…,Y_a-1)^T be an [(a-1)N]-vector with Y_k=(Y_k1,…,Y_kN)^T an N-vector and Y_ki equal to  1/2(the number of alleles of type k in individual i). If a particular allele k is suspected to be associated with the disease, the locus might be treated as biallelic k/non-k and the test performed just as described in the previous case. Arguably, when there is no prior idea of which allele might be associated with the disease, a more general alternative model should be considered. As a generalization of the biallelic case, we consider E(Y)=μ=(μ₁,…,μ_a-1)^T, where μ_k=(p_k+s₁r_k,…,p_k+s_Nr_k)^T with s_i=1 if i is a case and s_i=0 if i is a control. Here, we write p=(p₁,…,p_a-1)^T and r=(r₁,…,r_a-1)^T, and we assume 0<p_k+r_k<1 and 0<p_k<1 for all k. As in the biallelic case, we allow for a very general form for the covariance matrix of Y. When r=0, this matrix is Σ=F⊗K (⊗ is defined in appendix A), where F is the (a-1)×(a-1) matrix of the form

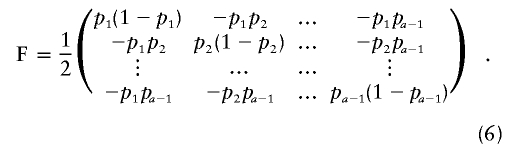Note that, in the biallelic case, F reduces to  1/2p(1-p) and Σ= 1/2p(1-p)K, as given in the “Biallelic Case” subsection above. We show in appendix A that, in this case,

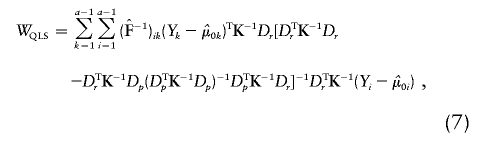where, for all k, 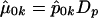, and 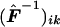is the (i,k) entry of F evaluated at 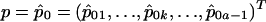. Here, 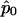is the quasi-likelihood estimator of p when r=0. For each k, 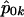is calculated using eq. (2) with Y replaced by Y_k (Wu et al. [2000] and M.S.M., X. Wu, and C.O., unpublished data). In this case, we also expect the null distribution of W_QLS to be ∼χ² with (a-1) df, and we examine the accuracy of this approximation in the “Results” section. In a manner similar to the biallelic case, when the N subjects belong to F independent families, W_QLS is computed as in eq. (7) with all the terms of the form X^TK^-1B in this formula—where X and B are N-vectors: either D_p, D_r or 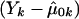—computed as 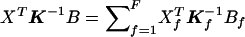, where X_f and B_f are the N_f-subvectors of X and B corresponding to the N_f members of the f family.

General Framework for the QLS and χ² Tests

The W_QLS statistic can be seen as a particular case of a more general class of linear statistics of the form 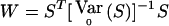, where S=V^TY with V≠0 a known [N(a-1)×(a-1)] matrix and E₀(S)=0. E₀(S) and 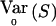are, respectively, the expectation and the variance of S when r=r₀. 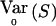depends on p and, in practice, is computed at 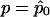. In what follows, we refer to this class of linear statistics as the “W class.” In the biallelic case, we can define V_QLS=V₁, where V₁=K^-1D_r-(D^T_rK^-1D_p)(D^T_pK^-1D_p)^-1K^-1D_p. Then, 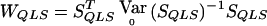, where S_QLS=V^T_QLSY (this result can be obtained by inserting eq. [2] into eq. [4] and moving all the factors of 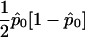into the variance term). More generally, we show, in appendix B, that, in the multiallelic case, we have a similar result with V_QLS=I_a-1⊗V₁, where I_a-1 is the identity matrix of dimension (a-1).

In the special case when the correlations among all the individuals, as well as between the two alleles of an individual, are zero, the classical case-control χ² test for association also fits in the W class of statistics. For a biallelic locus, V_χ²=V₂, where V₂=D_r-(D^T_rD_p)(D^T_pD_p)^-1D_p (note that V₂ is just V₁ with K replaced by I). Indeed, 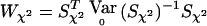with S_χ²=V^T_χ²Y is equal to the classical case-control χ² test statistic, as shown in appendix B. The multiallelic case is similar, with V_χ²=I_a-1⊗V₂ (see appendix B).

Correction Factor for the Classical χ² Test

One way to extend the classical χ² test so that it is valid when the above correlations are not zero, is to use the same S_χ²=V^T_χ²Y and recompute 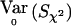to take into account the correlations. In the biallelic case, this is done by making use of the fact that 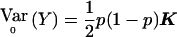, rather than  1/2p(1-p)I. We call the resulting statistic “W_χ²corr,” and we have

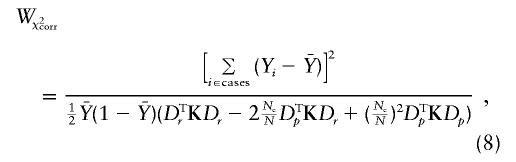where 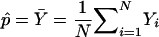has been substituted for p.

Let ρ_χ²corr be the correction factor to be applied to the W_χ² to have a valid test. W_χ²corr=ρ_χ²corrW_χ² with

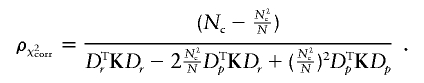Note that ρ_χ²corr depends only on the sample composition (i.e., who are the cases and who are the controls), not on allele-frequency estimates. It can be shown that the same correction applies when there are a alleles at a locus, so that ρ_χ²corrW_χ² approximately follows a χ² distribution with (a-1) df under the null hypothesis. Here again, if the N individuals belong to F independent families, W_χ²corr and ρ_χ²corr can be computed as above with all the terms of the form X^TKB (where X and B are N-vectors) in these formulas, computed as .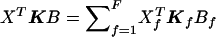

Null Distribution of the W_QLS and W_χ²corr Statistics

To determine whether the χ² approximation provides the correct type I error for the tests based on W_QLS and W_χ²corr, we performed simulations based on three different real case-control samples of Hutterites from South Dakota. The Hutterites are a North American religious isolate that originated in eastern Europe and whose entire population can be traced back to 90 ancestors in the 1700s/1800s. Sample 1 consisted of 701 Hutterites who were phenotyped for atopy, defined as a positive skin-prick testing (+SPT) to at least 1 of 14 airborne allergens. This sample included 310 individuals with atopy and 391 controls (no +SPT to any of the 14 allergens tested). Sample 2 consisted of 156 individuals with BHR and 434 controls without any asthma symptoms or BHR. Sample 3 consisted of the same 434 controls and 76 individuals out of the 156 cases of sample 2 with self-reported asthma symptoms and a doctor’s diagnosis of asthma and BHR. The latter phenotype will be referred to as “asthma” in what follows. The details of the phenotype have been described elsewhere (Ober et al. 2000). The complete genealogy of these 719 different individuals was constructed from a Hutterite pedigree of ⩾12,000 individuals. This yielded a 1,623-person pedigree that included all known ancestors of the individuals in the three samples. The inbreeding coefficients for all 719 individuals, as well as the kinship coefficients between any pair of individuals in each sample, were computed on the basis of the 1,623-person pedigree, using the algorithm of Boyce (1983). Mean values of the inbreeding and kinship coefficients for the three samples are presented in table 1. Two smaller subsamples were also considered, to evaluate the effect of sample size on the type I error. Sample 4 consisted of the 76 cases from sample 3 and 76 controls randomly drawn from the 434 corresponding controls. Sample 5 consisted of 30 cases randomly drawn from the 76 cases in sample 3 and 30 controls randomly drawn from the corresponding 434 controls.

Table 1.

Mean Inbreeding and Kinship Coefficients in Cases and in Controls from Three Hutterite Samples

Sample	Size	KinshipCoefficient	InbreedingCoefficient
+SPT:
Cases	310	.0436	.0363
Controls	391	.0419	.0321
BHR:
Cases	156	.0423	.0337
Controls	434	.0426	.0348
Asthma:
Cases	76	.0445	.0336
Controls	434	.0426	.0348

Genotype information for markers unlinked to the phenotypes under study was simulated by randomly drawing alleles for the founders of the 1,623-person pedigree with fixed allele frequencies and then simulating the Mendelian transmission of these alleles throughout the pedigree. The validity of the χ² null distribution was assessed by comparing the proportion of simulations showing a statistic whose value is greater than the χ² threshold for a nominal type I error and the value of this nominal type I error.

Power of the W_QLS and W_χ²corr Statistics

We show, in appendix C, that, under certain regularity conditions, W_QLS is asymptotically the locally most powerful test of the W class of linear tests described earlier. We provide here analytical power calculations for W_QLS and W_χ²corr to quantify the difference between the two tests. The basic assumption underlying these calculations is that, under the alternative hypothesis H₁, both W_QLS and W_χ²corr have a noncentral χ² distribution with the respective noncentrality parameters λ_QLS and λ_χ²corr. (For instance, this would hold asymptotically for local alternatives [i.e., alternatives that are close to the null] under certain conditions on K.) λ_QLS is obtained by calculating W_QLS with Y replaced by E_H1(Y), where E_H1(Y) is the expectation of Y under the alternative hypothesis H₁. Similarly, λ_χ²corr is equal to W_χ²corr computed with Y replaced by E_H1(Y). We focus, in what follows, on the biallelic case. Using the expression of W_QLS as a function of S_QLS given earlier, we have

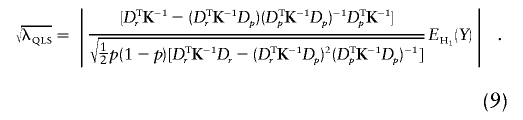The alternative presented in (3) may also be written as E_H1(Y)=pD_p+rD_r. Thus,

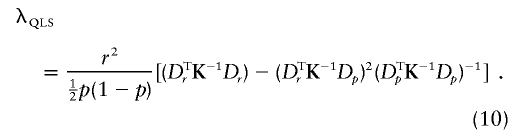Similarly, it comes from eq. (8) that

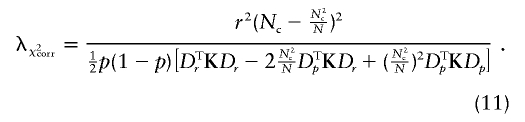For fixed values of (p,r) defining an alternative, the power of W_QLS and W_χ²corr for a nominal type I error α is β_QLS=1-ℛ_λQLS,1(K_α,1) and β_χ²corr=1-ℛ_λχ²corr,1(K_α,1), respectively, where K_α,1 is the upper αth quantile of a χ²₁ distribution and where ℛ_λ,1 is the distribution function of a noncentral χ²₁ with noncentrality parameter λ.

Testing Candidate Genes for Asthma in the Hutterites

The W_QLS and the W_χ²corr statistics were used to test the association between asthma, BHR, and atopy and 48 biallelic markers located in 35 different genes that were selected because of their known or suspected role in the inflammatory process. Typing was done by multiplex PCR and an immobilized-probe linear-array system (LAS) (Mirel et al. 2002). These genes (n = number of polymorphisms per gene) included interleukin 4 (IL4 [MIM 147780], n=1), interleukin 4 receptor α chain (IL4RA [MIM 147730], n=3), interleukin 13 (IL13 [MIM 147683], n=1), β₂-adrenergic receptor (ADRB2 [MIM 109690], n=3), intercellular adhesion molecule 1 (ICAM1 [MIM 147840], n=2), vascular cell adhesion molecule 1 (VCAM1 [MIM 192225], n=1), E-selectin (SELE [MIM 131210], n=1), P-selectin (SELP [MIM 173610], n=2), Fcε receptor β chain (FCERB1 [MIM 147138], n=1), monocyte differentiation antigen CD14 (CD14 [MIM 158120], n=1), uteroglobin (UGB [MIM 192020], n=1), transforming growth factor β1 (TGFB1 [MIM 190180], n=1), Eotaxin (SCYA11 [MIM 601156], n=2), chemokine receptor 2 (CCR2 [MIM 601267], n=1), chemokine receptor 3 (CCR3 [MIM 601268], n=1), chemokine receptor 5 (CCR5 [MIM 601373], n=2), T cell–specific transcription factor 7 (TCF7 [MIM 189908], n=1), interleukin 9 (IL9 [MIM 146931], n=1), interleukin 1 α chain (IL1A [MIM 147760], n=1), interleukin 1 β chain (IL1B [MIM 147720], n=2), interleukin 5 receptor α chain (IL5RA [MIM 147851], n=1), interleukin 6 (IL6 [MIM 147620], n=2), interleukin 10 (IL10 [MIM 124092], n=1), complement 3 (C3 [MIM 120700], n=1), complement 5 (C5 [MIM 120900], n=1), colony-stimulating factor 2 (CSF2 [MIM 138960], n=1), cytotoxic T lymphocyte–associated protein (CTLA4 [MIM 123890], n=2), leukotriene C4 synthase (LTC4S [MIM 246530], n=1), nitrous oxide synthetase 3 (NOS3 [MIM 163729], n=2), nitrous oxide synthetase 2A (NOS2A [MIM 163730], n=1), stromal cell–derived factor 1 (SDF1 [MIM 600835], n=1), lymphotoxin α (LTA [MIM 153440], n=1), tumor necrosis factor (TNF [MIM 191160], n=2), vitamin D receptor (VDR [MIM 601769], n=1), and group-specific component (GC [MIM 139200], n=1). Full descriptions of the polymorphisms included in this study are available at the authors' Web site (Association Studies in Hutterites). The samples 1, 2, and 3 (described in the “Null Distribution of the W_QLS and W_χ²corr Statistics” subsection above) corresponding to the three phenotypes—atopy, BHR, and asthma, respectively—were used to conduct the analysis. The association between these 48 SNPs and the three phenotypes was also tested in the Hutterites, using the transmission/disequilibrium test (TDT), as implemented in ASPEX (Hinds and Risch 1999), considering all the cases for which parental genotypes were available.

Results

Null Distribution of the W_QLS and W_χ²corr Statistics

Table 2 presents the results of simulation studies in samples 1 (+SPT), 2 (BHR), and 3 (asthma), assessing the empirical type I error of both the QLS and the corrected χ² statistics when the χ² distribution is used as the null distribution of the statistics. Four different choices of allele-frequency distribution are considered. The results of the noncorrected χ² test are also displayed, to highlight the increase in type I error when interindividual correlations are neglected. For a given sample, this increase shows nonnegligible variation from one allele case to another, even though the correction factor ρ_χ²corr does not depend on allele frequency. This presumably reflects the fact that W_χ²corr is only χ² distributed and that, in finite samples, the accuracy of the χ² approximation varies slightly, depending on the allele-frequency distribution. In our largest sample, sample 1, the real type I error for the noncorrected χ² with a nominal P value of 5% may be as large as 18% in the three-allele case. For both the QLS and the corrected χ² tests, the nominal type I error lies within the 95% CI of the real type I errors in all three samples for two of the three biallelic situations considered and for the triallelic situation. Similar results are obtained for the two smaller Hutterite subsamples, as can be seen in table 3. When the allele frequency becomes low (0.05), the χ² approximation seems to be slightly conservative or anticonservative for both tests in all five samples, a deviation possibly due to small numbers of observations of the minor allele when its frequency is low. Even though not exhaustive, these results tend to confirm that the χ² distribution is a reasonably good approximation of the null distribution of these two tests, as long as neither the allele frequency nor the sample size is too small. The sample size and allele frequency required for the χ² distribution to hold depend on the relationship among the individuals of the sample and are likely to differ from one population sample to another. We would recommend that exact simulations be performed for confirmation in case of a significant result associated with a small number of alleles in the case and/or the control sample.

Table 2.

Empirical Type I Error of the QLS Test, the Corrected Case-Control χ² Test, and the Noncorrected χ² Test Estimated with 5,000 Simulations in Three Hutterite Samples^[Note]

	Empirical Type I Error with Nominal Type I Error of
	.05			.01
Number of Alleles (Frequency) and Test	+SPT	BHR	Asthma	+SPT	BHR	Asthma
2 (.5/.5):
QLS	.052	.046	.055	.013	.011	.012
Corrected χ2	.055	.050	.054	.009	.013	.011
Noncorrected χ2	.145	.071	.071	.054	.021	.019
2 (.2/.8):
QLS	.045	.050	.047	.010	.010	.010
Corrected χ2	.055	.056	.049	.010	.010	.010
Noncorrected χ2	.140	.072	.069	.054	.016	.017
2 (.05/.95):
QLS	.041	.038	.045	.013	.013	.014
Corrected χ2	.045	.050	.042	.008	.008	.012
Noncorrected χ2	.123	.066	.060	.043	.043	.016
3 (.3/.3/.4):
QLS	.055	.055	.056	.013	.011	.012
Corrected χ2	.054	.055	.051	.010	.014	.012
Noncorrected χ2	.180	.082	.079	.073	.020	.020

Note.— Values outside the 95% CI of the nominal type I error are underlined.

Table 3.

Empirical Type I Error of the QLS Test and the Corrected χ² Test Estimated with 5,000 Simulations, for a Nominal Type I Error of .01 in Smaller Hutterite Samples and for Biallelic Markers^[Note]

	Empirical Type I Error in
	76 Cases/76 Controlswith Allele Frequency of			30 Cases/30 Controlswith Allele Frequency of
Test	.5	.2	.05	.5	.2	.05
QLS	.012	.012	.019	.012	.01	.01
Corrected χ2	.012	.012	.004	.012	.009	.0024

Note.— Values outside the 95% CI of the nominal type I error are underlined.

Power of the W_QLS and W_χ²corr Statistics

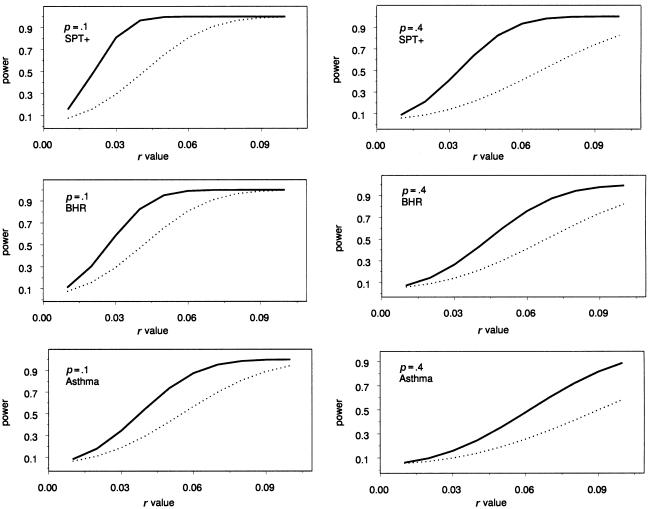
Figure 1 displays the power of both the W_QLS and W_χ²corr statistics based on the analytical power calculations, for various alternatives defined by (p,r) pairs (allele frequency in the controls and difference in allele frequency between cases and controls), using the three different Hutterite samples described above. Note that these power calculations are expected to be more accurate for smaller values of r, which represent alternative models close to the null.

Figure 1.

Power with a 5% nominal type I error of the QLS test (solid lines) and the corrected χ² test (dotted lines) for different alternative models defined by (p, r) pairs in three different Hutterite case-control samples: +SPT, BHR, and asthma. Power is presented as a function of r for two different values of p.

The corresponding noncentrality parameter ratios (λ_QLS/λ_χ²corr) are 4.01 for sample 1, 2.36 for sample 2, and 2.14 for sample 3. These ratios depend only on the sample composition (i.e., the actual choice of cases and controls) and not on the alternative model, as can be seen from eqs. (10) and (11). In every situation considered, the approximate power calculated for W_QLS is higher than that calculated for W_χ²corr, and, in fact, we show in appendix C that λ_QLS⩾λ_χ²corr. The difference in power between the two tests tends to become smaller for small values of r, but the gain in power when using W_QLS instead of W_χ²corr remains nonnegligible. This point is of particular interest, because small values of r are more likely to occur in real data sets. Indeed, the difference in allele frequencies between cases and controls would reach its maximum when the marker is the functional variant. However, the most common situation is that the marker has an allele that is in linkage disequilibrium with the functional variant, corresponding to smaller values of r.

Testing Candidate Genes for Asthma in the Hutterites

The results for all the 48 SNPs with a noncorrected P value <.05 for at least one of the three tests (QLS test, corrected χ² test, or TDT) are presented in table 4 for asthma, BHR, and atopy. As expected, the number of observations available for the two case-control tests is larger than that for the TDT. Although, for example, 269 atopy cases and 323 controls are genotyped for the Val640Leu amino acid polymorphism in SELP (SELP_640), only 136 heterozygous parents are available for the TDT. Two association signals reached the 5% significance threshold after adjustment for 105 tests (35 different genes tested for three phenotypes), using the Bonferroni correction (P=.000476): SELP_640 and atopy, using the QLS test, and SCYA11_−1328 and BHR, using the corrected χ² test. If we consider the uncorrected threshold of .05, association signals were detected when the QLS test was used, with 15 other polymorphisms when the corrected χ² test was used but with only 3 polymorphisms when the TDT was used and none of the polymorphisms reached the significance threshold. Interestingly, the smallest P values obtained using the corrected χ² test and the QLS test were not systematically observed at the same loci. Except for the associations between CSF2_117 and atopy, which had a P value <.01 with both tests (P=.0087 with the corrected χ² test and P=.0038 with the QLS test) and between NOS3_298 and asthma, which had a P value close to .01 (P=.0084 with the corrected χ² test and P=.011 with the QLS test), all other association signals with a P value <.01 were observed with only one of the two tests (SCYA11_−1328 and asthma, SCYA11_−1328 and BHR, and SDF1_3UTR and asthma, using the corrected χ² test; LTC4S_444 and BHR, C3_102 and atopy, and SELP_640 and atopy, using the QLS test). Even though the QLS test is locally more powerful than the corrected χ² test under certain regularity conditions, the probability that the corrected χ² test provides a smaller P value than the QLS test in any particular case is not negligible. Furthermore, we have not studied the power of both tests when the alternative is not local (e.g., in the event of strong difference in allele frequency between cases and controls; note that analytic power calculations are not feasible for that case). In particular, the results shown on figure 1 were valid for values of r close to 0. We cannot rule out the possibility that the corrected χ² test might perform better for some alternatives, as suggested by the results of our data analysis.

Table 4.

Results of Association Studies with Asthma, BHR, and Atopy, Using the QLS Test, the Corrected χ² Test, and the TDT^[Note]

					P
Phenotypeand RS Number	Marker	Nc	Nt	p	χ2corr	QLS	TDT	TR:NT
Asthma:
1801157	SDF1_3UTRa	65	357	.64	.00087	.037	.032	22:9
4795895	SCYA11_−1328b	65	362	.79	.0096	.14	.38	14:20
1799983	NOS3_298c	72	404	.52	.0084	.011	.89	26:24
25882	CSF2_117d	66	372	.84	.037	.04	.83	11:9
17611	C5_802e	66	362	.53	.034	.04	1.0	21:20
1800872	IL10_−571f	65	366	.55	.033	.077	.65	18:22
1042713	ADRB2_16g	71	400	.64	.025	.97	1.0	27:27
BHR:
361525	TNF_−238h	147	409	.87	.043	.46	.74	23:20
4795895	SCYA11_−1328b	135	262	.79	.00038	.099	.33	29:38
1799983	NOS3_298c	144	404	.52	.013	.018	.26	55:43
1137933	NOS2A_346i	136	370	.76	.046	.12	.61	28:33
730012	LTC4S_−444j	133	354	.8	.06	.002	.47	22:28
25882	CSF2_117d	136	372	.83	.21	.04	.4	29:22
1800872	IL10_−571f	134	366	.56	.035	.19	.19	42:45
6133	SELP_640k	137	372	.82	.11	.012	.027	43:24
Atopy:
2569190	CD14_−260l	259	319	.61	.27	.03	.2	87:70
1800779	NOS3_−922m	285	361	.56	.36	.034	1.0	89:89
5742909	CTLA4_−318n	261	320	.77	.013	.013	.51	59:67
25882	CSF2_117d	265	330	.81	.0087	.0038	.05	63:42
2230199	C3_102o	238	297	.72	.64	.0049	.23	46:34
2290608	IL5R_−80p	258	326	.93	.028	.074	.45	34:27
6133	SELP_640k	269	323	.82	.068	.000002	.0014	87:49
1041163	VCAM1_−1594q	271	330	.91	.49	.017	.48	40:33

Note.— SNPs with an associated P value <.05 for at least one of the three tests are reported, and P values <.05 are underlined. Descriptions of the SNPs can be found on the dbSNP Home Page, using their reference SNP (RS) number. The associated alleles are underlined in the footnotes below. The number of genotypes available in cases (N_c) and controls (N_t), the major allele frequency in the case-control sample as a whole (p) and the number of transmitted:nontransmitted major alleles in the TDT sample (TR:NT) are displayed.

^aG→A in 3′ UTR in SDF1.

^bG→A in promoter region position −1328 in SCYA11 (eotaxin).

^cGlu 298Asp in NOS3.

^dIle 117Thr in CSF2.

^eVal 802Ile in C5.

^fC→A in promoter region position −571 in IL10.

^gGly16 Arg in ADRB2.

^hG→A in promoter region position −238 in TNF.

ⁱC→T synonymous change (Asp346) in NOS2A.

^jA→C in promoter region position −444 in LTC4S.

^kVal640Leu in SELP.

^lC→T in promoter region position −260 in CD14.

^mA→G in promoter region position −922 in NOS3.

ⁿT→C in promoter region position −318 in CTLA4.

^oArg102Gly in C3.

^pG→A in promoter region position −80 in IL5R.

^qT→C in promoter region position −1594 in VCAM1.

Discussion

Recent progress in unraveling the genetic complexity of common diseases suggests that susceptibility is due to numerous genetic factors with modest effects. In this context, the study of isolated populations with negligible migration will continue to be important, because the relative genetic (and often environmental) homogeneity may result in less complex underlying models of susceptibility. In such studies, however, limited sample sizes can be a serious problem. Making use of all affected individuals, not only those for whom parents are available (as in the TDT), will increase the power to detect susceptibility loci. However, to use case-control association tests, rather than family-based association tests, one needs to correct for the relatedness among individuals. In populations with known genealogy, it is preferable to use this information. This is the rationale for developing the QLS test described in the present article. Indeed, making use of the quasi-likelihood framework, we were able to derive a valid test for allelic association in the presence of strong but known correlations among alleles. We showed that this approach may be more powerful than simply correcting the variance of the χ² test under certain conditions and is asymptotically the locally most powerful test in a general class of linear tests. Furthermore, we detected a highly significant association by use of this test.

Recent attempts to correct association tests either for unknown population stratification and cryptic relatedness (Devlin and Roeder 1999) or for the sampling of related subjects in outbred populations (Slager and Schaid 2001) used the Armitage trend test (Armitage 1955), which is genotype based rather than allele based. Indeed, as shown by Sasieni (1997) and further explored by Devlin and Roeder (1999), both the Armitage trend test and the allele-based test contrast allelic frequencies between cases and controls, while considering an additive effect for alleles. In addition, the Armitage trend test corrects for possible departure from Hardy-Weinberg equilibrium in the sample, whereas the allelic test does not. Apart from genotyping errors, departures from Hardy-Weinberg equilibrium in isolated populations such as the Hutterites are mainly due to nonnegligible inbreeding (Bourgain et al. 2002). The QLS test presented here, which is performed conditional on the pedigree structure and explicitly models inbreeding, is thus likely to be a correct test for allelic association even though it is performed at the level of alleles rather than genotypes. We showed how the QLS test may also be used in outbred populations when relatives of any kind are sampled. We should stress that, for this approach to be correct in outbred pedigrees, no departure from Hardy-Weinberg equilibrium should be observed at the loci under study. We did not compare the power of the Slager and Schaid (2001) approach with ours, because we focused on pedigrees that are too complex to be handled by their method. We believe that in simpler pedigrees the Slager and Schaid (2001) approach might perform better than the corrected χ² test presented here, because the former method uses a corrected variance, computed conditional on the IBD information obtained from the pedigree data, whereas our method uses an unconditional corrected variance (exact computation of the conditional variance is infeasible in complex pedigrees). With regard to the comparison between the corrected χ² test and the QLS test in small pedigrees, it is not obvious which test would be more powerful. The outcome might depend on the kind of correlations among the individuals in the sample, as well as on the informativeness of the markers used in the analysis. We note that, if desired, a QLS-type version of the Slager and Schaid (2001) approach could be performed, in small pedigrees, that should be more powerful than both our QLS approach and their approach.

The controversy as to whether case-control tests are preferable to family-based association tests has been ongoing for several years (Morton and Collins 1998; Risch and Teng 1998; McGinnis 2000). In the present article, we did not formally compare the power of the QLS test and the TDT. We note that the TDT can be expressed as a conditional-likelihood–score test (Clayton 1999), whereas our approach is an unconditional QLS test, which can be viewed as an approximation to the unconditional-likelihood–score test. The unconditional approach would be expected to perform better in the absence of confounding population substructure. However, the formal comparison of these two tests is not straightforward, because the QLS test is only an approximation to the unconditional-likelihood–score test. Furthermore, the correction for relatedness among individuals may be interpreted as a reduction of the effective sample size. Indeed, the weight associated with an allele in the W_QLS statistic decreases as the amount of relatedness of this allele with other alleles of the sample increases. The difference in effective sample size between the QLS test and the TDT is thus not as large as it might first appear. No general statement on power comparison can be made from our analysis of real data, because none of the genes investigated have been definitively established as risk factors for asthma, BHR, or atopy. Nonetheless, no associations were detected by the TDT that were not detected by the QLS test, and, in each case, the association signal was stronger when the QLS test was used. A number of quite significant associations would have been missed if we used only the TDT.

The most significant association among the 48 markers examined in the present study was between a polymorphism at amino acid 640 (Val→Leu) in SELP and atopy, detected by the QLS test (P=.000002) and the TDT (P=.0014). Although associations between polymorphisms in SELP and asthma-related phenotypes have not been reported previously, P-selectin is an outstanding functional candidate. Indeed, P-selectin is an adhesion molecule expressed on the surface of activated platelets and endothelial cells. It contributes to both bronchoconstriction and inflammation in murine models of allergic airway reactivity (Lukacs et al. 2002). The results of this study indicate that the common Val630 allele is a risk allele for atopy. The other significant association observed in this study was between a promoter polymorphism in SCYA11 (−1328G→A) and BHR, detected by the corrected χ² test (P=.000383). The −1328A allele was significantly associated with BHR and with asthma (P=.00956), although the latter association likely reflects the fact that our definition of asthma included BHR. The SCYA11 gene encodes eotaxin, the predominant eosinophil chemoattractant involved in allergic inflammation. Another variant in the promoter region of this gene was associated with IgE level in patients with atopic dermatitis (AD) but not with AD itself or asthma (Tsunemi et al. 2002). Thus, variation in this gene may influence a variety of atopic phenotypes. Other novel associations identified in the present study are between asthma and the 880G allele in the 3′ UTR of SDF1 and between atopy and the 102Gly allele in C3. These genes are both good functional candidates for asthma-related phenotypes. SDF1 encodes a small chemokine (C-K-C motif) that is a highly potent lymphocyte chemoattractant and is the principal ligand for CXCR4, which is also a coreceptor for CD4. Furthermore, the 3′ UTR polymorphism investigated in this study has been associated with delayed progression to AIDS (Winkler et al. 1998), suggesting that its role as a viral receptor might influence asthma susceptibility. C3 deficiency in an allergen-induced model of airway allergy was associated with diminished airway responsiveness and lung eosinophilia (Drouin et al. 2001). Thus, variation in this gene may influence allergic responses, as indicated by our study. Most of the remaining associations detected in the present study, including many of the more modest associations, have been reported elsewhere for the same or related phenotypes (Genetic Association Database.

Finally, we believe that the two tests presented here are not only of general interest for studies involving related individuals but may also be particularly interesting tools to take full advantage of founder populations for gene mapping of complex traits.

Appendix A : Expression of W_QLS in the Multiallelic Case

Notation: Given the n×m matrix A with (i,j)th element a_ij and the p×q matrix B with (i,j)th element b_ij, their Kronecker product, denoted A⊗B, is the np×mq matrix with block structure

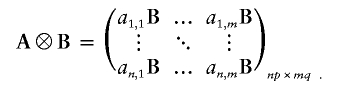Consider a locus with a distinct alleles. Define p=(p₁,…p_a-1)^T as the (a-1)-vector of control allele frequencies, and define r=(r₁,…r_a-1)^T as the (a-1)-vector of differences in allele frequencies between cases and controls. Our model stipulates that under the null hypothesis, r=r₀=0, in which case we obtain E₀(Y)=μ₀=p⊗D_p and 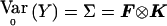with K defined in eq. (1) and F defined in eq. (6). Our model for the alternative hypothesis specifies E(Y)=μ=p⊗D_p+r⊗D_r, and, as in the biallelic case, we allow Var(Y)=Ω to depend on both r and p, provided that, when r=0, Ω=Σ and that Ω be differentiable and invertible. Let D_π=∂μ/∂p and D_ρ=∂μ/∂r. D_π and D_ρ are N(a-1)×(a-1) matrices with the kth column equal to ∂μ/∂p_k and ∂μ/∂r_k, respectively. Then D_π=I_a-1⊗D_p and D_ρ=I_a-1⊗D_r, where I_a-1 is the identity matrix of dimension (a-1). U_r(r₀,p)=D^T_ρΣ^-1(Y-μ₀) becomes U_r(r₀,p)=(I_a-1⊗D_r)^T(F⊗K)^-1(Y-p⊗D_p). From the properties of the Kronecker product (e.g., see Schott 1996), it follows that 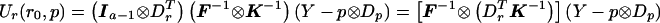and .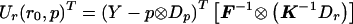

Similarly, 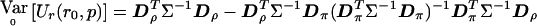becomes 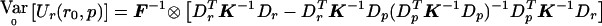. Then, evaluating 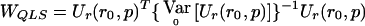at 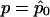(the quasi-likelihood estimator of p when r=r₀), we get

where 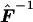corresponds to matrix F^-1 evaluated at 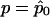. Eq. (7) is easily derived from the latter expression of W_QLS.

Appendix B : General Framework for the QLS and the χ² Test in the Multiallelic Case

In the multiallelic case, using the framework presented in appendix A, we note that 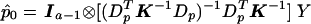. Define V_QLS=I_a-1⊗V₁ with V₁ given in the text and let S_QLS=V^T_QLSY. We note that 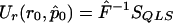. We have 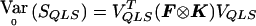. Because p is unknown, we evaluate 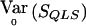at 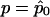to obtain . Then 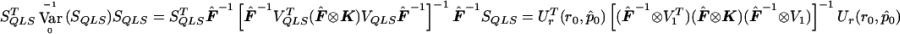. Note that 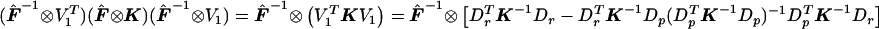, which matches the formula for 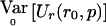given in appendix A once 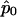is substituted in for p. Thus, .

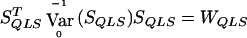A possible expression for the classical χ² test for case-control association in the biallelic case is

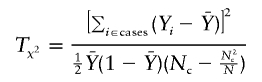with 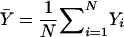. We note that T_χ² may also be written

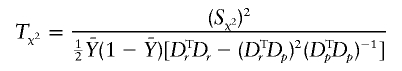with S_χ²=[D^T_r-(D^T_rD_p)(D^T_pD_p)^-1D^T_p]Y=V^T₂Y. When the correlations among all the individuals as well as between the two alleles of an individual are zero then the variance of Y when r=r₀ is 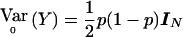where I_N is the N×N identity matrix. Thus, 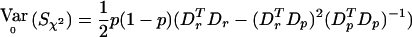. If 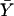is used as an estimator of p to compute 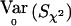, then

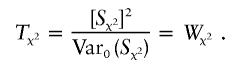Similarly, in the multiallelic case, 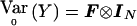. Thus, S_χ²=V^T_χ²Y with V_χ²=I_a-1⊗V₂ and 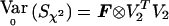. Finally,

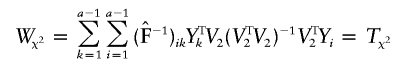Appendix C : Proof That the QLS Test Is Asymptotically the Locally Most Powerful Test of the W Class

We focus here on the biallelic situation. Consider the statistics of the W class described in the text, that is, 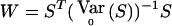with S=V^TY, V≠0 and known, E₀(S)=0. Under the alternative hypothesis, E_H1(Y)=pD_p+rD_r. Under the null hypothesis, r=0. E₀(S)=0 implies that pV^TD_p=0, which must hold for any p, so that V^TD_p=0. As described in the text, 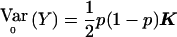, where K is the correlation matrix described in eq. (1). Thus, 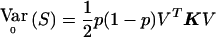and

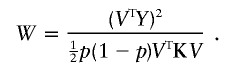If we assume that W has a χ² distribution under the null hypothesis and a noncentral χ² distribution with noncentrality parameter λ under local alternatives, the locally most powerful statistic of this class is the one maximizing the value of λ over all V≠0, such that V^TD_p=0. By definition 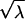is the expectation of 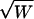under the alternative hypothesis; thus,

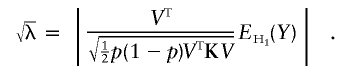In practice, p is a nuisance parameter, and we use its estimator 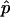. Under certain regularity conditions, this is asymptotically equivalent to the case in which the true p is used. In what follows, we use the true value of p and will thus derive the asymptotic value of λ:

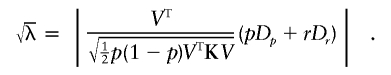Maximizing λ is thus equivalent to maximizing

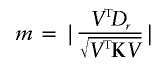over all V≠0, such that V^TD_p=0.

We first consider a modified version of the problem by maximizing

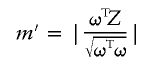over all ω≠0 such that ω^TR=0 with Z and R being N-vectors and R≠0. By definition, |ω^TZ|=|ω||Z||cos(θ_(ω,Z))|, where θ_(ω,Z) is the angle between ω and Z. Thus, m^′=|Z||cos(θ_(ω,Z))|, and we need only to maximize cos(θ_(ω,Z)) over all ω≠0 subject to ω^TR=0. By geometry, the maximizing ω, ω_max, is any scalar multiple of the projection of Z onto the subspace orthogonal to R. Thus, ω_max∝(I_N-R(R^TR)^-1R^T)Z, where I_N is the N×N identity matrix (e.g., see Schott 1996).

We consider now the initial problem. K being symmetric positive definite, we can derive its Cholesky decomposition K=C^TC, where C is an invertible upper triangular matrix. Define ω by ω=CV. Because C is invertible, V≠0⇔ω≠0. Furthermore, V^TD_p=0⇔ω^TC^-TD_p=0, and we have

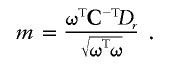Define R=C^-TD_p and Z=C^-TD_r. We get from the previous modified version of the problem that

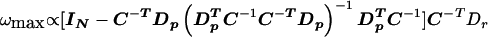and the corresponding V is

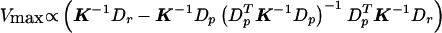. Note that V_max∝V_QLS so that

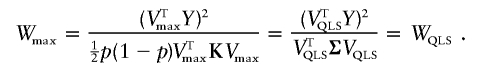It follows that, when p is known, the noncentrality parameter for W_QLS is larger than that for any other statistic in the W class. When p is unknown, we argue that replacement of p by

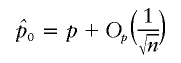makes W_QLS asymptotically the locally most powerful test in the W class. Note that all our data are correlated with an n×n correlation matrix K. Thus, whether or not we have (i) W asymptotically χ² under the null and (ii) noncentral χ² for local alternatives and (iii)

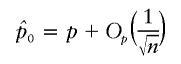for local alternatives, will depend on assumptions about how K behaves as n→∞. Subject to regularity conditions on K ensuring that statements (i), (ii), and (iii) hold, then W_QLS will be asymptotically the locally most powerful test in the W class.