Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 1997 Jul;73(1):306–317. doi: 10.1016/S0006-3495(97)78071-8

Analysis of birefringence decay profiles for nucleic acid helices possessing bends: the tau-ratio approach.

E Vacano 1, P J Hagerman 1
PMCID: PMC1180932  PMID: 9199795

Abstract

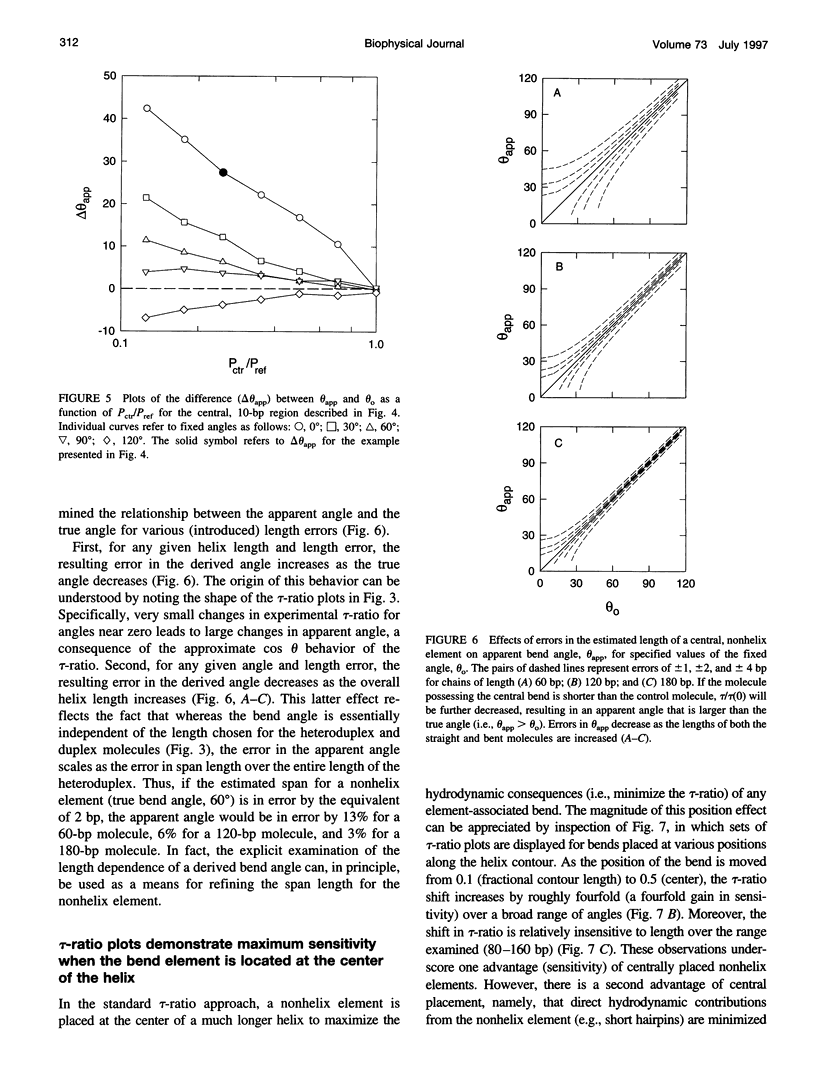
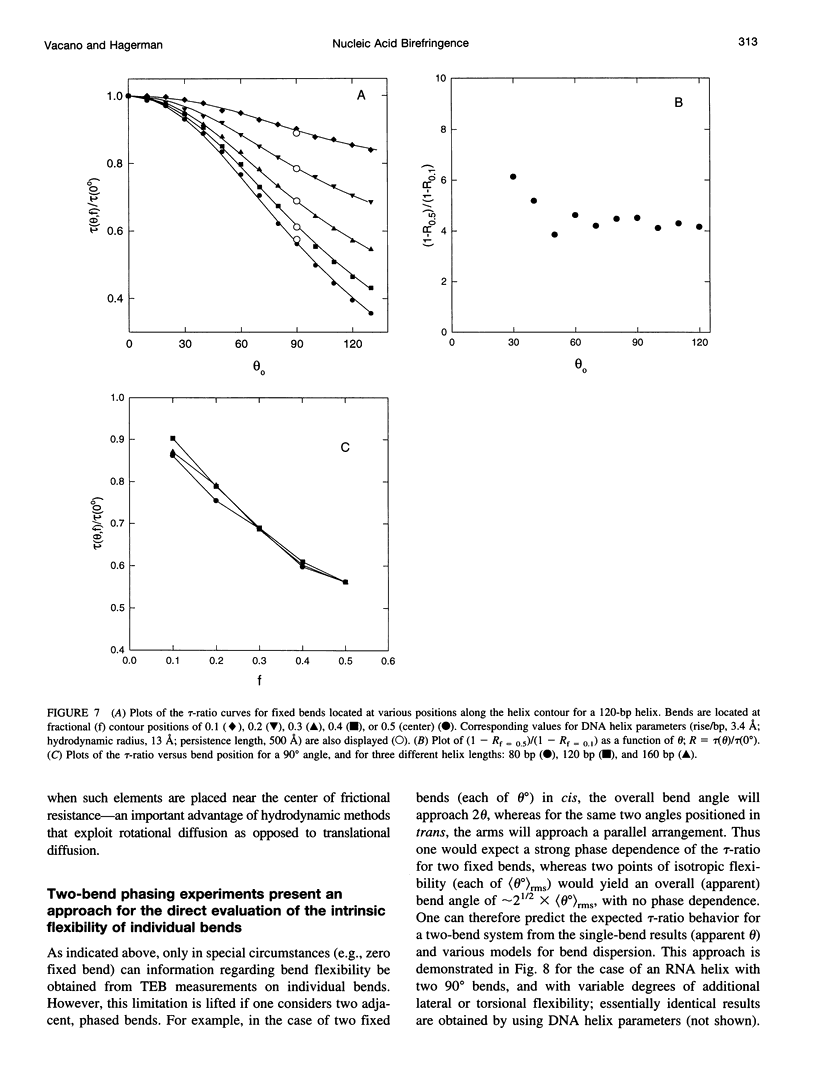
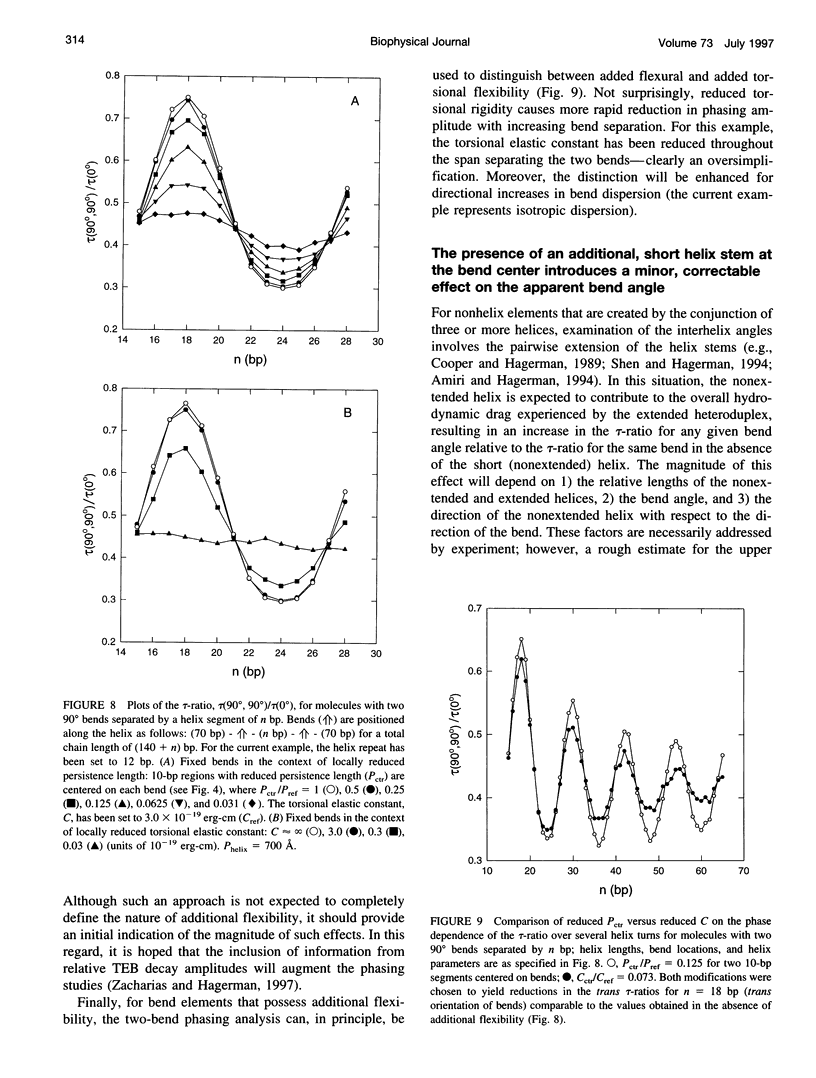
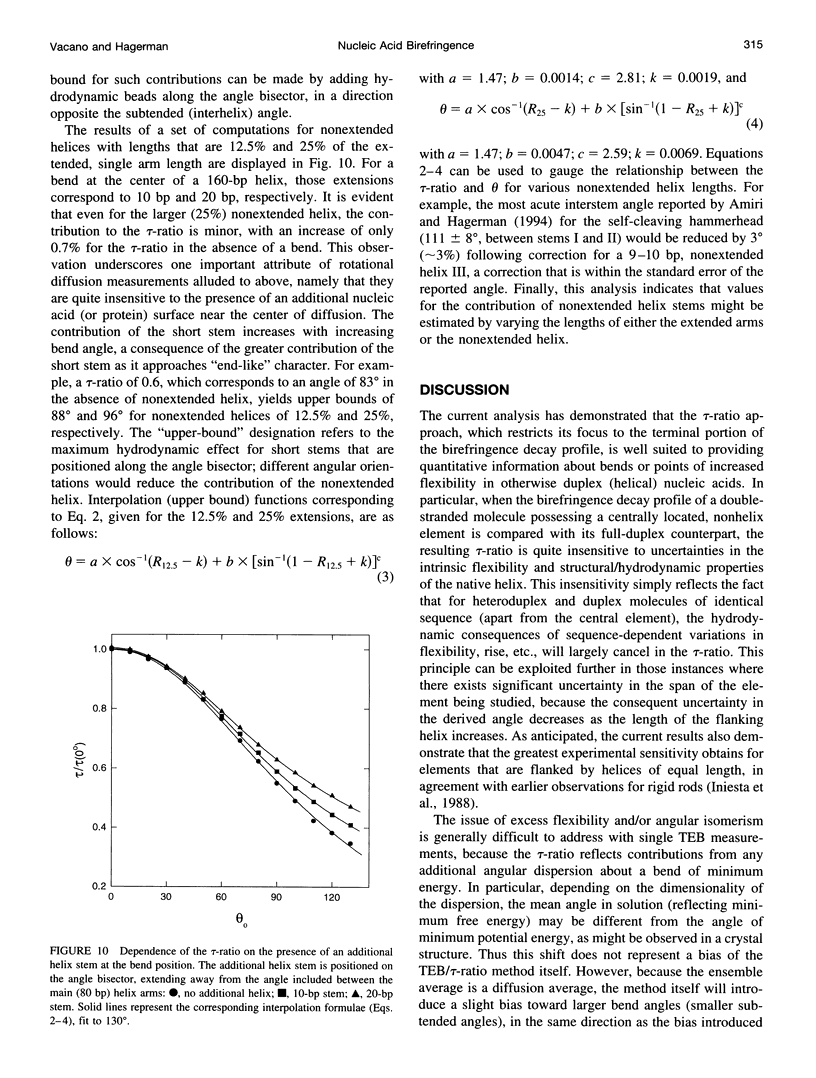
For nucleic acid helices in the 100-200-bp range, a central bend or point of flexibility increases the rate of rotational diffusion. In a transient electric birefringence (TEB) experiment, this increase is manifest as a reduction in the terminal (slowest) birefringence decay time. Previous experimental and theoretical work has demonstrated that the ratio of the decay times for a bent/flexible molecule and its fully duplex (linear) counterpart represents a sensitive, quantifiable measure of the apparent bend angle (tau-ratio approach). In the current work, we have examined the influence of helix parameters (e.g., persistence length, helix rise, diameter) on the tau-ratio for a given bend. The tau-ratio is found to be remarkably insensitive to variations and/or uncertainties in the helix parameters, provided that one employs bent and control molecules with the same sequence and length (apart from the bend itself). Although a single tau-ratio determination normally does not enable one to distinguish between fixed and flexible bends, such a distinction can be made from a set of tau-ratios for molecules possessing two variably phased bends. A number of additional uncertainties are examined, including errors in the estimation of the dimensions of nonhelix elements that are responsible for bends; such errors can, in principle, be estimated by performing a series of measurements for molecules of varying length.

Full text

PDF
306

Images in this article

307FIGURE 1
on p.307

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Amiri K. M., Hagerman P. J. Global conformation of a self-cleaving hammerhead RNA. Biochemistry. 1994 Nov 15;33(45):13172–13177. doi: 10.1021/bi00249a003. [DOI] [PubMed] [Google Scholar]
  2. Charney E. Electric linear dichroism and birefringence of biological polyelectrolytes. Q Rev Biophys. 1988 Feb;21(1):1–60. doi: 10.1017/s0033583500005011. [DOI] [PubMed] [Google Scholar]
  3. Cooper J. P., Hagerman P. J. Geometry of a branched DNA structure in solution. Proc Natl Acad Sci U S A. 1989 Oct;86(19):7336–7340. doi: 10.1073/pnas.86.19.7336. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Diekmann S., Hillen W., Jung M., Wells R. D., Pörschke D. Electric properties and structure of DNA-restriction fragments from measurements of the electric dichroism. Biophys Chem. 1982 May;15(2):157–167. doi: 10.1016/0301-4622(82)80028-8. [DOI] [PubMed] [Google Scholar]
  5. Friederich M. W., Gast F. U., Vacano E., Hagerman P. J. Determination of the angle between the anticodon and aminoacyl acceptor stems of yeast phenylalanyl tRNA in solution. Proc Natl Acad Sci U S A. 1995 May 23;92(11):4803–4807. doi: 10.1073/pnas.92.11.4803. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Garcia de la Torre J. G., Bloomfield V. A. Hydrodynamic properties of complex, rigid, biological macromolecules: theory and applications. Q Rev Biophys. 1981 Feb;14(1):81–139. doi: 10.1017/s0033583500002080. [DOI] [PubMed] [Google Scholar]
  7. García Molina J. J., López Martínez M. C., García de la Torre J. Computer simulation of hydrodynamic properties of semiflexible macromolecules: randomly broken chains, wormlike chains, and analysis of properties of DNA. Biopolymers. 1990 May-Jun;29(6-7):883–900. doi: 10.1002/bip.360290603. [DOI] [PubMed] [Google Scholar]
  8. García de la Torre J., Bloomfield V. A. Conformation of myosin in dilute solution as estimated from hydrodynamic properties. Biochemistry. 1980 Oct 28;19(22):5118–5123. doi: 10.1021/bi00563a028. [DOI] [PubMed] [Google Scholar]
  9. García de la Torre J., Mellado P., Rodes V. Diffusion coefficients of segmentally flexible macromolecules with two spherical subunits. Biopolymers. 1985 Nov;24(11):2145–2164. doi: 10.1002/bip.360241110. [DOI] [PubMed] [Google Scholar]
  10. Hagerman P. J. Evidence for the existence of stable curvature of DNA in solution. Proc Natl Acad Sci U S A. 1984 Aug;81(15):4632–4636. doi: 10.1073/pnas.81.15.4632. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hagerman P. J. Flexibility of DNA. Annu Rev Biophys Biophys Chem. 1988;17:265–286. doi: 10.1146/annurev.bb.17.060188.001405. [DOI] [PubMed] [Google Scholar]
  12. Hagerman P. J., Ramadevi V. A. Application of the method of phage T4 DNA ligase-catalyzed ring-closure to the study of DNA structure. I. Computational analysis. J Mol Biol. 1990 Mar 20;212(2):351–362. doi: 10.1016/0022-2836(90)90130-E. [DOI] [PubMed] [Google Scholar]
  13. Hagerman P. J. Sometimes a great motion: the application of transient electric birefringence to the study of macromolecular structure. Curr Opin Struct Biol. 1996 Oct;6(5):643–649. doi: 10.1016/s0959-440x(96)80031-5. [DOI] [PubMed] [Google Scholar]
  14. Highsmith S., Kretzschmar K. M., O'Konski C. T., Morales M. F. Flexibility of myosin rod, light meromyosin, and myosin subfragment-2 in solution. Proc Natl Acad Sci U S A. 1977 Nov;74(11):4986–4990. doi: 10.1073/pnas.74.11.4986. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Highsmith S., Wang C. C., Zero K., Pecora R., Jardetzky O. Bending motions and internal motions in myosin rod. Biochemistry. 1982 Mar 16;21(6):1192–1197. doi: 10.1021/bi00535a013. [DOI] [PubMed] [Google Scholar]
  16. Iniesta A., Díaz F. G., García de la Torre J. Transport properties of rigid bent-rod macromolecules and of semiflexible broken rods in the rigid-body treatment. Analysis of the flexibility of myosin rod. Biophys J. 1988 Aug;54(2):269–275. doi: 10.1016/S0006-3495(88)82956-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kebbekus P., Draper D. E., Hagerman P. Persistence length of RNA. Biochemistry. 1995 Apr 4;34(13):4354–4357. doi: 10.1021/bi00013a026. [DOI] [PubMed] [Google Scholar]
  18. Leehey M. A., Squassoni C. A., Friederich M. W., Mills J. B., Hagerman P. J. A noncanonical tertiary conformation of a human mitochondrial transfer RNA. Biochemistry. 1995 Dec 19;34(50):16235–16239. doi: 10.1021/bi00050a001. [DOI] [PubMed] [Google Scholar]
  19. Levene S. D., Wu H. M., Crothers D. M. Bending and flexibility of kinetoplast DNA. Biochemistry. 1986 Jul 15;25(14):3988–3995. doi: 10.1021/bi00362a003. [DOI] [PubMed] [Google Scholar]
  20. Mellado P., Iniesta A., Diaz F. G., García de la Torre J. Diffusion coefficients of segmentally flexible macromolecules with two subunits: a study of broken rods. Biopolymers. 1988 Nov;27(11):1771–1786. doi: 10.1002/bip.360271107. [DOI] [PubMed] [Google Scholar]
  21. Schellman J. A. Flexibility of DNA. Biopolymers. 1974 Jan;13(1):217–226. doi: 10.1002/bip.1974.360130115. [DOI] [PubMed] [Google Scholar]
  22. Shen Z., Hagerman P. J. Conformation of the central, three-helix junction of the 5 S ribosomal RNA of Sulfolobus acidocaldarius. J Mol Biol. 1994 Aug 19;241(3):415–430. doi: 10.1006/jmbi.1994.1517. [DOI] [PubMed] [Google Scholar]
  23. Stellwagen N. C. Transient electric birefringence of two small DNA restriction fragments of the same molecular weight. Biopolymers. 1991 Nov;31(13):1651–1667. doi: 10.1002/bip.360311318. [DOI] [PubMed] [Google Scholar]
  24. Taylor W. H., Hagerman P. J. Application of the method of phage T4 DNA ligase-catalyzed ring-closure to the study of DNA structure. II. NaCl-dependence of DNA flexibility and helical repeat. J Mol Biol. 1990 Mar 20;212(2):363–376. doi: 10.1016/0022-2836(90)90131-5. [DOI] [PubMed] [Google Scholar]
  25. Zacharias M., Hagerman P. J. Bulge-induced bends in RNA: quantification by transient electric birefringence. J Mol Biol. 1995 Mar 31;247(3):486–500. doi: 10.1006/jmbi.1995.0155. [DOI] [PubMed] [Google Scholar]
  26. Zacharias M., Hagerman P. J. Influence of static and dynamic bends on the birefringence decay profile of RNA helices: Brownian dynamics simulations. Biophys J. 1997 Jul;73(1):318–332. doi: 10.1016/S0006-3495(97)78072-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Zacharias M., Hagerman P. J. The bend in RNA created by the trans-activation response element bulge of human immunodeficiency virus is straightened by arginine and by Tat-derived peptide. Proc Natl Acad Sci U S A. 1995 Jun 20;92(13):6052–6056. doi: 10.1073/pnas.92.13.6052. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Zacharias M., Hagerman P. J. The influence of symmetric internal loops on the flexibility of RNA. J Mol Biol. 1996 Mar 29;257(2):276–289. doi: 10.1006/jmbi.1996.0162. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES