Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 1997 Sep;73(3):1337–1354. doi: 10.1016/S0006-3495(97)78167-0

Permeation through the calcium release channel of cardiac muscle.

D Chen 1, L Xu 1, A Tripathy 1, G Meissner 1, B Eisenberg 1
PMCID: PMC1181034  PMID: 9284302

Abstract

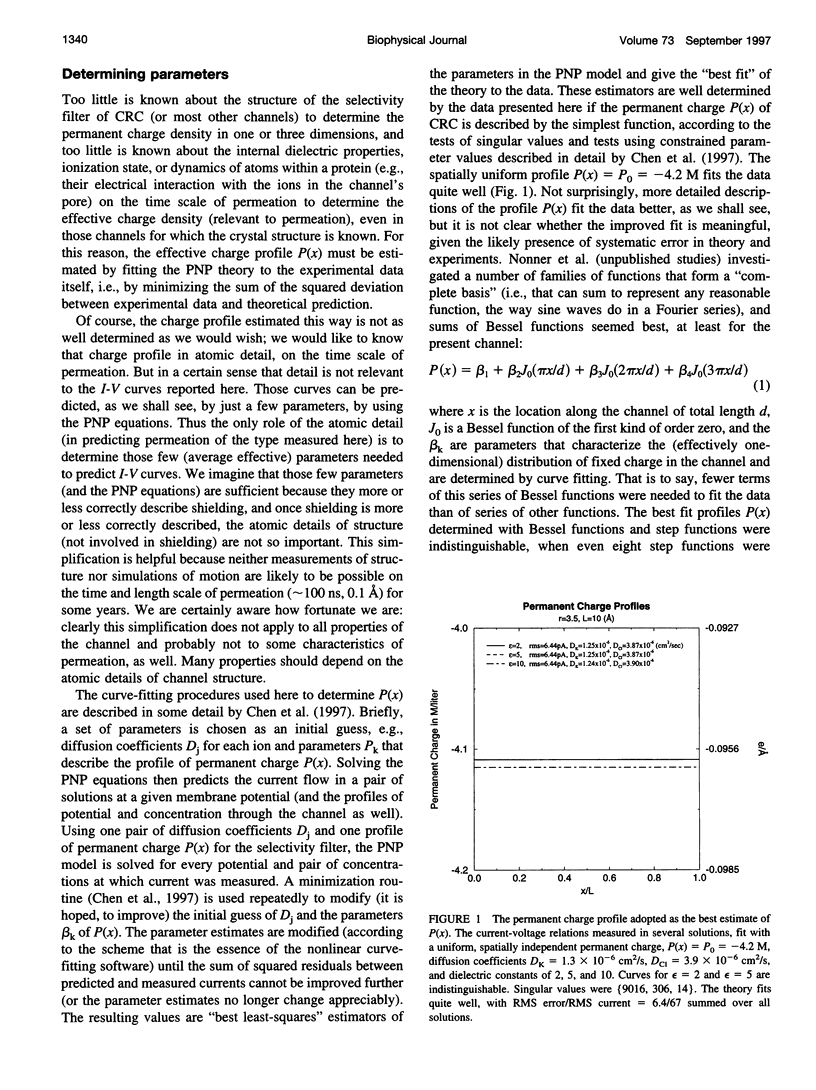
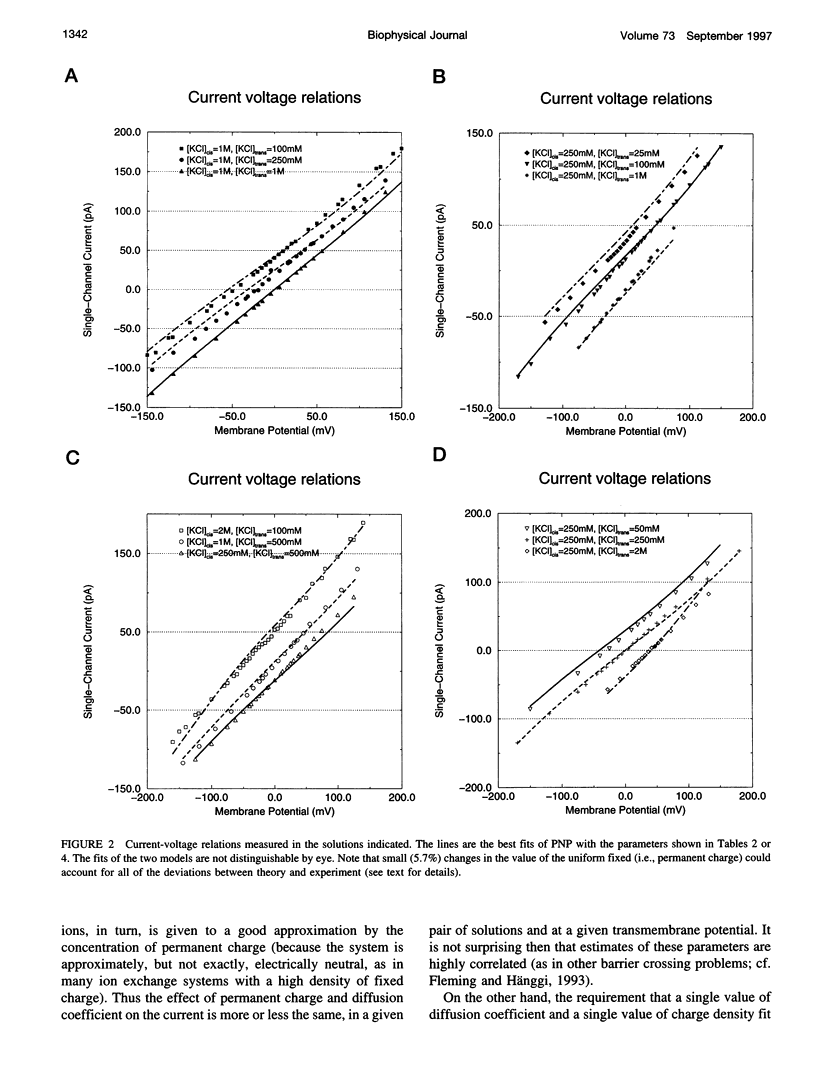
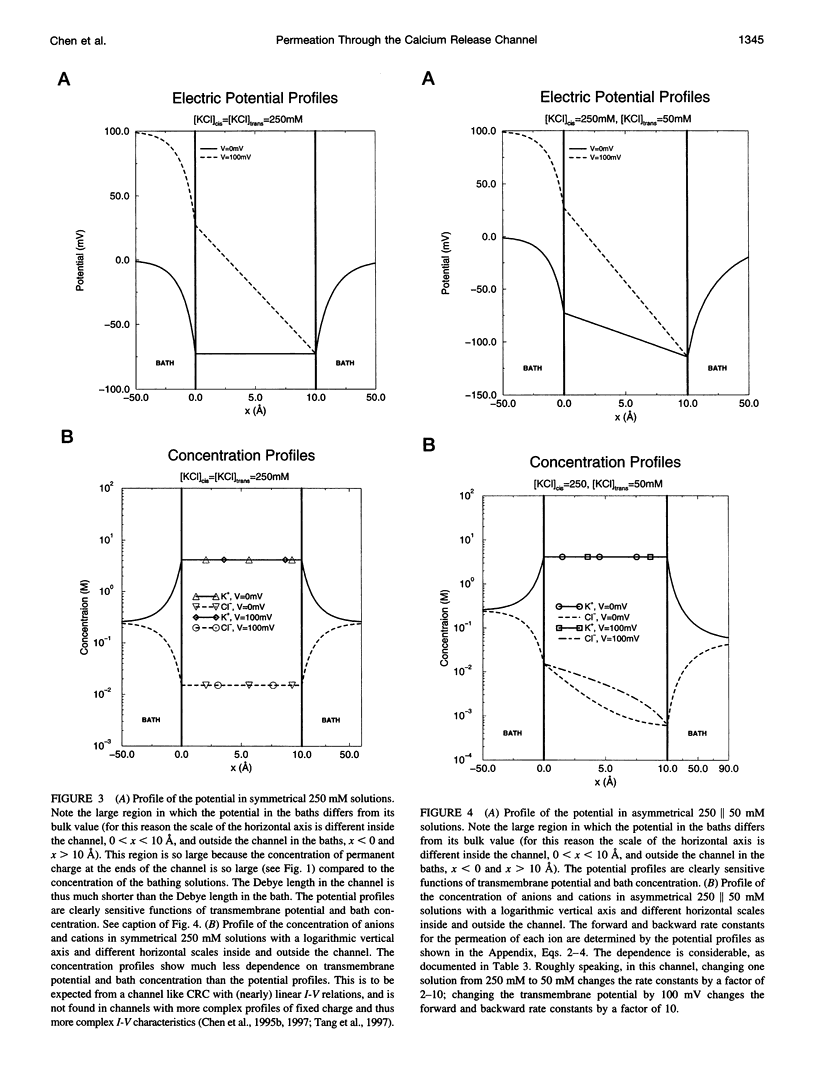
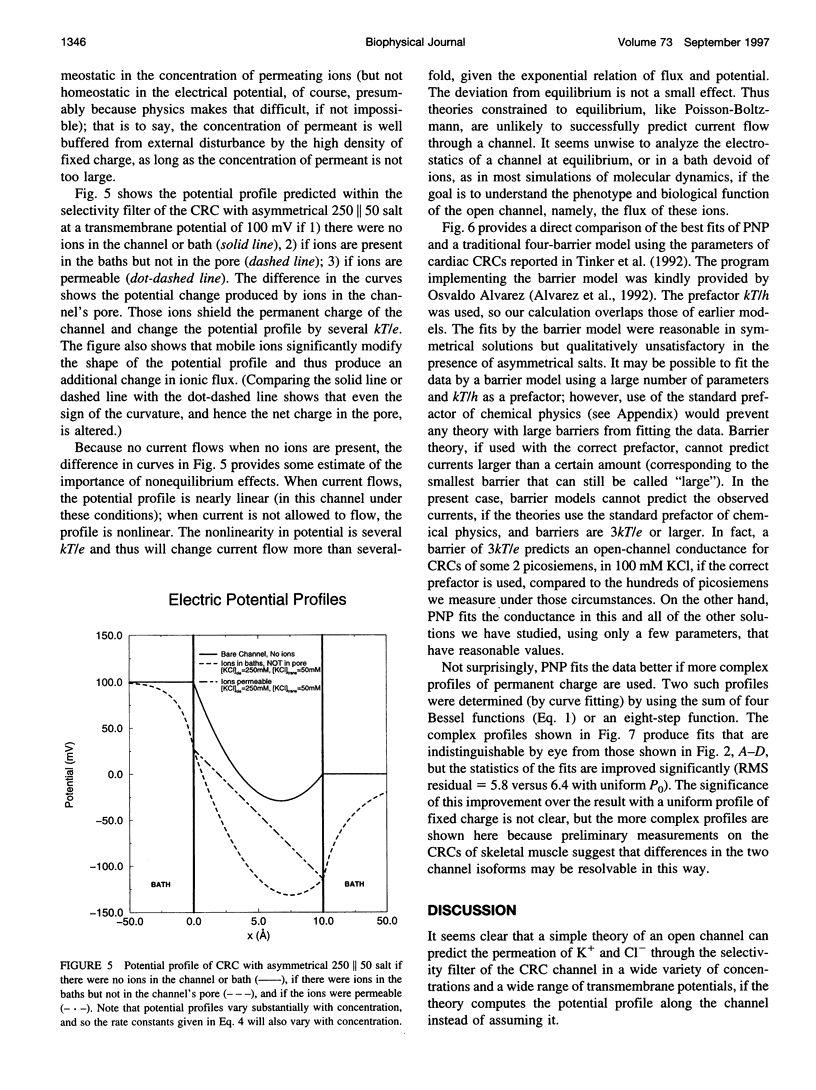
Current voltage (I-V) relations were measured from the calcium release channel (CRC) of the sarcoplasmic reticulum of cardiac muscle in 12 KCl solutions, symmetrical and asymmetrical, from 25 mM to 2 M. I-V curves are nearly linear, in the voltage range +/- 150 mV approximately 12kT/e, even in asymmetrical solutions, e.g., 2 M // 100 mM. It is awkward to describe straight lines as sums of exponentials in a wide range of solutions and potentials, and so traditional barrier models have difficulty fitting this data. Diffusion theories with constant fields predict curvilinear I-V relations, and so they are also unsatisfactory. The Poisson and Nernst-Planck equations (PNP) form a diffusion theory with variable fields. They fit the data by using adjustable parameters for the diffusion constant of each ion and for the effective density of fixed (i.e., permanent) charge P(x) along the channel's "filter" (7-A diameter, 10 A long). If P(x) is described by just one parameter, independent of x (i.e., P(x) = P0 = -4.2 M), the fits are satisfactory (RMS error/RMS current = 6.4/67), and the estimates of diffusion coefficients are reasonable D(K) = 1.3 x 10(-6) cm2/s, D(Cl) = 3.9 x 10(-6) cm2/s. The CRC seems to have a small selectivity filter with a very high density of permanent charge. This may be a design principle of channels specialized for large flux. The Appendix derives barrier models, and their prefactor, from diffusion theories (with variable fields) and argues that barrier models are poor descriptions of CRCs in particular and open channels in general.

Full text

PDF
1337

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Alvarez O., Villarroel A., Eisenman G. Calculation of ion currents from energy profiles and energy profiles from ion currents in multibarrier, multisite, multioccupancy channel model. Methods Enzymol. 1992;207:816–854. doi: 10.1016/0076-6879(92)07058-v. [DOI] [PubMed] [Google Scholar]
  2. Andersen O. S., Koeppe R. E., 2nd Molecular determinants of channel function. Physiol Rev. 1992 Oct;72(4 Suppl):S89–158. doi: 10.1152/physrev.1992.72.suppl_4.S89. [DOI] [PubMed] [Google Scholar]
  3. Barkai E, Eisenberg RS, Schuss Z. Bidirectional shot noise in a singly occupied channel. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1996 Aug;54(2):1161–1175. doi: 10.1103/physreve.54.1161. [DOI] [PubMed] [Google Scholar]
  4. Bek S., Jakobsson E. Brownian dynamics study of a multiply-occupied cation channel: application to understanding permeation in potassium channels. Biophys J. 1994 Apr;66(4):1028–1038. doi: 10.1016/S0006-3495(94)80884-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chen D. P., Barcilon V., Eisenberg R. S. Constant fields and constant gradients in open ionic channels. Biophys J. 1992 May;61(5):1372–1393. doi: 10.1016/S0006-3495(92)81944-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chen D. P., Eisenberg R. S. Flux, coupling, and selectivity in ionic channels of one conformation. Biophys J. 1993 Aug;65(2):727–746. doi: 10.1016/S0006-3495(93)81099-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chen D. P., Eisenberg R. S., Jerome J. W., Shu C. W. Hydrodynamic model of temperature change in open ionic channels. Biophys J. 1995 Dec;69(6):2304–2322. doi: 10.1016/S0006-3495(95)80101-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chen D., Eisenberg R. Charges, currents, and potentials in ionic channels of one conformation. Biophys J. 1993 May;64(5):1405–1421. doi: 10.1016/S0006-3495(93)81507-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chen D., Lear J., Eisenberg B. Permeation through an open channel: Poisson-Nernst-Planck theory of a synthetic ionic channel. Biophys J. 1997 Jan;72(1):97–116. doi: 10.1016/S0006-3495(97)78650-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chiu S. W., Jakobsson E. Stochastic theory of singly occupied ion channels. II. Effects of access resistance and potential gradients extending into the bath. Biophys J. 1989 Jan;55(1):147–157. doi: 10.1016/S0006-3495(89)82786-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cooper K. E., Gates P. Y., Eisenberg R. S. Diffusion theory and discrete rate constants in ion permeation. J Membr Biol. 1988 Dec;106(2):95–105. doi: 10.1007/BF01871391. [DOI] [PubMed] [Google Scholar]
  12. Cooper K. E., Gates P. Y., Eisenberg R. S. Surmounting barriers in ionic channels. Q Rev Biophys. 1988 Aug;21(3):331–364. doi: 10.1017/s0033583500004480. [DOI] [PubMed] [Google Scholar]
  13. Cooper K., Jakobsson E., Wolynes P. The theory of ion transport through membrane channels. Prog Biophys Mol Biol. 1985;46(1):51–96. doi: 10.1016/0079-6107(85)90012-4. [DOI] [PubMed] [Google Scholar]
  14. Coronado R., Morrissette J., Sukhareva M., Vaughan D. M. Structure and function of ryanodine receptors. Am J Physiol. 1994 Jun;266(6 Pt 1):C1485–C1504. doi: 10.1152/ajpcell.1994.266.6.C1485. [DOI] [PubMed] [Google Scholar]
  15. Crouzy S., Woolf T. B., Roux B. A molecular dynamics study of gating in dioxolane-linked gramicidin A channels. Biophys J. 1994 Oct;67(4):1370–1386. doi: 10.1016/S0006-3495(94)80618-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Dani J. A., Levitt D. G. Water transport and ion-water interaction in the gramicidin channel. Biophys J. 1981 Aug;35(2):501–508. doi: 10.1016/S0006-3495(81)84805-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Eisenberg R. S. Channels as enzymes. J Membr Biol. 1990 Apr;115(1):1–12. doi: 10.1007/BF01869101. [DOI] [PubMed] [Google Scholar]
  18. Eisenberg R. S. Computing the field in proteins and channels. J Membr Biol. 1996 Mar;150(1):1–25. doi: 10.1007/s002329900026. [DOI] [PubMed] [Google Scholar]
  19. Eisenman G., Horn R. Ionic selectivity revisited: the role of kinetic and equilibrium processes in ion permeation through channels. J Membr Biol. 1983;76(3):197–225. doi: 10.1007/BF01870364. [DOI] [PubMed] [Google Scholar]
  20. Fabiato A. Calcium-induced release of calcium from the cardiac sarcoplasmic reticulum. Am J Physiol. 1983 Jul;245(1):C1–14. doi: 10.1152/ajpcell.1983.245.1.C1. [DOI] [PubMed] [Google Scholar]
  21. Goldman D. E. POTENTIAL, IMPEDANCE, AND RECTIFICATION IN MEMBRANES. J Gen Physiol. 1943 Sep 20;27(1):37–60. doi: 10.1085/jgp.27.1.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. HODGKIN A. L., KATZ B. The effect of sodium ions on the electrical activity of giant axon of the squid. J Physiol. 1949 Mar 1;108(1):37–77. doi: 10.1113/jphysiol.1949.sp004310. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hille B. Ionic selectivity, saturation, and block in sodium channels. A four-barrier model. J Gen Physiol. 1975 Nov;66(5):535–560. doi: 10.1085/jgp.66.5.535. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hille B., Schwarz W. Potassium channels as multi-ion single-file pores. J Gen Physiol. 1978 Oct;72(4):409–442. doi: 10.1085/jgp.72.4.409. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Honig B., Nicholls A. Classical electrostatics in biology and chemistry. Science. 1995 May 26;268(5214):1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
  26. Levitt D. G. Comparison of Nernst-Planck and reaction rate models for multiply occupied channels. Biophys J. 1982 Mar;37(3):575–587. [PMC free article] [PubMed] [Google Scholar]
  27. Levitt D. G. Exact continuum solution for a channel that can be occupied by two ions. Biophys J. 1987 Sep;52(3):455–466. doi: 10.1016/S0006-3495(87)83234-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Levitt D. G. Interpretation of biological ion channel flux data--reaction-rate versus continuum theory. Annu Rev Biophys Biophys Chem. 1986;15:29–57. doi: 10.1146/annurev.bb.15.060186.000333. [DOI] [PubMed] [Google Scholar]
  29. McLaughlin S., Mulrine N., Gresalfi T., Vaio G., McLaughlin A. Adsorption of divalent cations to bilayer membranes containing phosphatidylserine. J Gen Physiol. 1981 Apr;77(4):445–473. doi: 10.1085/jgp.77.4.445. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. McLaughlin S. The electrostatic properties of membranes. Annu Rev Biophys Biophys Chem. 1989;18:113–136. doi: 10.1146/annurev.bb.18.060189.000553. [DOI] [PubMed] [Google Scholar]
  31. Meissner G. Ryanodine activation and inhibition of the Ca2+ release channel of sarcoplasmic reticulum. J Biol Chem. 1986 May 15;261(14):6300–6306. [PubMed] [Google Scholar]
  32. Meissner G. Ryanodine receptor/Ca2+ release channels and their regulation by endogenous effectors. Annu Rev Physiol. 1994;56:485–508. doi: 10.1146/annurev.ph.56.030194.002413. [DOI] [PubMed] [Google Scholar]
  33. Melzer W., Herrmann-Frank A., Lüttgau H. C. The role of Ca2+ ions in excitation-contraction coupling of skeletal muscle fibres. Biochim Biophys Acta. 1995 May 8;1241(1):59–116. doi: 10.1016/0304-4157(94)00014-5. [DOI] [PubMed] [Google Scholar]
  34. Ríos E., Pizarro G. Voltage sensor of excitation-contraction coupling in skeletal muscle. Physiol Rev. 1991 Jul;71(3):849–908. doi: 10.1152/physrev.1991.71.3.849. [DOI] [PubMed] [Google Scholar]
  35. Schneider M. F. Control of calcium release in functioning skeletal muscle fibers. Annu Rev Physiol. 1994;56:463–484. doi: 10.1146/annurev.ph.56.030194.002335. [DOI] [PubMed] [Google Scholar]
  36. Smith J. S., Imagawa T., Ma J., Fill M., Campbell K. P., Coronado R. Purified ryanodine receptor from rabbit skeletal muscle is the calcium-release channel of sarcoplasmic reticulum. J Gen Physiol. 1988 Jul;92(1):1–26. doi: 10.1085/jgp.92.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Tinker A., Lindsay A. R., Williams A. J. A model for ionic conduction in the ryanodine receptor channel of sheep cardiac muscle sarcoplasmic reticulum. J Gen Physiol. 1992 Sep;100(3):495–517. doi: 10.1085/jgp.100.3.495. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Tinker A., Williams A. J. Measuring the length of the pore of the sheep cardiac sarcoplasmic reticulum calcium-release channel using related trimethylammonium ions as molecular calipers. Biophys J. 1995 Jan;68(1):111–120. doi: 10.1016/S0006-3495(95)80165-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Tripathy A., Meissner G. Sarcoplasmic reticulum lumenal Ca2+ has access to cytosolic activation and inactivation sites of skeletal muscle Ca2+ release channel. Biophys J. 1996 Jun;70(6):2600–2615. doi: 10.1016/S0006-3495(96)79831-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Tu Q., Vélez P., Brodwick M., Fill M. Streaming potentials reveal a short ryanodine-sensitive selectivity filter in cardiac Ca2+ release channel. Biophys J. 1994 Dec;67(6):2280–2285. doi: 10.1016/S0006-3495(94)80713-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Warshel A., Russell S. T. Calculations of electrostatic interactions in biological systems and in solutions. Q Rev Biophys. 1984 Aug;17(3):283–422. doi: 10.1017/s0033583500005333. [DOI] [PubMed] [Google Scholar]
  42. Wier W. G. Cytoplasmic [Ca2+] in mammalian ventricle: dynamic control by cellular processes. Annu Rev Physiol. 1990;52:467–485. doi: 10.1146/annurev.ph.52.030190.002343. [DOI] [PubMed] [Google Scholar]
  43. Williams A. J. Ion conduction and discrimination in the sarcoplasmic reticulum ryanodine receptor/calcium-release channel. J Muscle Res Cell Motil. 1992 Feb;13(1):7–26. doi: 10.1007/BF01738423. [DOI] [PubMed] [Google Scholar]
  44. Xu L., Mann G., Meissner G. Regulation of cardiac Ca2+ release channel (ryanodine receptor) by Ca2+, H+, Mg2+, and adenine nucleotides under normal and simulated ischemic conditions. Circ Res. 1996 Dec;79(6):1100–1109. doi: 10.1161/01.res.79.6.1100. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES