Abstract
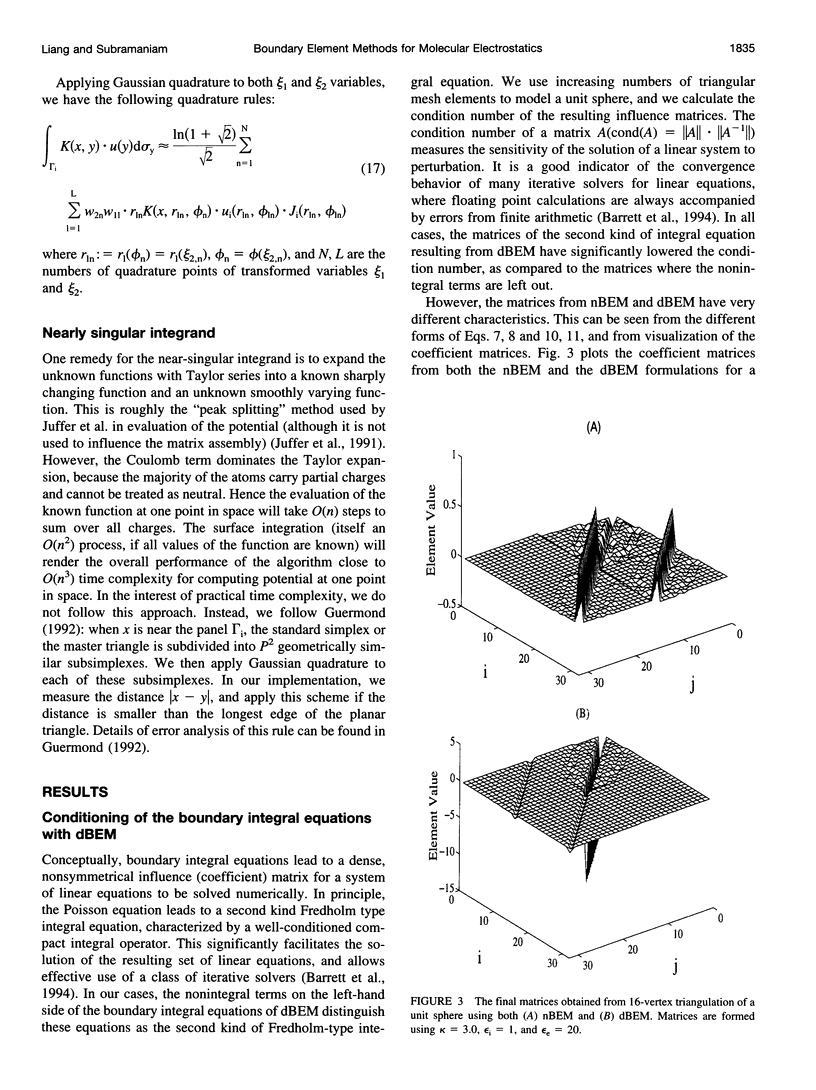
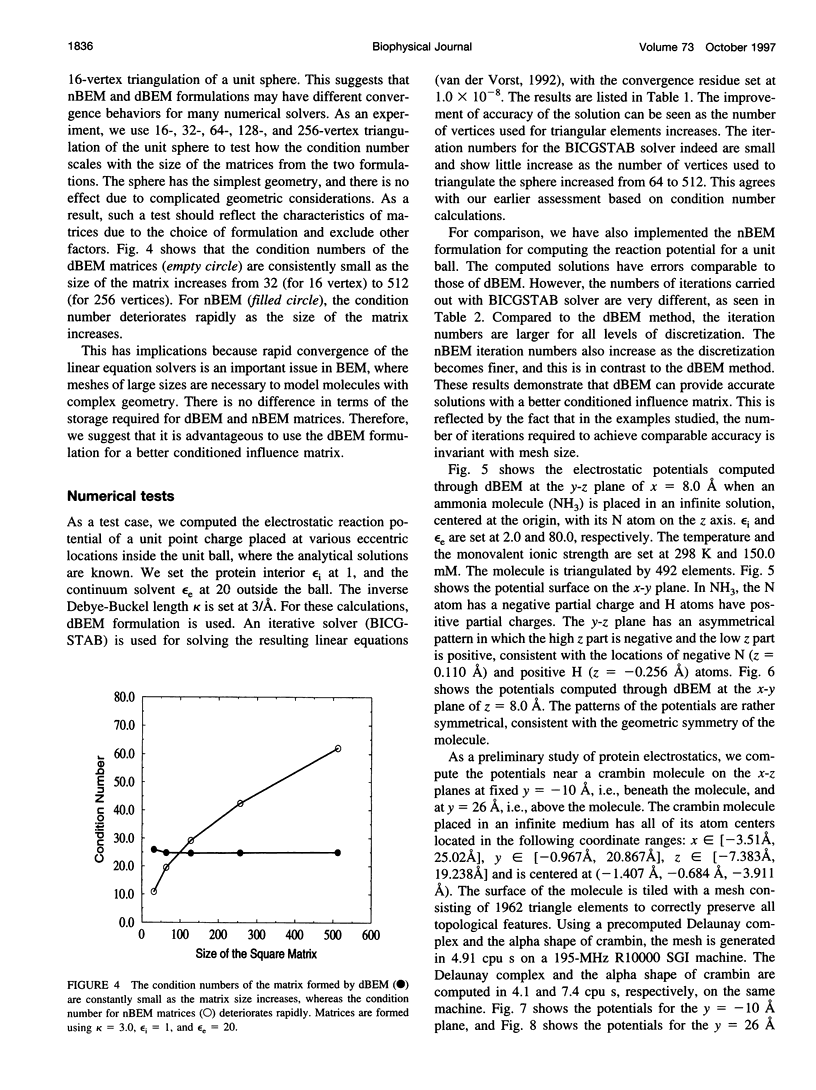
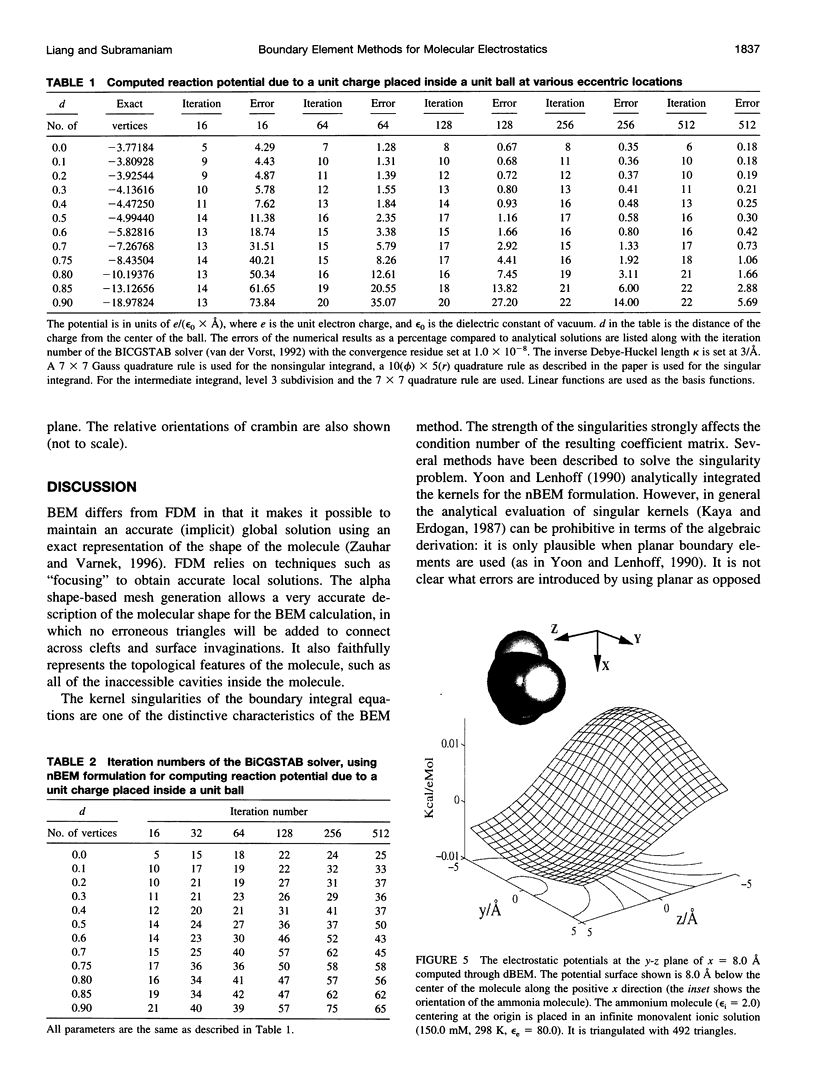
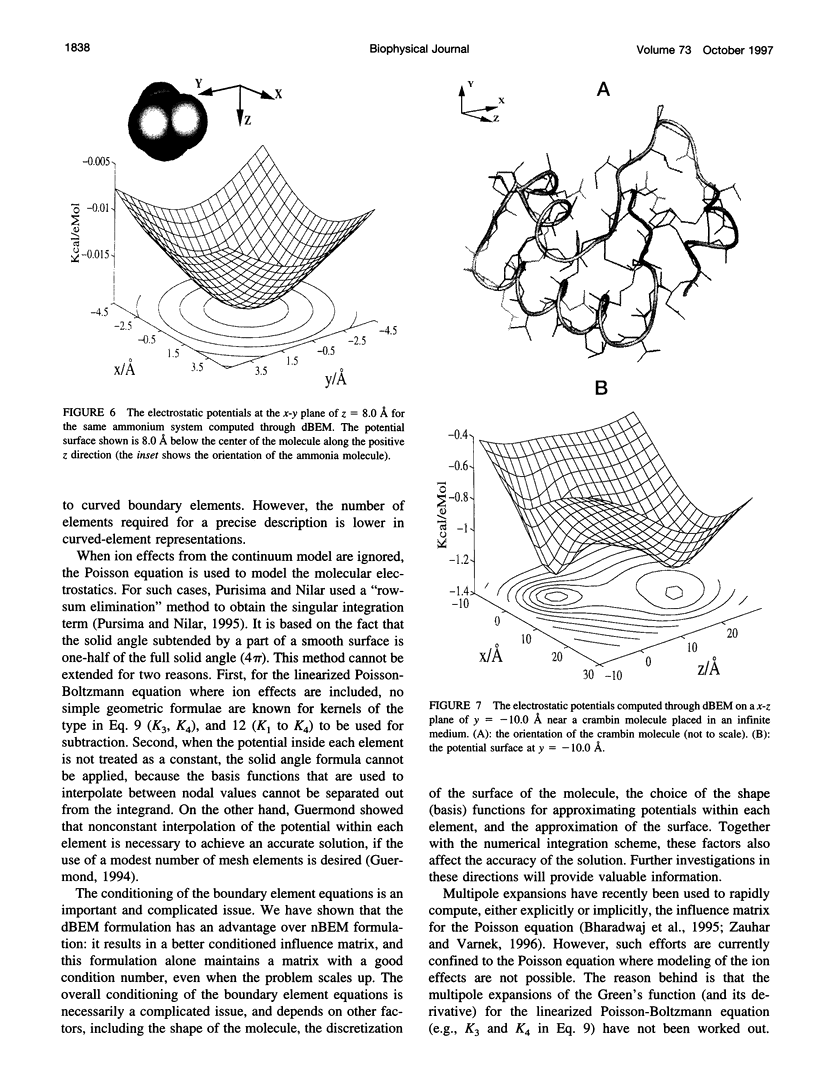
In continuum approaches to molecular electrostatics, the boundary element method (BEM) can provide accurate solutions to the Poisson-Boltzmann equation. However, the numerical aspects of this method pose significant problems. We describe our approach, applying an alpha shape-based method to generate a high-quality mesh, which represents the shape and topology of the molecule precisely. We also describe an analytical method for mapping points from the planar mesh to their exact locations on the surface of the molecule. We demonstrate that derivative boundary integral formulation has numerical advantages over the nonderivative formulation: the well-conditioned influence matrix can be maintained without deterioration of the condition number when the number of the mesh elements scales up. Singular integrand kernels are characteristics of the BEM. Their accurate integration is an important issue. We describe variable transformations that allow accurate numerical integration. The latter is the only plausible integral evaluation method when using curve-shaped boundary elements.
Full text
PDF







Images in this article
Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Gilson M. K., Rashin A., Fine R., Honig B. On the calculation of electrostatic interactions in proteins. J Mol Biol. 1985 Aug 5;184(3):503–516. doi: 10.1016/0022-2836(85)90297-9. [DOI] [PubMed] [Google Scholar]
- Klapper I., Hagstrom R., Fine R., Sharp K., Honig B. Focusing of electric fields in the active site of Cu-Zn superoxide dismutase: effects of ionic strength and amino-acid modification. Proteins. 1986 Sep;1(1):47–59. doi: 10.1002/prot.340010109. [DOI] [PubMed] [Google Scholar]
- Lee B., Richards F. M. The interpretation of protein structures: estimation of static accessibility. J Mol Biol. 1971 Feb 14;55(3):379–400. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
- Rashin A. A., Iofin M., Honig B. Internal cavities and buried waters in globular proteins. Biochemistry. 1986 Jun 17;25(12):3619–3625. doi: 10.1021/bi00360a021. [DOI] [PubMed] [Google Scholar]
- Sharp K. A., Honig B. Electrostatic interactions in macromolecules: theory and applications. Annu Rev Biophys Biophys Chem. 1990;19:301–332. doi: 10.1146/annurev.bb.19.060190.001505. [DOI] [PubMed] [Google Scholar]
- Warwicker J., Watson H. C. Calculation of the electric potential in the active site cleft due to alpha-helix dipoles. J Mol Biol. 1982 Jun 5;157(4):671–679. doi: 10.1016/0022-2836(82)90505-8. [DOI] [PubMed] [Google Scholar]
- Zauhar R. J., Morgan R. S. A new method for computing the macromolecular electric potential. J Mol Biol. 1985 Dec 20;186(4):815–820. doi: 10.1016/0022-2836(85)90399-7. [DOI] [PubMed] [Google Scholar]
- Zhou H. X. Boundary element solution of macromolecular electrostatics: interaction energy between two proteins. Biophys J. 1993 Aug;65(2):955–963. doi: 10.1016/S0006-3495(93)81094-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H. X. Brownian dynamics study of the influences of electrostatic interaction and diffusion on protein-protein association kinetics. Biophys J. 1993 Jun;64(6):1711–1726. doi: 10.1016/S0006-3495(93)81543-1. [DOI] [PMC free article] [PubMed] [Google Scholar]







