Selecting a Maximally Informative Set of Single-Nucleotide Polymorphisms for Association Analyses Using Linkage Disequilibrium

Abstract

Common genetic polymorphisms may explain a portion of the heritable risk for common diseases. Within candidate genes, the number of common polymorphisms is finite, but direct assay of all existing common polymorphism is inefficient, because genotypes at many of these sites are strongly correlated. Thus, it is not necessary to assay all common variants if the patterns of allelic association between common variants can be described. We have developed an algorithm to select the maximally informative set of common single-nucleotide polymorphisms (tagSNPs) to assay in candidate-gene association studies, such that all known common polymorphisms either are directly assayed or exceed a threshold level of association with a tagSNP. The algorithm is based on the r² linkage disequilibrium (LD) statistic, because r² is directly related to statistical power to detect disease associations with unassayed sites. We show that, at a relatively stringent r² threshold (r²>0.8), the LD-selected tagSNPs resolve >80% of all haplotypes across a set of 100 candidate genes, regardless of recombination, and tag specific haplotypes and clades of related haplotypes in nonrecombinant regions. Thus, if the patterns of common variation are described for a candidate gene, analysis of the tagSNP set can comprehensively interrogate for main effects from common functional variation. We demonstrate that, although common variation tends to be shared between populations, tagSNPs should be selected separately for populations with different ancestries.

Introduction

SNPs represent the most frequent form of polymorphism in the human genome. In multiple-gene surveys, estimates of nucleotide diversity in the human genome range between 3.7×10^-4 and 8.3×10^-4 differences per base pair (Wang et al. 1998; Cambien et al. 1999; Cargill et al. 1999; Halushka et al. 1999; Sachidanandam et al. 2001; Stephens et al. 2001a). From these and other studies of nucleotide diversity, it has been estimated that a common SNP (an SNP with a minor-allele frequency [MAF]>10%) occurs once every ∼600 bp (Kruglyak and Nickerson 2001). Given that the average gene in the human genome spans ∼27 kb (Lander et al. 2001; Venter et al. 2001), ∼50 common polymorphisms may be present in such a gene.

Although the number of common variants per gene is finite, the throughput of current genotyping technologies is inadequate for genotyping all existing common variants in all but the smallest of genes (Nickerson et al. 2000). Consequently, the issue of how to select a maximally informative set of common polymorphisms (tagSNPs) for association analyses is generating considerable interest; early publications on this topic focused on simply resolving common haplotypes (Johnson et al. 2001), and more quantitative methods have been described that minimize the number of tagSNPs required for this task (Zhang et al. 2002b; Ackerman et al. 2003; Ke and Cardon 2003; Meng et al. 2003). However, the relationship between tagSNPs selected for haplotype resolution and power to detect disease risk associated with existing polymorphism has been addressed only partially, by use of methods for maximizing haplotype information content for a given number of markers (Zhang et al. 2002a; Stram et al. 2003; Weale et al. 2003).

Genotypes at common SNPs <10 kb apart tend to be correlated; linkage disequilibrium (LD) describes the relationship between genotypes at a pair of polymorphic sites. Several popular statistics exist for describing LD; the two most frequently used are D′ and r² (sometimes referred to as “Δ²”) (Devlin and Risch 1995). |D^′|=1 if neither site has experienced recurrent mutation or gene conversion and if there has been no recombination between the sites. “|D^′|=1” can be described as “complete LD,” because the allelic association is as strong as possible, given the allele frequencies at the two sites. However, genotypes can be perfectly correlated between sites only if their MAFs are the same. Only when genotypes are perfectly correlated does r²=1, which can be described as “perfect LD.”

To date, most candidate-gene studies have directly analyzed the association between disease status and a small number of candidate SNPs that have known or predicted functional consequences (Collins et al. 1997; Botstein and Risch 2003). That study design can easily determine whether a given variant confers significant risk of disease. An alternative to direct analysis of functional SNPs in candidate genes is indirect analysis by use of a dense set of assayed SNPs (Collins et al. 1997). Indirect analysis does not require a priori identification of functional SNPs; rather, it assumes that genotypes at unassayed, risk-related SNPs will be correlated with one or more assayed SNPs. Statistical power to detect unassayed, disease-associated polymorphisms depends on the correlation (r²) between the unassayed site and an assayed site. The relationship between r² and power is relatively simple to calculate, given an r² between an assayed polymorphism and a disease-associated polymorphism. The power to detect the disease-associated polymorphism indirectly in N samples is equivalent to power to detect it directly in Nr² samples (Pritchard and Przeworski 2001).

We have developed a simple greedy algorithm for identifying sets of tagSNPs in a candidate gene, such that all polymorphisms above a specified frequency threshold either are directly assayed or exceed a specified level of r² with an assayed polymorphism. Given a population of cases and controls, the allele frequency and r² thresholds can be specified to yield a given level of power to detect a disease association with any common SNP in the gene. We find that, at a relatively stringent r² threshold (r²>0.8), the selected tagSNPs resolve >80% of all existing haplotypes. We have implemented the algorithm in a program that will identify bins of tagSNPs at a user-specified minimum-allele frequency and at minimum r² between tagSNPs and unassayed SNPs. Users may also specify mandatory tagSNPs, when prior hypotheses exist as to which SNPs might be functionally important (e.g., nonsynonymous coding region SNPs [cSNPs] or SNPs in known regulatory regions).

Material and Methods

tagSNP Selection

We developed a greedy algorithm to identify subsets of tagSNPs for genotyping, selected from all SNPs exceeding a specified MAF threshold. Starting with all SNPs above the MAF threshold, the single site exceeding the r² threshold with the maximum number of other sites above the MAF threshold is identified. This maximally informative site and all associated sites are grouped as a bin of associated sites. Not all SNPs within the bin are interchangeable, because pairwise association is not an associative property: if r² exceeds the threshold for SNP pairs A/B and B/C, r² for SNP pair A/C might not exceed the threshold. Thus, because the bin is initially ascertained using a single SNP, all pairwise r² within bin are re-evaluated, and any SNP exceeding threshold r² with all other sites in the bin is specified as a tagSNP for the bin. Thus, one or more SNPs within a bin are specified as “tagSNPs,” and only one tagSNP would need to be genotyped per bin. The tagSNP can be selected for assay on the basis of genomic context (coding vs. noncoding or repeat vs. unique), ease of assay design, or other user-specified criteria.

The binning process is iterated, analyzing all as-yet-unbinned SNPs at each round, until all sites exceeding the MAF threshold are binned. Each bin is reported as a set of all SNPs in the bin as well as the subset of tagSNPs within the bin, each of which is above the r² threshold with all other SNPs in the bin. If an SNP does not exceed the r² threshold with any other SNP in the region, it is placed in a singleton bin.

Samples

Forty-seven unrelated individuals were resequenced: 24 individuals from the Coriell African American 50 panel (Coriell samples NA17101–NA17116 and NA17133–NA17140) and 23 European subjects from the CEPH families (NA06990, NA07019, NA07348, NA07349, NA10830, NA10831, NA10842–NA10845, NA10848, NA10850–NA10854, NA10857, NA10858, NA10860, NA10861, NA12547, NA12548, and NA12560).

Sequencing

The SeattleSNPs Program for Genomic Applications (PGA) resequences candidate genes involved in inflammatory processes in humans. For all genes analyzed, we resequenced the genomic region spanning the longest reference transcript in LocusLink, including introns, as well as an average of 2.5 kb 5′ of the gene and 1.5 kb 3′ of the gene. Only autosomal genes with >85% complete resequencing coverage of the genomic region were included in these analyses. Overlapping PCRs were designed for the reference sequence by use of the program PCRoverlap (Rieder et al. 1999). Templates were amplified using the Elongase kit from Invitrogen on MJR Tetrad thermal cyclers. Samples were sequenced using Big Dye Terminator chemistry (Applied Biosystems) on ABI 3700 and ABI 3730 instruments. Detailed protocols for PCR and sequencing are available at the University of Washington–Fred Hutchinson Cancer Research Center Web site.

Sequence data were assembled into contigs by use of Phred (Ewing and Green 1998; Ewing et al. 1998), Phrap, and Consed (Gordon et al. 1998). Polymorphic sites were identified using PolyPhred, version 4.05 (Nickerson et al. 1997). At insertion-deletion polymorphisms, the sequence analysts manually genotyped each sample and designed primers from the other strand to sequence beyond the indel. All polymorphic sites flagged by PolyPhred were reviewed to remove a few false positives associated with biochemical artifacts, such as GC compressions, unincorporated dye terminators, and heterozygous insertion-deletion polymorphisms.

Data quality was assessed in a number of ways. We trimmed each chromatogram to remove low-quality sequence (Phred score <25), resulting in analyzed reads averaging >450 bp, with an average Phred quality of 40. We obtained second-strand confirmation from a different sequencing primer at 66% of all polymorphic sites and third-strand confirmation at 33% of all polymorphic sites. We observed all three possible genotypes (heterozygotes and homozygotes for each allele) for 38% of common polymorphic sites, with an average Phred quality >45 (1/50,000 probability of being incorrectly assigned). The average flanking-sequence quality associated with polymorphic sites (±5 bp on each side of the polymorphic site) was >40. We independently verified 110 of the identified common sites by Taqman allelic discrimination, using an ABI 7900 (Livak 1999); >99% of Taqman genotypes were concordant with the sequence data.

Calculating r²

African American and European American populations were analyzed independently. Within a given gene, two SNP haplotype frequencies were estimated using standard methods for all pairs of SNPs (Hill 1974), and r² was calculated from the inferred haplotype frequencies (Hill and Robertson 1968).

To compare results from LD-based selection with those from random SNP selection, in each gene, the number of tagSNP bins was determined at each r² threshold. An equal number of SNPs then was selected at random from the set of all SNPs >10% MAF, and r² was measured between the random set and all SNPs above the MAF threshold. Random selection was repeated 100 times to determine the average number of SNPs in each gene exceeding the r² threshold with the randomly selected set of SNPs.

To determine the relationship between LD-selected tagSNPs and haplotypes, haplotypes were inferred independently, using PHASE, version 1.0.1 (Stephens et al. 2001b), on all sites with >10% MAF in each population. Then the number of haplotypes inferred using all sites was compared with the number of haplotypes resolved using only one tagSNP per bin. These data were compared either as the actual number of haplotypes resolved or as the effective number of haplotypes resolved (n_e), calculated in equation (1), where p_i is the frequency of the ith haplotype:

For comparison with haplotype-based tagSNP selection methods, we first identified haplotype “blocks” as regions with little evidence of historical recombination between common SNPs, through use of a defined set of rules (Gabriel et al. 2002). tagSNPs were selected, using the program tagsnps.exe (Stram et al. 2003) to identify a minimal set of tagSNPs that optimize the predictability of common haplotypes by use of the statistic r²_h. We ran the program with the following parameters: common haplotypes were defined as “the minimal set of haplotypes that covers 80% of existing haplotypes,” and sets of tagSNPs resolving the common haplotypes were selected at an r²_h threshold of 0.7, because the number of selected tagSNPs at this threshold was comparable to the number of tagSNPs selected using the LDSelect algorithm at an r² threshold of 0.5. When genes contained more than one block, tagSNPs were selected independently within each block.

htSNPs were also identified using the program HaploBlockFinder. HaploBlockFinder requires inferred haplotypes as input, so we used PHASE, version 2.0, and inferred haplotypes for the complete gene within each population. HaploBlockFinder was run with defined blocks by haplotype diversity within each block (Patil et al. 2001), and htSNPs were selected within each block for 80% coverage (program parameters −A2 −C0.8 −T1 −P0.8).

Results

We tested the LD-select algorithm on a set of 100 candidate genes resequenced in 24 African Americans and 23 European Americans. These genes averaged 16.5 kb in length, with the longest at 45 kb. In this set of genes, 8,877 SNPs were observed overall, with 7,793 in the African American population and 4,620 in the European American population, for an average SNP density of 1 every 200 bp. A small number of triallelic SNPs were observed, but they were excluded from this analysis. The observed nucleotide diversity (π) was 9.1×10^-4 in African Americans, 6.6×10^-4 in European Americans, and 8.4×10^-4 in the combined population, which are similar results to those of previous large-scale genomic surveys (Wang et al. 1998; Cambien et al. 1999; Cargill et al. 1999; Halushka et al. 1999; Sachidanandam et al. 2001; Stephens et al. 2001a). With common variation defined as “an SNP with MAF>10%,” 3,178 common SNPs were identified in the African American population, and 2,375 common SNPs were identified in the European American population. Thus, the average observed frequency of SNPs with an MAF >10% was every 500 bp in African Americans and every 700 bp in European Americans, as predicted elsewhere (Kruglyak and Nickerson 2001).

Coding sequences (CDS) accounted for slightly more than 8% of the scanned sequence (135 kb), for an average of 1.35 kb of CDS per gene. Four hundred two SNPs were observed within CDS, of which 277 were nonsynonymous, changing amino acids. By comparison, UTRs accounted for slightly more than 5% of the scanned sequence (77 kb), and 497 SNPs were observed in UTRs; thus, SNP density in coding regions is clearly lower than in other contexts. Of the nonsynonymous cSNPs, 78 were common in African Americans, 63 were common in European Americans, and only 44 were common in both populations. Thus, less than one common nonsynonymous cSNP was observed per gene, so a direct analysis of putatively functional common variation would not be possible in many genes. However, as mentioned above, an average of 20–30 common variants were identified in each gene (depending on population); therefore, even in the absence of coding changes, a considerable amount of common polymorphism exists within each gene. Analysis of common, noncoding variants can test the alternative hypothesis that functional SNPs reside in noncoding regions.

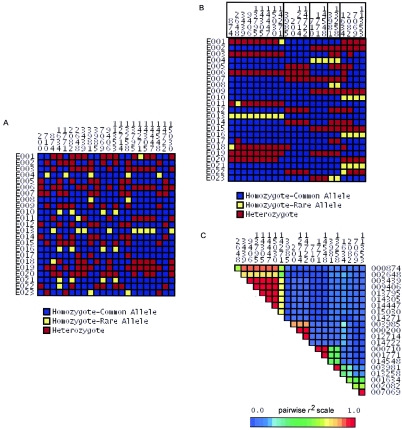
Variation discovery results for an average-sized candidate gene are shown in figure 1. We resequenced a total of 15,152 bp across the β-2 bradykinin receptor (BDKRB2) and identified 77 SNPs over all, with 28 SNPs with >10% MAF in either African Americans or European Americans. Twenty-two SNPs with MAF>10% were observed in the European American population (fig. 1A). When the samples are rearranged so that SNPs with similar patterns of genotype are adjacent (fig. 1B), it is clear that many SNPs exhibit very similar patterns of genotype. When we considered the 22 common SNPs in European Americans, just 11 unique patterns of genotype were observed, and some of those patterns were extremely similar. Pairwise r² between sites (fig. 1C) shows groups of sites with similar patterns of genotype as red triangles above the diagonal, indicating that r² is near 1.

Figure 1.

Common variation and LD in European Americans at BDKRB2. At the BDKRB2 gene, 22 SNPs with MAF>10% were described for the European American samples (A). Patterns of genotype at each SNP are shown as a visual genotype plot, in which each column represents a site and each row represents a sample. Genotype is color coded, as shown, with SNPs presented in the order they were identified across the gene. Patterns of genotype are clearly similar for many SNPs (e.g., sites 10922 and 12574) but not necessarily for adjacent SNPs. The same data are shown in panel B, with the order of SNPs rearranged such that each SNP is adjacent to SNPs with similar patterns of genotype. Among the 22 SNPs, the LD-based SNP-selection algorithm identified five bins of tagSNPs at an r² threshold of 0.5. tagSNP bins are boxed (B). The LD statistic r² describes the similarity of pattern between pairs of polymorphic sites: pairwise r² between SNPs is shown for the same order of SNPs as in panel B, and bins of SNPs with similar patterns are visible as reddish triangles above the diagonal (C).

Pairwise SNP Association Analysis

Because the theoretical variance of any single r² measurement is quite large (Ewens 1979), we modeled the patterns of LD across candidate genes, using coalescent simulated data (Hudson 2002) to determine the relationship between observed r² in a small SNP discovery population and true r² in the overall population. Modeled data demonstrated that the true distribution of r² in regions of ∼15 kb is skewed to extreme values (near 0 or near 1), with a dramatic increase in variance for comparisons involving SNPs with <10% MAF (data not shown). Therefore, we limited the present analysis to sites with >10% MAF.

In simulated data, the frequency with which the observed r² in 24 individuals exceeded a given r² threshold when the true r² in 10,000 individuals did not exceed that threshold increases dramatically for r² thresholds <0.5; therefore, thresholds >0.5 appear to yield more reliable results in this sample size (Carlson et al. 2003). Reliable tagSNP identification at lower r² thresholds or MAF thresholds will require larger resequencing data sets. Therefore, we suggest the use of r² thresholds >0.5 until larger resequencing data sets become available.

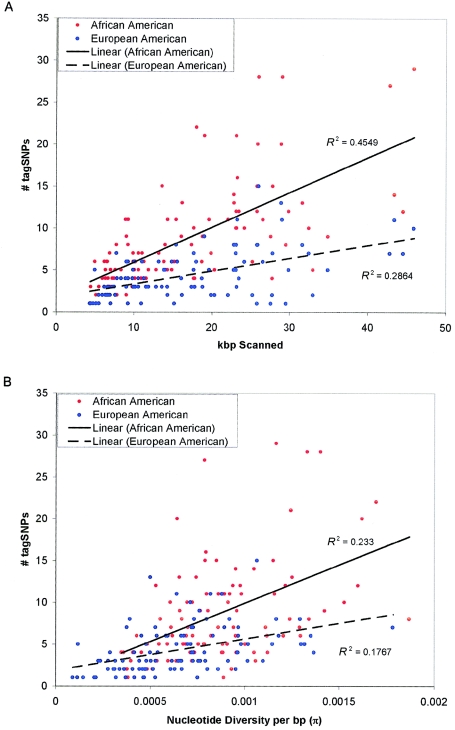
The set of tagSNP bins identified in BDKRB2 at threshold r²>0.5 and with MAF>10% in the European American sample is shown in figure 1B. Five bins of tagSNPs were identified: one bin of nine SNPs, two bins of four SNPs, one bin of three SNPs, and one bin of two SNPs. The pattern of genotypes within each bin clearly is very similar. The number of tagSNP bins selected for each of the 100 genes at threshold r²>0.5 and with MAF>10% is shown in figure 2A and table 1. As expected, the minimal number of tagSNP bins tends to be larger in the African American population, reflecting both higher nucleotide diversity and weaker LD in that population.

Figure 2.

tagSNPs per gene, with threshold r²>0.5 and MAF>10%. The complete genomic region of 100 genes was resequenced in 24 unrelated African American and 23 unrelated European American samples. Within each population, tagSNPs were selected from all SNPs with MAF>10% at an r² threshold of 0.5. A, The number of tagSNPs selected in each gene under these parameters, plotted against the size of the genomic region for each gene. Although there is a clear trend toward more tagSNPs in larger genes, there is considerable variance in the required tagSNP density in both populations. B, The number of tagSNPs selected in each gene, plotted against nucleotide diversity (π) per base pair. Thus, variance in tagSNP density between genes reflects both variation in nucleotide diversity and variation in the average extent of LD within genes. Within each gene, a greater number of tagSNPs is generally required in the African American population, reflecting both greater nucleotide diversity and shorter range LD, relative to the European American population.

Table 1.

Comparison of SNPs at Different Frequencies and Thresholds in Two Populations

			African Americans					European Americans
				No. of					No. of
						tagSNPs at					tagSNPs at
Gene	GenBank Accession Numbera	No. ofBase Pairs Scanned	Nucleotide Diversity(π×10-4)	SNPs	Common SNPs	r2>0.5	r2>0.8	Nucleotide Diversity(π×10-4)	SNPs	Common SNPs	r2>0.5	r2>0.8
ACE	AY436326	22,122	9.22	83	44	11	21	6.31	43	27	2	5
AGT	AY436323	15,593	12.97	91	43	6	16	13.51	84	52	6	10
AGTR1	AY436325	45,926	11.67	253	95	29	42	7.14	128	74	10	18
APOB	AY324608	44,547	5.31	159	43	12	20	3.77	79	32	7	11
BDKRB2	AF378542	14,050	6.68	61	19	8	12	7.00	49	22	5	9
BF	AF551848	9,956	5.92	30	11	6	6	5.30	26	6	3	4
CCR2	AF545480	10,073	6.75	41	12	5	8	5.85	22	19	6	7
CD36	AY095373	29,921	9.79	167	49	12	25	7.16	80	35	5	8
CEBPB	AY193834	4,508	7.22	13	6	3	3	4.70	10	3	1	2
CRF	AF410771	9,293	7.99	38	16	11	15	7.21	24	14	4	6
CRP	AF449713	6,715	10.51	30	14	4	7	5.05	13	5	3	3
CSF2	AF373868	5,992	11.24	30	9	4	7	6.68	17	9	2	3
CSF3	AF388025	5,527	8.91	28	4	1	2	8.62	17	8	2	2
CSF3R	AY148100	18,843	9.60	99	29	9	13	6.17	52	23	3	10
DCN	AF491944	34,947	8.06	141	38	9	14	1.20	40	8	5	5
F10	AF503510	28,937	6.42	98	33	20	27	5.01	63	28	13	18
F11	AY191837	26,603	8.87	120	51	11	22	6.65	63	41	6	10
F12	AF538691	10,616	6.12	44	10	7	8	4.17	22	10	4	6
F2	AF478696	20,407	5.93	90	15	5	10	4.78	57	8	2	5
F2R	AF391809	24,231	6.96	94	34	10	13	5.36	52	28	6	12
F2RL1	AF400075	17,715	7.36	98	19	4	7	6.41	43	24	5	8
F2RL2	AF374726	9,273	13.42	61	24	8	12	11.82	37	22	6	7
F2RL3	AF384819	10,214	7.27	42	19	6	12	6.60	25	16	3	6
F3	AF540377	16,114	6.57	61	19	9	12	5.41	26	19	4	6
FGA	AF361104	9,947	3.99	23	6	3	5	3.18	17	5	3	3
FGB	AF388026	11,604	4.56	45	7	4	4	7.93	36	24	3	3
FGG	AF350254	10,168	3.49	21	7	4	4	2.28	12	6	3	3
FGL2	AF468959	6,382	4.14	19	5	4	4	2.78	6	2	2	2
FSBP	AF487652	9,846	5.96	31	11	3	5	5.01	26	12	4	5
GP1BA	AF395009	6,241	8.23	27	9	6	6	7.67	21	8	3	4
HMGCR	AY321356	27,810	3.61	69	17	4	7	4.08	49	20	2	4
ICAM1	AY225514	17,731	6.08	61	19	10	13	5.28	39	19	7	10
IFNG	AF375790	7,665	4.87	28	5	5	5	4.62	13	7	2	4
IL10	AF418271	7,879	9.32	26	13	2	3	9.66	24	17	4	4
IL10RA	AY195619	19,942	7.00	69	31	7	14	5.17	49	16	2	7
IL11	AY207429	8,964	9.85	40	17	11	14	7.30	24	15	4	6
IL12A	AF404773	11,330	9.65	52	21	6	9	7.88	29	23	4	4
IL12B	AF512686	14,902	7.86	52	19	5	6	5.95	33	23	6	6
IL13	AF377331	6,919	8.62	27	12	7	12	4.46	16	6	2	3
IL17B	AF386077	9,077	4.85	32	7	2	4	7.28	22	15	3	3
IL19	AF390905	10,998	7.14	43	13	4	5	4.18	24	8	1	2
IL1A	AF536338	17,849	9.57	78	38	4	7	10.99	50	44	3	4
IL1B	AY137079	17,447	5.54	51	21	8	15	4.45	35	17	3	7
IL1R1	AF531102	27,864	7.91	134	38	15	24	7.21	85	40	7	15
IL1R2	AY124010	23,160	16.00	188	85	12	23	10.20	101	80	5	7
IL1RN	AY196903	19,677	11.59	146	37	11	16	13.19	91	69	5	11
IL2	AF359939	6,752	3.79	20	3	2	2	3.57	10	5	3	4
IL20	AF402002	6,634	6.91	25	7	6	6	4.73	17	5	2	4
IL21R	AY064474	25,844	8.52	116	35	15	21	7.34	76	36	8	17
IL22	AF387519	8,393	10.04	46	12	5	10	9.62	28	18	4	5
IL24	AY062931	10,628	7.56	41	16	5	6	6.50	24	14	3	3
IL2RB	AF517934	26,029	13.31	148	66	28	42	10.65	100	59	15	18
IL3	AF365976	6,387	5.47	27	6	5	5	3.07	9	4	2	3
IL4	AF395008	22,845	9.53	105	45	14	29	4.80	56	25	5	6
IL4R	AF421855	25,917	16.21	179	78	20	38	11.69	118	58	8	18
IL5	AF353265	5,186	5.14	16	4	2	3	0.92	3	1	1	1
IL6	AF372214	7,526	8.80	41	10	4	6	9.14	26	12	3	6
IL8	AF385628	7,035	6.89	35	9	5	5	4.66	9	7	1	1
IL9	AF361105	6,676	6.40	28	8	3	6	3.64	14	7	2	2
IRAK4	AY186092	33,033	7.87	153	34	5	14	3.15	72	5	2	4
JAK3	AF513860	19,067	12.46	113	48	21	27	7.62	56	31	9	14
KEL	AY228336	25,850	9.38	128	50	12	22	1.47	47	2	1	2
KLK1	AY094609	9,922	12.93	63	24	7	14	13.00	46	27	5	6
KLKB1	AY190920	31,670	12.53	165	74	13	27	12.95	128	88	8	14
LDL	AY324609	42,873	7.87	178	60	27	38	7.29	109	65	7	17
LTA	AY070490	5,033	9.54	20	10	6	6	11.48	19	14	5	8
LTB	AY070219	4,412	3.84	16	2	1	1	2.07	7	2	1	1
MC1R	AF514787	6,545	12.06	36	14	6	8	9.55	22	11	2	4
MMP3	AF405705	11,904	8.85	50	17	5	9	7.56	35	16	3	4
NOS3	AF519768	23,307	7.95	102	33	16	21	6.41	54	34	11	13
PLAU	AF377330	9,274	8.87	30	17	4	6	7.52	23	13	1	3
PLAUR	AY194849	23,187	12.47	166	44	21	29	7.99	94	18	8	11
PON1	AF539592	29,052	14.02	175	89	28	44	8.80	121	55	11	25
PON2	AY210982	32,487	9.13	137	60	10	20	8.94	101	72	7	13
PROC	AF378903	12,877	9.09	52	25	5	12	10.18	39	28	3	7
PROCR	AF375468	6,968	5.37	15	9	3	3	6.10	14	8	2	2
PROZ	AF440358	14,366	8.63	86	24	11	15	8.04	46	27	2	3
REN	AY436324	13,640	11.52	78	28	15	24	6.67	46	16	3	7
SCYA2	AF519531	9,070	7.66	38	15	9	10	6.79	25	14	6	8
SELE	AF540378	13,892	11.20	86	25	6	9	9.83	70	20	5	9
SELP	AF542391	43,454	10.50	254	72	14	34	8.20	141	64	11	18
SERPINA5	AF361796	7,806	18.68	61	29	8	11	17.84	41	25	7	4
SERPINC1	AF386078	15,208	6.19	43	18	6	12	3.21	27	13	1	10
SERPINE1	AF386492	13,208	11.13	85	25	7	11	9.68	48	27	6	8
SFTPA1	AY198391	23,126	15.28	170	71	10	21	9.68	153	29	7	10
SFTPA2	AY206682	18,039	16.95	152	60	22	30	8.34	111	23	6	12
SFTPB	AF400074	11,094	9.42	49	21	7	9	4.55	18	11	6	7
SFTPD	AY216721	23,538	12.17	151	42	12	20	13.68	134	51	4	10
SMP1	AF458851	25,269	6.93	90	37	6	9	3.40	39	12	2	2
STAT6	AF417842	18,769	4.30	53	13	6	10	2.89	22	12	4	6
TGFB3	AY208161	23,236	7.24	81	32	10	21	4.82	50	24	3	4
THBD	AF495471	7,254	4.10	24	6	4	4	2.79	14	4	3	3
TNFAIP1	AY065346	14,331	4.79	53	10	5	5	2.39	19	6	3	3
TNF	AY066019	4,830	4.71	21	2	1	1	3.72	12	2	1	2
TNFRSF1A	AY131997	16,207	7.44	60	26	13	17	4.80	26	14	2	4
TRPV5	AY206695	29,555	12.41	180	69	8	18	2.15	66	9	1	1
TRPV6	AY225461	27,629	14.24	142	74	9	18	1.16	63	1	1	1
VCAM1	AF536818	22,868	6.55	102	24	13	14	3.93	39	21	8	11
VEGF	AF437895	15,442	8.95	64	26	11	20	9.21	49	25	8	10
VTN	AF382388	5,559	10.59	28	11	3	4	5.29	15	4	1	2

^aPolymorphisms identified in these GenBank records by the SeattleSNPs PGA or the Pharmacogenetics and Risk of Cardiovascular Disease project were included in the analysis.

Also as expected, the number of tagSNP bins tends to increase with gene size in both populations, although considerable variance in site-set density was observed, probably reflecting the recombinational history of each gene, as well as the variance in the nucleotide diversity of each gene. Genes with few recombinant chromosomes would tend to require fewer tagSNPs than highly recombinant genes of similar size; for example, PON1 and TRPV5 have similar size and nucleotide diversity in the African American population, but PON1 requires 28 tagSNPs at an r² threshold of 0.5, compared with 9 at TRPV6. In this population, we identified seven haplotype blocks in PON1 compared with three in TRPV6, which would be consistent with elevated rates of recombination in PON1 and could explain the large number of tagSNP bins required for this gene. Similarly, genes with high nucleotide diversity tend to require more tagSNPs than low-diversity genes (fig. 2B), although this trend is more subtle.

We implemented LD-based tagSNP selection as a greedy algorithm; to test the performance of this algorithm, we compared against the results from an exhaustive search for the minimal set of tagSNPs for which all common SNPs are either directly assayed or exceed a specified r² threshold. The computational burden of the exhaustive algorithm was excessive for solutions with more than seven tagSNPs, so we limited our testing to genes with fewer than seven tagSNP bins identified by the greedy algorithm. In the European sample, at an r² threshold of 0.5, 78 genes were identified with less than seven tagSNP bins. In all 78 genes, the minimal number of tagSNPs identified using the exhaustive search was the same as the number of tagSNP bins identified using the greedy algorithm. Thus, although the greedy algorithm is not guaranteed to minimize the number of tagSNP bins, in this data set, the greedy algorithm appears to yield results that are comparable to the results of an exhaustive algorithm, at considerable computational savings.

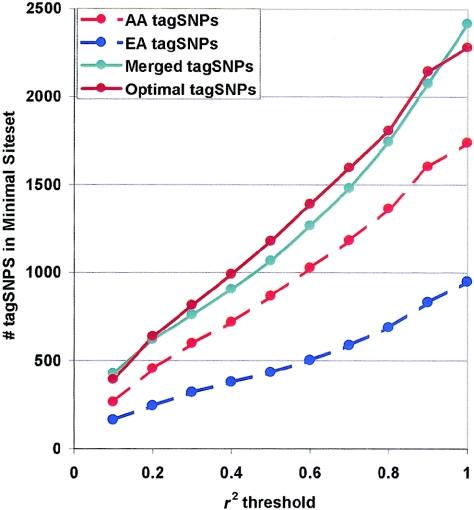
The total number of tagSNP bins identified in the 100-gene set is shown for a range of r² thresholds in figure 3. As expected, the number of tagSNP bins increases as the stringency of the r² threshold increases; the increase in the number of tagSNP bins was observed to be roughly linear with increasing r² thresholds. In the African American population, 867 tagSNP bins were identified at r²>0.5, or an average of 9 tagSNP bins per gene, and 1,366 tagSNP bins were identified at r²>0.8, or an average of almost 14 tagSNPs per gene. Similarly, in the European American population, 435 tagSNP bins were identified at r²>0.5, and 689 tagSNP bins were identified at r²>0.8, for an average of 4 and 7 tagSNP bins per gene, respectively. Some genes were observed with dramatically different numbers of tagSNPs between populations (e.g., TGFB3 with 10 tagSNPs in African Americans and 3 tagSNPs in Europeans, at an r² threshold of 0.5). Some but not all of these differences reflected dramatic differences in nucleotide diversity (e.g., KEL, TRPV5, and TRPV6).

Figure 3.

Total tagSNP bins in 100 genes, versus threshold r². At each r² threshold, tagSNP bins were identified for 100 genes within African American (“AA tagSNPs”) and European American (“EA tagSNPs”) populations. As expected, more tagSNP bins were identified in African American samples than in European American samples. To measure the effects of population stratification on the LD-select algorithm, tagSNPs were also selected from merged African American and European American populations (“Merged tagSNPs”). The minimal set of tagSNPs relevant to both populations was also assembled at each r² threshold as the union of the tagSNP sets selected in each subpopulation (“Optimal tagSNPs”); this set was larger than the tagSNP set in either subpopulation alone but considerably smaller than the sum of the population-specific site sets, reflecting the fact that many (but not all) tagSNPs were useful in both populations.

To determine whether tagSNPs are population specific, we tested tagSNPs identified in each ethnic population (European American or African American) against all common variants in the other population. At an r² threshold of 0.5, 867 tagSNPs were identified in African Americans, and 1,911 of 2,375 (80%) common SNPs in Europeans were either directly assayed or exceeded r²=0.5 with the African American tagSNP set. Thus, at this r² threshold, the tagSNPs identified in the African American sample perform well in the European American samples, although at a cost of assaying roughly twice as many tagSNPs as the tagSNP set derived directly from European Americans (435 tagSNPs). Conversely, at an r² threshold of 0.5, the 435 European American tagSNPs either directly assayed or exceeded r²=0.5, with only 1,028 of 3,178 (32%) common SNPs in African Americans, indicating that the tagSNP set assembled in European Americans is clearly inadequate for use in the African American population.

LD is sensitive to population stratification. When subpopulations have significantly different allele frequencies, LD between a pair of SNPs in the combined population can be stronger than in either subpopulation, and this will cause the LD-selection algorithm to bin sites inappropriately. To examine the effects of population stratification on LD selection, we selected tagSNPs from merged African American and European American populations at an r² threshold of 0.5. When we tested the merged tagSNP set against each subpopulation separately, in European Americans, 5% of common SNPs did not exceed r²=0.5 with any selected tagSNP and, in African Americans, 15% of common SNPs did not exceed r²=0.5 with any selected tagSNP. Thus, within each subpopulation, a significant fraction of unassayed sites were below the r² threshold with the merged tagSNP set, which demonstrates the hazards of tagSNP selection in a stratified population. The effects of admixture within individuals are considerably more difficult to assess and have been left for future analysis.

Haplotype and LD Selection

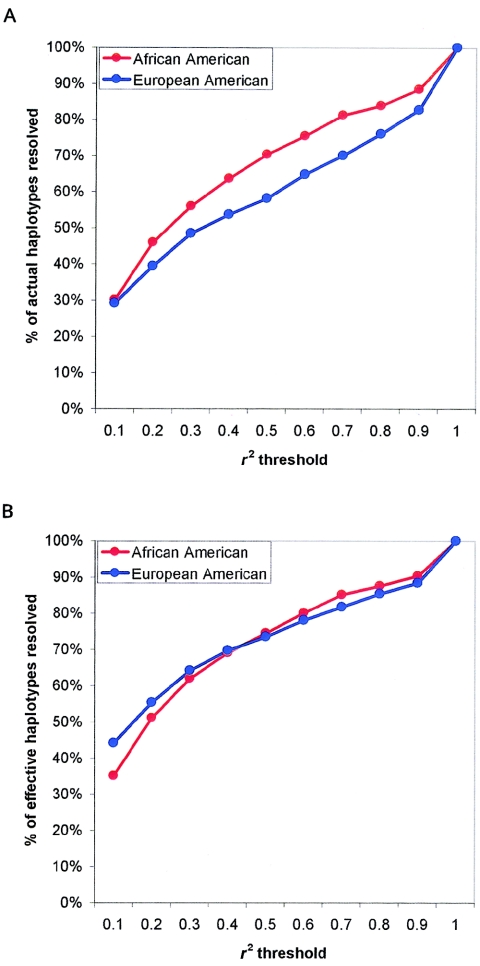
Under certain circumstances, haplotypes may be a useful way to reduce the complexity of candidate-gene association analyses. Discrimination between common haplotypes is more useful than discrimination between rare haplotypes; a convenient statistic to describe the number of common haplotypes is the effective number of haplotypes (the reciprocal of the haplotype homozygosity) analogous to the effective number of alleles at a single polymorphic site (Wright 1931). We inferred haplotypes in each population by use of PHASE (Stephens et al. 2001b), and we investigated the relationship between the LD-selected minimal set of tagSNPs and haplotype by comparing the actual (fig. 4A) and effective (figure 4B) number of haplotypes resolved with the minimal tagSNP set, as compared with haplotypes inferred using all common SNPs. In the data from European Americans, at an r² threshold of 0.5, the LD-selected tagSNP set resolved 58% of actual haplotypes and 74% of effective haplotypes. The greater fraction of effective than actual haplotypes resolved demonstrates how the LD-based algorithm resolves common haplotypes more effectively than rare haplotypes. At the same r² threshold, 70% of actual and 75% of effective haplotypes were resolved in African Americans. At an r² threshold of 0.8, 76% of actual and 85% of effective haplotypes were resolved in European Americans, and 84% of actual and 88% of effective haplotypes were resolved in African Americans, demonstrating the utility of LD-selected tagSNPs in haplotype resolution.

Figure 4.

The relationship between LD-selected tagSNPs and haplotypes. For each gene, haplotypes were inferred computationally. Results are shown as the fraction of haplotypes resolved using only LD-selected tagSNPs, relative to haplotypes resolved using all common SNPs. Results are shown across a range of r² values in each population (A). The effective number of haplotypes weights the number of haplotypes by frequency, with common haplotypes more heavily weighted. For each gene, the fraction of effective haplotypes resolved using only LD-selected tagSNPs, relative to effective haplotypes resolved, by use of all common SNPs is shown across a range of r² values in each population (B). For r² thresholds >0.5, >80% of effective haplotypes were resolved, demonstrating how, at adequately stringent r² thresholds, LD-selected tagSNPs efficiently resolve common haplotypes.

Comparison with Other tagSNP-Selection Methods

At present, knowledge of common genetic variation is incomplete for the majority of genes (Carlson et al. 2003); therefore, marker selection for association analysis in such genes is effectively random. To compare the efficiency of SNPs selected at random with tagSNPs identified using LD select, sets of common SNPs that were equal in number to the LD-selected tagSNPs at each r² threshold were selected at random, with a minimum of one randomly selected SNP per gene. For example, at r²>0.5, there were 867 LD-selected tagSNP bins for African American data, so 867 common SNPs were selected for each random SNP set. For 250 random samples of 867 common SNPs from the African American data, an average of 2,326 of 3,224 (72%) common SNPs exceeded r²=0.5. Similarly, there were 435 tagSNP bins at r²>0.5 for European Americans, and, in 250 random samples of 435 common SNPs from the European population, on average, 1,802 of 2,388 (76%) common SNPs exceeded r²=0.5 with the randomly selected set of SNPs. Across the entire range of r² values analyzed, 70%–80% of all existing common SNPs were above the r² threshold with randomly selected sets of SNPs (table 2).

Table 2.

Comparison of tagSNPs and Random SNPs at Various r² Thresholds in Two Populations

	African Americansa		European Americansb
r2 Threshold	No. oftagSNPs Bins	Random SNP Ascertained	No. oftagSNPs Bins	Random SNP Ascertained
.1	268	2,500	165	1,973
.2	456	2,451	247	1,906
.3	598	2,397	323	1,866
.4	720	2,337	380	1,822
.5	867	2,326	435	1,803
.6	1,028	2,297	504	1,783
.7	1,186	2,278	588	1,777
.8	1,366	2,313	689	1,774
.9	1,606	2,319	832	1,758

^aIn the African American population, 3,178 tagSNPs were identified.

^bIn the European American population, 2,375 tagSNPs were identified.

An alternative method for selecting a subset of SNPs to genotype is haplotype based: haplotype-tagging SNPs (htSNPs) are selected to optimize resolution of existing haplotypes. This type of SNP selection is generally applied to small segments of the genome with limited haplotype diversity, sometimes referred to as “haplotype blocks.” We adapted the haplotype block definition from Gabriel et al. (2002) to identify haplotype blocks in our data set. Haplotype blocks could not be assigned in two genes in African Americans (FGB and LTB) and four genes in European Americans (IL5, LTB, TRPV6, and TNF), because the genes contained zero or only one SNP with >20% MAF. In addition, haplotype blocks were not identified in nine genes in African Americans (BDKRB2, FGL2, IFNG, IL11, IL13, IL3, STAT6, THMDN, and TNF) and six genes in European Americans (FGL2, FGG, IL2, IL9, KELL, and THMDN), even though adequate numbers of high-frequency SNPs were present to define a block, generally reflecting small gene size as well as low levels of LD between SNPs with >20% MAF. Considering only the 89 genes for which one or more haplotype blocks could be identified in the African American sample, 216 haplotype blocks were identified: 2,080 common SNPs fell within blocks, 878 common SNPs were between blocks, and 159 SNPs were between a block and the end of the resequenced region. In consideration of only the 90 genes for which one or more haplotype blocks could be identified in European Americans, 149 blocks were identified, with 1,834 SNPs within blocks, 355 between, and 160 ambiguous.

We compared two htSNP selection algorithms against LDSelect. First, 800 htSNPs were selected, through use of an htSNP-selection algorithm (Stram et al. 2003), in the 89 genes with at least one haplotype block in the African American population, at an r²_h threshold of 0.7. This is quite similar to the number of tagSNPs identified in these genes and in this population with LD selection at an r² threshold of 0.5 (806 tagSNPs), so we determined how many common SNPs showed r²>0.5 with the htSNPs: 2,640 of 3,117 (85%). Similarly, in the European American population, 417 htSNPs were selected using the haplotype-based algorithm, again comparable to the 431 tagSNPs selected by the LD-based algorithm at the r² threshold 0.5. For the haplotype-selected set of htSNPs in European Americans, 2,041 of 2,381 (86%) common SNPs showed r²>0.5.

We also tested the HaploBlockFinder program (Zhang and Jin 2003) for identification of htSNPs, which automatically defines blocks within a set of inferred haplotypes. By use of a chromosomal-coverage block definition, 535 blocks were identified in Africans, and 223 blocks were identified in Europeans Americans. The large number of blocks observed, relative to the Gabriel et al. (2002) definition, was at least partially attributable to the fact that HaploBlockFinder allows blocks consisting of a single SNP: 196 blocks containing a single SNP were identified in African Americans and 60 in European Americans. For the African American population, 1,250 htSNPs were selected, and 469 htSNPs were selected for the European American population. Again, we determined how many common SNPs showed r²>0.5 with the selected htSNPs: 2,790 of 3,117 (89%) in African Americans and 1,839 of 2,381 (77%) in European Americans. Thus, although htSNPs are superior to randomly selected SNPs, LD-selected tagSNPs more comprehensively describe common patterns of variation for a given number of assayed SNPs than either alternative.

Discussion

Several strategies exist for candidate-gene association studies. It is not unreasonable to test for association between candidate SNPs with predicted function (e.g., nonsynonymous cSNPs) and phenotype, but this type of polymorphism is relatively rare, whereas 20–30 common polymorphisms exist per gene in our data set, and it is not yet possible to predict whether most noncoding polymorphisms might have functional consequences. A major drawback of testing candidate SNPs directly is that a lack of association with a candidate SNP does not rule out functionally important changes at nearby SNPs, except those that are in tight LD with the candidate SNP. An alternative strategy is to test a set of densely spaced SNPs for disease association and to rely on LD between the genotyped SNPs and unassayed SNPs to detect functional variants that cannot be predicted a priori. To design such a study, it is necessary to define common variants in a region, as well as the patterns of LD between these variants. It is currently feasible to resequence the complete genomic region of an average-sized gene in a modestly sized polymorphism-discovery population, thereby defining patterns of LD. Rational selection of a subset of sites that provides maximum information about common variation in the region is then possible on the basis of the observed patterns of LD between common SNPs.

We have developed a simple greedy algorithm to efficiently identify optimized subsets of SNPs for assay using observed patterns of LD. tagSNPs are selected for assay, such that all common SNPs either are directly assayed or exceed a threshold level of LD (r²) with an assayed SNP. Thus, to assay all SNPs in the gene at a given r² threshold, it is necessary to genotype only the minimal set of tagSNPs. We applied this algorithm at a range of stringencies to define the minimal set of tagSNPs for the set of 100 candidate genes in two ethnic populations.

At the relatively lenient threshold of r²>0.5, the average map density was 5.2 tagSNPs per 10 kb in African Americans and 2.6 tagSNPs per 10 kb in European Americans; at a more stringent threshold (r²>0.8), map densities were 8.25 tagSNPs per 10 kb and 4.2 tagSNPs per 10 kb, respectively. Extrapolating to 35,000 genes with an average of 27 kb, ∼250,000 tagSNPs would be required to cover all genic regions in European Americans at an r² threshold of 0.5, or 400,000 at an r² threshold of 0.8. Similarly, ∼500,000 tagSNPs would be required to cover all genic regions in African Americans at an r² threshold of 0.5, or 800,000 at an r² threshold of 0.8.

It is important to keep in mind that these map densities reflect the most informative possible set of tagSNPs, whereas random SNP–selection strategies would require denser maps to achieve similar power. In a comparison with an equal number of randomly selected SNPs, ∼75% of common SNPs were above the r² threshold of the random set.

It has been observed that many short segments of the genome (<20 kb) appear to have experienced little or no recombination and that there are a small number of haplotypes within these segments. These segments have been termed “haplotype blocks,” and significant efforts are under way to map the extent of such blocks and to identify SNPs that describe variation within them (Patil et al. 2001; Gabriel et al. 2002). However, fully describing existing patterns of variation requires knowledge of the evolutionary relationships between the haplotypes, even in nonrecombinant regions. Some SNPs will be specifically associated with a single haplotype, whereas other SNPs will be associated with clades of related haplotypes.

At an adequately stringent r² threshold (r²>0.8), LD-selected tagSNPs describe both haplotype-specific and clade-specific patterns of variation, because the LD-selection algorithm reduces the set of all sites to bins of sites with similar patterns of genotype. For example, given five haplotypes in a hypothetical nonrecombinant region, there are seven possible patterns of variation, some haplotype specific and others restricted to groups of related haplotypes (fig. 5). Because the tagSNP bins describe unique patterns of SNPs without reference to haplotype, at an adequately stringent r² threshold, there would be seven bins of tagSNPs in this region. Thus, association analyses that make use of the LD-selected minimal site set can detect either haplotype-specific or clade-specific effects within each nonrecombinant region, without prior inference of haplotypes.

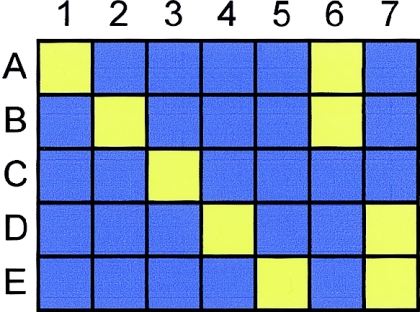
Figure 5.

tagSNP bins and the evolutionary relationships between haplotypes. A hypothetical nonrecombinant region with five existing haplotypes is shown, with each row (A–E) representing a haplotype and each column (1–7) representing an SNP with a unique pattern of alleles. The common allele is shown as blue and the rare allele as yellow. There are five possible patterns (1–5) that are haplotype specific, and two (6 and 7) that are specific to clades of related haplotypes. LD-based tagSNP selection at an adequately stringent r² threshold would identify all seven patterns in this hypothetical region. Thus, directly testing LD-selected tagSNPs can identify disease associations with either specific haplotypes or with clades of related haplotypes.

Given the fact that blocks with limited haplotype diversity exist, it is important to understand the patterns of recombination at the boundaries of these blocks. A small number of recombination hotspots have been confirmed (Chakravarti et al. 1984; Jeffreys et al. 2001), and some analyses have suggested the presence of recombination hotspots between blocks, but simulations with uniform recombination rates have also been shown to generate “blocks” (Subrahmanyan et al. 2001). It is likely that, in some instances, the observed boundaries of nonrecombinant regions reflect recurrent recombination events at a single hotspot but that others reflect a single recombinant chromosome that has drifted to high frequency in the population.

Under a hotspot model, LD should be low for all site pairs spanning the recombination hotspot, whereas, under a drift model, LD would be reduced only for sites where the alleles differed on the two ancestral haplotypes involved in the recombination event, and LD would remain strong across the hotspot for all other sites. Thus, where block boundaries reflect a small number of recombination events, genotypes will not be independent between adjacent blocks, and the optimal set of sites for a region that spans multiple blocks can be smaller than the sum of the optimal sets of sites when each block is considered independently. The LD-selection algorithm does not require prior specification of haplotype block boundaries, and it will find an optimal set of tagSNPs for a given region, regardless of recombination history.

To compare the LD-selected tagSNPs with htSNPs selected on the basis of haplotype blocks, we determined the block structure of the genes in our data set using the haplotype block definition of Gabriel et al. (2002). The large number of common SNPs that did not fall within blocks has important ramifications for SNP-selection algorithms that assume block structure, given that only SNPs within blocks are considered for selection as htSNPs. We selected htSNPs using two programs—tagsnps.exe (Stram et al. 2003) and HaploBlockFinder—and we found that the htSNPs selected with either algorithm did modestly better than random SNPs in describing patterns of common variation, as measured by the fraction of all common variants above the LD threshold for a given set of SNPs. However, LD-selected tagSNPs are more powerful than an equivalent number of either haplotype-selected htSNPs or randomly selected SNPs for detecting the simplest possible scenario, in which disease risk is directly associated with a single allele at a single SNP.

The LD-selection algorithm assumes that LD between SNPs reflects the evolutionary relationship between those sites within a population, reflecting demographic events such as population expansion and contraction, selective pressure, and recombination. Therefore, the LD-selection algorithm is sensitive to population stratification, which can generate artifactual LD between otherwise unrelated sites. As a consequence, tagSNPs should be selected in unstratified populations, when possible. The advantages of tagSNP selection within ethnic populations are twofold: in lower-diversity populations, the set of tagSNPs selected within the population will be considerably smaller than in the combined population; in higher diversity populations, unassayed SNPs will better correlate with the minimal set of tagSNPs selected within the population than will tagSNPs from the combined population. After tagSNP bins are identified in each subpopulation, the minimal site set relevant to multiple populations can easily be assembled.

In conclusion, resequencing a modest number of samples can define all common SNPs in a candidate gene, as well as the patterns of LD between these SNPs. We have described an efficient greedy algorithm to identify an optimal set of tagSNPs that describe these patterns. Because the LD between unassayed SNPs and tagSNPs is defined, testing the tagSNPs for main effects on disease status or severity provides reasonable power to detect risk directly associated with any allele or genotype at any common SNP in the candidate gene. At an adequately stringent r² threshold (r²>0.5), the tagSNPs also efficiently resolve haplotype and could be used to test for haplotype-related risks. The LD-based tagSNP-selection algorithm is robust for recombination history within the gene and does not require accurate prediction of functional SNPs within candidate genes. Software implementing the LD-selection algorithm is implemented in the SeattleSNPs vg2 program. A stand-alone version is also available from the authors on request. The distributed version allows users to specify allele-frequency thresholds, r² thresholds, and mandatory markers to include or exclude as tagSNPs.