Novel Analytical Methods Applied to Type 1 Diabetes Genome-Scan Data

Abstract

Complex traits like type 1 diabetes mellitus (T1DM) are generally taken to be under the influence of multiple genes interacting with each other to confer disease susceptibility and/or protection. Although novel methods are being developed, analyses of whole-genome scans are most often performed with multipoint methods that work under the assumption that multiple trait loci are unrelated to each other; that is, most models specify the effect of only one locus at a time. We have applied a novel approach, which includes decision-tree construction and artificial neural networks, to the analysis of T1DM genome-scan data. We demonstrate that this approach (1) allows identification of all major susceptibility loci identified by nonparametric linkage analysis, (2) identifies a number of novel regions as well as combinations of markers with predictive value for T1DM, and (3) may be useful in characterizing markers in linkage disequilibrium with protective-gene variants. Furthermore, the approach outlined here permits combined analyses of genetic-marker data and information on environmental and clinical covariates.

Introduction

The incidence of type 1 diabetes (T1DM, IDDM [MIM 222100]) varies globally (Onkamo et al. 1999; Karvonen et al. 2000). Scandinavia is a high-incidence area, with incidence rates in childhood from 15–20 per 100,000 inhabitants per year in Denmark to >40 in Finland. Very recent data suggest that the incidence of T1DM is rising, including in already-high-incidence regions like Scandinavia (Onkamo et al. 1999; Karvonen et al. 2000; Svensson et al. 2002). The etiology of T1DM is unknown, but interaction of genetic and environmental factors seems necessary for disease development.

Several recent and ongoing studies are primarily aiming at unraveling the genetic basis of the disease. Focus has been on whole-genome screenings of families with affected sib pairs (ASPs) to detect chromosomal regions with evidence of linkage (Davies et al. 1994; Hashimoto et al. 1994; Concannon et al. 1998; Mein et al. 1998; Cox et al. 2001; European Consortium for IDDM Genome Studies [ECIGS] 2001). This approach has demonstrated the polygenic nature of T1DM. Thus, evidence for linkage to T1DM has been reported for >20 markers at a level of significance of P<.05 (nominal P value) (Pociot and McDermott 2002). However, it has not been possible to replicate the majority of the originally identified loci in later and larger whole-genome scans, and this has led to skepticism about this approach (Lernmark and Ott 1998; Altmüller et al. 2001).

Current methods for evaluating genome-scan data have typically been performed by searching for the marginal effects of a single putative trait locus. Complex traits like those of T1DM, however, may be the result of interactions at several trait loci, so the power to detect linkage may be increased by searching for several trait loci at once (Dupuis et al. 1995; Blangero and Almasy 1997). Methods for searching for multiple trait loci include stratifying on evidence for linkage at one locus while searching for another (Buhler et al. 1997; Farrall 1997; Cox et al. 1999). Most of these methods focus on two-loci traits, usually under the assumption that these trait loci are unrelated to each other, and their statistical usefulness for genomewide searches for susceptibility genes are not fully understood.

To overcome the built-in limitations of the statistical methods, we see a need to explore new strategies for detecting sets of marker loci linked to multiple interacting disease genes—also across different chromosomes. The use of artificial neural networks has been proposed as such an approach (Lucek and Ott 1997; Lucek et al. 1998; Bhat et al. 1999; Curtis et al. 2001; Marinov and Weeks 2001; Ritchie et al. 2003). Data mining was also suggested as a method of fulfilling this requirement and was proposed for analyzing genome-scan data (Anonymous 1999) and has been applied to the analysis of a limited number of SNPs (Weir et al. 1999) and, recently, to genomewide simulation data from the Genetic Analysis Workshop 12 (Flodman et al. 2001). Data mining techniques include predictive modeling, clustering analysis, dependency modeling, data summarization, and change and deviation detection based on, for example, decision-tree and artificial-neural-network approaches.

We have used data mining to examine the possible very-complex interaction of genes underlying T1DM. The analyses are on a model-free, nonparametric basis. The idea of applying data-mining technology to genomewide linkage data is attractive, in that it should be able to detect complex nonlinear interactions between multiple-trait loci.

We have tested whether this approach could identify the chromosomal regions found already with nonparametric linkage (NPL) analysis of the same data set as proof of concept, whether novel markers and/or marker combinations of predictive value could be identified, and, finally, whether such information could also be used to characterize the nondiabetic status.

Subjects and Methods

Genome-Scan Data

Rather than using simulated data, we have chosen to apply and evaluate the method on our recently published genome-scan data (ECIGS 2001). The data set results from analyses of 318 microsatellite markers in 331 multiplex families from Denmark and Sweden. These families included 375 ASPs, 188 unaffected sib pairs, and 564 discordant sib pairs, for a total of 1,586 individuals. Data were not completely compatible in the two data sets (i.e., from Denmark and Sweden). To overcome that, and to obtain the most robust training and testing, 14 markers (of the 318 originally included) were excluded at this point: 2 markers on chromosome 7, 2 on chromosome 4, and 3 on chromosome 17. The remaining seven were single markers on different chromosomes.

Since unaffected individuals might be genetically susceptible and later develop T1DM, the stabilization age was established. This means that individuals younger than a certain age were excluded from some of the models used to identify specific effects. A population-specific stabilization age was determined on the basis of the 95% age-at-onset fractal, which was age 36 years in the Swedish and age 40 years in the Danish populations. This resulted in a reduction in individuals to 1,329, of which 56% had T1DM. Chromosome X data were not included in the analysis.

Data Mining

The mathematical framework for data mining has been described in detail elsewhere (Bradley et al. 1999). In brief, these methods are different from traditional statistical methods by being algorithms that have to be “trained” on the basis of knowledge/information in a database. Such inductive algorithms are useful for regression, classification, and segmentation of data. Inductive algorithms contain large numbers of parameters, which, through the training procedure, are adjusted automatically. The aim of the training procedure is to make the inductive model “as good as possible” to predict one or more output variables on new input data. To ensure that the trained model is as good as possible, it is important to avoid “overtraining” of the model. This means that the performance (i.e., misclassification rate) on training data and new data should be comparable. This is referred to as the ability of the models to generalize.

Rather than using the specific alleles of each marker—that is, the genotype (the two alleles)—we used the sum of the alleles. As an alternative to the sum, the two-dimensional set of numbers (x, y), where x and y correspond to the exact allele calling, was considered. Problems with this representation include the very large number of values each marker can have (100–200) in relation to the population size of the present study. The sum is symmetrical and is used as an integer, keeping the number of parameters at a low level (10–20) for each marker.

The two main approaches of data mining used in the present study were based on decision trees and artificial neural networks.

Decision Trees

Decision-tree learning can provide an informative model through which predictive rules are induced to solve classification problems (Breiman et al. 1984). The method uses a process known as recursive partitioning. Two decision-tree models were used in the present study, the C5.0 algorithm implemented in Clementine software, version 6.5 (SPSS), and the Tree Node software implemented in Enterprise Miner (SAS Institute).

Each of these trees applies entropy as a measure of information (see the appendix), which is used in the process of splitting the population into smaller and more-clean subgroups. Unlike neural networks, decision trees can handle data with missing values (any marker may contain blank values). Handling missing values is a delicate matter, in the sense that there is no consensus for selecting the one best procedure for doing so. In the current data set, the number of missing values for individual markers varied from 0.5% to 39%. The treatment of missing values by different algorithms differs at several points (see the appendix).

Marginal Markers and Marginal Trees

The tree algorithm might not always be able to identify signals from neighboring markers, for example, if they belong to the same haplotype block. In this situation, the tree will most likely find only one of the markers. We therefore introduce the concept of marginal markers. The first marginal marker is determined as the root of a pruned tree trained on all data. This is defined as the first marginal tree. The second marginal marker is then found as the root in a pruned tree trained on the same data set but without the first marker. This is defined as the second marginal tree. This process is continued until there are no markers left with enough information content to generate a tree. We adjusted the pruning parameters in such a way that the pruned marginal trees ended up using ∼15 markers. The C5.0 algorithm, which is a modification of the well-known C4.5 algorithm (Quinlan 1992), was used to identify the marginal markers.

Interaction between Markers

We assume that the predictive signal from a marker is correlated to the gain in entropy (also known as cross-entropy) caused by the marker’s binary split of the data set into cleaner subgroups. The basic idea is to search for combination of markers (i.e., interaction between markers) producing splits with high gain in entropy and thereby producing clean subgroups.

We have used the Tree Node in Enterprise Miner (SAS) to perform interaction analyses, because this tool is designed to perform the tedious but very important step of finding trees (rules) that have the same performance on the training and validation data set (i.e., ability to generalize) and produce clean groups. The performance is measured by the misclassification rate, R(T) (fraction of false positives and false negatives to the total number), of the tree T. Through use of stratification rules (e.g., nationality and affected status), data were divided into a training set containing 70% of the data and a validation set containing the remaining (30%) data. Training continues until all terminal nodes reach a minimum size (in the present study, selected as 19). After training was accomplished, manual inspection of the graph 1-R(T) for the validation data set indicated how to select the best subtree, TS, to avoid overtraining. Selected subtrees were then searched for terminal leaves with clean subgroups in the training and validation data so the R(T) value would be identical for the training and the validation sets—which is very important.

Neural-Networks Analysis

Neural networks consist of layers of nodes, in which the first one is the input layer and the last one the output layer. In between may be one or more “hidden” layers. Information is passed from one layer to the next in such a way that the input to a receiving node is the weighted output from all nodes in the previous layer. The output values from hidden nodes are normally a nonlinear function of the received input.

We have used three different models, all of the Multi-Layer Perceptrons (MLP) type (Bishop 1995). In these models, the input variables are transformed to binary variables corresponding to the number of categories for the variable. To obtain more-complex decision functions, the inputs are fed into a number of perceptron nodes, each with its own set of weight and threshold. The outputs of these nodes are then input into another layer of nodes, and so on. Hence, the output of the final layer of nodes is the output of the entire network. For the current analyses, we have used neural networks with one hidden layer and one, three, and six hidden nodes. In addition, the models differentiate in initialization and convergence values. For networks with one or six hidden neurons, 10 initial analyses with random parameters were used to identify the most robust training on the following number of iterations (maximum number of iterations for models with one or six hidden neurons was 500 and 200, respectively). The most robust parameter—that is, with the minimum error function—was used as the starting point for the analysis of the test data. For networks with three hidden neurons, 20 initial analyses were used (maximum iterations: 200). The Levenberg-Marquardt training testing procedure was selected, which stops the iterations when overtraining begins (Marquardt 1963).

Neural-network analysis was performed in different ways:

• 1. Searching predictive signals from neighboring markers in one chromosomal region. For this purpose, we have used neural networks trained on one window containing five neighboring markers. The network is expected to modify the weights so the marker alleles (genotypes) predict affection status—that is, so they recognize those markers located near the disease loci.

• 2. Searching predictive signals from interaction analysis between two different chromosomal regions. In this case, we have used models with two windows, each containing three neighboring markers. Again, the networks are expected to modify the weights so the interactions between marker alleles predict affection status; that is, recognizing interactions between markers in different chromosomal regions.

• 3. Validation of multiple loci interactions identified by decision-tree analysis. It was tested whether neural networks could confirm the most-significant rules found by decision trees involving several markers.

Software

We used SAS base, graph, insight, and stat, version V8; Enterprise Miner, version 4.1, from SAS Institute; and Clementine, version 6.5, from SPSS. All programs were run on a PC platform with Windows 2000 Professional (Microsoft).

Results

Decision-Tree Analyses

Table 1 shows the 26 markers identified by the decision-tree analyses in ranked order; that is, according to information determined by the GainRatio. Following the identification of these 26 markers, no additional markers with marginal effects could be identified.

Table 1.

The Marginal Markers Identified with Highest GainRatio

Ranka	Marker	Map Location(Kosambi cM)b	Groupc	GainRatio(× 1,000)	Single-Point NPL Scored
1	TNFA	45.85	a	13.58	36.97
2	D7S527	97.38	b	9.49
3	D6S300	103.45	c	8.45	4.27
4	D8S1771	50.05		6.99
5	D16S3131	50.60	d	5.71	2.36 (D16S407–D16S287)
6	D16S407	18.07	d	5.40	2.36 (D16S407–D16S287)
7	D9S147E	31.6		5.20
8	D3S1263	36.10		5.13
9	D2S206	240.79	e	5.10
10	D10S191	37.90	f	5.09
11	D8S504	.45		4.86
12	D16S423	10.36	d	4.78	2.36 (D16S405–D16S287)
13	D6S273	44.96	a	4.77	4.270
14	D6S314	143.40	c	4.56
15	D10S583	115.27		4.45	.90
16	D12S87	51.99		4.44
17	D18S57	62.84		4.27
18	D16S287	37.9	d	4.03	2.36 (D16S405–D16S287)
19	D8S88	102.62		3.87	1.388e
20	D5S429	179.11		3.56
21	D5S419	39.99		3.39	1.93 (D5S407)
22	D2S12522	260.63	e	3.09
23	TH	.55		3.06
24	D7S524	108.59	b	2.94	1.00e
25	D10S189	19.00	f	2.37
26	D17S798	53.41		2.32

^aRank refers to GainRatio value.

^bMap position is from Marshfield (Center for Medical Genetics).

^cMarkers belonging to the same chromosome region (<40 cM).

^dSingle-point NPL scores (ECIGS 2001). These values are from the analysis of the total Scandinavian population, whereas data mining was applied only to data sets from Denmark and Sweden.

^eValues obtained for either the Danish or Swedish population, whereas the NPL scores for these loci for the entire Scandinavian data set were <.85.

As seen in table 1, 14 of the 26 markers could be arranged in six groups according to their chromosomal location (groups a–f [table 1]). Markers were grouped when they appeared to cover the same signal; that is, corresponding to intervals <40 cM. It is interesting that most of the markers that could not be grouped with others were ranked low. For comparison, the single-point LOD scores (for regions with LOD scores >1) obtained by conventional NPL analysis of the data by ANALYZE (ECIGS 2001) are also shown in table 1. This demonstrated that data-mining analyses identified the most important observations from our classical linkage analyses. TNFA (marker for HLA, IDDM1) was the single marker with highest predictive value. Four markers covering a 39-cM region on chromosome 16, D16S423–D16S3131, were also identified as having high predictive value. In addition, the method identified regions on chromosomes 7 and 8 to be the most prominent novel regions of relevance for T1DM prediction. It is noteworthy that the method identified the INS locus (defined by the TH marker) as well.

Interaction Analysis

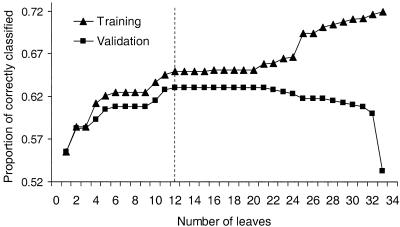
For the five marginal markers with highest GainRatios, interaction analyses were performed as described in the “Subjects and Methods” section. The total number of markers was 304, and, for each marker, the sum of the alleles had a range of 10–15 different values. A first step in the modeling was a reduction (filtering) of the number of markers to ∼80; that is, each of the five marginal trees was pruned to ∼15 markers, and no marker was recorded more than once, although a marker could be included in several marginal trees. An example of R(T) graphs for training and validation data sets are shown in figure 1. The curves show the proportion correctly classified in the training set (70% of total) and validation set (30% of total). From these graphs, the best subtrees were selected, marked by the vertical dotted line. These subtrees were then searched for terminal leaves with clean subgroups, in which R(T) had the same value in training and validation data sets. This resulted in the rules shown in table 2, in which the identified rules are based on group sizes 19–72. As an example, the exact rule for one of these trees (#6963) is given: if TNFA⩾19.5, D8S88<10.5, D16S320<16.5, D5S428<14.5, D6S300⩾11.5, and D7S486>21.5, then 18 (95%) of 19 subjects are correctly classified as having T1DM.

Figure 1.

Proportion of correctly classified subjects (1-R(T)) in the training set (-▪- curve; 70% of all data) and in the validation data set (--▴-- curve; 30% of total data), by use of the rules derived from the training data set. As training continues—that is, the number of leaves increases—more markers are selected, leading to improvement in correct classification on the training set. In the beginning of training, the correct classification rate 1-R(T) on the validation set is seen to follow the training set up to 12 leaves. After 20 leaves, 1-R(T) for the validation set begins to fall, indicating overtraining of the tree. The vertical dashed line marks the early stoppage; that is, the point from which subtrees were selected for further interaction analysis.

Table 2.

Interaction Analyses Based on Rules from Decision Trees^[Note]

Decision Tree Identified Rules and Markers	Status	No. Correct/No. (%)
Rules from tree 8415:
TNFA, D1S228, D5S419, D11S35, D16S407	T1DM	48/56 (86)
TNFA, D1S228, D5S419, D11S35, D1S468, D14S74	Non-T1DM	25/30 (83)
TNFA, D11S35, D13S173, D17S798, D19S225	Non-T1DM	25/25 (100)
Rule from tree 1081:
TNFA, D20S199, D6S300, D16S407, D3S1297, D3S1282	Non-T1DM	45/51 (88)
Rules from tree 9926:
TNFA, D5S407	T1DM	60/72 (83)
TNFA, D21S65, D16S407, D9S144, D17S789	T1DM	35/40 (88)
Rule from tree 454:
TNFA, D5S407, D17S934, D14S74	T1DM	25/28 (89)
Rule from tree 6963:
TNFA, D8S88, D16S320, D5S428, D6S300, D7S486	T1DM	18/19 (95)
Rules from tree 7328:
D7S527, D4S403	T1DM	21/24 (88)
D7S527, D16S407, D5S410, D21S270, D2S177, D8S284	T1DM	21/21 (100)
D7S527, D16S407, D6S314, D6S320, D17S798, D6S273	T1DM	21/21 (100)

Note.— Selected examples of rules generated for the first two marginal markers and for marginal marker number 15; that is, TNFA and D7S527. The first column shows six rules and, for three of them, two or three subleaves of the rule. Column 2 shows whether the established rule is predictive for T1DM or non-T1DM status, whereas the last column shows the number and percent of correctly classified individuals and of the total number of individuals in each group defined by the rule.

We then estimated the probability of finding an almost-clean subgroup of size n without any prior information. We supposed that the probability p(D=1)=0.56 and p(D=2)=0.44 in the random experiment, drawing n individuals from a population of 1,329 can be applied in a binomial distribution, B[x,n,p(D=1)], is a reasonable assumption, as long as n≪1,329. The number of individuals with D=1 is called x. The binomial distribution B(x,n,p) can be approximated by a normal distribution Φ(z), where z is determined by z=(x-n^*p)/√[n^*p^*(1-p)]. This approximation is valid as long as min[n^*p,n^*(1-p)]>5 (a rule of thumb generally accepted). From such calculations, we found all probabilities of finding an “almost-clean” subgroup of the defined sizes with no prior information to be ∼10⁻⁵.

Neural-Network Analyses

Neural-network analyses essentially identified the same regions in single-marker analyses as found by the decision-tree algorithms, although the data were more complex to interpret. The three neural-network models used showed similar data, and data shown are mean values of these models. Examples of data for chromosomes 6, 7, and 8 are shown in table 3, in which the markers of the separate windows (five marker windows) are shown. A plus sign (+) denotes significant predictive value of the markers. Markers in bold italics were also defined by the decision-tree–based methods and are likely to concur with this prediction. For chromosome 6, these markers include D6S273, TNFA, D6S300, and D6S314; for chromosome 7, they were D7S524 and D7S527; and for chromosome 8, the markers were D8S1771 and D8S88.

Table 3.

Neural-Network Analysis of Single Markers (Five-Marker Window)

Chromosomeand Windowa	Markersb	Predictionc
5:
1	D6S470, D6S260, D6S276, D6S273, TNFa	+
2	D6D260, D6S276, D6S273, TNFa, D6S291	+
3	D6S276, D6S273, TNFa, D6S291, D6S1650	+
4	D6S273, TNFa, D6S291, D6S1650, D6S402	+
5	TNFa,D6S291, D6S1650, D6S402, D6S286	+
6	D6S291, D6S1650, D6S402, D6S286, D6S300	−
7	D6S1650, D6S402, D6S286, D6S300, D6S283	−
8	D6S402, D6S286, D6S300, D6S283, D6S268	−
9	D6S286, D6S300, D6S283, D6S268, D6S287	−
10	D6S300, D6S283, D6S268, D6S283, D6S262	+
11	D6S283, D6S268, D6S283, D6S262, D6S314	+
12	D6S268, D6S283, D6S262, D6S314, D6S290	−
13	D6S283, D6S262, D6S314, D6S290, D6S305	−
14	D6S262, D6S314, D6S290, D6S305, D6S264	−
15	D6S314, D6S290, D6S305, D6S264, D6S281	−
7:
1	D7S531, D7S513, D7S507, D7S493, D7S629	−
2	D7S513, D7S507, D7S493, D7S629, D7S484	−
3	D7S513, D7S507, D7S493, D7S629, D7S519	−
4	D7S507, D7S493, D7S629, D7S519, D7S502	−
5	D7S493, D7S629, D7S519, D7S502, D7S669	+
6	D7S629, D7S519, D7S502, D7S669, D7S524	+
7	D7S519, D7S502, D7S669, D7S524, D7S527	+
8	D7S502, D7S669, D7S524, D7D527, D7S486	+
9	D7S669, D7S524, D7S527, D7S486, CFTR	−
10	D7S524, D7S527, D7S486, CFTR, D7S530	+
11	D7S527, D7S486, CFTR, D7S530, D7S684	+
12	D7S486, CFTR, D7S530, D7S684, D7S483	−
13	CFTR, D7S530, D7S684, D7S483, D7S550	−
8:
1	D8S504, D8S503, D8S552, D8S261, D8S1771	−
2	D8S503, D8S552, D8S261, D8S1771, D8S283	−
3	D8S552, D8S261, D8S1771, D8S283, D8S285	+
4	D8S261, D8S1771, D8S283, D8S285, D8S260	+
5	D8S1771, D8S283, D8S285, D8S260, D8S286	−
6	D8S283, D8S285, D8S260, D8S286, D8S273	−
7	D8S285, D8S260, D8S286, D8S273, D8S88	+
8	D8S260, D8S286, D8S273, D8S88, D8S257	+
9	D8S286, D8S273, D8S88, D8S257, D8S281	−
10	D8S273, D8S88, D8S257, D8S281, D8S198	+
11	D8S88, D8S257, D8S281, D8S198, D8S284	+
12	D8S257, D8S281, D8S198, D8S284, D8S272	+

^aWindows on chromosome 6, 7, and 8, used for training and prediction of diabetes, with neural networks. Each window contains five consecutive markers. A new window is defined by moving the gate one marker.

^b All the marginal markers identified by decision trees (in bold italics [see table 1]) on chromosome 6 and 7 are recognized by the neural networks. For chromosome 8, all marginal markers are recognized by the neural networks, with the exception of the first marker, D8S504, on chromosome 8.

^cA plus sign (+) indicates that the markers of a specific window have an increased predictive value; a minus sign (−) indicates that no increased predictive value was observed.

For interaction analyses, a double-window approach was used; that is, looking for interaction between two sets of markers. Window one includes markers 1, 2, and 3 of a certain chromosome; window two includes markers 2, 3, and 4; window three includes markers 3, 4, and 5; and so on, to windows including all 314 markers. Shown in table 4 are all observations with the highest increase (i.e., >8%) in prediction by interaction of markers of the two windows. Data shown represent the mean value of the three models tested. To generate these outputs, we set a cut-off at 20; that is, rules (interactions) were recorded when all markers used for defining the rule were complete in ⩾200 individuals. The exact numbers are shown in table 4. These analyses suggested evidence for several different interactions—that is, between chromosomes 1 and 16; between chromosome 6 (TNFA) and regions on chromosomes 1, 2, 4, 5, 6, 7, 10, 11, 16, or 17; and between chromosomes 12 and 17.

Table 4.

Interaction Analyses Based on Neural Network^[Note]

	Three Consecutive Markers in Window
Combinationa	1	2	Nb	Predictive Valuec(%)
1	D1S199, D1S470, D1S255	D6S273, TNFA, D6S291	259	8
2	D1S249, D1S229, D1S103	D6S273, TNFA, D6S291	251	8
3	D1S508, D1S228, D1S199	D16S503, D16S515, D16S516	207	9
4	D2S177, D2S123, D2S139	D6S276, D6S273, TNFA	244	9
5	D4S418, D4S405, D4S398	D6S276, D6S273, TNFA	226	9
6	D4S398, D4S392, D4S1538	D6S276, D6S273, TNFA	263	8
7	D4S413, D4S2979, D4S415	D6S276, D6S273, TNFA	283	8
8	D4S418, D4S405, D4S398	D6S273, TNFA, D6S291	220	9
9	D5S428, D5S409, D5S421	D6S276, D6S273, TNFA	264	9
10	D5S210, D5S410, D5S422	D6S305, D6S264, D6S281	201	9
11	D6S276, D6S273, TNFA	D6S268, D6S287, D6S262	229	10
12	D6S273, TNFA, D6S291	D6S268, D6S287, D6S262	220	10
13	D6S276, D6S273, TNFA	D6S287, D6S262, D6S314	244	9
14	D6S276, D6S273, TNFA	D7S484, D7S519, D7S502	207	9
15	D6S276, D6S273, TNFA	D8S552, D8S261, D8S1771	215	9
16	D6S276, D6S273, TNFA	D9S43, D9S15, D9S175	237	10
17	D6S273, TNFA, D6S291	D9S43, D9S15, D9S175	225	10
18	D6S276, D6S273, TNFA	D9S15, D9S175, D9S1843	208	9
19	D6S276, D6S273, TNFA	D10S537, D10S201, D10S583	209	8
20	D6S276, D6S273, TNFA	D10S583, D10S192, D10S190	229	9
21	D6S273, TNFA, D6S291	D10S583, D10S192, D10S190	221	8
22	D6S276, D6S273, TNFA	D10S192, D10S190, D10S217	241	9
23	D6S276, D6S273, TNFA	D10S190, D10S217, D10S212	244	9
24	D6S276, D6S273, TNFA	D11S569, D11S899, D11S904	239	9
25	D6S273, TNFA, D6S291	D11S569, D11S899, D11S904	232	10
26	D6S273, TNFA, D6S291	D12S368, D12S83, D12S43	260	10
27	D6S276, D6S273, TNFA	D14S51, D14S267, D14S1010	208	10
28	D6S287, D6S262, D6S314	D16S261, D16S411, D16S415	210	8
29	D6S273, TNFA, D6S291	D16S516, D16S289, D16S422	250	9
30	D6S276, D6S273, TNFA	D17S926, D17S513, D17S786	225	8
31	D6S276, D6S273, TNFA	D17S799, D17S953, D17S798	230	9
32	D6S273, TNFA, D6S291	D17S799, D17S953, D17S798	228	9
33	D6S276, D6S273, TNFA	D18S52, D18S62, D18S53	221	9
34	D11S569, D11S899, D11S904	INT2, D11S916, D11S901	214	8
35	D12S99, D12S77, D12S358	D17S799, D17S953, D17S798	207	9

Note.— Interaction analysis using a double-window approach, with three consecutive markers in each window (see text for details).

^aThirty-five combinations were observed with ⩾8% increase in prediction.

^bN = the total number of individuals with complete genotyping for this rule.

^cThe exact increase in predictive value.

Comparison of Results from Decision-Tree and Neural-Network Analyses

The decision-tree– and neural-network–based methods may not identify the exact same marker for a susceptibility locus, owing to the different algorithms on which the methods are based, as well as the way they handle missing values and information obtained from unaffected individuals. However, substantial overlap of identified markers was obtained using both approaches. This was the case for both single-marker and interaction analyses, although some markers showed up only in one of the analyses.

Marginal markers found by decision trees were compared with those markers found by neural networks through use of one window. A high degree of overlap between results from the different models was observed, as exemplified by comparison of markers in tables 1 and 3.

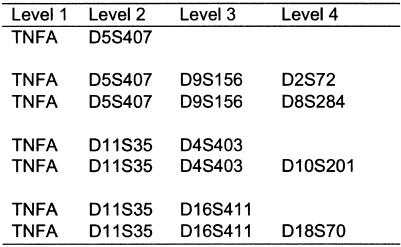
Generally, it is difficult to compare interaction analysis performed by decision trees and neural networks, owing to problems caused by different ways of handling missing values. As an example, we have compared the performance of a neural network trained at a window holding 10 markers, which were found as the uppermost four levels in the first marginal tree with TNFA as the root of the tree. A neural network with three hidden neurons was trained looking for consensus between the two different models. The results are shown in figure 2. It should be noted that the 10 markers analyzed have several missing values, which cannot be handled by a neural-network model, and, therefore, training and validation data are reduced by ∼50%. A weight matrix for the neural-network training was therefore developed (table 5). Table 5 shows that TNFA, D5D407, D11S35, D16S411, D4S403. and D18S70 have high scores, indicating importance. Figure 2 is in accordance with several rules from the tree structure (table 2).

Figure 2.

Interacting markers identified both by decision-tree logarithms and neural networks. Markers shown are from the uppermost four levels in the first marginal tree, with TNFA as the root of the tree. Neural-network analyses were able to identify interaction between four markers (levels 1–4). There was substantial overlap between these observations and data obtained by decision tree–based analyses (see table 2). Including more levels or going to the next marginal marker (i.e., D7S527) did not reveal any significant observations.

Table 5.

Representation of the Weight Matrix for the Neural-Network Training Using 10 Markers^[Note]

	Marker Weight in Hidden Layer of Hidden Neuron
Markers Testedin Neural Network	H11	H12	H13
D10S201A	2.0484236754	4.6192772063	2.4947083718
D11S35A	−7.934751706	7.2841126372	−7.685113595
D16S411A	−6.959237296	−.039549253	−7.946016641
D18S70A	−8.479866259	−5.542465429	−.561232083
D2S72A	−.604908428	3.5962258611	−1.798954882
D4S403A	−5.651504639	.6727007998	−2.718476328
D5S407A	−3.016408132	−8.64709955	2.2380102222
D8S284A	−2.39344054	.1036999572	−2.983227802
D9S156A	−1.003564901	.4589297045	−.040987975
TNFAA	4.3589767151	6.1373890004	−9.450707354
Bias	6.2328088752	−3.232536179	6.1562568365
Output neuron	1.0260184223	−1.132891966	−.931969555
Bias output neuron	.8339701434

Note.— All hidden neurons and the output neuron have a bias, and they are all considered as weights, as outlined in equation A1 of the appendix. The data show that TNFA, D5D407, D11S35, D16S411, D4S403, and D18S70 have high scores, indicating importance. It is possible to calculate a measure for the importance of individual parameters. This measurement is often referred to as the sensitivity and the values of the sensitivity as the contribution values.

Discussion

The search for genes that predispose to T1DM provides an example of multiple genetic risk factors of varying effect. One locus has a major effect (HLA, IDDM1), whereas other loci have small—yet significant—individual effects. Furthermore, susceptibility may be due to loci that interact independently or may be dependent on the genotype at another locus. Thus far, the performed genome scans suggest extensive complexity and the need for developing new analytical tools.

We have used data-mining tools to analyze genome scan data from families with T1DM. Compared with most novel methods developed, data mining represents a combination of several methods that are based on pattern recognition. It is interesting that a few other methods using pattern recognition have recently been applied to genetic data (Nelson et al. 2001; Ritchie et al. 2001; Lauer et al. 2002). Data mining is not a new methodology, but it has only recently been applied to biological and genetic data (Bassett et al. 1999; Toivonen et al. 2000; Flodman et al. 2001; Perez-Iratxeta et al. 2002; van Driel et al. 2003). The advantage of inductive methods is that they can include a large number of variables and allow simultaneous testing of all markers in a single test and have the potential to model complex nonlinear relationships without the need to construct complicated statistical models.

The data-mining process identifies not only single markers versus disease, but also combinatorial marker-marker interactions as they relate to disease status. The training process finds and uses correlations between these to obtain the best possible prediction parameters. A trained inductive method can be used to analyze a set of new data, as well as for further training of the inductive algorithms. The quality and amount of the data sets used in the training procedure are important. The data input must be standardized and without duplications, and the larger the number of data sets with “important” information is, the more the validity of the output variable will increase.

First, we have used the sum of the alleles rather than the full genotype. This was done primarily to reduce the size of the parameter space. As shown in table 1, this transformation of the genotype allowed confirmation of observations from classical NPL analysis. We have made several permutation tests by permuting, for example, the disease status to confirm that the list of marginal markers shown in table 1 were indeed generated on the basis of information using the sum of alleles (data not shown). All the major linkage peaks from NPL analyses (ECIGS 2001) were also identified in the current analysis. It is interesting that the markers identified on chromosomes 2 and 10 correspond to linkage peaks found in other genome scans (Cox et al. 2001). In addition, we found evidence for novel regions influencing disease predisposition on chromosomes 7, 8, 9, and 3 (ranked order; table 1). Second, decision-tree and neural-network analyses were capable of identifying the same interacting markers, as exemplified in table 4 and figure 2, further supporting that data-mining methods may be of value in studies of the probably quite complex genetics of multifactorial diseases, in casu T1DM. Third, sets of combinations of relatively few markers can predict status as affected (T1DM) and unaffected (nondiabetic) (table 2). Even though the population sizes defined by such decision-tree rules are rather small, it might be hypothesized that combinations of only partly overlapping different markers could identify potentially different phenotypic subgroups of patients with T1DM. Since we found most of the probabilities for randomly picking such groups with no prior information to be ∼10⁻⁵, it can be concluded that the subgroups generated by pruning the trees are based on information achieved from entropy calculations of the genetic markers.

Of Danish patients with T1DM, ∼10% lack T1DM-predisposing HLA alleles (Pociot et al. 1994). Of particular interest may be that in the absence of HLA (TNFA) conferred risk, a relatively small number of markers in combination can correctly predict T1DM (table 2). A role for several of these markers when they occur in combinations with HLA (TNFA) is also evident from tables 2 and 4 and may suggest that genes located near these markers might be of particular relevance for T1DM pathogenesis.

It is interesting that combinations of few markers were also able to predict protection status. This may reflect the fact that protective HLA alleles are dominant (Undlien et al. 2001) and that most of the loci shown to be relevant for the genetics of the nonobese diabetic mouse—a model of T1DM in man—involve aberrations in protective mechanisms (Todd and Wicker 2001).

Furthermore, we identified interaction between loci on chromosomes 6 (HLA) and 4p, 5p, 11q, and 17q; between chromosomes 7 and 16; between chromosomes 2 and 8; between chromosomes 11p (INS) and 7; and between chromosomes 6q and 16. Interactions between loci on the same chromosome were also observed. Some of these interactions have also been observed in conditioned analyses of genome-scan data in other studies (Cox et al. 2001; ECIGS 2001).

A large body of evidence indicates that inherited genetic factors influence both susceptibility and resistance to the disease. Linkage analysis using ASPs is looking for increased sharing and therefore is not well suited for identifying protective gene variants. By including and analyzing information on unaffected individuals—including calculating a stabilization age—data mining may provide information on regions most likely to harbor protective variants. The present data suggest that, for example, the TNFA-D11S35-D13S173-D17S798-D19S225 combination may be of particular interest in this regard, since the rule defined by these markers gave rise to a subgroup of only nondiabetic subjects (table 2).

The results obtained by different methods in data mining indicate that the methods are robust to missing and erroneous data. Typically, linkage analysis is performed with likelihood-based methods. There are practical reasons for this but also limitations. The methods have been developed for analyzing monogenic diseases and are more suitable for those diseases than for complex ones. On the other hand, rigid statistical models give possibilities for constructing CIs and test statistics for significance testing, which is not straightforward in the approach presented here. However, the methods used in the present study split data into training and validation sets, and only results replicated in the validation sets are recorded. As seen from figure 1, the majority of rules generated in the training set did not apply to the validation set.

Complex diseases like T1DM are major challenges for gene mapping. It in interesting that the current analyses support the concept that epistasis is a ubiquitous component of the genetic architecture of common diseases and that complex interactions are more important than the independent main effects of any individual susceptibility gene, with the exception of HLA in T1DM. Environmental factors, gene-environment interactions, and gene-gene interactions may further complicate the genetic etiology. The power of linkage analysis to detect minor genes is low, even in large data sets. We believe that the approach adopted here may allow analyses of some of the complex characteristics as well.

It should be stressed that the purpose of the present study was to evaluate the strength of combining several analytical tools rather than to establish the best possible prediction tool for specific rules. The strategy used was primarily to establish rules for marker interactions with the ability to generalize by decision trees and then validate the rules by neural-network analysis. Thus, we have avoided overtraining of the models. An “overtrained” algorithm may be extremely predictive only for the particular data set used in the training procedure training, whereas a “properly trained” algorithm should be trained so that it becomes generally predictive for different data sets with the same overall genetic background, thus excluding “data set–specific” classification traits in the algorithms. It is obvious that such analyses can be expanded; for example, more neural–network architectures could be examined, since this was shown to be important when only neural networks are used for modeling gene-gene interactions (Marinov and Weeks 2001; Ritchie et al. 2003).

The current study, which is the first comprehensive data-mining analysis of genome-screen data, has defined a number of rules (interaction between loci) and could be viewed as a hypothesis-generating tool identifying interaction between genes close to the involved marker loci. Whereas this information may be directly valuable in screening for predisposition to diabetes, the specific genes, as well as the functional mechanisms behind the findings, should be further investigated.

In addition to genetic-marker data, information on environmental and clinical covariates may be included in the analyses. These may include nutritional factors, demographic data, information on infections, etc. Quantitative measurements related to T1DM diagnosis, like immune-response measurements or serum autoantibodies, may be included. Such measurements might actually have a simpler genetic basis than the disease per se, since the disease state may result from very complicated and heterogeneous processes. Consequently, we believe that the approach outlined in this study may have wide applicability to the analysis of complex diseases and pathways, including the analysis of a vast amount of complex data appearing from transcriptome and proteome analysis.

Appendix

Each marker is defined by the two specific alleles, the genotype. To use the information contained in the genotype of a marker, we introduce the sum of the alleles in the genotype. The sum is symmetrical and is used as an enteger, keeping the number of parameters on a low level (10–20) for each marker. A decision tree uses a process called recursive partitioning of the population in pure subgroups, in the sense that individuals in a subgroup belong to the same class. An important function in the partitioning is the entropy introduced by Shannon (1949).

Entropy

B is the total population and D is a categorical variable that equals 1 for individuals with diabetes and 2 for individuals without diabetes. s(M) is the sum of the alleles for a random marker M. A class division of M(B) into classes M_U and M_O, which are defined as 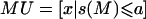and 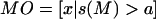, respectively, where a is the split value. In each of the two classes, M_U and M_O, the distribution of affected and unaffected is calculated. In general, if we are given a probability distribution P=(p1,p2,…,pn) then the information conveyed by this distribution, also called the “entropy of P,” is

Drawing a random individual from population B, the information I[M(B),D] for the class division M(B) is defined as the mean value:

where p(M_U) and p(M_O) are the probabilities for an individual to be drawn from M_U or M_O, and

and

where p(M_U_1), p(M_U_2), p(M_O_1), and p(M_O_2) are the probabilities for D=1 or D=2 in each of the partitions of B.

The difference in achieved information is the Gain, defined as

The Gain measure is used by the Tree Node in Enterprise Miner (SAS Institute). GainRatio is estimated by weighting the Gain with the information I[M(B)] of the class division M(B) and is used to compensate for skewed, but potentially interesting, distributions

and

The GainRatio measure is used by C5.0 in Clementine version 6.5 (SPSS).

Handling Missing Values

Missing values will often affect statistical models, and many models exclude incomplete data. If incomplete data are included in the models, their “hierarchical” ranking will often reflect the number of missing values for the different markers. Some of the models we have developed seem very robust, whereas others are more sensitive to missing data.

The tree node.—All observations having missing values for the marker under evaluation are assigned to have the same unknown value and are placed in the branch that makes the split have the highest Gain. The branch may or may not contain other observations.

The C5.0 algorithm.—Details about the C5.0 and C4.5 algorithms are reported by Quinlan (1992). It turns out that, when creating a split, observations with a missing value in the splitting variable (marker) are discarded when computing the reduction in entropy, and the entropy of a split is computed as if the split made an additional branch exclusively for the missing values. When applying a splitting rule to an observation with a missing value on the splitting variable, in case of a binary split, the observation is replaced by two observations, and each new observation is assigned a weight equal to the proportion of observations used to create the split sent into that branch.

The neural-network models.—Neural networks evaluate the influence of the variables, as described in equation A1 in the following section (“Neural-Network Models”). Opposite the trees, which evaluate the information in each variable separately before it is selected as a split variable, the neural networks treat combinations of variables. By this reasoning, we have to exclude all observations with missing values for the markers represented in the windows under evaluation. For some of the windows containing five or six markers, >50% of the observations have to be excluded.

Neural-Network Models

Following the outputs of the final layer of nodes in the network, binary variables are combined in a decision function of the form

where z is the frequency that needs to be modulated, X is the vector of independent variables, A is a matrix, b_i is a bias vector, and d is a scalar with parameters to be estimated, g and h are activation functions, c_i are weight parameters used for the linear combination of activation functions also to be estimated, and i denotes the number of hidden neurons; only one hidden layer is used in our model.

As activation function g for the hidden layer and h for the output layer, we have selected:

and

MLPs suffer from many problems; training may take several iterations to converge. Also, MLPs are prone to overfitting without some sort of capacity control. To control for capacity, we have used the methods of early stopping and network complexity. The method of early stopping tracks the performance of the network by use of a separate validation set. Typically, the error of the validation set will decrease as the network fits the data and then increase as the network fits the idiosyncrasies of the noise in the training data. Increasing the number of hidden nodes increases the expressiveness of the hypothesis space of the network (network complexity).