Abstract
One of the first and most important steps in planning a genetic association study is the accurate estimation of the statistical power under a proposed study design and sample size. In association studies for candidate genes or in fine-mapping applications, allele and genotype frequencies are often assumed to be known when, in fact, they are unknown (i.e., random variables from some distribution). For example, if we consider a diallelic marker with allele frequencies of 0.5 and 0.5 and Hardy-Weinberg proportions, the three genotype frequencies are often assumed to be 0.25, 0.50, and 0.25, and the statistical power is calculated. Unfortunately, ignoring this source of variation can inflate the estimated power of the study. In the present article, we propose averaging the estimates of power over the distribution of the genotype frequencies to calculate the true estimate of power for a fixed allele frequency. For the usual situation, in which allele frequencies in a population are not known, we propose placing a prior distribution on the allele frequency, taking advantage of any available genotype information. This Bayesian approach provides a more accurate estimate of power. We present examples for quantitative and qualitative traits in cohort studies of unrelated individuals and results from an extensive series of examples that show that ignoring the uncertainty in allele frequencies can inflate the estimated power of the study. We also present the results from case-control studies and show that standard methods may also overestimate power. As discussed in this article, the approach of fixing allele frequencies even if they are not known is the common approach to power calculations. We show that ignoring the sources of variation in allele frequencies tends to result in overestimates of power and, consequently, in studies that are underpowered. Software in C is available at http://www.ambrosius.net/Power/.
Introduction
In a genetic association study, the goal is to test for an association between one or more genetic variants and a phenotype of interest and to estimate the magnitude of the association. In these studies, tests are routinely conducted on functional polymorphisms, positionally selected polymorphisms, or haplotypes. SNPs are increasingly forming the backbone of these studies. Two different approaches are frequently used to identify the SNP characteristics assumed in the power analysis. In the first approach, a relatively small number of individuals (e.g., 10–20) is genotyped to verify previously identified SNPs and to obtain crude estimates of the allele frequencies. The SNPs that have some minimum allele frequency (e.g., 0.10) are then genotyped in the sample of interest, and a test for association is performed. In the second approach, one that is frequently employed in candidate-gene studies, polymorphisms are identified through a literature search or public databases, and allele frequency estimates from these published studies are then used to compute power. A critical assumption in these calculations is that the estimated allele frequencies from the small sample or other populations exactly equal the underlying allele frequencies in the population being considered. In general, the validity of this assumption is not explored and is seriously suspect because (1) there is important allele frequency heterogeneity across different populations, even within the same ethnic group, and (2) the estimates are merely estimates and are random variables from some often unknown distribution. For subsequent genotype-based analyses, power calculations often make the additional assumption that the genotype frequencies can be estimated from the assumed allele frequencies under the assumption of Hardy-Weinberg proportions. It is clear that, if genotype frequencies are known a priori, calculation of power can be performed using standard statistical methods and software (e.g., Elashoff 2000). We hold that allele and genotype frequencies are rarely known a priori when designing a study. An important, classic example of when genotype frequencies are known is when one wishes to calculate the ad hoc power to detect meaningful differences when the primary results are negative (see, e.g., Ghosh et al. 2000).
Power analysis methods have been well developed for continuous and binary phenotypes when the sample sizes in the two or more groups are fixed (i.e., when frequencies are known) (Searle 1971; Fleiss 1981; Sahai and Khurshid 1996). However, we were unable to find any previous work that deals with the problem of calculating power when the group sizes are not fixed but when they follow an assumed probability mass function. Lalouel and Rohrwasser (2002) provide a nice review of power analysis for case-control studies of genetic association. For family-based tests of association, there is considerable literature on the calculation of power. For example, power for the family of transmission/disequilibrium tests (TDT) (Spielman et al. 1993) has been examined extensively (Long and Langley 1999; Wang and Sun 2000; Deng and Chen 2001; Lange and Laird 2002; McGinnis et al. 2002; Shih and Whittemore 2002).
The idea of integrating over distributions of unknown parameters (i.e., allele frequency uncertainty in a sample) to estimate the power of genetic association studies was discussed by Schork (2002). In his article, Schork (2002) mentions that a beta prior might be used for allele frequencies and proposes using empirical estimation of the allele probability density function. Schork (2002) focuses on a case-control design and states that it would be of “great value” to explore other study designs and methods for quantitative traits.
In this article, we describe an approach and computer software (software in C is available at the authors' Web site) that computes power for candidate polymorphisms while accounting for allele frequency uncertainty under a cohort design for both qualitative and quantitative traits, as well as under a case-control design. In the case in which we know a priori the population allele or genotype frequencies, we propose to model the sample counts under a multinomial distribution and average the statistical power over this distribution. In the predominant situation, in which we do not know the population allele or genotype frequencies, we use Bayesian methods to expand upon the above approach by placing a beta prior distribution on the allele or genotype frequencies. We explore the effects of ignoring these two sources of variation via a series of examples and illustrate the methods with both quantitative and qualitative traits in cohort studies and case-control studies of unrelated individuals. The effect of ignoring these sources of variation can range from small to substantial, and it is important to calculate the magnitude of the effect when planning a candidate polymorphism association study.
Methods
We will begin by examining methods for cohort studies. Once we have developed these methods, we can modify them slightly for use in case-control studies.
Notation
We assume that we have a diallelic marker with alleles A and B, with genotypes in Hardy-Weinberg proportions, and that the population frequency of allele A is pA. We assume that we have a total sample of size N individuals, where n1 is the number of AA, n2 is the number of AB, and n3 is the number of BB individuals, such that n1+n2+n3=N. In designing most genetic association studies, we specify N and not the vector 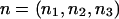 .
.
If we know n, the significance level of the test (α), the statistical test (T), the model (M), and the assumed alternative hypothesis (A), then we can calculate the statistical power through use of standard methods, which are described in the next subsection and in the appendix. Denote this power as 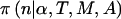 . For brevity of notation, we assume that α, T, M, and A are fixed, and we will denote power for a specific n simply as
. For brevity of notation, we assume that α, T, M, and A are fixed, and we will denote power for a specific n simply as 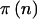 .
.
Standard Methods
If the subjects’ genotypes are known a priori, calculation of power can be performed using existing methods and software. For quantitative traits, the general linear model is used for most comparisons; for qualitative traits, Fisher’s exact test or the χ2 test are frequently used. Details of these methods are included in the appendix. Searle (1971) provides a discussion of methodology and power for the general linear model. Tests of proportions (Fisher’s exact and χ2 tests) are discussed by Sahai and Khurshid (1996) and Fleiss (1981). With a fixed sample size and a fixed alternative hypothesis, software readily exists to calculate power (e.g., Elashoff 2000). Unfortunately, subjects’ genotypes are rarely known a priori when designing a study. In a typical study, we recruit N subjects, collect genotypic and phenotypic data on them, and perform the analysis. In this case, the observed genotype frequencies are random variables.
Example
Let us first consider a simple example. Assume a dominant–mode-of-inheritance model in which genotypes AA and AB predispose individuals to one phenotype and genotype BB predisposes individuals to a different phenotype. Further assume that we are designing a study with eight subjects and could have anywhere from zero to eight AAs and ABs. If we have zero or eight, then there would be no power to detect a difference, because there would be no people in one of the two groups. As the number of AAs and ABs increases from zero to eight, the power will rise and then fall again. An example can be seen in table 1. In this example, we calculate power for a dominant effect when N=8 and α=0.05. For the quantitative trait, we assume that μAA=μAB=1, μBB=3, and that the within-group SD (σ) is 1, where μAA is the mean of the AA individuals. For the qualitative traits, we assume that the penetrances are 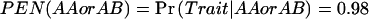 and
and 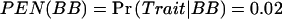 . The columns headed by
. The columns headed by 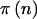 indicate the power to detect effects of these magnitudes if we observe the number of people indicated in the first two columns for quantitative and qualitative traits using the Fisher’s exact and arcsine methods. (For details, see the “Implementation Details” subsection and the appendix.) The example is artificial, because the differences are larger than would be expected in practice, but it serves to illustrate the point. Depending on the observed genotype distribution, the actual power can range considerably, as seen in the third through fifth columns. The last two columns of table 1 will be discussed in the “Motivational Example” subsection.
indicate the power to detect effects of these magnitudes if we observe the number of people indicated in the first two columns for quantitative and qualitative traits using the Fisher’s exact and arcsine methods. (For details, see the “Implementation Details” subsection and the appendix.) The example is artificial, because the differences are larger than would be expected in practice, but it serves to illustrate the point. Depending on the observed genotype distribution, the actual power can range considerably, as seen in the third through fifth columns. The last two columns of table 1 will be discussed in the “Motivational Example” subsection.
Table 1.
|
n |
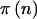 a a |
|||||
| nAA+nAB | nBB | QT | FE | AS | Wexpected | WBayesian |
| 0 | 8 | 0 | 0 | 0 | .0039 | .0220 |
| 1 | 7 | .3507 | 0 | .6729 | .0312 | .0725 |
| 2 | 6 | .5373 | .8508 | .8835 | .1094 | .1364 |
| 3 | 5 | .6295 | .8508 | .9412 | .2187 | .1874 |
| 4 | 4 | .6569 | .8508 | .9535 | .2734 | .2035 |
| 5 | 3 | .6295 | .8508 | .9412 | .2187 | .1779 |
| 6 | 2 | .5373 | .8508 | .8835 | .1094 | .1223 |
| 7 | 1 | .3507 | 0 | .6729 | .0312 | .0610 |
| 8 | 0 | 0 | 0 | 0 | .0039 | .0171 |
QT = quantitative trait; FE = Fisher's exact test; AS = arcsine approximation.
Multinomial Distribution
The above example illustrates the effect that the observed genotype frequencies have on power. Assume that pA is a known fixed quantity and that the alleles are in Hardy-Weinberg proportions. The observed genotype frequencies then follow a multinomial distribution,
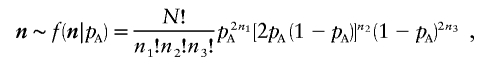 |
with expected counts E[n]=[Np2A,2NpA(1-pA),N(1-pA)2]. Assume for a moment that pA=0.5. We would then expect that 25% of our sample would be AA, 50% would be AB, and 25% would be BB, but there will be variability in these proportions. For example, if there were a total of 4 subjects, we would observe 1 AA, 2 ABs, and 1 BB with probability
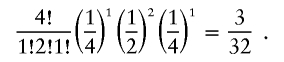 |
Similarly, if there were a total of 100 subjects, we would observe 25 AAs, 50 ABs, and 25 BBs with probability 0.0089.
For each realization of n, we can calculate power. Averaging across all possible realizations of n results in the expected power for a fixed pAas
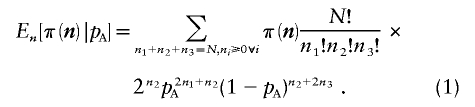 |
Beta Prior
In most problems, we do not know pA but either use an estimate of it from previous data or apply a plausible value. In this article, we will assume that the distribution of pA can be described, using a beta prior with parameters γ and δ, as
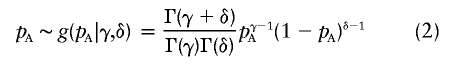 |
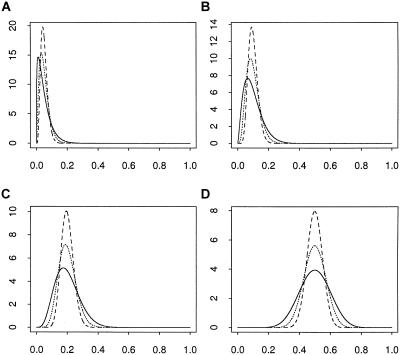
for γ⩾1 and δ⩾1. The mean of this distribution is γ/(γ+δ), and the variance is 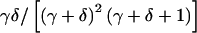 . By varying γ and δ, the mean can range between 0 and 1. The variance can be changed by scaling γ and δ by any positive constant, so long as min(γ,δ)⩾1. Examples of beta prior distributions are given in figure 1. We use a beta prior because it is constrained to [0,1], is quite flexible, and allows us to average over the prior distribution in closed form.
. By varying γ and δ, the mean can range between 0 and 1. The variance can be changed by scaling γ and δ by any positive constant, so long as min(γ,δ)⩾1. Examples of beta prior distributions are given in figure 1. We use a beta prior because it is constrained to [0,1], is quite flexible, and allows us to average over the prior distribution in closed form.
Figure 1.
Example of the beta prior. Within each figure, the three lines are for γ+δ=25, 50, and 100, with γ and δ chosen so that the means are 0.05 (A), 0.1 (B), 0.2 (C), and 0.5 (D). The curves become more concentrated (i.e., they have higher peaks) as γ+δ increases. In these examples, the distributions represented are for the less common alleles.
The question of how the choice of γ and δ affects power is an important one. To answer this question, let 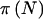 denote the power for a total sample of size N, taking into account the variability in genotype frequencies given pA and the uncertainty in pA. The function
denote the power for a total sample of size N, taking into account the variability in genotype frequencies given pA and the uncertainty in pA. The function 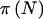 can be thought of as the average
can be thought of as the average 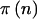 . Using properties of conditional expectations, we can write
. Using properties of conditional expectations, we can write 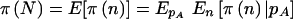 , where the inner expectation is taken with respect to the distribution of n conditional on pA, and the outer expectation is taken with respect to the distribution of pA. Note that the order of summation and integration can be exchanged, which allows the problem to be greatly simplified. After making the switch, we can collect the powers of pA and (1-pA) as 01p2n1+n2+γ-1A(1-pA)n2+2n3+δ-1dpA, which equals
, where the inner expectation is taken with respect to the distribution of n conditional on pA, and the outer expectation is taken with respect to the distribution of pA. Note that the order of summation and integration can be exchanged, which allows the problem to be greatly simplified. After making the switch, we can collect the powers of pA and (1-pA) as 01p2n1+n2+γ-1A(1-pA)n2+2n3+δ-1dpA, which equals
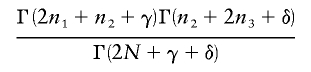 |
(equation 6.2.1 of Abramowitz and Stegun [1965]). The result is
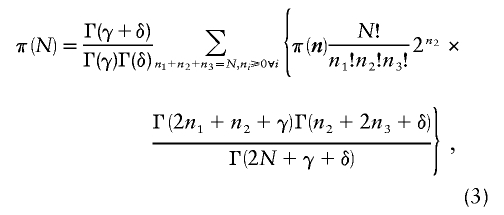 |
which is only slightly more difficult to evaluate than equation (1).
The question is, then: “What beta prior distribution do we assume for pA?” In the absence of previous data, we could assume that all values of pA are equally likely (i.e., a uniform prior). We could improve upon the uniform prior by genotyping a number of subjects to get an estimate of the allele frequency; if we use an elementary result in Bayesian statistics, and if we observe xA copies of the A allele in m individuals (2m alleles), then the posterior distribution of pA is (if we assume a uniform prior) 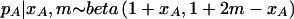 . This would be a reasonable prior distribution to use for the calculation of power. Alternatively, one could use nonstatistical arguments to justify the use of an empirical distribution from another population for the same SNP or from the same population for a different SNP. In any case, plots of equation (2) can be used to help decide on a reasonable prior distribution. Under the assumption of random mating within one population, it is reasonable to assume that the distribution of pA would be unimodal, which cannot be assumed in the situation discussed by Schork (2002). If the distribution is unimodal and restricted to the interval between 0 and 1, the family of beta distributions provides a rich set of possible distributions.
. This would be a reasonable prior distribution to use for the calculation of power. Alternatively, one could use nonstatistical arguments to justify the use of an empirical distribution from another population for the same SNP or from the same population for a different SNP. In any case, plots of equation (2) can be used to help decide on a reasonable prior distribution. Under the assumption of random mating within one population, it is reasonable to assume that the distribution of pA would be unimodal, which cannot be assumed in the situation discussed by Schork (2002). If the distribution is unimodal and restricted to the interval between 0 and 1, the family of beta distributions provides a rich set of possible distributions.
Implementation Details
We have implemented this approach in the C programming language and Proc-StatXact (Mehta and Patel 1999). We used utilities, a sorting algorithm, and the log-gamma function from Numerical Recipes (Press et al. 1992). We used DCDFLIB (Double precision Cumulative Distribution Function LIBrary) to calculate probabilities of the normal, χ2, and F distributions (Brown et al. 1997; software available from the Department of Biomathematics and Biostatistics Free Code Archive Web site). Our program is freely available at the authors' Web site. Some of the algorithms for calculating the multinomial probabilities are based on algorithms by Chasalow (2002) (software available from the Comprehensive R Archive Network Web site). Both equations (1) and (3) use 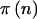 for all possible n. Note that the amount of computation time goes up as the square of N (run time is O[N2]) because there are (N+2)(N+1)/2 possible values of n.
for all possible n. Note that the amount of computation time goes up as the square of N (run time is O[N2]) because there are (N+2)(N+1)/2 possible values of n.
For quantitative traits, we have assumed use of the general linear model for hypothesis testing. Power for a fixed alternative hypothesis is calculated exactly for any sample size through use of methods described in detail in the appendix. For qualitative traits, we calculated power using Fisher’s exact test and the χ2 test. Fisher’s exact test is somewhat conservative for small sample sizes but does not rely on large sample approximations (Agresti 1990, pp. 65–66). In contrast, a χ2 test is less conservative but does require approximations based on the normal approximation to the binomial distribution. The calculations required to calculate 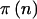 for Fisher’s exact test are quite complicated and difficult to program. Thus, we initially used Proc-StatXact to calculate
for Fisher’s exact test are quite complicated and difficult to program. Thus, we initially used Proc-StatXact to calculate 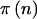 and read those values into our C program to calculate
and read those values into our C program to calculate 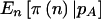 and
and 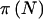 , using equations (1) and (3). We subsequently programmed Fisher’s exact test to create an entirely stand-alone program. In the examples shown in table 3, the differences between using Proc-StatXact’s implementation of Fisher’s exact test and ours never resulted in overall power differences >0.0003. Our program will either calculate power using our implementation of Fisher’s exact test or will read in power calculated externally (perhaps using Proc-StatXact).
, using equations (1) and (3). We subsequently programmed Fisher’s exact test to create an entirely stand-alone program. In the examples shown in table 3, the differences between using Proc-StatXact’s implementation of Fisher’s exact test and ours never resulted in overall power differences >0.0003. Our program will either calculate power using our implementation of Fisher’s exact test or will read in power calculated externally (perhaps using Proc-StatXact).
Table 3.
Comparison of Power Calculations for Qualitative Traits, using Fisher’s Exact Test and a Dominance Model[Note]
|
Parameters |
|||||||
| N | γ | δ | pA | 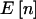 |
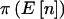 |
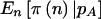 |
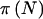 |
| 100 | 1 | 1 | .5 | (25,50,25) | .8973 | .8841 | .6046 |
| 100 | 5 | 5 | .5 | (25,50,25) | .8973 | .8841 | .7887 |
| 100 | 10 | 10 | .5 | (25,50,25) | .8973 | .8841 | .8310 |
| 100 | 5 | 45 | .1 | (1,18,81) | .8612 | .8483 | .8043 |
| 100 | 10 | 90 | .1 | (1,18,81) | .8612 | .8483 | .8263 |
| 100 | 100 | 900 | .1 | (1,18,81) | .8612 | .8483 | .8462 |
Note.— The AA and AB groups are compared with the BB group. Parameters include PEN(AAorAB)=0.5, PEN(BB)=0.15, and α=0.05.
If 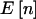 was not integer valued, we calculated the power at the bracketing values and took the minimum as the power for Fisher’s exact test. That is, if the expected group sizes were (5.5,14.5), we calculated power at (5,15) and (6,14) and took the minimum power, as would be done in practice, to be conservative. We implemented power estimation for the χ2 test using the arcsine approximation with formulas from Sahai and Khurshid (1996) (see the appendix). This approximation gives sample sizes that are too low and power that is too high (Sahai and Khurshid 1996) but has the advantage that it can be calculated for all n. Although there are formulas based on a corrected χ2 test that are too conservative (Sahai and Khurshid 1996), they all fail at the edges of the range of possible n. Because of this, we have chosen to simply use the arcsine approximation for our examples. This approximation may not be very good at the edges of the range of n, but, with moderately large values of N and
was not integer valued, we calculated the power at the bracketing values and took the minimum as the power for Fisher’s exact test. That is, if the expected group sizes were (5.5,14.5), we calculated power at (5,15) and (6,14) and took the minimum power, as would be done in practice, to be conservative. We implemented power estimation for the χ2 test using the arcsine approximation with formulas from Sahai and Khurshid (1996) (see the appendix). This approximation gives sample sizes that are too low and power that is too high (Sahai and Khurshid 1996) but has the advantage that it can be calculated for all n. Although there are formulas based on a corrected χ2 test that are too conservative (Sahai and Khurshid 1996), they all fail at the edges of the range of possible n. Because of this, we have chosen to simply use the arcsine approximation for our examples. This approximation may not be very good at the edges of the range of n, but, with moderately large values of N and 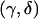 chosen so that p is unlikely to be near 0 or 1, the weight given
chosen so that p is unlikely to be near 0 or 1, the weight given 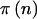 for extreme values of n is small. We have also implemented a general power calculation procedure for r×c tables (Lachin 1977) to allow for genotype-based (2×3) analyses. This method can also be used for dominance models.
for extreme values of n is small. We have also implemented a general power calculation procedure for r×c tables (Lachin 1977) to allow for genotype-based (2×3) analyses. This method can also be used for dominance models.
Case-Control Studies
For the case-control studies, we assume a fixed sample of N0 controls and N1 cases; we denote the number of controls with genotype AA as n01, the number with AB as n02, and the number with BB as n03. We similarly define n1j for cases. We assume that the allele frequencies differ between the controls and the cases, and we denote these as pA0 and pA1, respectively. We define n=(n01,n02,n03,n11,n12,n13) and test whether the allele frequencies are different between cases and controls. For the moment, we will combine individuals with genotypes AA and AB, to determine whether the proportion of individuals with at least one copy of A differs between cases and controls.
Let 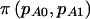 denote the power for detecting a difference between the cases and the controls in the proportion who are AA or AB when we assume that pA0 and pA1 are known. In the context of case-control studies,
denote the power for detecting a difference between the cases and the controls in the proportion who are AA or AB when we assume that pA0 and pA1 are known. In the context of case-control studies, 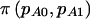 plays the same role as π(E[n]) does in cohort studies. For reasons that we will explain shortly, this additional notation is necessary to differentiate between case-control and cohort studies. Testing for a difference between cases and controls is simply a test of the equality of two proportions with group sizes N0 and N1 and proportions under the alternative hypothesis of
plays the same role as π(E[n]) does in cohort studies. For reasons that we will explain shortly, this additional notation is necessary to differentiate between case-control and cohort studies. Testing for a difference between cases and controls is simply a test of the equality of two proportions with group sizes N0 and N1 and proportions under the alternative hypothesis of 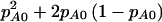 and
and 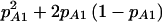 (again, under an assumption of Hardy-Weinberg proportions). We used the arcsine approximation to the χ2, Lachin’s method (Lachin 1977), or Fisher’s exact test to calculate the power of this comparison (see the appendix for details). This is the typical approach to calculating power for case-control studies.
(again, under an assumption of Hardy-Weinberg proportions). We used the arcsine approximation to the χ2, Lachin’s method (Lachin 1977), or Fisher’s exact test to calculate the power of this comparison (see the appendix for details). This is the typical approach to calculating power for case-control studies.
As was done in equation (1), we average over the multinomial distributions to calculate the average power for fixed pA0 and pA1 as
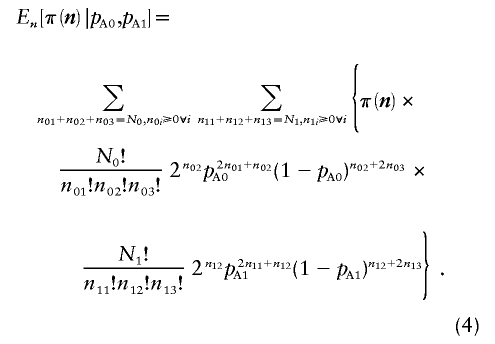 |
This is obviously considerably more complicated to evaluate because of the double summation required by the two multinomial distributions. Similarly, we can modify equation (3) to calculate the average power over two prior distributions. We assume that pA0∼beta(γ0,δ0) and pA1∼beta(γ1,δ1). This results in
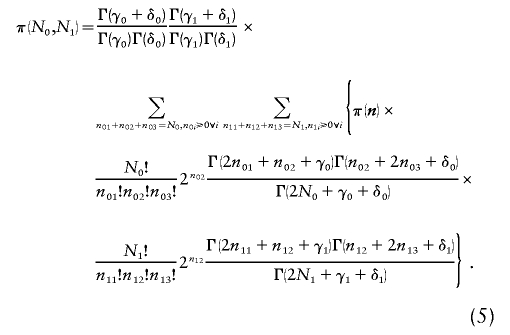 |
The execution time for equations (4) and (5) is O(N20N21), because there are (N0+2)(N0+1)(N1+2)(N1+1)/4 possible values of n.
Finally, we have to calculate 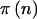 . Unlike in the cohort-study examples described above, the data are completely determined by n. We can simply perform the test at the α level, and then
. Unlike in the cohort-study examples described above, the data are completely determined by n. We can simply perform the test at the α level, and then 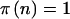 if it is significant and
if it is significant and 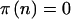 otherwise. This simplifies the calculations because we can calculate the sums only over n such that
otherwise. This simplifies the calculations because we can calculate the sums only over n such that 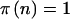 . Likewise, in a case-control study,
. Likewise, in a case-control study, 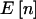 is fixed, and therefore
is fixed, and therefore 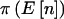 is either 0 or 1. The notation
is either 0 or 1. The notation 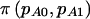 was introduced to allow us to differentiate between the usual power calculation for cohort studies,
was introduced to allow us to differentiate between the usual power calculation for cohort studies, 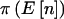 , and for case-control studies,
, and for case-control studies, 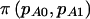 .
.
It is interesting to note that, for Fisher’s exact test and case-control studies, 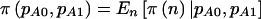 . This is because power for Fisher’s exact test is calculated as a weighted average over all possible tables with fixed sizes of N0 and N1 in exactly the same manner as we have proposed here (Mehta and Patel 1999).
. This is because power for Fisher’s exact test is calculated as a weighted average over all possible tables with fixed sizes of N0 and N1 in exactly the same manner as we have proposed here (Mehta and Patel 1999).
This section has focused on a dominant model. We have also implemented a genotype-based (2×3) analysis in which AA, AB, and BB are compared using a 2-df test and an allele-based analysis in which each allele is treated independently.
Results
Quantitative Traits for Cohort Studies
A comparison of power for a dominant 1-df alternative hypothesis for a quantitative trait is shown in table 2. The column with the header “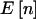 ” lists the expected number of counts in the three cells. The column under “
” lists the expected number of counts in the three cells. The column under “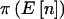 ” shows the power if we knew a priori that the observed n were
” shows the power if we knew a priori that the observed n were 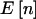 . The last two columns list the power when accounting for variability in n when pA is fixed
. The last two columns list the power when accounting for variability in n when pA is fixed 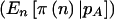 and variable
and variable 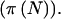 Several points should be noted. First,
Several points should be noted. First, 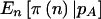 and
and 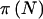 are generally smaller than π(E[n]). When the prior for pA is diffuse (small γ and δ), there is a larger difference than with a concentrated prior. Second, as γ and δ are increased while their ratio is held fixed,
are generally smaller than π(E[n]). When the prior for pA is diffuse (small γ and δ), there is a larger difference than with a concentrated prior. Second, as γ and δ are increased while their ratio is held fixed, 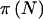 approaches
approaches 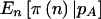 , which is the usual situation when prior uncertainty is reduced (i.e., when you are assuming more information). If we use a genotype-based 2-df genetic model instead of a quantitative dominant model, the results are similar.
, which is the usual situation when prior uncertainty is reduced (i.e., when you are assuming more information). If we use a genotype-based 2-df genetic model instead of a quantitative dominant model, the results are similar.
Table 2.
Comparison of Power Calculations for a Dominance Model for a Quantitative Trait[Note]
|
Parameters |
|||||||
| N | γ | δ | pA | 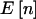 |
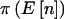 |
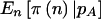 |
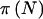 |
| 20 | 1 | 1 | .5 | (5,10,5) | .7358 | .6952 | .4937 |
| 20 | 10 | 10 | .5 | (5,10,5) | .7358 | .6952 | .6650 |
| 20 | 1,000 | 1,000 | .5 | (5,10,5) | .7358 | .6952 | .6949 |
| 40 | 1 | 1 | .5 | (10,20,10) | .9651 | .9488 | .6934 |
| 40 | 10 | 10 | .5 | (10,20,10) | .9651 | .9488 | .9102 |
| 40 | 1,000 | 1,000 | .5 | (10,20,10) | .9651 | .9488 | .9484 |
Note.— The AA and AB groups are compared with the BB group. Parameters include μ=(3,3,1), σ2=2, and α=0.05.
Qualitative Traits for Cohort Studies
Power for qualitative traits when Fisher’s exact test is used can be seen in table 3. In all examples, a dominant mode of inheritance is assumed for the trait. In general, 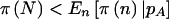 and
and 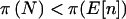 , but
, but 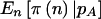 was not always <π(E[n]). The pattern is for the power to be overestimated when ignoring the sampling variability in n and the uncertainty in pA. Results using the arcsine approximation for 2×2 tables and genotype-based (2×3) analyses in which we allow three levels were similar but are not shown.
was not always <π(E[n]). The pattern is for the power to be overestimated when ignoring the sampling variability in n and the uncertainty in pA. Results using the arcsine approximation for 2×2 tables and genotype-based (2×3) analyses in which we allow three levels were similar but are not shown.
Case-Control Studies
Power for case-control studies using the arcsine approximation can be seen in table 4, in which a dominant model is assumed. In general, the pattern 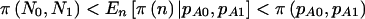 is the same as that seen for cohort studies. Similar results (not shown) were observed for a genotype-based model (2×3) and for an allele-based model (2×2) in which each allele is treated independently.
is the same as that seen for cohort studies. Similar results (not shown) were observed for a genotype-based model (2×3) and for an allele-based model (2×2) in which each allele is treated independently.
Table 4.
Comparison of Power Calculations for Case-Control Studies, using a Dominance Model[Note]
|
Parameters |
|||||||||||
| N0 | N1 | γ0 | δ0 | pA0 | γ1 | δ1 | pA1 | OR | π(pA0,pA1) | En[π(n)|pA0,pA1] | 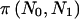 |
| 100 | 100 | 2 | 3 | .4 | 3 | 2 | .6 | 2.95 | .9067 | .9056 | .7646 |
| 100 | 100 | 20 | 30 | .4 | 30 | 20 | .6 | 2.95 | .9067 | .9056 | .7628 |
| 100 | 100 | 200 | 300 | .4 | 300 | 200 | .6 | 2.95 | .9067 | .9056 | .8794 |
| 300 | 200 | 22 | 28 | .44 | 28 | 22 | .56 | 1.90 | .8601 | .8561 | .6883 |
| 300 | 200 | 220 | 280 | .44 | 280 | 220 | .56 | 1.90 | .8601 | .8561 | .7972 |
| 300 | 200 | 2,200 | 2,800 | .44 | 2,800 | 2,200 | .56 | 1.90 | .8601 | .8561 | .8487 |
| 500 | 500 | 23 | 27 | .46 | 27 | 23 | .54 | 1.53 | .8323 | .8319 | .7002 |
| 500 | 500 | 230 | 270 | .46 | 270 | 230 | .54 | 1.53 | .8323 | .8319 | .7367 |
| 500 | 500 | 2,300 | 2,700 | .46 | 2,700 | 2,300 | .54 | 1.53 | .8323 | .8319 | .8169 |
Note.— The AA and AB groups are compared with the BB group. The arcsine approximation to the normal distribution was used for the calculation of 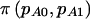 , and a χ2 test was used for the calculation of
, and a χ2 test was used for the calculation of 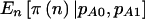 and
and 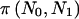 . The significance level is α=0.05 for all examples.
. The significance level is α=0.05 for all examples.
Examples
Motivational Example
We now return to the example described in the “Methods” section and table 1. The effect sizes were described previously. We assume the prior on pA to be 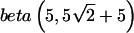 , which implies Pr(AAorAB)=Pr(BB)=0.5. The final two columns in table 1 are the weights given to the
, which implies Pr(AAorAB)=Pr(BB)=0.5. The final two columns in table 1 are the weights given to the 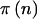 in equations (1) and (3). For the quantitative trait,
in equations (1) and (3). For the quantitative trait, 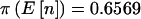 , En[π(n)|pA]=0.5945, and π(8)=0.5494. For the qualitative trait the patterns were similar:
, En[π(n)|pA]=0.5945, and π(8)=0.5494. For the qualitative trait the patterns were similar: 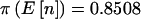 , En[π(n)|pA]=0.7909, and π(8)=0.7040 when Fisher’s exact test was used, and
, En[π(n)|pA]=0.7909, and π(8)=0.7040 when Fisher’s exact test was used, and 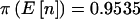 , En[π(n)|pA]=0.9078, and π(8)=0.8562 when the arcsine approximation was used. In all cases, incorporating sampling variability of n and uncertainty in the specification of pA results in substantially smaller estimates of power.
, En[π(n)|pA]=0.9078, and π(8)=0.8562 when the arcsine approximation was used. In all cases, incorporating sampling variability of n and uncertainty in the specification of pA results in substantially smaller estimates of power.
Example 2
The methods described in this article can be illustrated using an examination of SNPs in the gene encoding for the epithelial sodium channel (ENaC) of the kidney (Ambrosius et al. 1999). The study was approved by the institutional review board at Indiana University. Although multiple SNPs were examined in the hypertension study, we focus on one: an A→T substitution at amino acid 663 of the α subunit (αA663T). This study consists of a cohort of children in whom various markers of ENaC activity are measured and a case-control study of adults whom we examined for a relationship between hypertension (the case-control variable) and the SNPs. We report here only data from African Americans.
Allele frequencies for power calculations for cohort studies were estimated using data from the cohort of children. We observed 179 AA, 53 AT, and 3 TT individuals for α663. When an exact test was used (Louis and Dempster 1987), there was no evidence that the assumption of Hardy-Weinberg was inappropriate (P=1.0). On the basis of this, we assumed a beta(413,61) prior for α663A. (The prior parameters were calculated using the method described in the “Beta Prior” subsection of the “Methods” section: 413=1+2×179+53 and 61=1+53+2×3.) A plot of the prior shows that most of the mass is near 1, indicating that the wild-type allele is highly prevalent. We illustrate the proposed methods by examining power for a quantitative trait (log of the aldosterone:potassium ratio [nmol/mmol] in urine) in children and a qualitative trait (hypertension) in adults.
Specifically, three estimates of the sample size required for 80% power are illustrated: (1) one ignoring both the sampling variation about pA and the uncertainty in 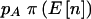 ; (2) one accounting for the sampling variation about pA but ignoring the uncertainty in pA,
; (2) one accounting for the sampling variation about pA but ignoring the uncertainty in pA, 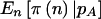 ; and (3) one accounting for both the sampling variation about pA and the uncertainty in pA,
; and (3) one accounting for both the sampling variation about pA and the uncertainty in pA, 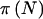 .
.
For the calculation of power for the case-control study, we note that there are 75 normotensive individuals (controls) with AA, 37 with AT, and 10 with TT genotypes for α663. There were 229 hypertensive individuals (cases) with AA, 78 with AT, and 9 with TT. There was no evidence that the assumption of Hardy-Weinberg equilibrium was inappropriate in hypertensive (P=0.51) or normotensive (P=0.12) individuals (Louis and Dempster 1987). The genotype frequencies correspond to prior distributions for the distribution of A of beta(188,58) for normotensive and beta(537,97) for hypertensive individuals. Because calculation of power for case-control studies is much more computationally intensive than for cohort studies, we report only the power estimates for N0=122 and N1=316 rather than calculating the required sample sizes for a given power.
Quantitative trait for cohort studies
In the original study, the outcome measurements (log of the aldosterone:potassium ratio [nmol/mmol] in urine) were made multiple times, and a repeated measures analysis of covariance model with a random effect for subject was used. Here, we assume one measurement will be made for each subject, and we will not adjust for covariates. The pooled SD was 0.97, with means of −1.45 (AA), −1.25 (AT), and −0.18 (TT). We calculated power to detect an effect of this magnitude through use of a 2-df null hypothesis at the 5% level, using the beta(413,61) prior described above. Using a simple power calculation, we would need 293 subjects to have 80% power (π(E[n])). Incorporating the variability of the multinomial distribution would result in 323 subjects being required 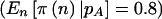 . Finally, incorporating the uncertainty in specification of the allele frequency would result in a sample size of 330 subjects
. Finally, incorporating the uncertainty in specification of the allele frequency would result in a sample size of 330 subjects 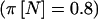 . As can clearly be seen, the sample size would be substantially underestimated if we did not account for the variability in allele frequency and the variability in observed genotype frequencies.
. As can clearly be seen, the sample size would be substantially underestimated if we did not account for the variability in allele frequency and the variability in observed genotype frequencies.
Case-control studies
As in the previous subsection, we grouped subjects into those with no copies and those with one or more copies of the α663T allele. On the basis of the priors described above, this results in an odds ratio of 0.553. That is, the odds of being AT or TT are 0.553 times higher in hypertensive individuals than in normotensive individuals. With N0=122 and N1=316, we calculated π(pA0,pA1)=0.7505, En[π(n)|pA0,pA1]=0.7590, and 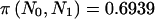 , using the arcsine approximation. It can be seen that we likely have less power than we expect, which follows the previous examples.
, using the arcsine approximation. It can be seen that we likely have less power than we expect, which follows the previous examples.
Discussion
Power calculations for genetic association tests typically assume fixed allele frequencies and ignore both sampling variation about and uncertainty in allele frequencies. We have described methodology and provided examples for power calculations of candidate polymorphisms that address sampling variability and allow for allele frequency uncertainty. Our results show that ignoring the variability in sample sizes among the different genotype groups and the uncertainty in allele frequencies can result in overestimation of power. Equivalently, it can result in an underestimate of the sample size needed for a specific power. The result of overestimating power—and thus either underrecruiting or having overly optimistic expectations—is to reduce the success of candidate gene and fine mapping studies. Ultimately, underpowered studies are a waste of financial, human, and sample resources. In our examples, the overestimation of power could be large or small. Given the potential impact of sample variability and allele frequency uncertainty on power estimates and the relative ease of addressing this variability in power calculations, we argue that sample variability should not be ignored and should be properly accounted for through use of the methods we have described.
The level of uncertainty in pA, as expressed by the prior, plays a large role in the calculation of power. One possible mechanism to specify the beta prior is to use available data for the polymorphism of interest from previous studies. This approach is reasonable, provided that the sample on which the previous study was based is from a population that is the same as or comparable to the sample in the present study. As has been well documented and is predicted from evolutionary models, allele frequencies will vary significantly between different populations. Thus, considerable care should be taken when borrowing data from other studies. Unlike the use of a single point estimate, as is typically used in genetic power calculations, the use of a distribution on pA can soften the blow of misspecification. One possible remedy to counteract concerns of population substructure is to widen the distribution of pA (i.e., decrease the prior parameters γ and δ by a multiplicative constant c). It is clear that the ideal solution would be to obtain a subsample of genotype data from the current population. We believe that it is better to have an average estimate of power for a study over a distribution of possible values of pA than an overestimate of power for a single estimate of pA. Failure to account for this uncertainty can lead to insufficiently powered studies and, ultimately, to a lack of success.
Schork (2002) discussed the potential value of averaging over unknown parameters for power calculations; he does not address the issue of integrating over genotype frequencies. Schork (2002) notes that the selection of the proper prior distribution may be difficult, but he does not provide guidance on how to make such a selection. Although we agree with Schork (2002) as per the selection of the exact distribution of the allele frequencies, we believe that often we do have some information. Appropriately incorporating that information greatly improves the quality of our power estimates compared with arbitrarily fixing allele frequencies and treating them as if they are known quantities. As discussed in the present article, fixing allele frequencies even if they are not known is the common approach to power calculations. We show that ignoring the sources of variation in allele frequencies tends to result in overestimates of power and, consequently, in studies that are underpowered. The current work contains a proposal for the selecting a prior distribution. An important additional advantage of our choice of a beta prior is that it allows us to switch the order of integration and summation in calculation of 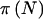 , which greatly reduces the complexity of equation (3). This exchange is not possible with an empirically derived prior distribution for the allele frequencies, as proposed by Schork (2002).
, which greatly reduces the complexity of equation (3). This exchange is not possible with an empirically derived prior distribution for the allele frequencies, as proposed by Schork (2002).
There are many obvious extensions of the current work. When studying a population composed of one or more subpopulations with differing allele frequencies (e.g., two different ethnic groups), a prior for each group might be useful. If we assume that the effect of the allele on the phenotype was the same for each group and that there was a group effect, then the statistical model might then contain a term for group and power could be calculated by integrating over both prior distributions. For cohort studies, the calculations would be similar to those presented here for case-control studies. In this article, we have used the proposed method for tests that use the general linear model for quantitative traits, using Fisher’s exact and χ2 tests for qualitative traits and using χ2 tests for case-control studies. The method can be used for any test, by using the appropriate 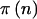 . We are currently working to extend this method to microsatellite markers, haplotypes, and the TDT. The effect likely will be larger for microsatellite markers and haplotypes, because of the greater number of allele variants.
. We are currently working to extend this method to microsatellite markers, haplotypes, and the TDT. The effect likely will be larger for microsatellite markers and haplotypes, because of the greater number of allele variants.
Acknowledgments
We acknowledge the financial support of National Institutes of Health grants M01-RR07122 (W.T.A.), P01-AR49084 (E.M.L. and C.D.L.), and R01-HL60944 (C.D.L.). Our thanks to J. Howard Pratt (Indiana University) for the data used in the example (funded by National Institutes of Health grant R01-HL35795). We would like to thank Stephen Rich for his thorough reading of this article and his many helpful suggestions. Finally, we would like to thank the anonymous reviewers, whose many suggestions resulted in a substantially improved manuscript.
Appendix : Details of Power Calculations
In this article, we have implemented software for the calculation of power for quantitative traits through use of the general linear model and for qualitative traits through use of Fisher’s exact test and the arcsine approximation to the χ2 test. The calculation of power for both approaches uses standard methods and is described here for completeness.
Quantitative Traits
Assume that we have a hypothesized alternative hypothesis where μ is a vector of length 3, containing the means of the three groups under the alternative. We assume that the within-group variance is σ2 and that the tests will be performed at the α level.
Assume that we are given the following parameters: the level of the test (α), the number of subjects with genotypes AA, AB, and BB 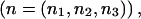 the assumed means under the alternative hypothesis (μ), the within-group variance (σ2), and the model (M). In this article, the model M will be a three-level (2-df) model in which the test is made using one-way analysis of variance, an additive model in which the test is made using linear regression, or a dominance-recessive model in which the AA and AB groups are pooled for comparison to the BB group. (Note that we can switch A and B to compare BB and AB to AA.) Finally, we assume that A and B are in Hardy-Weinberg proportions.
the assumed means under the alternative hypothesis (μ), the within-group variance (σ2), and the model (M). In this article, the model M will be a three-level (2-df) model in which the test is made using one-way analysis of variance, an additive model in which the test is made using linear regression, or a dominance-recessive model in which the AA and AB groups are pooled for comparison to the BB group. (Note that we can switch A and B to compare BB and AB to AA.) Finally, we assume that A and B are in Hardy-Weinberg proportions.
We use the theory of linear models to calculate power with any combination of the above parameters. Our approach follows that presented by Searle (1971). Write the model in matrix notation as Y=Xβ+ε, where X has N=n1+n2+n3 rows and k+1 columns. For the three-level model when all cell counts are positive (ni>0,∀i), k=2. For the linear (additive) and dominance-recessive models, k=1. We assume that X contains an intercept and can be rewritten as 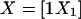 and that
and that 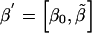 . Let
. Let 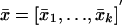 be the means of the columns of X1. Letting
be the means of the columns of X1. Letting 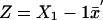 , we can calculate the noncentrality parameter as
, we can calculate the noncentrality parameter as 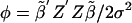 Let Fcrit satisfy
Let Fcrit satisfy 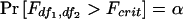 . Finally, the power is
. Finally, the power is 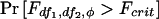 , which may be calculated using built-in functions in S-Plus or SAS. Note that, in S-Plus, φ is defined without the factor of 2 in the denominator.
, which may be calculated using built-in functions in S-Plus or SAS. Note that, in S-Plus, φ is defined without the factor of 2 in the denominator.
Three-Level Model
When fitting a three-level model, the matrix Z′Z is given by
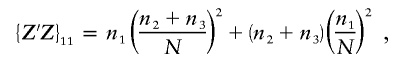 |
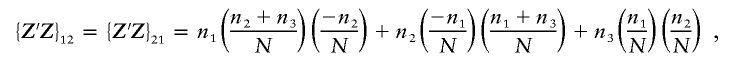 |
and
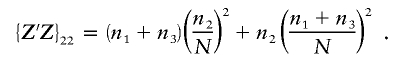 |
The term 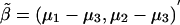 . If none of the cell sizes are 0, then df1=2 and df2=N-3. If only one of the cell sizes is 0, then df1=1 and df2=N-2. If two or more of the cell sizes is 0 or N=2, then the test cannot be performed, and the power is 0.
. If none of the cell sizes are 0, then df1=2 and df2=N-3. If only one of the cell sizes is 0, then df1=1 and df2=N-2. If two or more of the cell sizes is 0 or N=2, then the test cannot be performed, and the power is 0.
Additive Model
When fitting an additive model and the alternative hypothesis is specified as μ, we need to estimate the slope as a function of the number of copies of the B allele. We use a weighted regression with data 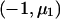 ,
, 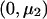 , and
, and 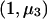 and weights n1, n2, and n3 and calculate
and weights n1, n2, and n3 and calculate 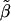 as the slope of these data. With this model, k=1,
as the slope of these data. With this model, k=1,
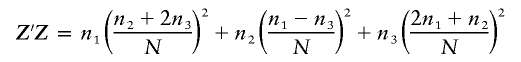 |
is a scalar, df1=1, and df2=N-2. If all subjects are of the same genotype 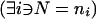 or if N⩽2, then the power is 0.
or if N⩽2, then the power is 0.
Dominant-Recessive Model
When fitting a dominant-recessive model, we need to estimate the effect size under the alternative hypothesis, as was done in the previous section. We use a weighted regression with data 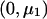 ,
, 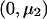 , and
, and 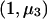 with weights n1, n2, and n3 and calculate
with weights n1, n2, and n3 and calculate 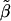 as the slope of these data. The matrix product
as the slope of these data. The matrix product
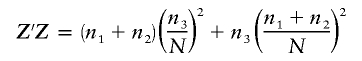 |
is a scalar, df1=1, and df2=N-2. If all or none of the subjects are homozygous for B or if N⩽2, then the power is 0.
Qualitative Traits
For examination of qualitative traits, we assume either a dominance or a genotype-based (2×3) model. For the former, this is equivalent to assuming that people with AA and AB genotypes are identical, and they are compared with the people with BB genotypes. For the latter, we compare AA with AB with BB through use of a 2-df test. Under the alternative hypothesis, we assume that the true phenotype penetrances are PEN(AAorAB) and PEN(BB) or PEN(AA), PEN(AB), and PEN(BB). Testing will be performed at the α level.
An excellent discussion of power for testing differences in proportions for the two-sample design can be found in the review article by Sahai and Khurshid (1996). In their article, they compare Fisher’s exact test to the χ2 test (with and without continuity correction). Fisher’s exact test is conservative, but it has the advantage that it does not rely on approximations. A discussion of power for χ2 tests for tables of arbitrary dimension is found in the article by Lachin (1977).
Fisher’s Exact Test
The calculation of power for Fisher’s exact test is quite complicated. Details can be found in Sahai and Khurshid (1996) and the Proc-StatXact manual (Mehta and Patel 1999). Instead of programming the calculations ourselves, we initially used Proc-StatXact to calculate 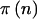 for each possible n. These values were then read into our C program and used to calculate
for each possible n. These values were then read into our C program and used to calculate 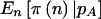 and
and 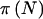 using equations (1) and (3). We subsequently programmed the calculations ourselves, to have a stand-alone program.
using equations (1) and (3). We subsequently programmed the calculations ourselves, to have a stand-alone program.
χ2 Test with Arcsine Approximation
The arcsine method is described by Sahai and Khurshid (1996), and power as a function of n1, n2, PEN(AAorAB), PEN(BB), and α is given in equation (48) of their article. Unfortunately, their formula is for a one-sided test, even though it is described as being for a two-sided test. However, a modification of the formula they present in their table II can be used to calculate the correct power. Specifically, let k=n2/n1,
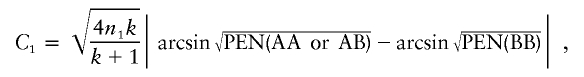 |
and 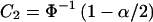 , where Φ(x) is the standard normal distribution function. The power is then Φ(C1-C2)+Φ(-C1-C2).
, where Φ(x) is the standard normal distribution function. The power is then Φ(C1-C2)+Φ(-C1-C2).
χ2 Test for an r×c Table
Power for a general r×c table is described by Lachin (1977). Let there be r treatment groups (indicated by the rows) and c classes (indicated by the columns). Let N be the total sample size and Ni the group sizes. Define Qi by Ni=NQi. Let ρ1ij denote the probability of being in column j conditional on being in row i under the assumed alternative hypothesis. Let αj=Σiρ1ijQi and δij=ρ1ij-αj. Define the noncentrality parameter as 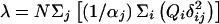 and df=(r-1)×(c-1). Let Ccrit satisfy
and df=(r-1)×(c-1). Let Ccrit satisfy 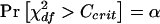 . Finally, the power is
. Finally, the power is 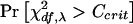 .
.
Electronic-Database Information
The URLs for data presented herein are as follows:
- Authors' Web site, http://www.ambrosius.net/Power/ (for software in C)
- Comprehensive R Archive Network, University of California, Los Angeles, http://cran.stat.ucla.edu/src/contrib/PACKAGES.html#combinat (for Combinat: combinatorics utilities version 0.0-2 [a package for R and S-Plus])
- Department of Biomathematics and Biostatistics Free Code Archive, M.D. Anderson Cancer Center, http://odin.mdacc.tmc.edu/anonftp/ (for DCDFLIB: library of C routines for cumulative distribution functions, inverses, and other parameters, release 1.1)
References
- Abramowitz M, Stegun I (1965) Handbook of mathematical functions with formulas, graphs, and mathematical tables. Dover Publications, New York [Google Scholar]
- Agresti A (1990) Categorical data analysis. John Wiley & Sons, New York [Google Scholar]
- Ambrosius W, Bloem L, Zhou L, Rebhun J, Snyder P, Wagner M, Guo C, Pratt J (1999) Genetic variants in the epithelial sodium channel in relation to aldosterone and potassium excretion and risk for hypertension. Hypertension 34:631–637 [DOI] [PubMed] [Google Scholar]
- Brown B, Lovato J, Russell K (1997) DCDFLIB: library of C routines for cumulative distribution functions, inverses, and other parameters, release 1.1. Technical report, University of Texas, Houston [Google Scholar]
- Chasalow S (2002) Combinat: combinatorics utilities version 0.0-2 (a package for R and S-Plus). Technical report, University of California, Los Angeles [Google Scholar]
- Deng H, Chen W (2001) The power of the transmission disequilibrium test (TDT) with both case-parent and control-parent trios. Genet Res 78:289–302 10.1017/S001667230100533X [DOI] [PubMed] [Google Scholar]
- Elashoff J (2000) nQuery advisor version 4.0: user’s guide. Statistical Solutions, Los Angeles [Google Scholar]
- Fleiss J (1981) Statistical methods for rates and proportions, 2nd ed. John Wiley & Sons, New York [Google Scholar]
- Ghosh S, Watanabe R, Hauser E, Langefeld C, Valle T, Magnuson V, Mohlke K, et al (2000) The Finland-United States investigation of non-insulin-dependent diabetes mellitus genetics (FUSION) study. I. An autosomal genome scan for genes that predispose to type 2 diabetes. Am J Hum Genet 67:1174–1185 [PMC free article] [PubMed] [Google Scholar]
- Lachin J (1977) Sample size determinations for r × c comparative trials. Biometrics 33:315–324 [PubMed] [Google Scholar]
- Lalouel L, Rohrwasser A (2002) Power and replication in case-control studies. Am J Hypertens 15:201–205 10.1016/S0895-7061(01)02285-3 [DOI] [PubMed] [Google Scholar]
- Lange C, Laird N (2002) Power calculations for a general class of family-based association tests: dichotomous traits. Am J Hum Genet 71:575–584 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long A, Langley C (1999) The power of association studies to detect the contribution of candidate genetic loci to variation in complex traits. Genome Res 9:720–731 [PMC free article] [PubMed] [Google Scholar]
- Louis E, Dempster E (1987) An exact test for Hardy-Weinberg and multiple alleles. Biometrics 43:805–811 [PubMed] [Google Scholar]
- McGinnis R, Shifman S, Darvasi A (2002) Power and Efficiency of the TDT and case-control design for association scans. Behav Genet 32:135–144 10.1023/A:1015205924326 [DOI] [PubMed] [Google Scholar]
- Mehta C, Patel N (1999) Proc-StatXact 4 for SAS users: statistical software for exact nonparametric inference. CYTEL Software Corporation, Cambridge MA [Google Scholar]
- Press W, Teukolsky S, Vetterling W, Flannery B (1992) Numerical recipes in C: the art of scientific computing, 2nd ed. Cambridge University Press, Cambridge [Google Scholar]
- Sahai H, Khurshid A (1996) Formulae and tables for the determination of sample sizes and power in clinical trials for testing differences in proportions for the two-sample design: a review. Stat Med 15:1–21 [DOI] [PubMed] [Google Scholar]
- Schork N (2002) Power calculations for genetic association studies using estimated probability distributions. Am J Hum Genet 70:1480–1489 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Searle S (1971) Linear models. John Wiley & Sons, New York [Google Scholar]
- Shih M, Whittemore A (2002) Tests for genetic association using family data. Genet Epidemiol 22:128–145 10.1002/gepi.0151 [DOI] [PubMed] [Google Scholar]
- Spielman R, McGinnis R, Ewens W (1993) Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM). Am J Hum Genet 52:506–516 [PMC free article] [PubMed] [Google Scholar]
- Wang D, Sun F (2000) Sample sizes for the transmission disequilibrium tests: TDT, S-TDT, and 1-TDT. Communications in statistics, part A: theory and methods 5–6:1129–1142 [Google Scholar]