A High-Density Admixture Map for Disease Gene Discovery in African Americans

Abstract

Admixture mapping (also known as “mapping by admixture linkage disequilibrium,” or MALD) provides a way of localizing genes that cause disease, in admixed ethnic groups such as African Americans, with ∼100 times fewer markers than are required for whole-genome haplotype scans. However, it has not been possible to perform powerful scans with admixture mapping because the method requires a dense map of validated markers known to have large frequency differences between Europeans and Africans. To create such a map, we screened through databases containing ∼450,000 single-nucleotide polymorphisms (SNPs) for which frequencies had been estimated in African and European population samples. We experimentally confirmed the frequencies of the most promising SNPs in a multiethnic panel of unrelated samples and identified 3,011 as a MALD map (1.2 cM average spacing). We estimate that this map is ∼70% informative in differentiating African versus European origins of chromosomal segments. This map provides a practical and powerful tool, which is freely available without restriction, for screening for disease genes in African American patient cohorts. The map is especially appropriate for those diseases that differ in incidence between the parental African and European populations.

Introduction

Admixture mapping (also known as “mapping by admixture linkage disequilibrium,” or MALD) offers an approach for performing a whole-genome linkage disequilibrium (LD)–based association scan at a fraction of the cost of haplotype or direct association mapping (Chakraborty and Weiss 1988; Risch 1992; Briscoe et al. 1994; Stephens et al. 1994; McKeigue 1997, 1998; Zheng and Elston 1999; McKeigue et al. 2000; Lautenberger et al. 2000; Pfaff et al. 2001; Smith et al. 2001; Halder and Shriver 2003; Hoggart et al. 2003). The idea of admixture mapping is to screen along the genome in patients such as African Americans or Hispanic Americans, whose genomes have chromosomal segments of different origins because of historic gene flow between different ethnic groups (e.g., African, European, and American Indian). The strategy is to identify a genomic region with an unusually high contribution of ancestry from one ancestral population, usually the population with the highest incidence of disease. Admixture mapping is expected to be particularly powerful for finding genes for diseases that differ strikingly in frequency across populations, because of the possibility that there may be genetic loci that underlie these differences. For example, multiple sclerosis is a good candidate for admixture mapping, because it is heritable and has a much higher genetic risk in European than African Americans (Kurtzke et al. 1979), and prostate cancer and end-stage renal disease are good candidates because their incidences are higher in people of African descent (Klag et al. 1997; Davey Smith et al. 1998).

The key advantage of admixture mapping is that it requires the study of substantially fewer genetic markers than do other methods of association mapping (haplotype or direct association studies). Because of the recent admixture of African Americans (within the last 20 generations), their genomes have not been shuffled much by recombination since population mixing began, and the stretches of identical ancestry should be many megabases in extent. As a result, although 10⁵–10⁶ markers may be necessary for whole-genome haplotype studies (Gabriel et al. 2002; Carlson et al. 2003), a couple thousand MALD markers typed in an admixed population cohort should be adequate to assess ancestry information genomewide.

Admixture mapping has not yet been successfully used to identify a disease gene, although theoretical and empirical studies of feasibility are encouraging (Chakraborty and Weiss 1988; Risch 1992; Briscoe et al. 1994; Stephens et al. 1994; McKeigue 1997, 1998; Zheng and Elston 1999; Lautenberger et al. 2000; McKeigue et al. 2000; Pfaff et al. 2001; Smith et al. 2001; Halder and Shriver 2003; Hoggart et al. 2003; Rosenberg et al. 2003; Patterson et al. 2004 [in this issue]). A major reason for the lack of results so far is that there has been limited availability of highly informative MALD markers—that is, those with known large differences in allele frequencies across major ethnic groups. Recently, the genotyping of hundreds of thousands of SNPs from several populations has improved the prospects for admixture mapping. Here we describe a high-density map of 3,011 SNPs, <1% of the screening database, that have been validated in a second and independent set of samples. In the accompanying article (Patterson et al. 2004 [in this issue]), we present methods that efficiently combine the information from neighboring, partially informative markers, to make estimates of ancestry that are suitable for disease gene discovery. The highly differentiated markers validated in this study, as well as the new methods, should facilitate admixture mapping as a powerful method for disease gene localization.

Methods

Building a Large Database of SNPs from Which to Choose an Admixture Map

The key resource for building an admixture map in African Americans is a very large database of genetic variants for which allele frequencies are known in populations of both European and African descent (table 1). Although most genetic variants have similar frequencies in these ancestral populations (Lewontin 1972; Nei and Roychoudhury 1982), a small fraction have large enough differences to be useful for admixture mapping.

Table 1.

Sources for SNPs Used To Build the Map

	No. of SNPs in
Sourcea	EntireDatabase	ValidatedMap of3,011	ReducedMap of2,154
TaqMan Assays-On-Demand SNP Genotyping Products database (De La Vega et al. 2002)	177,781	1,913	1,316
The SNP Consortium Allele Frequency Project (SNP Consortium Web site)	54,824	759	592
Applera Genomics Initiative exon resequencing database (Adams et al. 2002)b	266,135	304	219
Previously identified as informative for admixture analysis (Parra et al. 1998)	18	14	13
SNPs culled by D.R. from random published sources (especially Reich et al. 2003) and unpublished data	1,348	14	9
SeattleSNPs discovered by resequencing genes (UW-FHCRC Variation Discovery Resource Web site)	6,305	7	5
Totalb	∼450,000	3,011	2,154

^aMany SNPs had allele frequency information submitted from multiple sources. To create a nonredundant entry, we included frequency data only from the source in which the most samples were genotyped.

^bOnly 10,530 SNPs from the Applera gene resequencing database, those with SIC >0.1, were in the actual list from which SNPs were selected. This meant that the total number of SNPs in the list we analyzed was 250,806; however, the effective number used for choosing differentiated markers was thus larger, ∼450,000.

We combined SNPs from public and private databases to obtain a list of nonredundant markers with frequencies known in populations of both European and African descent (table 1). For each SNP, we recorded the frequencies, number of samples genotyped, physical position in the HG16 public genome assembly, and genetic position in the deCODE map (Kong et al. 2002). We eliminated SNPs from analysis if they appeared to have discrepant physical and genetic positions (that is, if they were within 100 kb on the physical map but appeared >0.5 cM apart on the genetic map).

Choosing Candidate SNPs for Follow-Up Experimental Validation

A computer program was written to select the best SNPs for admixture mapping from the database. The program chooses SNPs that are (1) evenly spaced on the genetic map and (2) maximally informative about ancestry at each point along the genome, in the sense of having high allele frequency differentiation. Thus, it attempts to choose an optimal set of SNPs for estimating ancestry at each point in the genome.

We implemented an iterative “greedy algorithm” to choose markers in the map. The algorithm repeatedly chooses the SNP that adds the most additional information to the set that has already been identified, taking into account the fact that some information may already be provided at the site of a candidate SNP by markers already chosen for the map. For simplicity, we make the approximation that all markers in an 8-cM window centered on the candidate SNP are fully “linked for admixture” and thus can be treated as a compound locus for the purpose of ancestry inference. We also assume that more-distant markers provide no information.

To assess how much additional information is provided by a candidate SNP, we calculated the mutual information (McEliece 2002) provided about ancestry with the candidate MALD marker added in, minus the information only from nearby markers. The formula for a multimarker genotype is similar to the Rosenberg et al. (2003) equation for “informativeness for assignment.” When a candidate SNP is considered alone or is >4 cM from any other SNPs, it is simply

with a₀₀=(1-m)×p^WA, a₀₁=m×p^EA, a₁₀=(1-m)×(1-p^WA), and a₁₁=m×(1-p^EA). Here, p^EA and p^WA are the SNP frequencies in European Americans and West Africans, and m is the proportion of European ancestry in African Americans, which we set to 0.21, although we found that SNP selection is not very sensitive to the choice of m. For the many SNPs in our data set for which no West African frequencies were available, we used an expectation-maximization algorithm (Dempster et al. 1977) to infer them from the African American frequencies.

The greedy algorithm described above was iteratively applied, each time choosing new markers for the map until the additional information provided by the SNP (SIC) fell below 0.035, at which point the algorithm terminated. Three additional criteria were applied for SNP selection:

• 1. Candidate SNPs were chosen for the map only if they were spaced at least 50 kb from all previously chosen ones.
• 2. The estimates of frequencies from the databases were adjusted to account for the fact that some SNPs may appear to be more attractive for admixture mapping simply because they are picked as the most extreme cases of differentiation from a database in which there is sampling fluctuation. Specifically, before applying the SNP selection algorithm, 1 was added to both the minor and major allele counts in the populations of European and African descent, to make their frequencies appear more similar. For SNPs with frequencies from less reliable pooled genotyping, the differentiation was reduced further by adding 25% to both the major and minor allele frequencies.
• 3. Finally, the estimates of frequencies were adjusted by transforming all estimates so that they were 7% closer to 0.5. This procedure encouraged the program to choose markers for the map even near the most informative SNPs, which is important because it means the map will have some power even if there are missing genotypes.

Procedure for Experimentally Validating SNPs

All SNPs in the map were revalidated by genotyping new population samples to determine their allele frequencies. Validation of SNPs was performed at two laboratories. About half were validated at the National Cancer Institute’s Laboratory of Genomic Diversity (Laboratory of Genomic Diversity Web site) in Maryland by the 5′ nuclease assay (TaqMan Assays-on-Demand or Assays-by-Design SNP Genotyping Products [Applied Biosystems]) (Livak 1999), and about half were genotyped at the Broad Institute in Massachusetts by primer-oligo base extension assay resolved by MALDI-TOF mass spectrometry on a chip (MassARRAY [Sequenom]) (Tang et al. 1999). A total of 3,340 SNPs were experimentally genotyped during the validation process, although, as described below, only a subset of 3,011 were considered robust enough to be included in the complete map and presented in table A (online only).

The great majority of revalidated SNPs (2,991 of 3,340) were genotyped in 78 European Americans (from Chicago or Baltimore), 120 sub-Saharan Africans (from Senegal, Ghana, Cameroon, or Botswana), 109 African Americans (from Chicago, Baltimore, Pittsburgh, or North Carolina), 40 Cantonese Chinese, and 29 Mexican Amerindians (table 2). For 1,136 SNPs (including 349 not studied in the main panel of samples), 78 European Americans (CEPH) and 73 sub-Saharan Africans (Beni from Nigeria) were genotyped. All samples were collected under institutional review board approval with informed consent for the genetic study at each collection site.

Table 2.

Characteristics of Samples

		Population ContributionAssessed by STRUCTUREa(%)
Sample Examined	n	European	African	Asian	Amerindian
European American:
Chicagob	39	98.4	.4	.7	.5
Baltimoreb	39	97.5	.4	.9	1.3
African American:
Chicagob,c	18	18.4	80.6	.7	.3
Pittsburghb,c	23	18.3	80.6	.6	.5
Baltimored	45	15.9	83.2	.5	.5
North Carolinac	23	18.8	79.6	.5	1.1
African:
Senegale	46	2.8	95	1.6	.6
Ghanaf	33	.1	99.8	.1	.1
Cameroong	20	.1	99.8	.1	.1
Botswanah	21	1.2	98.4	.3	.1
Chinese:
Cantonesei	40	.2	.1	98.9	.8
Amerindian:
Mexican Zapotecj	29	4.3	.3	.5	94.8

^aThe STRUCTURE analysis (Falush et al. 2003) was based on the 2,034 SNPs from the reduced 2,154-marker map that were genotyped in the samples above. The relative log likelihoods for the two-, three-, four-, five-, and six-population models in STRUCTURE (Falush et al. 2003) were −25055, −6612, 0, −756, and −667, respectively. We used a four-population model because it is most probable given the data.

^bFrom the Multicenter AIDS Cohort Study (Kaslow et al. 1987).

^cFrom the Multicenter Hemophilia Cohort Study (Goedert et al. 2002).

^dFrom the AIDS Link to Intravenous Experiences study (Vlahov et al. 1998).

^eSample from J.-L.S..

^fSample from S.M.W.

^gSample from S.A.T. (Tishkoff and Williams 2002).

^hSample from M.E. (Novitsky et al. 2001).

ⁱSample from Z.Y., G.T., and S.O. (unpublished data).

^jSample from Hollenbach et al. 2001.

Identifying a Subset of SNPs That Should Be Included in MALD Mapping Panels

Validated SNPs were included in the complete 3,011-marker map if they:

• 1. were genotyped successfully in at least 20 West Africans and 20 European Americans;
• 2. were in Hardy-Weinberg equilibrium in the parental populations (P>.005 by G test summing over all European American and West African populations for which data were available and a Hardy-Weinberg statistic could be calculated);
• 3. had a minimal level of informativeness (SIC >0.035 according to eq. [1], out of a maximum of 0.709) at the FY-null locus (also known as “Duffy”); and
• 4. were similar in frequency within continents (P>.002 in a G test in sub-Saharan African populations, excluding the more distantly related Botswana population, and P>.002 in European Americans).

Admixture Mapping Panel Free of Historic LD

Additional SNPs with low information were eliminated until the following were satisfied:

• 5. all SNPs in the map were spaced at least 50 kb from each other, and
• 6. all SNPs in the map were not in LD with any of the other SNPs (P>.0005 not correcting for multiple hypothesis testing) in the parental populations.

Evaluating the Power of the Map

The power to detect a disease locus through use of admixture mapping depends on two independent factors. First, there is the strength of the disease locus for which one is searching: the enrichment of one population’s ancestry at that point in the genome. The accompanying article by Patterson et al. (2004 [in this issue]) explores in detail how disease model affects the power of a study. Second, there is the quality of the map: how well one is able to estimate origins of chromosomal segments from genotyping data.

To analyze the quality of the map, we used an analysis described in detail in the appendix (online only). In brief, “map power” is calculated as a quotient: the number of samples required, given the imperfect map, divided by the number that would be necessary if one had a perfectly informative marker at every site. For example, at a point where map power is 1/3, one needs 3 times the sample size as would be necessary if one were trying to detect a locus near a marker (such as FY null) with full map power: where genotypes provide definitive information about whether patients have 0, 1, or 2 European-ancestry alleles. In practice, map power was calculated by simulating data sets containing a disease locus and evaluating how many samples were necessary to detect it with a given level of power, compared with a perfectly informative marker such as FY null (see the appendix [online only]).

The map power calculation is somewhat overoptimistic, in that it assumes that the frequencies of alleles in parental populations are known perfectly, but inaccuracies in these measurements may in fact reduce power. Extensive simulations were used to explore the importance of this effect. We found, for example, that a locus with a calculated map power of 70% may provide only 50% of the information of the FY null locus (see fig. 7 of Patterson et al. 2004 [in this issue]).

Data Analysis to Assess Admixture Mapping Parameters and Population Structure

The analysis from Patterson et al. (2004 [in this issue]), which is implemented in the software package ANCESTRYMAP, was used to estimate admixture mapping parameters. The STRUCTURE program (Pritchard et al. 2000) was employed to assess the relative contributions of different populations to the multiethnic data set, using admixture LD between markers as the basis for the inference (Falush et al. 2003).

Results

A Database of SNPs for Marker Selection

The SNPs for building the admixture map came from publicly available sources (mostly in dbSNP), as well as two commercial databases (Adams et al. 2002; De La Vega et al. 2002; Applied Biosystems myScience Web site) (table 1). The Applied Biosystems database consisted of 177,781 SNPs genotyped in 46 European Americans and 45 African Americans. These data were obtained while developing the Applied Biosystems TaqMan Assays-on-Demand Genotyping Products (De La Vega et al. 2002). The Applera Genomics Initiative database consisted of 266,135 SNPs discovered in 20 European Americans and 19 African Americans by resequencing exonic and promoter regions around 23,363 annotated human genes (Adams et al. 2002). The total size of the SNP collection that we mined to obtain maximally informative markers for African American admixture mapping was ∼450,000 (table 1).

Selection of MALD Marker SNPs and Experimental Validation

After each round of SNP selection and genotyping (typically 300–1,200 SNPs), the database was updated with the revised frequencies of the SNPs that were now validated, and the program was run again to select new SNPs. This iterative procedure made it possible to fill in holes in the map and to utilize new SNP allele frequencies from public and proprietary databases as they became available over the course of the project. Overall, 1,537 SNPs were genotyped only at the Laboratory of Genomic Diversity (1.3% missing data rate), and 1,770 SNPs were genotyped only at the Broad Institute (2.9% missing data rate). Of the 33 SNPs genotyped at both sites, 61 discrepancies were observed out of 11,847 genotypes obtained at least in duplicate (0.51%). This indicates an average error rate of ∼0.26%.

Selection of 3,011 Markers with High Frequency Differentiation across Populations

From the 3,340 experimentally revalidated SNPs, we selected 3,011 that are maximally informative for admixture mapping (table 1; also see table A [online only], a tab-delimited ASCII file that can be imported into a spreadsheet). The median allele frequency difference between West Africans and European Americans is 56%, and the median SIC according to equation (1) is 25% of the maximum. The allele frequency estimates obtained by our revalidation genotyping in each ethnic group, the map positions, and the flanking sequences for the SNPs are all presented in table A (online only). All markers in this map are freely and publicly available without restriction, and genotypes are available on request. Chromosomal maps, figures showing the positions of each of the MALD markers in the genome, are available from the Laboratory of Genomic Diversity Web site.

Power of 2,154 Widely Spaced Markers for Admixture Mapping

We further selected 2,154 SNPs that are optimized for current admixture mapping analysis strategies (e.g., Falush et al. 2003; Patterson et al. 2004 [in this issue]), in the sense of having no LD among them in the parental African and European populations. We calculated the power of this panel for admixture mapping, where map power is defined (as above) as the information provided by the map about ancestry at a given point in the genome, compared with what would be obtained from genotyping a 100% informative marker that perfectly differentiates between populations.

When we assess the power in African Americans, the average map power for a random position in the genome is 71%±9% of the maximum (mean ± SD) (figs. 1 and 2). The power for 50%-50% mixtures of Africans-Amerindians is 66%±11%, for Europeans-Amerindians is 30%±11%, and for Europeans–East Asians is 36%±11%. The fact that East Asians are slightly more distinctive than Amerindians as compared with Europeans may reflect a small amount of confounding European admixture among the Amerindian samples (table 2).

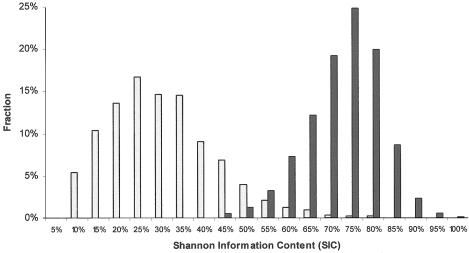
Figure 1.

Power of the individual 2,154 MALD markers (white bars), as a fraction of the maximum (power is calculated by eq. [1]). Power increases strikingly when the methods described by Patterson et al. (2004 [in this issue]) are used to combine data from multiple, closely linked markers (black bars).

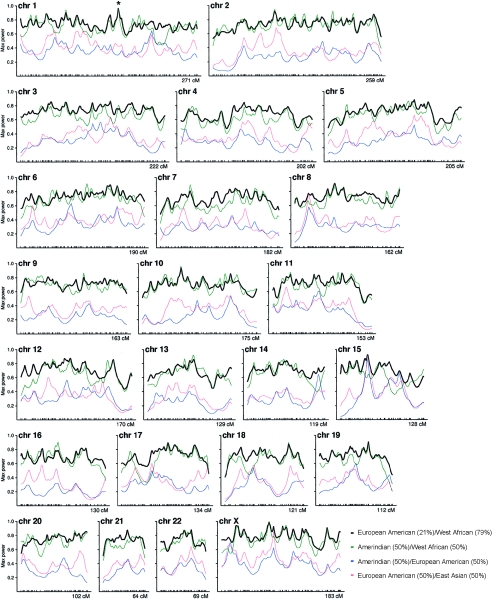
Figure 2.

Power of the 2,154-marker map as a fraction of what would be expected if there was full information about ancestry available at every point (e.g., nearly complete information [a value of 1 on the Y-axis] is available at Duffy on chromosome 1, indicated by a star). The black line is the power of the African American map under the assumption of an average of six generations since admixture (the power would be lower for individuals with more generations since admixture). We were also able to roughly estimate the quality of the map for studies involving Amerindian and East Asian mixtures under the assumption of six generations since admixture, although these estimates are less reliable because the sample sizes were smaller.

Figure 2 presents the distribution of map power across the genome. Because the average information content extracted from African American samples is 71%, at an average locus one needs to study 1/0.71=1.4 times as many samples to detect disease genes as would be necessary if one had full ancestry information. Uncertainties in the frequencies in the parental populations, however, mean that, in practice, these estimates are overoptimistic (see the “Methods” section and Patterson et al. 2004 [in this issue]). The true information content is ∼50%, comparable to the power of standard linkage maps (M. Daly, personal communication). Admixture genome scans using the present 2,154-marker map should therefore have double the sample size than would be necessary with a “perfect admixture map” in which every marker was as maximally differentiated as the FY null allele between the parental African and European populations. Calculations for such a “perfect admixture map,” for various disease models, are presented in the article by Patterson et al. (2004 [in this issue]). Power would be improved if extra information were incorporated from the full 3,011-marker map.

Subsets of SNPs for Estimating Population Ancestry

A subset of MALD markers can be genotyped to estimate the proportion of ancestry for each individual in a study (Parra et al. 1998). Genotyping such panels of markers allows researchers to search for evidence of genetic risk for a disease being higher in one ancestral population than another. For example, prostate cancer (Kittles et al. 2002), BMI (Fernandez et al. 2003), lupus (Molokhia et al. 2003), and several other traits (Halder and Shriver 2003) have all been genetically associated with the proportion of African ancestry. Estimating ancestry proportions in individuals is also useful for controlling for population stratification—systematic differences in ancestry between cases and controls—which can cause false positives in association studies (Pfaff et al. 2002; Hoggart et al. 2003; Freedman et al. 2004).

Table B (online only), a tab-delimited ASCII file that can be imported into a spreadsheet, provides lists of 100 SNPs spaced by at least 25 cM that are optimal for distinguishing four different mixtures and for making precise ancestry estimates. The average differences in allele frequencies are 78% (for African/European mixture), 85% (for African/American Indian mixture), 56% (for European/American Indian mixture), and 57% (for European/East Asian mixture).

Estimates of Admixture Mapping Parameters from the Genotyping Data in this Study

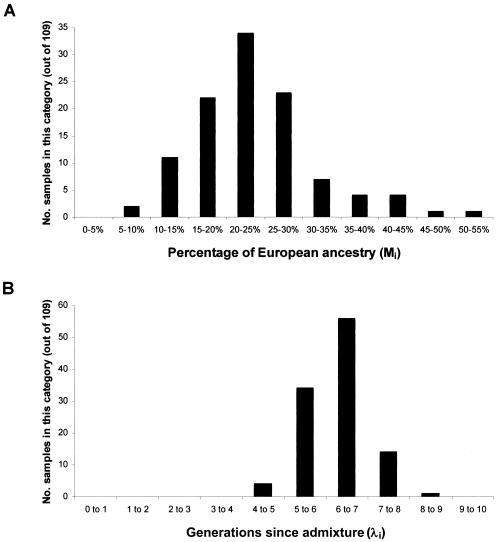
The ANCESTRYMAP software described in the accompanying article by Patterson et al. (2004 [in this issue]) was used to estimate parameters relevant to admixture mapping. First, the range of proportions of European ancestry was estimated for the 109 African American samples in this study (fig 3A). The range of estimates is 20%±8% (mean ± SD), slightly lower than the estimate of 21%±11% for 718 unrelated samples from the study by Patterson et al. (2004 [in this issue]). We note that 95% of the samples in this study are estimated to have 10%–90% European ancestry, in the range of maximal power for admixture mapping (Patterson et al. 2004 [in this issue]).

Figure 3.

A, Distribution of percentage of European ancestry (M_i) in 109 African American samples genotyped at 2,154 MALD markers (mean ± SD = 20% ± 8%). B, Distribution of estimated number of generations since admixture (λ_i) for 109 African Americans (mean ± SD = 6.3 ± 1.1). All estimates are generated by the ANCESTRYMAP software from the accompanying article by Patterson et al. (2004 [in this issue]). We emphasize that the number of “generations since admixture” is an average across a person’s lineages, since mixing between Africans and Europeans has occurred over many generations.

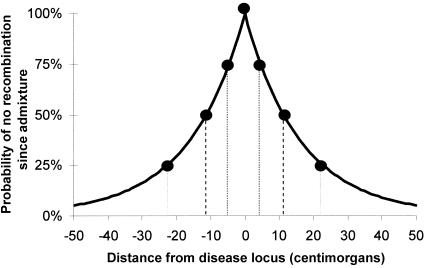
Second, we estimated the number of generations since admixture for each individual (fig. 3B). Since gene flow between European Americans and African Americans has occurred over many generations, the estimated number of generations since admixture should, in fact, be interpreted as an average across a person's different lineages (Stephens et al. 1994; Pfaff et al. 2001). We estimate 6.3±1.1 generations since admixture for these 109 samples, which is similar to the result of 6.0±1.6 for the 718 samples studied by Patterson et al. (2004 [in this issue]). We used this to estimate the probability of no recombination since admixture between a disease locus and neighboring sites; that is, the extent of admixture LD in the African American population (fig. 4). A peak of association is expected to fall to half its maximum LOD score within 11 cM of a disease locus, consistent with previous estimates of 10–20 cM for strong admixture LD in African Americans (Parra et al. 1998; Lautenberger et al. 2000; Collins-Schramm et al. 2003; Falush et al. 2003; Patterson et al. 2004 [in this issue]).

Figure 4.

Predicted probability of no recombination having occurred since admixture between a disease locus and a nearby marker locus, predicting the shape of a peak of association in an African American admixture study. The analysis was based on the distribution of the estimated number of generations since admixture (λ_i) values estimated from 109 African Americans (fig. 3B). We present the probability of a crossover between ancestry segments, as a function of the distance between a disease locus and mapping marker. At 4.5 cM, we expect the strength of association to drop to 75% of its maximum (measured as LOD or log of the P value). At 11 cM and 23 cM, the power drops to 50% and 25% of its maximum, respectively.

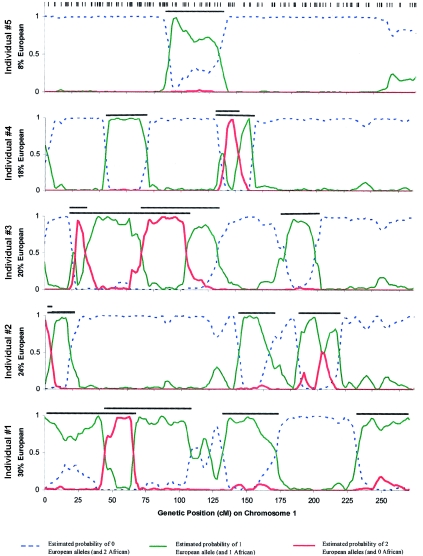
Third, we applied the Patterson et al. (2004 [in this issue]) analytic approach to chromosome 1 for 5 African American individuals, each with different percentages of European ancestry, selected from the 109 in this study. The analysis demonstrates clear transitions between segments of 0, 1, or 2 European alleles, with stretches of European and African ancestry extending for tens of megabases (fig. 5). To screen for disease genes on the basis of such data, the Patterson et al. (2004 [in this issue]) ANCESTRYMAP software combines these estimates across many individuals, searching for regions where the average proportion of African ancestry is higher (or lower) than the genomewide average.

Figure 5.

Estimates of ancestry along chromosome 1 for five African American samples, estimated by use of the Patterson et al. (2004 [in this issue]) ANCESTRYMAP software. The positions of the 169 markers in the map on chromosome 1 that were used for this inference are indicated by hash marks (inferred European chromosome segments are indicated by black bars). Sharp transitions between segments of 0, 1, or 2 European alleles are clear from the analysis, indicating the high resolution of the map.

Fourth and finally, application of the ANCESTRYMAP software allowed us to assess how closely the West African and European American populations corresponded to the true parental populations for African Americans. The software can estimate a parameter τ_E for Europeans and τ_A for Africans, indicating how much drift has occurred between the parental population and actual European American and West African samples that have been genotyped. An interpretation of τ_E and τ_A is that the true frequencies in the parental populations of African Americans are as close to those in the European American and West African controls as would be expected if the control sample frequencies were obtained by sampling τ_E alleles and τ_A alleles from the ancestral African American populations (e.g., Nicholson et al. 2002). The West Africans and European Americans are fairly close to the parental populations (τ_E=135; τ_A=242). For example, this means that if the true allele frequency of a SNP in the African ancestors of an African American sample was 30%, its frequency in the West African samples studied here is 95% likely to be in the range of 27%–33%. This is encouraging for potential applications of admixture mapping, but not surprising. As has been previously observed (Collins-Schramm et al. 2003), there is remarkable similarity in allele frequencies across all of West Africa, which is thought to be the source population for African Americans (perhaps because of the Bantu expansion across West Africa within the past 5,000 years). In addition, the 2,154 MALD markers chosen for the map were specifically selected not to differ strikingly in frequency across West African or European American populations, to minimize within-continent allele frequency divergences.

Analysis of Population Structure from the Genotyping Data

The STRUCTURE program (Pritchard et al. 2000; Falush et al. 2003), which clusters individuals into populations based on characteristic LD patterns between linked and unlinked loci, was used to assess population differentiation on the basis of the genotyping data from the main panel of 376 samples (table 2). The STRUCTURE analysis strongly supports the partition into four ancestral populations, corresponding to West Africans, Europeans, American Indians, and East Asians (table 2). The four African American populations were estimated to have 16%–19% European ancestry, consistent with the estimates of Parra et al. (1998). Modest admixture is also inferred for the other populations (e.g., European admixture in Amerindians and European admixture in Senegal and Botswana), although STRUCTURE does not provide statistical confidence about the presence of admixture.

Discussion

We have developed a high-density admixture map for studies in African Americans. This map contains 3,011 highly differentiated SNPs that are about five times more informative, on average, than a random microsatellite (Smith et al. 2001; Rosenberg et al. 2003). In the accompanying article (Patterson et al. 2004 [in this issue]), we present a method that allows for efficient use of this map. Other analysis methods, including those of McKeigue (1997, 1998) and Hoggart et al. (2003), as well as straightforward association tests (Chakraborty and Weiss 1988; Stephens et al. 1994), will also benefit from the admixture map. Diseases with strikingly different risks in populations of African and European descent (table 3) are particularly promising for admixture mapping in African Americans, as long as the difference in risk has a genetic underpinning and is not entirely due to environmental influences.

Table 3.

Candidate Diseases for Admixture Mapping in African Americans^[Note]

Disease	Relative Risk (95% CI)	Reference
Hepatitis C clearance	.19 (.10–.38)	Thomas et al. 2000
HIV vertical transmission	.30 (.10–.90)	Tess et al. 1998
Multiple sclerosis	.45 (.35–.55)	Kurtzke et al. 1979
Lung cancer	1.48 (1.38–1.67)	Davey Smith et al. 1998
Stroke	1.57 (1.27–1.94)	Davey Smith et al. 1998
End-stage renal disease	1.87 (1.47–2.39)	Klag et al. 1997
Intracranial hemorrhage	2.10 (1.44–3.06)	Davey Smith et al. 1998
Focal segmental glomerulosclerosis	2.43 (1.09–5.45)	Lopes et al. 1999
Prostate cancer	2.73 (2.13–3.52)	Davey Smith et al. 1998
Hypertensive heart disease	2.80 (2.03–3.86)	Davey Smith et al. 1998
Myeloma	3.14 (2.00–4.93)	Davey Smith et al. 1998

Note.— Relative risks given are for African Americans versus European Americans. Admixture mapping may also work for diseases with small incidence differences between African Americans and European Americans, because the risk may be differently distributed over loci. However, these should not be the first diseases to which the method is applied.

Comparable resources for admixture mapping in Hispanic populations or in Asian admixed groups are not yet available. Candidate SNPs have been identified by Parra et al. (1998) and Collins-Schramm et al. (2004), and our map contains several hundred markers that appear to be highly informative for both Hispanic and Asian admixture mapping (fig. 2). To build dense maps comparable to the one presented here for African Americans, it will be necessary to first mine large databases, such as those being developed in the international haplotype map project (International HapMap Consortium 2003), and then to validate candidate SNPs in a new and diverse sample set representative of the ancestral populations of Hispanic American and admixed Asian populations. The resulting marker maps will provide a powerful resource for admixture mapping of high-incidence disease-causing alleles in these populations.

The map of MALD markers that we have described and the methods presented in the accompanying article (Patterson et al. 2004 [in this issue]) now make high-density admixture mapping in African Americans practical. However, no new disease gene has ever been identified by admixture mapping, so validation of the approach will require the study of large collections of unrelated patients affected by disease. Only a few thousand markers need to be genotyped to perform a powerful admixture mapping study, and, thus, a whole-genome scan is practical with current technologies. Admixture mapping can, in theory, localize disease variants that differ strikingly in frequency across populations, to within 5–10 cM (fig. 4). This is a finer scale than linkage mapping but much rougher than haplotype-based association mapping. We conclude that admixture mapping provides a major new practical addition to the approaches available for discovering novel genes underlying the development of complex diseases.

Appendix: Calculating Information Content for an Admixture Map

We wish to test the relative power at each locus of a SNP map in an admixture study. We simplify the problem and assume that the average ancestry level of population A, M, is known, and that the population-dependent allele frequencies are also known.

Let us fix a locus t. ℋ=ℋ(t) is the hypothesis of a disease locus at t, ℋ₀ is the null hypothesis, X is the set of genotypes for an individual at our markers, A(t) is the number of chromosomes with ancestry from population A at t, and A(t)∈{0,1,2}. Write

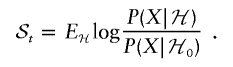Similarly, we define the “full score” as

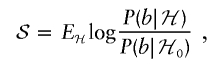where b is the number of chromosomes for the individual that have population A ancestry at locus t.

We wish to estimate 𝒮_t and will regard 𝒮_t/𝒮 as the multiplicative loss in sample size required to detect disease association at t over the size needed if we were to observe the ancestry at each chromosome locus. In other words, 𝒮 is the expected log factor for ℋ over ℋ₀ if we were to observe the ancestry of the chromosomes, and 𝒮_t/𝒮 is the relative power from observing only polymorphic markers and not ancestry. We believe that 𝒮_t/𝒮 will be roughly independent of the details and strength of the disease model.

𝒮 is easy to compute. We use an efficient combination of Monte-Carlo sampling and a control variate (Chen et al. 2000, p. 79) technique to estimate 𝒮_t. Now

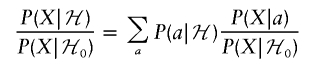and

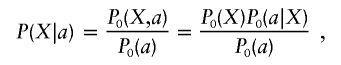writing P₀ as a shorthand for P|ℋ₀. Thus,

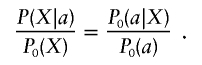Hence,

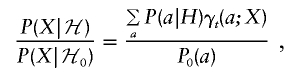where γ_t(a;X) is the posterior probability under ℋ₀ that A(t)=a.

Set

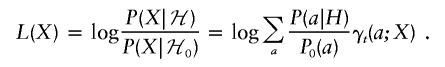Let 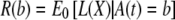. Note that L(X) conditional on A(t)=b is identically distributed under ℋ₀ and ℋ. This is the key remark. Then, .

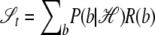Full power, if we observe the ethnicity b at t, is

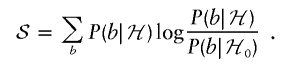Note that 𝒮 is nonnegative (it is a Kullback-Leibler distance).

𝒮 is easy to compute, given a disease model, and we will estimate 𝒮_t and thus 𝒮_t/𝒮. The simplest computation would be to perform a Monte-Carlo simulation, generating an ancestry sequence A and genotype sequence X. Then, we would accumulate observed values of L(X) into boxes labeled by “t” and “b” according to the values of A.

However, there are some refinements that make a huge difference to the sampling efficiency of the estimator. Pick a locus t. We describe a fair way, under the null model, to generate a sample (b,X) of the ancestry b at t and X. We generate a sequence of ethnicities A, using the Markov chain for A. Note that this is a Markov chain and that nothing is hidden. Then, generate X through use of P₀(X|A). So far, this is the same procedure as that described above. Now generate b, distributed as γ_t(b;X). Since X has the correct distribution P₀(X), and since we generate b according to the posterior P₀(b|X), this procedure is correct.

This argument shows that 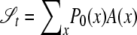, where

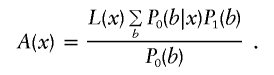Here we use P₁(b) as a shorthand for P(b∣ℋ). Similarly, we can write 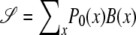, where

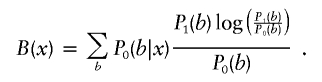Thus, 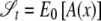, and 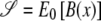. An extremely efficient means of estimating 𝒮_t is to use B(x) as a control variate. Draw N independent samples, x₁,x₂,…,x_N, and compute a_i=A(x_i) and b_i=B(x_i)-𝒮. The b_i have a mean of 0 by construction. Now regress B on A, minimizing 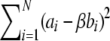as a function of β. We finally obtain our estimator for 𝒮_t as

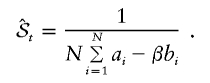This control variate technique is extremely efficient, since the correlation coefficient between A(x) and B(x) is usually >0.99.

We typically set N, the number of simulated genotype sets x_i, as N=10,000, and the power map estimates for the whole genome require only a few minutes of computation on a Compaq alpha.