Theoretical and Empirical Power of Regression and Maximum-Likelihood Methods to Map Quantitative Trait Loci in General Pedigrees

Abstract

Both theoretical calculations and simulation studies have been used to compare and contrast the statistical power of methods for mapping quantitative trait loci (QTLs) in simple and complex pedigrees. A widely used approach in such studies is to derive or simulate the expected mean test statistic under the alternative hypothesis of a segregating QTL and to equate a larger mean test statistic with larger power. In the present study, we show that, even when the test statistic under the null hypothesis of no linkage follows a known asymptotic distribution (the standard being χ²), it cannot be assumed that the distribution under the alternative hypothesis is noncentral χ². Hence, mean test statistics cannot be used to indicate power differences, and a comparison between methods that are based on simulated average test statistics may lead to the wrong conclusion. We illustrate this important finding, through simulations and analytical derivations, for a recently proposed new regression method for the analysis of general pedigrees to map quantitative trait loci. We show that this regression method is not necessarily more powerful nor computationally more efficient than a maximum-likelihood variance-component approach. We advocate the use of empirical power to compare trait-mapping methods.

Introduction

In human genetics, there is increasing interest in the dissection of genetic variation underlying continuously varying traits, because such traits may be genetically correlated with susceptibility to disease. Study designs to map QTLs include collections of sib pairs, small nuclear families, and general, complex pedigrees. For QTL analysis, a large number of methods have been proposed, including linear regression (see Feingold [2000] and T.Cuenco et al. [2003] for a description and discussion of regression methods), maximum-likelihood variance components (Goldgar 1990; Amos 1994; Fulker and Cherny 1996; Almasy and Blangero 1998), allele sharing (Risch and Zhang 1995), and Bayesian methods (e.g., Uimari and Sillanpaa 2001). In this article, we focus on regression and maximum-likelihood variance-component (VC) methods. To quantify the statistical power of different methods, either theoretical derivations (e.g., Williams and Blangero 1999; Sham et al. 2000a, 2000b; Sham and Purcell 2001; Visscher and Hopper 2001) or simulation studies (e.g., T.Cuenco et al. 2003 and Szatkiewicz et al. 2003) have been used. A commonly made assumption in the theoretical calculations is that, for a given location, a test statistic can be formulated that asymptotically has a central χ² distribution under the null hypothesis of no linkage and a noncentral χ² distribution under the alternative hypothesis of linkage. If that is true, then the relative power of different tests that have the same type I error rate can be quantified by calculating or simulating the expected test statistic under the alternative hypothesis (Dolan et al. 1999; Sham et al. 2002; T.Cuenco et al. 2003). The expected value of a χ² variate is a function of the degrees of freedom and the noncentrality-parameter (NCP). The mean and variance of a noncentral χ² distribution with k df are (k+λ) and 2(k+2λ), respectively, with λ as the NCP. Under the null hypothesis, λ=0, which gives a central χ². In simulation studies, the NCP can be estimated from either the empirical mean or variance of the test statistics.

For sibling pairs, it has been shown, both by theory and simulation, that regression methods are as powerful as maximum-likelihood VC methods (Sham and Purcell 2001; Visscher and Hopper 2001). When the total number of phenotypes (N) is fixed, an increase of the sibship size per nuclear family (s) gives more information on linkage, because the number of pairs in each family increases quadratically—[s(s-1)/2]—and the overall number of pairs increases linearly—[(s-1)N/2]—with sibship size. Analogously, more complicated pedigree structures provide more information than do small nuclear families for the same number of phenotypes, because all pairs of relatives can be considered simultaneously. There is some dispute, however, as to whether observations on different relative pairs within one pedigree can be treated as independent in analysis methods that are based on the sampling of independent pairs of relatives from the population (Lynch and Walsh 1998 [pp. 518] and references therein).

Regression methods are used widely in QTL mapping, because they are computationally efficient and lend themselves to resampling techniques, such as a permutation test to set significance thresholds (Churchill and Doerge 1996) and bootstrapping to estimate the CI of QTL location (Visscher et al. 1996). Recently, Sham et al. (2002) proposed a regression approach (herein referred to as “SR”) that can deal with general pedigrees and showed, by comparing the observed average test statistics from simulations, that this new approach had power superior to that of the VC method, while retaining the simplicity and robustness of regression methods. An interesting novelty of their approach was to model identity-by-descent (IBD) proportions as a function of observed trait values, instead of the usual modeling of trait values as a function of IBD proportions.

The aim of the present study was to compare and contrast regression and maximum-likelihood methods for sibling pairs, nuclear families, and complex pedigrees, in terms of theoretical and empirical power and computational efficiency.

Material and Methods

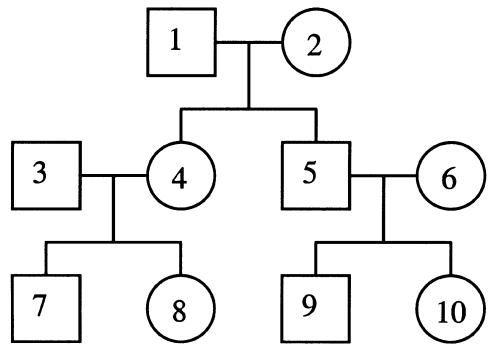
Phenotypic and marker data were simulated in nuclear families with sibship sizes varying from 2 to 10 and for the same cousin pedigree (fig. 1) that was used by Sham et al. (2002). A “perfect” marker was simulated so that the proportion of alleles that are identical-by-descent (IBD) between pairs of relatives was observed and had values of π=0, .5, or 1. A polygenic, additive QTL and residual random effect were simulated for each individual, conditional on the parental polygenic and QTL genotypes. For the nuclear families, phenotypes were simulated only for the siblings. The QTL effects in the founders were simulated from a normal distribution of QTL effects, which is consistent with an assumption of an infinite-allele model of random QTL effects. Diallelic QTLs were also simulated but gave similar results (not shown). The nuclear-family data were analyzed using the Haseman-Elston (HE) regression method (Haseman and Elston 1972), the Visscher-Hopper (VH) regression method (Visscher and Hopper 2001), and a maximum-likelihood VC method (Goldgar 1990; Amos 1994; Fulker and Cherny 1996; Almasy and Blangero 1998). For the regression methods, sibling pairs within a family were treated as if they were independent. The HE and VH regression analyses were performed using software written by the authors. The cousin pedigrees were analyzed using maximum-likelihood VCs and the regression method (SR) proposed by Sham et al. (2002). Merlin (Abecasis et al. 2002) was used for these analyses. For SR, the population mean, variance, and heritability need to be specified. True values of these parameters (i.e., those used to simulate the data) were used. Statistical tests were one-sided. Asymptotically, the test statistics from regression and maximum likelihood are presumed to have the same distribution, under the null hypothesis of no linked QTL, being 0 with a probability of .5 and following a χ² distribution with 1 df with a probability of .5 (Almasy and Blangero 1998; Sham and Purcell 2001; Visscher and Hopper 2001; T.Cuenco et al. 2003). For the present study, we use empirical type I error thresholds. Empirical power was calculated as the probability that the test statistic under the alternative hypothesis exceeded the significance threshold calculated from the empirical distribution under the null hypothesis. Type I error rate and empirical power were obtained from 2,000 simulations per set of parameters. For nuclear families, expected values of the NCP were calculated following Sham et al. (2002). Relative CPU time used by the four methods was compared. Calculations were performed on a virtual RAM disk so that the operation of raw data input/output of SR and VC were done in memory and can be ignored. Average CPU time was calculated from 100 replicates.

Figure 1.

Structure of the cousin pedigree

Results

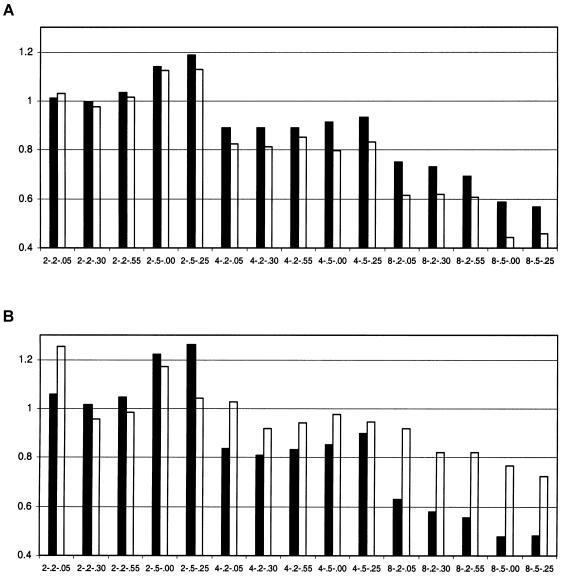
We first explored the empirical distributions of the test statistic obtained from the four methods for analysis of sibling data. The means and variances of the test statistics are shown in table 1. For the null hypothesis, the observed means are in good agreement with the expected values. Under the alternative hypothesis, the mean test statistic observed from the simulations is close to the simulation results shown by Sham et al. (2002), which is as expected, since we used the same method and software. As reported by Sham et al. (2002), the test statistics from SR are systematically larger than those from VC when the sibship size is >3. The empirical variances of the test statistic from regression methods are larger than those from VC, especially when the sibship size is large. For example, for a sibship size of 8 and a QTL heritability of 0.5, the variance of the HE test statistic is larger than that from VC, and the variance of the test statistic from SR is approximately twice that from VC (table 1). The NCPs estimated by equating the mean and the variance of the observed test statistics, with the appropriate expected moments of the noncentral χ² distribution, are given in table 2. If the observed test statistic follows a χ² distribution, the two estimates of the NCP should be identical. However, the estimated NCP obtained from the variance of the test statistic are inflated as the sibship size increases. With larger sibships, the estimated NCP from the empirical variance of the test statistic from SR are almost twice as large as those estimated from VH. Therefore, it appears that the test statistics from regression-based methods do not follow a noncentral χ² distribution when the family size is large. The ratios of the NCP calculated from the average test statistic and that calculated from the variance of test statistics are plotted in figure 2. All of the ratios tend to decrease as the family size increases. VC behaves the most regularly, in that the ratio is closest to 1.0 in all comparisons.

Table 1.

Mean and Variance of the Test Statistic (TS) for Each of the Four Analysis Methods, for Samples Consisting of 1,000 Phenotypes from Nuclear Families^[Note]

	Mean TS				Theoretical Mean TSc		Variance (TS)
Sibship Size,h2QTLa, and h2PGb	HE	VH	SR	VC	SR	VC	HE	VH	SR	VC
2:
.0:
.25	.50	.50	.50	.49	.50	.50	1.25	1.20	1.19	1.13
.50	.52	.53	.52	.53	.50	.50	1.38	1.42	1.37	1.43
.75	.52	.52	.52	.52	.50	.50	1.27	1.30	1.28	1.31
.2:
.05	2.51	3.52	3.51	3.29	3.62	3.63	7.96	11.79	11.49	9.30
.30	3.09	3.90	3.89	3.98	4.02	4.04	10.38	13.86	13.38	14.45
.55	4.18	4.85	4.82	4.98	4.86	4.90	14.31	17.17	16.61	18.19
.5:
.00	14.14	18.87	18.28	20.22	19.89	20.83	48.06	65.59	58.64	67.68
.25	19.37	23.30	22.33	26.77	25.13	27.00	63.92	80.93	69.66	100.72
4:
.0:
.25	.51	.51	.51	.49	.50	.50	1.29	1.36	1.36	1.23
.50	.51	.51	.51	.50	.50	.50	1.39	1.35	1.40	1.28
.75	.50	.50	.50	.48	.50	.50	1.27	1.25	1.24	1.14
.2:
.05	5.93	8.95	9.20	8.50	9.18	8.74	24.14	40.48	41.17	31.18
.30	7.70	10.16	11.10	10.50	11.07	10.49	32.04	46.97	51.90	43.38
.55	10.51	12.54	14.40	13.63	14.62	13.77	44.68	56.14	66.35	55.69
.5:
.00	40.44	55.29	58.52	57.90	63.93	58.76	174.70	274.89	272.00	235.11
.25	56.67	69.06	76.54	79.78	86.12	80.00	240.21	329.19	338.17	334.87
8:
.0:
.25	.52	.54	.54	.50	.50	.50	1.39	1.45	1.44	1.20
.50	.48	.50	.50	.47	.50	.50	1.25	1.46	1.39	1.13
.75	.49	.50	.52	.48	.50	.50	1.25	1.33	1.48	1.21
.2:
.05	12.76	19.93	21.38	17.77	21.01	17.93	64.78	125.32	131.78	75.00
.30	16.71	22.57	27.13	22.56	26.97	22.61	87.76	141.59	182.60	106.90
.55	23.41	28.25	37.01	30.39	37.49	30.66	131.50	181.16	261.05	145.45
.5:
.00	94.16	129.38	149.27	118.58	163.30	119.09	637.61	1165.91	1245.42	615.44
.25	131.64	160.88	200.71	164.20	229.06	164.59	923.16	1395.88	1660.64	903.14

Note.— The empirical mean and variance of the TS are based on 10,000 replicates.

^aProportion of the phenotypic variance due to QTL effects.

^bProportion of the phenotypic variance due to residual polygenic effects.

^cThe theoretical expected value of the test statistic was calculated as described by Sham et al. (2000a).

Table 2.

Empirical NCP under the Alternative Hypothesis from Samples of 1,000 Phenotypes from Nuclear Families

	NCP from Mean TSa				NCP from TS Varianceb
Sibship Size,h2QTL, and h2PG	HE	VH	SR	VC	HE	VH	SR	VC
2:
.2:
.05	1.5	2.5	2.5	2.3	1.5	2.4	2.4	1.8
.30	2.1	2.9	2.9	3.0	2.1	3.0	2.8	3.1
.55	3.2	3.9	3.8	4.0	3.1	3.8	3.7	4.0
.5:
.00	13.1	17.9	17.3	19.2	11.5	15.9	14.2	16.4
.25	18.4	22.3	21.3	25.8	15.5	19.7	16.9	24.7
4:
.2:
.05	4.9	8.0	8.2	7.5	5.5	9.6	9.8	7.3
.30	6.7	9.2	10.1	9.5	7.5	11.2	12.5	10.3
.55	9.5	11.5	13.4	12.6	10.7	13.5	16.1	13.4
.5:
.00	39.4	54.3	57.5	56.9	43.2	68.2	67.5	58.3
.25	55.7	68.1	75.5	78.8	59.6	81.8	84.0	83.2
8:
.2:
.05	11.8	18.9	20.4	16.8	15.7	30.8	32.4	18.3
.30	15.7	21.6	26.1	21.6	21.4	34.9	45.2	26.2
.55	22.4	27.3	36.0	29.4	32.4	44.8	64.8	35.9
.5:
.00	93.2	128.4	148.3	117.6	158.9	291.0	310.9	153.4
.25	130.6	159.9	199.7	163.2	230.3	348.5	414.7	225.3

^aE(TS)=1+NCP.

^bVar(TS)=2+4(NCP).

Figure 2.

Ratio of NCP values, calculated from the empirical mean divided by those from the empirical variance of the test statistic. The labels on the X-axis are in the format of s-h²_QTL-h²_PG, where s is the sibship size. A, Comparison between the HE (blackened bars) and VH (unblackened bars) methods. B, Comparison between the SR (blackened bars) and VC (unblackened bars) methods.

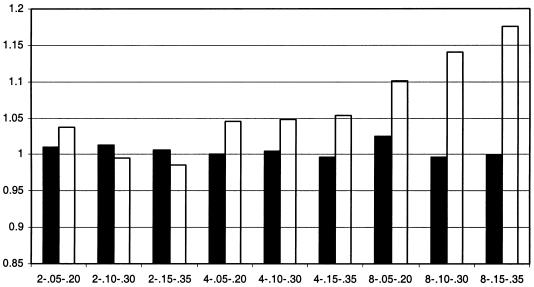
Empirical power at a one-sided significance level of 0.05 is shown in table 3. For all the scenarios considered, the HE method has the lowest power to detect the QTL, which was expected, because it utilizes least information on linkage (Wright 1997; Sham and Purcell 2001; Visscher and Hopper 2001). When the polygenic effects are small, the powers of VH, SR, and VC are very similar. For all scenarios considered, SR and VC have almost the same empirical power. A comparison of relative empirical power and mean test statistic is shown in figure 3. There is a clear trend of a proportional increase of the SR test statistic relative to the VC test statistic as the sibship size increases, whereas the relative power from the two methods remains similar. Hence, inference on the relative power based on the average test statistic may be misleading.

Table 3.

Empirical Power (%) for Analyses of Nuclear Families, at a Type I Error Rate of 5%^[Note]

Sibship Sizeand h2QTL	h2PG	HE(%)	VH(%)	SR(%)	VC(%)
2:
.05	.20	8.9	11.0	10.7	10.6
.10	.30	18.0	21.3	22.1	21.8
.15	.35	28.7	37.1	37.1	36.8
4:
.05	.20	15.0	18.2	18.5	18.5
.10	.30	33.2	42.5	43.7	43.5
.15	.35	61.8	71.5	75.1	75.3
8:
.05	.20	21.2	28.4	29.9	29.2
.10	.30	56.8	66.8	71.5	71.7
.15	.35	87.8	94.0	96.3	96.4

Note.— Results are based on 10,000 replicates.

Figure 3.

Ratio of empirical power (blackened bars) and of mean test statistic (unblackened bars), from SR divided by VC. The labels on the X-axis are in the format of s-h²_QTL-h²_PG, where s is the sibship size.

In addition to simulating the scenarios of Sham et al. (2002), we also explored the behavior of the test statistic when the proportion of phenotypic variance due to the QTL is very large (>0.5). For a large QTL variance, the mean test statistic, when simulating a diallelic QTL, was larger than the mean test statistic from a infinite-allele QTL (results not shown). In addition, SR was found to give lower mean test statistics and a downwardly biased estimate of the QTL variance compared with VC. In the extreme case of a QTL explaining 99% of the variance, the mean estimated proportion of variance due to the QTL was 0.75 with SR, whereas it was unbiased with VC.

Results from the complex cousin pedigree are shown in table 4. The mean test statistics from SR and VC are not significantly different, either from each other or from the results given by Sham et al. (2002), except for the last scenario shown in table 4. In this case, the mean of 91.2 with SR is significantly different from 94.6, the mean obtained with VC (table 1), and different from 93.68 and 93.41, the values reported by Sham et al. (2002) for SR and VC, respectively. (Note that, in table 7 of Sham et al. [2002], the columns for the “Perfect Marker” and “Diallelic Marker” were transposed.) Sham et al. (2002) observe a systematic difference in mean test statistic between SR and VC in the presence of a linked QTL, in particular, for the diallelic marker case. We reported only results for the perfect marker scenario but do not observe this trend for either situation. As for the case of large sibships, the empirical variances of the test statistic from SR are larger than those from VC. The estimated NCP from the mean and variance of the test statistic were calculated from the results of the five linked QTL scenarios in table 4. For SR, the ratio of the NCP calculated from the mean and variance of the test statistic varied from 0.80 to 0.90, whereas the corresponding range was 0.92–1.02 for the VC method. Hence, the distribution of the test statistic from VC appears to follow a standard noncentral χ² distribution more closely than the test statistic from SR, because the NCP parameter estimated from the mean and the variance of the distribution are more similar with VC.

Table 4.

Mean and Variance of Test Statistic from SR and VC from the Cousin Pedigree^[Note]

	Test Statistics
	SR		VC
θa, h2QTL,and h2PG	Mean	Variance	Mean	Variance
.5:
.0:
.25	.48	1.08	.46	1.02
.50	.50	1.17	.49	1.08
.75	.46	1.18	.45	1.10
.2:
.05	.49	1.10	.49	1.07
.30	.49	1.20	.49	1.16
.55	.50	1.29	.49	1.30
.5:
.00	.53	1.42	.55	1.49
.25	.52	1.43	.55	1.60
.0:
.2:
.05	11.5	49.0	11.0	41.0
.30	12.7	56.4	12.2	48.6
.55	16.6	72.3	16.0	64.5
.5:
.00	70.6	349.7	71.2	299.8
.25	91.2	427.8	94.6	407.6

Note.— Results are based on 2,000 replicates.

^aθ is the recombination fraction between the QTL and the marker.

The comparison of CPU time used by the four methods is given in table 5. For sibships of size 2–6, SR is faster than VC but an order of magnitude slower than HE or VH regression. For a sibship size of ⩾8, the CPU time for SR is substantially larger than for VC. For a sibship size of 12, the ratio of CPU time for SR and VC is ∼800 (results not shown). For the cousin pedigree, the two methods require comparable CPU time.

Table 5.

Relative CPU Time Usage^[Note]

Pedigree	HE and VH	VC	SR
Sibship size 2	1	10.1	3.4
Sibship size 3	1	9.9	3.5
Sibship size 4	1	11.3	4.2
Sibship size 5	1	11.2	4.9
Sibship size 6	1	12.1	9.2
Sibship size 8	1	14.8	129.0
Sibship size 10	1	16.8	2,682
Cousin	1a	83.6	70.8

Note.— Sibship size × number of families = 120. For each scenario, 100 repeats were performed.

^aHE an VH methods applied to all pairs of siblings in the cousin pedigree.

Discussion

With more than two siblings in a family, the genotypes and phenotypes of pairs of siblings are dependent (Hodge 1984). For example, in the case of three siblings, if two of the three possible pairs share both alleles IBD, then the third pair must also do so (see, e.g., Daly and Lander 1996). Correlated data can result in an increase in the variance of the test statistics. For example, if we duplicate a sample of size N to estimate the arithmetic mean, then the naive estimate of the sampling variance of the mean is σ²/(2N), whereas the actual variance is σ²/N—twice as large. When there is dependence in the data and this is ignored in the analysis and subsequent hypothesis testing, care should be taken with the interpretation of results. In particular, it may be incorrect to rely on P values that are calculated from an assumed asymptotic distribution of the test statistic or to use the expected test statistic to infer statistical power. Dolan et al. (1999) investigated the power of different analysis methods when sibling pairs, concordant and/or discordant for quantitative trait values, were ascertained using simulation studies. Comparison of power was made from the average test statistic, even though the authors showed that empirical type I error rates differed between analysis methods. It is not clear how differently the methods would perform if empirical power were used to assess performance. T.Cuenco et al. (2003) and Szatkiewicz et al. (2003) investigated power for selected sibling pairs only for methods that gave a “correct” type I error rate, but an “incorrect” type I error does not necessarily imply reduced power. The conclusions from our study regarding the VC and SR methods are not affected by assumptions regarding (in)dependence of correlated data, because both methods model the correlation between all siblings within a family.

It is interesting that Sham et al. (2002) presented not only simulation results for which the NCP of their regression method was larger than the corresponding NCP from the VC methods but also showed analytically that this difference was to be expected. In the appendix, we show why this does not imply that the SR is more powerful than VC for large sibships or complex pedigrees, and we conclude that the SR method is an approximation of the VC method.

How important is it that a statistical test for QTL linkage at a given genomic location asymptotically has a known distribution under the null hypothesis? In practice, with real data, there are a number of facts that question the importance of this property. First, “asymptotic” or equivalently “large sample” requirements are vague. For example, is a sample of 1,000 sibling pairs and a marker with 75% heterozygosity sufficient to calculate a P value from an asymptotic distribution? Second—and more important—in practice, a chromosome or genome scan is performed, and the test statistic of interest is the largest observed test statistic among a (large) number of tests. The largest test statistic has no simple distribution, although approximations have been suggested for dense maps of fully informative markers (e.g., by Lander and Botstein 1989 and Dupuis and Siegmund 1999), so the asymptotic behavior of the test statistic at a single location becomes less relevant for genome scans. However, looking at a single location enables a simpler comparison of analysis methods, and the ranking of methods for a single location is likely to hold for the more general situation of a genome scan. For simple pedigree structures, a permutation test (Churchill and Doerge 1994) is a simple and effective method for creating an empirical distribution of the test statistic under the null hypothesis, conditional on the observed data. For complex pedigrees, however, a simple permutation test is not obvious, because permuting phenotypes over genotypes (or vice versa) would break up polygenic-phenotypic as well as QTL-phenotypic relationships. Therefore, the extrapolation of the properties of a statistical test at a single locus to a genomewide scan is a useful alternative to genomewide parametric simulation studies.

For the four methods we studied, the HE regression method always had the lowest power. However, although the HE implicitly uses less information on linkage, it has been shown to be extremely robust to violations of assumptions regarding the distribution of the test statistic and robust to misspecification of trait parameters and normality (see, e.g., T.Cuenco et al. 2003). The VH-regression method is simple and efficient for unselected samples, but it has been shown to give “biased” type I error rates in selected samples. When the sibship size is large and the polygenic effect is large, the VH method is less powerful than SR and VC. The test statistic from the SR regression method does not follow a noncentral χ² distribution and consumes a great deal of CPU time for large sibships or complex pedigrees. However, its modeling of the proportion of alleles shared IBD as a function of quantitative trait value makes it particularly useful for analysis of selected samples (Sham et al. 2002). Of all methods studied, the VC method appears to be the most desirable when all of the properties are considered (type I error rate, empirical power, asymptotic distribution, and computing efficiency). In the case of selected samples for genotyping (e.g., discordant and concordant sibling pairs), with phenotypes available on the entire sample before selection, maximum-likelihood VC methods are typically not used for analysis (Szatkiewicz et al. 2003), mainly for computational reasons, although Dolan et al. (1999) used maximum likelihood (ML) with prior IBD probabilities to analyze large samples of simulated sibling pairs. A full joint segregation-linkage analysis of all phenotypic and marker data—that is, a VC analysis that uses the posterior IBD probabilities (conditional on marker data, if available, and phenotypes)—is computationally feasible for large samples of sibling pairs (say, >40,000 phenotypes) and should be more powerful than regression or VC methods that ignore the ungenotyped individuals.

Appendix: Expected-Likelihood Ratio Test Statistic for QTL Variance in Complex Pedigrees

The purpose of this appendix is to show equivalence between the approximations of Williams and Blangero (1999) and Sham et al. (2002) for the expected value of the NCP for VC and regression methods, respectively. Williams and Blangero (1999) used the asymptotic theory of likelihood-ratio test statistics to derive the NCP for an arbitrary pedigree structure. For a linear model of the data (y) containing random QTL effects (q), random polygenic effects (a), and residual effects (e), the covariance matrix, conditional on the observed IBD configuration matrix (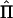), is

with A as the numerator relationship matrix (twice the kinship matrix). A Taylor series expansion of minus twice the log-likelihood ratio for H₀:θ=θ₀ against H₁:θ=θ₁ is,

with θ₁ as the true parameters under H₁ and θ₀ as the parameters under H₀ and θ₁₀ as the expected values of the parameter estimates for the reduced model when H₁ is true (Sorensen and Gianola 2002 [pp. 171–174]). The matrix 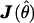is the observed information matrix for 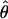under the full model and is the inverse of the asymptotic covariance matrix of 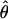. Its elements contain (second) differentials of the log likelihood, with respect to the unknown parameters, and are functions of Σ and 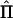(Williams and Blangero 1999). For a single data set, 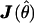represents the curvature of the log-likelihood function, with respect to the unknown parameters, and depends on data. When the expected information is used instead, the curvature reflects an average curvature over realizations of the data (see, e.g., Sorensen and Gianola 2002 [pp. 171–174]). Asymptotically, the likelihood-ratio test statistic is distributed as a (non)central χ², with NCP,

To derive analytical equations for statistical power—that is, independent of observed data—Williams and Blangero (1999) used the expected amount of information (minus the expected value of the second differential of the log-likelihood function, with respect to the parameters) in the above equation. The derivation of the expected NCP for a QTL-mapping pedigree, in the absence of observed IBD data, is more complicated than that of a “standard” design to estimate VCs, because the matrix 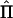varies over conceptual repeated samples. Hence, the information matrix needs to be a weighted average of all possible realizations of 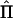. Williams and Blangero (1999) average over 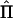but use a constant Σ evaluated at the reduced model [Σ₀=A(σ²_a+σ²_q)+Iσ²_e]. Asymptotically, use of either Σ₀ or a weighted average 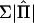should give equivalent results, but we have found that the approximations differ when the QTL heritability is large and/or when the sibship size is large. Williams and Blangero (1999) present a number of “exact” results (which strictly are only exact for an infinite sample size) for the expected NCP for particular designs. For sib pairs, their derivation shows that

with h²=a²+q², the total proportion of variance due to polygenic (a²) and QTL (q²) effects.

Sham et al. (2000a) showed that the exact value of the NCP is

where Σ_i is the covariance matrix for IBD realization i and p_i is the probability of that realization. For complex pedigrees, a Monte Carlo approximation of equation (A2) for a fully informative marker is easily obtained by gene-dropping simulations. We have found this to be a convenient and quick way to assess power for complex pedigrees, and it is much faster than simulating phenotypes and maximizing the likelihood for both hypotheses. Sham et al. (2002) use a Taylor series approximation to equation (A2) and note that this approximation is equivalent to the expectation of their regression-based test statistic. For sibships of size s, and under the assumption of a fully informative marker, the approximation is

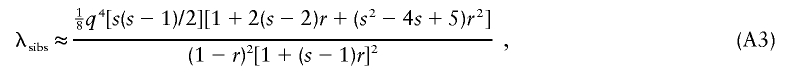with r as the average sib correlation in the population (Sham et al. 2002). Sham et al. (2002) note that, for large sibships, the NCP from equation (A3) is larger than that from equation (A2), and they conclude that, therefore, their regression method is more powerful than the VC method for large sibships. This conclusion is not justified, on the basis of these calculations, because equation (A3) is only an approximation of the exact NCP (eq. [A2]). In fact, equation (A3) is identical to the VC approximation used by Williams and Blangero (eq. [A1]). For the variance model used above, r= 1/2h². A substitution of this in equation (A3) with a setting of s=2 results in equation (A1). The same applies for the expression given by Williams and Blangero (1999) for s=3. Hence, the NCP for the regression method derived by Sham et al. (2002) is a second-order Taylor series approximation of the exact NCP for the likelihood-ratio test.

Sham et al. (2002) showed that their prediction of the NCP for their regression method closely matched their observed average test statistic with regression for sibships. Although it is not a formal proof, it appears that their regression method therefore also is an approximation of the VC method. For large sibships, the NCP for the regression method is larger than the NCP for maximum likelihood, but other examples can be given for which the expected NCP for the regression method is smaller than that for maximum likelihood. For example, for 500 sib pairs and a large QTL heritability (q²=0.9, a²=0), the NCP for regression and ML are 151 (through use of eq. [A1]) and 96 (through use of eq. [A2]), respectively.