Abstract
There is a growing recognition that gene conversion can be an important factor in shaping fine-scale patterns of linkage disequilibrium in the human genome. We devised simple multilocus summary statistics for estimating gene-conversion rates from genomewide polymorphism data sets. In addition to being computationally feasible for very large data sets, these summaries were designed to yield robust estimates of gene-conversion rates in the presence of variation in crossing-over rates. Using our summaries, we analyzed 21,840 biallelic single-nucleotide polymorphisms (SNPs) on human chromosome 21. Our results indicate that models including both crossing over and gene conversion fit the overall short-range data (0–5 kb) of chromosome 21 much better than do models including crossing over alone. The estimated ratio of gene-conversion rate to crossing-over rate has a range of 1.6–9.4, depending on the assumed conversion tract length (in the range of 500–50 bp). Removal of the 5,696 SNPs that occur in known mutational hotspots (CpG sites) did not significantly change our conclusions, suggesting that recurrent mutations alone cannot explain our data.
Introduction
Linkage disequilibrium (LD) refers to the nonrandom association between alleles at different loci, at a population level. With the availability of genomewide polymorphism data, LD has gained great theoretical and practical importance in the area of human genetics. Understanding the patterns of LD across the genome is crucial for both fine-scale mapping of disease genes and for making inferences about human population history. Such patterns are influenced by numerous forces. These include forces that affect the whole genome (e.g., population growth) as well as forces that affect individual loci (e.g., natural selection). In particular, genetic exchange mechanisms play a key role in shaping the LD patterns within a population. New alleles that arise by mutation are in strong association with alleles at the surrounding loci. These associations get broken down when alleles are shuffled between chromosomes at the time of meiosis. Thus, LD between any two alleles decays with time.
Current meiotic modes allow for two different mechanisms of allelic exchange. Central to many biological models that describe these mechanisms is a structure called the “Holliday junction” (Holliday 1964). “Holliday junction” refers to a four-way DNA intermediate that arises when homologous chromosomes overlap for strand exchange. Resolution of these intermediates results in the transfer of short stretches of DNA between chromosomes. However, this process is not always accompanied by the reciprocal exchange of larger chromosomal segments (Carpenter 1984). We use “crossing over” to denote the reciprocal exchange of large chromosomal fragments, “gene conversion” to denote short exchanges between chromosomes that are not accompanied by crossing over, and “recombination” to denote both gene conversion and crossing over. We refer to the stretch of DNA transferred during a gene-conversion event as a “conversion tract.”
Although both crossing over and gene conversion reduce the levels of LD over time, the effects are qualitatively different. The rate of decay of LD by crossing over increases as the distance between the markers increases. In contrast, the rate of decay of LD by gene conversion is independent of the marker spacing for distances greater than the length of a conversion tract (Andolfatto and Nordborg 1998; Wiehe et al. 2000). Thus, whereas crossing over is the major determinant of LD for distant sites, the added effects of gene conversion cannot be ignored for closely linked sites (Andolfatto and Nordborg 1998).
Short-range patterns of LD can lead to spurious inferences about population history and effective population size when gene conversion is not taken into account. Gene conversion can also have significant implications in disease mapping and association studies. A wide variation in the rate of conversion across the genome would create distortions in an LD map based on crossing over alone and, in turn, would adversely affect results from whole-genome association studies (Clark et al. 2003). Since the decay of LD by gene conversion becomes independent of distance as the marker spacing increases, high conversion rates will make LD much less informative for mapping purposes.
Population genetic models that incorporate both gene conversion and crossing over in the coalescent have recently been developed (Wiuf and Hein 2000). Many recent studies have also indicated that gene conversion may be frequent in the human genome. Ardlie et al. (2001) determined SNP genotypes in 68 STSs and found much less LD among SNPs within very short physical distances than expected on the basis of population genetics theory. They concluded that gene conversion was the most likely explanation for this observation. Frisse et al. (2001) applied a generalization of an estimation method developed by Hudson (2001) to data from a 20-kb region in the genome and found that the estimated ratio of gene-conversion to crossing-over rates is 7.3 for a mean tract length of 500 bp. Analysis of several genomic regions in humans further supports the idea that local LD is less than expected and that the discrepancy can be easily explained by gene conversion (Przeworski and Wall 2001).
In this article, we present simple summary statistics to estimate gene-conversion rates from population genetic data (SNPs) and to distinguish evolutionary scenarios including gene conversion from those including crossing over alone. Our analysis was focused on gene conversion rather than crossing over, and our summary statistics were designed to separate the effects of the former from those of the latter, as far as possible. Using coalescent simulations, we first evaluated the performance of our method under the standard model of gene conversion, as well as under some nonstandard models. We found that our method works better than comparable existing methods for estimating the conversion rate (whereas the opposite was true for the rate of crossing over), and the estimates seemed to be robust to variation in the crossing-over rates. We then applied our summaries to 21,840 biallelic SNPs from 20 independent copies of human chromosome 21 (data set of Patil et al. [2001] that was also used by Innan et al. [2003]; see also the National Center for Biotechnology Information [NCBI] Web site) and estimated the average rate of gene conversion in the data. Finally, we examined the fit of the overall data to some simple population genetic models without conversion and checked for multiple “hits” in CpG sites. Our results suggest that gene-conversion events make a major contribution to the decay of short-range LD in chromosome 21.
Material and Methods
Models and Simulations
Coalescent theory provides an efficient framework for simulating population genetic data (Kingman 1982; Nordborg 2001). We simulated data under the coalescent, assuming no population structure, a large constant population size (N), no selection, and the infinite-sites model for mutations (i.e., every mutation affects a unique site). All of our simulations involved 200-kb DNA sequences (a region large enough to encompass the phenomenon of interest yet small enough for computational feasibility), a sample size of n=18 (to match the data; see below), and a uniform population mutation rate θ=4Nu=140 (estimates from Innan et al. [2003]). Here, u denotes the per-generation probability of a mutation event per sequence. Only the nonsingleton SNPs (i.e., SNPs with minor allele count >1) in any simulated data set were used for further analysis.
We considered models with both uniform and nonuniform crossing over along the sequence. For modeling nonuniform crossing over, we assumed that there are 1-kb regions with elevated crossing-over rates (i.e., hotspots) once every 40 kb, on average. A significant percentage (x) of all crossing-over events happen within these hotspots, whereas the rest of the events happen in the intervening regions. Crossing over within hotspots as well as within nonhotspot regions is assumed to be uniform. All hotspots have identical (higher) levels of crossing over. Similarly, all nonhotspot regions also have identical (lower) levels of crossing over.
For modeling gene conversion, we used the coalescent with both crossing over and gene conversion, as described by Wiuf and Hein (2000). Gene-conversion tracts are assumed to be geometrically distributed, with a mean length L, whereas the population crossing-over rate ρ (i.e., 4Nr) and population gene-conversion rate γ (i.e., 4Nc) are uniform along the sequence. Here, r denotes the per-generation, per-sequence probability of a crossing-over event, and c denotes the per-generation, per-sequence probability of a gene-conversion event. Note that this model is equivalent to the assumption that events occur with a total rate of ρ+γ and that each event results in crossing over with probability ρ/(ρ+γ) and in gene conversion otherwise. The ratio of the rate of gene conversion to the rate of crossing over (i.e., γ/ρ or c/r) is denoted by f. In addition to this standard model of gene conversion, we simulated data under an alternate model in which crossing over is nonuniform and gene conversion is uniform (program available at the Nordborg Lab Web site). The model of nonuniform crossing over here assumes that 50% of all crossing-over events occur in hotspots that are 1 kb in length (Wall and Pritchard 2003).
We also simulated data with population structure and population growth. Population structure is simulated using a symmetric two-island model with equal migration rates (4Nom) between the two subpopulations, where m denotes the per-generation, per-sequence probability of a migration event and No is the size of a subpopulation. The two subpopulations are also assumed to be equal in size and to have identical mutation (u) and recombination (r) rates. For simulation of population growth, the ancestral population size is assumed to have been constant until t generations ago, after which it grew exponentially to the current population size. Time is scaled nonlinearly during the exponential growth phase. Both the structure and growth models are described in detail by Nordborg (2001).
Rejection Method
A simple rejection scheme is used to estimate parameters such as the population crossing-over rate (ρ), population gene-conversion rate (γ), etc. Under this scheme, we simulated data sets for different parameter values and computed summary statistics. We then accepted a data set if all of its summaries were within 20% of the observed values. Otherwise, we rejected it. The likelihood of a set of parameter values was approximated as the fraction of data sets that were accepted for that set (for details about rejection methods, see Weiss and von Haeseler [1998] and Marjoram et al. [2003]).
Summary Statistics
We now describe the summary statistics used in our analysis. A pair of SNPs is called “incompatible” if all four possible haplotypes are observed in the sample and called “compatible” otherwise. Under the infinite-sites model for mutations, incompatibility is evidence for at least one crossing-over or gene-conversion event between the two loci (Hudson and Kaplan 1985).
Consider three SNPs A, B, and C, ordered from left to right. SNPs are defined to be in pattern a if: A and B are incompatible, B and C are incompatible, and A and C are compatible.
Now consider four SNPs A, B, C, and D, ordered from left to right. SNPs are defined to be in pattern b if: A and D are incompatible and B and C are incompatible.
Let p(a) and p(b) denote the fraction of all triplets and quadruplets with the outer SNPs within 5 kb that show patterns a and b, respectively. We used p(a) and p(b) jointly to estimate the gene-conversion rate. Thus, under our rejection method, we accepted a data set if both p(a)and p(b) were within 20% of the observed values. Note that patterns a and b reflect the potential effects of a single gene-conversion and crossing-over event. Patterns of type a can arise from a single gene-conversion event affecting the middle SNP in a triplet. Similarly, patterns of type b can result from a single crossing-over event between the inner SNPs in a quadruplet.
The Chromosome 21 Data
We analyzed the chromosome 21 data of Patil et al. (2001), who identified 35,989 SNPs in a 33-Mb region in the q arm of this chromosome, after masking 33% of the sequence as repeats. The SNPs were obtained by resequencing 20 independent copies of the chromosome from a worldwide sample. For the current study, we used 21,840 biallelic nonsingleton SNPs from a 28-Mb region on the largest contig, NT_002836 (NCBI). A singleton SNP can never form an incompatible pair, so singletons are excluded in our analysis. This data set contains a large amount of missing data. On average, data from 3.9 chromosomes are missing per SNP site.
To avoid biases of sample size due to missing data, we consider a pair of SNPs as compatible or incompatible on the basis of a random sample of 18 chromosomes alone. This random sample should satisfy the following two conditions: (1) there is no missing data at either SNP site and (2) there are nonsingleton SNPs at either SNP location.
To calculate p(a) and p(b), we chose only those triplets and quadruplets in which we can find such a random sample for all the pairs of interest. The sample size of 18 was chosen to give a large enough number of triplets and quadruplets in the short range. All in all, we used 191,189 triplets and 787,264 quadruplets to calculate p(a) and p(b).
Results
Choice of Summary Statistics
A serious difficulty in estimating the gene-conversion rate is distinguishing between gene conversion and crossing over. A single summary statistic cannot efficiently distinguish models with both crossing over and gene conversion from models with higher crossing over alone. Furthermore, patterns based on pairs of sites alone are not effective in teasing apart the effects of gene conversion and crossing over (example in fig. 1). For that reason, we have chosen a combination of summaries based on triplets and quadruplets of loci.
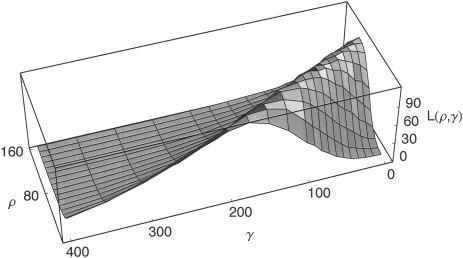
Figure 1.
A likelihood surface of chromosome 21 data that is based on the fraction of short-range (0–5 kb) incompatible SNP pairs alone. ρ denotes the crossing-over rate, γ denotes the gene-conversion rate, and L(ρ,γ) is the product of the likelihood and an arbitrary constant. Note that estimates of gene conversion decrease rapidly with increasing crossing-over rates and eventually reach zero. A single pairwise summary cannot distinguish between the effects of gene conversion and those of crossing over.
Both crossing over and gene conversion increase p(a) and p(b). However, the joint distribution of p(a) and p(b) in the presence of gene conversion alone is different from the distribution with crossing over alone (see fig. 2).
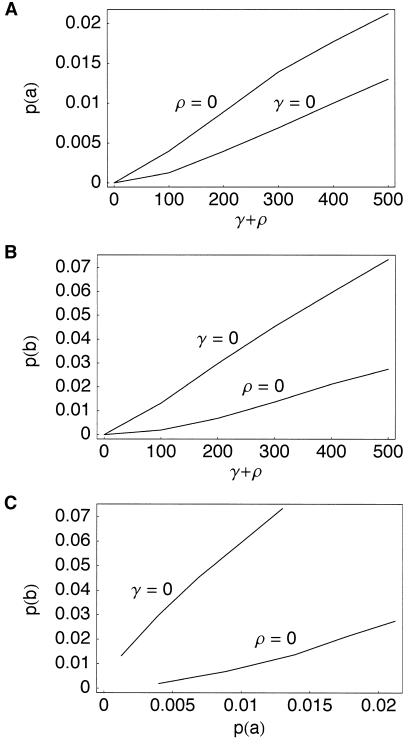
Figure 2.
Expected values of p(a) and p(b), from simulations under models with uniform crossing over alone (γ=0) and uniform gene conversion alone (ρ=0) at differing rates. Expectations were calculated from 1,000 simulations of 200-kb sequences, with θ=140. For models with gene conversion alone, the mean conversion-tract length was fixed at L=500 bp.
Accuracy of Estimation
Many different methods for estimation of crossing-over rates from population genetic data are currently available (e.g., Kuhner et al. 2000; Nielsen 2000; Hudson 2001). Our primary goal is to estimate gene conversion rather than crossing over. In this section, we evaluate the performance of our summaries, under the standard model of gene conversion, and compare it with the composite likelihood method of Hudson (used by Frisse et al. [2001]). We also test our method under some nonstandard models and show that our summaries provide robust estimates of the gene-conversion rate.
We first simulated 1,000 data sets each for different combinations of crossing-over and gene-conversion rates, under the standard model of gene conversion (i.e., with uniform crossing over and gene conversion and with geometrically distributed tract length). The mean conversion tract length (L) was fixed at 500 bp. For each simulated data set, we calculated p(a) and p(b) and estimated gene-conversion and crossing-over rates using the rejection method. Under this method, we simulated 8,000 data sets each, under the same model, for a grid of ρ (0-160) and γ (0-400) values and determined the approximate maximum-likelihood estimate (MLE) of gene conversion (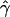 ) and crossing over (
) and crossing over (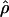 ) for all the 1,000 data sets. Table 1A shows the results of estimates obtained for our simulated data sets. We find that the accuracy of our estimates of gene conversion (i.e., the fraction of times
) for all the 1,000 data sets. Table 1A shows the results of estimates obtained for our simulated data sets. We find that the accuracy of our estimates of gene conversion (i.e., the fraction of times  for a simulated data set is within a factor of 2 of the true γ value) generally decreases as the relative amount of crossing over increases, and vice versa. The method seems to be slightly biased toward underestimating the gene-conversion rate. The distribution of
for a simulated data set is within a factor of 2 of the true γ value) generally decreases as the relative amount of crossing over increases, and vice versa. The method seems to be slightly biased toward underestimating the gene-conversion rate. The distribution of 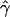 is highly skewed (fig. 3A). The expected value is higher than the true one, although we underestimate more often than we overestimate.
is highly skewed (fig. 3A). The expected value is higher than the true one, although we underestimate more often than we overestimate.
Table 1.
Performance of p(a) and p(b)
| A. Data Simulated with Uniform Crossing Over and Uniform Conversion of γ and ρ | |||||||
| Rate |
|||||||
| ρ | γ |
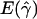 a a
|
g(γ)b | B(γ)c |
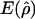 a a
|
g(ρ)b | B(ρ)c |
| 20 | 40 | 48.45 | .57 | .50 | 26.33 | .61 | .52 |
| 40 | 40 | 45.53 | .52 | .55 | 49.06 | .70 | .48 |
| 60 | 40 | 42.83 | .44 | .58 | 72.08 | .74 | .45 |
| 30 | 20 | 27.08 | .43 | .55 | 36.07 | .62 | .50 |
| 30 | 40 | 45.98 | .52 | .54 | 38.44 | .57 | .48 |
| 30 | 60 | 67.49 | .62 | .49 | 37.50 | .55 | .50 |
| B. Data Simulated with Nonuniform Crossing Over and Uniform Conversion of γ and ρ | |||||||
| Rate |
|||||||
| ρ | γ |
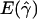 a a
|
g(γ)b | B(γ)c |
 a a
|
g(ρ)b | B(ρ)c |
| 20 | 40 | 46.31 | .58 | .52 | 28.16 | .63 | .47 |
| 40 | 40 | 43.66 | .51 | .58 | 48.33 | .67 | .51 |
| 60 | 40 | 43.17 | .47 | .57 | 64.51 | .77 | .52 |
| 30 | 20 | 25.96 | .36 | .61 | 37.70 | .58 | .46 |
| 30 | 40 | 47.41 | .49 | .52 | 36.83 | .54 | .52 |
| 30 | 60 | 67.14 | .54 | .54 | 35.98 | .49 | .53 |
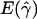 and
and  denote the averages of the MLEs of gene conversion (
denote the averages of the MLEs of gene conversion (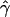 ) and crossing over (
) and crossing over (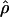 ) rates for the 1,000 data sets simulated at the corresponding crossing-over (ρ) and gene-conversion (γ) rate.
) rates for the 1,000 data sets simulated at the corresponding crossing-over (ρ) and gene-conversion (γ) rate.
g(γ) and g(ρ) denote the fraction of times 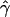 and
and 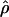 for a simulated data set is within a factor of 2 of the true γ and ρ, respectively (Wall 2000).
for a simulated data set is within a factor of 2 of the true γ and ρ, respectively (Wall 2000).
B(γ) and B(ρ) denote the fraction of times 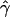 and
and 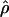 are less than their true values, given that they are not equal to their true values.
are less than their true values, given that they are not equal to their true values.
Figure 3.
The distribution of MLEs of gene conversion (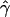 ) for 1,000 data sets, each simulated at uniform crossing-over rate ρ=40 and uniform gene conversion rate γ=40 (A) and at nonuniform crossing over ρ=40 and uniform gene conversion rate γ=40 (B).
) for 1,000 data sets, each simulated at uniform crossing-over rate ρ=40 and uniform gene conversion rate γ=40 (A) and at nonuniform crossing over ρ=40 and uniform gene conversion rate γ=40 (B).
We then considered the effects of departures from the standard modeling assumptions. Many assumptions made by the standard model of gene conversion are not accurate. For example, a model with uniform crossing over is not realistic. There is evidence that crossing-over rates vary substantially across the human genome at all scales (Fullerton et al. 1994; Dunham et al. 1999; Innan et al. 2003). Hotspots of crossing over are also known to exist in certain regions of the genome (see, e.g., Jeffreys et al. [2001]). To investigate whether crossing-over hotspots affect the accuracy of our estimates, we simulated data sets under an alternate model of gene conversion, with nonuniform crossing over and uniform gene conversion for the same set of parameter values as before. We then estimated 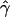 and
and 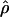 under the standard model of gene conversion for these data sets, as before. Table 1B shows the results obtained for these data sets. We found that values of g(γ) in table 1B are similar to those in table 1A. Thus, the presence of crossing-over hotspots does not decrease the accuracy of our gene-conversion estimates. The distribution of
under the standard model of gene conversion for these data sets, as before. Table 1B shows the results obtained for these data sets. We found that values of g(γ) in table 1B are similar to those in table 1A. Thus, the presence of crossing-over hotspots does not decrease the accuracy of our gene-conversion estimates. The distribution of 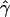 for this scenario is shown in figure 3B. In figure 3A and 3B, we see that a significant fraction of estimates are zeroes. This may be due to the relatively small value of γ (40). The data simulated with gene conversion shows enormous deviation from the median values of p(a) and p(b), which can lead to both overestimates and underestimates. However, whereas overestimates can be arbitrarily high, underestimates are bounded by zero. After a certain extent, any further deviation from the median values in a direction of underestimates—for example, lower p(a) and higher p(b)—results only in γ=0 and not lower than that. Thus, deviations to zero and beyond zero both add up at γ=0.
for this scenario is shown in figure 3B. In figure 3A and 3B, we see that a significant fraction of estimates are zeroes. This may be due to the relatively small value of γ (40). The data simulated with gene conversion shows enormous deviation from the median values of p(a) and p(b), which can lead to both overestimates and underestimates. However, whereas overestimates can be arbitrarily high, underestimates are bounded by zero. After a certain extent, any further deviation from the median values in a direction of underestimates—for example, lower p(a) and higher p(b)—results only in γ=0 and not lower than that. Thus, deviations to zero and beyond zero both add up at γ=0.
To compare our method with that used by Frisse at al. (2001), we simulated 500 data sets of 200-kb sequences, under both the standard and alternate model of gene conversion for the same parameter values as shown in table 1A and 1B. We then estimated gene conversion and crossing over in these data sets, using the program maxhap, which uses a generalization of Hudson’s composite pairwise likelihood method. For this estimation, ρ per base pair was set in the range of 0.00005–0.0008, with a starting value of 0.0002, whereas f was set in the range of 0–15, with intervals of 0.5. The mean conversion tract length L was fixed at 500 bp. Table 2A and 2B show the results of estimates obtained using Hudson’s method. We found that the accuracy of gene-conversion estimates based on our method was roughly twofold higher than the composite likelihood approach, although Hudson’s method gave better estimates of the crossing-over rate. Estimates of γ based on maxhap are also more likely to be underestimates than overestimates, for these set of parameters.
Table 2.
Performance of Hudson’s Pairwise Composite Likelihood Method
| A. Data Simulated with Uniform Crossing Over and Uniform Conversion | |||||||
| Rate |
|||||||
| ρ | γ |
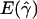 a a
|
g(γ)b | B(γ)c |
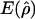 a a
|
g(ρ)b | B(ρ)c |
| 20 | 40 | 38.02 | .25 | .64 | 20.78 | .80 | .55 |
| 40 | 40 | 33.82 | .21 | .71 | 44.22 | .84 | .49 |
| 60 | 40 | 42.10 | .21 | .68 | 64.10 | .85 | .48 |
| 30 | 20 | 29.82 | .13 | .66 | 31.84 | .82 | .53 |
| 30 | 40 | 38.08 | .25 | .67 | 31.63 | .84 | .51 |
| 30 | 60 | 44.82 | .28 | .72 | 33.07 | .81 | .49 |
| B. Data Simulated with Nonuniform Crossing Over and Uniform Conversion | |||||||
| Rate |
|||||||
| ρ | γ |
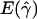 a a
|
g(γ)b | B(γ)c |
 a a
|
g(ρ)b | B(ρ)c |
| 20 | 40 | 29.01 | .26 | .73 | 21.05 | .81 | .54 |
| 40 | 40 | 23.06 | .14 | .81 | 40.71 | .83 | .56 |
| 60 | 40 | 18.43 | .17 | .85 | 58.60 | .90 | .58 |
| 30 | 20 | 14.95 | .12 | .78 | 29.17 | .83 | .59 |
| 30 | 40 | 22.55 | .21 | .80 | 30.85 | .82 | .54 |
| 30 | 60 | 36.45 | .28 | .77 | 30.94 | .83 | .55 |
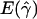 and
and 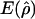 denote the averages of the MLEs of gene-conversion (
denote the averages of the MLEs of gene-conversion ( ) and crossing-over (
) and crossing-over (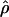 ) rates for the 500 data sets simulated at the corresponding crossing-over (ρ) and gene-conversion (γ) rate.
) rates for the 500 data sets simulated at the corresponding crossing-over (ρ) and gene-conversion (γ) rate.
g(γ) and g(ρ) denote the fraction of times 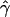 and
and 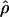 for a simulated data set is within a factor of 2 of the true γ and ρ, respectively (Wall 2000).
for a simulated data set is within a factor of 2 of the true γ and ρ, respectively (Wall 2000).
B(γ) and B(ρ)denote the fraction of times 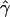 and
and  are less than their true values.
are less than their true values.
Another unrealistic assumption in the standard model of gene conversion is the absence of population structure. Population structure is a well-documented phenomenon in human populations (e.g., Cavalli-Sforza et al. 1994). The observed levels of LD will be higher in samples drawn from structured populations, as compared with samples drawn from a panmictic population. This is because haplotypes from different subpopulations will not have as much chance to recombine as will those under panmixia. Our concern here was that population structure might create effects similar to gene conversion on the joint distribution of our summaries. To check if population subdivision alone can inflate our estimates of γ, we simulated 800 data sets, each under the symmetric two-island model with no gene conversion for various crossing-over and migration rates. We also simulated data sets for the same crossing-over rates without population structure. We then calculated the MLEs of the gene-conversion rate for both scenarios, under the standard model of gene conversion, as before, and compared the results (table 3). As can be seen from table 3, estimates of gene conversion for data simulated under population structure are not substantially higher than estimates obtained for a panmictic population. In other words, there is no indication that presence of population structure alone mimics the effects of gene conversion on our statistics.
Table 3.
Estimates of Gene Conversion with Population Structure and Crossing Over Alone
| ρa and 4Nomb | Pc |
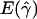 d d
|
| 40: | ||
| 1 | .850 | 6.28 |
| 10 | .839 | 6.58 |
| 20 | .856 | 6.19 |
| 50 | .873 | 5.83 |
| 100 | .866 | 5.79 |
| Panmictic-inf | .880 | 5.32 |
| 60: | ||
| 1 | .805 | 8.79 |
| 10 | .816 | 8.18 |
| 20 | .817 | 8.25 |
| 50 | .821 | 9.22 |
| 100 | .808 | 8.73 |
| Panmictic-inf | .828 | 8.81 |
| 80: | ||
| 1 | .761 | 12.35 |
| 10 | .758 | 11.19 |
| 20 | .775 | 11.26 |
| 50 | .772 | 11.41 |
| 100 | .766 | 11.85 |
| Panmictic-inf | .773 | 11.53 |
ρ (4Nr) denotes the population crossing-over rate based on the total population size (N).
4Nom is the population-migration rate, where m is the probability of migration per generation per sequence and No is the size of subpopulations.
P denotes the fraction of the 800 simulated data sets for which the MLE of gene-conversion rate (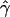 ) is ⩽10.
) is ⩽10.
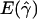 denotes the average of the MLE of gene conversion (
denotes the average of the MLE of gene conversion (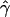 ) for the 800 data sets simulated at a particular crossing-over rate (ρ) and population model.
) for the 800 data sets simulated at a particular crossing-over rate (ρ) and population model.
Although population structure does not inflate our estimates of gene conversion, we see that E[ ] is considerably larger than zero in table 3. This shows that our summaries are not completely effective in distinguishing gene conversion from crossing over alone in data sets of our size (200 kb). It is fortunate that the chromosome 21 data set that we plan to analyze is much larger (28 Mb) than the data sets we used in our simulations. Since the values of our summaries in this data set are approximately equivalent to an average of many independent sequences, our ability to distinguish gene conversion from crossing over is expected to be much higher. The accuracy of our estimates will also be higher for such large data sets. Therefore, we are convinced that our summaries will provide good estimates of the gene-conversion rate for the chromosome 21 SNPs.
] is considerably larger than zero in table 3. This shows that our summaries are not completely effective in distinguishing gene conversion from crossing over alone in data sets of our size (200 kb). It is fortunate that the chromosome 21 data set that we plan to analyze is much larger (28 Mb) than the data sets we used in our simulations. Since the values of our summaries in this data set are approximately equivalent to an average of many independent sequences, our ability to distinguish gene conversion from crossing over is expected to be much higher. The accuracy of our estimates will also be higher for such large data sets. Therefore, we are convinced that our summaries will provide good estimates of the gene-conversion rate for the chromosome 21 SNPs.
Analysis of Chromosome 21 Data
The Average Gene-Conversion Rate in Chromosome 21
The observed values of p(a) and p(b) for this data set are 0.00463 and 0.0105, respectively. Both gene-conversion (γ) and crossing-over (ρ) rates for chromosome 21 were estimated, under the standard model of gene conversion. Rather than estimating the mean length of a conversion tract, we used the rejection method to obtain the MLEs of gene-conversion rate for two illustrative values of the tract length, L=500 bp and L=50 bp. We also generated likelihood surfaces of ρ and γ for these tract lengths (figs. 4 and 5).
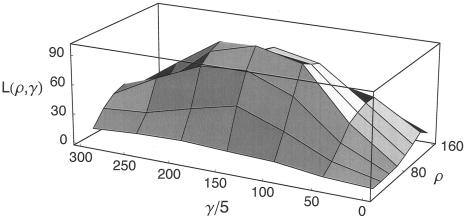
Figure 4.
The likelihood surface of chromosome 21 data based on p(a) and p(b), for a mean tract length L=500 bp. Likelihoods were calculated from 8,000 simulations of 200-kb sequences for different rates of crossing over (ρ=0–160) and gene conversion (γ=0–300). L(ρ,γ) roduct of the likelihood and an arbitrary constant. The peak is seen at ρ=80 and γ=125.
Figure 5.
The likelihood surface of chromosome 21 data based on p(a) and p(b), for a mean tract length L=50 bp. Likelihoods were calculated from 2,500 simulations of 200-kb sequences for different rates of crossing over (ρ=0–160) and gene conversion (γ=0–1,500). L(ρ,γ) denotes the product of the likelihood and an arbitrary constant (1,500). The peak is seen at ρ=80 and γ=750.
The MLEs for L=500 bp are 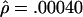 and
and 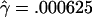 per base pair (f=1.6), whereas, for L=50 bp, they are
per base pair (f=1.6), whereas, for L=50 bp, they are 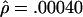 and
and 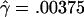 per bp (f=9.4). Under the assumption that the prior distribution is uniform, our likelihood surfaces represent the posterior distribution of ρ and γ. We used these likelihoods to compute ∼95% credible intervals for γ. For L=500 bp, a 95% credible interval of γ per base pair is 0.00020–0.00175, whereas, for L=50 bp, this interval is 0.00125–0.00750.
per bp (f=9.4). Under the assumption that the prior distribution is uniform, our likelihood surfaces represent the posterior distribution of ρ and γ. We used these likelihoods to compute ∼95% credible intervals for γ. For L=500 bp, a 95% credible interval of γ per base pair is 0.00020–0.00175, whereas, for L=50 bp, this interval is 0.00125–0.00750.
A highly desirable feature of these surfaces is that the estimates of gene conversion seem to be independent of the crossing-over rates (in contrast to fig. 1). Thus, our method is robust to errors in the estimates of crossing-over rates. Note that the estimated conversion rate always depends on the assumed conversion tract length. As the length of the conversion tract decreases, the estimated rate of gene conversion increases. This is because smaller tracts have a lower chance of including an SNP than do longer tracts; therefore, we need such conversion events to happen more often. Since the effects of high gene-conversion rates with small tracts will be similar to the effects of lower conversion rates with longer tracts (particularly in a range where tracts are short and mostly affect only a single marker or less), it is hard to estimate both these parameters independently from LD data.
Spatial Variation in Gene-Conversion and Crossing-Over Rates
We looked at the spatial variation in  and
and  by computing these parameters for large overlapping 2-Mb windows along chromosome 21. Correlation calculation shows that our estimates of gene conversion and crossing over are not significantly correlated (R=0.07575; P=.7073). We also constructed ∼95% credible intervals for these estimates (fig. 6A and 6B). For most windows, the chromosomal average of
by computing these parameters for large overlapping 2-Mb windows along chromosome 21. Correlation calculation shows that our estimates of gene conversion and crossing over are not significantly correlated (R=0.07575; P=.7073). We also constructed ∼95% credible intervals for these estimates (fig. 6A and 6B). For most windows, the chromosomal average of  falls well within the 95% credible intervals. However, the region between 12 and 14 Mb appears to have a gene-conversion rate that is substantially higher than the chromosomal average.
falls well within the 95% credible intervals. However, the region between 12 and 14 Mb appears to have a gene-conversion rate that is substantially higher than the chromosomal average.
Figure 6.
The MLEs of gene conversion ( ) and crossing over (
) and crossing over (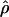 ) for overlapping 2-Mb windows along chromosome 21. The X-axis denotes the location corresponding to the center of the 2-Mb windows, and the error bars indicate ∼95% credible intervals. The horizontal line denotes the chromosomal average of the parameters.
) for overlapping 2-Mb windows along chromosome 21. The X-axis denotes the location corresponding to the center of the 2-Mb windows, and the error bars indicate ∼95% credible intervals. The horizontal line denotes the chromosomal average of the parameters.
Can We Reject Models with No Gene Conversion?
To check if we can reject models without gene conversion, we compared the observed 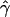 for our data with a distribution of values of
for our data with a distribution of values of 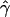 obtained for large data sets simulated under different models of crossing over alone. We first simulated 500 data sets of five independent 200-kb sequences, under models of both uniform and nonuniform crossing over for differing rates, and we calculated the average p(a) and p(b). On the basis of these summaries, we determined the
obtained for large data sets simulated under different models of crossing over alone. We first simulated 500 data sets of five independent 200-kb sequences, under models of both uniform and nonuniform crossing over for differing rates, and we calculated the average p(a) and p(b). On the basis of these summaries, we determined the 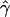 , under the standard model of gene conversion, for all our simulated data sets using the rejection method. The mean tract length was fixed at 500 bp, and we estimated
, under the standard model of gene conversion, for all our simulated data sets using the rejection method. The mean tract length was fixed at 500 bp, and we estimated 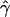 in the same way as we did for the chromosome 21 SNPs. We then calculated the fraction of data sets (Z) for which
in the same way as we did for the chromosome 21 SNPs. We then calculated the fraction of data sets (Z) for which  is at least as high as the
is at least as high as the 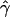 value we observed in chromosome 21.
value we observed in chromosome 21.
The human population is known to have experienced dramatic growth during recent times. To investigate the effects of a changing population size, we also simulated similar data sets (i.e., 500 data sets of five independent 200-kb sequences) with uniform crossing over alone and with different scenarios of population growth. The model of population growth assumes exponential growth from an ancestral population size of 104 to a current population size of 6×109. The different scenarios make different assumptions about the time (t) at which this growth started. We then calculated  (under the standard model of gene conversion for a mean tract length of 500 bp) for data simulated under growth and determined Z.
(under the standard model of gene conversion for a mean tract length of 500 bp) for data simulated under growth and determined Z.
In all these large data sets simulated with crossing over alone, we almost never observed a value of 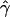 that was as high as the value observed for the chromosome 21 data (maximum observed Z=0.004). Therefore, we reject the null hypothesis of no gene conversion for our data. However, we caution here that a realistic model of crossing over might be very different from the models that we have considered here. For example, very little is known about the length, density, and overall distribution of recombination hotspots in the human genome. It is possible that there exist alternative models of nonuniform crossing over that might fit this data set better (e.g., regional variation in crossing over combined with hotspots or some alternate distribution of crossing-over hotspots).
that was as high as the value observed for the chromosome 21 data (maximum observed Z=0.004). Therefore, we reject the null hypothesis of no gene conversion for our data. However, we caution here that a realistic model of crossing over might be very different from the models that we have considered here. For example, very little is known about the length, density, and overall distribution of recombination hotspots in the human genome. It is possible that there exist alternative models of nonuniform crossing over that might fit this data set better (e.g., regional variation in crossing over combined with hotspots or some alternate distribution of crossing-over hotspots).
Effect of Recurrent Mutation
Recurrent mutations can inflate the apparent level of recombination observed in the data. More importantly, they can mimic the patterns produced by gene-conversion events by disrupting short-range LD. Therefore, if recurrent mutation is frequent, we may overestimate the average rate of gene conversion in our data. CpG sites have roughly tenfold higher mutation rate than do other sites and thus have a high chance of being subject to recurrent mutations (Templeton et al. 2000). Consequently, to explore whether recurrent mutation events might be influencing our estimates, we removed the 5,696 SNPs in the data that occur in CpG sites and recalculated p(a) and p(b). We found that the change in the observed values of our summaries was insignificant (new p(a)=0.0044 and new p(b)=0.0112, respectively). Thus, CpG sites do not seem to be inflating our estimates of gene-conversion rate, which suggests that recurrent mutation is not a major explanation for the pattern of LD on chromosome 21.
Discussion
We have shown that a model with uniform crossing over alone is not compatible with the overall short-range data from chromosome 21. In addition, some plausible models of nonuniform crossing over or population growth alone cannot explain our data. A more realistic model of genetic exchange that includes both gene conversion and crossing over fits our data much better than do models with crossing over alone. We estimate a substantial amount of gene conversion on chromosome 21. Our estimates do not appear to be inflated by either recurrent mutations at CpG sites or the presence of population structure alone. In short, it seems that gene conversion is necessary to explain our data.
Although both crossing over and gene conversion cause the decay of pairwise LD, the effects on multiple loci is likely to be different. A single gene-conversion event can create the equivalent of two crossing-over events, with respect to the middle SNP in a triplet. In contrast to two crossing-over events, a gene-conversion event of this type does not affect the association between the two outer SNPs. Therefore, the outer SNPs can still be strongly associated with each other even if both are unassociated with the middle SNP. When we consider four loci, every crossing-over event that happens between the inner SNPs is also a crossing-over event between the outer SNPs, whereas this is not always true for gene conversion with short tracts (mean length <1 kb). Thus, p(b) is more sensitive to crossing over than to gene conversion with short tracts. These differential effects on multilocus summaries can help us to distinguish between these two mechanisms of recombination.
The triplet patterns that we describe are robust estimators of the gene-conversion rate. Compared with other summaries (e.g., the fraction of incompatible SNP pairs), they are less sensitive to changes in crossing-over rates. If gene conversion follows the model of Wiehe et al. (2000) (i.e., conversion events never affect more than one SNP, either because tracts are short or because SNPs are sparse), our four-locus summaries can be modified into a robust estimator of crossing-over rate from short-range data (0–5 kb). We call these patterns of type c. Consider four loci A, B, C, and D, located in that order on the chromosome. We define SNPs to be in pattern c if: A and B are compatible, B and C are incompatible, C and D are compatible, and A and D are incompatible. Note that this pattern can arise from a single crossing-over event between B and C, whereas it requires two gene-conversion or recurrent mutation events. In addition, unlike gene-conversion or recurrent mutation events, a single crossing-over event of this type does not affect the association between A and B or between C and D.
Compared with the composite-likelihood method of Hudson (used by Frisse et al. [2001]), our rejection method appears to be better at estimating the gene-conversion rate and worse at estimating the crossing-over rate. An interesting question for the future is whether it might be possible to improve our estimates of crossing over by adding additional summary statistics. This will be necessary for addressing questions concerning variation in the ratio of gene-conversion rate to crossing-over rate (i.e., f) across the genome. Our main goal here was to construct an estimator of gene conversion that was robust to variation in the crossing-over rates. To explore the relationship between these two processes, accurate estimates of both will be needed.
Gene-conversion rates have been estimated from experiments in some eukaryotes. For example, typical values of f in yeast and fruit flies are close to 2 and 4, respectively. Conversion tracts are estimated to be in the range of 350–2,000 bp in these organisms. Not much experimental data is available for humans, except from a few individual loci. Single-sperm analysis of the HLA-DPB1 locus seems to support very short conversion tract lengths of ∼54–132 bp and very high gene-conversion rates relative to crossing-over rates (f>20) (Zangenberg et al. 1995). Recent experiments by Jeffreys and May (2004) identified highly localized gene-conversion activity (hotspots) in some crossing-over hotspots in humans. Their study suggests that the mean length of tracts associated with crossing-over is ∼460 bp and gene-conversion tracts are in the range of 55–290 bp. Jeffreys and May estimate f in the DNA3 hotspot to be ∼2.7, but they point out that this may be an underestimate, since tract lengths affect the proportion of conversion events that are experimentally detectable. For our data set, the highest likelihood was observed at f=1.6 for a mean tract length of 500 bp. Decreasing the mean tract length to 50 bp greatly increases our estimates of γ and f (9.4).
We did not explicitly distinguish recurrent mutations from gene conversion in our analysis. Although most SNPs are thought to arise from unique mutational events, CpG dinucleotides and repetitive elements in the human genome are believed to be highly mutable and can therefore mutate more than once at the same position (Templeton et al. 2000). The SNPs in chromosome 21 were obtained after masking large amounts of repetitive DNA. In addition to this, excluding SNPs that occurred in CpG sites did not alter our summaries substantially. Nevertheless, there is a chance that certain unknown sequence motifs in DNA are subject to mutations at a rate much higher than the average. If conversion tracts happen to be considerably longer than the average spacing between markers, there are four-locus patterns that can serve as robust estimators of gene conversion in the presence of recurrent mutations. We refer to these as patterns of type d. Consider four loci A, B, C, and D, located in that order on the chromosome. SNPs are defined to be in pattern d when: A and B are incompatible, B and C are compatible, C and D are incompatible, and A and D are compatible. Note that this pattern can arise from a single gene-conversion event that affects both B and C but will require two crossing-over or recurrent-mutation events. Unlike recurrent-mutation or crossing-over events, a gene-conversion event of this type will not affect the association between A and D or B and C. On the other hand, distinguishing between recurrent mutations and gene conversion with very short tracts seems to be a more difficult problem and will be the topic of future work.
Several recent studies have suggested that LD in the human genome has a “blocklike” structure (e.g., Patil et al. 2001). Haplotype blocks are defined as a series of consecutive SNPs that are in complete or near complete LD with one another. It has generally been assumed that the presence of haplotype blocks provides evidence of fine-scale variations in crossing-over rates, with blocks corresponding to regions of reduced crossing-over rates and interblock regions corresponding to hotspots of crossing over. The usefulness of this concept in association studies will be more limited if regions with reduced crossing over in the genome can still have high levels of gene conversion. For example, the haplotype block study of Wall and Pritchard (2003) examined several data sets in humans and found that higher-than-expected recombination over short distances within blocks was consistent with the gene-conversion hypothesis. If gene-conversion rates are also highly variable across the human genome (as the experiments of Jeffreys and May [2004] suggest), the efficacy of future association studies will depend on local patterns of both crossing over and gene conversion.
Acknowledgments
We are thankful to Perlegen Sciences for the data used in this study. We also thank Jeff Wall, Noah Rosenberg, and Chris Toomajian for helpful suggestions and comments about the manuscript. This work was supported, in part, by National Institutes of Health Center for Excellence in Genomic Science grant 1 P50 HG002790-01A1.
Electronic-Database Information
The URLs for data presented herein are as follows:
- National Center for Biotechnology Information (NCBI), http://www.ncbi.nlm.nih.gov/SNP/snp_viewBatch.cgi?sbid=4649 (for details about the 21,840 SNPs [from ss3996755 to ss4018594])
- Nordborg Lab, http://walnut.usc.edu/programs (for the program for simulating data with uniform gene conversion and nonuniform crossing over [to be made available July 2004])
- Perlegen Sciences, http://www.perlegen.com/haplotype/ (for the data set used for this study [publicly available])
References
- Andolfatto P, Nordborg M (1998) The effect of gene conversion on intralocus associations. Genetics 148:1397–1399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ardlie K, Liu-Cordero SN, Eberle MA, Daly M, Barrett J, Winchester E, Lander ES, Kruglyak L (2001) Lower-than-expected linkage disequilibrium between tightly linked markers in humans suggests a role for gene conversion. Am J Hum Genet 69:582–589 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter ATC (1984) Meiotic roles of crossing-over and of gene conversion. Cold Spring Harbor Symp Quant Biol 49:23–26 [DOI] [PubMed] [Google Scholar]
- Cavalli-Sforza LL, Menozzi P, Piazza A (1994) The history and geography of human genes. Princeton University Press, Princeton [Google Scholar]
- Clark AG, Nielsen R, Signorovitch J, Matise TC, Glanowski S, Heil J, Winn-Deen ES, Holden AL, Lai E (2003) Linkage disequilibrium and inference of ancestral recombination in 538 single-nucleotide polymorphism clusters across the human genome. Am J Hum Genet 73:285–300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunham I, Shimizu N, Roe BA, Chissoe S, Hunt AR, Collins JE, Bruskiewich R, et al (1999) The DNA sequence of human chromosome 22. Nature 402:489–495 10.1038/990031 [DOI] [PubMed] [Google Scholar]
- Frisse L, Hudson RR, Bartoszewicz A, Wall JD, Donfack J, Di Rienzo A (2001) Gene conversion and different population histories may explain the contrast between polymorphism and linkage disequilibrium levels. Am J Hum Genet 69:831–843 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fullerton SM, Harding RM, Boyce AJ, Clegg JB (1994) Molecular and population genetic analysis of allelic sequence diversity at the human β-globin locus. Proc Natl Acad Sci USA 91:1805–1809 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holliday R (1964) A mechanism for gene conversion in fungi. Genet Res 5:282–287 [DOI] [PubMed] [Google Scholar]
- Hudson RR (2001) Two-locus sampling distributions and their applications. Genetics 159:1805–1817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR, Kaplan NL (1985) Properties of the number of recombination events in the history of a sample of DNA sequences. Genetics 111:147–164 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Innan H, Padhukasahasram B, Nordborg M (2003) The pattern of polymorphism on human chromosome 21. Genome Res 13:1158–1168 10.1101/gr.466303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffreys AJ, Kauppi L, Neumann R (2001) Intensely punctuate meiotic recombination in the class II region of the major histocompatibilty complex. Nat Genet 29: 217–222 10.1038/ng1001-217 [DOI] [PubMed] [Google Scholar]
- Jeffreys AJ, May CA (2004) Intense and highly localized gene conversion activity in human meiotic crossover hotspots. Nat Genet 36:151–156 10.1038/ng1287 [DOI] [PubMed] [Google Scholar]
- Kingman JFC (1982) The coalescent. Stochast Proc Appl 13:235–248 10.1016/0304-4149(82)90011-4 [DOI] [Google Scholar]
- Kuhner M, Yamato KJ, Felsenstein J (2000) Maximum likelihood estimation of recombination rates from population genetic data. Genetics 156:1393–1401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marjoram P, Molitor J, Plagnol V, Tavare S (2003) Markov chain Monte Carlo without likelihoods. Proc Natl Acad Sci USA 100:15324–15328 10.1073/pnas.0306899100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R (2000) Estimation of population parameters and recombination rates from single-nucleotide polymorphisms. Genetics 154:931–942 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg M (2001) Coalescent theory. In: Balding DJ, Bishop M, Cannings C (eds) Handbook of statistical genetics. John Wiley, Chichester, United Kingdom, pp 213–238 [Google Scholar]
- Patil N, Berno AJ, Hinds DA, Barrett WA, Doshi JM, Hacker CR, Kautzer CR, Lee DH, Marjoribanks C, McDonough DP, Nguyen BT, Norris MC, Sheehan JB, Shen N, Stern D, Stokowski RP, Thomas DJ, Trulson MO, Vyas KR, Frazer KA, Fodor SP, Cox DR (2001) Blocks of limited haplotype diversity revealed by high resolution scanning of human chromosome 21. Science 294:1719–1723 10.1126/science.1065573 [DOI] [PubMed] [Google Scholar]
- Przeworski M, Wall JD (2001) Why is there so little intragenic linkage disequilibrium in humans? Genet Res 77:143–151 10.1017/S0016672301004967 [DOI] [PubMed] [Google Scholar]
- Templeton AR, Clark AG, Weiss KM, Nickerson DA, Boerwinkle E, Sing CF (2000) Recombinational and mutational hotspots within the human lipoprotein lipase gene. Am J Hum Genet 66:69–83 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wall JD (2000) A comparison of estimators of the population recombination rates. Mol Biol Evol 17:156–163 [DOI] [PubMed] [Google Scholar]
- Wall JD, Pritchard JK (2003) Assessing the performance of the haplotype block model of linkage disequilibrium. Am J Hum Genet 73:502–515 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss G, von Haeseler A (1998) Inference of population history using a likelihood approach. Genetics 149:1539–1546 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiehe T, Mountain J, Parham P, Slatkin M (2000) Distinguishing recombination and intragenic gene conversion by linkage disequilibrium patterns. Genet Res 75:61–73 10.1017/S0016672399004036 [DOI] [PubMed] [Google Scholar]
- Wiuf C, Hein J (2000) The coalescent with gene conversion. Genetics 155:451–462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zangenberg G, Huang MM, Arnheim N, Erlich H (1995) New HLA-DPB1 alleles generated by interallelic gene conversion detected by analysis of sperm. Nat Genet 10:407–444 [DOI] [PubMed] [Google Scholar]