Abstract
We studied the effect of transmission-ratio distortion (TRD) on tests of linkage based on allele sharing in affected sib pairs. We developed and implemented a discrete-trait allele-sharing test statistic, Sad, analogous to the Spairs test statistic of Whittemore and Halpern, that evaluates an excess sharing of alleles at autosomal loci in pairs of affected siblings, as well as a lack of sharing in phenotypically discordant relative pairs, where available. Under the null hypothesis of no linkage, nuclear families with at least two affected siblings and one unaffected sibling have a contribution to Sad that is unbiased, with respect to the effects of TRD independent of the disease under study. If more distantly related unaffected individuals are studied, the bias of Sad is generally reduced compared with that of Spairs, but not completely. Moreover, Sad has higher power, in some circumstances, because of the availability of unaffected relatives, who are ignored in affected-only analyses. We discuss situations in which it may be an efficient use of resources to genotype unaffected relatives, which would give insights for promising study designs. The method is applied to a sample of pedigrees ascertained for asthma in a chromosomal region in which TRD has been reported. Results are consistent with the presence of transmission distortion in that region.
Introduction
Transmission-ratio distortion (TRD) is a departure from Mendel’s law of independent segregation of alleles. Classic examples of TRD include the t complex in mice and segregation distorter in Drosophila (see, e.g., Lyttle [1993]). In humans, evidence of TRD has been found in several locations, including the Xp11.4 region (Naumova et al. 1998), in which, among male offspring, inheritance is biased in favor of the grandpaternal allele. Causes of TRD are numerous. It can occur, for example, in the region of a gene under selection, causing postfertilization loss. Eaves et al. (1999) found excess transmission of one class of alleles (on the basis of allele size) of a variable-number-of-tandem-repeats polymorphism of the insulin gene (INS on 11p15.5) in samples not ascertained because of disease status. The polymorphism regulates expression of both INS and IGF2, the insulinlike growth factor 2 gene; lower expression of alleles from another size-related class is thought to reduce the chances of survival in utero. TRD may also be caused by meiotic drive. Pardo-Manuel de Villena et al. (2000) showed that meiotic drive, at the second meiotic division, was responsible for the observed maternal TRD at the Om locus in mice. It was subsequently observed that the level of meitoic drive was correlated with the maternal X chromosome inactivation phenotype (de la Casa-Esperón et al. 2002).
In general, linkage methods based on allele sharing evaluate the correlation between a measure of the trait value (quantitative or discrete) in pairs of relatives and a function of the number of alleles shared identical by descent by the pair—in other words, cosegregation of the trait and genetic markers. Trait-independent TRD (i.e., TRD that is not the result of ascertainment based on disease status or trait value) in a chromosome region can bias inference of linkage obtained from the results of widely used methods (Greenwood and Morgan 2000). For discrete traits, searching for excess allele sharing among affected individuals does not constitute a test of linkage per se. Rather, the procedure tests for Mendelian segregation among them; linkage to a putative disease gene is only one possible explanation for the observed deviation from Mendelian inheritance. Hence, trait-independent TRD has a direct effect on test statistics based on allele sharing, when used as a test of linkage for discrete traits. Although a potential source of bias and of inflation of the estimate of risk, TRD does not have a strong effect on the power to detect linkage, as long as the deviation from Mendelian segregation is modest (Greenwood and Morgan 2000).
For tests of linkage based on transmission disequilibrium, Spielman et al. (1993) advocated the use of data from unaffected children for their transmission/disequilibrium test (TDT) statistic when the possibility of TRD exists. Validation of a significant TDT result can also be assessed using the TDTDS test statistic of Deng et al. (2002), a TDT-like statistic that uses discordant sib-pair–parent tetrads and tests for both TRD and linkage.
In the context of allele sharing, we developed a discrete-trait test of linkage for affected sib pairs (ASPs) at autosomal loci that is based on the Spairs test statistic of Whittemore and Halpern (1994), that incorporates unaffected relatives, and that is less sensitive to trait-independent TRD. In particular, sibships with both affected and discordant sib pairs have an unbiased contribution to the test, under the null hypothesis of no linkage. Because our test statistic evaluates excess sharing of alleles in ASPs and lack of sharing of alleles in phenotypically discordant pairs of relatives (sib pairs or others), when available, the power of the test may be augmented.
The development of our test statistic was motivated by a linkage signal in asthma-ascertained pedigrees in a region of chromosome 6 shown by Naumova et al. (2001) to be subject to TRD. Naumova et al. (2001) evaluated TRD in selected imprinted gene regions that were associated with embryo development. The grandparental origin of transmitted marker alleles in or near these regions was evaluated to relate errors in imprinting to TRD. Naumova et al. (2001) hypothesized that improperly erased grandparental-imprinting marks in the germ line could cause embryonic loss and, thus, TRD. In the 6q25.3 region, the IGF2R gene (insulin-like growth factor 2/mannose-6-phosphate receptor [location based on the July 2003 freeze of the Human Genome Browser]) was selected because it is expressed in the embryo and placenta and is a growth repressor (although imprinting of that gene—possibly polymorphic imprinting—is not well established [Xu et al. 1993; Ogawa et al. 1993]). Polymorphisms in the IGF2R gene and one microsatellite marker were used to evaluate differences in transmission of grandparental alleles, according to the sex of the parent and sex of the grandchild, in 31 three-generation CEPH families unselected for disease. They found that mothers tended to transmit the grandmaternal allele to their offspring, irrespective of offspring sex, in an ∼3:2 ratio (P=.008). No significant deviation from the expected 1:1 ratio was observed in transmissions from fathers. An analysis of the linkage signal in the ongoing asthma project illustrates our method.
Subjects and Methods
A Discrete-Trait Allele-Sharing Test of Linkage
We describe a simple allele-sharing test statistic, incorporating the genotypes of unaffected relatives, that is less sensitive to trait-independent TRD when used as a test of linkage. The basis of this approach is that, in a region in which TRD occurs, the number of alleles shared by members of phenotypically discordant pairs (one affected and one unaffected individual) should be as high as the number shared by members of affected pairs with the same relationship, if the region is not linked to any gene contributing to the risk of developing the disease under study. The discordant pairs can be viewed as control individuals, reducing the potential bias that arises from TRD. In addition, incorporation of these phenotypically discordant pairs may contribute to the power to detect linkage, since, in a region linked to a disease gene, discordant pairs should share alleles less often than expected under Mendelian inheritance. This expected lack of sharing provides additional information about the segregation of the putative disease gene.
For a given pedigree, let V be a random variable representing the descent path (Thompson 2000)—or “inheritance vector,” in the nomenclature of Kruglyak et al. (1996)—of the alleles in the pedigree. If M represents the marker data available for the pedigree on a particular chromosome, then, at a specific chromosomal position l, V has conditional probability distribution Pl(v|M), where v is a realization of V (a distribution that can be computed by software such as GENEHUNTER, by use of the Lander-Green algorithm [Lander and Green 1987] and MERLIN, by use of a sparse binary trees algorithm [Abecasis et al. 2002], to name two). Let A denote an informative affected pair of relatives (here, we focus on ASPs), of which there are NA in the pedigree, and let D denote an informative discordant pair, of which there are ND in the pedigree. A pair is informative if the number of alleles shared identical by descent is not a priori fully known. For example, if the possibility of inbreeding in the genealogy is excluded, a parent-child combination is uninformative, since parents and children always share one allele identical by descent, whereas a pair of unrelated individuals share no alleles identical by descent (see Génin and Clerget-Darpoux [1996] and Leutenegger et al. [2002] for the effects of sampling in an inbred population on allele-sharing tests of linkage).
If the descent path in the pedigree is v, let SA(v) be the number of alleles shared identical by descent in affected pair A, and let SD(v) be the number of alleles shared identical by descent in discordant pair D. Given the descent path, these quantities are easily computed. The proposed test statistic, Sad (where ad=affected/discordant), is based on the differences
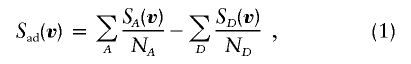 |
which are averaged over the possible realizations of V, conditional on the marker data at position l:
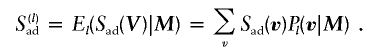 |
Note that, if no discordant pairs are available, the second sum in equation (1) is empty, and Sad reduces to the Spairs score of Whittemore and Halpern (1994). We then normalize Sad by subtracting its expectation (μ0) and dividing the result by its SD (σ0), both taken under the null hypothesis of Mendelian segregation (or equivalently, under the prior uniform probability distribution of V), to obtain the standardized score
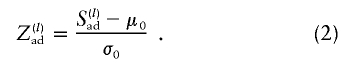 |
The scores of all pedigrees are then added, with selection of pedigree weights such that the sum of the squared weights, over all pedigrees, is one (Kruglyak et al. 1996) (note that this approach is different from the one of Whittemore and Halpern [1994], in which the sum of scores of pedigrees is normalized). Then, under the assumption that families are unrelated and on the basis of sample size considerations, an approximate α-level test of linkage consists of rejecting the null hypothesis of no linkage, when the weighted sum of Z(l)ad is above the 100×(1-α)th percentile of the standard normal distribution.
This normalized test statistic has the same disadvantage as do others that are based on different score functions, in that its variance (with expectation taken with respect to a probability distribution over all possible genotypes M, not to be confused with the expectation under the distribution of V) is <1, if the conditional distribution Pl(v|M) does not have its total mass at a single point; information is then said to be imperfect (Kruglyak et al. 1996). To correct for incompleteness of the data, the likelihood approach of Kong and Cox (1997) can be taken. The result would be a test statistic Zlr,ad (lr=likelihood ratio, after the notation of Kong and Cox [1997]) that has a variance of 1.
Models of TRD
We formulate a model of TRD that is based on preferential transmission of grandparental alleles, motivated by the findings of Naumova et al. (2001). Let m and M represent the paternal and maternal alleles, respectively, in males and let f and F represent the paternal and maternal alleles, respectively, in females. In a region unlinked to a disease-susceptibility gene, let δm=1-δM be the probability of a male transmitting his paternal allele, and let δf=1-δF be the probability of a female transmitting her paternal allele. The bias is defined as
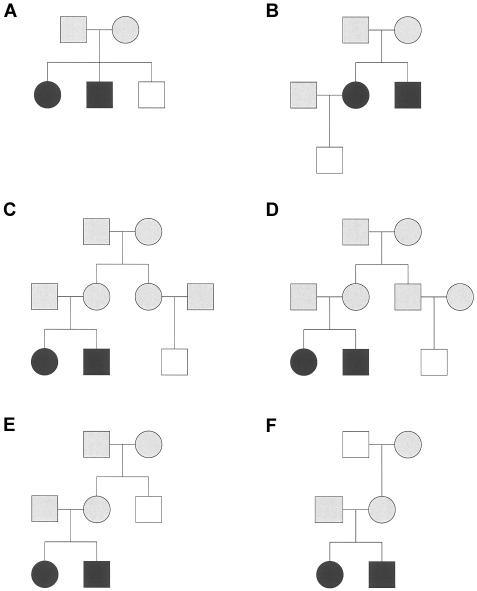
where E(S|δm,δf) denotes the expectation of a scoring function S (either Spairs or Sad), if the true transmission parameters are δm and δf. Under the null hypothesis of no linkage, the expectation is taken with respect to the a priori distribution of V (dropped from the notation for simplicity), which depends on δm and δf. For selected pedigrees (fig. 1), algebraic expressions for the bias were found.
Figure 1.
Six pedigrees with discordant pairs. Individuals depicted by blackened symbols are affected. Individuals depicted by unblackened symbols are unaffected. We have no phenotypic data for individuals depicted by gray symbols.
A second model of TRD is based on allelic preferential transmission. At a biallelic locus, heterozygous individuals tend to transmit a specific allele (found in frequency p in the population) to their offspring with probability s. Effects of this model on the bias were surveyed through simulations. A computer program, SimM (Lemire Web site), was designed to perform gene-dropping simulations, allowing for TRD.
Power Calculations
For selected pedigrees (e.g., fig. 1), gene-dropping simulations were performed for perfectly informative markers by assignment of unique alleles to all founders. We simulated two marker loci, M1 and M2, and one disease locus, D, with the order and intermarker distances
All individuals are genotyped. The disease model is defined by the susceptibility allele frequency and penetrances. To evaluate the power of Sad and Spairs, we computed the sample size Nad and Npairs required to achieve a power of 80% for a nominal type I error of α=0.1%. We used a normal approximation for the distribution of Zad and Zpairs (the equivalent of eq. [2] for Spairs), under the null hypothesis of Mendelian inheritance. The power of a statistic based on a score S then depends only on the mean and SD of S, under the alternative hypothesis (the model). These parameters were estimated with at least 50,000 simulated replicates—as many as 300,000 for low-penetrance models for which the mean to be estimated is small and thus require greater precision.
We also generated a population of sibships, with size modeled after a Poisson distribution, with a mean of 2 siblings, truncated at 7 siblings. Through a single affected proband, 400 sibships were ascertained with at least one affected sibling and one unaffected sibling, randomly selected among all affected members of the simulated population. All siblings are phenotyped and genotyped at the two highly informative markers M1 and M2, each with 10 equifrequent alleles. Parental genotypes are not available. The statistics Zlr,ad and Zlr,pairs (Kong and Cox 1997) were computed, and power was calculated as the proportion of 1,000 replicates with test statistics greater than or equal to the ⩾99th percentile of a standard normal distribution.
Asthma Study Data
We computed the Zlr,ad and the Zlr,pairs test statistics on data collected from families from the Saguenay Lac Saint-Jean region of Quebec. More than 225 families were recruited on the basis of a single asthmatic proband from each family who fulfilled at least two of the following three criteria: (1) a minimum of three clinic visits for acute asthma within 1 year, (2) two or more asthma-related hospital admissions within 1 year, and (3) steroid dependency, as defined by either 6 mo of oral or 1 year of inhaled corticosteroid use. All subjects gave informed consent. Genomewide genotyping was performed on a subset of these families with at least one asthmatic or atopic pair—some consisting of multiplex, multigenerational families—with a set of 396 polymorphic microsatellite markers, followed by fine mapping in selected regions (results to be published). For the present study, 15 microsatellite markers (average heterozygosity 0.71) were chosen in the neighborhood of the 6q25.3 region. The sex-averaged genetic map of Marshfield (Center for Medical Genetics) was used (Broman et al. 1998).
Implementation
We implemented the Sad test statistic, with a modified version of GENEHUNTER 2.1r3 (Kruglyak et al. 1996; Kruglyak and Lander 1998), called “GENEHUNTER++sad” (Lemire Web site), which also integrates the specific code lines of GENEHUNTER-PLUS (Kong and Cox 1997).
Results
Bias for Selected Pedigree Types
The bias of Sad compared with Spairs may be reduced, completely or partially, but it may even be larger, depending on the relationship between the affected and unaffected individuals and the model for TRD. We illustrate the bias for selected pedigree types.
Consider a nuclear family with three siblings, two of whom are affected (fig. 1A). There is one ASP, A, and there are two discordant sib pairs, D1 and D2. Calculation of the joint distribution of SA and SD1+SD2 is straightforward, if we proceed by conditioning on SA—and on the origin of the shared alleles, if necessary. This distribution is given in table 1 (where we let Δm=2δmδM and Δf=2δfδF), as are the corresponding values of Sad. Taking the expectation of Sad, with respect to the distribution from table 1, we obtain E(Sad|δm,δf)=0 for all possible values of δm and δf. The test statistic is thus unbiased in this case. This could have been intuitively argued, and the intuitive argument helps to show that Sad is unbiased for nuclear families with more than two affected siblings, as long as there is at least one unaffected sibling. In equation (1), if both sums on the right-hand side involve pairs of only the same kinship, then both sums have the same expected value, irrespective of the distribution of V, as long as it is independent of disease status. This includes the prior uniform distribution over realizations of V, and distributions that depend on only δm and δf. Hence, Sad has an expectation of 0 and is, moreover, unbiased.
Table 1.
Joint Distribution of SA and SD1+SD2a
| SA | SD1+SD2 | Sad | Joint Distribution |
| 0 | 2 | −1 | ΔmΔf |
| 1 | 3 | - 1/2 | Δm+Δf-3ΔmΔf |
| 2 | 4 | 0 | 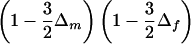 |
| 1 | 1 | 1/2 | ΔmΔf |
| 2 | 2 | 1 | 1/2(Δm+Δf-3ΔmΔf) |
| 2 | 0 | 2 | 1/4ΔmΔf |
For the pedigree shown in figure 1A.
By use of table 1 for computation of the marginal distribution of SA, the bias of the Spairs test statistic for any pedigree with a single ASP can be shown to be b(δm,δf)=1-Δm-Δf.
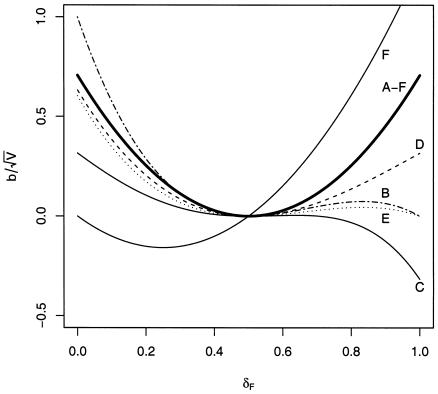
The statistic Sad is not unbiased for the other pedigrees of figure 1. For these, figure 2 illustrates the bias divided by the SD of the statistic under Mendelian segregation (the normalized bias, under Mendelian inheritance) of Sad and Spairs, when TRD comes only from the maternal side, as a function of the probability of mothers transmitting the grandmaternal allele.
Figure 2.
Graph of bias divided by the SD under Mendelian segregation (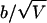 ) of Spairs (thick line) and Sad (thin lines) for the pedigrees (A to F) shown in figure 1, under TRD coming from the maternal side.
) of Spairs (thick line) and Sad (thin lines) for the pedigrees (A to F) shown in figure 1, under TRD coming from the maternal side.
Pedigree F (fig. 1) shows one grandparent with unknown status; this requires some additional comments. A trio that consists of two grandparents from the same parental side and one grandchild is uninformative for the total number of alleles shared by the three, which always equals 1. Hence, if both grandparents share the same disease status, they will contribute neither to Sad (when they are both unaffected) nor to Spairs (when they are both affected). On the other hand, the trio would be informative if the two grandparents were phenotypically discordant, since the Sad statistic depends on the contrast between the number of alleles shared by the grandparent-grandchild affected pair and the grandparent-grandchild phenotypically discordant pair: this number is not a priori fully known. However, the phenotypically discordant grandparent-grandchild pair would not add additional information about the segregation of susceptibility genes that could not be obtained from the affected grandparent-grandchild pair.
We find two instances in which the bias of Sad is larger, as shown by the lines of figure 2, pertaining to pedigrees B and F. In the former pedigree, which shows a phenotypically discordant pair formed by an unaffected nephew and an affected uncle, the normalized bias is higher only when the mother tends to transmit the grandpaternal allele (actually, only when δF is less than ∼0.3). For the latter pedigree, the apparent large bias (in absolute value) observed is a consequence of the model chosen for TRD, which is grandparental-origin dependent. Note that if the grandmother had been unaffected instead of the grandfather, we would have seen the mirror image (about δf=0.5) of line F in figure 2.
If both parents are subject to the same level of TRD, the normalized bias of Sad is increased in all cases and, except for pedigree F, is symmetric, positive, and smaller than the normalized bias of Spairs (data not shown).
Since the large bias observed in the case of pedigree F is a consequence of the chosen model, we simulated TRD on the basis of allelic preferential transmission (see the “Subjects and Methods” section). For a perfectly informative marker at the same genetic position as the distorted locus, we estimated the normalized bias of Spairs and Sad with 20,000 replicates. Results are shown in table 2. For this model of TRD, the bias of Sad is lower, although only slightly, than the bias of Spairs in pedigree F. This result also holds true for the other pedigrees of figure 1, with larger differences.
Table 2.
Normalized Bias of Spairs and Sad for Allele-Specific TRD[Note]
|
Normalized Bias for Allele-Specific TRD with Probability (s) |
||||
| Frequency (p)and Pedigree | .6 | .7 | .8 | .9 |
| .2: | ||||
| A–F | .0071 | .091 | .19 | .34 |
| B | .0097 | .015 | .047 | .070 |
| C and D | .014 | .016 | .046 | .037 |
| E | −.0023 | .014 | .050 | .093 |
| F | .0059 | .084 | .17 | .30 |
| .35: | ||||
| A–F | .027 | .10 | .24 | .44 |
| B | .0057 | .046 | .090 | .15 |
| C and D | .017 | .014 | .058 | .087 |
| E | .00075 | .037 | .052 | .11 |
| F | .027 | .097 | .22 | .39 |
| .5: | ||||
| A–F | .033 | .11 | .24 | .42 |
| B | .013 | .050 | .11 | .21 |
| C and D | .011 | .022 | .065 | .11 |
| E | .0036 | .026 | .061 | .084 |
| F | .028 | .097 | .21 | .38 |
Note.— Normalized bias of Spairs (shown in bold italics) and Sad for alleles in frequency p that are preferentially transmitted by heterozygous individuals, with probability s. For Sad, pedigree A is unbiased.
True Type I Errors
Figure 2 shows the normalized bias for both Spairs and Sad for selected pedigree types. A sample of N pedigrees of the same type would give rise to an approximate true type I error of
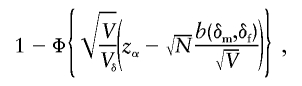 |
by use of the central limit theorem, where b(δm,δf) is the bias of S for that pedigree type (see eq. [3]), Vδ=Var(S|δm,δf), V=Var(S| 1/2, 1/2), Φ is the cumulative distribution function of a standard normal distribution, and zα=Φ-1(1-α) is its quantile of order 1-α. Since 1-Φ is a decreasing function, the true type I error of the test is an increasing function of the sample size, except perhaps when the bias is negative and the variance ratio is not too large. Table 3 shows the true type I error of Spairs that can be expected for samples of varying sizes of nuclear families with two and three affected siblings and varying levels of TRD that comes from either one or both parents. For modest deviations from the Mendelian rules of inheritance, the true type I errors are reasonably close to the nominal one and only slowly increase with the sample size. As the deviation becomes more important, the true type I error increases rapidly with the sample size. On the other hand, every ASP pedigree with at least one genotyped unaffected sibling has an unbiased contribution to the test based on Sad.
Table 3.
True Type I Errors Associated with Spairs[Note]
|
True Type I Errors with Distortion of |
||||||
| 13:12, with TRD from |
6:5, with TRD from |
3:2, with TRD from |
||||
| No. of AffectedSiblings and Sample Size | One Parent | Both Parents | One Parent | Both Parents | One Parent | Both Parents |
| 2: | ||||||
| 100 | .0103 | .0106 | .0117 | .0136 | .0204 | .0389 |
| 400 | .0106 | .0113 | .0136 | .0182 | .0390 | .116 |
| 1,600 | .0113 | .0127 | .0182 | .0315 | .116 | .475 |
| 6,400 | .0127 | .0160 | .0315 | .0820 | .475 | .986 |
| 3: | ||||||
| 100 | .0106 | .0113 | .0137 | .0183 | .0384 | .105 |
| 400 | .0112 | .0125 | .0176 | .0293 | .0971 | .367 |
| 1,600 | .0124 | .0153 | .0283 | .0678 | .362 | .931 |
| 6,400 | .0152 | .0224 | .0662 | .243 | .938 | 1.00 |
Note.— These results are for a nominal level of 1%, for nuclear families with two or three affected siblings and varying degrees of TRD.
Power Calculations
Power calculations were performed for sibships, such as that depicted in figure 1A and similar sibships, under different disease models (defined by the mode of inheritance, the susceptibility-allele frequency, and the penetrances), all with a 15% disease prevalence in the population. We varied the sibship size from 3 to 5 and the number of affected individuals from 2 to 3. Parental genotypes are available. Results are shown in table 4. Except for sibships of size 4 with a single unaffected individual, power is generally increased by the addition of the unaffected individuals. Although this may be expected because of the availability of additional individuals who are ignored in affected-only analyses, we note that, in certain circumstances, genotyping the extra siblings, when available, may be an efficient strategy. For example, with three siblings, whereas Spairs would effectively need the genotyping of four of the five (or 80%) family members, the ratios shown in table 4 are generally less than or slightly above 80%, which means that the effective total number of individuals required to achieve the desired power is generally smaller or similar when Sad is used on all five members rather than when Spairs is used with only four of the five members. In certain circumstances, when the sibling recurrence risk is low, genotyping only the affected individuals is more efficient, but then the unbiasedness of Sad for the effects of TRD may be an additional incentive for genotyping the unaffected sibling, when available.
Table 4.
Results of Power Calculations Performed on Sibships of Various Size[Note]
|
Value for Total Sibship Size |
||||||||
| 3 Total, 2 Affected (80b) |
4 Total, 2 Affected (67b) |
4 Total, 3 Affected (83b) |
5 Total, 3 Affected (71b) |
|||||
| Model, Penetrances for Genotypes, KS (%),and Markera | Nad | Nad:Npairsc | Nad | Nad:Npairsc | Nad | Nad:Npairsc | Nad | Nad:Npairsc |
| Recessive (q = .316): | ||||||||
| DD = .08, Dd = .08, dd = .78, KS = 25.9: | ||||||||
| M1 | 61 | .68 | 55 | .6 | 26 | .87 | 17 | .65 |
| M2 | 92 | .68 | 81 | .58 | 38 | .86 | 25 | .66 |
| DD = .10, Dd = .10, dd = .60, KS = 20.5: | ||||||||
| M1 | 199 | .78 | 183 | .65 | 74 | 1 | 54 | .78 |
| M2 | 299 | .78 | 269 | .66 | 111 | 1.03 | 78 | .79 |
| DD = .12, Dd = .12, dd = .40, KS = 16.7: | ||||||||
| M1 | 1,756 | .83 | 1,609 | .73 | 533 | 1.18 | 416 | .93 |
| M2 | 2,819 | .81 | 2,430 | .72 | 801 | 1.2 | 640 | .92 |
| DD = .13, Dd = .13, dd = .33, KS = 15.9: | ||||||||
| M1 | 6,302 | .96 | 5,788 | .72 | 1,973 | 1.28 | 1,591 | .95 |
| M2 | 9,640 | .97 | 8,365 | .72 | 2,983 | 1.3 | 2,341 | .93 |
| Dominant (q = .0513): | ||||||||
| DD = .08, Dd = .78, dd = .78, KS = 29.5: | ||||||||
| M1 | 68 | .5 | 67 | .42 | 26 | .68 | 18 | .51 |
| M2 | 102 | .5 | 98 | .42 | 38 | .66 | 27 | .51 |
| DD = .10, Dd = .60, dd = .60, KS = 22.4: | ||||||||
| M1 | 230 | .66 | 213 | .56 | 68 | .87 | 52 | .66 |
| M2 | 344 | .66 | 328 | .57 | 99 | .86 | 76 | .64 |
| DD = .12, Dd = .40, dd = .40, KS = 17.3: | ||||||||
| M1 | 1,672 | .75 | 1,708 | .67 | 448 | 1.12 | 387 | .82 |
| M2 | 2,622 | .72 | 2,436 | .65 | 657 | 1.11 | 584 | .82 |
| DD = .13, Dd = .33, dd = .33, KS = 16.2: | ||||||||
| M1 | 5,854 | .87 | 6,012 | .73 | 1,563 | 1.18 | 1314 | .93 |
| M2 | 9,848 | .89 | 8,863 | .74 | 2,234 | 1.14 | 1,987 | .93 |
| Additive (q = .1): | ||||||||
| DD = .08, Dd = .43, dd = .78, KS = 22.4: | ||||||||
| M1 | 241 | .78 | 193 | .67 | 98 | .98 | 70 | .77 |
| M2 | 360 | .78 | 276 | .66 | 144 | .99 | 100 | .76 |
| DD = .10, Dd = .35, dd = .60, KS = 18.8: | ||||||||
| M1 | 743 | .82 | 635 | .72 | 273 | 1.13 | 211 | .85 |
| M2 | 1,095 | .82 | 923 | .73 | 406 | 1.13 | 305 | .82 |
| DD = .12, Dd = .26, dd = .40, KS = 16.1: | ||||||||
| M1 | 6,534 | .94 | 6,316 | .79 | 1,873 | 1.22 | 1,585 | .94 |
| M2 | 9,760 | .92 | 9,524 | .8 | 2,756 | 1.26 | 2,350 | .94 |
| DD = .13, Dd = .23, dd = .33, KS = 15.6: | ||||||||
| M1 | 21,369 | .9 | 20,561 | .85 | 8,562 | 1.32 | 5,163 | .91 |
| M2 | 40,511 | .88 | 38,026 | .92 | 13,052 | 1.28 | 8,387 | .94 |
Note.— Parental genotypes are available. The nominal type I error is 0.1%. Parameters are estimated from at least 50,000 simulated replicates.
Penetrances are given in terms of the genotypes at the disease locus, where d is the susceptibility allele, with frequency q. KS is the sibling recurrence risk for the disease model. In all cases, the disease prevalence is 15%.
Percentage of individuals used by Spairs.
Ratio Nad:Npairs of the required number of pedigrees of a single type to achieve a power of 80% for the Sad statistic (Nad) and the Spairs statistic (Npairs), calculated at marker M1 and marker M2.
In sibships of size 4 with a single unaffected individual, a loss of power is observed. Note that, here, unless all three affected siblings share both their alleles (which is a single configuration of the 16 possible descent paths of alleles), the unaffected individual will always share alleles with at least one affected sibling. This may explain the loss of power. We note, however, that, by adding a second unaffected sibling, this almost-obligate sharing of alleles is balanced by an increase in statistical information, and we observe a gain in power.
For the other pedigrees shown in figure 1, the number of additional individuals beyond the ASP and their parents is too large to make it an efficient use of resources to genotype them all (with the technical exception of pedigree F; see below), especially since Sad still has bias due to TRD (fig. 2 and table 2). If the genotypic data are otherwise already available, then some power may be gained, depending on the structure of the pedigrees and the mode of inheritance. For completeness, we computed the power for the remaining pedigrees of figure 1. Results are shown in table 5.
Table 5.
Results of Power Calculations Performed for Pedigrees[Note]
|
Value for Pedigree |
|||||||||
| B |
C or D |
E |
Fb |
||||||
| Model, Penetrances for Genotypes, KS (%),and Markera | Nad | Nad:Npairs | Nad | Nad:Npairs | Nad | Nad:Npairs | Nad | Nad:Npairs | Nad:N*pairs |
| Recessive (q = .316): | |||||||||
| DD = .08, Dd = .08, dd = .78, KS = 25.9: | |||||||||
| M1 | 238 | 1.9 | 111 | 1.08 | 102 | 1.04 | 65 | .63 | 1.03 |
| M2 | 373 | 1.97 | 168 | 1.08 | 156 | 1.05 | 94 | .6 | 1.07 |
| DD = .10, Dd = .10, dd = .60, KS = 20.5: | |||||||||
| M1 | 538 | 1.82 | 288 | 1.1 | 261 | 1.08 | 145 | .67 | 1.01 |
| M2 | 841 | 1.86 | 459 | 1.12 | 411 | 1.1 | 211 | .63 | 1.05 |
| DD = .12, Dd = .12, dd = .40, KS = 16.7: | |||||||||
| M1 | 3,582 | 1.93 | 1,862 | 1.13 | 2,067 | 1.11 | 1,020 | .73 | .95 |
| M2 | 5,364 | 1.97 | 2,746 | 1.17 | 2,955 | 1.1 | 1,365 | .68 | 1 |
| DD = .13, Dd = .13, dd = .33, KS = 15.9: | |||||||||
| M1 | 8,738 | 1.1 | 7,824 | 1.2 | 7,106 | 1.16 | 3,791 | .68 | .99 |
| M2 | 13,875 | 1.07 | 11,714 | 1.32 | 9,413 | 1.18 | 4,590 | .66 | 1 |
| Dominant (q = .0513): | |||||||||
| DD = .08, Dd = .78, dd = .78, KS = 29.5: | |||||||||
| M1 | 124 | .66 | 109 | .84 | 106 | .79 | 40 | .35 | 1.33 |
| M2 | 199 | .71 | 166 | .86 | 163 | .8 | 55 | .32 | 1.41 |
| DD = .10, Dd = .60, dd = .60, KS = 22.4: | |||||||||
| M1 | 371 | .9 | 260 | .92 | 255 | .86 | 91 | .35 | 1.34 |
| M2 | 591 | .98 | 389 | .94 | 372 | .87 | 125 | .32 | 1.4 |
| DD = .12, Dd = .40, dd = .40, KS = 17.3: | |||||||||
| M1 | 3,203 | 1.27 | 2,283 | .95 | 2,237 | 1.07 | 572 | .37 | 1.33 |
| M2 | 5,250 | 1.44 | 3,340 | .95 | 3,113 | 1.07 | 773 | .3 | 1.42 |
| DD = .13, Dd = .33, dd = .33, KS = 16.2: | |||||||||
| M1 | 6,277 | .92 | 6,634 | 1.01 | 6,431 | .89 | 1,992 | .41 | 1.26 |
| M2 | 9,939 | .89 | 7,482 | .98 | 10,494 | .9 | 2,643 | .38 | 1.29 |
| Additive (q = .1): | |||||||||
| DD = .08, Dd = .43, dd = .78, KS = 22.4: | |||||||||
| M1 | 414 | 1.05 | 281 | .93 | 268 | .88 | 113 | .39 | 1.3 |
| M2 | 662 | 1.07 | 406 | .93 | 426 | .88 | 151 | .36 | 1.34 |
| DD = .10, Dd = .35, dd = .60, KS = 18.8: | |||||||||
| M1 | 1,286 | 1.08 | 872 | .95 | 827 | .94 | 314 | .41 | 1.28 |
| M2 | 1,990 | 1.09 | 1,257 | .92 | 1,227 | .96 | 429 | .37 | 1.32 |
| DD = .12, Dd = .26, dd = .40, KS = 16.1: | |||||||||
| M1 | 9,079 | 1.19 | 5,626 | .98 | 6,100 | .81 | 2,136 | .5 | 1.18 |
| M2 | 12,193 | 1.08 | 9,176 | .92 | 10,731 | .9 | 2,971 | .47 | 1.21 |
| DD = .13, Dd = .23, dd = .33, KS = 15.6: | |||||||||
| M1 | 22,717 | 1.09 | 27,662 | 1.17 | 23,556 | 1.12 | 12,015 | .28 | 1.49 |
| M2 | 45,148 | 1.17 | 30,897 | 1.14 | 45,072 | 1.01 | 20,300 | .18 | 1.69 |
Note.— Pedigree labels refer to figure 1. All individuals are genotyped.
Penetrances are given in terms of the genotypes at the disease locus, where d is the susceptibility allele, with frequency q. KS is the sibling recurrence risk for the disease model. In all cases, the disease prevalence is 15%.
For pedigree F, N*pairs is related to the power of Spairs if the grandmother's status was affected instead of unknown.
The differences in Npairs values for the different ASP pedigree types are explained by the different ascertainment schemes. For example, by selecting only ASPs with an unaffected cousin (pedigrees C and D), we effectively reduced the genetic effect in favor of phenocopy effects; hence, the reduced power compared with the unrestricted selection of ASPs. Similarly, by selecting nuclear families with exactly one unaffected sibling (pedigree A), we may end up with a suboptimal ascertainment scenario. For pedigree F, we ascertained families with phenotypically discordant grandparents, treating the affected grandparent as having an unknown status. As mentioned above, the number of alleles that a grandchild shares with one grandparent can be obtained from the number that he or she shares with the other grandparent. The Sad statistic for pedigree F (with an affected grandparent treated as having an unknown disease status) is thus very similar to the Spairs computed for the affected trio and differs only with respect to how pairs are weighted: with Spairs, all pairs have the same weight, whereas, with Sad (ignoring the affected grandparent), grandparent-grandchild pairs weigh half as much as the ASP. We compared the power of Spairs (ignoring the affected grandparent) with the power of Spairs computed for the affected trio (N*pairs in table 5). The power of Sad compares to the power of Spairs only for recessive disease models, but it is less powerful otherwise.
Designs in which it is desirable to genotype unaffected siblings include those for diseases with late onset, in which, in the absence of parental data, unaffected siblings are appropriate controls for follow-up association studies (Curtis 1997; Spielman and Ewens 1998). We thus also performed gene-dropping simulations, again without TRD effects, under the scenario of unavailability of parental data. We ascertained 400 families through a single affected proband with at least one affected sibling, randomly selected from all affected members of a simulated population (see the “Subjects and Methods” section). Six low-penetrant disease models were used from the models of table 4. To correct for incompleteness of the data, the method of Kong and Cox (1997) is used with Spairs and Sad. Note that, for the reconstruction of the parental genotypes, it is assumed that random mating occurs. Two strategies are investigated: one in which a single unaffected sibling is genotyped (say, the oldest) and one in which all unaffected siblings are genotyped. In practice, for late-onset diseases, it may be desirable to genotype only unaffected siblings on the basis of suitable age-cutoff considerations (Majewski 2001). Results from 1,000 replicates are given in table 6, for a nominal type I error of 1%. For the former scenario, 400 unaffected siblings are genotyped, whereas, for the latter, the average number of unaffected siblings that are genotyped has a range of 798–817, depending on the disease model. The mean number of affected individuals has a range of 860–873. In both cases, the power is augmented by consideration of the unaffected siblings, but, for low-penetrance models, results show that it is not worthwhile to genotype more than one unaffected sibling. Note that, for those low-penetrant models, much larger samples are needed.
Table 6.
Power of Spairs and Sad in the Absence of Parental Genotypes[Note]
|
Power |
|||
| Model, Penetrances for Genotypes, KS (%),and Markera | Spairs | Sad(one) | Sad(all) |
| Recessive (q = .316): | |||
| DD = .12, Dd = .12, dd = .40, KS = 16.7: | |||
| M1 | .369 | .386 | .453 |
| M2 | .300 | .272 | .337 |
| DD = .13, Dd = .13, dd = .33, KS = 15.9: | |||
| M1 | .099 | .103 | .098 |
| M2 | .076 | .073 | .076 |
| Dominant (q = .0513): | |||
| DD = .12, Dd = .40, dd = .40, KS = 17.3: | |||
| M1 | .313 | .371 | .439 |
| M2 | .249 | .276 | .308 |
| DD = .13, Dd = .33, dd = .33, KS = 16.2: | |||
| M1 | .106 | .106 | .116 |
| M2 | .086 | .085 | .097 |
| Additive (q = .1): | |||
| DD = .12, Dd = .26, dd = .40 KS = 16.1: | |||
| M1 | .097 | .103 | .126 |
| M2 | .080 | .066 | .087 |
| DD = .13, Dd = .23, dd = .33, KS = 15.6: | |||
| M1 | .037 | .046 | .038 |
| M2 | .034 | .035 | .029 |
Note.— Power of Spairs and Sad under six different models, without TRD effects, for 400 ascertained sibships of various sizes. Two genotyping scenarios are considered: typing one unaffected sibling or all unaffected siblings. Parental genotypes are unavailable. Power is estimated at markers M1 and M2 from 1,000 simulated replicates, for a nominal level of 1%.
Penetrances are given in terms of the genotypes at the disease locus, where d is the susceptibility allele, with frequency q. KS is the sibling recurrence risk for the disease model. In all cases, the disease prevalence is 15%.
Finally, we investigated the effects of TRD on the power to detect linkage with Sad, under the above scenario with a single unaffected sibling genotyped. Marker M1 was taken to be under the influence of disease-independent TRD, in which grandparental chromosomes segregate in a 3:2 ratio from a single parent, in a 3:2 ratio from both parents, and in a 3:1 ratio from both parents. We observed loss of power—or bias toward the null—in the cases we considered (see table 7). This loss of power is marginal when the TRD is small, but it is more important as the distortion grows.
Table 7.
Power of Sad under the Effects of TRD[Note]
|
Power |
||||
| Model, Penetrances for Genotypes, KS (%),and Markera | No TRD | 3:2 (one) | 3:2 (both) | 3:1 (both) |
| Recessive (q = .316): | ||||
| DD = .12, Dd = .12, dd = .40, KS = 16.7: | ||||
| M1 | .386 | .381 | .364 | .258 |
| M2 | .272 | .283 | .267 | .174 |
| DD = .13, Dd = .13, dd = .33, KS = 15.9: | ||||
| M1 | .103 | .105 | .090 | .071 |
| M2 | .073 | .075 | .068 | .051 |
| Dominant (q = .0513): | ||||
| DD = .12, Dd = .40, dd = .40, KS = 17.3: | ||||
| M1 | .371 | .363 | .304 | .218 |
| M2 | .276 | .278 | .253 | .152 |
| DD = .13, Dd = .33, dd = .33, KS = 16.2: | ||||
| M1 | .106 | .095 | .083 | .046 |
| M2 | .085 | .071 | .063 | .045 |
| Additive (q = .1): | ||||
| DD = .12, Dd = .26, dd = .40, KS = 16.1: | ||||
| M1 | .103 | .097 | .082 | .045 |
| M2 | .066 | .071 | .066 | .036 |
| DD = .13, Dd = 2, dd = .33, KS = 15.6: | ||||
| M1 | .046 | .024 | .034 | .011 |
| M2 | .035 | .020 | .027 | .007 |
Note.— Power of Sad under the effects of TRD, for sibships of varying sizes with a single unaffected sibling genotyped and without parental data. Distortions are in ratio 3:2 coming from a single parent, 3:2 coming from both parents, and 3:1 coming from both parents.
Penetrances are given in terms of the genotypes at the disease locus, where d is the susceptibility allele, with frequency q. KS is the sibling recurrence risk for the disease model. In all cases, the disease prevalence is 15%.
Although pedigrees with discordant sib pairs but without ASPs could be included in the analysis, this decision should be made in the light of the work of Risch (1990) and Rogus and Krolewski (1996): it may be advantageous when the recurrence risk for a given relative is high enough (in the case, for example, of a highly penetrant dominant disease) but not efficient if that risk is <50%. In all cases, as mentioned by Rogus and Krolewski (1996), a proper and adequate definition of the unaffected status is required.
Application to an Asthma Study
For the present study, we used data from families with two or more affected siblings, artificially treating other asthmatic relatives as having an unknown phenotype. The intention was to consider only pedigrees that are similar, in terms of diagnosis, to the pedigrees shown in figure 1. Our sample consisted of 61 families, 21 of which had phenotypically discordant pairs: 14 pedigrees in which the discordant pairs are sibling pairs, 2 in which they are cousin pairs, and 5 in which they are avuncular pairs. Working under the hypothesis that TRD is grandparental-origin dependent, we did not consider grandparent-grandchild discordant pairs.
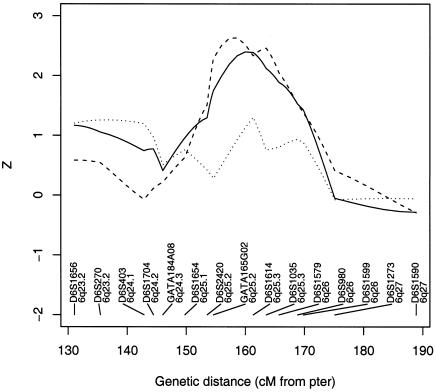
We focused on the region surrounding 6q25.3. Markers in this region that were selected for the present study are shown in figure 3. Excess sharing of alleles among asthmatic individuals was observed. Figure 3 shows a maximum score of Zlr,pairs=2.40 (P=.0082), on the basis of the exponential model of Kong and Cox (1997), with the Spairs statistic, in the interval between markers GATA165G02 and D6S1614, in the neighborhood of 6q25.3. Since the excess sharing could be a consequence of parent-of-origin–dependent TRD, we looked at parent-specific allele sharing. We measured parent-specific sharing by artificially analyzing all affected siblings as half-siblings with distinct mothers or fathers, depending on the desired parental origin of sharing. Sharing is higher from the maternal side than from the paternal side (fig. 3), a result consistent with the observations of Naumova et al. (2001).
Figure 3.
Zlr,pairs allele-sharing statistic of Kong and Cox (1997) among asthmatic siblings (solid line). Also shown are parent-specific allele-sharing statistics: maternal allele sharing (dashed line) and paternal allele sharing (dotted line).
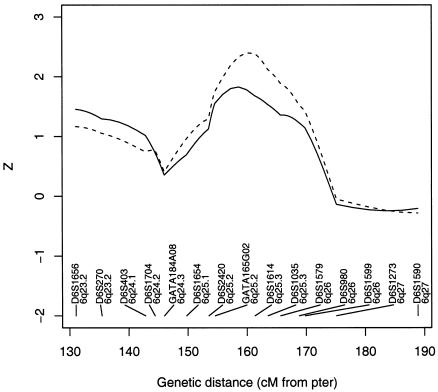
We computed the Sad score with GENEHUNTER++sad (Lemire Web site) for the data set consisting of all 61 pedigrees. Results are shown in figure 4. We observe a decreased value for the Zlr,ad test statistic (1.78; P=.038) compared with Zlr,pairs at the position of the maximum Zlr,pairs. Even though the families with phenotypically discordant pairs are modest in size, the differences between the two statistics are important.
Figure 4.
Zlr,pairs (dashed line) and Zlr,ad (solid line) test statistics in a sample of 61 pedigrees, 36 of whom have phenotypically discordant pairs.
Discussion
We have developed a novel allele-sharing statistic that uses discordant pairs of relatives as a control against the possible bias caused by TRD. In regions under TRD, our statistic is unbiased for the common design of sampling ASPs, if unaffected siblings are also sampled. Moreover, for this design, because the method combines the lack of sharing of alleles in discordant sib pairs and the excess sharing of alleles in ASPs to find evidence for linkage, incorporating unaffected siblings in the analysis improves the power to detect linkage. Power may also be increased by consideration of other relative pairs, to control, to a lesser extent, for TRD. However, we want to stress the fact that, if faced with the decision to genotype either an affected sibling or an unaffected one, then, in terms of power alone, it is preferable to genotype the affected sibling, with perhaps the exception of diseases with very high sibling recurrence risk (Risch 1990).
The Sad statistic has some limitations. For example, an ASP with an unaffected sibling has an unbiased contribution to Sad, but it would become biased by adding other unaffected nonsibling relatives to the pedigree. Moreover, for general pedigrees with multiple affected relatives, bias and power issues are still unaddressed, and use of Sad may not be appropriate. The intuitive argument used to show the unbiasedness of Sad in the case of nuclear families with affected and unaffected siblings can provide some insights for a statistic applicable to general pedigrees. Perhaps a more convenient statistic to use would be of the form
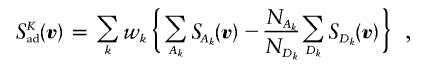 |
where pairs are grouped on the basis of their kinship k (with relative types possibly being weighted differently), among which the totals of the number of alleles shared are computed. Thus, when available, an affected relative pair would have a matched phenotypically discordant pair to control for TRD, and phenotypically discordant pairs would be used only if an affected pair of the same kinship contributes to the statistic. Implementation of SKad is pending.
The original linkage result for the asthma trait in the 6q25.3 region is only modest and cannot be considered significant in the context of a whole-genome scan. The result, nevertheless, shows that there is significant distortion from Mendelian inheritance in the region, given the prior evidence of TRD, but, specific to our sample of only modest size, the question remains as to whether it is due to asthma-independent TRD or a putative asthma-related gene with weak and possibly parent-of-origin effects. The 6q25 region under study contains one candidate gene that could play a role in the airway hyperresponsiveness and asthma: the vasoactive intestinal peptide gene (VIP), which is a potent relaxant of the airway smooth muscle (Ollerenshaw et al. 1989; Berisha et al. 2002; Hasaneen et al. 2003). Parent-of-origin effects have been shown to play a role in allergic diseases, especially in atopy, in which the chance of an atopic mother transmitting the disease is four times as high as transmission from an atopic father (Cookson 2002). Note that, in our analysis, we used a sex-averaged genetic map. Misspecification of map distances may result in an increase in type I error and may reduce the power when linkage is present (Halpern and Whittemore 1999; Daw et al. 2000). Moreover, the use of a sex-averaged map may result in incorrectly inferred imprinting effects, when genetic distances differences between males and females are important (Mukhopadhyay and Weeks 2003).
Although the application of our method to the asthma study focused on a single region suspected to be under the influence of TRD, Sad is appropriate for genomewide linkage studies. Interpretation of genomewide linkage results for complex diseases can then be based on guidelines such as the locus-counting method (Wiltshire et al. 2002), which compares the number of independent regions of the genome showing evidence for linkage with that expected under the null hypothesis of no linkage. An unbiased statistic may be particularly well suited for the locus-counting approach, since the method relies on the hypothesis of Mendelian inheritance throughout the genome, a hypothesis not supported by the recent findings of Zöllner et al. (2004), who observed evidence of extensive TRD in the genome. Consequently, unless an unbiased statistic is used to assess linkage, the shift of the observed distribution of the number of independent regions showing evidence for linkage (with respect to varying linkage-assessment thresholds), compared with the null distribution, may be inflated.
TRD is a confounding factor for tests based on allele sharing in affected relative pairs, and its effects were overlooked over the years, despite clear comments made in that regard early in the development of family-based tests that look for transmission disequilibrium (e.g. Spielman et al. 1993). A report of a sex-specific distorted region (10p) in CEPH families (Paterson and Petronis 1999) generated replies from groups who previously reported linkage of schizophrenia to 10p (Faraone et al. 1999; Schwab et al. 1999). These groups addressed the issue of possible TRD in the region, and it was found to have little impact on the magnitude of their original results. It is our opinion that recognizing the existence of possible confounding factors and taking them into account can only strengthen linkage results.
Commenting on the lack of studies of normal sib pairs, Edwards (2003) mentioned that “[the affected sib pair] family of surveys [is] one of the largest undertaken in the absence of controls.” In this regard, the recent contributions of Paterson et al. (2003) to the Genetic Analysis Workshop 13, as well as the work of Zöllner et al. (2004), are further steps in a whole-genome–scan context toward the identification of loci under the influence of TRD.
Acknowledgments
The authors thank Celia Greenwood, Anna Naumova, J. Loredo-Osti, and two anonymous reviewers for helpful comments on earlier versions of the manuscript. This research was supported by the Canadian Institutes of Health Research (CIHR) (support to T.J.H. and C.L.) and by the Networks of Centres of Excellence program—the Canadian Genetic Diseases Network and the Mathematics of Information Technology and Complex Systems (support to K.M.). C.L. is supported by the Fonds pour la recherche en santé du Québec. T.J.H. is recipient of an Investigator Award from CIHR and a Clinician-Scientist Award in Translational Research from the Burroughs Wellcome Fund.
Appendix
The joint distribution of SA (we consider a single ASP) and 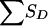 for pedigrees C, D, and E of figure 1 can be obtained from tables 8 and 9. Table 8 shows the joint distribution for the value of SA and the grandparental origin of the maternal allele shared by the ASP, if any. Table 9 shows the conditional distribution of
for pedigrees C, D, and E of figure 1 can be obtained from tables 8 and 9. Table 8 shows the joint distribution for the value of SA and the grandparental origin of the maternal allele shared by the ASP, if any. Table 9 shows the conditional distribution of 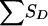 , given the grandparental origin of the maternal allele shared by the ASP. The joint distribution of SA and
, given the grandparental origin of the maternal allele shared by the ASP. The joint distribution of SA and 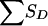 (and then the distribution of the values of Sad) is obtained by multiplication of the conditional and joint unconditional probabilities, summing these products when necessary. Table 10 applies to pedigree B of figure 1, in which it is easier to obtain the distribution of SD (here, there is only a single discordant pair) conditional on the number of alleles shared by the ASP, along with the grandparental origin of the allele shared. Given the information shown in table 8, the value of
(and then the distribution of the values of Sad) is obtained by multiplication of the conditional and joint unconditional probabilities, summing these products when necessary. Table 10 applies to pedigree B of figure 1, in which it is easier to obtain the distribution of SD (here, there is only a single discordant pair) conditional on the number of alleles shared by the ASP, along with the grandparental origin of the allele shared. Given the information shown in table 8, the value of 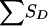 for pedigree F of figure 1 is readily obtained.
for pedigree F of figure 1 is readily obtained.
Table 8.
Joint Distribution of SA
| ASP Maternal Allele Shared and SAa | Joint Probabilityb |
| None: | |
| 0 | ΔfΔm |
| 1 | Δf(1-Δm) |
| f: | |
| 1 | Δmδ2f |
| 2 | (1-Δm)δ2f |
| F: | |
| 1 | Δmδ2F |
| 2 | (1-Δm)δ2F |
f=the grandpaternal allele; F=the grandmaternal allele.
The joint distribution of the number of alleles shared by a single ASP and the grandparental origin of the maternal allele shared, if any.
Table 9.
Probability Distributions for ∑ SD of Pedigrees C, D, and E
|
Conditional Probabilityb for |
|||
ASP Maternal Allele Shared and 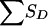 a a
|
Pedigree C | Pedigree D | Pedigree E |
| None: | |||
| 0 | ΔfδF+Δmδf | Δmδm+ΔfδM | ΔfΔm |
| 1 | (1-Δf)δF+(1-Δm)δf | (1-Δm)δm+(1-Δf)δM | Δf(1-Δm)+Δm(1-Δf) |
| 2 | 0 | 0 | (1-Δf)(1-Δm) |
| f: | |||
| 0 | Δm+(1-Δm)δF | Δm+(1-Δm)δM | Δm |
| 2 | (1-Δm)δf | (1-Δm)δm | 1-Δm |
| F: | |||
| 0 | Δf+(1-Δf)δf | Δf+(1-Δf)δm | Δf |
| 2 | (1-Δf)δF | (1-Δf)δM | 1-Δf |
f=the grandpaternal allele; F=the grandmaternal allele.
Probability distributions for 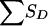 of pedigrees C, D, and E (fig. 1), conditional on the grandparental origin of the maternal allele shared by the ASP.
of pedigrees C, D, and E (fig. 1), conditional on the grandparental origin of the maternal allele shared by the ASP.
Table 10.
Pedigree B Distributions[Note]
| SA (Allele Shared), Probabilitya, and SD | Conditional Probability |
| 0: | |
| ΔmΔf: | |
| 0 | 1 |
| 1 (f): | |
| (1−Δm)Δf: | |
| 0 | δF |
| 1 | δf |
| 1 (F): | |
| Δm(1−Δf): | |
| 0 | δf |
| 1 | δF |
| 2: | |
| (1−Δm)(1−Δf): | |
| 1 | 1 |
Note.— Distributions are related to pedigree B of figure 1.
The joint event representing the number of alleles shared by the ASP and the allele that is shared (f=a shared paternal allele; F=a shared maternal allele). The distribution of SD is conditional on this joint event.
Electronic-Database Information
The URLs for data presented herein are as follows:
- Center for Medical Genetics, http://research.marshfieldclinic.org/genetics/ (for the Marshfield Clinic marker order and genetic distance between markers)
- Lemire Web site, http://www.genome.mcgill.ca/~mlemire/ (for GENEHUNTER++sad and SimM)
References
- Abecasis GR, Cherny SS, Cookson WO, Cardon LR (2002) Merlin—rapid analysis of dense genetic maps using sparse gene flow trees. Nat Genet 30:97–101 10.1038/ng786 [DOI] [PubMed] [Google Scholar]
- Berisha HI, Bratut M, Bangale Y, Colasurdo G, Paul S, Said SI (2002) New evidence for transmitter role of VIP in the airways: impaired relaxation by a catalytic antibody. Pulm Pharmacol Ther 15:121–127 10.1006/pupt.2001.0337 [DOI] [PubMed] [Google Scholar]
- Broman KW, Murray JC, Sheffield VC, White RL, Weber JL (1998) Comprehensive human genetic maps: individual and sex-specific variation in recombination. Am J Hum Genet 63:861–869 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cookson W (2002) Genetics and genomics of asthma and allergic diseases. Immunol Rev 190:195–206 10.1034/j.1600-065X.2002.19015.x [DOI] [PubMed] [Google Scholar]
- Curtis D (1997) Use of siblings as controls in case-control association studies. Ann Hum Genet 61:319–333 10.1017/S000348009700626X [DOI] [PubMed] [Google Scholar]
- Daw EW, Thompson EA, Wijsman EM (2000) Bias in multipoint linkage analysis arising from map misspecification. Genet Epidemiol 19:366–380 [DOI] [PubMed] [Google Scholar]
- de la Casa-Esperón E, Loredo-Osti JC, Pardo-Manuel de Villena F, Briscoe TL, Malette JM, Vaughan JE, Morgan K, Sapienza C (2002) X chromosome effect on maternal recombination and meiotic drive in the mouse. Genetics 161:1651–1659 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng H-W, Chen W-M, Recker RR (2002) Transmission disequilibrium test with discordant sib pairs when parents are available. Hum Genet 110:451–461 10.1007/s00439-002-0675-9 [DOI] [PubMed] [Google Scholar]
- Eaves IA, Bennett ST, Forster P, Ferber KM, Ehrmann D, Wilson AJ, Bhattacharyya S, Ziegler A-G, Brinkmann B, Todd JA (1999) Transmission ratio distortion at the INS-IGF2 VNTR. Nat Genet 22:324–325 10.1038/11890 [DOI] [PubMed] [Google Scholar]
- Edwards JH (2003) Sib-pairs in multifactorial disorders: the sib-similarity problem. Clin Genet 63:1–9 12519363 [DOI] [PubMed] [Google Scholar]
- Faraone SV, Meyer J, Matise T, Svrakic D, Pepple J, Malaspina D, Suarez B, Hampe C, Chan G, Aelony A, Friedman JH, Kaufmann C, Cloninger CR, Tsuang MT (1999) Suggestive linkage of chromosome 10p to schizophrenia is not due to transmission ratio distortion. Am J Med Genet 88:607–608 [DOI] [PubMed] [Google Scholar]
- Génin E, Clerget-Darpoux F (1996) Consanguinity and the sib-pair method: an approach using identity by descent between and within individuals. Am J Hum Genet 59:1149–1162 [PMC free article] [PubMed] [Google Scholar]
- Greenwood CMT, Morgan K (2000) The impact of transmission-ratio distortion on allele sharing in affected sibling pairs. Am J Hum Genet 66:2001–2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halpern J, Whittemore AS (1999) Multipoint linkage analysis: a cautionary note. Hum Hered 49:194–196 10.1159/000022874 [DOI] [PubMed] [Google Scholar]
- Hasaneen NA, Foda HD, Said SI (2003) Nitric oxide and vasoactive intestinal peptide as co-transmitters of airway smooth-muscle relaxation: analysis in neuronal nitric oxide synthase knockout mice. Chest 124:1067–1072 10.1378/chest.124.3.1067 [DOI] [PubMed] [Google Scholar]
- Kong A, Cox NJ (1997) Allele-sharing models: LOD scores and accurate linkage tests. Am J Hum Genet 61:1179–1188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruglyak L, Daly MJ, Reeve-Daly MP, Lander ES (1996) Parametric and nonparametric linkage analysis: a unified multipoint approach. Am J Hum Genet 58:1347–1363 [PMC free article] [PubMed] [Google Scholar]
- Kruglyak L, Lander ES (1998) Faster multipoint linkage analysis using Fourier transforms. J Comput Biol 5:1–7 [DOI] [PubMed] [Google Scholar]
- Lander ES, Green P (1987) Construction of multilocus genetic linkage maps in humans. Proc Natl Acad Sci USA 84:2363–2367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leutenegger A-L, Génin E, Thompson EA, Clerget-Darpoux F (2002) Impact of parental relationships in maximum lod score affected sib-pair method. Genet Epidemiol 23:413–425 10.1002/gepi.10190 [DOI] [PubMed] [Google Scholar]
- Lyttle TW (1993) Cheaters sometimes prosper: distortion of Mendelian segregation by meiotic drive. Trends Genet 9:205–210 10.1016/0168-9525(93)90120-7 [DOI] [PubMed] [Google Scholar]
- Majewski J (2001) To type or not to type: the use of unaffected siblings in nonparametric linkage analysis. Genet Epidemiol Suppl 21:S522–S527 11793730 [DOI] [PubMed] [Google Scholar]
- Mukhopadhyay N, Weeks DE (2003) Linkage analysis of adult height with parent-of-origin effects in the Framingham Heart Study. BMC Genet Suppl 4:S76 14975144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naumova AK, Greenwood CMT, Morgan K (2001) Imprinting and deviation from Mendelian transmission ratios. Genome 44:311–320 10.1139/gen-44-3-311 [DOI] [PubMed] [Google Scholar]
- Naumova AK, Leppert M, Barker DF, Morgan K, Sapienza C (1998) Parental origin–dependent, male offspring–specific transmission-ratio distortion at loci on the human X chromosome. Am J Hum Genet 62:1493–1499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa O, McNoe LA, Eccles MR, Morison IM, Reeve AE (1993) Human insulin-like growth factor type I and type II receptors are not imprinted. Hum Mol Genet 2:2163–2165 [DOI] [PubMed] [Google Scholar]
- Ollerenshaw S, Jarvis D, Woolcock A, Sullivan C, Scheibner T (1989) Absence of immunoreactive vasoactive intestinal polypeptide in tissue from the lungs of patients with asthma. N Engl J Med 320:1244–1248 [DOI] [PubMed] [Google Scholar]
- Pardo-Manuel de Villena F, de la Casa-Esperón E, Briscoe TL, Sapienza C (2000) A genetic test to determine the origin of maternal transmission ratio distortion: meiotic drive at the mouse Om locus. Genetics 154:333–342 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paterson AD, Petronis A (1999) Transmission ratio distortion in females on chromosome 10p11-p15. Am J Med Genet 88:657–661 [DOI] [PubMed] [Google Scholar]
- Paterson AD, Sun L, Liu X-Q (2003) Transmission ratio distortion in families from the Framingham Heart Study. BMC Genet Suppl 4:S48 14975116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risch N (1990) Linkage strategies for genetically complex traits. II. The power of affected relative pairs. Am J Hum Genet 46:229–241 [PMC free article] [PubMed] [Google Scholar]
- Rogus JJ, Krolewski AS (1996) Using discordant sib pairs to map loci for qualitative traits with high sibling recurrence risk. Am J Hum Genet 59:1376–1381 [PMC free article] [PubMed] [Google Scholar]
- Schwab SG, Wildenauer DB, Hallmayer J (1999) No evidence for segregation distortion in females in a sample of 72 families with schizophrenia with potential linkage to chromosome 10p14-p11. Am J Med Genet 88:750–751 [DOI] [PubMed] [Google Scholar]
- Spielman RS, Ewens WJ (1998) A sibship test for linkage in the presence of association: the sib transmission/disequilibrium test. Am J Hum Genet 62:450–458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spielman RS, McGinnis RE, Ewens WJ (1993) Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM). Am J Hum Genet 52:506–516 [PMC free article] [PubMed] [Google Scholar]
- Thompson EA (2000) Statistical inference from genetic data on pedigrees. NSF-CBMS Regional Conference Series in Probability and Statistics. Vol 6. Institute of Mathematical Statistics, Beachwood, OH [Google Scholar]
- Whittemore AS, Halpern J (1994) A class of tests for linkage using affected pedigree members. Biometrics 50:118–127 [PubMed] [Google Scholar]
- Wiltshire S, Cardon LR, McCarthy MI (2002) Evaluating the results of genomewide linkage scans of complex traits by locus counting. Am J Hum Genet 71:1175–1182 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y, Goodyer CG, Deal C, Polychronakos C (1993) Functional polymorphism in the parental imprinting of the human IGF2R gene. Biochem Biophys Res Commun 197:747–754 10.1006/bbrc.1993.2542 [DOI] [PubMed] [Google Scholar]
- Zöllner S, Wen X, Hanchard NA, Herbert MA, Ober C, Pritchard JK (2004) Evidence for extensive transmission distortion in the human genome. Am J Hum Genet 74:62–72 [DOI] [PMC free article] [PubMed] [Google Scholar]