Abstract
Genomewide linkage scans have traditionally employed panels of microsatellite markers spaced at intervals of ∼10 cM across the genome. However, there is a growing realization that a map of closely spaced single-nucleotide polymorphisms (SNPs) may offer equal or superior power to detect linkage, compared with low-density microsatellite maps. We performed a series of simulations to calculate the information content associated with microsatellite and SNP maps across a range of different marker densities and heterozygosities for sib pairs (with and without parental genotypes), sib trios, and sib quads. In the case of microsatellite markers, we varied density across 11 levels (1 marker every 0.5, 1, 2, 3, 4, 5, 6, 7, 8, 9, or 10 cM) and marker heterozygosity across 6 levels (2, 3, 4, 5, 10, or 20 equally frequent alleles), whereas, in the case of SNPs, we varied marker density across 4 levels (1 marker every 0.1, 0.2, 0.5, or 1 cM) and minor-allele frequency across 7 levels (0.5, 0.4, 0.3, 0.2, 0.1, 0.05, and 0.01). When parental genotypes were available, a map consisting of microsatellites spaced every 2 cM or a relatively sparse map of SNPs (i.e., at least 1 SNP/cM) was sufficient to extract most of the inheritance information from the map (>95% in most cases). However, when parental genotypes were unavailable, it was important to use as dense a map of markers as possible to extract the greatest amount of inheritance information. It is important to note that the information content associated with a traditional map of microsatellite markers (i.e., 1 marker every ∼10 cM) was significantly lower than the information content associated with a dense map of SNPs or microsatellites. These results strongly suggest that previous linkage studies that employed sparse microsatellite maps could benefit substantially from reanalysis by use of a denser map of markers.
The past few years have witnessed an explosion in the number of linkage studies of complex diseases and traits (Kostanje and Paigen 2002). Typically, these studies have involved genomewide scans that use low-density maps of microsatellite markers that are spaced at intervals of ∼10 cM across the genome. To maximize the chances of detecting linkage, it is critical that any map of markers extracts the optimum amount of inheritance information (Kruglyak and Lander 1995; Kruglyak 1997).
More recently, the discovery of SNPs and the development of automated high-throughput genotyping methods have enabled investigators to type thousands of markers across the genome quickly and economically. Although SNPs are biallelic and usually have lower heterozygosities than microsatellite markers, they are present at a greater density throughout the genome and are associated with lower genotyping error rates than their microsatellite counterparts (Kennedy et al. 2003). Indeed, there is growing evidence that a map of closely spaced SNPs may offer several advantages over low-density microsatellite maps, including superior power to detect linkage (Kruglyak 1997; Wilson and Sorant 2000; Goddard and Wijsman 2002; Matise et al. 2003; Middleton et al. 2004) and improved localization of the underlying disease/trait locus (John et al. 2004). However, previous simulation studies have only examined sparse maps of SNPs, with a limited range of pedigree structures. For example, the highest density that Kruglyak (1997) examined was 1 SNP/cM, and this was only in the case of cousin pairs for which parental genotypes were available. Very recently, reanalysis of existing microsatellite scans with a denser map of SNPs found significant linkages missed by the initial scans (Middleton et al. 2004). Given that SNP technology has evolved to allow high-throughput, high-density genotyping at densities >1 SNP/cM, it is important to determine whether high-density maps offer significant benefits over lower-density maps, in terms of power to detect linkage. In this study, we examined the information content associated with both microsatellite and high-density SNP maps in the context of the most common types of pedigree designs—nuclear family and sibling studies. In particular, we were interested not only in the conditions under which a dense map of SNPs might provide an advantage over traditional microsatellite maps but also in what the optimal density of markers might be for each of these pedigree structures.
For all simulations, we segregated 100-cM chromosomes in 200 pedigrees. Pedigrees consisted of either a sib pair with parental genotypes or a sib pair, trio, or quad without parental genotypes. In the case of the microsatellite maps, we simulated equally spaced markers every 0.5, 1, 2, 3, 4, 5, 6, 7, 8, 9, or 10 cM, with each marker consisting of 2, 3, 4, 5, 10, or 20 equally frequent alleles. In the case of the SNP maps, we varied the spacing of the markers so that SNPs were equally spaced every 0.1, 0.2, 0.5, or 1 cM. We also varied the minor-allele frequency (MAF) of the SNPs across seven levels: 0.5, 0.4, 0.3, 0.2, 0.1, 0.05, and 0.01. This range of parameters encompasses all currently available SNP and microsatellite linkage panels, including the commercially available 4,600- and 10,000-SNP panels (Oliphant et al. 2002; Matsuzaki et al. 2004), the 300–400-microsatellite sets widely used in the Applied Biosystems and Cooperative Human Linkage Center collections (Dib et al. 1996; Broman et al. 1998), and the recent deCODE set of 1,068 microsatellite markers (Helgadottir et al. 2004). Information content was computed using the program MERLIN (Abecasis et al. 2002) and was averaged over the 100 simulations either at the marker closest to the middle of the chromosome or halfway between the two markers closest to the middle of the chromosome (Kruglyak 1997).
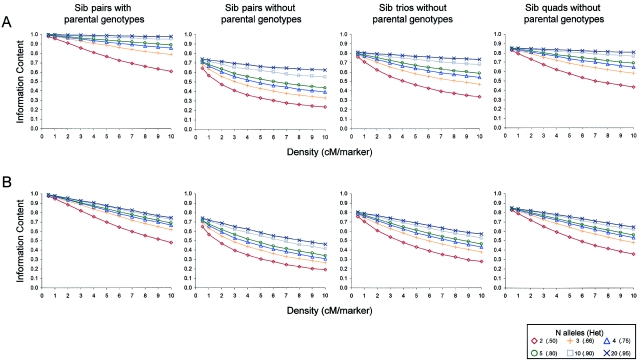
Figure 1 displays the information content associated with microsatellite maps across the different heterozygosities, marker densities, and pedigree structures. As expected, information content increased with heterozygosity and was greatest at markers and lowest in between markers. Information content also increased with marker density, although this depended strongly on the availability of parental genotypes. When parents were genotyped, a density of 1 microsatellite every 1 or 2 cM was sufficient to extract nearly 100% of the inheritance information from the map (see left-hand panels in fig. 1). Thus, when parental genotypes are available, there is little point in genotyping at a density >1 microsatellite/2 cM. However, most linkage studies have employed a sparse map of 300–400 microsatellite markers, which are spaced every 10 cM, on average, across the genome (Altmüller et al. 2001). With this map, the information content dipped to ∼70% in between markers. Even recent scans that have employed a denser panel of ∼1,600 microsatellite markers from the deCODE set (i.e., ∼1 marker/3 cM) do not quite extract the maximum amount of inheritance information and could benefit from an increase in marker density (e.g., Helgadottir et al. 2004).
Figure 1.
Information content for microsatellites, as a function of marker density (X-axis) and marker heterozygosity (colored lines). Information content is calculated at the middle marker of the chromosome (A) and halfway between the two middle markers (B).
In contrast, when parental genotypes were unavailable, the information content associated with the highest density of microsatellites we examined was only ∼70%—approximately the same as that associated with a sparse map of microsatellite markers when parents were genotyped. We note that, although it would be theoretically possible to examine higher densities of microsatellite markers in our simulations, this would be unrealistic, since the density of microsatellites in the human genome is not much greater than 1 marker/0.5 cM. Most alarming, the information content associated with a traditional map of microsatellites (i.e., 1 marker/10 cM) was as low as ∼30% in between markers. This figure is dramatically lower than the figure of 58% reported by Kruglyak (1997) in the case of cousin pairs with parental genotypes available. Since the expected LOD score, and therefore the power of linkage analysis, is proportional to the amount of information extracted from the map (Kruglyak 1997), this result suggests that the majority of sib-pair linkage studies that have used the typical sets of 300–400 microsatellite markers have been seriously underpowered.
A previous study by Kruglyak and Lander (1995) reported trends similar to our results, but with higher values for information content. For example, in the case of sib pairs without parental genotypes, Kruglyak and Lander (1995) reported that the information content associated with a microsatellite map of 1 marker/10 cM was >60% (as compared with our figure of ∼30%). The reason for this discrepancy is that Kruglyak and Lander (1995) used an older definition of information content that was based on the variance associated with the distribution of estimated identical-by-descent probabilities. This has since been shown to be inferior to an entropy-based measure (the classical measure of information content) that scales linearly with the expected LOD score (Kruglyak 1997). We used this more-appropriate entropy measure, as implemented in MERLIN (Abecasis et al. 2002).
Table 1 displays the information content associated with SNP maps as a function of marker density, allele frequency, and pedigree structure. Increasing the density of SNPs has little effect when parents have been genotyped, since, even at relatively low densities (e.g., 1 SNP/cM [∼3,000 SNPs genomewide]), the majority of inheritance information has been extracted from the pedigree. Therefore, if parents can be genotyped, a sparse map of SNPs should suffice. In contrast, when parental genotypes were not available, increasing the marker density significantly increased the amount of inheritance information extracted—in some cases, by ⩾20%. This effect was most marked for sib pairs and decreased as more siblings were added to the pedigree. This is expected, since typing additional siblings increases certainty about inheritance, even at sparse marker densities. We note that when parents were not typed, increasing the density of markers beyond ∼2–5 SNPs/cM (6,000–15,000 SNPs total) produced increasingly diminishing returns. In the end, it will be the investigator who decides whether the additional cost associated with genotyping at a higher density is worth the small gain in information. Finally, we note that, except in the case of rare SNPs (<5% MAF), allele frequency was far less important in determining information content than SNP density (Kruglyak 1997).
Table 1.
Information Content Calculated at SNP Markers as a Function of Marker Density, MAF, and Pedigree Structure[Note]
|
Information Content for SNPs with MAF of |
|||||||
| Pedigree Structureand Map Density | .5 | .4 | .3 | .2 | .1 | .05 | .01 |
| Sib pairs with parental genotypes: | |||||||
| 1 SNP/1 cM | .957 (.944) | .954 (.942) | .944 (.933) | .918 (.910) | .837 (.831) | .704 (.700) | .297 (.297) |
| 1 SNP/.5 cM | .980 (.974) | .979 (.974) | .973 (.967) | .959 (.954) | .918 (.915) | .836 (.834) | .468 (.468) |
| 1 SNP/.2 cM | .992 (.990) | .992 (.990) | .990 (.988) | .985 (.983) | .969 (.968) | .935 (.935) | .706 (.706) |
| 1 SNP/.1 cM | .996 (.995) | .996 (.995) | .994 (.993) | .993 (.992) | .985 (.984) | .968 (.968) | .840 (.840) |
| Sib pairs without parental genotypes: | |||||||
| 1 SNP/1 cM | .568 (.563) | .562 (.557) | .542 (.538) | .504 (.501) | .417 (.415) | .324 (.323) | .117 (.117) |
| 1 SNP/.5 cM | .641 (.638) | .638 (.636) | .623 (.620) | .594 (.592) | .521 (.520) | .437 (.436) | .194 (.194) |
| 1 SNP/.2 cM | .703 (.702) | .703 (.702) | .693 (.692) | .670 (.669) | .635 (.634) | .572 (.571) | .340 (.340) |
| 1 SNP/.1 cM | .725 (.725) | .720 (.720) | .723 (.722) | .710 (.710) | .684 (.684) | .645 (.645) | .455 (.455) |
| Sib trios: | |||||||
| 1 SNP/1 cM | .709 (.703) | .703 (.697) | .691 (.685) | .654 (.650) | .567 (.565) | .451 (.450) | .173 (.173) |
| 1 SNP/.5 cM | .760 (.757) | .757 (.754) | .749 (.747) | .727 (.725) | .669 (.668) | .582 (.581) | .284 (.284) |
| 1 SNP/.2 cM | .792 (.791) | .793 (.792) | .787 (.786) | .778 (.777) | .752 (.752) | .704 (.704) | .465 (.465) |
| 1 SNP/.1 cM | .803 (.803) | .803 (.802) | .799 (.799) | .795 (.795) | .785 (.784) | .757 (.757) | .594 (.594) |
| Sib quads: | |||||||
| 1 SNP/1 cM | .796 (.789) | .793 (.786) | .779 (.773) | .751 (.747) | .672 (.668) | .548 (.546) | .218 (.217) |
| 1 SNP/.5 cM | .827 (.824) | .827 (.824) | .819 (.816) | .805 (.802) | .761 (.759) | .682 (.681) | .353 (.353) |
| 1 SNP/.2 cM | .845 (.843) | .844 (.843) | .842 (.841) | .837 (.835) | .821 (.820) | .785 (.785) | .560 (.560) |
| 1 SNP/.1 cM | .849 (.849) | .850 (.849) | .848 (.847) | .846 (.845) | .838 (.838) | .822 (.822) | .687 (.687) |
Note.— Values inside parentheses refer to information content calculated halfway between the two middle markers.
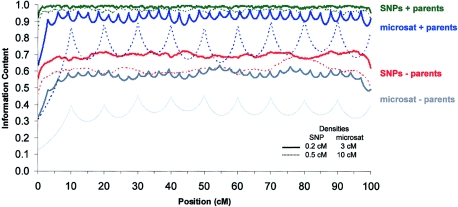
Which is superior in terms of extracting inheritance information—a dense map of SNPs or a map of microsatellites? A comparison of figure 1 and table 1 shows that, in most cases, a very dense map of SNPs (i.e., 1 SNP/0.1 cM) performs similarly to, or only marginally better than, a relatively dense map (i.e., 1 marker/0.5 cM) of microsatellite markers. It is important to note that a dense map of SNPs extracts considerably more information than a sparse map of 300–400 microsatellites (fig. 2). For example, in the case of sib pairs without parental genotypes, reanalysis with a map consisting of 5 SNPs/cM (∼15,000 SNPs) across the genome, which is close to the density offered by some current gene chips (Matsuzaki et al. 2004), would approximately double the inheritance information extracted from the sib pair. Such a map of SNPs would offer greater power than that associated with the densest microsatellite panels currently available (fig. 2). SNPs also have some advantages relative to microsatellites, in that they are associated with a lower genotype error (Kennedy et al. 2003) and are amenable to automation and thus may be cheaper in terms of cost and labor.
Figure 2.
Information content associated with a single 100-cM simulated region for a variety of SNP and microsatellite panels. Each line is representative of a marker panel currently available. Broken lines represent sparse marker densities (1 SNP/0.5 cM or 1 microsatellite/10 cM), and unbroken lines represent dense maps (1 SNP/0.2 cM or 1 microsatellite/3 cM). All simulations were conducted for one sib pair per family; color coding shows the presence or absence of parental genotypes, as labeled in the margin. All SNPs had MAFs of 30%, and all microsatellites had five equally frequent alleles (or heterozygosities of 0.80).
These results point to some clear guidelines for genotyping in linkage studies, but it is important to note some assumptions on which they are based. First, we have assumed that an accurate genetic map of SNP markers is available, when this may not be the case in reality. Misspecification of genetic distances may result in decreased power to detect linkage (Daw et al. 2000). Although locations of SNPs could be interpolated by use of currently available maps, the best option would be the construction of a genetic map of SNPs like the deCODE microsatellite map (Kong et al. 2002). Also, we have assumed the absence of linkage disequilibrium in the calculation of information content at very high marker densities. The software package MERLIN uses a modification of the Lander-Green algorithm, which assumes linkage equilibrium between genetic markers (Abecasis et al. 2002). It has been demonstrated that this algorithm can give misleading results with missing data in the presence of linkage disequilibrium (Schaid et al. 2002). Although several recent studies have shown that the extent and distribution of linkage disequilibrium is extremely variable throughout the genome, in most cases significant linkage disequilibrium does not influence markers separated by >0.1 cM in outbred populations (Dawson et al. 2002; Phillips et al. 2003; Ke et al. 2004). Last, we have not investigated the effect that genotyping error may have on the results of these simulations. It is well known that multipoint linkage analysis is extremely sensitive to genotyping error and that error rates as small as 1% can significantly decrease the power to detect loci (Douglas et al. 2000; Abecasis et al. 2001). Thus, if an increase in marker density also increases the number of genotyping errors present in the data, the net effect may actually be a decrease in the power to detect linkage. We suggest that the consequences of genotyping error for high-density linkage scans be thoroughly investigated in future studies.
The present findings suggest a number of guidelines for genotyping in linkage studies. First, genotyping parents is the most effective way to ensure that the maximum amount of inheritance information is extracted from any panel of markers. This holds true regardless of marker density and regardless of whether SNPs or microsatellite markers are typed. Of course, it is not always possible to genotype parents, as is often the case in late-onset diseases and psychiatric disorders. One compromise is to genotype additional siblings. Such a strategy not only increases the amount of inheritance information extracted from the marker panel but also provides a more powerful analysis, since more pairwise comparisons are provided in the relationship (Dolan et al. 1999; Williams and Blangero 1999).
Second, performing genomewide linkage analysis by use of a dense map of SNPs is preferable to performing linkage analysis by use of a sparse map of microsatellites. When parental genotypes are available, a moderately dense map of SNPs or microsatellites should suffice (i.e., ∼1 marker/1 cM in the case of SNPs and 1 marker/2 cM in the case of microsatellites). When parental genotypes are unavailable, the higher the density of markers, the better.
Finally, the very low values of information content associated with sparse panels of microsatellite markers suggest that previous linkage studies that have employed these panels would benefit substantially from reanalysis with a dense map of SNPs. This is particularly true for sib-pair studies in which parents have not been genotyped. Several recent studies that have reanalyzed existing microsatellite scans with a denser map of SNPs have found either suggestive or significant linkages missed by the initial scans (John et al. 2004; Middleton et al. 2004). Our results suggest that reanalysis with a denser map of markers will result in a substantial gain in the power to detect linkage.
Acknowledgments
This work was supported by Affymetrix, the Wellcome Trust, the SNP Consortium, the National Institutes of Health (EY-126562 [to L.R.C]), and the Medical Research Council (G9801327).
References
- Abecasis GR, Cherny SS, Cardon LR (2001) The impact of genotyping error on family-based analysis of quantitative traits. Eur J Hum Genet 9:130–134 [DOI] [PubMed] [Google Scholar]
- Abecasis GR, Cherny SS, Cookson WO, Cardon LR (2002) Merlin—rapid analysis of dense genetic maps using sparse gene flow trees. Nat Genet 30:97–101 10.1038/ng786 [DOI] [PubMed] [Google Scholar]
- Altmüller J, Palmer LJ, Fischer G, Scherb H, Wjst M (2001) Genomewide scans of complex human diseases: true linkage is hard to find. Am J Hum Genet 69:936–950 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broman KW, Murray JC, Sheffield VC, White RL, Weber JL (1998) Comprehensive human genetic maps: individual and sex-specific variation in recombination. Am J Hum Genet 63:861–869 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daw EW, Thompson EA, Wijsman EM (2000) Bias in multipoint linkage analysis arising from map misspecification. Genet Epidemiol 19:366–380 [DOI] [PubMed] [Google Scholar]
- Dawson E, Abecasis G, Bumpstead S, Chen Y, Hunt S, Beare DM, Pabial J, et al (2002) A first-generation linkage disequilibrium map of human chromosome 22. Nature 418:544–548 10.1038/nature00864 [DOI] [PubMed] [Google Scholar]
- Dib C, Faure S, Fizames C, Samson D, Drouot N, Vignal A, Millasseau P, Marc S, Hazan J, Seboun E, Lathrop M, Gyapay G, Morissette J, Weissenbach J (1996) A comprehensive genetic map of the human genome based on 5,264 microsatellites. Nature 380:152–154 10.1038/380152a0 [DOI] [PubMed] [Google Scholar]
- Dolan CV, Boomsma DI, Neale MC (1999) A note on the power provided by sibships of sizes 2, 3, and 4 in genetic covariance modeling of a codominant QTL. Behav Genet 29:163–170 10.1023/A:1021687817609 [DOI] [PubMed] [Google Scholar]
- Douglas JA, Boehnke M, Lange K (2000) A multipoint method for detecting genotype errors and mutations in sibling-pair linkage data. Am J Hum Genet 66:1287–1297 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goddard KAB, Wijsman EM (2002) Characteristics of genetic markers and maps for cost-effective genome screens using diallelic markers. Genet Epidemiol 22:205–220 10.1002/gepi.0177 [DOI] [PubMed] [Google Scholar]
- Helgadottir A, Manolescu A, Thorleifsson G, Gretasdottir S, Jonsdottir H, Thorsteinsdottir G, Samani NJ, et al (2004) The gene encoding 5-lipoxygenase activating protein confers risk of myocardial infarction and stroke. Nat Genet 36:233–239 10.1038/ng1311 [DOI] [PubMed] [Google Scholar]
- John S, Shephard N, Liu G, Zeggini E, Cao M, Chen W, Vasavda N, Mills T, Barton A, Hinks A, Eyre S, Jones KW, Ollier W, Silman A, Gibson N, Worthington J, Kennedy GC (2004) Whole-genome scan, in a complex disease, using 11,245 single-nucleotide polymorphisms: comparison with microsatellites. Am J Hum Genet 75:54–64 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ke X, Hunt S, Tapper W, Lawrence R, Stavrides G, Ghori J, Whittaker P, Collins A, Morris AP, Bentley D, Cardon LR, Deloukas P (2004) The impact of SNP density on fine-scale patterns of linkage disequilibrium. Hum Mol Genet 13:577–588 10.1093/hmg/ddh060 [DOI] [PubMed] [Google Scholar]
- Kennedy GC, Matsuzaki H, Dong S, Liu WM, Huang J, Liu G, Su X, Cao M, Chen W, Zhang J, Liu W, Yang G, Di X, Ryder T, He Z, Surti U, Phillips MS, Boyce-Jacino MT, Fodor SP, Jones KW (2003) Large scale genotyping of complex DNA. Nat Biotechnol 21:1233–1237 10.1038/nbt869 [DOI] [PubMed] [Google Scholar]
- Kong A, Gudbjartsson DF, Sainz J, Jonsdottir GM, Gudjonsson SA, Richardsson B, Sigurdardottir S, Barnard J, Hallbeck B, Masson G, Shlien A, Palsson ST, Frigge ML, Thorgeirsson TE, Gulcher JR, Stefansson K (2002) A high-resolution map of the human genome. Nat Genet 31:241–247 [DOI] [PubMed] [Google Scholar]
- Kostanje R, Paigen B (2002) From QTL to gene: the harvest begins. Nat Genet 31:235–236 10.1038/ng0702-235 [DOI] [PubMed] [Google Scholar]
- Kruglyak L (1997) The use of a genetic map of biallelic markers in linkage studies. Nat Genet 17:21–24 10.1038/ng0997-21 [DOI] [PubMed] [Google Scholar]
- Kruglyak L, Lander ES (1995) Complete multipoint sib-pair analysis of qualitative and quantitative traits. Am J Hum Genet 57:439–454 [PMC free article] [PubMed] [Google Scholar]
- Matise TC, Sachidanandam R, Clark AG, Kruglyak L, Wijsman E, Kakol J, Buyske S, et al (2003) A 3.9-centimorgan-resolution human single-nucleotide polymorphism linkage map and screening set. Am J Hum Genet 73:271–284 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuzaki H, Loi H, Dong S, Tsai YY, Fang J, Law J, Di X, Liu WM, Yang G, Liu G, Huang J, Kennedy GC, Ryder TB, Marcus GA, Walsh PS, Shriver MD, Puck JM, Jones KW, Mei R (2004) Parallel genotyping of over 10,000 SNPs using a one-primer assay on a high-density oligonucleotide array. Genome Res 14:414–425 10.1101/gr.2014904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middleton FA, Pato MT, Gentile KL, Morley CP, Zhao X, Eisner A, Brown A, Petryshen TL, Kirby AN, Medeiros H, Carvalho C, Macedo A, Dourado A, Coelho I, Valente J, Soares MJ, Ferreira CP, Lei M, Azevedo MH, Kennedy JL, Daly MJ, Sklar P, Pato CN (2004) Genomewide linkage analysis of bipolar disorder by use of a high-density single-nucleotide-polymorphism (SNP) genotyping assay: a comparison with microsatellite marker assays and finding of significant linkage to chromosome 6q22. Am J Hum Genet 74:886–897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliphant A, Barker DL, Stuelpnagel JR, Chee MS (2002) BeadArray technology: enabling an accurate, cost-effective approach to high-throughput genotyping. Biotechniques Suppl: 56–58, 60–61 [PubMed] [Google Scholar]
- Phillips MS, Lawrence R, Sachidanandam R, Morris AP, Balding DJ, Donaldson MA, Studebaker JF, et al (2003) Chromosome-wide distribution of haplotype blocks and the role of recombination hot spots. Nat Genet 33:382–387 10.1038/ng1100 [DOI] [PubMed] [Google Scholar]
- Schaid DJ, McDonnell SK, Wang L, Cunningham JM, Thibodeau SN (2002) Caution on pedigree haplotype inference with software that assumes linkage equilibrium. Am J Hum Genet 71:992–995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams JT, Blangero J (1999) The power of variance component linkage analysis to detect quantitative trait loci. Ann Hum Genet 63:545–563 10.1046/j.1469-1809.1999.6360545.x [DOI] [PubMed] [Google Scholar]
- Wilson AF, Sorant AJ (2000) Equivalence of single- and multilocus markers: power to detect linkage with composite markers derived from biallelic loci. Am J Hum Genet 66:1610–1615 [DOI] [PMC free article] [PubMed] [Google Scholar]