No “Bias” Toward the Null Hypothesis in Most Conventional Multipoint Nonparametric Linkage Analyses

To the Editor:

We would like to comment on the Schork and Greenwood (2004) article dealing with the inherent “bias” toward the null hypothesis in the context of nonparametric linkage analysis. The authors point out that, in certain situations, a loss of evidence for linkage can result from the practice of assigning expected allele-sharing values to affected relative pairs that are uninformative for their identity-by-descent (IBD) status. They explained this by setting up a likelihood function and studying its properties by simulation, clearly illustrating the negative impact of using expected IBD values for uninformative pairs. However, we would like to point out that their likelihood does not reflect how the majority of nonparametric linkage analysis programs compute statistics in practice. Indeed, the “problem” has been known and well discussed for years. Some of the concerns we discuss here have also been raised by Cordell (2004).

Schork and Greenwood (2004) set up the likelihood formulation as follows. Let n_i be the number of sib pairs sharing i alleles IBD (i=0, 1, or 2). If all families had unambiguous IBD sharing, then the LOD score evaluated at the sharing vector (p₀, p₁, p₂) is calculated as

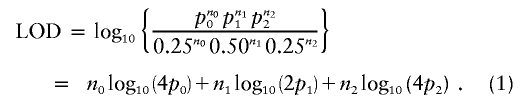In their model, Schork and Greenwood (2004) said that fully uninformative sibling pairs contribute 0.25, 0.50, and 0.25, respectively, to the counts n₀, n₁, and n₂ used in equation (1). If so, then the presence of uninformative sib pairs can lower the LOD score. However, in most software implementations, expected allele-sharing values are not used to compute nonparametric LOD scores. For example, consider the maximum LOD score (MLS) statistic proposed by Risch (1990). Let w_i be the probability of the observed marker phenotypes of the pair, given that they share i alleles IBD (i=0, 1, or 2). Then, the likelihood of the observed marker data for the pair is given by

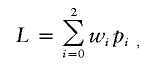where p_i is the posterior probability that the pair shares i alleles IBD, given that both members of the pair are affected. Suppose, in addition, that we know that n_2,1 pairs share either 2 or 1 alleles, n_2,0 pairs share either 2 or 0 alleles, n_1,0 pairs share either 1 or 0 alleles, and n_un is the number of pairs that are fully uninformative. According to Risch (1990), the LOD score can be written as

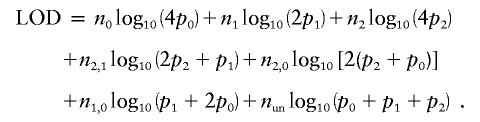Maximizing this likelihood gives consistent and asymptotically unbiased estimates of the IBD-sharing probabilities. Cordell (2004) confirms this by simulation.

To verify that most implementations of nonparametric linkage statistics are not altered by uninformative families, we used FastSLINK (Ott 1989; Weeks et al. 1990; Cottingham et al. 1993) to simulate 200 fully genotyped affected–sib-pair families under disease model 1 of Schork and Greenwood (2004). The disease locus was completely linked to a two-allele marker with equally frequent alleles. We then used a variety of programs to compute linkage statistics on two data sets: (1) all 200 families and (2) the 147 families that remained after removal of the fully uninformative families. As shown in table 1, the majority of the linkage statistics, as implemented in widely used software, are exactly the same for the two data sets.

Table 1.

Comparison of Linkage Statistics Analyses Using All 200 Families and Using Only the 147 Informative Families

	Result for
Statistic and Software	All 200 Families	147 Informative Families	Reference
Mean test Z value:
SIBPAL	14.07	17.56	Haseman and Elston 1972
MLS LOD score (2 df):
SPLINK	36.34	36.34	Holmans 1993
MLS LOD score (1 df):
GeneHunter	22.20	22.20	Kruglyak and Lander 1995
ASPEX sib_phase	22.20	22.20	Hinds and Risch 1996
NPL Sall Z score:
GeneHunter	6.70	7.82	Kruglyak et al. 1996
Allegro	7.82	7.82	Gudbjartsson et al. 2000
Merlin	7.82	7.82	Abecasis et al. 2002
GeneHunter-Plus Sall LOD score:
GeneHunter-Plus	22.20	22.20	Kong and Cox 1997
Allegro	22.20	22.20	Gudbjartsson et al. 2000
Merlin	22.20	22.20	Abecasis et al. 2002

There are two statistics in table 1 that are less significant when all 200 families are used than when the uninformative families are removed. These two statistics are the GeneHunter NPL S_all Z score and the SIBPAL mean test Z value. In both of these cases, the reduction in evidence for linkage is caused by the use of the “perfect data approximation” to compute the variance of the statistics. The “perfect data approximation” performs well if most of the families are informative for IBD sharing, but, as the proportion of uninformative families increases, it becomes increasingly conservative, leading to a loss of power (Kruglyak et al. 1996). In fact, the loss of power due to “bias” that Schork and Greenwood (2004) identify is, mathematically, exactly the samething as the loss of power due to the “perfect data approximation.”

The negative effects of the “perfect data approximation” can be illustrated by a simple example. Consider the sib-pair IBD-sharing statistic

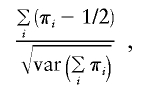where π_i is the estimated proportion of alleles shared IBD for the ith affected sib pair. Suppose we have two data sets: (1) 50 fully informative affected–sib-pair families and (2) 50 fully informative and 50 uninformative families. Suppose π_i in our fully informative families takes on the values 0, 1/2, and 1, with probabilities1/8, 1/2, and 3/8, respectively, whereas π_i is 1/2 in our uninformative families. The numerator of the statistic is identical for both data sets. However, different approaches to computing the variance in the denominator can lead to different statistic values for the two data sets. Under the “perfect data approximation,” the value of the statistic is 2.50 for the first data set and 1.77 for the second data set—an undesirable reduction in the evidence for linkage. Use of the correct variance (given that the number of uninformative families remains constant) leads to statistic values of 2.50 for both data sets. Another option is to use the empirical variance, which reflects the alternative hypothesis rather than the null hypothesis and can be quite powerful; the empirical variance gives an expected IBD-sharing statistic of 2.50 for both example data sets. A score test using empirical variances was one of the best statistics in a recent evaluation of methods for QTL mapping using selected sibling pairs (T.Cuenco et al. 2003).

To avoid the negative consequences of using the “perfect data approximation,” Kong and Cox (1997) proposed a nonparametric statistic that performs much better in the presence of uninformative families. This statistic has been implemented in GeneHunter-Plus (Kong and Cox 1997), Allegro (Gudbjartsson et al. 2000), and Merlin (Abecasis et al. 2002) and, as illustrated by our simple simulation experiment in table 1, is insensitive to the presence of fully uninformative families. Similarly, in the context of the Haseman-Elston (HE) test (Haseman and Elston 1972), in which trait values are regressed on IBD sharing, the problem of using estimated IBD sharinghas long been recognized. For example, Kruglyak and Lander (1995) developed a missing-value regression approach to compute a modified HE test that has much better behavior in the presence of uninformative families than the original test.

Whereas it is always useful to remind the scientific community that proper statistical analyses of linkage data requires deep insight into the potential weaknesses of the chosen methodology and software implementation, we feel that Schork and Greenwood’s concerns are overstated. Indeed, as we have shown, not only has this potential problem been known since at least the mid-1990s, but, in addition, the majority of implementations of linkage statistics in commonly used software do not suffer from this “bias” toward the null hypothesis in the presence of uninformative families. Furthermore, the use of highly informative markers in a multipoint analysis will result in very few families being fully uninformative for IBD sharing.