Increasing the Power and Efficiency of Disease-Marker Case-Control Association Studies through Use of Allele-Sharing Information

Abstract

Case-control disease-marker association studies are often used in the search for variants that predispose to complex diseases. One approach to increasing the power of these studies is to enrich the case sample for individuals likely to be affected because of genetic factors. In this article, we compare three case-selection strategies that use allele-sharing information with the standard strategy that selects a single individual from each family at random. In affected sibship samples, we show that, by carefully selecting sibships and/or individuals on the basis of allele sharing, we can increase the frequency of disease-associated alleles in the case sample. When these cases are compared with unrelated controls, the difference in the frequency of the disease-associated allele is therefore also increased. We find that, by choosing the affected sib who shows the most evidence for pairwise allele sharing with the other affected sibs in families, the test statistic is increased by >20%, on average, for additive models with modest genotype relative risks. In addition, we find that the per-genotype information associated with the allele sharing–based strategies is increased compared with that associated with random selection of a sib for genotyping. Even though we select sibs on the basis of a nonparametric statistic, the additional gain for selection based on the unknown underlying mode of inheritance is minimal. We show that these properties hold even when the power to detect linkage to a region in the entire sample is negligible. This approach can be extended to more-general pedigree structures and quantitative traits.

Introduction

Mapping studies of complex disease often involve case-control disease-marker association studies (Risch 2000; Cardon and Bell 2001). A sample of affected cases is compared with a suitable control group to test for association between allelic variants and disease status. These studies currently are conducted in candidate genes and linkage candidate regions and, as our understanding of variation in the genome improves (Patil et al. 2001; Dawson et al. 2002; Gabriel et al. 2002), soon will be conducted genomewide. Usually, to canvass adequately a region of interest for association, many markers must be genotyped. The exact density of markers required to sample the variation adequately depends on the extent and pattern of linkage disequilibrium in the region (Abecasis et al. 2001; Carlson et al. 2003). In addition, because modest effect sizes are expected for loci predisposing to complex diseases (Risch 2000), hundreds or even thousands of individuals may be required to obtain sufficient power to detect association. Hence, depending on the size of the region, association studies may require the genotyping of hundreds of thousands of markers in thousands of individuals. Although much progress has been made in developing accurate, high-throughput SNP genotyping (Sachidanandam et al. 2001; Syvanen 2001; Oliphant et al. 2002; Olivier et al. 2002), association studies can be costly and require substantial effort, making efficient study design important.

One strategy for improving the power of genetic studies is to select individuals who are most likely to carry genetic risk factors. These genetically loaded individuals or families presumably provide a stronger signal and facilitate identification of the variant(s) responsible for disease. Standard designs include choosing individuals with an early age at onset (e.g., Hall et al. 1992), a more severe form of the disease (e.g., Goldstein et al. 1987), and/or a family history of disease (e.g., Go et al. 1983; Valle et al. 1998). Identifying genetically loaded individuals in this manner will continue to be an attractive approach for disease-marker association studies, in particular. Risch and Teng (1998) showed that affected individuals with at least one affected sibling carried more copies of the disease allele, on average, than did singleton cases, resulting in increased power of association tests when cases with affected sibs are chosen for study.

Selecting individuals with multiple affected family members is effective in part because chromosomes that occur in multiple affected individuals are more likely to carry disease alleles. An even more effective approach to obtaining a case sample enriched for genetic risk factors may be to select individuals that carry these shared chromosomes. Allele-sharing information could be used to identify families showing excess allele sharing in a region of interest and/or the individuals within each family who show the most allele sharing with other affected family members. By carefully selecting families and/or individuals on the basis of increased allele sharing, we might increase the frequency of the disease-associated allele in the case sample and thereby increase the power of association studies. Using allele-sharing information may also be a more efficient use of genotyping resources. In addition to defining a potentially more informative sample, a strategy that uses individuals only from the families with excess allele sharing requires fewer individuals be genotyped. Given fixed genotyping resources, this allows more markers to be screened for association, providing a more dense coverage of a region.

Evidence for linkage to a region of interest in the overall sample is not required to use allele-sharing information to select cases. However, the application of a case-selection approach that uses allele-sharing information is most natural in the context of a linkage candidate region, where the case and control samples may be derived from families in the linkage sample, independent samples, or a combination of the two. In the case of sibship designs, perhaps the simplest (and often the default) approach is to type one or more randomly selected affected individuals from each sibship in the linkage sample along with a set of suitably chosen controls. Although this is certainly reasonable, we might obtain a more informative sample for detecting disease-marker association by exploiting the evidence for linkage to the region.

Selecting families that show evidence for linkage to a region for further study has been suggested and implemented previously in the context of linkage candidate regions (e.g., Horikawa et al. 2000; Van Eerdewegh et al. 2002; Kim et al. 2003), but the properties of the approach have not been evaluated systematically. Davis et al. (2001) used information from multiple covariates to identify families that contributed to the evidence for linkage to the region for further study. In contrast, to our knowledge, using allele-sharing information to select individuals within each family who show maximal sharing with other affected individuals is a new approach and has been neither applied nor described.

In this article, we compare three case-selection strategies that use allele-sharing information with a strategy that selects a single individual from each family at random when affected sibships have been collected for study. Specifically, we compare the strategies in terms of statistics of the form 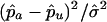, where 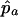and are the estimated marker allele frequencies in the affected cases and unaffected controls, respectively, and 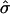is the estimated SD of the difference. Because an increase in 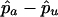due to selection of sibships may result in a sample size reduction that increases 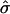, we investigate whether the increase in is enough to compensate for the loss in sample size. We evaluate multiple disease models, varying the frequency of the disease-predisposing variant and its impact on disease risk. We show that enriching the case sample for alleles that are shared by multiple affected individuals can increase the power and genotyping efficiency of case-control studies in the context of affected sibship designs. We show that this is true even when the power to detect linkage to a region in the entire sample is negligible. We also describe how the approach might be extended to more general pedigree structures, quantitative traits, and DNA pooling studies.

Methods

We consider the problem of selecting a set of unrelated cases (one per family) from a set of sibships, each with two or more affected individuals. These cases could then be genotyped and used to evaluate evidence for association in a typical case-control setting. (See the “Discussion” section for comments on markers typed in multiple affected individuals per family.) Our goals are to choose individuals who maximize the expected allele-frequency difference between cases and controls and to use genotyping resources efficiently.

Definitions and Assumptions

By either ignoring or using allele-sharing information in choosing affected sibships and affected individuals within those sibships, we consider four case-selection strategies: (i) one sib randomly chosen from each sibship (“all-random,” or AR), (ii) one sib with the most evidence for sharing with other sibs chosen from each sibship (“all-best,” or AB), (iii) one sib randomly chosen only from sibships with evidence for linkage (“linked-random,” or LR), and (iv) one sib with the most evidence for sharing with other sibs chosen only from sibships with evidence for linkage (“linked-best,” or LB).

For simplicity, we assume that a sample of unrelated, unaffected individuals well matched to the case individuals is available to serve as controls. Let p be the population allele frequency of the disease-predisposing variant D, and let q=1-p. Let p_a and p_u be the frequency of D in affected cases and unaffected controls, respectively, and let p_a|SS be the expected frequency of D in cases selected by strategy SS∈{AR,AB,LR,LB}. Similarly, let Δp_SS be the expected difference in the disease-allele frequency between cases and controls and N_SS be the expected number of cases for strategy SS. For simplicity, we assume that the number of controls, N, is equal to the number of affected sibships, so that N=N_AR=N_AB⩾N_LR=N_LB.

We consider one-locus, two-allele disease models with penetrances f_i=Pr(Disease|i copiesof D), population prevalence K=q²f₀+2pqf₁+p²f₂ and attributable fraction . For dominant, additive, and recessive models, setting K, AF, and p completely specifies the disease model. By definition, f₀=K(1-AF). For dominant models, 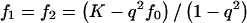. For additive models, 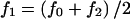and 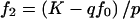. For recessive models, f₁=f₀ and . The genotype relative risk associated with having i copies of the disease allele compared with 0 copies is GRR_i=f_i/f₀.

Selecting Sibships on the Basis of Allele Sharing

To identify sibships showing evidence for linkage, we use identity-by-descent (IBD) sharing scores. Several such scores have been proposed, with the goal of identifying families that demonstrate excess allele sharing consistent with linkage (e.g., Whittemore and Halpern 1994; McPeek 1999; Sengul et al. 2001). Regardless of which score, S, is chosen, the conditional expected sharing score (given the marker data for the affected sibship), S_i, is calculated for each sibship i and standardized under the null hypothesis of no linkage. We define a sibship as showing evidence for linkage if the standardized sharing score NPL=[S-E₀(S)]/SD₀(S) for the sibship is (i) strictly >0, corresponding to more IBD sharing than expected under no linkage or (ii) ⩾0, which excludes only those families with less sharing than expected under no linkage. The first definition requires clear excess allele sharing but results in a smaller sample than does the second definition. Here, E₀(S) and SD₀(S) represent the mean and standard deviation of the sharing score S under no linkage.

We employ the scores S_pairs and S_all (Whittemore and Halpern 1994). S_pairs measures pairwise IBD allele sharing among all affected members of a family. In the case of sibships, S_pairs can be written as 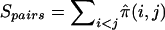, where 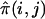is the estimated proportion of alleles shared IBD by sibs i and j, and the sum is taken over all sib pairs (i,j) in the sibship. The alternative score, S_all, gives more weight to sibships in which multiple sibs share the same allele IBD. S_all is defined as 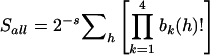, where h is one of the 2^s possible sets of alleles generated by choosing one allele from each of the s affected sibs within the sibship, and b_k(h) is the number of times parental allele k appears in h. For sib pairs and trios, S_all is equal to S_pairs after standardization (Sengul et al. 2001).

Selecting Individual Sib(s) with the Most Evidence for Sharing with other Affected Sibs

Once a sibship has been chosen for inclusion (either because all families will be included or on the basis of allele sharing), we next choose which individual from that sibship to include. We define the sib-specific S_pairs score for sib j as , where the sum is taken over only those sib pairs that include sib j. Similarly, we define a sib-specific S_all score as 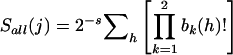, where the product is over only the two alleles of sib j instead of over all four parental alleles. We identified the sib(s) with the highest sib-specific sharing score as the “best” sib(s). For sib pairs, both sibs have the same sharing score, and so there is no difference between the “best” and “random” strategies.

Table 1 displays the parental allele assignments that correspond to unique IBD configurations for sibship sizes s=2–5 (Sengul et al. 2001). Columns 2 and 3 indicate whether the NPL_pairs and NPL_all scores for each configuration are greater (+), less than (−), or equal to (0) 0. Column 4 indicates which sibs have the highest sib-specific sharing score for each configuration. For all configurations but one, the sib-specific S_pairs(j) and S_all(j) scores select the same sib(s). As a specific example, table 2 displays the sibship S_pairs score, sib-specific S_pairs(j) scores, and expected disease-allele frequencies under a disease model for each unique IBD configuration for an affected sib trio.

Table 1.

Sibship IBD Configurations^[Note]

No. of Affected Sibsand Configuration	NPLpairsa	NPLalla	BestSib(s)	Pr0b
2:
13 13	+	+	13	.250
13 14	0	0	13 14	.500
13 24	−	−	13 24	.250
3:
13 13 13	+	+	13	.063
13 13 14	+	+	13	.375
13 13 24	−	−	13	.188
13 14 23	−	−	13	.375
4:
13 13 13 13	+	+	13	.016
13 13 13 14	+	+	13	.125
13 13 14 14	+	+	13 14	.094
13 13 13 24	0	−	13	.063
13 13 14 23	0	−	13	.188
13 13 14 24	−	−	13 14c	.375
13 13 24 24	−	−	13 24	.047
13 14 23 24	−	−	Any	.094
5:
13 13 13 13 13	+	+	13	.004
13 13 13 13 14	+	+	13	.039
13 13 13 14 14	+	+	13	.078
13 13 13 13 24	+	+	13	.020
13 13 13 14 23	+	+	13	.078
13 13 13 14 24	0	−	13	.156
13 13 14 14 23	0	−	13	.234
13 13 13 24 24	−	−	13	.039
13 13 14 24 24	−	−	14	.117
13 13 14 23 24	−	−	13	.234

Note.— Alleles 1 and 2 are maternal, and alleles 3 and 4 are paternal.

^aIBD configuration has NPL score less than (−), equal to (0), or greater than (+) 0.

^bProbability of IBD configuration under the null hypothesis of no linkage.

^cThe 13 genotype has the highest S_pairs(j) score, and the 14 genotype has the highest S_all(j) score.

Table 2.

S_pairs, Sib-Specific S_pairs(j), and Disease-Allele Frequencies with Three Affected Sibs^[Note]

Sib Configuration
Sib A	Sib B	Sib C	Spairs	Spairs(A)	Spairs(B)	Spairs(C)	pa(A)	pa(B)	pa(C)	Pr(Configuration|Model)
13	13	13	3	2	2	2	.40	.40	.40	.067
13	13	14	2	1.5	1.5	1	.37	.37	.33	.384
13	13	24	1	1	1	0	.33	.33	.26	.183
13	14	23	1	1	.5	.5	.33	.29	.29	.366

Note.— Additive disease model: K=.10, AF=.15, and p=.20, corresponding to f₀=.0850, f₁=.1225, and f₂=.1600.

Comparison of Selection Strategies

To compare the strategies, we considered three criteria. First, we computed Δp_SS=p_a|SS-p_u and the proportional increase in Δp_SS for each of the allele sharing–based strategies (AB, LR, and LB) compared with the AR strategy (e.g., 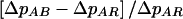). Second, as a measure of the relative power of the selection strategies, we computed the ratios of the test statistics for each of the strategies to the statistic for the AR strategy (e.g., T²_AB/T²_AR). We considered test statistics of the form

These statistics follow a χ² distribution asymptotically and increase linearly with sample size. Third, we computed the per-genotype contribution to each test statistic as I_SS=T²_SS/(N_SS+N), as a measure of the informativeness of the selected individuals, and computed the ratios of the per-genotype contributions (e.g., I_AB/I_AR) to compare the efficiency of the strategies in terms of use of genotyping resources.

Case Disease-Allele Frequencies when IBD Is Known: Analytic Calculations

We initially considered the situation in which IBD at the disease locus is known. For affected sibships of size s=2–5 and for each SS and disease model, we calculated the expected value of the disease-allele frequency p in the affected sib selected for genotyping, p_a|SS(s), under a given disease model as

where n_D|SS is the expected number of copies of D in the individual selected by strategy SS for inheritance vector v, and the sum is taken over all possible inheritance vectors for a sibship of size s. An inheritance vector specifies the grandparental origin of each allele in a sibship and therefore captures the IBD information for the sibship. To calculate the allele frequency for sibships selected on the basis of allele sharing, we restrict the sum in equation (1) to inheritance vectors in L={v:NPL(v)>0} or {v:NPL(v)⩾0}. Similarly, the proportion of sibships included for the two “linked” strategies can be written as . Let g_f and g_m be the ordered genotypes for the father and mother, respectively, and let Pr(g_f), Pr(g_m), and Pr(v) be the prior probabilities of g_f, g_m, and v.

Since

and Pr(v)=4^-s for all v,

The Pr(sib j affected|v,g_f,g_m) terms are simple functions of the penetrance functions f_i.

We calculated p_a|SS(s) for models with prevalence K=.01–.10 at .01 intervals, AF=.05–1 at .05 intervals, and disease-allele frequency p=.0025–.9975 at .0025 intervals. Because of our interest in complex diseases, we focus our attention on models for which the genotype relative risk GRR₂⩽3. We also repeated the calculation of p_a|SS(s) for each SS under the assumption that the sibship included 1 or 2 unaffected sibs in addition to the s=2–5 affected sibs.

Case Disease-Allele Frequencies when IBD Is Unknown: Simulation

Since IBD is generally not known with certainty for studies of affected sibships, we performed computer simulations to compare the four case-selection strategies when the IBD status of the sibs is incompletely known because of partially informative markers and missing parental genotypes. Table 3 describes the one-locus, two-allele disease models we considered. We chose these models to examine the properties of the strategies over a range of values of AF, p, GRR₂, and sibling recurrence risk ratio, λ_s, when each of these characteristics was held constant.

Table 3.

Characteristics of Simulated Disease Models^[Note]

Model	K	AF	p	GRR2	λs
I:
Dominant	.10	.20	.15	1.9	1.1
Additive	.10	.20	.15	2.7	1.1
Recessive	.10	.20	.15	12.1	1.5
II:
Dominant	.10	.50	.25	3.3	1.1
Additive	.10	.50	.25	5.0	1.2
Recessive	.10	.50	.25	17.0	2.3
III:
Dominant	.11	.54	.35	3.0	1.1
Additive	.09	.41	.35	3.0	1.1
Recessive	.09	.20	.35	3.0	1.1

Note.— Additional settings were considered for analytical calculations.

For each of the disease models in table 3, we generated 1,000 replicate samples of 500 affected sibships with s=2–4 affected sibs. We assumed a 100-cM map of markers with four equally frequent alleles (H=.75) evenly spaced at a 5- or 1-cM density, with the disease locus centered between two markers in the middle of the map. We used the Haldane (1919) no-interference map function to convert map distances to recombination fractions. We generated parental chromosomes on the basis of the population allele frequencies and under the assumption of Hardy-Weinberg and linkage equilibrium, and we generated offspring chromosomes allowing for recombination according to the genetic map. We determined whether each individual was affected on the basis of the penetrance function for his/her genotype and kept only those sibships with all siblings affected. For linkage analyses, we removed the disease locus genotypes and all parental genotypes.

We calculated the Kong and Cox (1997) LOD scores for the entire sample and for each sibship through use of the Merlin software package (Abecasis et al. 2002; Merlin Web site). Since it is typical to examine regions near modest linkage peaks in complex disease genome scans, we initially simulated samples until we had 1,000 replicates with maximum LOD score (MLS) ⩾1. We also performed the simulations with no minimum threshold requirement for the MLS. For each replicate, we based the selection of cases on allele sharing information at the position of the MLS and then also at the true disease-locus position. This procedure allowed us both to mimic a typical follow-up study and to compare selection at the MLS to that at the true position. Because the distribution of NPL_pairs scores is not discrete when IBD is estimated rather than known, capturing families that have scores near that expected under no linkage (equivalent to IBD-known NPL_pairs scores of 0) requires using a cutoff that is slightly <0 for sibship sizes 2 and 4. We investigated several such cutoffs and found that results were very similar when selection was based on a cutoff between −0.25 and −0.45, and we report results based on a cutoff of −0.35.

Results

IBD Known at Disease Locus: Analytic Calculations

In what follows, we give the results for selection based on S_pairs and sib-specific S_pairs(j) scores and note differences associated with using the S_all and S_all(j) scores. Figure 1 shows the results for each comparison criterion for additive models with a GRR₂⩽3. Results were similar for dominant and recessive models (see figs. A and B [online only]).

Figure 1.

Additive models with GRR₂ ⩽3, mean ± 2 SD. A, Proportional increase in disease-allele frequency difference for sharing-based strategies compared with the AR strategy. B, Ratio of test statistics for sharing-based strategies to test statistic for the AR strategy. C, Ratio of per-genotype information for sharing-based strategies to per-genotype information for the AR strategy.

Figure A.

Dominant models with GRR₂ ⩽3, mean ± 2 SD. A, Proportional increase in disease-allele frequency difference for sharing-based strategies compared with the AR strategy. B, Ratio of test statistics for sharing-based strategies to test statistic for the AR strategy. C, Ratio of per-genotype information for sharing-based strategies to per-genotype information for the AR strategy.

Figure B.

Recessive models with GRR₂ ⩽3, mean ± 2 SD. A, Proportional increase in disease-allele frequency difference for sharing-based strategies compared with the AR strategy. B, Ratio of test statistics for sharing-based strategies to test statistic for the AR strategy. C, Ratio of per-genotype information for sharing-based strategies to per-genotype information for the AR strategy.

Proportion of Sample Size Retained for “Linked” Strategies

Under the null hypothesis of no linkage, 25% of sib pairs have NPL_pairs >0. The corresponding proportions are 44%, 23%, and 22% for sibships with s=3, 4, and 5 affected sibs, respectively. For NPL_pairs ⩾0, these proportions are 75%, 44%, 48%, and 61%. Given linkage, these proportions are increased. Despite these increases, for most of the disease models we considered, unless the sibship sample is sufficiently large that ⩽25% of the sample provides adequate power, the reduction in sample size for the NPL_pairs >0 selection outweighs any increase in the disease-allele frequency for the two “linked” strategies for sibship sizes of 2, 4, and 5. Hence, we give results for the less restrictive NPL_pairs ⩾0 selection for the remainder of this article, unless otherwise noted.

Difference in Disease-Allele Frequency between Cases and Controls

The expected difference in the disease-allele frequency between cases and controls, Δp, is increased for the two “best” strategies compared with the AR strategy for every disease model in which AF is <.95. In addition, with the exception of dominant models with p>.98 for s=5 sibs, Δp is greater for the LR strategy than for the AR strategy for all models with GRR₂ ⩽3. It is surprising that the LR strategy becomes less useful as the GRR₂ increases. Still, disease models with 3<GRR₂⩽10 for which Δp decreases for the LR strategy are generally limited to models with large AFs (>90% have AF >.50).

Regardless of selection strategy, the mean expected disease-allele frequency difference between cases and controls increases with sibship size (data not shown). Within each sibship size, the largest average Δp is seen for the LB strategy. Table 4 gives specific examples of how the disease frequency increases when the case group is enriched for cases with additional affected family members and evidence for sharing with other affected siblings for several models with disease prevalence K=.10 and AF=.15. Although the absolute increases in Δp can be small, the proportional increases in Δp are meaningful (fig. 1A). The proportional increase in Δp is largest for small values of AF and GRR₂.

Table 4.

Disease-Allele Frequency in Controls and Selected Case Groups^[Note]

	Frequency in Group
p andModel	Control	SingletonCase	ASPCase	LinkedASPCase	AffectedTrioCase	AffectedTrio BestCase	LinkedAffectedTrio Case	LinkedAffected TrioBest Case
.20:
Dominant	.194	.253	.282	.291	.309	.324	.333	.341
Additive	.193	.260	.295	.306	.331	.348	.361	.371
Recessive	.187	.320	.467	.506	.646	.690	.750	.778
.50:
Dominant	.497	.525	.536	.540	.547	.553	.556	.559
Additive	.496	.538	.556	.562	.574	.583	.589	.595
Recessive	.492	.575	.618	.631	.662	.681	.697	.709

Note.— K=.10; AF=.15.

Relative Power of the Selection Strategies

Across every disease model considered, the expected test statistic for the AB strategy was greater than that for the AR strategy, since Δp was increased without reducing the sample size. For many models, the expected test statistic of the LB strategy was also increased compared with the AR strategy while requiring fewer genotypes. With the exception of dominant models for sibships with s=3 or 4 affected sibs, the average ratio of the test statistics comparing the LB strategy with the AR strategy is ⩾1 for models with GRR₂ ⩽3. In contrast, the mean ratios for the dominant models are 0.90±.06 and 0.95±.05 for 3 and 4 affected sibs, respectively. For sibship sizes s=3–5, the test statistic for the LR strategy was reduced, on average, compared with the AR strategy, since the increase in Δp was insufficient to outweigh the loss in sample size. The increases in the test statistics associated with the two “best” strategies indicate that these two strategies have greater power, on average, than the AR strategy. The magnitudes of these increases necessarily vary by disease model.

For additive models, the AB strategy has the greatest power for sibship sizes s=3–5 and is associated with an average 26%±1%, 21%±1%, and 31%±1% increase in the test statistic compared with the AR strategy, for sibship sizes of 3, 4, and 5, respectively (fig. 1B). Recall that the AB and AR strategies are equivalent for 2 sibs. The corresponding average increases in the test statistic for the LB over the AR strategy for additive models are 5%±1%, 2%±5%, 7%±5%, and 19%±3% for sibship sizes 2, 3, 4, and 5, respectively. The ability to type fewer individuals on each marker allows more markers to be typed, which, in turn, provides better coverage of the region. Given fixed genotyping resources, for additive models with GRR₂ ⩽3, ∼14%, 38%, 34%, and 24% more markers could be typed, on average, for 2, 3, 4, and 5 sibs, respectively, using the LB strategy as opposed to the AR strategy, while maintaining or increasing power. Since the proportion of sibships selected under each of the disease models is similar, the potential increase in the number of markers typed is similar for dominant and recessive models.

Relative Per-Genotype Information Gain

Each of the three sharing-based strategies is more efficient in the per-genotype contribution to the test statistic than the AR strategy. The LB strategy is the most efficient strategy, with an average 20%, 41%, 43%, and 47% larger per-genotype contribution to the test statistic than the AR strategy for additive models with GRR₂ ⩽3 for sibship sizes of 2, 3, 4, and 5, respectively (fig. 1C). These results suggest that, if genotyping costs are the limiting factor for a study, the LB strategy is the most efficient use of genotyping resources.

Unaffected Sibs in Sibship

When we assume that the sibship includes either 1 or 2 unaffected sibs in addition to s affected sibs, results are very similar. For all models with GRR₂ ⩽3, the disease-allele frequency in chosen affected sibs is lower than when we assume no affected siblings. At the same time, the proportional increase in Δp achieved by using the linkage-based strategies is slightly greater (on the order of 0.5%–1.5%), on average, compared with sibships with no unaffected sibs.

Differences between S_pairs and S_all

The results described above are for selection of sibships and sibs on the basis of the S_pairs and S_pairs(j) statistics, respectively. Results are very similar for selection based on S_all and S_all(j). Recall that NPL_pairs and NPL_all are identical for sib pairs and trios. For sibships with 4 or 5 affected sibs, the proportional increase in Δp in the more restrictive NPL_all selection is not enough to outweigh the loss in sample size when testing for association.

IBD Unknown at Disease Locus: Simulation

Table 5 shows the mean proportional increase in Δp for each of the strategies compared with the AR strategy for NPL_pairs selection, for each of the additive models we considered. Table 6 similarly shows the mean ratios of the test statistics. Each table includes the mean proportional increase or ratio based on the IBD-known analytic calculation and based on selection at the true disease-locus position for simulations in which we required no minimum MLS. Each table also includes selection based on the true position of the disease locus and the position of the MLS for 1- and 5-cM marker spacing for the simulations in which we required an MLS ⩾1. Many modest linkage signals may be false, and no strategy will legitimately improve the evidence for association in this case. To examine the situation in which these peaks are indicative of a true linkage signal, we restricted our results based on the MLS position in both tables to those with an MLS ⩾1 within 10 cM on either side of the true disease-locus position. Results were nearly identical when we used all replicates with an MLS ⩾1 within 20 cM on either side of the true position.

Table 5.

Mean Proportional Increase in Disease-Allele Frequency Difference when IBD Status Is Unknown

	Mean Proportional Increase inDisease-Allele Frequency Difference for
	2 AffectedSibs			3 AffectedSibs			4 AffectedSibs
Model andSimulationConditiona	AB	LR	LB	AB	LR	LB	AB	LR	LB
Model I:
Expected	.00	.11	.11	.13	.22	.29	.11	.14	.27
Actual, all	.00	.11	.11	.13	.22	.29	.11	.13	.26
Actual, MLS ⩾1	.00	.11	.11	.13	.21	.28	.10	.13	.25
1 cM	.00	.09	.09	.12	.18	.26	.10	.12	.24
5 cM	.00	.09	.09	.11	.16	.23	.10	.09	.21
Model II:
Expected	.00	.08	.08	.11	.13	.18	.09	.07	.18
Actual, all	.00	.08	.08	.11	.12	.18	.09	.07	.17
Actual, MLS ⩾1	.00	.08	.08	.11	.12	.18	.09	.07	.17
1 cM	.00	.07	.07	.10	.11	.17	.08	.06	.17
5 cM	.00	.06	.06	.10	.10	.16	.09	.05	.15
Model III:
Expected	.00	.09	.09	.12	.16	.22	.09	.09	.20
Actual, all	.00	.09	.09	.11	.15	.22	.09	.09	.20
Actual, MLS ⩾1	.00	.09	.09	.12	.15	.22	.09	.09	.20
1 cM	.00	.08	.08	.11	.13	.20	.09	.08	.19
5 cM	.00	.07	.07	.10	.11	.18	.09	.06	.16

^aExpected = selection based on analytic calculation when IBD known; Actual, all = selection based on the true disease-locus position with data generated at 1-cM marker density and analyzed every 0.5 cM, no minimum MLS; Actual, MLS ⩾1 = selection based on the true disease-locus position with data generated at 1-cM marker density and analyzed every 0.5 cM, MLS ⩾1; 1 and 5 cM = selection based on position of MLS ⩾1 with data generated at 1- and 5-cM marker density, respectively, and analyzed every 0.5 cM.

Table 6.

Mean Ratio of Test Statistics when IBD Status Is Unknown

	Mean Test Statistic Ratio for
	2 Affected Sibs			3 Affected Sibs			4 Affected Sibs
Model andSimulationConditiona	AB	LR	LB	AB	LR	LB	AB	LR	LB
Model I:
Expected	1.00	1.01	1.01	1.24	.83	.91	1.21	.80	.98
Actual, all	1.00	.99	.99	1.25	.82	.91	1.21	.80	.99
Actual, MLS ⩾1	1.00	.99	.99	1.24	.83	.92	1.20	.80	.99
1 cM	1.00	.99	.99	1.23	.82	.92	1.19	.81	.97
5 cM	1.00	.96	.96	1.21	.79	.89	1.20	.82	1.00
Model II:
Expected	1.00	1.01	1.01	1.26	.86	.97	1.23	.83	1.06
Actual, all	1.00	1.00	1.00	1.26	.84	.95	1.22	.83	1.07
Actual, MLS ⩾1	1.00	.99	.99	1.26	.84	.95	1.22	.83	1.06
1 cM	1.00	.98	.98	1.25	.84	.95	1.21	.83	1.05
5 cM	1.00	.95	.95	1.23	.81	.92	1.22	.84	1.06
Model III:
Expected	1.00	1.03	1.03	1.26	.88	1.00	1.22	.84	1.07
Actual, all	1.00	1.02	1.02	1.26	.87	.99	1.22	.85	1.08
Actual, MLS ⩾1	1.00	1.02	1.02	1.27	.88	1.00	1.22	.85	1.09
1 cM	1.00	1.01	1.01	1.25	.88	1.00	1.21	.85	1.07
5 cM	1.00	.97	.97	1.23	.85	.97	1.21	.87	1.08

^aExpected = selection based on analytic calculation when IBD known; Actual, all = selection based on the true disease-locus position with data generated at 1-cM marker density and analyzed every 0.5 cM, no minimum MLS; Actual, MLS ⩾1 = selection based on the true disease-locus position with data generated at 1-cM marker density and analyzed every 0.5 cM, MLS ⩾1; 1 and 5 cM = selection based on position of MLS ⩾1 with data generated at 1- and 5-cM marker density, respectively, and analyzed every 0.5 cM.

We find that each of the strategies performs very similarly to expectations based on the IBD-known case for these additive models and for the dominant and recessive models (data not shown). These results highlight the fact that, even in cases in which the power to detect linkage is negligible in the entire sample, using allele-sharing information within a reasonable distance of the disease-locus position to choose families and individuals can increase the power to detect association. Aside from showing that selection based on the MLS is nearly as good as that based on the true disease-locus position, the results based on the true position are relevant for candidate gene studies, in which selection may be based on the position of the putative disease gene rather than the MLS and can be performed in the absence of an interesting MLS value.

Discussion

We considered four case-selection strategies when affected sibships have been collected. Each strategy uses one affected individual from each sibship and compares these cases with a sample of unrelated controls. We found that the case sample could be enriched for the disease allele by choosing the affected sib that showed the most evidence for pairwise sharing with the other affected sibs in the sibship. When a “best sib” was chosen from each of the sibships in the linkage sample (i.e., the AB strategy), the test statistic was greater than the AR test statistic for all disease models considered and was increased by >20%, on average. This increase indicates that the power to detect association is increased over a broad range of disease models compared with randomly choosing one sib. When the best sib was chosen only from sibships showing evidence for linkage (i.e., the LB strategy), the magnitude of the test statistic was generally maintained compared with randomly choosing one sib from each of the sibships, whereas the number of individuals genotyped per marker was reduced. Given fixed genotyping resources, this decrease in the sample size allows more markers to be typed in a region.

Even though we selected the best sib with a mode-of-inheritance–free statistic, the best sib often had the most copies of the disease allele in the sibship. In cases in which the sib with the most copies was not chosen (e.g., more than one sib with same sharing score but different genotypes), the loss of information was minimal. If the full parametric disease model were known, the average proportional increase in Δp would change by a factor of 1.024 (±.017), 1.007 (±.008), and 1.002 (±.002) over all of the dominant, additive, and recessive models considered with K=.10, respectively, for the AB strategy. Results were very similar for the LB strategy. Hence, our best-sib selection is nearly as good as selection based on the (unknown) underlying mode of inheritance.

Each of the sharing-based strategies was more efficient than the AR strategy, in terms of per-genotype information gain. The LB strategy was the most efficient over a broad range of disease models and was, on average, 20%–47% more efficient than the AR strategy for additive models with a GRR₂ ⩽3 and was 17%–32% and 23%–55% more efficient for dominant and recessive models, respectively.

Practical Considerations

These results suggest that the choice between strategies will depend on the characteristics of the underlying sample. For affected sibships of size 2, the two equivalent “linked” strategies have similar power to the “all” strategies and are, on average, 17%–23% more efficient, in terms of per-genotype information, compared with the “all” strategies. For sibships of size 3–5, if having maximum power to detect association with a particular marker is of primary concern, then the AB strategy is preferred, since it results in the largest mean test statistic of all the selection strategies. If, however, the power associated with the LB strategy is deemed sufficient for a given sample and allocation of resources is of primary concern, then the LB strategy is superior, since it allows more markers to be genotyped.

Even if the decision is made to genotype sibs from all of the sibships in the linkage sample, either of the two “linked” strategies can be performed as an interesting subanalysis. Since we do not expect the “linked” case group to have greater power than the entire case group, the objective of these analyses would likely be to see whether the estimated frequency of the putative disease allele was greater in the “linked” group for a given marker. For the additive simulation models, we saw an increase in the frequency of the disease allele in >95% of the replicate data sets for sib pairs when selection of the linked sibships was based on the position of an MLS within 10 cM on either side of the true disease locus. We performed a similar simulation for an even more modest additive model: λ_s=1.02, GRR₂=1.9, and Δp=12%. In this case, the disease-allele frequency increased in 67% of the replicates when selection was based on the position of the MLS and in 83% of replicates when selection was based on the true position of the disease locus. Hence, such an increase for a given marker is evidence in support of that marker being relevant to disease status, but the absence of such an increase does not necessarily indicate that the marker is unrelated to disease.

We note that we have assumed that the goal of the association studies considered here is to identify disease-predisposing variants rather than to carefully characterize their impact on disease risk in a specific population. Certainly, population-based samples of cases and controls are necessary for such characterization, and any sample selected to enrich for disease-predisposing variants is inappropriate for that purpose. We also note that the three sharing-based strategies do require that region-specific genotyping sets be created when more than one region is of interest. Whether this poses a problem for a particular lab will depend on the scale of the project and available technical resources.

Alternative Study Designs

There are several alternatives to a study design that uses one individual each from affected sibships and compares those cases to unrelated controls. For case-control studies, cases may be singleton cases or those with other affected family members. Although it is often simpler and less expensive to collect singleton cases, cases with affected relatives can provide a more powerful sample for association even when only one of the sibs from each family is genotyped (Risch and Teng 1998). The increase in power is largely due to the increase in the expected disease-allele frequency in individuals from families with multiple affected individuals rather than to the increased sample size achieved when multiple sibs are included in an analysis.

If multiple sibs have been genotyped for a given marker, it is best to use all of those sibs in analyses, since this generally results in more-efficient estimates of the disease-allele frequency and, hence, more-powerful tests (see, e.g., Li and Boehnke 2001). This is clearly the case for those markers used to assess allele-sharing information, and methods that appropriately account for the correlation among related cases are available for this situation (Slager and Schaid 2001). We considered the case in which one sib per family would be typed in the follow-up association study, since, given fixed genotyping resources and large regions of interest, many investigators initially type many markers in only one sib per family. Genotyping all affected individuals in each family would be more powerful but perhaps not as cost effective. Although beyond the scope of this article, it would certainly be useful to compare the cost efficiency of a design that uses all available affected family members with the design strategies investigated here.

An alternative to using unrelated controls is to use family-based sibling controls (Boehnke and Langefeld 1998; Spielman and Ewens 1998; Abecasis et al. 2000; Martin et al. 2000). Although our strategies are not limited to using unrelated controls, we chose to use unrelated controls because, in most cases, tests that use sibling controls are much less powerful (Boehnke and Langefeld 1998; Risch and Teng 1998). In addition, the potential increase in the contrast between cases and controls that is due to careful selection of sibships is limited, because the frequency of the disease allele may be increased in the unaffected as well as the affected sibs. For investigators who do not have a sample of unrelated controls, the AB strategy is likely preferred, since the case sample can be enriched for the disease allele without correspondingly increasing the frequency of the disease-allele in the unaffected sibling control.

Extensions

We may extend this work in several ways. First, we assumed that only affected sibs were used in the selection of the best sib. If unaffected sibs have also been collected and typed on the markers used for measuring allele-sharing, it should be possible to use these sibs to choose between affected sibs with the same sharing score. If two or more sibs have the same sharing score but different genotypes, then the sib(s) that share the fewest alleles with the unaffected sibs should be more likely to be carrying the disease allele. The choice between sibs with the same sharing score also could be based on other factors, such as disease severity or age at onset.

Second, several investigators have suggested using pools of multiple DNA samples for genotyping, rather than individuals, as a screening tool in the first phase of an association study (e.g., Arnheim et al. 1985; Barcellos et al. 1997; Wolford et al. 2000; Mohlke et al. 2002). This approach reduces the number of genotypes that need to be determined but introduces measurement error associated with creating the pools and estimating the allele frequency in the pools. If we assume that the error due to pooling in the allele frequency estimate is constant across sample sizes, then the sampling variability is the only component of variance that increases for the two “linked” strategies. Whether the LB or AB strategy would be optimal will depend on the relative magnitude of the pooling variance. If the pooling variance is large compared with the sampling variance, then the LB strategy may be superior, since it results in the largest increase in the difference in frequency of the disease allele between cases and controls. If the pooling variance is proportionally small, then the AB strategy is likely superior, since it does not result in a decrease in sample size that increases the sampling variance.

Third, these strategies could also be extended to general pedigrees. The principles of the strategies would remain the same, but the choice of scoring statistic—S_pairs, S_all, or some other—might become more important. Fourth, these strategies might be extended to association studies in regions of quantitative trait linkage (Camp et al. 2001; Sham et al. 2002). As before, the notion is that, among sibs (or other relatives) with similar phenotypes, those that have the most evidence for IBD sharing in a QTL linkage region should be more likely to carry the allele(s) that is influencing variation in that quantitative trait.

In summary, we have compared four different case-selection strategies, in terms of the relative magnitude of the association test statistic and per-genotype information gain. We found that, by selecting individuals most likely to be carrying chromosomes shared by multiple affected individuals, we could increase the test statistic and therefore improve power and increase the genotyping efficiency of disease-marker association studies. These results emphasize the utility, in terms of power and efficiency of genotyping resource allocation, of study designs that use cases from families with multiple affected individuals. These comparisons should be helpful to investigators planning association studies, particularly in linkage candidate regions.