Multiple Comparisons in Studies of Gene × Gene and Gene × Environment Interaction

To the Editor:

Complex diseases are (by definition) influenced by multiple genes, environmental factors, and their interactions. There is currently a strong interest in studies testing for association between combinations of these factors and disease, in part because genes that affect the risk of disease only in the presence of another genetic variant or particular environment may not be detected in a marginal (gene-by-gene) analysis (Culverhouse et al. 2002). Such studies raise the problem of multiple comparisons. Even when a small number of candidate genes and environmental factors is examined, a large number of possible interactions may need to be tested, as illustrated by a recent article in The American Journal of Human Genetics (Bugawan et al. 2003).

Bugawan et al. (2003) investigated potential interaction between the IL4R locus and five tightly linked SNPs in the IL4 and IL13 loci on chromosome 5, through use of a sample of 90 patients with type I diabetes and 94 population-based controls. They independently tested each of the chromosome 5 SNPs for interaction with IL4R, through use of logistic regression (cf. their table 7), and corrected for multiple comparisons through use of a permutation procedure. They concluded that there is statistically significant evidence for an epistatic interaction between at least one of the chromosome 5 SNPs and the IL4R locus. However, the authors’ permutation procedure does not have the desired statistical property—that is, it rejects the global null hypothesis of no interaction too often when none of the estimated interaction parameters differ from their null value. In this letter, I discuss why their procedure fails, present several alternatives, and compare the performance of these alternatives in a small simulation study.

The procedure presented by Bugawan et al. (2003) amounts to plugging the order statistics for the observed p values, p₍₁₎,…,p₍₅₎, into their joint cumulative distribution function under the null: p=F₀(p₍₁₎,…,p₍₅₎)=Pr(P₍₁₎⩽p₍₁₎,…,P₍₅₎⩽p₍₅₎). (Here, italicized uppercase letters refer to random variables, and lowercase letters refer to observed values of the corresponding variables. This differs from the notation in the Bugawan et al. [2003] article.) The authors estimate F₀ by permuting case-control labels 200 times and calculating the ordered p values for each permutation.

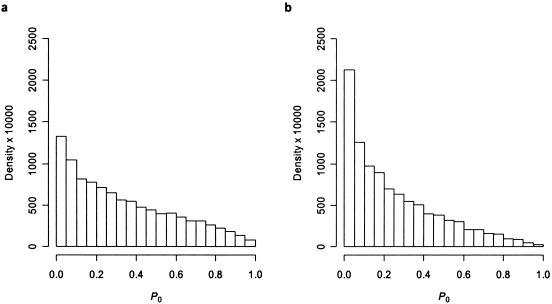
A simple example shows that this approach is inappropriate. Consider the p values from two independent tests, P₁ and P₂. If we assume a large enough sample size, P₁ and P₂ are independently uniform on (0,1) under the null, and, hence, the cumulative distribution function for the associated order statistics, F₀(p₍₁₎,p₍₂₎), is P₍₁₎(2p₍₂₎-p₍₁₎) (Bickel and Doksum 1977). The distribution of P=F₀(P₍₁₎,P₍₂₎) under the global null is shown in figure 1a. P does not have a uniform distribution under the null, as we expect for a p value. In this case, a test that rejects the global null hypothesis that both tests are null when P<.05 would have a type I error rate between 10% and 15%. As shown in figure 1b, the magnitude of the type I error rate increases as the number of independent tests increases.

Figure 1.

Density of global p values for the multiple-comparisons procedure used by Bugawan et al. (2003) under the global null hypothesis for two independent tests (a) and three independent tests (b). In panel a, P₀≡F₀(P₍₁₎,P₍₂₎), where P₁ and P₂ are independently uniform on (0,1) and F₀ is the cumulative distribution function of the order statistics, as discussed in the text. In panel b, P₀≡F₀(P₍₁₎,P₍₂₎,P₍₃₎), where P₁, P₂, and P₃ are independently uniform on (0,1). Densities are estimated from 10,000 Monte Carlo replicates.

There are several alternative, theoretically justified and simple procedures that correct for multiple comparisons, besides the notoriously conservative Bonferroni correction. Simes’s test (Simes 1986), for example, controls the overall significance level (also known as the “familywise error rate”) when the tests are independent or exhibit a special type of dependence (Sarkar 1998). Simes’s test rejects the global null hypothesis that all K test-specific null hypotheses are true if p_(k)⩽αk/K for any k in 1,…,K. Simulation results reported in table 1 suggest that Simes’s test has the appropriate false-positive rate, even when the tests are correlated.

Table 1.

Observed False-Positive Rates (False-Discovery Rates) for Procedures with Nominal 5% Rates in the Context of Testing Five Possible Gene × Gene Interactions, Calculated from 500 Simulated Data Sets^[Note]

	False-Positive Rate under Model
Procedurea	Null I	Null II
CDF	.194	.214
Simes	.032	.036
RSimes	.048	.058
	False-Discovery Rate under Model
	Null I	Null II
BHD	.014	.014
DRW	.050	.070

Note.— Six SNPs were simulated for 100 cases and 100 controls. The first SNP had mutant-allele frequency of .2; the other five SNPs were generated independently of the first by sampling five-SNP haplotypes with frequencies similar to those given in table 5 of Bugawan et al. (2003). Under model Null I, none of the SNPs were associated with disease. Under Null II, each mutant allele for the first SNP doubles disease risk, but the remaining five SNPs are not associated with disease. The multiple-comparisons procedures are applied to the p values from five Wald tests for interaction based on the logistic model Pr(disease)=α+β₁SNP₁+βSNP_i+β_intSNP^*₁SNP_i, analogous to that of Bugawan et al. (2003).

^a“CDF” denotes the cumulative distribution function procedure used by Bugawan et al. (2003); “Simes” is the standard Simes’s test; “RSimes” is Simes’s test applied to p values calculated by comparing the observed p values to the distribution of p values generated by permuting the outcome variable 200 times; “BHD” is the Benjamini and Hochberg step-up procedure corrected for general dependency (Benjamini and Yekutieli 2001) (the usual step-up procedure is identical to Simes’s test in this case); and “DRW” is the related procedure proposed by Devlin et al. (2003).

Other approaches with particular appeal in the context of multiple-gene and multiple-environmental-factor studies aim to control the false-discovery rate—that is, the expected proportion of rejected null hypotheses that are falsely rejected. This approach is particularly useful when a portion of the null hypotheses can be assumed false, as in microarray studies. Devlin et al. (2003) recently proposed a variant of the Benjamini and Hochberg (1995) step-up procedure that controls the false-discovery rate when testing a large number of possible gene × gene interactions in multilocus association studies. The Benjamini and Hochberg procedure is related to Simes’s test; setting k^*=maxk such that p(k)⩽αk/K, it rejects all k^* null hypotheses corresponding to p₍₁₎,…,p_(k^*). In fact, the Benjamini and Hochberg procedure reduces to Simes’s test when all null hypotheses are true (Benjamini and Yekutieli 2001).

Devlin et al.’s (2003) proof for the validity of their false-discovery-rate procedure requires that the analyzed genes be statistically independent. This is not the case for the IL4 and IL13 SNPs studied by Bugawan et al. (2003), but the simulation results in table 1 suggest that Devlin et al.’s (2003) procedure controls the false-discovery rate even when the analyzed genes are correlated.

The p values reported in table 7 of Bugawan et al. (2003) do not lead to any significant results at the .05 level when any of the alternative procedures discussed here are used.

Clearly, effective methods are needed for adjusting for multiple comparisons when testing for association between multiple factors and complex disease. On the one hand, blithely reporting any results marginally “significant” at the .05 level or relying on outdated and ill-performing stepwise model-building procedures (see, e.g., Burnham and Anderson [2002] and Devlin et al. [2003]) will lead to spurious results, expensive follow-up studies with little chance of replication, and confusion. On the other hand, overly conservative procedures will create missed opportunities. Although the procedures discussed here are known to control the familywise error rate or false-discovery rate in particular situations (e.g., independent covariates), their performance in more general situations needs further investigation.