Revisiting the Clinical Validity of Multiplex Genetic Testing in Complex Diseases

To the Editor:

The usefulness of genetic testing to identify high-risk patients for common multifactorial diseases is subject to debate. Optimism about the public health opportunities is counterbalanced with skepticism, since genetic factors appear to play a role in only a minority of patients with complex diseases, the number of genes involved is large, and their penetrance is incomplete (Holtzman and Marteau 2000; Vineis et al. 2001).

In last March's issue of the Journal, Yang and colleagues addressed the question of whether prediction of disease is improved by multiplex genetic testing (Yang et al. 2003). At first sight, their results seem promising. In a simulation study, they considered five genetic tests (g₁–g₅), which each could have a positive (g_i=1) or negative result (g_i=0). Yang et al. used the likelihood ratio to indicate the magnitude of change in disease probability before and after genetic testing. Positive test results have a likelihood ratio >1, which means that the posterior disease probability is higher than the prior probability. Negative test results have a likelihood ratio <1. The combined likelihood ratio of several independent test results can be obtained by multiplying their individual likelihood ratios. Using these principles, Yang et al. showed that combining information on five genetic factors and one environmental exposure in one multiplex test may increase a 5% baseline risk to 88.9%, which was considerably higher than the posterior probabilities obtained by testing for the single genes (7.8%–16.4%). In addition, they demonstrated using empirical data from a study on deep venous thrombosis that the posterior probability of venous thrombosis was substantially higher when three genes, factor V Leiden, G20210A prothrombine, and protein C deficiency, were considered simultaneously (61.6%), rather than each gene alone (1.2%–3.1%). These estimates are correct, but they do not demonstrate the clinical validity of multiplex genetic testing, as the authors concluded. There are four reasons for this.

First, Yang et al. based their conclusion on only one outcome of the composite test—that is, the combination of positive results on all individual tests. Although Yang et al. acknowledged in their discussion that this concerns only a small proportion of the population, they did not quantify the size of the proportion. From multiplication of the prevalences of the test results, we calculate that the 18-fold increase in probability of disease in the simulated data was found in 0.0006% (6 per million) of all subjects and the 100-fold increase in the risk of venous thrombosis in only 0.0004% (4 per million). This low prevalence of high-risk combinations of genes may limit the clinical usefulness of genetic testing.

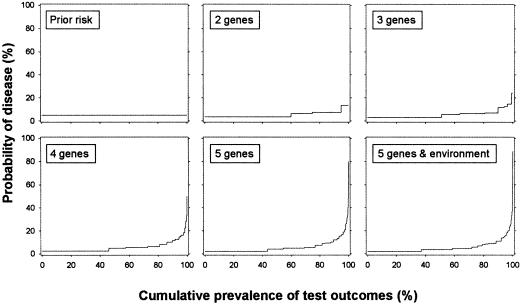
The second point is related to this issue. Yang et al. presented disease probabilities for subjects who had positive results on all single tests, but they did not report the probabilities for subjects who had combinations of both positive and negative results. The posterior probabilities and prevalences of all test result combinations are presented in figure 1. This figure demonstrates that the probabilities that Yang et al. had reported are the highest points in each of the graphs. Although these probabilities increase when genes are added, the probabilities of all other test result combinations do not rise accordingly. This is explained by the fact that positive results on each single test increase the combined likelihood ratio. This implies that the posterior probabilities reported by Yang et al. increase by definition when tests are added. In all other combinations with one or more negative test results, the likelihood ratios of negative results on the single tests will decrease the overall likelihood ratio. For the majority of subjects, the benefits of multiplex genetic testing in terms of the difference between the prior and posterior probability are less profound.

Figure 1.

Probability of disease before and after testing for multiple genes and environmental exposure. The two-gene test has 4 (2²) possible test results, the three-gene test has 8 (2³) results, and so on. The posterior probability of disease for each combination of test results is obtained from the regression equations in table 1 of Yang et al. (2003).The prevalence of each combination is calculated by multiplying the probabilities of positive (p) and negative (1-p) test results of each single test. For example, for the two-gene test we calculate that 60% ([1−0.25] × [1−0.20] × 100) of the individuals will have negative results on both tests and 15% ([1−0.25] × 0.20 × 100) will have a negative result on test 1 and a positive result on test 2. To facilitate presentation of all results, a cumulative prevalence (X-axis) was calculated, which was obtained by summing the prevalences after ranking the outcomes on their posterior probability.

A third point is that each genetic test that was added by Yang et al. was a stronger predictor of disease than those already considered in the multiplex test. The relative risks of the positive test results increased from 1.5 to 3.5, with likelihood ratios ranging from 1.6 to 3.7. This implies that the increase in the likelihood ratio of the composite test results may not only be due to the addition of tests but probably also to their higher predictive values. If the likelihood ratio of each single test had been 1.7, similar to the first test, then the combined likelihood ratio for subjects who had positive results on all five tests would have been 14.2, much lower than the 77.6 reported by Yang et al. This demonstrates that the substantial increase in the likelihood ratio was largely explained by the increasing predictive value of the single genes. In general, the added value of expanding a multiplex test will depend on the predictive value of each individual genetic test.

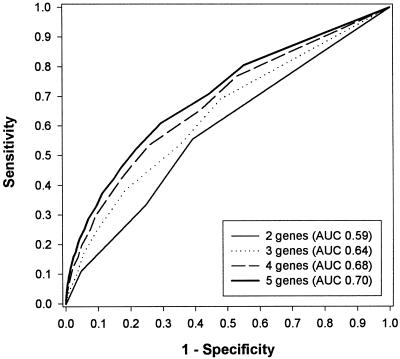
The fourth point concerns the most important conclusion of the authors that multiplex genetic testing has the potential to improve the clinical validity of predictive testing for common multifactorial diseases. This conclusion was based on the substantial increase in the probability of disease of individuals who had positive results on all single tests. However, the clinical validity of a test does not depend on the posterior probability for a few subjects, but on its ability to discriminate between the probability of disease in subjects who will develop the disease and those who will not. The discriminative ability of a test is commonly evaluated by its sensitivity and specificity. The sensitivity of a test is the percentage of positive test results among subjects who will develop the disease, and the specificity is the percentage of negative test results among subjects who will not develop the disease. On a perfect, or “gold-standard,” test, all subjects who will develop the disease have a positive test result (sensitivity = 1), and all subjects who will not develop the disease have a negative result (specificity = 1). For composite tests, positive and negative results are defined by a cutoff value of the disease probability. The sensitivity and specificity of a composite test may differ, depending on the cutoff probability that is chosen. Therefore, the sensitivity and specificity are calculated for each possible cutoff value of the probability and plotted in a so-called receiver-operating–characteristic (ROC) curve (Hanley and McNeil 1982). The area under the ROC curve (AUC) indicates the discriminative ability of a composite test. The discriminative ability is perfect if the AUC is 1, whereas an AUC of 0.50 indicates a total lack of discrimination (Hanley and McNeil 1982). If one is interested in whether genetic tests can improve the accuracy of prediction above and beyond certain minimum levels of sensitivity or specificity, one may also consider analyses of a partial AUC (e.g., Thompson and Zucchini 1989). The ROC curves for the composite tests considered by Yang et al. are presented in figure 2. The total AUC increases from 0.59 for the two-gene test to 0.70 for the five-gene test, which means that adding genes improves the discriminative ability of the multiplex genetic test. Also here, one may question whether this increase was due to the addition of genes or to their increasing predictive values. To examine this, we considered the relative risks in equal steps from 1.5 to 1.7, rather than from 1.5 to 3.5, which is more realistic for genetic factors in common diseases. With these lower relative risks, the AUC of the two-gene test was 0.57 and that of the five-gene test was 0.61. This difference between the AUCs was smaller than that obtained from the data from Yang et al., which implies that also the increase in the discriminative ability of their multiplex tests is largely explained by the increasing predictive value of the added tests.

Figure 2.

ROC curves for the multiplex genetic tests of Yang et al. (2003).

What can we learn from the ROC curve about the clinical validity of genetic testing? The aim of genetic screening is often to select high-risk subjects for preventive treatment or intensified surveillance programs. For this purpose, the sensitivity of the test should be high so that most (future) patients are identified by a positive test result. A high specificity of the test is desired to increase the efficiency of screening, because then the number of subjects who are unnecessarily selected for preventive interventions is minimized. From figure 2 it follows that a sensitivity of 0.80, which means that still 20% of the patients are missed by the screening program, is accompanied by a specificity of 0.45. The latter means that 55% of all subjects who will not develop the disease will be classified falsely. In a population in which 95% of the individuals will not develop the disease, as in the study of Yang et al., this means that 52% will undergo unnecessary preventive treatment. When a sensitivity of 0.90 is chosen, the percentage of all subjects who are unnecessarily selected is 73%. In comparison, the sensitivity and specificity of mammography in a large population–based breast cancer screening program were 0.75 and 0.92, respectively (Carney et al. 2003). Thus, the multiplex genetic tests of Yang et al. are by no means efficient screening strategies.

In conclusion, the clinical usefulness of genetic testing should be evaluated by ROC analysis. Using this approach for the data of Yang et al., we found that the discriminative ability of the multiplex genetic test increased by the addition of more genes but that its performance for use as a screening instrument was rather inefficient. It remains to be investigated whether these results are representative of the prediction of common disease by multiplex genetic tests that include genetic factors with low mutation prevalence and low relative risks. In that case, alternative statistical strategies are needed to increase the potential clinical application of selective genetic testing.