Evolutionary cycles of cooperation and defection

Abstract

The main obstacle for the evolution of cooperation is that natural selection favors defection in most settings. In the repeated prisoner's dilemma, two individuals interact several times, and, in each round, they have a choice between cooperation and defection. We analyze the evolutionary dynamics of three simple strategies for the repeated prisoner's dilemma: always defect (ALLD), always cooperate (ALLC), and tit-for-tat (TFT). We study mutation–selection dynamics in finite populations. Despite ALLD being the only strict Nash equilibrium, we observe evolutionary oscillations among all three strategies. The population cycles from ALLD to TFT to ALLC and back to ALLD. Most surprisingly, the time average of these oscillations can be entirely concentrated on TFT. In contrast to the classical expectation, which is informed by deterministic evolutionary game theory of infinitely large populations, stochastic evolution of finite populations need not choose the strict Nash equilibrium and can therefore favor cooperation over defection.

In the prisoner's dilemma, two players have the choice to cooperate or to defect. Both obtain payoff R for mutual cooperation, but a lower payoff P for mutual defection. If one individual defects, while the other cooperates, then the defector receives the highest payoff T whereas the cooperator receives the lowest payoff S. We have T > R > P > S. Defection dominates cooperation: in any mixed population, defectors have a higher fitness than cooperators.

As is standard in repeated games, new strategies become possible when the game is repeated, and these strategies can lead to a wider range of equilibrium outcomes (1–8). In particular, in the infinitely repeated prisoner's dilemma, cooperation becomes an equilibrium outcome, but defection remains an equilibrium as well (9, 10). To select between these equilibria, the authors of refs. 11–13 looked at the replicator dynamic on a continuum population, and the authors of refs. 14 and 15 applied variants of evolutionary stability to repeated games with complexity costs. These solution concepts do not have explicit dynamics and are based on models with a continuum population.

Our goal is to study explicit evolutionary dynamics in a large but finite population. To explicitly model evolutionary dynamics, the space of possible strategies must be restricted. In this article, we explore the evolutionary dynamics of three strategies: always defect (ALLD), always cooperate (ALLC), and tit-for-tat (TFT). TFT cooperates in the first move and then does whatever the opponent did in the previous move. Ever since Axelrod's celebrated computer tournaments (16), TFT is a world champion in the repeated prisoner's dilemma, although it has some weaknesses and has at times been defeated by other strategies (11, 12, 17). For our purpose here, these weaknesses are not important. We conjecture that similar results hold for other reciprocal strategies, such as generous-tit-for-tat (11) or win–stay, lose–shift (12, 18), which is also known as perfect-tit-for-tat (15).

We consider a finitely repeated game with an average number of rounds, m. TFT is a conditional strategy, whereas the other two strategies are unconditional. Therefore, it is natural to include a complexity cost for TFT (14): the payoff for TFT is reduced by a small constant c. The payoff matrix is given by

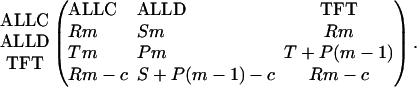[1]

The pairwise comparison of the three strategies leads to the following conclusions. (i) ALLC is dominated by ALLD, which means it is best to play ALLD against both ALLC and ALLD. (ii) TFT is dominated by ALLC. These two strategies cooperate in every single round, but the complexity cost of TFT implies that ALLC has a higher payoff. (iii) If the average number of rounds exceeds a minimum value, m > [(T - P + c)/(R - P)], then TFT and ALLD are bistable. This result means that, choosing between ALLD and TFT, each strategy is a best response to itself.

Let us now consider traditional evolutionary game dynamics of all three strategies as given by the replicator equation (19–21). This approach describes deterministic selection in infinitely large populations. The frequency of a strategy increases at a rate given by the difference between its fitness and the average fitness of the population. The fitness of a strategy is the expected payoff from the game assuming many random encounters with other individuals. In this framework, any mixed population of ALLC, TFT, and ALLD will converge to a pure ALLD population. The state where everybody plays ALLD is the only stable equilibrium.

This outcome does not surprise us. From the payoff matrix (1), we see that ALLD is the only evolutionarily stable strategy (ESS) and the only strict Nash equilibrium (22–24). If everybody uses ALLD, then every other strategy has a lower fitness. Therefore, no mutant strategy can invade an ALLD population. In contrast, neither TFT nor ALLC nor any mixed population has this property.

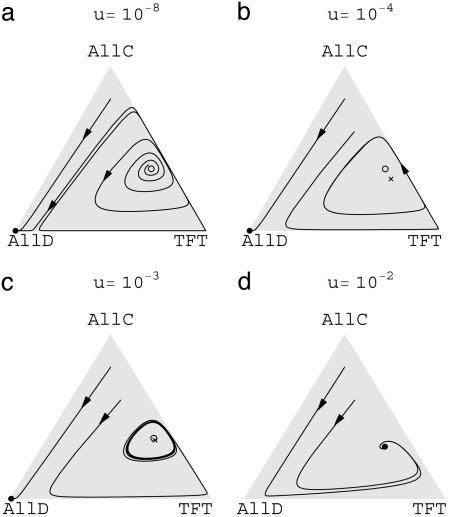
We can extend the replicator equation and consider selection and mutation in a deterministic framework. In the resulting “replicator–mutator equation” (see Appendix), deterministic evolutionary dynamics remain essentially the same for very small mutation rates: all trajectories starting in the interior converge to a population that consists of almost only ALLD players. We call this equilibrium “almost ALLD.” For small or zero mutation rates, there is also an unstable mixed equilibrium containing all three strategies. When there are no mutations, the proportion of ALLD players in this equilibrium is c/[(m - 1)(P - S)] and thus can be made arbitrarily small by increasing the number of rounds or by reducing the complexity cost. If the mutation rate exceeds a critical value, a stable limit cycle forms around this mixed equilibrium, so that there are two basins of attraction. Certain initial conditions converge to almost ALLD, whereas others converge to the limit cycle. For even larger mutation rates, almost ALLD loses stability, and the limit cycle becomes a global attractor. There is another critical mutation rate, where the limit cycle disappears and all trajectories converge to a stable mixed equilibrium containing all three strategies. Fig. 1 illustrates these deterministic dynamics.

Fig. 1.

Deterministic replicator dynamics of an infinite population with different mutation rates u. Filled circles represent stable stationary points; open circles represent unstable stationary points. The times symbol in b and c (×) indicates the time average of the limit cycle. The payoffs in the prisoner's dilemma game are T = 5, R = 3, P = 1, and S = 0.1; the expected number of rounds is m = 10, and the complexity cost for TFT is c = 0.8.

Let us now move from deterministic evolution of infinite populations to stochastic evolution of finite populations (25–31). We study a frequency-dependent Moran process (30–32) with mutation. In each time period, an individual is chosen for reproduction with a probability proportional to its fitness. The offspring replaces a randomly chosen individual. The total population size is constant. With a small mutation probability, the offspring does not use the same strategy as the parent, but one of the two other strategies. A precise description of the stochastic process is in the Appendix. Reproduction can be interpreted genetically or culturally. In the latter case, successful strategies spread by learning (or imitation) from one individual to another.

The evolutionary dynamics of this stochastic process differ from the deterministic approach. In the limiting case of very small mutation rates, the stochastic process does not converge to ALLD, but instead there are endless oscillations from ALLC to ALLD to TFT and back to ALLC. For a long time, the population is almost homogeneous for one strategy, but then a mutant is produced that generates a lineage that takes over the population. The transition rate from one homogeneous population to the next is given by the product of the population size, N, times the mutation rate u, times the fixation probability of the mutant in the resident population. The oscillations tend to revolve in one direction, because the transitions from ALLC to ALLD, from ALLD to TFT, and from TFT to ALLC are much more likely than the corresponding reverse transitions.

Surprisingly, the time average of these oscillations can be entirely dominated by TFT. This means that, for most of the time, the population is in a state that consists of only TFT players. This observation is of interest because, in the limit of very small mutation rates, an infinite population chooses defection, but a finite population (of the right size) chooses reciprocity. This is a remarkable result, given that the payoff matrix (1) clearly indicates that ALLD is the only strict Nash solution and the only evolutionarily stable strategy. We observe that neither concept implies evolutionary success in the stochastic setting of finite populations.

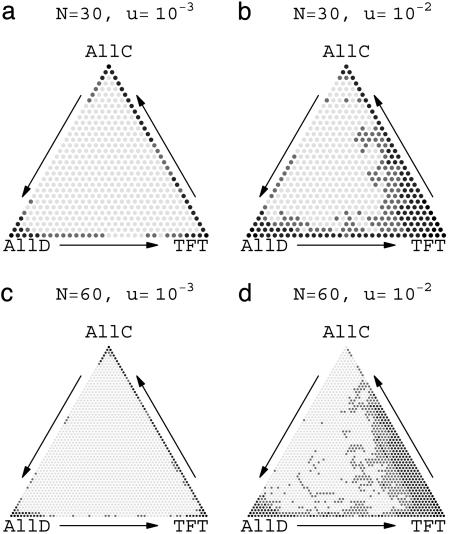
The Appendix contains a theorem that states that the stochastic process has a time average that is arbitrarily close to TFT. More precisely, for a suitable range of population sizes, the population consists most of the time of only TFT players, provided that the average number of rounds m of the repeated prisoner's dilemma is large enough. Fig. 2 shows the (stationary) distribution of the stochastic process for numerical simulations.

Fig. 2.

Frequencies of visits of the Moran process for different population sizes N and different mutation rates u. Dark points correspond to states that are often visited. Most points in the interior of the state space are rarely visited; transitions from ALLC to ALLD and from ALLD to TFT are faster than those from TFT to ALLC. The process spends most of the time at or near the state where everyone plays TFT. For the smaller mutation rate, the concentration of the stationary density to the vertices is more strongly pronounced. The payoffs are T = 5, R = 3, P = 1, and S = 0.1; the expected number of rounds is m = 10, and the complexity cost for TFT is c = 0.8. The arrows indicate the direction of the stochastic oscillations.

The transition rate from an ALLD population to a TFT population is Nuρ, where ρ is the fixation probability of a single TFT player in an ALLD population. The transition rate from a TFT to an ALLC population is of order u, because ALLC and TFT are nearly neutral given a small complexity cost of TFT. The transition rate from an ALLC to an ALLD population is of order Nu, because ALLD has a strong selective advantage. Therefore, the most rapid transition is from ALLC to ALLD. If Nρ > 1, then the transition from ALLD to TFT is faster than the transition from TFT to ALLC. In this case, the population consists most often of TFT players.

A natural extension of our work would be to accommodate the possibility that players make mistakes, so that there is a small probability that a realized action is different from the intended action (15). This extension seems to be particularly relevant when the number of rounds is large. In two recent articles (33, 34), Brandt and Sigmund studied the effects of errors in a deterministic model for the evolution of an infinite population of ALLC, ALLD, and TFT players.

Evolutionary game theory of the last two decades has largely focused on deterministic descriptions of infinitely large populations. Most of our intuitions about evolutionary dynamics come from this important tradition (20, 21). In this article, we have shown that the intrinsic stochasticity of finite populations can lead to surprising outcomes. Instead of convergence to the only strict Nash solution (ALLD), we observe oscillations from ALLD to TFT to ALLC and back to ALLD, with a time average that is concentrated on TFT. Stochastic evolution in finite populations leads to a natural selection of reciprocity.

Appendix

Deterministic Replicator Dynamics. Deterministic evolutionary game dynamics are given by the replicator equation (19–21):

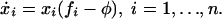Here x_i denotes the frequency of strategy i. The payoff matrix is A = [a_ij]. The fitness of strategy i is f_i = Σ_j x_ja_ij. The average fitness of the population is φ = Σ_i x_i f_i. Note that Σ_i x_i = 1.

Deterministic Replicator Dynamics with Mutations. Frequency-dependent selection and mutation can be described by the replicator–mutator equation:

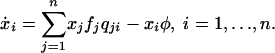Here, q_ij denotes the probability that strategy i generates an offspring using strategy j. In Fig. 1, q_ij = u for i ≠ j, and q_ii = 1 - 2u.

Stochastic Dynamics in Finite Populations. Consider a population of size N and let u ≥ 0 denote the mutation probability. Let A = (a_ij)³_i,j=1 be a positive payoff matrix. We define a frequency dependent Moran process X(t) = X(t; μ, N, A), t = 0, 1, 2,..., on the state space

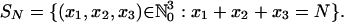Here x_i denotes the number of players using strategy i. If the population is in state (x₁, x₂, x₃) with x_i ≥ 1, then the fitness of individuals using strategy i is

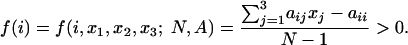We subtract a_ii because the individual does not interact with itself. In each time step, we choose one individual for reproduction and one for death. The probability that an individual with strategy i reproduces is given by x_i f(i)/Σ_j x_j f(j). The probability that the offspring of this individual will use strategy i is 1 - 2u. With probability u, the offspring will use one of the two other strategies. The offspring is replacing a randomly chosen individual; an individual using strategy i is removed with probability x_i/N. This algorithm defines a Markov chain on S_N. If u > 0, the stochastic process has no absorbing states, and the transition matrix is irreducible. Therefore, there is a well defined unique stationary distribution π = π(s; u, N, A), s ∈ S_N, determined by the left-hand eigenvector associated with the unique largest eigenvalue 1.

Limit Distribution for Small Mutations. Consider the homogeneous states s₁ = (N, 0, 0), s₂ = (0, N, 0), s₃ = (0, 0, N). Let ρ_ij(N, A) be the probability that the no-mutation process {X(t; 0, N, A)} gets absorbed in s_j if initially every individual but one plays i and one plays j. To determine the limit of the stationary distribution as the mutation rate goes to zero, we consider an associated Markov chain on the reduced state space {s₁, s₂, s₃} with transition matrix 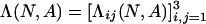, where

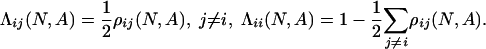For every N and every positive payoff matrix A, the matrix Λ(N, A) is positive. Therefore, there is a unique positive vector

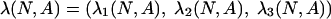such that

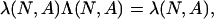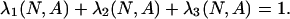It can be shown that

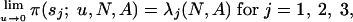[2]

and for every s ∈ S_N{s₁, s₂, s₃},

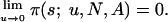Note that f(i, x₁, x₂, x₃; N, A), ρ_ij(N, A), Λ(N, A) and λ(N, A) depend continuously on A.

Returning to the prisoner's dilemma game, fix payoffs,

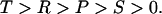Identify strategies 1:AllC, 2:AllD, 3:TFT. Let c ∈ [0, S) be the overall cost of playing TFT. For every expected number of rounds m ≥ 1, let

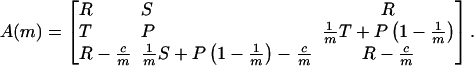The following theorem states that, for a suitable range of population sizes, the population consists most of the time of TFT players, provided that the average number of rounds is large enough.

Theorem. Given ε > 0, there exists a population size N₀ such that the following holds. For every N₁ > N₀, there exists 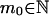such that, for every m ≥ m₀, there is u₀(m)> 0, such that

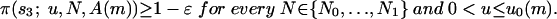A proof of the theorem is given in ref. 35. Here, we provide only a sketch of the proof. In the first step, we consider the Moran process corresponding to the prisoner's dilemma game with infinitely many rounds. The payoff matrix is given by

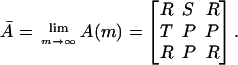We examine the asymptotic behavior of the fixation probabilities ρ_ij(N, Ā) for the no-mutation process as N → ∞. In the second step, we turn to the associated Markov chain on the reduced state space {s₁, s₂, s₃}. We use the results from the first step to determine the behavior of the stationary distribution λ(N, A as N → ∞. It turns out that

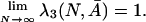[3]

Thus, in the infinitely repeated prisoner's dilemma, the associated Markov chain spends nearly all of the time at TFT when N is large. On the other hand, it can be shown that, for any finite number of rounds,

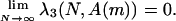[4]

In the third step, we deduce that λ₃(N, A(m)) is close to 1 provided that (i) m and N are large enough (see Eq. 3) and (ii) N is not too large (see Eq. 4). To return from the associated Markov chain to the original chain on the whole state space S_N, we finally use the limit relation (2).