Structure, function, and evolution of transient and obligate protein–protein interactions

Abstract

Recent analyses of high-throughput protein interaction data coupled with large-scale investigations of evolutionary properties of interaction networks have left some unanswered questions. To what extent do protein interactions act as constraints during evolution of the protein sequence? How does the type of interaction, specifically transient or obligate, play into these constraints? Are the mutations in the binding site of an interacting protein correlated with mutations in the binding site of its partner? We address these and other questions by relying on a carefully curated dataset of protein complex structures. Results point to the importance of distinguishing between transient and obligate interactions. We conclude that residues in the interfaces of obligate complexes tend to evolve at a relatively slower rate, allowing them to coevolve with their interacting partners. In contrast, the plasticity inherent in transient interactions leads to an increased rate of substitution for the interface residues and leaves little or no evidence of correlated mutations across the interface.

The recent debate on the degree of constraint that protein–protein interactions confer on protein evolution (1–4) has highlighted the problems of reliability in high-throughput interaction data and the processing and interpretation of those data. With increasing amounts of data on protein–protein interactions for several species as well as the emphasis on representing and understanding basic biological processes in terms of networks of interactions, it is important to focus on the precise definition and classification of these underlying interactions. Some computational analyses tend to group together disparate datasets originating from different experimental methods to get more robust answers (5), which sometimes tends to blur the definitions of the nodes and edges of the merged networks. Although the simplest approach to networks as sets of binary interactions provides some rudimentary understanding of the data, the more realistic and nuanced view in terms of modular complexes and subcomplex structures is needed, and such characterizations have recently started appearing in the literature (6).

An important distinction between transient and obligate protein–protein interactions, overlooked in many studies, has important implications for the construction of protein interaction networks. Constructing a network with each node representing a single protein sequence is hardly realistic from a biological perspective. It is well known that many proteins exist as parts of permanent obligate complexes such as multisubunit enzymes, which may often fold and bind simultaneously (7, 8). Other interactions are fleeting encounters between single proteins or the aforementioned larger complexes (9). These often include complexes involved in enzyme–inhibitor, enzyme–substrate, hormone–receptor, and signaling–effector types of interactions. The distinction between such interactions is not always well understood, and the classification is sometimes difficult. A study relying primarily on more controlled interaction datasets and taking into account the nature of the complexes found that interactions does place a constraint on sequence divergence (10). However, this analysis was able to provide only cursory answers, because the conservation was analyzed indirectly, by comparing whole sequences instead of the specific residues participating in interactions. One would expect the most reliable answers to come from structural analyses, but in the past, those have been limited by the number of available structures. Most studies tended to focus on homodimers, and the results on the significance of conservation in transient and obligate heteromeric protein interfaces have been conflicting (11–13).

Here we take a multifaceted approach by looking at the structure, function, and sequence evolution of interacting proteins of different types. Because protein complexes for which the structure has been solved are the best-studied examples of protein interactions available, we take a structure-driven approach, compiling our dataset from the Protein Data Bank (14) and then extending the analysis to related sequences. We address the question of constraint that protein interactions confer on protein evolution by compiling a sufficiently large structure-based dataset and focusing on the specific residues participating in the interaction. In addition, we differentiate the effects of transient and obligate interactions and relate these differences to the structural and functional properties of the proteins involved. Although we have previously shown that transient and obligate interfaces can be distinguished based purely on properties of interfaces structure (15), here we focus on how such differences could come about from an evolutionary perspective. We consider the differences in substitution rates between whole sequences of proteins involved in the two types of interaction as well as the rates of specific structural features, interfaces, and protein cores. Furthermore, we measure the extent of coevolution between interacting proteins that can be detected both from full sequences as well as from the specific interacting residues.

Methods

Dataset. We have previously compiled a nonredundant structural dataset of protein–protein interactions derived from the Protein Data Bank and manually separated it into permanent and transient classes (15). We have updated and refined the dataset for this study. Briefly, the dataset consists of 212 transient and 115 obligate protein complexes. Two complexes were considered nonredundant if the domains in contact belonged to a different structural classification of protein (16) family–family pairs. Note that a protein may be represented multiple times as part of different nonredundant complexes. Slightly different subsets of this initial dataset were used in different parts of the analysis, depending on the availability other relevant information. Ninety-one transient and 41 obligate complexes were used for analysis of residue conservation, 78 and 92 for distance matrix correlation analysis, 51 and 61 for mutual information-(MI) based coevolution analysis, and 143 and 97 for Gene Ontology (GO) functional annotation analysis (www.geneontology.org).

Residue surface accessibility was calculated with naccess (17). A residue was categorized as surface if it had >1% relative solvent accessibility. Interface residues were defined as having lost >1% relative solvent accessibility upon complex formation.

Functional Correspondence. The number of shared GO functional annotations between the complex components was counted below the fourth level of the hierarchy to avoid matches between very general nondescriptive terms.

Conservation Score. The conservation score for multiple sequence alignments (MSAs) from hssp (18) was computed based on von Neumann entropy (VNE), a modified Shannon entropy, as described (13):

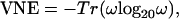[1]

where ω is a matrix given by the product of amino acid frequencies in an alignment position and a similarity matrix such as blosum50 (19):

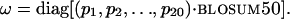[2]

In addition, we applied a correction for the actual surface buried by a given residue as suggested by Elcock and McCammon (20).

Coevolution Metrics. MSAs for coevolution calculations were obtained from a maximum of three psi-blast (21) iterations against SWISS-PROT/TrEMBL (22) with a conservative e-value cutoff of 1 × 10^-5. Whole-protein sequences were used in psi-blast runs, preventing domain drift by forcing portions of the query present in the crystal structures to match. Alignments were further refined with the program muscle (23). Each pair of alignments was required to have hits in at least 10 species. We then selected the best hit from each species and ordered the alignments from interacting proteins so the species matched by using the mirror tree method proposed by Pazos and Valencia (24). All-against-all distance matrices containing representations of phylogenetic trees for each alignment were derived from the MSAs. The matrices were then used to compute the linear correlation coefficient r, which implicitly measures the similarity between the trees. Statistical significance of the correlations was obtained by bootstrapping as described by Goh et al. (25) For each pair of matrices, we generated 1,000 matrices with randomly permuted distances and computed the correlation coefficients r_rand. We then computed a z score by using that background distribution

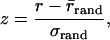[3]

where σ_rand is the standard deviation of r_rand. The P value for the correlation was then obtained from the complement error function. Complexes resulting in correlations with P values ≤0.01 were used in subsequent analysis.

MI between MSA alignment columns corresponding to contacting residues was computed with the equation

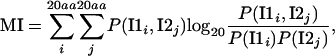[4]

where i and j are residue types in the two alignment columns corresponding to sequences of interactor 1 (I1) and interactor 2 (I2). To ensure that MI is not overestimated, we considered only those alignment column pairs that resulted in statistically significant MI estimates corrected for insufficient sampling bias (26). Statistical significance was estimated by permuting the order in the alignment columns 1,000 times and recalculating MI. Only those alignment column pairs that resulted in P values ≤0.01 were used in subsequent analysis.

Substitution Rates. To calculate the substitution rates, we obtained orthologous pairs between human and six other species: Mus musculus, Gallus gallus, Xenopus tropicalis, Danio rerio, Drosophila melanogaster, and Caenorhabditis elegans by finding reciprocal best hits and aligning them with the sequences of the proteins in the complex crystal structures. Percentage sequence identity values were converted to substitution rates by using the formula q = ln(1 + 2d)/2d described by Grishin (27), correcting for variation in amino acids and sites, where q is percent identical sites, and d is the substitution rate. For comparative substitution rate analysis, orthologous pairs were obtained by finding blast reciprocal best hits with an e-value ≤1 × 10^-10. To associate each orthologous pair with the most sequence-similar crystallized complex, we selected those orthologs that resulted in the best blast hits against the crystallized sequences, averaged over all interacting proteins in a complex.

Unless otherwise noted, statistical significance of the difference between distributions was assessed by the Wilcoxon rank test.

Results

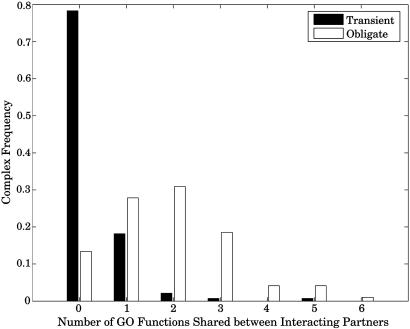
Correspondence Between Structure and Function. To be sure that our manual classification of obligate/transient interactions is appropriate, we checked the correspondence between our classification and the GO ontology (28). This was achieved by comparing the functional annotation of the components of the complex. Specifically, we counted the number of GO molecular functions that two components of the complex had in common. The calculation was restricted to the fourth level and lower in the GO graph to avoid comparing unspecific high-level and “unknown” annotations. From the distributions in Fig. 1, it is evident that most transient complexes do not share any functional annotations between the complex components, whereas many obligate complexes do. The difference does not come from a systematic discrepancy in the amount of annotation for the different types of complexes (Table 3, which is published as supporting information on the PNAS web site). The difference between the distributions in Fig. 1 is highly significant as calculated by the Wilcoxon rank sum test, resulting in a P value <10^-29. In a previous study, we achieved a 91% success rate in distinguishing between transient and obligate interactions based on the structural features of the protein complexes (15). This, in turn, implies a significant correspondence between structural features and functional annotation of protein complexes.

Fig. 1.

Components of many transient protein complexes share no functional annotation with other components, whereas many obligate complexes do.

Interface Conservation of Interacting Protein Partners. There have been a few recent studies investigating the conservation of interacting proteins. Teichmann (10) compared the sequence identities of orthologous pairs of yeast proteins from Saccharomyces cerevisiae and Schizosaccharomyces pombe. She used the MIPS database (29), with some additional manual curation to classify the complexes, and compared overall sequence identity between the classes. The reported average sequence identities were 46%, 41%, and 38% for stable, transient, and putatively noninteracting proteins, respectively, with statistically significant differences between all groups. Based on these results, Teichmann (10) suggested that the increased pattern of conservation must be a function of the surface area of the protein buried upon complex formation and thus subject to evolutionary constraint. This argument is supported by previous data on the sizes of obligate and transient interfaces as well as some additional considerations presented. Although the effect of interface size and the number of residues involved on the overall sequence conservation is evident, the degree of evolutionary constraint on the residues in different types of interfaces remains unclear. Is the difference in overall sequence identity between transient and obligate interactors solely due to the number of residues involved, or are there also differences in how strongly those residues are conserved?

More recently, Caffrey et al. (13) examined a relatively large dataset of complexes, primarily comparing the residue conservation at the interface with exposed noninterface residues. The results indicate that both obligate and transient interfaces are significantly more conserved than other surface residues. Caffrey et al. (13) also noted that obligate interfaces had fewer gaps in the MSAs than transient interfaces. However, the comparison of transient and obligate heterodimers was limited by the small number of transient complexes, 10 protein sequences from eight complexes.

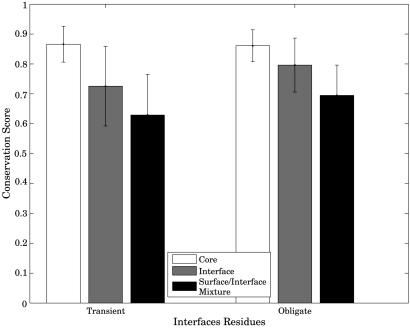
Starting with our original set of structures, we found 91 transient and 41 obligate nonredundant protein complexes resulting in 103 and 71 respective MSAs with sufficient number of sequences. The comparison of the conservation score (see Methods) among the core, interface, and other surface residues for obligate and transient heterodimers is presented in Fig. 2. Note that the extent of conservation of residues labeled Interface/Surface Mixture is provided for completeness, and these values cannot be regarded as true estimates of noninteracting protein surface. Indeed, we would like to argue that given a particular complex interface, noninteracting surface residues do not provide a good estimate of conservation of residues lacking the evolutionary constraint imposed by protein interaction. Moreover, it is very difficult to estimate the degree of conservation of such residues, because they are very likely to participate in interactions that we are not aware of. Within our dataset, there are examples of protein families that participate in multiple interactions, both obligate and transient. The family of small G proteins is a good extreme example of the phenomenon. This is one of the best structurally studied families with the G protein being cocrystallized in >30 complexes with multiple interactors (30). At least for this particular family of proteins, there are virtually no surface residues that we can call “noninteracting.” Although the situation may be less extreme for many other proteins that are not signaling hubs, the general principle remains that the surface residues can at best serve to provide the upper limit of the degree of evolutionary conservation, because they are likely to be contaminated with interacting residues. In addition, often only a fragment or an interacting domain is crystallized, which means that some of the residues “on the surface” of the domain are actually buried in interactions with other domains of the protein. This helps explain the results in Fig. 2 showing that “surface/interface” residue conservation follows a pattern similar to interface residues. The reason is that “surface/interface” residues really represent a mixture of interacting and noninteracting residues and can thus be used only as an upper bound estimate on the conservation of noninteracting surface.

Fig. 2.

Comparison of conservation of core, interface, and other residues in transient and obligate protein complexes. Note that the surface/interface residue mixtures are included for completeness and can be thought of only as the upper bound estimates of the conservation of noninteracting residues. Please see text for details.

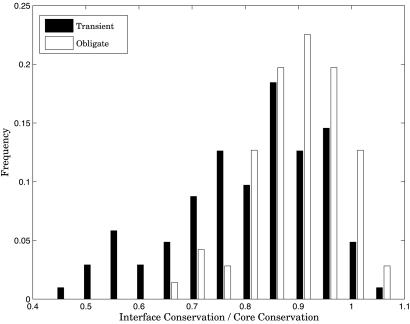
As expected, the selective constraints become comparatively relaxed from core to interface to surface residues. Within each class of complexes, the differences in conservation score are all highly significant, with P values ranging from 10^-6 to 10^-16 (Table 1). In this study, however, we are more interested in the differences in conservation between the interface residues of the two types of protein interactions. Table 2 reports the significance as obtained from the Wilcoxon rank tests, with core residues not showing a difference. This is expected, because the core residues should not be subject to constraint due to protein interactions irrespective of the type of interaction. The conservation of core residues, however, does vary substantially from protein to protein due to a variety of evolutionary pressures we cannot account for. We, therefore, report P values obtained from comparison of interface residues, normalized by the conservation of core residues of the respective proteins, which increases the significance by an order of magnitude (Table 2). The distributions of relative interface conservation in Fig. 3 show a highly significant difference between obligate and transient complexes with P value = 4.2 × 10^-5.

Table 1. P values from comparison of distributions of conservation scores for different residue types.

Residue	Core vs. interface	Interface vs. surface	No. of MSAs
Transient	2.2 × 10-16	9.5 × 10-7	103
Obligate	5.6 × 10-6	8.1 × 10-9	71

Table 2. P values from comparison of distributions of conservation scores for different complex types.

Complex	Transient vs. permanent P value
Core	0.82
Interface	3.5 × 10-4
Interface/core	4.3 × 10-5

Fig. 3.

Comparison of interface conservation score distributions for obligate and transient complexes, normalized by core residue conservation. Obligate interface residues are significantly more conserved.

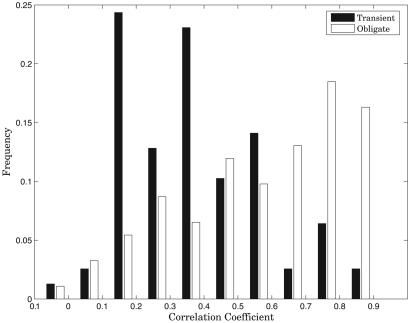
Coevolution of Obligate and Transient Interacting Partners. It has been suggested anecdotally and recently shown on larger datasets that interacting proteins tend to coevolve (i.e., undergo mutations that correlate with corresponding mutations in the binding site of the interacting partner) to preserve the functionality of the interaction (1, 24, 31, 32). The observation that transient interfaces evolve faster than obligate ones leads to the hypothesis that correlated mutations are less likely to be fixed in transient than in obligate interacting partners. To test this hypothesis, we followed the approach suggested by Pazos and Valencia (24) selecting complexes, for which at least 10 species had an ortholog for all interacting components of the complex. The analysis was repeated with second-best hits to assess the validity of our ortholog selection (see Supporting Text and Tables 4 and 5, which are published as supporting information on the PNAS web site). The MSAs were filtered to keep the best hit in each species and reorganized to ensure that the species order was the same for interacting components. We were then able to calculate correlations between the distance matrices derived from MSAs of interacting partners. The distributions of correlation coefficients for the two types of complexes are compared in Fig. 4. Clearly, obligate complexes are subject to constraints forcing compensatory mutations to a much greater extent than the transiently interacting ones. The difference is highly significant, with a P value of 5.6 × 10^-8. On average, the individual correlations computed for obligate complexes turn out to be much more statistically significant than those for transient complexes as computed with a bootstrap analysis (see Methods). The average z scores are 12.5 and 37.6 for transient and obligate correlation coefficients, respectively. We also compared the relevant subsets of the structural classification of the protein-derived dataset analyzed by Kim et al. (32) and obtained similar results (data not shown).

Fig. 4.

Comparison of the extent of coevolution of transient and obligate complex components as assessed by correlations of distance matrices derived from MSAs. Only complexes producing alignments with correlations significant at 0.01 level are included. The correlations are significantly higher for obligate complexes.

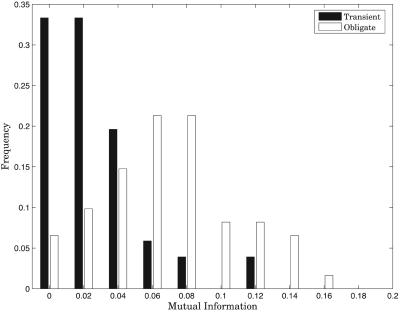
Analysis of entire protein sequences, although strongly suggestive of differences in evolutionary patterns between the two types of interactions, does not address the specific mutations at the relatively small percentage of sites involved in the interaction. We therefore repeated the above coevolution analysis, zeroing in on the complex interfaces to see whether the pattern persisted on that level. Computing MI between MSA columns that corresponded to interacting interface residues allowed us to directly measure the effect of protein interaction as a functional constraint on the evolution of those residue positions. The dataset had to be reduced for this analysis, because we could use only those complexes for which we could find a sufficient number of alignment columns corresponding to interface positions. Fig. 5 clearly shows that obligate complexes exhibit much stronger residue interdependence across the interface than transient complexes (P value, 2.1 × 10^-9). Indeed, a large fraction of transient complexes show near-zero MI between contacting residues.

Fig. 5.

Comparison of the extent of coevolution of transient and obligate complexes as assessed by MI between MSA columns corresponding to interacting interface residues. Only those alignment columns are included that result in MI estimates significant at the 0.01 level as computed by bootstrapping. The largest fraction of transient complexes exhibits nearzero information.

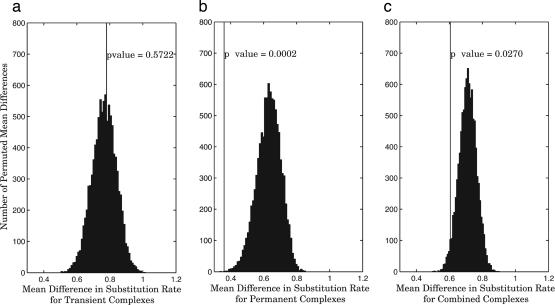
Similarity of Substitution Rates. The comparative analysis of coevolution presented above using MSAs lacks an important dimension, time, or more precisely, rate. Proteins that are subject to higher substitution rates may not have as much “time” to coevolve and preserve the interaction interface. Fraser et al. (1) use the difference between evolutionary rates of interacting protein partners to suggest coevolution. They compared this difference with a distribution of randomly paired proteins using yeast/worm orthologs and show that true interacting partners evolve at significantly more similar rates. Because most crystallized proteins come from higher eukaryotes, we could not make a direct comparison but carried out a similar analysis with human–fly orthologs. Fig. 6c shows that when both types of complexes are analyzed together, we can detect a weakly significant similarity (P value = 0.027) between the rates of substitution, as compared with randomly paired proteins. However, upon separation of the dataset into obligate and transient, we see that the weak significance of the combined dataset was most likely the result of the strong effect exhibited by obligate complexes (P value = 2 × 10^-4), whereas the transient complexes themselves show no significance in this type of analysis.

Fig. 6.

When comparing the extent of coevolution of protein complex components, separating the dataset into transient (a) and obligate (b) classes shows that the statistical significance observed in the combined set (c) is entirely due to the effects of obligate complexes. Here, the extent of coevolution was computed as the difference in the rate of substitution between the complex components in human–fly orthologous pairs. Vertical lines with labeled P values correspond to mean differences, as compared with distributions of 10,000 randomized pairings.

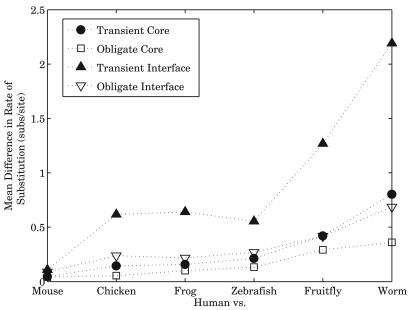
Although comparing substitution rates of whole protein sequences provides some insight, different parts of the sequence, especially in multidomain proteins, may be subject to different pressures and thus evolve at different rates. Availability of detailed structural information makes it possible to “zoom in” on the residues involved in interaction. We extended the approach above by comparing the rates of substitution between interacting partners across a range of evolutionary distances by detecting human orthologs in five additional species and repeating the analysis, while making a distinction between core and interface residues. For each of the six species, we compute the mean difference in the rates of substitution between interacting partners for core and interface residues. The means are presented in Fig. 7, with interface residues from transient complexes showing the greatest mean difference, as expected. The difference in means between transient interface residues and all others was statistically significant with P values < 0.002. These results show that proteins involved in obligate interactions tend to evolve at more similar rates than those that interact transiently. This makes sense in the context of different levels of conservation and the coevolutionary differences presented above: proteins subject to stronger pressure due to the obligate nature of their interaction are more likely to coevolve at similar rates, thus giving them a chance to undergo correlated, perhaps compensatory, substitutions, preserving the interaction.

Fig. 7.

Extending the analysis in Fig. 6 to orthologous pairs between human and six other higher eukaryotes, we show that, on average, interface residues of transient complexes coevolve to a lesser extent (have greater mean difference in substitution rates) than all other core and interface residues from both types of complexes. The organisms on the x axis are ordered by increasing sequence similarity from human, thus representing a measure of evolutionary distance.

Discussion

The degree to which proteins are subject to constraints due to their interactions with other proteins has been a subject of some debate. We believe this work addresses the question at its core, by looking at specific residues involved in the interaction and avoiding the high false-positive rates in large genome-wide screens. The results clearly show differences in the degree of evolutionary constraint depending on whether the proteins interact transiently or represent components of an obligate protein complex. The evolutionary evidence corroborates previous findings that suggested there are differences in the types of atomic contacts the proteins make across the interface (15).

Some key ideas about the effect of protein interactions on protein evolution have recently been formulated by Papp et al. (33) in a so-called “balance hypothesis,” suggesting that a stoichiometric imbalance of components of protein complexes can be deleterious. Although the authors do not make an explicit distinction between the types of interactions, they use data that primarily include yeast obligate complexes to support their claims. According to the balance hypothesis, the organism's sensitivity to the dosage of protein complex components leads to specific predictions about gene family size. Single gene duplications lead to immediate stoichiometric imbalance, which would be counterselected. Thus we expect smaller family sizes for genes encoding protein complex components and, specifically, fewer paralogs. Papp et al. (33) show that this indeed holds true in yeast. To see how the two types of interactions play into the balance hypothesis, we compared family size and fraction of paralogs in our datasets. We find that transient complex components on average belong to larger families than obligate complexes (means 191.4 and 134.9, respectively, with P value = 4.4 × 10^-5). Furthermore, transient complexes have more than double the mean number of paralogs per represented species (means 4.3 and 1.9 for transient and obligate, respectively, with P value = 2.5 × 10^-10). We can therefore conclude that, although there are not enough data to determine whether dosage sensitivity plays a role in transient protein interactions, this effect is easily detectable in obligate complexes relative to transient ones insofar as this can be corroborated with gene family sizes.

Together, the results of analyses of rates of evolution and coevolution paint a coherent picture. Residues on the protein surface that are involved in obligate interactions are under greater pressure and thus are likely to evolve at a slower rate. This slower rate allows for better-coordinated substitutions between contacting residues, resulting in a greater degree of coevolution. On the other hand, the very nature of transient interactions requires faster adaptation to possible mutations at the interface of the interacting partner resulting in greater plasticity of transient interfaces. Data show that the difference in the degree of constraint that interactions place on sequence divergence in transient and obligate complexes is not just a result of the greater proportion of residues involved in the interaction but actually is due to comparatively relaxed pressures on transient complexes. The difference in selective pressure makes it more difficult to detect correlated mutations across the interfaces of transient complexes.