Noise-induced stability in dryland plant ecosystems

Abstract

Dryland plant ecosystems tend to exhibit bistable dynamics with two preferential configurations of bare and vegetated soils. Climate fluctuations are usually believed to act as a source of disturbance on these ecosystems and to reduce their stability and resilience. In contrast, this work shows that random interannual fluctuations of precipitation may lead to the emergence of an intermediate statistically stable condition between the two stable states of the deterministic dynamics of vegetation. As a result, there is an enhancement of ecosystem resilience and a decrease in the likelihood of catastrophic shifts to the desert state.

It is commonly accepted that dryland ecosystems tend to exhibit two preferential states, corresponding to desert and vegetated land (1, 2). The existence of these two stable states usually is associated with positive feedbacks between vegetation and its most limiting resource, water (e.g., ref. 1). Natural and anthropogenic disturbances act on these bistable ecosystems, inducing catastrophic shifts to the stable state of homogeneous, unvegetated land (2-4). The strength of disturbances able to induce phase transitions to a different stable state is known as ecosystem resilience (3, 5). After the transition to the desert state has taken place, only a significant increase in resource availability (i.e., rainfall) can destabilize the desert state and reestablish a vegetation cover. This view of drylands as bistable ecosystems apparently contrasts with the existence of a middle ground between desert and completely vegetated landscapes. Recent studies (6, 7) have shown that spatial heterogeneities and lateral redistribution of resources can explain the emergence of local-scale vegetation patterns and the consequent existence of an intermediate stable condition of vegetation between the two stable states of the system (3). In this work, we demonstrate that a similar result can be obtained without invoking the effect of spatial heterogeneities: we start from a minimalist model of the bistable vegetation dynamics and show how random interannual fluctuations of precipitation typical of arid climates (8-11) lead to the emergence of an intermediate statistically stable configuration between the two preferential states of the bistable deterministic dynamics. This phenomenon of noise-induced stability has remarkable ecohydrological significance. In fact, it implies that, instead of acting as a source of disturbance, interannual rainfall fluctuations are able to induce stability and enhance the resilience of water-limited ecosystems.

Soil moisture is the key variable explaining the effect of climate fluctuations on vegetation. Positive feedbacks often exist between vegetation and soil moisture. Two different mechanisms are often invoked to explain these feedbacks at different scales. At the regional or subcontinental scales vegetation may affect the rainfall regime (12) as suggested by simulations with global and regional circulation models (13, 14). At smaller (plot-to-landscape) scales a positive feedback explains the existence of moister soils beneath vegetation canopies with respect to adjacent bare-soil plots. This feedback has often been attributed to the larger infiltration capacity of vegetated soils (1), due to their lower exposure to rain-splash compaction and the higher hydraulic conductivity resulting from root action. This mechanism is invoked by a number of competition-facilitation models of pattern formation (3, 6, 7, 15). Others (16-18) argue that soil moisture-vegetation feedbacks could be associated with the lower evapotranspirational losses from subcanopy soils, compared with evaporation from bare-soil plots. The ecological significance of this feedback is that in some regions the establishment of new seedlings can occur only in vegetated soil plots.

Methods

To investigate the effect of the feedback between soil moisture and vegetation dynamics, we model the soil water balance for a shallow soil layer of thickness, Z, as (19)

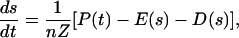[1]

where s is the relative soil moisture (0 ≤ s ≤1), n is the soil porosity, and P(t) is the infiltrating precipitation, while E(s) and D(s) are soil moisture losses associated with evapotranspiration (evaporation only, for bare soils) and drainage (20, 21), respectively. Because of the pulsing character and the rapid variability of soil moisture typical of arid environments (8), we interpret Eq. 1 at the daily time scale and model precipitation as a sequence of rainy days using a marked Poisson process of storm occurrence at rate λ, with each storm having random depth exponentially distributed with mean α. Rainfall infiltration, R(t), is equal to the whole storm depth or to the soil storage capacity, (1 - s)nZ, whichever is less, whereas rainfall excess is assumed to be lost from the system as surface runoff. D(s) is modeled as a function of soil moisture, D(s) = K_s[e^β(s-sfc) - 1]/[e^β(1-sfc) -1] when s is greater than field capacity, s_fc, while D(s) is zero for s ≤ s_fc. K_s is the saturated hydraulic conductivity, and β is a parameter of the moisture retention curves (20).

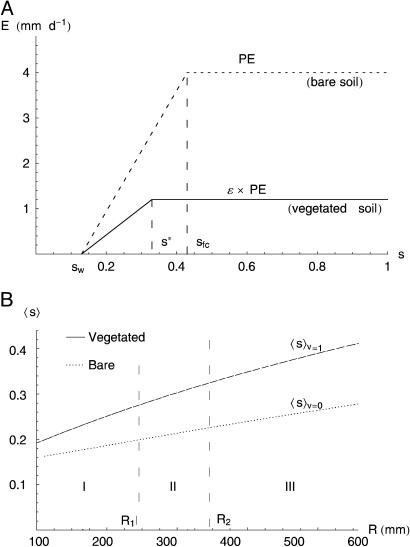
To account for the vegetation-soil moisture feedback, we reduce soil moisture losses from (shallow) vegetated soils (Fig. 1A) by taking the maximum rate of evapotranspiration as a fraction, ε, of the potential evaporation, PE, from bare soil. The lower evapotranpirational losses from the top soil beneath vegetation canopies is because vegetation takes up water from a deeper soil column than the shallow layer affected by bare-soil evaporation (22, 23), whereas the atmospheric evaporative demand on bare and vegetated soil is about the same. Thus, E(s) is expressed as a function of soil moisture (24, 25) and vegetation biomass, V, as shown in Fig. 1 A for the cases of bare (i.e., V = 0) and completely vegetated (i.e., V = V_max) soil plots. We denote V_max the maximum vegetation biomass (26) sustainable with the available resources (e.g., nutrients, light, and space) and the existing disturbance regime (e.g., herbivores and fires). We characterize the growing-season soil moisture through its average value, 〈s〉, using existing analytical solutions (20) of Eq. 1. Fig. 1B shows an example of the dependence of 〈s〉 on the normalized vegetation biomass, v = V/V_max, and precipitation, R, in the growing season. Three different regimes can be defined, depending on the possible fitness of vegetation to soil moisture conditions: for small values of R (e.g., R less than a threshold value, R₁) the soil water content is too low for the establishment of vegetation and only the bare-soil state (i.e., v = 0) is stable; for large values of R (e.g., R greater than another threshold value, R₂) water stress does not occur, regardless of the amount of existing biomass, suggesting that the state v = 0 is unstable, whereas v = 1 is stable. In intermediate conditions (i.e., R₁ ≤ R ≤ R₂) average soil moisture is too low for the establishment of vegetation in bare soil, whereas in completely vegetated plots (v = 1) the soil available water is sufficient for the existing vegetation. This finding suggests that in this interval, the system is bistable, i.e., both bare and completely vegetated soils are stable configurations. The same dynamical behavior would emerge regardless of the specific mechanisms [e.g., evaporative losses (17, 18) or infiltration (1)] responsible for the dependence of 〈s〉 on v shown in Fig. 1B.

Fig. 1.

Effect of vegetation on the soil water balance. (A) Dependence of evapotranspiration on (shallow) soil moisture. Bare-soil (i.e., V = 0) evaporation linearly increases from zero at the hygroscopic point, s_h, to potential evaporation, PE, at field capacity, s_fc (24), and remains constant for s ≥ s_fc. In completely vegetated plots (i.e., V = V_max), unstressed evapotranspiration occurs for s greater than a critical value s^*. For s < s^*, evapotranspiration linearly decreases, due to stomata regulation (19, 20, 25). E = 0 when s is less than the permanent wilting point, s_w. Soil parameters are for sandy soils (s_h ≅ s_w = 0.13; s^* = 0.33; s_fc = 0.42). PE is 4 mm/d, and the maximum rate of evapotranspiration from the top 10 cm of soil (Z = 10 cm) is ε·PE with ε = 0.3. The use of different values of ε does not alter the general results of this study. (B) Average seasonal soil moisture calculated with Eq. 1 as a function of R for bare (〈s〉_v=0) and completely vegetated (〈s〉_v=1) soils. The other parameters (n = 0.38; K_s = 2,000 cm·d^-1; β = 12.5, α = 10 mm·d^-1; ε = 0.3, growing season length of 180 d) are typical of sandy soils and arid climates (e.g., ref. 20).

We study the year-to-year variability of vegetation through a minimalist model that captures the main features of vegetation dynamics, including the soil moisture-vegetation feedbacks shown in Fig. 1B

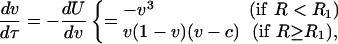[2a] [2b]

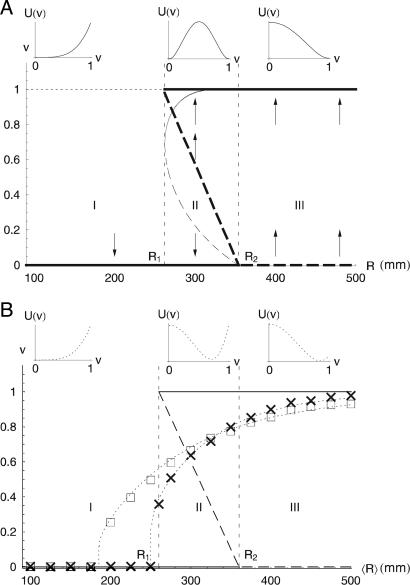
with U being the potential function (Fig. 2A) and τ = at the dimensionless representation of time, t, with respect to the “inertia,” a, of vegetation. c is an unstable state, which depends on R, as c = (R₂ - R)/(R₂ - R₁) for R > R₁ (Fig. 2). The cubic polynomial on the right-hand side of Eq. 2 induces the three regimes described in ref. 27. In fact, a sign analysis of Eq. 2 suggests that bare soil (v = 0) is a stable state only for R < R₂, whereas for larger values of R it becomes unstable. v = 1 exists as a stable state only for R > R₁ (Fig. 2 A, thick lines). For R₁ < R < R₂, Eq. 2 has two stable configurations (v = 0, 1) separated by an unstable state (v = c). For R < R₁, c = 0 and there is no stable state at v = 1; thus, Eq. 2b degenerates into Eq. 2a. For R > R₂, the system has both a stable (v = 1) and an unstable (v = 0) state, whereas the stable state at v = c < 0 has no physical meaning.

Fig. 2.

Stable and unstable states of the system. (A) Deterministic stable (solid thick lines) and unstable (dashed thick lines) states of Eq. 2 with R₁ = 260 mm and R₂ = 360 mm. The plots on the top represent the shapes of the deterministic potentials, U(v), associated with the different regimes of the dynamics. The arrows indicate the convergence toward a stable state. The thin, curved line represents stable (solid) and unstable (dashed) states of the growth-death model with k = 2 and B = 20 (〈s〉_v=0 and 〈s〉_v=1 depend on R as in Fig. 1B). (B) Noise-induced statistically stable states of the stochastic dynamics. Numerically calculated values of the modes of v (from Eq. 2) are shown with crosses (σ_R = 0.4〈R〉) and squares (σ_R = 0.6〈R〉). The thin dotted lines show the modes of v analytically calculated from Eq. 4 by using equation 25 in ref. 28. The agreement between numerical and analytical solutions suggests that c = c⁺ is a suitable mathematical approximation for the calculation of the modes of v. The stochastic potential functions associated with Eq. 4 are shown (dotted lines) in the plots on the top for the cases of 〈R〉 = 150, 310, and 410 mm, with σ_R = 0.6〈R〉. The shapes of deterministic and stochastic potentials indicate the emergence of noise-induced stability.

This mathematical representation of vegetation dynamics, Eq. 2, can be obtained from a simple growth-death model of dryland vegetation. For example, the net growth rate can be modeled as proportional to existing vegetation biomass, v, available resources, 1 - v, and photosynthetic rate, which, in turn, (linearly) depends on 〈s〉. Drought-induced death rates can be expressed as proportional to the existing biomass and to the water stress, (s^* - 〈s〉)^k, with s^* being the point of incipient water stress (Fig. 1 A). Thus, vegetation dynamics can be expressed as

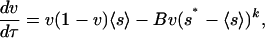[3]

with B and k accounting for the relative importance of growth and death processes. It is assumed that no drought-induced death occurs in the absence of water stress (i.e., B = 0 for 〈s〉 ≥ s^*), whereas the dependence of 〈s〉 on v is expressed as 〈s〉 = (1 - v)〈s〉_v=0 + v〈s〉_v=1, with 〈s〉_v=0 and 〈s〉_v=1 depending on R (Fig. 1B). This expression in the growth-death model gives a cubic polynomial with coefficients depending on R. The roots of this polynomial (Fig. 2 A, thin line) are equilibrium states of the dynamics and have similar properties to those of Eq. 2.

Results

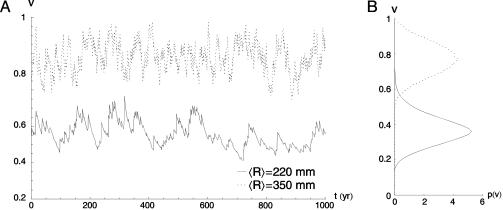
To investigate the effect of interannual rainfall fluctuations on vegetation dynamics we treat R as an uncorrelated random variable, with mean 〈R〉, standard deviation σ_R, and gamma distribution p(R). The use of other distributions would not alter the dynamical behavior of the system. The effect of noise is to switch the dynamics between two different regimes: with probability 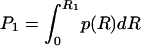, R is < R₁ and Eq. 2 is dv/dt = -v³, whereas with probability (1 - P₁), R exceeds R₁, and the process is governed by Eq. 2b with c depending on R. Thus, noise affects the number and location (on the v-axis) of stable states and alters the potential barrier between states. Quite surprisingly, by numerical integration of Eq. 2, we find (Fig. 2B) that random interannual fluctuations of precipitation stabilize the system around an unstable state of the underlying deterministic dynamics (Fig. 3). This noise-induced stable state does not necessarily coincide with the (deterministic) unstable state of equilibrium (Fig. 2B, dashed lines). Within a relatively broad range of values of R, the probability distribution of v exhibits only one mode (Fig. 3B) between 0 and 1. This stable state would not exist without the random forcing (i.e., the interannual rainfall fluctuations) as indicated by the shape of the deterministic potential function (Fig. 2 A).

Fig. 3.

Emergence of noise-induced statistically stable states in two examples of time series (A) and probability distributions (B) of vegetation generated by Eq. 2 for two different values of 〈R〉 and σ_R = 0.6〈R〉. The other parameters are 〈R₁〉 = 260 mm, 〈R₂〉 = 360 mm, and a = 0.05 yr^-1.

The modes of v (Fig. 2B, squares and crosses) are the preferential states of the system and also can be determined analytically through a probabilistic model able to capture the fundamental properties of these dynamics. To this end, we take c as a constant and replace it with the value c⁺, corresponding to the conditional average of R for R > R₁, c⁺ = c(R⁺) with 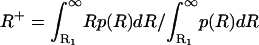(the use of the average value of c conditioned on R > R₁ is motivated by the fact that c appears only in Eq. 2b). The temporal dynamics of vegetation can be then represented as

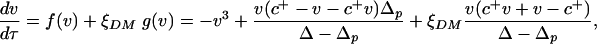[4]

where ξ_DM is a zero-mean dichotomic Markov process (28), assuming values Δ_p and Δ. The two functions g(v) and f(v) are determined in a way that dv/dt = -v³ when ξ_DM = Δ_p, and dv/dt = v(1 - v)(v - c⁺) when ξ_DM = Δ. The transition probabilities between the two states of ξ_DM are k_Δp = (1 - P₁) and k_Δ = P₁. The states Δ_p and Δ need to satisfy the condition Δ_pk_Δ + Δk_Δp = 0 for ξ_DM to be a zero-mean process. The analytical solution of Eq. 4 provided by ref. 28 is used here to calculate the modes of v and the stochastic potential, U, associated with Eq. 4 (Fig. 2B, dotted lines). This analysis shows that there is a range of values of 〈R〉 in which the stochastic dynamics have only one preferential state, whereas the stable states, v = 0 and v = 1, of the deterministic dynamics become unstable. We note that this behavior is a consequence of the threshold nature of the system Eq. 2 forced by noise. The threshold at R = R₁, i.e., abrupt disappearance of the stable vegetated state in dry climates, is due to the feedback between soil moisture and vegetation.

Discussion and Conclusions

We name the emergence of a statistically stable state (Fig. 2B) noise-induced stability and interpret it as an effect of noise on the shape of the potential function (29). This effect resembles the case of noise-enhanced stability (30, 31), although it is here observed through the emergence of unimodal behavior in the distribution of v. This finding has important ecological implications. Climate fluctuations are often considered as a source of disturbance (10) and, as such, are believed to enhance the likelihood of catastrophic shifts to the desert state or to control the transitions between preferential states in bistable dynamics (11). The emergence of a noise-induced stable configuration suggests that rainfall fluctuations unlock the system from these preferential states and stabilize the dynamics at halfway between conditions of bare soil and full vegetation cover.

Interestingly, Fig. 2B also shows that, for realistic values of σ_R/〈R〉 (9, 32), noise-induced statistically stable states may exist within a range of values of 〈R〉 wider than the interval [R₁, R₂] of the underlying bistable deterministic dynamics and that this range broadens with increasing noise intensities (i.e., with increasing σ_R/〈R〉). The possible existence of a noise-induced statistically stable state for values of 〈R〉 < R₁ prevents the occurrence of the desert conditions that would take place in the absence of rainfall fluctuations. In fact, v = 0 becomes unstable in the presence of the stochastic forcing as evidenced both by numerical simulations and by the shape of the stochastic potential (Fig. 2B). For even lower values of 〈R〉, the noise-induced stable state abruptly disappears, and the only stable configuration becomes v = 0. The width of the interval in which noise-induced stability exists decreases with decreasing values of σ_R. The transition from noise-induced stable and bistable dynamics abruptly occurs as σ_R/〈R〉 tends to 0. For 〈R〉 > R₂, rainfall fluctuations act as a disturbance on vegetation, in that the system is stable at values of v smaller than the stable state, v = 1, of the deterministic dynamics. However, for relatively large values of 〈R〉, the mode of v reaches v = 1, suggesting that the effect of climate fluctuations in subhumid and humid ecosystems is minimal. The disappearance of bistability for R₁ < 〈R〉 < R₂ reduces the likelihood of catastrophic shifts to the desert state. This finding implies that stronger disturbances (e.g., multidecadal trends in precipitation) are needed to drive the system into the desert state, suggesting that interannual rainfall variability enhances the resilience of dryland ecosystems.