Abstract
Phosphoglycerate kinase (PGK) is found to be controlled by a 25Mg2+-related magnetic isotope effect. Mg2+ nuclear spin selectivity manifests itself in PGK-directed ADP phosphorylation, which has been clearly proven by comparison of ATP synthesis rates estimated in reaction mixtures with different Mg isotopy parameters. Both pure 25Mg2+ (nuclear spin 5/2, magnetic moment +0.85) and 24Mg2+ (spinless, nonmagnetic nucleus) species as well as their mixtures were used in experiments. In the presence of 25Mg2+, ATP production is 2.6 times higher compared with the yield of ATP reached in 24Mg2+-containing PGK-based catalytic systems. The chemical mechanism of this phenomenon is discussed. A key element of the mechanism proposed is a nonradical pair formation in which 25Mg+ radical cation and phosphate oxyradical are involved.
Keywords: 25Mg
In one of their brilliant papers, Weber and Senior (1) pointed out that, despite great progress in our knowledge on the structure and our understanding of the molecular dynamics and functioning of ATP-synthesizing enzymes, the chemical mechanism of phosphorylation remains enigmatic: “Our understanding of ATP synthesis remains rudimentary in molecular terms.” Thus, our current understanding of ATP-synthesizing enzymes is still rudimentary at the molecular level and the key reaction responsible for the formation of the energy-carrying chemical bond P—O—P remains obscure. Indeed, the structures of the protein parts and catalytic sites of phosphorylating enzymes, such as ATP synthase, creatine kinase, and phosphoglycerate kinase (PGK) (2-10), are well known. There is an understanding of their functioning as molecular rotary motors (referring to ATP synthase) or molecular pumps (creatine kinase, for instance); however, within the area of enzymatic reaction chemistry, all ideas are limited to speculations circulating mostly around nucleophilic mechanisms.
An insight into the chemical mechanism follows from a recently discovered and remarkable phenomenon: a dependence of the phosphorylating activity of enzymes on Mg isotopy (11,12). This unusual effect was found for creatine kinase and ATP synthase (13). The rate of ATP production by enzymes in which the Mg2+ ion has magnetic nucleus 25Mg (nuclear spin, 5/2; magnetic moment, -0.855 Bohr magneton) was shown to be two to three times higher than that induced by the same enzymes carrying spinless, nonmagnetic nuclei 24Mg and 26Mg. The discovery of this attention-catching isotope effect convincingly and unequivocally demonstrates that enzymatic phosphorylation is an ion-radical, electron-spin-selective process in which Mg ion Mg2+ manifests itself as a reagent.
The present study deals with our search for other examples of nuclear spin selectivity in biological processes. PGK (EC 2.7.11.08), a typical two-domain enzyme catalyzing the transfer of a phosphate group from α-phosphoglycerate to ADP, which leads to ATP production in eukaryotic cells (14), has been chosen for this purpose. Like creatine kinase, PGK contains Mg2+ in its nucleotide binding site and is a molecular compressor in which a relative domain flexibility brings substrates, phosphoglycerate, and ADP in close proximity, compresses them, and urges to react. Again, there are still open questions concerning the chemical mechanism of this reaction and, particularly, the function of the Mg ion, which is assumed either to compensate for negative charges of the phosphates, to assist in the distribution of negative charge on the leaving group, or to stabilize and orient partners along the reaction trajectory.
To find answers to these questions, we have investigated the 25Mg2+-related magnetic isotope effect in PGK-directed catalysis.
Experimental Procedures
Purified pig skeletal muscle PGK samples were kindly donated by L. Gergely (Institute of Biophysics, Hungarian Academy of Sciences, Szeged, Hungary). The enzyme samples used were electrophoretically homogenous, as tested by the nondenaturing 7.5-12.0% polyacrylamide gel gradient separation method according to Davis (15). Isotopically pure (99.9% 25Mg and 99.9% 24Mg) MgCl2 for optimal composition of the incubation media was obtained from 25MgO and 24MgO (RAS Isotope Center, Obninsk, Russia) by using a routine acidic treatment. α[32P]Phosphoglycerate [21-28 Ci/mmol (1 Ci = 37 GBq); Amersham Pharmacia] was used in all measurements of PGK-specific activity, which has been expressed in [32P]ATP cpm per mg of protein (16).
For protein estimations, a conventional Bradford procedure was applied (16). To isolate the ATP fraction from postincubation and preincubation mixtures, our HPLC technique (ODS-S5CN reversed-phase separation column, 10-60% pyridine linear gradient) was used (17). All incubation mixtures used were balanced for catalysis-optimal conditions according to ref. 14.
For Mg isotope ratio monitoring, isotope mass spectrometry was applied by using the VGS Prism 2000 elemental analyzer/gas-isotope ratio mass spectrometer (Carlo Erba Reagenti, Milan) (18). To determine the total amount of Mg, atomic absorption spectrometry was performed with a QL 400 AA spectrophotometer (Zeiss) (19).
For all data presented, mean values of six measurements were estimated with Dunnett's nonparametric method suitable in n ≤ 8 cases (20).
Results and Discussion
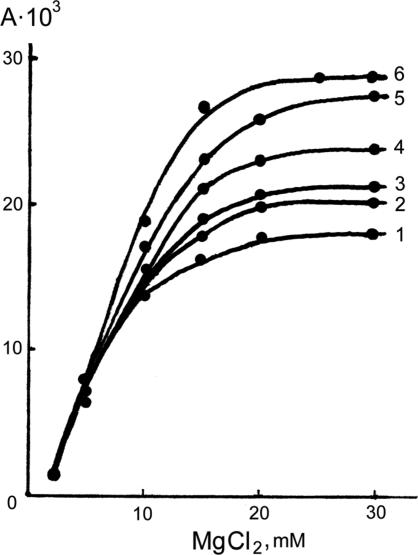
Enzymatic Activity as a Function of MgCl2 Concentration. Fig. 1 shows a dependence of the rate of ATP formation from phosphoglycerate and ADP on the MgCl2 concentration. Each one of the dots on any curve in Fig. 1 was determined as a result of the reaction mixture incubation in a number of tests, with several preprogrammed MgCl2 concentrations and 60 min of incubation per run. After a 40-min incubation, the reaction rate reaches its limit, does not depend on incubation time, and remains constant. This rate corresponds to an equilibrium condition of a system in which Mg is equilibrially distributed between the enzyme protein and a surrounding solution.
Fig. 1.
PGK activity as a function of total MgCl2 concentration with the following ratios of isotopes: line 1, 25Mg/24Mg = 0/1; line 2, 25Mg/24Mg = 1/10; line 3, 25Mg/24Mg = 1/3; line 4, 25Mg/24Mg = 1/1; line 5, 25Mg/24Mg = 3/1; and line 6, 25Mg/24Mg = 1/0. Enzyme-specific activity (A) was estimated as the amount of labeled ATP formed in 1 min by 1 mg of PGK at optimal conditions ([32P]ATP cpm per mg of PGK).
The ATP synthesis rate increases after the MgCl2 concentration increase until it reaches its top limit. This rate increase indicates a saturation of enzyme catalytic sites with Mg ions and, hence, their transfer to the reactive state. Once the reaction rate limit is reached (i.e., as soon as all catalytic sites become activated toward ATP synthesis by being filled up with Mg), the formation of ATP is, in fact, optimized. In this case, however, the protein Mg content is rather low compared with the total amount of Mg in the surrounding solution, which means that the constant of Mg2+ enzyme binding is not high.
Enzymatic Activity as a Function of Mg Isotopy. A remarkable property of PGK clearly seen in Fig. 1 is that its activity depends on the Mg isotope composition. An ATP synthesis upper rate limit (once it is reached, all catalytic sites are turned on) goes up after the increase of 25Mg contribution to the 25MgCl2/24MgCl2 mixture.
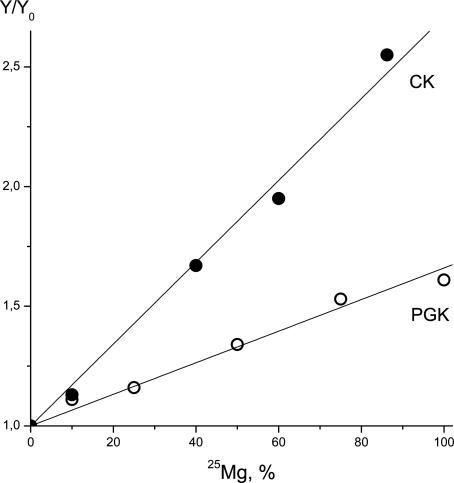
The Y/Y0 ratio, where Y stands for the ATP synthesis rate exclusively in the presence of 25Mg2+ and Y0 stands for the same reaction rate estimated in the presence of 24Mg2+ ions (no 25Mg2+ added in the mixture), is always >1.0. Therefore, the Y/Y0 index shows a linear correlation with a share of 25Mg in a total Mg pool (Fig. 2).
Fig. 2.
Catalytic activities of PGK and creatine kinase (CK) as a function of a share of 25Mg isotope in a total Mg pool.
Dependence of the PGK activity on Mg nuclear magnetic moment means that the 25Mg ion participates in the ADP phosphorylation process as a chemical reagent. Moreover, the mere fact of such a dependence proves undoubtedly that the magnetic isotope effect operates in the enzymatic reaction studied, which correlates well with the effect we observed recently in our study on phosphorylation directed by creatine kinase and ATPase (11, 12). Nuclear spin dependence proves unequivocally that the PGK-promoted phosphorylation is an ion-radical process backed by nuclear spin selectivity. In the next section, we propose and discuss a mechanism of this spin selectivity.
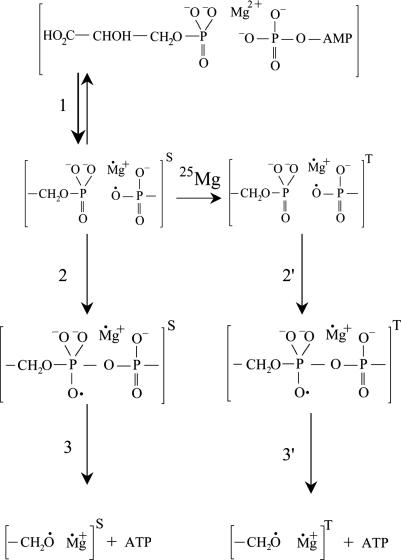
Nuclear Spin-Selective Reaction Mechanism. A 25Mg2+-related magnetic isotope effect is almost identical to the effect we found earlier in a similar reaction directed by creatine kinase. Therefore, the chemical mechanism of PGK-promoted phosphorylation looks similar to the mechanism for creatine kinase (Scheme 1).
Scheme 1.
Chemical mechanism of phosphorylation by PGK.
As seen from Scheme 1, the first and primary step of the process is an electron transfer from the ADP phosphate anion group located near the terminal Mg2+ (Scheme 1, reaction 1). This transfer generates a primary ion-radical pair (IRP) composed of monovalent radical cation Mg+ and an oxyradical of ADP. For simplicity, the IRP created in a catalytic site of phosphoglycerate and ADP is displayed in abbreviated form by terminal groups of reagents.
The primary IRP generated by the electron transfer from ADP to Mg2+ is in a singlet spin state just like any thermally generated radical pair because spin in this process is conserved. The next step is the phosphorylation itself, which occurs as an attack on the P=O chemical bond of phosphoglycerate by an ADP oxyradical (Scheme 1, reaction 2). Generated in this addition reaction, another oxyradical decomposes via β-scission of the P—O chemical bond (Scheme 1, reaction 3) and produces ATP and a final radical pair of glycerate radical and Ṁg+ ion. This final pair regenerates the Mg2+ ion and glycerate via spin-allowed back electron transfer.
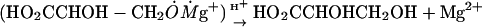 |
The rate of ADP phosphorylation along a singlet channel (Scheme 1, reactions 1, 2, and 3) is restricted by the spin-allowed back electron transfer in a primary IRP. This reaction regenerates the starting reagents and, hence, decreases the yield of ATP. However, in the presence of 25Mg, a new, additional channel of phosphorylation appears. The primary singlet IRP, generated in an active site of 25Mg-PGK, experiences a fast spin conversion into the triplet state induced by hyperfine coupling between the magnetic moment of an unpaired electron and the nuclear magnetic moment of 25Mg. The triplet IRP is chemically identical to the singlet pair, but, in this pair, back electron transfer is spin-forbidden, so this new channel is open for the phosphorylation only and provides an additional yield of ATP.
Triplet channel of transformation of the primary IRP in Scheme 1, reactions 2′ and 3′, is chemically identical to that of the singlet pair. The back electron transfer along this channel is spin-forbidden except for the final pair (-CH2Ȯ Ṁg+), in which it is allowed because of the fast spin relaxation of the glycerate oxyradical. Spin forbiddance in this pair no longer exists, and the pair regenerates glycerate and Mg2+ ion similarly to that in the singlet channel.
It should be pointed out that the mechanism proposed has nothing to do with a commonly accepted electrophylic mechanism of enzymatic catalysis in which a metal ion is supposed to interact with an unbound phosphoryl oxygen atom to polarize the P—O bond and enhance the electrophilicity of the phosphorus to be attacked by the phosphate group of phosphoglycerate. In the present ion-radical mechanism, Mg2+ ion is considered to be a reagent, and the most convincing evidence in favor of this mechanism is the nuclear spin dependence of the reaction rate. No other mechanism is able to describe this unusual but firmly established dependence.
A Phosphorylation Kinetic Scheme. A reaction scheme of enzymatic phosphorylation may be easily transformed into a kinetic one (Scheme 2). This scheme presumes a formation of an IRP within an enzyme-catalytic site. This process runs with a k0 rate constant owing to the electron transfer from the ADP phosphate group to Mg2+ (Scheme 1). IRP may regenerate both initial reagents because of back electron transfer running, with a k-1 rate constant. Also, IRP may generate ATP after two additive channels, with rate constants kn and km. These channels are chemically identical, although the first one is not dependent on the 25Mg2+ ions, whereas the second one relates completely to 25Mg2+-containing enzyme molecules. A total rate of ATP synthesis should be determined as the sum of rates estimated for both channels:
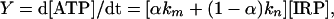 |
[1] |
where α is a share of catalytic sites occupied by 25Mg2+, which is supposed to be equal to the 25Mg2+ share in a whole catalytic system because the isotope effect in the Mg2+ binding constant is negligible and can be ignored. The [ATP] and [IRP] values are related to ATP concentration and IRP stationary concentration, respectively. The latter value is determined by kinetic equation
 |
[2] |
where [CS] is the enzyme catalytic site. By solving these two equations, one can derive
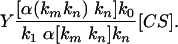 |
[3] |
When 25Mg is absent in a reaction mixture (α = 0), Y = Y0. Then, from Eq. 3 follows
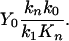 |
[4] |
Scheme 2.
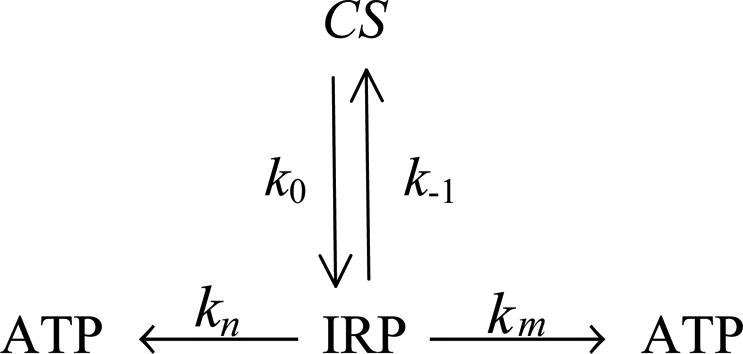
Kinetic scheme of phosphorylation by PGK.
From Eqs. 3 and 4, the following ratio is found:
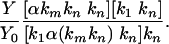 |
[5] |
This equation predicts a rather complex Y/Y0 dependence on α; however, experimental dependence (Fig. 2) is found to be linear with a high degree of accuracy. A linear Y/Y0 = f(α) dependence follows from Eq. 5 only on the condition that
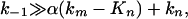 |
[6] |
which means that the back electron transfer in the IRP is the fastest process and that the ATP synthesis rate is controlled by chemical transformations in this pair (Scheme 1, reactions 2 and 3).
Under the condition of Eq. 6, Eq. 5 transforms into
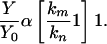 |
[7] |
Comparing this ratio with an experimentally estimated dependence, Y/Y0 = f(α) (Fig. 2), the km/kn index for PGK is found to be equal to 2.6. Therefore, the ATP synthesis rate constant is 2.6 times higher in 25Mg-operating enzyme compared with the same enzyme molecule with a nonmagnetic 24Mg isotope in the catalytic site. Note that creatine kinase manifests an even higher value: km/kn = 3.7 (Fig. 2).
Conclusions
A fundamental result of this study is the fact that the functioning of PGK is indeed controlled by the nuclear spin of the Mg2+ ion. Nuclear spin selectivity of the phosphorylation reaction operates in a primary IRP generated by electron transfer from ADP to Mg2+ ion. The rate of phosphorylation in 24,26Mg-PGK is suppressed by reversible back electron transfer. In 25Mg-PGK, a fast singlet-triplet conversion of the primary IRP induced by hyperfine coupling of an unpaired electron with the magnetic moment of the 25Mg nucleus competes successfully with the back electron transfer and results in a highly efficient channel of ATP production.
Hyperfine electron-nuclear coupling is a driving force of singlet-triplet spin conversion; a quantitative measure of the coupling is a hyperfine constant for the Mg+ radical-cation, which is known to be equal to 600 MHz in plasma (21) and 595 MHz in solids (22). The rate corresponding to the hyperfine coupling constant is a measure of the rate of a singlet-triplet conversion in the primary IRP, which is ≈6 × 108 s-1. Because this spin process competes with a back electron transfer, one can estimate the rate constant lower limit of the back electron transfer to be 6 × 108 s-1.
Acknowledgments
We thank Mr. Igor Kozin and Mrs. Olga Nenasheva for technical assistance. This work was supported by Russian Federation Ministry of Science Grant NSH-1221-2003.03.
Author contributions: A.L.B. designed research; D.A.K., M.A.O., and A.A.M. performed research; A.L.B., D.A.K., M.A.O., and A.A.M. analyzed data; and A.L.B. wrote the paper.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: PGK, phosphoglycerate kinase; IRP, ion-radical pair.
References
- 1.Weber, J. & Senior, A. (2000) Biophys. Biochim. Acta. 1458, 300-310. [DOI] [PubMed] [Google Scholar]
- 2.Oster, G. & Wang, H. (2000) J. Bioenerg. Biomembr. 32, 459-468. [DOI] [PubMed] [Google Scholar]
- 3.Oster, G. & Wang, H. (2002) Biophys. Biochim. Acta 1458, 1458-1496. [DOI] [PubMed] [Google Scholar]
- 4.Oster, G. (2002) Nature 417, 25-29. [DOI] [PubMed] [Google Scholar]
- 5.Yasuda, R., Noji, H., Yoshida, M., Kinosita, K. & Itoh, H. (2001) Nature 410, 898-903. [DOI] [PubMed] [Google Scholar]
- 6.Noji, H. & Yoshida, M. (2001) J. Biol. Chem. 276, 1665-1672. [DOI] [PubMed] [Google Scholar]
- 7.Sambongi, Y., Iko, Y., Tanabe, M., Omote, H., Iwamoto-Kihara, A., Ueda, I., Yanagida, T., Wada, I. & Futai, M. (1999) Science 286, 1722-1728. [DOI] [PubMed] [Google Scholar]
- 8.Rondelez, Y., Tresset, G., Nakashima, T., Kato-Yamada, Y., Fujita, H., Takeuchi, S. & Noji, H. (2005) Nature 433, 773-778. [DOI] [PubMed] [Google Scholar]
- 9.Merli, A., Szilagyi, A., Flachner, B., Rossi, G. & Vas, M. (2002) Biochemistry 41, 111-118. [DOI] [PubMed] [Google Scholar]
- 10.Flachner, B., Kovari, Z., Varga, A. & Vas, M. (2004) Biochemistry 43, 3436-3444. [DOI] [PubMed] [Google Scholar]
- 11.Buchachenko, A. L., Kouznetsov, D. A., Arkhangelsky, S.E., Orlova, M. A., Markaryan, A., Berdieva, A. G. & Khasigov, P. Z. (2005) Dokl. Biochem. Biophys. 396, 197-199. [DOI] [PubMed] [Google Scholar]
- 12.Buchachenko, A. L., Kouznetsov, D. A., Arkhangelsky, S. E., Orlova M.A. & Markaryan, A. (2005) Mitochondrion 5, 67-72. [DOI] [PubMed] [Google Scholar]
- 13.Buchachenko, A. L., Kouznetsov, D. A., Arkhangelsky, S. E. & Orlova, M. A. (2005) Biophysics, in press.
- 14.Lody, K. S., Loevenhaupt, K., Gergely, A. S. (2000) J. Biophys. 44, 261-267. [Google Scholar]
- 15.Davis, K. L. (1979) in Electrophoresis (McMillan, New York), pp. 45-67.
- 16.Arno, J. J., Ballot, J. K., Sawell, J., Tomeshima, A. S. & Okada, J. (1996) J. Appl. Enzymol. 16, 486-496. [Google Scholar]
- 17.Kouznetsov, D.A., Arkhangelsky, S. E., Berdieva, A. G., Khasigov, P. Z. & Orlova, M. A. (2004) Isot. Environ. Health Stud. 40, 221-228. [DOI] [PubMed] [Google Scholar]
- 18.Laurettes, J. K., De Dreaux, J. T., Berthault-Greauvexelle, A. S., Dupont, T. & Pitot, H. (2002) in Analytical Techniques in Organomercurial Studies, ed. Braundt, G. (Antwerp Univ. Press, Antwerp, Belgium), pp. 89-112.
- 19.Orchaev, S. K., Byrkov, S. T. & Allershayev, S. K. (2003) Spectrometry, eds. Ionov, S. K., Levadova, P. S. & Lomonosov, M. V. (Moscow State Univ. Press, Moscow).
- 20.Dunnett, A. S., Rosenbrough, J. S., Barthels, A. K. & Donowaugh, S. S. (1999) in Biometrics (Research, Raleigh-Durham, NC), pp. 100-111.
- 21.Powell, H. F., van Eijkelenborg, M. A., Irwine, W., Segal, D. M. & Phompson, R. C. (2002) J. Phys. B. 35, 205-211. [Google Scholar]
- 22.Brom, J. M. & Weltner W. (1973) J. Chem. Phys. 58, 5322-5330. [Google Scholar]