Abstract
Self-assembled DNA delivery systems based on anionic lipids (ALs) complexed with DNA mediated by divalent cations have been recently introduced as an alternative to cationic lipid–DNA complexes because of their low cytotoxicity. We investigate AL–DNA complexes induced by different cations by using synchrotron small angle x-ray scattering and confocal microscopy to show how different ion-mediated interactions are expressed in the self-assembled structures and phase behavior of AL–DNA complexes. The governing interactions in AL–DNA systems are complex: divalent ions can mediate strong attractions between different combinations of the components (such as DNA–DNA and membrane–membrane). Moreover, divalent cations can coordinate nonelectrostatically with lipids and modify the resultant membrane structure. We find that at low membrane charge densities AL–DNA complexes organize into a lamellar structure of alternating DNA and membrane layers crosslinked by ions. At high membrane charge densities, a new phase with no analog in cationic lipid–DNA systems is observed: DNA is expelled from the complex, and a lamellar stack of membranes and intercalated ions is formed. For a subset of the ionic species, high ion concentrations generate an inverted hexagonal phase comprised of DNA strands wrapped by ion-coated lipid tubes. A simple theoretical model that takes into account the electrostatic and membrane elastic contributions to the free energy shows that this transition is consistent with an ion-induced change in the membrane spontaneous curvature, c0. Moreover, the crossover between the lamellar and inverted hexagonal phases occurs at a critical c0 that agrees well with experimental values.
Keywords: colloids, like-charge attraction, membrane, self-assembly, x-ray
Gene therapy using either viral or synthetic vectors is currently one of the most promising strategies for developing cures for many hereditary and acquired diseases. Protocols have been approved for cancer, hemophilia, cystic fibrosis, neuromuscular disorders, and others (1). Although synthetic nonviral systems such as cationic liposomes generally transfect less efficiently than viruses, they have a number of advantages, such as high DNA packaging capacity and low immunogenicity. Cationic lipid (CL)–DNA complexes have emerged as one of the major nonviral DNA delivery platforms (1–7) and have been used to transfect a broad range of cell types and to deliver to cancer vaccines (8–10).
Anionic lipids (ALs) occur naturally in eukaryotic cell membranes, and DNA delivery systems based on ALs have recently been examined as an alternative to CLs because of their low cytotoxicity (11–13). ALs can be complexed with anionic DNA via interaction with multivalent cations such as Ca2+ and have been shown to successfully transfer oligonucleotides. An outstanding problem of this approach is the inefficient association between the ALs and DNA molecules, which is attributed to their like-charge electrostatic repulsion.
Rational design of AL–DNA vectors requires a coherent understanding of their structures and interactions. A useful starting point is the physics governing the analogous CL–DNA complexes (7, 14–30). DNA and CLs self-assemble into condensed multilamellar complexes, where parallel DNA chains are confined between lipid sheets (14, 15). By lowering the membrane's bending rigidity or changing its spontaneous curvature, an inverted hexagonal phase with an enhanced tendency for membrane fusion can be formed, in which DNA chains coated by lipid monolayers are packed into a 2D columnar hexagonal array (15). In these self-assembled complexes, the CL head groups neutralize the phosphate groups on the DNA chains, effectively releasing the counterions previously bound electrostatically to lipids and DNA, thus gaining translational entropy (23). The pioneering studies have shown that physical parameters, such as self-assembled nanostructure and membrane charge density, are crucial elements in transfection efficiency (31).
In this article, we systematically investigate the structure and interactions of AL–DNA complexes in the presence of different divalent cations. Although cationic membranes are attracted to DNA mainly via entropic forces because of counterion release, anionic membranes require multivalent cations to mediate attractions to anionic DNA through direct electrostatic “bridging” interactions (32). Further, the addition of multivalent ions can mediate strong attractions between different combinations of the constituents (membrane–membrane and DNA–DNA) (33, 34). Finally, divalent cations can also coordinate nonelectrostatically with lipid molecules and modify membrane structure (33).
We find that at low membrane charge densities AL–DNA complexes self-assemble into a lamellar structure, with alternating layers of like-charged DNA and anionic membranes bound together with divalent cations (Fig. 1A). As the membrane charge density is increased, we find a new phase with no analog in CL–DNA systems: DNA is systematically expelled from the complex, and the divalent ions mediate attractions between anionic membrane sheets to form a lipid lamellar stack (Fig. 1B). Divalent ions differ in their tendency to coordinate nonelectrostatically with lipids. Zn2+ ions are known to have strong nonelectrostatic interactions with lipids, involving significant dehydration of the lipid headgroups, whereas others such as Mg2+ have a much smaller effect (33). We find that as the global Zn2+ concentration is increased both lamellar phases are destabilized. The system instead forms an inverted hexagonal phase, comprised of a hexagonal array of divalent cation-coated DNA strands wrapped in turn by anionic membrane monolayers (Fig. 1C). Although Zn2+ is known to adhere to both lipids and DNA, we suggest that the change in AL–DNA structure is caused primarily by a cation-induced change in the membrane spontaneous curvature c0. Using simple theoretical considerations, we show that the expected crossover between the lamellar phase and hexagonal phase occurs at a critical c0 close to the experimentally observed values.
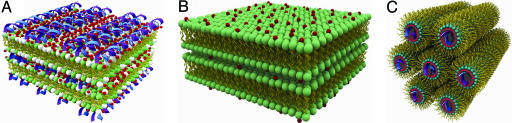
Fig. 1.
Schematic pictures of AL–DNA self-organized structures mediated by divalent cations. (A) Condensed DNA–ion–membrane lamellar structure with alternating layers of DNA and anionic membranes glued together by divalent cations. (B) Condensed ion–membrane lamellar structure in which charged membranes stacks are held together by divalent cations. (C) 2D inverted hexagonal structure in which hexagonal arrays of divalent cations coated DNA strands wrapped in the anionic membrane monolayer tubes.
Materials and Methods
DNA Preparation. Two kinds of dsDNA were used to ensure generality of the results. Monodisperse λ-phage DNA [48,502 bp (New England Biolabs)] was ethanolprecipitated (35) and resuspended in Millipore water at 10 mg/ml. The residual ion concentration is low («10 mM), so entropic effects from counterion release are expected to be small. Polydisperse calf thymus DNA, average length ≈75,000 bp (Amersham Pharmacia Biosciences), was dissolved in Tris-EDTA buffer (pH 8) then precipitated and resuspended in Millipore water at 10 mg/ml. For experiments with single-stranded polynucleotides, poly(A) (Amersham Pharmacia Biosciences) was used without further purification.
Liposome Preparation. Anionic membranes comprised of binary mixtures of the negatively charged lipid 1,2-dioleoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (sodium salt) (DOPG) and the homologous neutral lipid dioleoyl phosphatidyl choline (DOPC) (Avanti Polar Lipids) were used. Stock solutions of DOPG and DOPC (30 mg/ml) were mixed at the desired ratio. The mixture was dried under dry N2, and then desiccated under vacuum overnight. Millipore water was added to the dried lipids to obtain liposome solutions (25 mg/ml), which were then incubated at 37°C overnight. The resultant solution was sonicated to clarity and extruded through a 0.2-μm pore-size Nucleopore filter.
AL–DNA Complexes. DNA solutions, liposome solutions, and divalent salt stock solutions (MgCl2, CaCl2, CoCl2, CdCl2, MnCl2, and ZnCl2) were mixed to yield AL–DNA complexes at different global salt concentrations. The DNA-to-lipid charge (D/L ratio) stoichiometry is defined as the total charge of DNA divided by the total charge of the anionic DOPG lipids.
X-Ray Diffraction. AL–DNA complexes were sealed in quartz capillaries for small angle x-ray scattering (SAXS) experiments. For in-house SAXS experiments, CuKα radiation (λ = 1.54 Å) is monochromatized and focused by using Osmic multilayer optics and colliminated to a final beam size of ≈0.8 × 0.8 mm2. Scattered radiation is collected on a Bruker 2D wire detector (pixel size 105 μm). For SAXS experiments at the Stanford Synchrotron Radiation Laboratory (Palo Alto, CA) (BL4–2), 8.98-kev x-rays were focused to a size of ≈0.2 × 0.2 mm2. The scattered radiation is collected by using a MAR-Research (Hamburg) charge-coupled device (CCD) detector (pixel size 79 μm). For the SAXS experiments at the Advanced Photon Source (Argonne, IL, UNICAT BL-34ID), 9.93-keV x-rays were focused to ≈0.3 × 0.3 mm2. Diffraction data were recorded by using a Roper Scientific (Trenton, NJ) CCD detector (pixel size 22.5 μm). The 2D SAXS data from all set-ups were checked for mutual consistency. No radiation damage was observed for the exposure times used.
Confocal Microscopy. A Leica SP-2 confocal microscopy system was used to image the AL–DNA complexes in sequential line scan mode. YOYO-1 (excitation/emission 488/509 nm, Molecular Probes) was used to dye DNA solutions (≈0.1 mg/ml) with a dye loading of ≈1 in 30 DNA bp. 1,2-Dioleoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (ammonium salt), excitation/emission 550/590 nm, (Avanti Polar Lipids, Alabaster, AL) was used as the membrane dye. The weight ratio of the fluorescent lipid vs. total lipid content was set at 0.2%.
Model. We model how AL–DNA lipoplex's electrostatic and membrane elastic properties may compete to determine the phase stability. The model considers two equilibrium AL–DNA structures: lamellar and hexagonal. We use free energy estimates for these phases to calculate the range of membrane spontaneous curvatures for which the hexagonal structure is more stable than the lamellar. The total free energy is expressed as a sum of two contributions, FC = Felec + Felas. The first term represents the electrostatic interaction free energy between DNA and lipid, and the second represents the elastic free energy associated with bending the lipid layer.
For concreteness, we consider a solution containing a charge-to-neutral lipid ratio of φeff = N+/(N+ + N0), where N+ and N0 are the number of positively charged (Zn2+ bound AL) and net-neutral lipids, assuming that only these two lipids species are found in solution. We now briefly outline the terms and assumptions included in evaluating the lipoplex free energy.
Hexagonal Complexes. The elastic free energy per area associated with bending a lipid layer in the hexagonal complex can be accounted for by using the Helfrich free energy Felas = 1/2 k (c – c0)2, where k is the bending rigidity of the lipid layer, c = 1/Rm is the lipid layer curvature (Rm is the lipid radius of curvature), and c0 is the lipid's spontaneous curvature, defined as the curvature at which the bending free energy is minimum. This simplified expression ignores contributions to the free energy from saddle-splay curvature, because here we compare only the lamellar and hexagonal complexes. An additional elastic contribution is expected from the stretching of lipids facing the hexagonal interstices, dictated by space filling. This contribution is typically small, ≈0.1 kBT per lipid (T, temperature, kB, Boltzmann constant).
We model DNA as a charged rod of radius RD = 10 Å and a linear charge density along its backbone of e/b, where e is the elementary charge, and b = 1.7 Å is the average distance between charges along DNA. The total number of DNA charges in solution is D/b, with D the total length of DNA in solution. The ratio of lipid to DNA charges is therefore ρ = bN+/D; at the “isoelectric” point ρ = 1. As previously shown, we can estimate Felec by considering a capacitor-like model for DNA–lipid interactions (17). The free energy of the capacitor per length is Felec = (kBTlB/b2)ln(Rm/RD). Here, Rm is taken to be 13 Å and lB is the Bjerrum length ≈7.1 Å at room temperature.
Lamellar Complexes. Because only the interlayer spacing could be obtained from the diffraction pattern, we assume an average DNA–DNA spacing in the lamellar complex, based on the experimental evidence that all DNA is complexed, and adopt a simple cell model for lamellar complexes similar to that found in CL–DNA complexes. When all lipid and DNA is incorporated in complexes (one phase), the distance between strands is assumed to be d = aρ/2φeffb, where a = 70 Å2 is the area per lipid. The elastic bending energy is calculated as for the hexagonal phase. For a flat bilayer of area 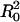 , a frustration energy Felas ≈ k is associated with deforming two monolayers into the joint flat configuration.
, a frustration energy Felas ≈ k is associated with deforming two monolayers into the joint flat configuration.
The electrostatic energy Felec can be evaluated by using a full free energy calculation based on the Poisson-Boltzmann equation as described (23, 28). In the following we set the charging free energy for the lamellar complex to zero in a relative scale and measure that of the hexagonal complex with respect to it.
Results and Discussion
Divalent ions can mediate interactions in AL–DNA complexes by three types of association: ion-mediated adhesion between ALs and DNA, ion-mediated adhesion between lipids on different membrane sheets, and ion-mediated interactions between lipids within a membrane sheet (assuming divalent ions do not induce significant attraction between DNA). Each of these can dominate under different physical conditions, and we expect this hierarchy of interactions to be expressed in the phase behavior of the AL–DNA system.
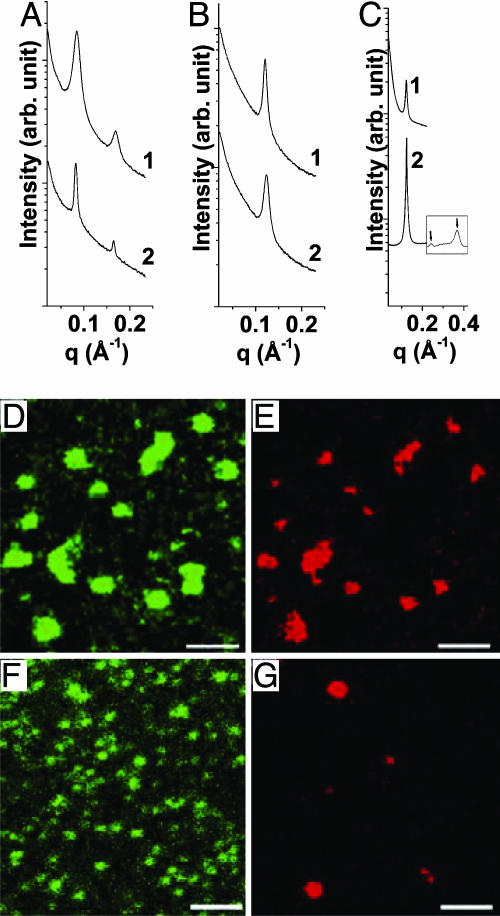
Transition Between Lamellar DNA–Ion–Membrane Complex and Lamellar Ion–Membrane Complex Coexisting with Expelled DNA. Complexes formed between ALs and DNA self-assemble into different structures at different membrane charge densities. At low membrane charge densities (DOPG/DOPC = 50/50 or less), AL–DNA complexes can organize into a lamellar DNA–ion–membrane structure, with alternating layers of DNA and anionic membranes “glued” together with divalent cations. We find this behavior in the intermediate concentration range (≈50–200 mM) for all of the divalent cations investigated (Mg2+, Ca2+, Zn2+, Co2+, Cd2+, and Mn2+). Representative SAXS data for AL–DNA complexes is shown in Fig. 2A ([M2+] = 50 mM for the different divalent cation species M, D/L = 4). Two sharp peaks are observed, corresponding to harmonics of the (001) peak of a 1D lamellar structure. The lamellar stack has a periodicity of 76.1 and 74.8 Å for DOPG/DOPC = 30/70 complexes made with Ca2+ and Cd2+, respectively. Similar diffraction signatures can be observed for Mg2+, Zn2+, Co2+, and Mn2+ ions. This periodicity corresponds well to the combined thickness of one DOPG/DOPC = 30/70 lipid bilayer (δm ≈ 48 Å), one layer of DNA (diameter ≈20 Å) and one layer of divalent counterions (≈4 Å each) at each of the two DNA–membrane interfaces.
Fig. 2.
Multiple lamellar phases can be formed with anionic lipids, DNA, and divalent cations. (A and B) SAXS data for the condensed DNA–ion–membrane lamellar complexes (30/70 DOPG/DOPC, A) and ion–membrane lamellar complexes (100/0 DOPG/DOPC, B) for different divalent cations (curve 1, [Cd2+] = 50 mM; curve 2, [Ca2+] = 50 mM). (C) A SAXS comparison of ion–membrane lamellar complex in the presence of expelled DNA (curve 1) with corresponding complex condensed with ions and ALs only (with no DNA) (curve 2). The equally spaced higher-order harmonics (data taken at a different resolution) indicate a lamellar phase. In both cases the membrane is 100/0 DOPG/DOPC and [Zn2+] = 100 mM. Note that the spatial periodicity is the same. (D–G) Confocal microscope pictures of AL–DNA complexes (D/L = 4). At low membrane charge density (D and E: 30/70 DOPG/DOPC membrane, [Zn2+] = 50 mM) DNA (green) is colocalized with anionic membranes (red) in every AL–DNA complex particle, whereas at high membrane charge density (F and G: 100/0 DOPG/DOPC membrane, [Zn2+] = 100 mM) the locations of the anionic membranes (green) are not correlated with that for DNA (red). DNA is expelled from the AL–DNA lamellar phase when increasing membrane charge density. (Scale bars: 2 μm.)
In contrast to CL–DNA structures, no in-plane DNA correlation is visible. The absence of an observable DNA peak may be caused by weak in-plane DNA ordering, which can, for example, be disrupted by ion-induced DNA kink formation at high Zn2+ densities (36, 37) or DNA–DNA crosslinking and condensation when Cd2+ or Mn2+ ions are used (34). The D/L has no influence on the lamellar DNA–ion–membrane structure. Moreover, the condensed DNA–ion–membrane lamellar structure is very stable; SAXS experiment showed that no structure changes occurred after storage for >18 months.
At high membrane charge densities, the lamellar periodicity, d, decreases by ≈25 Å. Data for representative DOPG/DOPC = 100/0 complexes are shown in Fig. 2. The measured values for d are 51.1 and 51.9 Å for Ca2+ and Cd2+, respectively. This periodicity is consistent with the combined thickness of one lipid bilayer plus one layer of ions (δm ≈45 Å for DOPG/DOPC = 100/0, dion ≈4Åfor the ions). These spacings are identical to those of the anionic membranes complexed with divalent ions in the absence of DNA. For example, for DOPG/DOPC = 100/0at[Zn2+] = 100 mM with no DNA, the lamellar periodicity is 51.1 Å, which is the same as the corresponding periodicity from Zn2+-induced DNA–ion–membrane complexes (Fig. 2C). Fig. 2C also shows the existence of equally spaced higher harmonics characteristic of lamellar phases. This is strong evidence that DNA is expelled from AL–DNA complexes with high membrane charge densities, which assemble into a lipid-only lamellar stack mediated by divalent cations. We speculate that the DNA may be generating the density fluctuations responsible for the difference in small-q small angle scattering in Fig. 2C, but more work is required to confirm this hypothesis.
To show the release of DNA from these lamellar complexes, we examined the interactions between fluorescently labeled anionic membranes and DNA by using confocal microscopy. For DNA and low charge density anionic membranes, typical confocal microscopy images are as shown in Fig. 2 (30:70 DOPG/DOPC membrane, D/L = 4, [Zn2+] = 50 mM). Fig. 2 D and E shows images for DNA (green) and membranes (red), respectively from the same location. DNA colocalizes with anionic membranes in every AL–DNA complex particle. This observation contrasts with confocal microscopy images for complexes formed between high charge density anionic membranes and DNA (100:0 DOPG/DOPC membrane, D/L = 4, [Zn2+] = 100 mM). Fig. 2 F and G shows images for DNA (green) and membranes (red), respectively from the same location. The membrane component is precipitated into dense, individual particles of different sizes by Zn2+ ions, whereas DNA is distributed almost homogeneously in the field of view (Fig. 2F). It is possible that some of the DNA may be crosslinked by the Zn2+ at some locations. It is clear, however, that DNA and anionic membranes are no longer associated with one another.
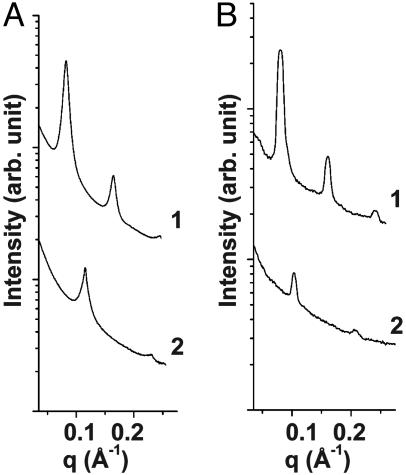
The relative stability of the two types of lamellar AL–DNA complexes, the DNA–ion–membrane lamellar phase (which forms at low membrane charge density) and the ion–membrane lamellar phase (which forms at high membrane charge density), changes as a function of divalent ion concentration. For AL–DNA complexes with low membrane charge density, a transition between the two lamellar phases occurs with divalent cation concentration. Typical SAXS data for AL–DNA complexes (DOPG/DOPC = 50/50) are shown in Fig. 3. For complexes at [Zn2+] = 20 mM, a lamellar phase with periodicity of 54.6 Å is observed (Fig. 3A, curve 2), which is consistent with the condensed ion–membrane lamellar structure, indicating the membranes prefer to adhere to one another and that DNA is excluded. For complexes at [Zn2+] = 50 mM (Fig. 3A, curve 1), three orders of diffraction peaks indicate that the lamellar periodicity expands to 76.4 Å, which corresponds well to one 50/50 DOPG/DOPC membrane bilayer (δm ≈47 Å), one DNA layer, and two layers of Zn2+ ions. This observed periodicity indicates the formation of the condensed DNA–ion–membrane lamellar phase. A similar transition occurs for AL–DNA complexes with DOPG/DOPC = 30/70 membranes (Fig. 3B).
Fig. 3.
Structural transition between two lamellar phases as a function of salt concentration. SAXS data for the AL–DNA complexes comprised of calf thymus DNA with 50/50 DOPG/DOPC membrane (curve 1, [Zn2+] = 50 mM; curve 2, [Zn2+] = 20 mM) (A) and 30/70 DOPG/DOPC membrane (curve 1: [Mg2+] = 50 mM; curve 2: [Mg2+] = 20 mM) (B). The AL–DNA complexes change from a DNA–ion–membrane lamellar structure (curve 1) to an ion-membrane lamellar structure (curve 2) as the ion concentration is decreased.
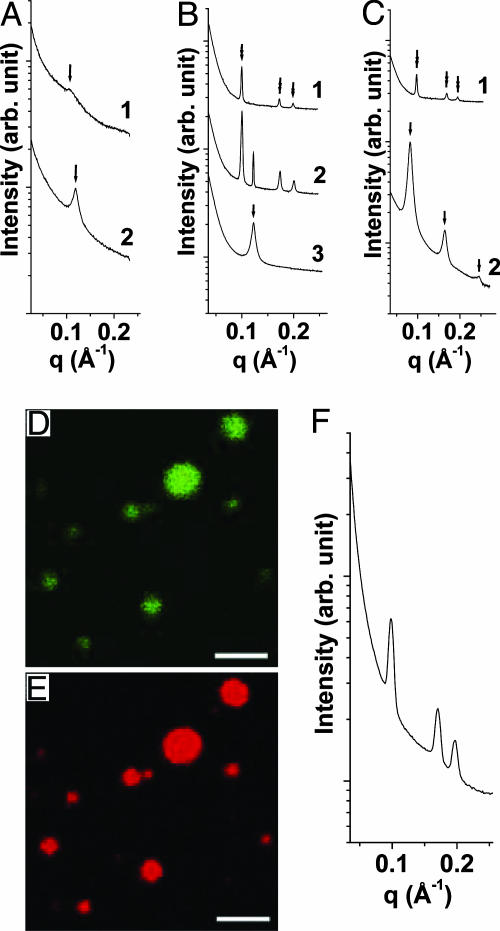
Inverse Hexagonal DNA–Ion–Membrane Complexes. At high enough divalent ion concentrations, screening must eventually dominate and the ion-mediated lamellar structures are expected to dissociate. This is, in fact, what we observe for most of the ions (such as Mg2+ and Ca2+), as illustrated by the SAXS data for AL–DNA complexes (DOPG/DOPC = 70/30, D/L = 4) induced by Mg2+ ions (Fig. 4A). As [Mg2+] is increased from 50 to 500 mM, the lamellar periodicity increases from 52.8 to 59.8 Å. Moreover, the first-order diffraction peak has decreased to ≈1/20 of its original intensity, indicating that the lamellar correlations are significantly weaker.
Fig. 4.
Lamellar and inverted hexagonal phases of AL–DNA complexes. (A) AL–DNA complexes dissociate at high salt for most divalent ions, as seen in an example using Mg2+-induced complexes formed with DOPG/DOPC = 70/30 membranes and calf thymus DNA (curve 1, [Mg2+] = 500 mM; curve 2, [Mg2+] = 50 mM). The intermembrane distance increases and the correlation peak is significantly weaker for the high salt complex. (B and C) For curvature-inducing ions such as Zn2+, an inverted hexagonal phase is formed instead at high salt, as seen for complexes formed with 100/0 DOPG/DOPC membranes (curve 1, [Zn2+] = 500 mM; curve 2, [Zn2+] = 300 mM; curve 3, [Zn2+] = 100 mM) (B) and for complexes formed with 50/50 DOPG/DOPC membranes (curve 1, [Zn2+] = 500 mM; curve 2, [Zn2+] = 50 mM) (C). Peaks under arrow and double arrow correspond to lamellar structure and hexagonal structure scatterings, respectively. (F) SAXS data for AL–single-stranded poly(A) complex indicate no significant change in the lattice parameter compared with dsDNA, so membranes do not adhere conformally to the DNA (the membrane is 50/50 DOPG/DOPC and [Zn2+] = 500 mM). (D and E) Confocal microscope pictures show that DNA (green) and membrane (red) are colocalized in AL–DNA inverted hexagonal complexes (D/L = 4, DOPG/DOPC = 100/0 membrane, [Zn2+] = 500 mM). (Scale bars: 2 μm.)
Zinc ions represent a class of ions that can strongly interact nonelectrostatically with lipids (25, 33), which is reflected in the self-assembly of Zn2+-induced AL–DNA complexes, qualitatively different from those induced by other divalent ions. At high concentrations, Zn2+ induces a transition from the two lamellar structures to a DNA–ion–membrane inverse columnar hexagonal structure. For high charge density membranes (100/0 DOPG/DOPC membrane, D/L = 4), SAXS data indicates a transition from the condensed ion–membrane lamellar phase to the inverted hexagonal phase (Fig. 4B). For [Zn2+] = 100 mM (Fig. 4B, curve 3), the diffraction peak corresponds to a spacing of 51.5 Å, which is the signature periodicity of the condensed ion–membrane lamellar phase. For [Zn2+] = 500 mM (Fig. 4B, curve 1), this series of peaks has been replaced by three new diffraction peaks at 0.100, 0.173, and 0.200 Å–1. These peak positions have the characteristic 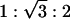 ratios for a 2D hexagonal structure. At [Zn2+] = 300 mM (Fig. 4B, curve 2) a coexistence between the lamellar and hexagonal phases can be seen. The same phase behavior has been observed for DNA complexed with DOPG/DOPC = 70/30 membranes. The unit cell parameter of this hexagonal structure is
ratios for a 2D hexagonal structure. At [Zn2+] = 300 mM (Fig. 4B, curve 2) a coexistence between the lamellar and hexagonal phases can be seen. The same phase behavior has been observed for DNA complexed with DOPG/DOPC = 70/30 membranes. The unit cell parameter of this hexagonal structure is 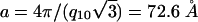 , which corresponds quite well to the thickness of one 100/0 DOPG/DOPC membrane bilayer (δm ≈45 Å) plus the diameter of one DNA chain (≈20 Å) and two Zn2+ ions (2 × 4 Å). This agreement suggests that this is an inverted hexagonal phase comprised of DNA strands wrapped by ion-coated lipid tubes.
, which corresponds quite well to the thickness of one 100/0 DOPG/DOPC membrane bilayer (δm ≈45 Å) plus the diameter of one DNA chain (≈20 Å) and two Zn2+ ions (2 × 4 Å). This agreement suggests that this is an inverted hexagonal phase comprised of DNA strands wrapped by ion-coated lipid tubes.
A transition from the condensed DNA–ion–membrane lamellar phase to the inverted hexagonal phase can be observed in AL–DNA complexes with low charge density membranes. SAXS data for AL–DNA complexes (DOPG/DOPC = 50/50, D/L = 4) is shown in Fig. 4C. At[Zn2+] = 50 mM (Fig. 4C, curve 2), the equally spaced diffraction peaks indicate the existence of the DNA–ion–membrane lamellar phase with a periodicity of 76.4 Å. At [Zn2+] = 500 mM (Fig. 4C, curve 1), the system self-assembles into a 2D inverted columnar hexagonal phase. The peaks under the double arrow in Fig. 4C have positions 0.096, 0.166, and 0.192 Å–1, which has the 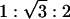 ratio of the inverted hexagonal phase with unit cell parameter a = 75.6 Å. A similar transition is seen in AL–DNA complexes with 30/70 DOPG/DOPC membranes.
ratio of the inverted hexagonal phase with unit cell parameter a = 75.6 Å. A similar transition is seen in AL–DNA complexes with 30/70 DOPG/DOPC membranes.
Using confocal microscopy, we verified that these inverted hexagonal AL–DNA complexes are comprised of both DNA and anionic membranes (Fig. 4 D and E, 100/0 DOPG/DOPC membrane, D/L = 4, [Zn2+] = 500 mM). Fig. 4 D and E corresponds to images for DNA and membranes, respectively. Clearly, DNA and membrane components are colocalized in each of the spheroidal aggregates, as expected.
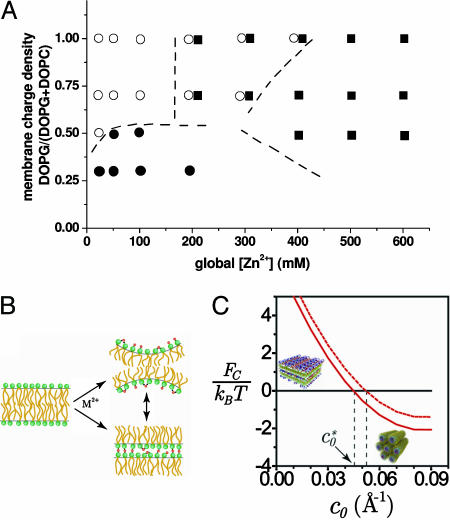
It is interesting to assess whether the formation of the hexagonal phase is caused by the electrostatic adhesion of the membrane to the surface of DNA via the Zn2+ cations. Fig. 4F shows SAXS data from inverted hexagonal AL–DNA complexes formed with single-stranded polynucleotide [poly(A)] rather than dsDNA. Three peaks at positions 0.098, 0.170, and 0.196 Å–1 can clearly be observed, which have the characteristic ratios of 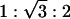 from a hexagonal structure with lattice parameter a = 74.0 Å. The effective diameter of single-stranded poly(A) is approximately half that of dsDNA. However, the size of the hexagonal unit cell parameter, a, is similar to that obtained from AL–DNA complexes with dsDNA. This result clearly demonstrates that the membrane does not follow the curvature of the DNA surface via ion-mediated interactions. It also suggests that there may be an optimum ion-induced curvature (minimum “tube radius”) for the membrane. We have also examined complexes that form between Zn2+ and the same lipids in the absence of DNA, and a cubic phase is observed. This finding not only emphasizes the role of Zn2+ in inducing a nonzero lipid spontaneous curvature, but also suggests a role for DNA in the redistribution of curvature into the cylindrical pores that encapsulate DNA in the inverted-hexagonal phase. The behavior of AL–DNA is summarized in the phase diagram in Fig. 5A.
from a hexagonal structure with lattice parameter a = 74.0 Å. The effective diameter of single-stranded poly(A) is approximately half that of dsDNA. However, the size of the hexagonal unit cell parameter, a, is similar to that obtained from AL–DNA complexes with dsDNA. This result clearly demonstrates that the membrane does not follow the curvature of the DNA surface via ion-mediated interactions. It also suggests that there may be an optimum ion-induced curvature (minimum “tube radius”) for the membrane. We have also examined complexes that form between Zn2+ and the same lipids in the absence of DNA, and a cubic phase is observed. This finding not only emphasizes the role of Zn2+ in inducing a nonzero lipid spontaneous curvature, but also suggests a role for DNA in the redistribution of curvature into the cylindrical pores that encapsulate DNA in the inverted-hexagonal phase. The behavior of AL–DNA is summarized in the phase diagram in Fig. 5A.
Fig. 5.
The effect of specific ion–lipid interactions on AL–DNA phase behavior. (A) Phase diagram for the AL–DNA–Zn2+ system. Shown are condensed ion–membrane lamellar complexes (○), condensed DNA–ion–membrane lamellar complexes (•), and condensed 2D inverse hexagonal DNA–ion–membrane structures (▪). Approximate phase and coexistence boundary lines are shown. (B) Schematic representation of divalent-mediated changes in intrinsic membrane curvature and intermembrane binding. (C) Model complex free energy for the lamellar (in black, set to zero) and hexagonal (in red) complexes per one DNA charge as a function of membrane curvature for φeff = 0.5 in the isoelectric case. Curves are shown for 1 mM (solid line) and 30 mM (dotted line) salt solutions.
Modeling the Lamellar to Hexagonal Transition. Modeling the effect of divalent ions on interactions between colloids by using simple mean-field theories is notoriously difficult. While attraction between like-charged objects is often found experimentally for divalent and trivalent ions, this attraction cannot be accounted for by using Poisson-Boltzmann theory for point-like ions alone; the effect of correlations between charges is not included in this type of approach (32). Additional nonelectrostatic contributions to the free energy are also often key, because many divalent and trivalent ions tend to adhere strongly to lipid molecules. Zinc ions, for example, are known to bind to both charged and uncharged lipids, changing the bilayer effective surface charge density and elastic bending properties with concomitant lipid headgroup dehydration (see Fig. 5B) (25, 38). In contrast, whereas Zn2+ is also known to interact with DNA, this interaction alone is insufficient to cause DNA collapse in solution (34).
We use here a phenomenological description of the effect of Zn2+ ions, because its quantitative effect on membrane elastic properties and the dependence on ion concentration in the bulk are unknown. Nonelectrostatic coordination of Zn2+ ions to DNA or lipids is taken into account in two ways. First, we assume an effective Zn2+ contribution to the lipid's tendency to form aggregates with a curved interface; we neglect the effect of Zn2+ binding on the bending rigidity k. Second, we assume that the DNA–lipid complexes may be viewed as an overcharged membrane interacting with an oppositely charged DNA. Membrane-adhering Zn2+ ions mediate the attraction of lipid to DNA.
These assumptions allow us to regard the complex as an analog of a CL–DNA complex, with Zn2+ bound lipids filling the role of CLs. For CL–DNA complexes, experiment and theory have shown that when equal numbers of DNA and lipid charges interact in solution (the “isoelectric point”) apposed charged surfaces interact in the complexes with almost no mobile counterions present, caused by their release into the bulk. Based on previous calculations, we extend this approach and consider isoelectric AL–DNA-Zn2+ complexes to estimate the electrostatic energy of the complex by using simple expressions such as the charging energy of a capacitor, detailed in Materials and Methods (17, 28, 39). We then determine the relative stability (free energy) of each phase by using simplified expressions for electrostatic and membrane elastic contributions to the free energy, while accounting for ideal mixing of charged and uncharged lipids in the 2D membrane plane.
Phase Stability. Fig. 5C shows the complex free energy of the lamellar and hexagonal complexes versus membrane spontaneous curvature for a single DNA charge. We assume membrane rigidity of k = 10 kBT, membrane charged/total lipid composition φeff = 0.5, and divalent salt concentration of 1 or 30 mM. We also assume that the curvature of the lipid interface in the hexagonal complex is c = 1/13 Å–1, matching closely the ranges of radii found in the AL–DNA Zn2+ phases at high [Zn2+]. Note that the model concentrates on the AL–DNA lamellar-hexagonal transition and does not take into account the possible formation of other phases such as the collapsed lamellar lipid-only phase, other lipid and lipoplex phases, or the possibility that at high salt concentrations both phases become unstable and tend to disintegrate.
For low membrane spontaneous curvature, Fig. 5C shows that the lamellar configuration is preferred because of the large unfavorable bending energy in the hexagonal complex. However, at a certain Zn2+-induced spontaneous curvature 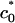 the free energies of the lamellar and hexagonal complexes become equal, indicating that the cost of bending the lipid layer around DNA exactly matches the direct electrostatic energy with the entropic gain of expelling an additional number of bound counterions from the tightly wrapped hexagonal phase. The crossover region is in the range
the free energies of the lamellar and hexagonal complexes become equal, indicating that the cost of bending the lipid layer around DNA exactly matches the direct electrostatic energy with the entropic gain of expelling an additional number of bound counterions from the tightly wrapped hexagonal phase. The crossover region is in the range 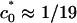 to 1/23 Å–1. The higher the salt concentration, the less the gain from direct electrostatic interactions, and the closer the membrane spontaneous curvature must match that of DNA to achieve wrapping. Interestingly,
to 1/23 Å–1. The higher the salt concentration, the less the gain from direct electrostatic interactions, and the closer the membrane spontaneous curvature must match that of DNA to achieve wrapping. Interestingly, 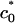 only weakly depends on solution ionic strength, indicating that only a small number of counterions are expected to still reside in the isoelectric complex and screen direct electrostatic interactions. We emphasize that
only weakly depends on solution ionic strength, indicating that only a small number of counterions are expected to still reside in the isoelectric complex and screen direct electrostatic interactions. We emphasize that 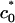 is the transition point between the lamellar and inverted hexagonal phases and therefore not necessarily the measured curvature of the tubes in the hexagonal complexes.
is the transition point between the lamellar and inverted hexagonal phases and therefore not necessarily the measured curvature of the tubes in the hexagonal complexes.
When comparing the two phases, our model accounts for a competition of counterion release, electrostatic matching, and membrane elastic deformations. We find that the strong binding energies of Zn2+ to lipid (and to a lesser extent to DNA) that are expected to play a crucial role in complexing lipid and DNA also play a role in the transition from lamellar to hexagonal structures through their effect on membrane's spontaneous curvature.
Conclusions
We have investigated AL–DNA complexes induced by a range of divalent ions to show how different ion-mediated interactions are expressed in the self-assembled structures. The condensed ion–membrane lamellar phase, which requires ion-mediated adhesion between membrane sheets, occurs at high membrane charge densities. The condensed DNA–ion–membrane lamellar phase, made possible by ion-mediated DNA–membrane contacts, occurs at low membrane charge densities. A transition between the two lamellar structures as a function of salt can occur. For extremely high salt levels, ion-mediated interactions between lipids in a given membrane dominate and an inverted hexagonal phase with encapsulated DNA may form. We suggest that the effect of ion binding on lipid's spontaneous curvature is sufficient to explain the lamellar to inverted hexagonal transition.
Acknowledgments
We thank Ilya Koltover, Don Rau, Horia Petrache, and Adrian Parsegian for helpful discussions. This work was supported in part by the U.S. Department of Energy, Division of Materials Sciences under Award DEFG02-91ER45439 through the Frederick Seitz Materials Research Laboratory at the University of Illinois at Urbana–Champaign, the National Science Foundation Nanoscience and Engineering Initiative, and the Petroleum Research Fund.
Author contributions: G.C.L.W. designed research; H.L. and D.H. performed research; H.L., D.H., and G.C.L.W. analyzed data; and H.L., D.H., and G.C.L.W. wrote the paper.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: AL, anionic lipid; CL, cationic lipid; SAXS, small angle x-ray scattering; DOPG, 1,2-dioleoyl-sn-glycero-3-[phospho-rac-(1-glycerol)]; DOPC, dioleoyl phosphatidyl choline; D/L, DNA-to-lipid charge ratio.
References
- 1.Templeton, N. S. (2004) Gene Therapy: Therapeutic Mechanisms and Strategies (Dekker, New York), 2nd Ed.
- 2.Felgner, P. L., Gadek, T. R., Holm, M., Roman, R., Chan, H. W., Wenz, M., Northrop, J. P., Ringold, G. M. & Danielsen, M. (1987) Proc. Natl. Acad. Sci. USA 84, 7413–7417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Felgner, P. L. & Ringold, G. M. (1989) Nature 337, 387–388. [DOI] [PubMed] [Google Scholar]
- 4.Fraley, R., Subramani, S., Berg, P. & Papahadjopoulos, D. (1980) J. Biol. Chem. 255, 10431–10435. [PubMed] [Google Scholar]
- 5.Safinya, C. R. (2001) Curr. Opin. Struct. Biol. 11, 440–448. [DOI] [PubMed] [Google Scholar]
- 6.Barenholz, Y. (2001) Curr. Opin. Colloid Interface Sci. 6, 66–77. [Google Scholar]
- 7.Podgornik, R., Harries, D., Strey, H. H. & Parsegian, V. A. (2004) in Gene Therapy: Therapeutic Mechanisms and Strategies, ed. Templeton, N. S. (Dekker, New York), 2nd Ed., pp. 301–332.
- 8.Stopeck, A. T., Hersh, E. M., Brailey, J. L., Clark, P. R., Norman, J. & Parker, S. E. (1998) Cancer Gene Ther. 5, 119–126. [PubMed] [Google Scholar]
- 9.Chesnoy, S. & Huang, L. (2000) Annu. Rev. Biophys. Biomol. Struct. 29, 27–47. [DOI] [PubMed] [Google Scholar]
- 10.Nabel, G. J., Nabel, E. G., Yang, Z. Y., Fox, B. A., Plautz, G. E., Gao, X., Huang, L., Shu, S. Y., Gordon, D. & Chang, A. E. (1993) Proc. Natl. Acad. Sci. USA 90, 11307–11311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fillion, P., Desjardins, A., Sayasith, K. & Lagace, J. (2001) Biochim. Biophys. Acta Biomembr. 1515, 44–54. [DOI] [PubMed] [Google Scholar]
- 12.Lakkaraju, A., Dubinsky, J. M., Low, W. C. & Rahman, Y. E. (2001) J. Biol. Chem. 276, 32000–32007. [DOI] [PubMed] [Google Scholar]
- 13.Patil, S. D. & Rhodes, D. G. (2000) Nucleic Acids Res. 28, 4125–4129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Radler, J. O., Koltover, I., Salditt, T. & Safinya, C. R. (1997) Science 275, 810–814. [DOI] [PubMed] [Google Scholar]
- 15.Koltover, I., Salditt, T., Radler, J. O. & Safinya, C. R. (1998) Science 281, 78–81. [DOI] [PubMed] [Google Scholar]
- 16.Gershon, H., Ghirlando, R., Guttman, S. B. & Minsky, A. (1993) Biochemistry 32, 7143–7151. [DOI] [PubMed] [Google Scholar]
- 17.May, S. & Ben-Shaul, A. (1997) Biophys. J. 73, 2427–2440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dan, N. (1998) Biochim. Biophys. Acta Biomembr. 1369, 34–38. [DOI] [PubMed] [Google Scholar]
- 19.Sternberg, B., Sorgi, F. L. & Huang, L. (1994) FEBS Lett. 356, 361–366. [DOI] [PubMed] [Google Scholar]
- 20.Simberg, D., Danino, D., Talmon, Y., Minsky, A., Ferrari, M. E., Wheeler, C. J. & Barenholz, Y. (2001) J. Biol. Chem. 276, 47453–47459. [DOI] [PubMed] [Google Scholar]
- 21.Pitard, B., Aguerre, O., Airiau, M., Lachages, A. M., Boukhnikachvili, T., Byk, G., Dubertret, C., Herviou, C., Scherman, D., Mayaux, J. F. & Crouzet, J. (1997) Proc. Natl. Acad. Sci. USA 94, 14412–14417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bruinsma, R. (1998) Eur. Phys. J. B 4, 75–88. [Google Scholar]
- 23.Wagner, K., Harries, D., May, S., Kahl, V., Radler, J. O. & Ben-Shaul, A. (2000) Langmuir 16, 303–306. [Google Scholar]
- 24.Barreleiro, P. C. A., Olofsson, G. & Alexandridis, P. (2000) J. Phys. Chem. B 104, 7795–7802. [Google Scholar]
- 25.Binder, H., Arnold, K., Ulrich, A. S. & Zschornig, O. (2001) Biophys. Chem. 90, 57–74. [DOI] [PubMed] [Google Scholar]
- 26.Kennedy, M. T., Pozharski, E. V., Rakhmanova, V. A. & MacDonald, R. C. (2000) Biophys. J. 78, 1620–1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Huebner, S., Battersby, B. J., Grimm, R. & Cevc, G. (1999) Biophys. J. 76, 3158–3166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Harries, D., May, S., Gelbart, W. M. & Ben-Shaul, A. (1998) Biophys. J. 75, 159–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Radler, J. O. (2001) in Electrostatic Effects in Soft Matter and Biophysics, eds. Holm, C., Kekicheff, P. & Podgornik, R. (Kluwer, Dordrecht, The Netherlands), pp. 441–458.
- 30.Lasic, D. D., Strey, H., Stuart, M. C. A., Podgornik, R. & Frederik, P. M. (1997) J. Am. Chem. Soc. 119, 832–833. [Google Scholar]
- 31.Lin, A. J., Slack, N. L., Ahmad, A., Koltover, I., George, C. X., Samuel, C. E. & Safinya, C. R. (2000) J. Drug Target. 8, 13–27. [DOI] [PubMed] [Google Scholar]
- 32.Lau, A. W. C., Pincus, P., Levine, D. & Fertig, H. A. (2001) Phys. Rev. E 63, 051604. [DOI] [PubMed] [Google Scholar]
- 33.Arnold, K. (1995) in Structure and Dynamics of Membranes, eds. Lipowsky, R. & Sackmann, E. (Elsevier, Amsterdam), pp. 903–957.
- 34.Rau, D. C. & Parsegian, V. A. (1992) Biophys. J. 61, 246–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sambrook, J., Fritsch, E. F. & Maniatis, T. (1989) Molecular Cloning: A Laboratory Manual (Cold Spring Harbor Lab. Press, Plainview, NY), 2nd Ed.
- 36.Han, W. H., Dlakic, M., Zhu, Y. W. J., Lindsay, S. M. & Harrington, R. E. (1997) Proc. Natl. Acad. Sci. USA 94, 10565–10570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nickol, J. & Rau, D. C. (1992) J. Mol. Biol. 228, 1115–1123. [DOI] [PubMed] [Google Scholar]
- 38.Ortiz, A., Killian, J. A., Verkleij, A. J. & Wilschut, J. (1999) Biophys. J. 77, 2003–2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Harries, D., Ben-Shaul, A. & Szleifer, I. (2004) J. Phys. Chem. B 108, 1491–1496. [Google Scholar]