Chemical exchange 2D IR of hydrogen-bond making and breaking

Abstract

The involvement of chemical exchange in 2D IR heterodyne echo spectroscopy is characterized through the hydrogen-bond exchange between CH₃OH and the CN of CH₃CN. The exchange dynamics on the hydrogen-bond potential surfaces associated with different quantum states of the high-frequency CN stretching mode contributes to strong cross peaks between CN groups in two different chemical configurations and provides firm evidence of the hydrogen exchange between them. In analogy with NMR, the chemical exchange is seen in both slow and dynamic regimes. The relative magnitudes of the cross peaks at various population periods measure the picosecond regime time constants for H-bond transfer, whereas the temperature dependences indicate that the activation energy for the exchange from the H-bonded state to the free state is ≈6.2 kJ·mol^–1. The results suggest that the hydrogen-bond dynamics is very similar in both vibrational quantum states of CN, suggesting that this stretching mode is not strongly coupled to the H-bond breaking reaction coordinate. The likely manifestations of chemical exchange in 2D IR experiments are discussed.

Vibrational spectroscopy has provided important experimental access to the microscopic aspects of ultrafast hydrogen-bond processes in complex systems. The dynamics of OH or OD stretching vibrational modes in water (1–10) or alcohol oligomers (11), the vibrations of molecular (12, 13) and atomic (14) aqueous ions, and the N–H and CO stretching modes, including those in peptides or proteins in water (15–23) and alcohols (24), are very sensitive to and correlated with the structural and dynamical properties of hydrogen bonds. In principle, the shape of the conventional IR absorption spectrum provides information on the equilibrium dynamics of a hydrogen-bonded system. However, in many cases, the line shapes are determined by population lifetimes and spectral diffusion processes that often cannot be reduced to the unique set of parameters needed to describe the frequencies and amplititudes of coupled solvent nuclear motions. With the help of multidimensional nonlinear spectroscopic techniques in the IR spectral region, it has become possible to probe these hydrogen-bond dynamics and extract more details on the structures and dynamics with high time resolution (25). Dynamical information on the O–H, O–D, and N–H stretching modes of intermolecular hydrogen-bonded systems such as alcohols, water, and amides has been obtained in the form of vibrational lifetimes, energy transfer, hydrogen-bond breaking and reforming rates, and the time dependence of spectral diffusion. In addition, the motions of hydrogen bonds in peptides and liquids are of importance in many chemical and biological processes. In protein secondary structures, the amide carbonyl group is very often involved in hydrogen bonding to water, N–H groups, or both. Much remains to be learned from experiments on the vibrational populations and coherences about the dynamics of these hydrogen bonds for a wide range of environments. In the present work, we describe an approach called chemical exchange 2D IR that can have wide applicability for the study of such ultrafast dynamics.

Chemical exchange processes in equilibrium dynamics have been studied since the earliest days of NMR, and one of the most important common uses of 1D and 2D NMR methods has been in the determination of rate constants (26). The same general concepts should be applicable to the recent technique of 2D IR (27, 28) that is more fully described in recent reviews (29–32). However, the time scales of the exchanges observed with 2D IR will be shifted into the picosecond/femtosecond regime because the most accurate exchange data are obtained when the reaction rate is fast compared with the population relaxation time but slow compared with the spectral parameters affected by the exchange. In the presence of chemical exchange, the usual fluctuating frequency in the nonlinear response function (29, 33) must incorporate transitions between the exchanging states. In this study, we report results on the (methyl) alcohol OH···NC–Me hydrogen bond exchange, which will be examined through the fluctuations in the CN frequency at ≈2,250 cm^–1. This case is one in which, on the picosecond time scale, the CN vibrational frequency fluctuates between that found in a free structure and an H-bonded structure.

The 2D IR is a three-pulse experiment. After a vibrational coherence time, τ, the system enters a population period for time T after which it is driven into a new coherent state from which a signal field is detected at time t. In a chemical exchange experiment, the coherence, initially associated with one chemical state, may be transferred to another chemical species during the delay periods. The presence of deterministic processes in the vibrational dynamics requires that the third-order responses due to the various Liouville pathways involved in 2D IR be modified. The essential difference with the picture in the absence of exchange is that the phase evolutions of the vibrational coherences, which are represented by the integrated frequency fluctuations caused by the interactions of the vibrator with the medium, contain components where the system jumps back and forth stochastically between a small number of identifiable chemical states. In the vibrational response functions that are used in conventional nonlinear spectroscopy, the number of these states may become very large, and the phase evolution characterizes the dynamics of a nearly continuous, inhomogeneous distribution of frequencies. One of the advantages of 2D IR in exchange studies of spectrally isolated (even uncoupled) vibrators is that the existence of chemical exchange can be firmly established from the existence of the cross peaks. In the present study, we give quantitative consideration to the exchange processes that occur during the population period and comment on the existence of dynamic exchange during the coherence evolution and detection periods.

Materials and Methods

Materials. A solution of 1.5 M CH₃CN in MeOH was used for the 2D IR experiments. The optical density of the sample was ≈0.1 with a 25-μm path length CaF₂ cell. FTIR spectra of solutions of CH₃CN in MeOH with different concentrations were recorded at various temperatures ranging from –17°C to 60°C. The relative intensities of the CN stretching mode region in the FTIR spectra were essentially independent of concentration.

The 2D IR Method. Fourier-transform limited 75-fs pulses with a center frequency of 2,250 cm^–1 were used in the 2D IR experiments. Three of these pulses, each with energy of 400 nJ and wave vectors k₁, k₂, and k₃, were incident on the sample. The phase-matched signal at wave vector –k₁+k₂+k₃ was detected by heterodyning it with a local oscillator pulse that always preceded the signal pulse by a fixed interval of ≈1.5 ps. The interval between pulses 1 and 2 is denoted as τ, that between pulses 2 and 3 is denoted as T, and that between pulse 3 and the detected signal is denoted as t. The rephasing sequence is one in which the beam k₁ arrives earlier than k₂ by an amount τ. The sequence when k₂ arrives earlier than k₁ by τ is named the nonrephasing sequence. The signal and local oscillator pulses were combined at the focal plane of a monochromator having a 64-element mercury–cadmium–telluride array detector (InfraRed Associates, Stuart, FL). Each detector element is 200 μm in width and 1 mm in height. The focal length of the monochromator is 270 mm, and the groove density of the grating used in our experiments was 120 lines per mm. The raw data collected by using this method was in the form of a 2D array of time τ in 2-fs steps from –6 to 6 ps and wavelength in ≈6-nm steps. To obtain absorptive or correlation spectra, rephasing and nonrephasing 2D frequency spectra were added. The waiting time, T, was varied from 0 to 10 ps with 1-ps intervals. Details of the 2D IR data processing are described in refs. 21 and 23. In general, the experiment yields a function S(τ, t, T) of the three time intervals which can be double Fourier-transformed along τ and t into the 2D spectra 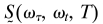for each population interval T.

Results and Discussion

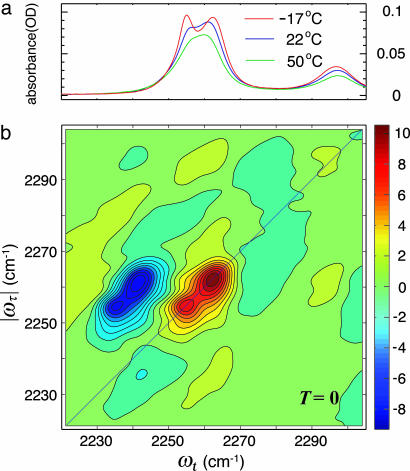
Fig. 1a shows the FTIR spectra of the samples at various temperatures in the region of the CN stretch. The IR spectrum in the CN region shown in Fig. 1 consists of two bands, each having a width of ≈8cm^–1 and separated by ≈8cm^–1. One band (A) is at the CN···H-bonded frequency of 2,262 cm^–1 (ε_max ≈ 35 M^–1·cm^–1) seen in water and the other (B) is assigned as the free CN frequency of 2,254 cm^–1 seen in polar nonhydroxyllic solvents (34). The relative intensity of these two bands changes dramatically with temperature in the range –30°C to 60°C, and beyond ≈50°C, it begins to coalesce into one band as shown in Fig. 1. This phenomenon was first reported in ref. 34, but it was not explained. These features strongly suggested to us that the CN is making and breaking its H bond to the alcohol on the picosecond time scale at ≈300 K.

Fig. 1.

Linear and 2D IR spectra of acetonitrile in methanol. (a) Linear FTIR spectra of CH₃CN in MeOH at various temperatures. (b) The real part of the absorptive 2D IR spectrum of CH₃CN in MeOH at T = 0 at –17°C, displaying a wide frequency range. The band at 2,297 cm^–1, a combination band of the CH bend and CC stretch of acetonitrile, has cross peaks with the other transitions.

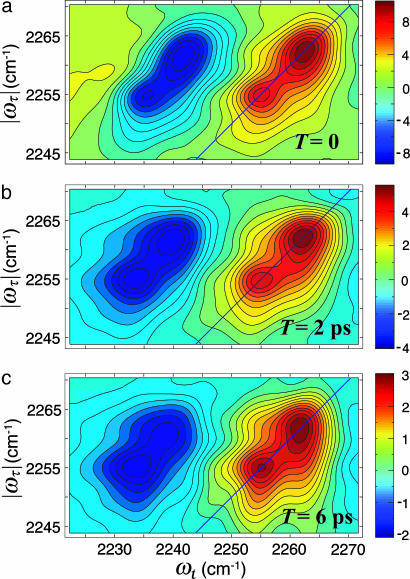
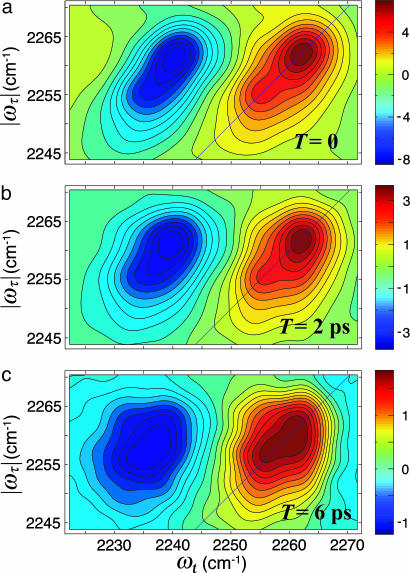
The 2D IR spectrum of a single vibrator would consist of a peak on the diagonal corresponding to the v = 0 → v = 1 part of the signal and a peak shifted to lower values of ω_t by the diagonal anharmonicity, which for the CN stretch is 18.9 ± 0.2 cm^–1 for both the free and bound states. The main nonlinear results are shown in Fig. 1b, which shows an overview of the 2D IR spectrum, and Figs. 2 and 3, which show the 2D IR spectra in the region of the CN stretch for three population times at two temperatures. A collection of many such 2D IR data sets and the derived 2D heterodyned transient grating data, S̃(τ = 0, ω_t, T), yielded the population relaxation times of the v = 1 states of the free and bonded CN stretch as 5 ± 0.5 ps, so these decays contribute only ≈12.5% to the full widths of the IR spectra. The key experimental observations are the clear existence of cross peaks between the A (H-bonded CN) and B (free CN) diagonal 2D IR peaks and their dependence on temperature. Furthermore, the 2D IR spectra of the v = 1 → v = 2 and the v = 0 → v = 1 spectral regions are well enough separated by 18.9 cm^–1 that they can be interpreted and discussed separately. Qualitatively, the appearance of the 2D IR spectra in the v = 1 → v = 2 and the v = 0 → v = 1 spectral regions is very similar. They have approximately the same dynamical parameters based on shape, cross peaks, and time dependence. The overall width is somewhat larger for the v = 1 → v = 2 region. However, in both cases, one can see the cross peaks evolve from very weak to significant over the population time T range of ≈0 to 6 ps.

Fig. 2.

The real part of the purely absorptive 2D IR spectrum of CH₃CN in MeOH at various waiting times, T, at –17°C. (a) T = 0. (b) T = 2 ps. (c) T = 6 ps.

Fig. 3.

The real part of the purely absorptive 2D IR spectrum of CH₃CN in MeOH at various waiting times, T, at 22°C. (a) T = 0. (b) T = 2 ps. (c) T = 6 ps.

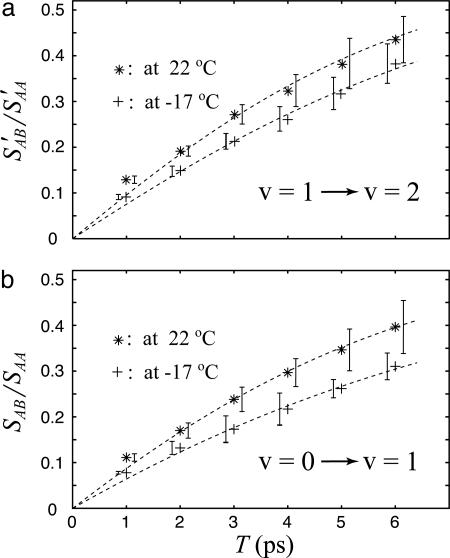
To obtain the ratio of the integrated cross peak to diagonal peak signals that are plotted in Fig. 4, the 2D spectrum 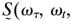0) at T = 0 was subtracted from the spectra 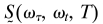at various T values to obtain spectra that contain only the cross peaks. The shapes of the cross peaks were very similar to those of the diagonal peaks, so integrated areas could be obtained from the residual peak heights. At each T value, the ratios of the integrated 2D spectra are defined as S_AB/S_AA (or S′_AB/S′_AA for the v = 1 → v = 2 region). The relationships of these parameters to the hydrogen-bond dynamics are deduced from a simple theory in the text that follows. The waiting time T dependence of these ratios is plotted on Fig. 4.

Fig. 4.

Time evolution of the cross peaks in 2D IR. (a) Relative magnitudes at 22°C (*) and –17°C (+) of the cross-to-diagonal peak ratio S_AB′/S_AA′ versus T in the v = 1 → v = 2 region. The dashed lines are fits to 0.77 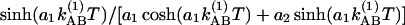with parameters of a₁ = 1.14, a₂ = 0.123, and 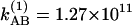s^–1 at 22°C and a₁ = 1.165, a₂ = 0.142, and 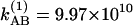s^–1 at –17°C. (b) Relative magnitudes at 22°C (*) and –17°C (+) of the cross-to-diagonal peak ratio S_AB/S_AA versus T in the v = 0 → v = 1 region. The dashed lines are fits to 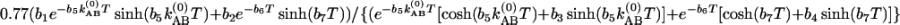with parameters of b₁ = 0.858, b₂ = 0.877, b₃ = 0.142, b₄ = 0.123, b₅ = 1.165, b₆ = 3.448 × 10¹¹ s^–1, b₇ = 1.448 × 10¹¹ s^–1, and 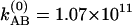s^–1 at 22°C and b₁ = 0.837, b₂ = 0.858, b₃ = 0.163, b₄ = 0.142, b₅ = 1.195, b₆ = 3.17 × 10¹¹ s^–1, b₇ = 1.162 × 10¹¹ s^–1, and 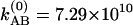s^–1 at –17°C.

Chemical Exchange 2D IR. The starting point for an analysis of the chemical exchange 2D IR is an enumeration of the appropriate Liouville paths. The pathways that contribute to the signal involve the usual ones for two independent oscillators (29) plus those with exchange. We use A and B to represent the two chemically different configurations. In the present example, A and B represent H-bonded and non-H-bonded structures, but the results are more general than that. For example, A and B might represent a molecule in two different states or two different conformations or isomeric structures. The various terms that add to give the 2D IR signals each depend on the product of three factors or propagators, one for each of the time intervals involved in the nonlinear process described earlier. The first factor describes the coherence evolution of the phase initiated by the first pulse. During this period, the effects of the relaxation of inhomogeneous distributions of frequencies, the population relaxations, and the fluctuations of the phase arising from the chemical exchange must be incorporated. The second factor describes the evolution during the population period and contains the intrinsic irreversible relaxations and the chemical exchange. Because of exchange, the system may not be in the same population state, A or B, at the beginning and the end of this period. The third term in the product represents the propagation of the vibrational coherence that gives rise to the photon echo or radiating macroscopic polarization and incorporates the same physical processes as in the first term. If either of these coherent factors begins by being associated with the A state, it may end by being associated with either the A or B states if reversible exchange occurs during the period. When the exchange is slow compared with other coherence dephasing mechanisms, it can be omitted from the first and third factors to yield the slow exchange equations. This condition is analogous to the “slow exchange” limit in NMR, although slow in the present case most often will mean picoseconds or faster. Vibrational transitions in solutions should be separated by ≈15 cm^–1 to be resolved, and they will be averaged only if the exchange rate exceeds ≈1 ps^–1. If this limit is appropriate at a particular temperature, at higher temperatures the approximation will begin to break down. In the opposite extreme, when the exchange is the dominant dephasing mechanism, there is dynamic averaging, and the nonlinear spectrum collapses into one transition at the mean frequency value. In the intermediate case, both the vibrational frequency fluctuations determining the spectral diffusion and the chemical exchange contribute to the spectral shapes in the 2D IR spectra.

In the slow exchange case, the diagonal signal from the v = 0 → v = 1 region of the A subpopulation is

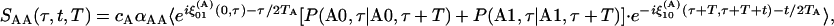[1]

where ξ^(A)_0i(t₁, t₂) is the phase accumulated in the time between t₁ and t₂ while the subset A molecules are in the coherence ρ_0i, c_A is the mole fraction of the species A, and P(Ai, t₁|Bj, t₂) is the probability that the system will occupy a subpopulation of states B at time t₂ if it is in subset A at t₁. The angle brackets in Eq. 1 represent an ensemble average. The population relaxation time of the v = 1 state of A is denoted by T_A. The factor α_AA is a relative signal strength factor depending on the product of the four transition dipoles involved in the signal creation and, in the case of Eq. 1, symbolizes 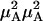. The diagonal elements of the B structures have the same form, with B replacing A. Note that the exchange of A and B will in principle contribute to the line widths and introduce cross peaks into the 2D IR spectrum during the coherence and detection periods. However, a cross term will certainly arise if there is chemical exchange between the A and B populations during the waiting time T. For example, in the v = 0 → v = 1 region with the initial coherence in the A group, the cross peak signal is

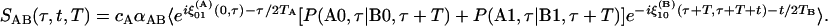[2]

The result for coherence initially in the B group is obtained by interchanging A and B in Eq. 2. The signals in the region of the v = 1 → v = 2 transitions, S′_AA(τ, T, t) and S′_AB(τ, T, t) have the same general form as Eqs. 1 and 2 but are shifted by the diagonal anharmonicity and contain the kinetic coefficients of only the v = 1 state. The 2D IR spectra as functions of ω_τ and ω_t in the limit of Eqs. 1 and 2 are formed by the double Fourier transforms along τ and t. There are simple dynamical models that yield useful indications of what is expected in general cases.

The simplest model is pure slow chemical exchange without dynamic averaging: In this picture, the contributions of the jumps between the different chemical states to the phase evolution are neglected. The conditional probabilities are easily deduced in terms of the kinetic parameters of the process A⇄B for the case that the forward and backward rate coefficients associated with the v = 0 state are 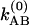and 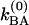, and those of v = 1 are 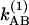and 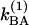. The coefficient 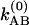corresponds to the transfer into the B molecules of the population created in the ground vibrational state of A that still contains the phase memory introduced by the first pulse; 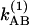refers to this transfer for the v = 1 population. The existence of cross peaks in the 2D IR spectrum is proof of the chemical exchange and the spatial proximity of the A and B states. The phase stored in the A state is transferred to the B state and vice versa. The conditional probabilities are

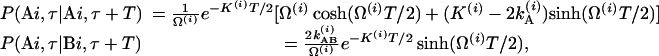[3]

and the other two probabilities are obtained by interchanging A and B. The total decay rate constants for the A and B states are 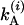and 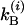, corresponding to the population decay rate coefficients plus exchange. The total relaxation rate is 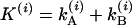and 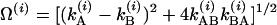for each of the vibrational states v = i. If the two T₁ times are equal, then the factor Ω⁽ⁱ⁾ becomes .

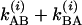Hydrogen-Bond Exchange Parameters. A useful experimental quantity is the total integrated area of each of the diagonal and cross peaks in the 2D IR spectrum obtained by setting τ and t equal to zero in Eqs. 1 and 2. They are determined by the kinetic factors for most dynamical models, and they can be measured experimentally when the peaks corresponding to the different Liouville pathways are sufficiently well separated in the 2D (ω_τ, ω_t) frequency space. The peak heights are also easily computed in terms of the relaxation rates.

The language of transient gratings is helpful in the discussion of these 2D IR spectra. To establish the 2D IR spectra in the v = 0 → v = 1 region, the first two pulses introduce population gratings into the sample. One corresponds to bleached ground state molecules, having the form sin[ω₀₁τ + xΔk], and the other corresponds to a population of v = 1 states of the oscillator, cos[ω₀₁τ + xΔk], where Δk is the difference in wave vector, 4πv̄ sinθ/2, between pulses 1 and 2, x is a displacement, and ω₀₁ is a particular vibrational frequency from the distribution. For a pulse wave number of v̄ ≈ 1,600 cm^–1 and an angle θ between the k₁ and k₂ beams of 10°, the population grating spacing is 35 μm. The grating phase, ω₀₁τ, which contains the memory of the coherence evolution, represents a frequency grating because of the distribution of absorbing frequencies (35). The effect of exchange on the photon echo depends on the time evolution of this memory. The v = 1 memory is destroyed by relaxation of the v = 1 population. The v = 0 grating is removed by relaxation processes that restore the distribution of frequencies originally stamped on the ground state by the excitation pulses. The latter grating might not be erased with the relaxation time of the v = 1 state. However, the 2D IR spectrum in the v = 1 → v = 2 region arises only from a v = 1 grating. As the system undergoes hydrogen-bond making or breaking, the large macroscopic spatial gratings will be maintained while the coherence memory content of the population distributions becomes reversibly associated with the interchanging chemical species. Therefore, the dynamics of the cross peaks in the v = 0 → v = 1 region will depend on the kinetics of exchange in both the v = 0 and the v = 1 states of CN, whereas those in the v = 1 → v = 2 region depend only on the exchange in the v = 1 state.

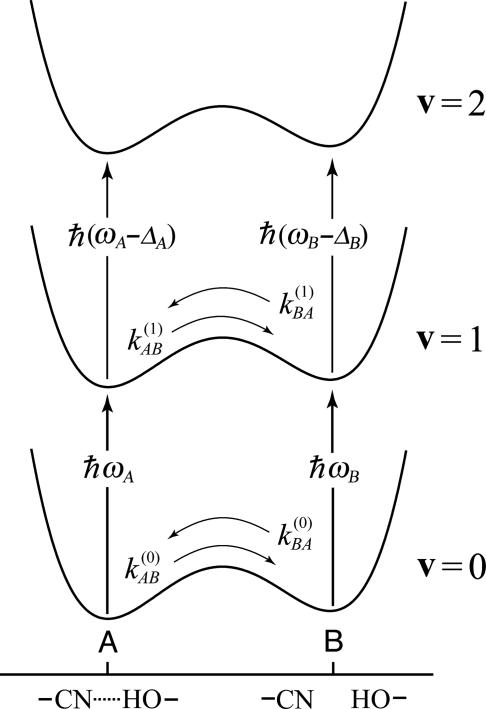
The foregoing analysis shows that the 2D IR chemical exchange spectrum is expected to differ significantly from what is usually seen in NMR. Most significantly, it will display the v = 1 → v = 2 transitions separately from the v = 0 → v = 1 transitions, so the proton dynamics of the different quantum states of the CN group should enter directly into the spectrum. A typical disposition of energy levels is illustrated in Fig. 5, which shows the free energy as a function of the H-bond coordinate for each of the high-frequency states. Furthermore, the dynamics of the inhomogeneous distributions contribute to the responses, as do the population relaxation times of each of the states involved. However, the vibrational dynamics, in particular the frequency correlation functions, renders the vibrational case to have content beyond the rate coefficients for the exchange. In the simplest possible case of slow exchange, the rate coefficients appear because the populations interconvert during the waiting time T, and the measured time constant corresponds to the sum of the forward and backward reaction rate coefficients. Although the relevant Liouville paths are analogous to those in NMR, the 2D IR signals incorporate an average over the dynamic distribution of vibrational frequencies. In general, the exchange is also occurring during the coherence and detection times, which will be discussed later as dynamic exchange.

Fig. 5.

Schematic representation of the free energy along a low-frequency hydrogen-bond coordinate for the CN stretch mode in its v = 0, v = 1, and v = 2 states.

In a linear FTIR spectrum, the absorption is proportional to 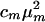, whereas in a heterodyned 2D IR spectrum, the signal is proportional to 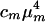, where c_m and μ_m represent the mole fraction and transition dipole in state m, respectively. By comparing the linear FTIR and 2D IR spectra we find μ_A:μ_B = 1:0.88 and c_A:c_B = 1:0.73 at –17°C. The A⇄B equilibrium constant yields the ground state free-energy difference ΔG⁽⁰⁾ = 700 J·mol^–1. The free-energy difference ΔG⁽¹⁾ = 600 J·mol^–1 for v = 1 is obtained by subtracting the 8-cm^–1 difference in the v = 0 → v = 1 transition frequencies for the states A and B. From the relation 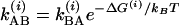, we obtain 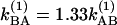at 256 K and 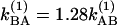at 295 K. By investigating the T dependence of the ratio of cross peaks to the diagonal peaks in the v = 1 → v = 2 region, we can directly measure the exchange rate in the v = 1 state, because the 2D (ω_τ, ω_t) domain spectra depended only on the dynamics of v = 1 states. Fig. 4a shows the observed and calculated from Eq. 3 values of S′_AB/S′_AA as a function of T in the v = 1 → v = 2 region from which we estimate k_AB = 9.97 × 10¹⁰ s^–1 at –17°C and 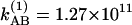s^–1 at 22°C, leading to relaxation rates of Ω⁽¹⁾ = 2.32 × 10¹¹ s^–1 at –17°C and Ω⁽¹⁾ = 2.90 × 10¹¹ s^–1 at 22°C. In v = 1, the activation energy for hydrogen exchange from the H-bonded state to the free state is found to be ≈3.9 ± 0.5 kJ·mol^–1 (≈3.3 ± 0.5 kJ·mol^–1 for the back exchange). By analysis of the relative magnitudes of the cross and diagonal peaks in the v = 0 → v = 1 region, we can obtain values for the relaxation Ω⁽⁰⁾. Unlike the cross peaks in the v = 1 → v = 2 region, however, those in the v = 0 → v = 1 region depend on the dynamics occurring on both v = 0 and v = 1 surfaces. The relative magnitude of a cross peak to a diagonal peak (S_AB/S_AA) in the v = 0 → v = 1 region is shown in Fig. 4b. With the help of the determination of Ω⁽¹⁾ from the analysis in the v = 1 → v = 2 region, we can obtain the ground state exchange rate, Ω⁽⁰⁾, independently. After fitting the data in Fig. 4b we estimate 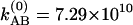s^–1 at –17°C and 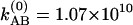s^–1 at 22°C. Therefore, in v = 0, the relaxation rates are Ω⁽⁰⁾ = 1.74 × 10¹¹ s^–1 at –17°C and Ω⁽⁰⁾ = 2.49 × 10¹¹ s^–1 at 22°C, leading to an activation energy for H-bond dissociation of ≈6.2 ± 1.5 kJ·mol^–1 (≈5.5 ± 1.5 kJ·mol^–1 for the back exchange). At ≈300 K, the exchange rate for the v = 1 states is ≈20% faster than that in v = 0, corresponding to the activation energy for the exchange in the v = 1 states being 65% of that in v = 0.

The making and breaking of the H bonds between acetonitrile and methanol is somewhat slower than the hydrogen-bond dynamics in neat methanol. The small activation enthalpy is suggested to be the result of a cooperative transition state in which an OH is H-bonded to both acetonitrile and to another methanol molecule. Because the H bonds between alcohols and between alcohol and acetonitrile (36) have similar enthalpy, the free-energy difference between the bonded and free states of the CN group is understandably small. The attempt frequency of ≈γ = 10¹² s^–1 obtained by writing the exchange rates in the form γe^–E/k_BT is very close to a characteristic relaxation time of liquid methanol that dominates the dipole fluctuations (37). The relatively weak sensitivity of the H-bond dynamics to the vibrational quantum number is consistent with the observation apparent from Figs. 2 and 3 that the anharmonicities of the A and B states are equal: In both results, the CN potential energy surface is not very sensitive to the hydrogen-bond formation. This situation is quite different to that for H-bonded NH and OH groups (25).

Dynamic Exchange. The spectrum in Fig. 2 at T = 0 exhibits weak cross peaks having ≈10% of the signal strength of the diagonals. The pulse width is ≈80 fs, so population exchange in the pulse overlap regime could not possibility yield cross peaks that exceed ≈1% of the diagonals. Therefore, dynamic exchange is occurring. In dynamic exchange, the rate coefficients k_AB and k_BA must be considered to contribute significantly to the dephasing of the coherences in a process that involves the vibrational coherence jumping back and forth between H-bonded and non-H-bonded structures. The observation of cross peaks at T = 0 implies that the spectral shapes depend on the exchange relaxation. Also notable is the apparent decrease in the frequency separation between A and B with temperature, evident by comparing Figs. 2 and 3. The averaging is also seen from the linear spectrum as a function of temperature: As seen in Fig. 1, the separation between the two exchanging peaks is decreasing with increasing temperature. Furthermore, the FTIR spectrum collapses into a single line at ≈50°C (34). If we assume that exchange occurs by means of a Kubo–Anderson two-state jump process (38) to account for the randomly interrupted deterministic motion between the two chemical states, the parameters presented here from the nonlinear spectra in the slow exchange limit provide a very satisfactory description of both the nonlinear and the dynamic averaging of the linear FTIR spectrum over the whole temperature range.

Consequences of Exchange. The slow and dynamic chemical exchange reported in this work for spectrally separated chemical states is very likely to be occurring in many systems where the transitions are more strongly overlapped and the contribution from the exchange is not so obvious. In these cases, the cross peaks created by the exchange alter the shape of the 2D IR spectra and obviate the relationships between spectral line shapes and correlation functions that do not explicitly include exchange. For example, the presence of a distribution of structures normally will elongate the 2D IR spectra along the frequency diagonal. The width of the 2D IR spectrum along the line perpendicular to the diagonal is usually much narrower, because the static distribution of frequencies does not contribute to it. However, the underlying exchange coupling peaks will influence the shape in this perpendicular direction and therefore must be incorporated explicitly to extract a meaningful picture of the dynamics from the line shapes. This situation may be especially important for the biological examples of polar amide carbonyls and N–H groups in water where there may be a small number of distinct hydrogen-bonded configurations that are exchanging. A similar picture would prevail if the exchanging states corresponded to two or more thermally interchangeable isomers or vibrational modes of a molecule rather than two different molecule solvent configurations. A more detailed analysis of the 2D IR will require quantitative consideration of the correlated fluctuations of the vibrational frequencies in the different chemical states. Whereas in NMR the nuclear spin functions centered on different molecules are uncorrelated (26), this situation is not necessarily the case for 2D IR when the spectral diffusion may be comparable with the jump rate. A main advantage of 2D IR experiments on exchange concerns the ability to measure simultaneously all of the kinetically relevant states, which will greatly simplify the treatment of more complex kinetic networks. Furthermore, no exchanges will occur during the femtosecond pulse excitation. The 2D IR experiment has the additional advantage that angular information on the CN bond axis in the two states could be obtained from the cross peak intensity for various pulse polarizations (39, 40).

Conclusions

The application of chemical exchange 2D IR to hydrogen-bond dynamics has addressed directly the differences in the exchange for the vibrational ground and excited states and allowed characterization of the activation of H-bond making and breaking events through temperature-dependence studies. This type of exchange may be common but hidden in conventional IR spectral bandwidths, so its signatures through 2D IR in cases such as those presented here are important and possibly wide-spread. When the number of exchanging states becomes large and they are not as well separated in frequency as in the present example, the response tends to the more common form involving a smooth Gaussian distribution of frequency fluctuations. There are other well known examples of dynamic chemical exchange effects on linear (41–45) and pump/probe IR spectroscopy (25) that could be readily accessed by using the heterodyne echo method with the aim of determining exchange dynamics in different vibrational quantum states and elucidating the coherence transfer mechanisms.