Numerical computation of diffusion on a surface

Abstract

We present a numerical method for computing diffusive transport on a surface derived from image data. Our underlying discretization method uses a Cartesian grid embedded boundary method for computing the volume transport in a region consisting of all points a small distance from the surface. We obtain a representation of this region from image data by using a front propagation computation based on level set methods for solving the Hamilton–Jacobi and eikonal equations. We demonstrate that the method is second-order accurate in space and time and is capable of computing solutions on complex surface geometries obtained from image data of cells.

We consider the problem of computing the solution to the diffusion equation on a surface.

[1]

[2]

where 𝒮 is a surface in . Our interest is motivated by problems in systems biology. Processes such as cellular metabolism, locomotion, and chemotaxis are mediated in part by diffusive transport on the membrane, represented by Eq. 1. In particular, we want to be able to compute high-fidelity solutions to these problems, in which the surface is obtained from image data of actual cells.

Traditional approaches to solving partial differential equations on surfaces have been based either on a global representation of the surface, such as a triangularization, or on local representations, such as with local coordinate representations, stitched together by using techniques such as multiblock or overset grids. In either case, both the construction of such representations and the design of discretizations of Eq. 1 based on them have algorithmic difficulties and complications beyond those arising when the domain is a subset of . In this article, we present an approach to this problem that avoids many of these difficulties. It is based on recent developments in both numerical methods for solving partial differential equations in complex geometries and mathematical methods for detecting features in image data. In our approach, we solve the heat equation on an annular domain consisting of all the points within a small distance ε of 𝒮.

[3]

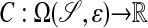[4]

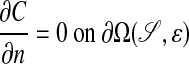[5]

[6]

This problem is solved by using a Cartesian grid embedded boundary method (1, 2), in which Eq. 3 is discretized on any domain in 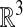on a finite volume grid constructed by intersecting the domain with rectangular grid cells. A representation of the annular region for which the requisite intersection information is obtained from image data by using the previously described methods (3) that represent the surface in terms of a solution to a Hamilton–Jacobi equation. Specifically, we obtain from this process a function whose values are the signed distance from the surface, defined in an annular region around the surface. Using such an implicit function representation for , it is routine to compute the required intersection information. In ref. 4, a similar approach to the one described here has been used to simulate biomedical fluid flow problems starting from images derived by using the described methods (3) from MRI data. The application to surface transport both imposes a different set of requirements and provides some opportunities for simplification.

The idea of solving this problem on a Cartesian mesh discretization on 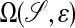was used previously (5). In that case, the partial differential equation being solved was the original surface equation (Eq. 1), extended in a natural way to the annular region. Such an approach leads to complicated difference approximations of the metric terms in the surface derivatives. In addition, Δ^surf is highly degenerate when viewed as an operator on functions in 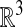. For example, in the case where 𝒮 is a plane, any function that depends on the coordinate direction orthogonal to 𝒮 is in the null space of Δ^surf. This complicates the construction of implicit time discretizations that require the solution of linear systems derived from discretizing Δ^surf.

The present approach avoids both of these problems. The finite volume approximations to Δ are relatively simple, and when combined with standard implicit discretizations in time, lead to linear systems that permit the use of efficient iterative methods such as multigrid. The cost is that the solution to Eq. 3 is only an approximation to the solution to Eq. 1. However, we show that the approximation is O(ε²). Since ε can be chosen to be a fixed multiple of the mesh spacing, this leads to error that is comparable to the other discretizations errors in a second-order accurate method.

Thin-Layer Asymptotics

Let 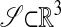denote a compact, smooth, orientable surface, with orientation defined by a unit normal field n. Then there exists a finite collection of smooth maps of the form,

[7]

such that union of the range of these maps cover 𝒮, and, for ε sufficiently small, the extensions

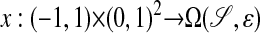[8]

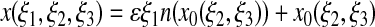[9]

have nonsingular Jacobians and ranges whose union covers 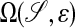. In that case, x(ξ₁, ξ₂, ξ₃) is the unique point in 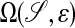that is a signed distance εξ₁ from x₀(ξ₂, ξ₃).

For any smooth coordinate mapping, we have

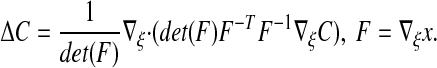[10]

For the coordinate mapping (Eq. 9) this leads to the following form for the diffusion equation (Eq. 3).

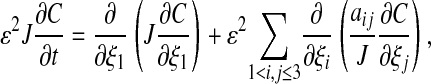[11]

where

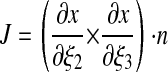[12]

and

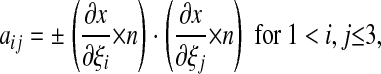[13]

where ± = + if i = j, ± = – if i ≠ j. We can compute J and a_ij as functions of ε.

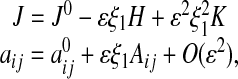where the quantities J⁰, 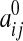, H, K, and A_ij depend only on ξ₂, ξ₃. In particular, the surface Laplacian Δ^surf appearing in Eq. 1 can be written in terms of the ξ₂, ξ₃ coordinate system.

[14]

[15]

We now show that as ε → 0, a solution to Eq. 3 differs from a solution to Eq. 1 by O(ε²). To do this, we expand C in powers of ε,

[16]

and equate terms in Eq. 11 corresponding to the same power of ε. We will further assume that the derivatives of C with respect to all of the original spatial variables and time are independent of ε, so that no inverse powers of ε appear from differentiating with respect to time or the mapped variables. This will be the case, for example, if the initial data are independent of ξ₁.

First, we note that the homogeneous Neumann boundary condition in Eq. 3 becomes

[17]

Furthermore, differentiating Eq. 16 with respect to ε implies that Eq. 17 must hold for each of the C^(p) separately. Then we have:

• p = 0:

  [18]

  and Eq. 17 implies that C⁽⁰⁾ is independent of ξ₁.
• p = 1:

  [19]

  Again, by Eq. 17 C⁽¹⁾ is independent of ξ₁.
• p = 2: After rearranging terms, and recalling that C⁽⁰⁾ and C⁽¹⁾ are independent of ξ₁, we have

  [20]

  The right side is independent of ξ₁, and by Eq. 17 it must be identically zero. i.e., C⁽⁰⁾ satisfies Eq. 14. In addition, C⁽²⁾ is independent of ξ₁.

• p = 3: Similarly to the case p = 2 we have

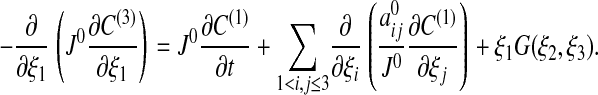[21]

It follows from C⁽¹⁾ being independent of ξ₁ and Eq. 17 that C⁽¹⁾ satisfies Eq. 14.

From this argument we see that C⁽⁰⁾ + εC⁽¹⁾ satisfies Eq. 14, which implies that C itself differs from a solution to Eq. 14 by O(ε²).

Even though the analysis was carried out given specific assumptions about the initial data, the conclusion appears to be robust relative relaxing the assumptions. In particular, we continue to observe in our numerical calculations nearly invariant behavior of the solution in the direction normal to the surface for problems with forcing of Eq. 1 with a source term; for long-time integration of the equations; and for initial data that varies in the normal direction. Qualitatively, this is not surprising: diffusion in the normal direction relaxes to a local steady state very rapidly relative to the time scale for diffusion in the tangential direction.

Embedded Boundary Discretization

The underlying discretization of space is given by rectangular control volumes on a Cartesian grid: 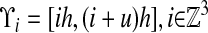, h is the mesh spacing, and u is the vector whose entries are all ones. The geometry is represented by the intersection of the irregular domain Ω with the Cartesian grid. We obtain control volumes 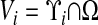and faces 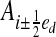, which are the intersection of ∂V_i with the coordinate planes {x: x_d = (i_d + 1/2 ± 1/2)h}. Here e_d is the unit vector in the d direction. We also define 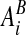to be the intersection of the boundary of the irregular domain with the Cartesian control volume: .

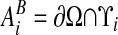To construct finite difference methods, we will need only a small number of real-valued quantities that are derived from these geometric objects.

• Areas and volumes are expressed in dimensionless terms: volume fractions κ_i = |V_i|h^–3, face apertures 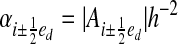and boundary apertures .

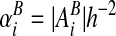• The locations of centroids, and the average outward normal to the boundary are given exactly by:

where n^B is the outward normal to ∂Ω, defined for each point on ∂Ω. We assume that we can compute estimates of these quantities that are accurate to O(h²).

Using just these quantities, we can define conservative discretizations for the divergence operator. Let be a function of x. Then

[22]

where Eq. 22 is obtained by replacing the integrals of the normal components of the vector field with the values at the face centroids. We obtain the spatial discretization from replacing 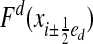with difference approximations. Following refs. 1 and 2, we define the discrete Laplacian,

[23]

where the fluxes satisfy

[24]

Here the sum over faces and the weights correspond to bilinear interpolation of the centered difference approximations to the centroid location. Then we solve

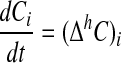[25]

by discretizing in time with a second-order accurate, L₀-stable implicit Runge–Kutta method (6). The resulting method provides uniformly second-order accurate solutions and is amenable to the use of geometric multigrid solvers for solving the resulting linear systems. This approach can be generalized to include the effect of source terms; for details, see refs. 1 and 2.

Grid Generation

To carry out the numerical procedure outlined in the previous section, it is necessary to generate the geometric data obtained from intersecting with rectangular grid cells, i.e., the areas, volumes, and centroids defined above. To do this, we compute on a Cartesian grid the representation of the domain as an implicit function:

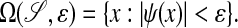[26]

Given the values of ψ on the grid, it is a routine exercise in quadrature to compute the intersection information we require to O(h²) accuracy. In this section, we will describe how we obtain such an implicit function starting from image data.

Typically, we are given image data in the form of intensities G = G(x) evaluated on a rectangular grid in three dimensions. In this work, the images are given as a collection of deconvolution microscopy images where each x – y slice contains gray scale values in the range [0, 1] (Fig. 1). The goal of this method is to find a surface that lies along high values of the gradient ∇G, as that indicates a sharp change in image intensity. Additional requirements need to be imposed, since in a typicalimage, the gradient is noisy, and there can be both missing edges caused by imaging effects and multiple possible edges caused by internal structures. Following ref. 3, we can formulate this problem as a front propagation problem, to be solved by using level set methods to solve the associated Hamilton–Jacobi equation (7):

[27]

Here the set {x: ψ(x, t) = 0} corresponds to the location of the front at time t, with the front located initially outside the surface to be detected, and

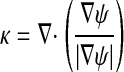is the curvature. The functions F and 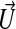are chosen so that the front is attracted to the maximum value of |∇G|, while g is chosen to constrain the curvature of the front, thus preventing the front from propagating through small gaps in the image data representation of the surface.

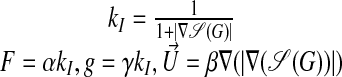The operator 𝒮 is a Gaussian smoothing operator, chosen to reduce the noise in the image data. The parameters α, β, and γ are currently chosen by trial and error, usually by running the detection code on 2D slices of the data, which takes a few seconds per run on a workstation (computing a 3D solution typically takes a few minutes). When the solution to Eq. 27 reaches a steady state, we expect the zero set of ψ to correspond to the outermost surface in the image. In practice, one solves the equations for a fixed time (e.g., t = 1) and adjusts the parameters α, β, and γ so that a solution sufficiently close to a steady state is obtained. Since we are interested in the solution only within a small distance of the propagating front, we use the previously described technique (8) to perform the calculation only in a narrow band near the front. Finally, we require not only the location of the front, but that ψ be a distance function defined within an ε distance on either side of the front. We use the previously described method (9) to compute extensions of F, gκ, and away from the zero set at each time step so that the time evolution tends to preserve the property that the solution satisfies the eikonal equation |∇ψ| = 1 and is therefore a signed distance function. In particular at the end of the calculation we expect the condition (Eq. 26) to be satisfied. We also postprocess the solution by solving the eikonal equation by using the previously described method (10, 11) to eliminate numerical error in the signed distance property that may have accumulated in the course of the time evolution.

Fig. 1.

2D slices through a gray-scale image of an hl-60 cell (15) obtained by using deconvolution microscopy. Image is ≈2,000 times actual size.

Results

We show results for two examples. In the first, the surface 𝒮 in a sphere of radius r₀ = 0.4. In spherical coordinates, the initial data is C^surf (θ, φ, t = 0) = cos(φ), for which the exact solution is

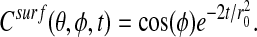We compute the solution on a spherical shell as in Eq. 3 for h = 1/32, 1/64, 1/128, with ε = 3h. Since the sphere can be specified analytically as a signed distance function, this calculation will test only the accuracy of the method for discretizing the diffusion equation. We advance the solution in time until the accumulated time is 0.1 by using a time step Δt = h/2. At the final time the magnitude of the solution has decreased by approximately a factor of 4. Fig. 2 shows the computed solution on the outer surface of the sphere. Fig. 3 shows the corresponding error, given as the difference between the computed solution and the exact solution extended to the entire spherical shell to be constant in the radial direction. Table 1 contains various norms of the error, where the integral norms (L¹ and L²) are computed by computing a consistent approximation to the integrals over 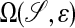divided by 2ε. In the limit of vanishing ε, these estimates converge to an estimate of the appropriate integrals over 𝒮. The L^∞ norm is computed as the maximum over all cells of the absolute value. For all three norms, the method is seen to be second order accurate. This is consistent with the modified equation analysis (1, 2, 12).

Fig. 2.

Computed solution on the spherical shell using 128³ grid points.

Fig. 3.

Slices through the spherical shell showing the difference between the computed solution and the exact solution using 128³ grid points.

Table 1. Solution error for h = 1/32, 1/64, 1/128.

L1 norm	Rate	L2 norm	Rate	L∞ norm	Rate
1.989444e-03		2.424191e-03		5.636316e-03
4.859636e-04	2.03	5.719458e-04	2.08	1.255820e-03	2.17
1.201429e-04	2.02	1.390271e-04	2.04	2.828283e-04	2.15

The second example demonstrates the end-to-end capability. We generate a signed distance representation of the image in Fig. 1, then use it to compute the grid intersection information required to discretize the solution to the diffusion equation in the annular region. In Figs. 4 and 5, the initial condition for this problem was a two-valued function: on a circular patch on the flat underside of the surface we set C = 10; everywhere else C = 0. The time step was 5.0 s, which is ≈30 times the maximum time step for an explicit method on this problem.

Fig. 4.

Solution for diffusion equation for a 256 × 256 × 128 grid at time = 50 s. The time step is 5.0 s.

Fig. 5.

Solution for diffusion equation for the 256 × 256 × 128 grid at time = 100 s. The time step is 5.0 s.

There are a number of directions in which we intend to take this work. The diffusion solver described here is the core of a multicompartment model currently under development for reaction-diffusion processes in cells. Transport in both the membrane and the cytosol is represented by using the embedded boundary approach, with coupling to chemical reaction terms in both regions, and spatially and state-dependent fluxes representing transport coupling the membrane and the interior of the cell. We would also like to extend this approach to other partial differential equations representing mechanical processes on the surface of the cell, including the representation of the membrane as an elastic or viscoelastic medium, coupling the ideas discussed here to the versions of embedded boundary method for hyperbolic problems described (13), extended to moving boundaries following ref. 14.