Coherent locomotion as an attracting state for a free flapping body

Abstract

A recent experiment [Vandenberghe, N., Zhang, J. & Childress, S. (2004) J. Fluid Mech. 506, 147–155] has shown that an axle-mounted blade can spontaneously rotate when oscillated (or “flapped”) above a critical frequency in a fluid. To understand the nature of flapping locomotion we study numerically the dynamics of a simple body, flapped up and down within a viscous fluid and free to move horizontally. We show here that, at sufficiently large “frequency Reynolds number,” unidirectional locomotion emerges as an attracting state for an initially nonlocomoting body. Locomotion is generated in two stages: first, the fluid field loses symmetry by an instability similar to the classical von Kármán instability; and second, precipitous interactions with previously shed vortical structures “push” the body into locomotion. Body mass and slenderness play central and unexpected roles in each stage. Conceptually, this work demonstrates how locomotion can be transduced from the simple oscillations of a body through an interaction with its fluid environment.

A common strategy for locomotion through a fluid uses appendages, such as wings or fins, flapping perpendicularly to the direction of travel (1). This strategy is in marked difference to strategies, using propellers or screws, ciliary waves, or rowing with limbs or oars, which explicitly move fluid in the direction opposite to travel. Flapping locomotion is also never observed for microorganisms moving at low Reynolds number. We consider a rigid body of simple shape, here an ellipse of major (minor) axis length L (W), with uniform mass density ρ_b. The body translates with velocity u_b = (u_b, v_b) (without rotation) in the infinite x-y plane through a 2D viscous fluid of density ρ and viscosity μ. We specify its vertical motion as y_b(t) =–Acos(2π ft) (in technical parlance this is a heaving body). Hence, L is a characteristic length and Af is a characteristic velocity, which defines the frequency Reynolds number Re_fr = ρ(Af)L/μ. The surrounding fluid is governed by the 2D incompressible Navier–Stokes equations:

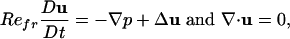[1]

with u = (u, v) the fluid velocity, p the pressure, and D/Dt the material time derivative. Eq. 1 is in nondimensional form with Re_fr its sole control parameter.

An important element of this study is that the horizontal motion of the body is not specified, as in many other studies (2–5), but rather is determined by the fluid force acting at its boundary through Newton's second law:

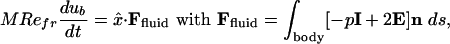[2]

where M = (ρ_b/ρ) · (A₀/L²), with A₀ the body area, and n the outward normal. The fluid stress tensor, –pI + 2E with E the symmetric rate-of-strain tensor, encodes pressure (first term) and viscous stresses (second term). Eqs. 1 and 2 together with u|_body = u_b, close this coupled body-fluid system, for which the sum of horizontal body and fluid momentum is an invariant. Newton's law has been coupled to the Navier–Stokes equations previously to study fundamental flow-body interactions such as bodies rising and falling in a fluid (6, 7) and cylinders mounted in a steady flow (8). Besides Re_fr, important control parameters are the body aspect ratio L/W, the dimensionless stroke amplitude A/L [set to 1/2 to simplify the problem; this value has been observed in experiments to lead to efficient flapping flight (5)], and the density ratio ρ_b/ρ. This last parameter is interesting as, if large, it can be considered as partially accounting for the inertia of an attached, nonoscillating body.

We have simulated this coupled body-fluid system by using a numerical method based on the “vorticity-stream-function” formulation of Eq. 1 and a mixed Fourier/finite-difference discretization. The vorticity, ω = v_x – u_y, measures the local rate-of-rotation of the fluid. Vorticity is transported and diffused according to Re_fr Dω/Dt = Δω, (the curl of Eq. 1). Our method is fourth-order accurate in space and second-order in time, with the vorticity diffusion term treated implicitly. Related formulations have been developed by E and Liu (9) and Wang (2). The numerical grid conforms to and moves with the elliptical body and has an outer boundary that is typically many body diameters away from the body itself. Boundary conditions on the outer boundary simulate the fluid dynamics in the far field, by setting the values of the stream function to correspond to purely translational velocity (minus the body velocity in the physical frame) and the values of vorticity to zero (see ref. 10 for further details). In these simulations, the vertical motion of the body is specified, and the horizontal motion is studied after the imposition of perturbations in horizontal velocity (u_b ≈ 10^–12 to 10^–2). The initial fluid velocity is zero everywhere, and the sum of horizontal body and fluid momentum is conserved to within 0.03% of the eventual steady-state magnitudes of each of the summands. Hence, any horizontal motion of the body significantly above the level of the perturbation is achieved only through a momentum exchange with the fluid.

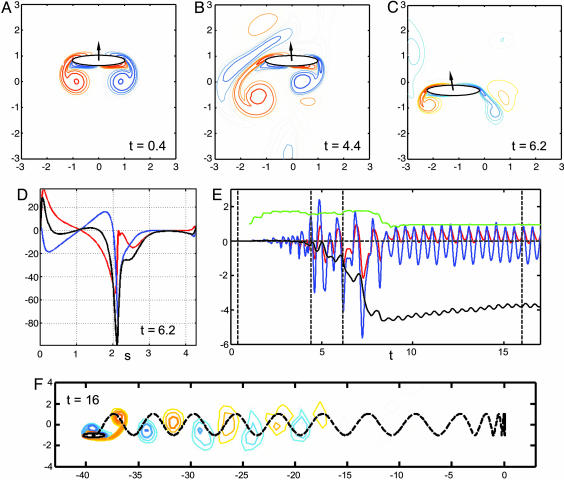
First, we find that if the body flaps at sufficiently small Re_fr the state of no horizontal body motion is stable; horizontal motions imposed transiently on the flapping body rapidly dissipate and the fluid resumes a left-right symmetric dynamics (in qualitative appearance, like Fig. 1A). At higher Re_fr the body dynamics is dramatically different. Fig. 1 (and Movie 1, which is published as supporting information on the PNAS web site) shows a simulation for an elliptical body (of aspect ratio 5:1) that illustrates the stages leading to “takeoff.” At early times (0 < t < 0.5), during an imposed horizontal perturbation (u_b ≈ 10^–2), the flow appears very nearly symmetric (Fig. 1 A). However, when the horizontal motion evolves freely under fluid forcing (t > 0.5), this initial perturbation grows in time and the fluid motions become increasingly asymmetric as the body both sheds vorticity into the fluid and interacts with vorticity already there (Fig. 1B).

Fig. 1.

The body and fluid dynamics (shown as a contour plot of the vorticity field) during the stages of takeoff for a flapping body in a sample case. The body aspect ratio is 5:1, body density is 32 times fluid density, and Re_fr = 35. For the first upstroke (0 < t < 0.5), a positive horizontal velocity perturbation is prescribed, increasing to 0.2% of the peak vertical velocity; subsequently the horizontal velocity is set by horizontal fluid forces. (A) Startup motion and flow are nearly vertically symmetric, so horizontal forces on the body are small. (B) Nearly four periods after the body is freed, the flow has become very asymmetric, while the body velocity is still nearly vertical because of body inertia. (C) The body collides with a previously shed vortex at t = 6.2, which decreases suction at the right edge by creating a vortex dipole. (D) The horizontal component of the pressure (blue) and viscous (red) stresses acting on the surface of the body, at the instant shown in C. The black line is the sum of the stresses. The arc length around the body surface (moving counterclockwise) is denoted by s, with the right edge at s = 0 and left edge at s = 2.14. The peak near s = 0 has a much smaller magnitude than the trough at s = 2.14, coincident with the formation of a vortex dipole at s = 0. (E) The horizontal pressure (blue line) and viscous (red line) forces acting on the body as a function of time. Dashed lines mark the instants of B, C, and F. Also shown is horizontal velocity of the body, u_b(t) (black line), which shows quasi-steady locomotion for t ≳ 8. The green line shows the negative (for separation from other graphs) of cycle-averaged input power P(t), defined as 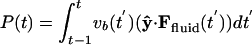.(F) The subsequent vortex street and center-of-mass trajectory (dotted line) in the quasi-steady state of unidirectional (leftward) flight. Shed vortices form a staggered array with net fluid momentum directed away from the body.

Fig. 1F shows the body and surrounding vorticity field after 16 flapping periods, by which time the body is moving steadily to the left and leaving behind a staggered array of positive and negative vortices. As is typical of flapping flight (4), a vortex is shed near the trailing edge of the body into the fluid during an upstroke (positive vorticity) or downstroke (negative vorticity). During a half-stroke the developing leading-edge vortex remains bound to the body and typically merges into and strengthens the trailing-edge vortex of the same sign that is produced during the following half-stroke. The vortex wake resembles a von Kármán vortex street behind a bluff body in a flow, but with vortices of reversed sign (11); this “inverse von Kármán street” has been observed in numerous experimental and numerical studies of flapping foils and in the carangiform mode of fish swimming (12).

In numerous simulations we have observed characteristic events that move the system into locomotion; an example is shown in Fig. 1C. Into its sixth cycle of flapping the body is moving upward and shedding oppositely signed vortices from its two edges. However, the right edge is colliding with a positively signed vortex that was shed from the opposite edge as the body was flapped downward on the previous half-cycle. This “free” vortex, at one point a full body length away, now forms part of a vortex dipole that subsequently carries fluid momentum away from the body. The horizontal fluid stresses around the body (Fig. 1D) show the effect of this interaction. There is a large suction force at the left edge, associated with vorticity creation. In symmetric flapping, an opposite suction force would act at the right edge, but this force has been reduced by the formation of the vortex dipole. This imbalance in suction force seems to initiate the locomotion of the body, and after a nearly identical dipole ejection on the next upward stroke, the body settles into steady locomotion. In other simulations locomotion is instead initiated by the collision of an incipient leading edge vortex with a vortex of the same sign. This merging strengthens the resultant shed vortex, leading to a larger, unbalanced suction force at the leading edge.

Horizontal fluid forces show clearly the importance of these collisions in the transition to locomotion. The dynamics unfold in three stages (Fig. 1E). First, by studying carefully the growth of horizontal velocity from very small initial amplitudes it can be shown that the initial growth of horizontal velocity (0 ≲ t ≲ 3) is exponential in time; this is the signature of a linear instability. Second is a transition period (3 ≲ t ≲ 8) typified by complex, large-amplitude temporal and spatial dynamics, during which the viscous and (dominant) pressure forces act generally in the same direction. The transition period ends with one or more vortex collisions, the timing of which depends on how the asymmetric flow field develops, and can be sensitive to initial conditions. Finally, as locomotion is achieved (t ≳ 8), the forces move rapidly toward a 1/2-periodic dynamics with cycle-averaged force on the body essentially zero. Pressure forces are predominantly in the direction of motion, and viscous forces are in the opposite direction. We also find that the cycle-averaged “input power” (Fig. 1E, green line) required to move the body vertically increases substantially with the loss of flow symmetry, but is followed by a drop of nearly 50% with the onset of locomotion.

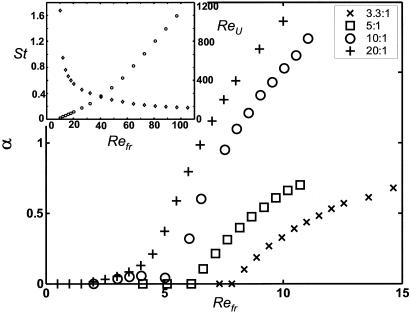
The initial loss of flow symmetry is similar to the classical von Kármán instability of the symmetric wake behind a bluff body, as both lead to alternating shedding of vortices above a critical Reynolds number (13). We have systematically studied the response to small initial horizontal velocities for vertically oscillated, elliptical bodies and find clear evidence for either exponential growth from (or decay to) the zero horizontal state as a function of Re_fr. Fig. 2 shows the calculated growth rate with an apparently sharp transition to instability occurring at moderate Re_fr. This transition Re_fr is apparently independent of mass ratio ρ_b/ρ, suggesting that the instability is that of the fluid flow alone and not of the coupled body-fluid system.

Fig. 2.

The growth rate of the linear instability in |u_b| ∼ 10^αt, as a function of Re_fr for four aspect ratios. The nonmonotonicity of the growth rate for the 10:1 case coincides with a change from linear growth with a single frequency (which occurs with the 20:1 body) to linear growth with a second, lower frequency (which occurs with the 5:1 and 3.3:1 bodies). (Inset) The cycle-averaged horizontal speed during steady locomotion, Re_U, (○, right axis) for a 10:1 body with ρ_b/ρ = 32, and the corresponding Strouhal number (⋄, left axis), as a function of Re_fr.

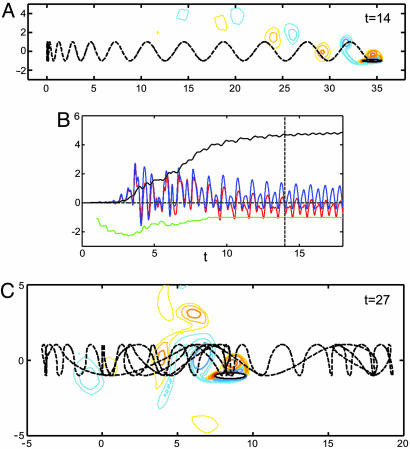
Body shape and mass are central to whether and how a coherently locomoting state is achieved. Fig. 3 A and B (and Movie 2, which is published as supporting information on the PNAS web site) shows the trajectory and integrated horizontal forces on a more slender body (10:1). We find generally that thinner bodies move more directly and smoothly into steady locomotion, as shown by the predominantly single-signed fluid forces in the transition period (4 ≲ t ≲ 9). Also, viscous forces play a larger role. Fig. 3C (and Movie 3, which is published as supporting information on the PNAS web site) illustrates the effect of body mass on the attainment of steady locomotion. Fig. 3C shows the apparently chaotic dynamics of a body that is lighter (“neutrally buoyant”) than that in Fig. 1, but otherwise identical in shape and Re_fr. The motion of this light body is highly sensitive to the instantaneous fluid forces on it, and thus it cannot sustain locomotion against a period of drag, even with the additional inertia caused by the added mass effect [the increased force per unit body acceleration required to accelerate a body in fluid versus a massless medium (14)]. However, light, yet more slender, bodies seem less susceptible to fluid force fluctuations.

Fig. 3.

The body dynamics for a more slender body and for a lighter body. (A) The trajectory of a body with the same mass as in Fig. 1, with the same start-up condition and Re_fr, but which is more slender (aspect ratio 10:1). The wake consists of paired vortices at an oblique angle. (B) The horizontal pressure (blue line) and viscous (red line) forces acting on the body as a function of time. The dashed line marks the instant of A. The horizontal velocity, u_b(t) (black line), shows a more gradual ramp-up than in Fig. 1. The input power P(t) (green line) again drops when steady locomotion is achieved. (C) The trajectory of a body with the same aspect ratio as in Fig. 1, but lighter (ρ_b/ρ = 1), at the same Re_fr and with the same start-up condition.

Fig. 2 shows that thinner bodies have a smaller critical Re_fr for the symmetry-breaking instability. Furthermore, for the 10:1 and 20:1 bodies the growth rate approaches zero more smoothly at the critical Re_fr. Fig. 2 Inset shows the average body velocity U (in the locomoting state) for a 10:1 body, expressed as the translational Reynolds number, Re_U = ρUL/μ, over a broad range of Re_fr. There are three points worth noting. First, there is an apparently linear onset of translational motion at a positive 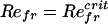. Second, the putative bifurcation point 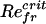is greater than the critical Re_fr of symmetry breaking. Third, Re_U increases monotonically with Re_fr and increases with apparent linearity for large Re_fr. For large Re_fr the corresponding Strouhal numbers, St = 2Re_fr/Re_U, have an asymptotic value slightly <0.2, which is at the lower end of the range (0.2 < St < 0.4) observed for efficient animal locomotion (15).

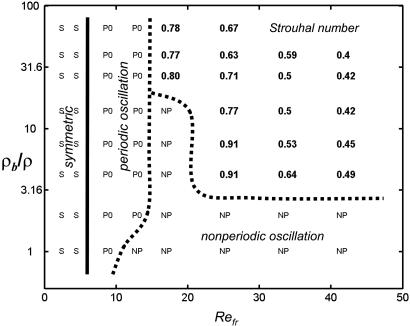
The examples of Fig. 3 give a sense of the physical constraints that delineate the regime of coherent locomotion accessible from rest. We have quantified this further by scanning the (Re_fr, ρ_b/ρ) parameter space for a 10:1 body aspect ratio (Fig. 4). As expected, below a transition Re_fr (apparently independent of ρ_b/ρ) we find that the state of no horizontal motion is apparently stable (Movie 4, which is published as supporting information on the PNAS web site). Above the transition Re_fr there is an intermediate region in which the body does not coherently locomote, but engages in a variety of periodic, quasi-periodic, or apparently chaotic dynamics. The periodic dynamics (Movie 5, which is published as supporting information on the PNAS web site) consist of regular horizontal oscillations, typically locked to a multiple of the flapping period. For small mass ratios, an increase in Re_fr brings a progressive loss of periodicity, leading to the irregular dynamics exemplified by Fig. 3C. For larger mass ratios, an increase of Re_fr leads to a locomoting state that shows decreased St with increased Re_fr (consistent with Fig. 2 Inset). Increasing the aspect ratio of the body decreases the ranges, in both Re_fr and ρ_b/ρ, of the various nonlocomoting states, and eases the transition to locomotion.

Fig. 4.

The final state of u_b, as a function of Re_fr, and ρ_b/ρ (ratio of body to fluid density), for a body of aspect ratio 10:1. For each point, the same start-up as in Fig. 1 is used. The “symmetric” region (points marked S) consists of runs in which u_b did not increase above the initial u_b of 0.01 during 80 periods of vertical flapping. “Periodic oscillation” (P0) means the horizontal velocity repeats to within 5% over at least five consecutive time intervals of the same length, with mean value < 0.1, corresponding to back-and-forth horizontal motion about a fixed point. “Nonperiodic oscillation” (NP) means the horizontal velocity did not meet the periodicity criterion during 80 flapping periods. The numbers indicate the mean Strouhal number for the case of steady locomotion, in which the horizontal velocity repeats to within 5% over at least five consecutive flapping periods, with mean value >0.1.

These results demonstrate how locomotion can arise “naturally” as an attracting dynamical state. We find that the interaction of the body with previously shed vortices can both enhance thrust during locomotion and provide the initial thrust that drives the body into locomotion. It has been conjectured that hovering insects enjoy enhanced lift because of the collision of their wings with previously shed vortices (16). Elaborations of our study include questions about the consequence of an attached and towed body (whose effect is approximated in the mass of the flapping wing), optimality in wing shapes and motions to obtain locomotion (including explicitly broken fore-aft symmetry), and the dynamics of bodies with purely internal forcing. The general 3D case introduces additional degrees of freedom that make the problem far more complex than we have considered here. However, simulations of 2D flapping airfoils undergoing prescribed motions can show good quantitative agreement with experimental studies of 3D finite-span wings, for the case when the vortex shedding is induced primarily by the reversal of the stroke direction (17), as it is in the present study. Complementary to the present study are recent numerical studies (4, 5) for flapping bodies whose translational motion is specified, and which identify a moderate Reynolds number below which thrust forces rapidly decrease. Our results show that spontaneous rotation of a flapped, axle-mounted wing seen in experiment (18) is observed in the more physically relevant regime of translation and demonstrate the critical effects of body mass and shape. Our study suggests, too, that the higher critical flapping frequency and the subcritical, hysteretic transition to rotation observed in the experiment may have resulted from axle-bearing friction. Taken together, those studies (4, 5, 18) and ours may also provide a fluid-dynamical explanation as to why some organisms change their locomotory strategy with increases in swimming speed [e.g., the mollusk Clione antarctica moves from using ciliary bands to flapping wings (19)] and suggest one possible origin of animal locomotion through the interaction of an oscillating body or appendage with its fluid environment.