Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 1997 Jan;72(1):397–407. doi: 10.1016/S0006-3495(97)78680-6

Identification and interpretation of complexity in sedimentation velocity boundaries.

B Demeler 1, H Saber 1, J C Hansen 1
PMCID: PMC1184330  PMID: 8994626

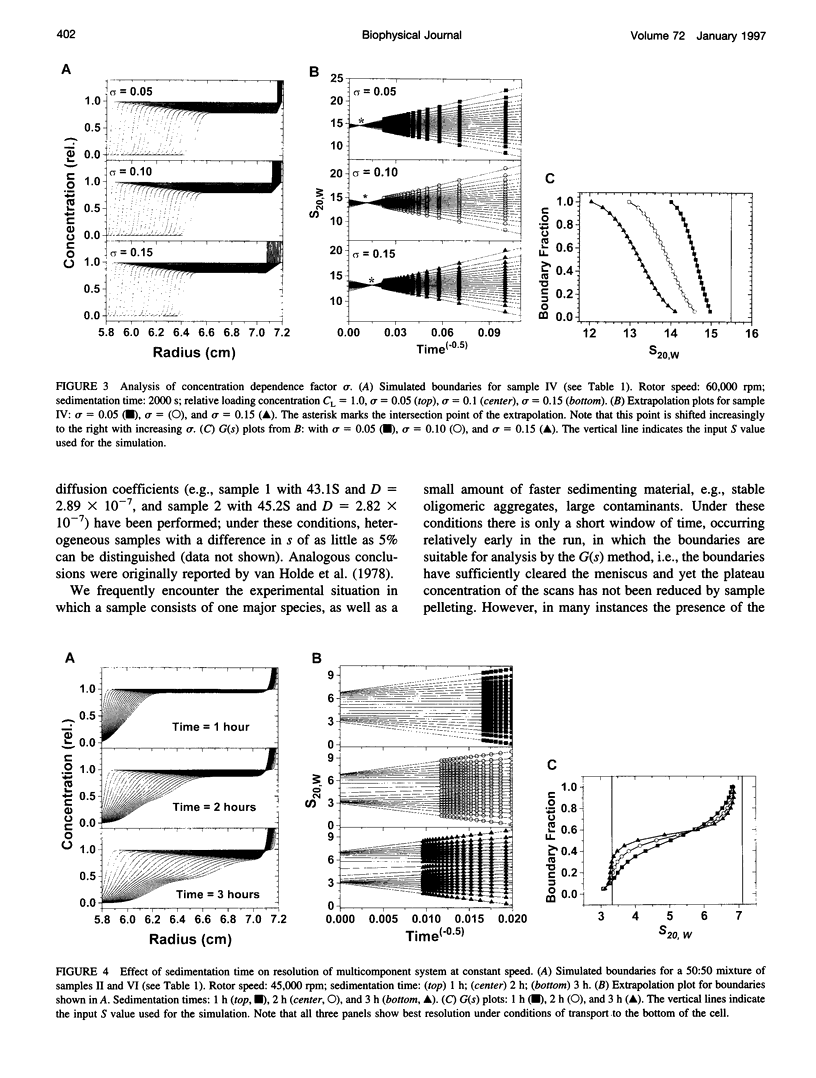
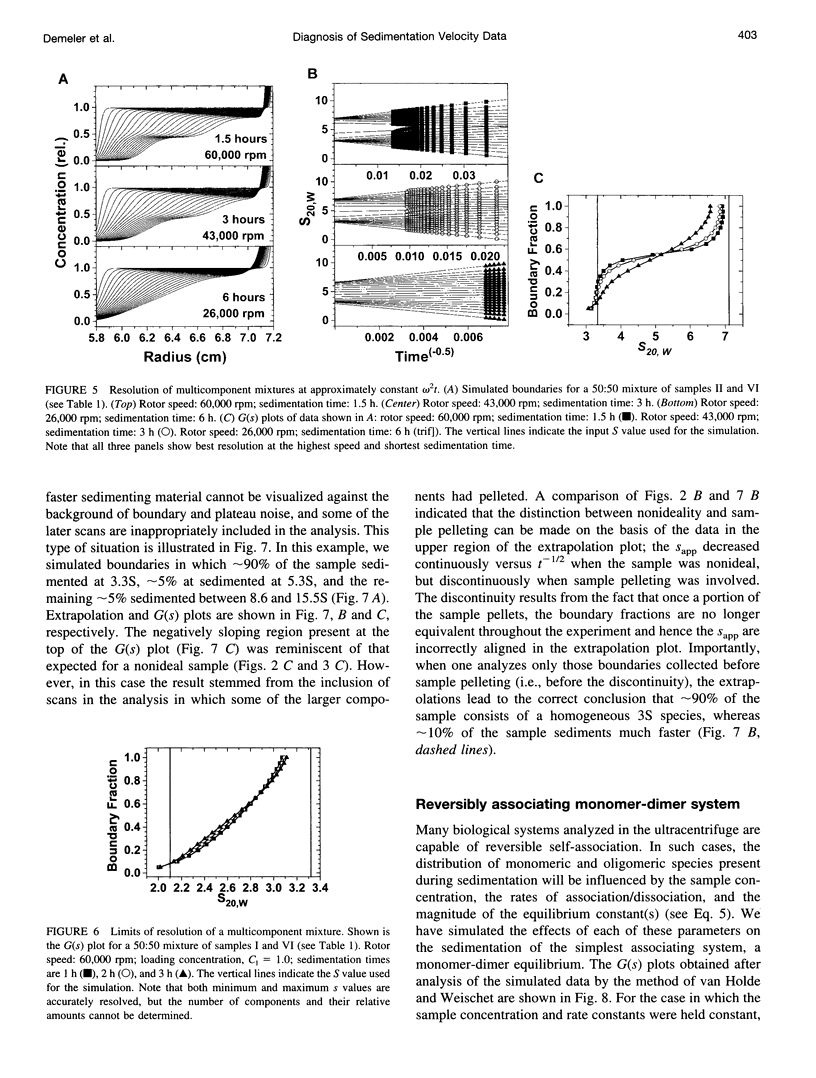
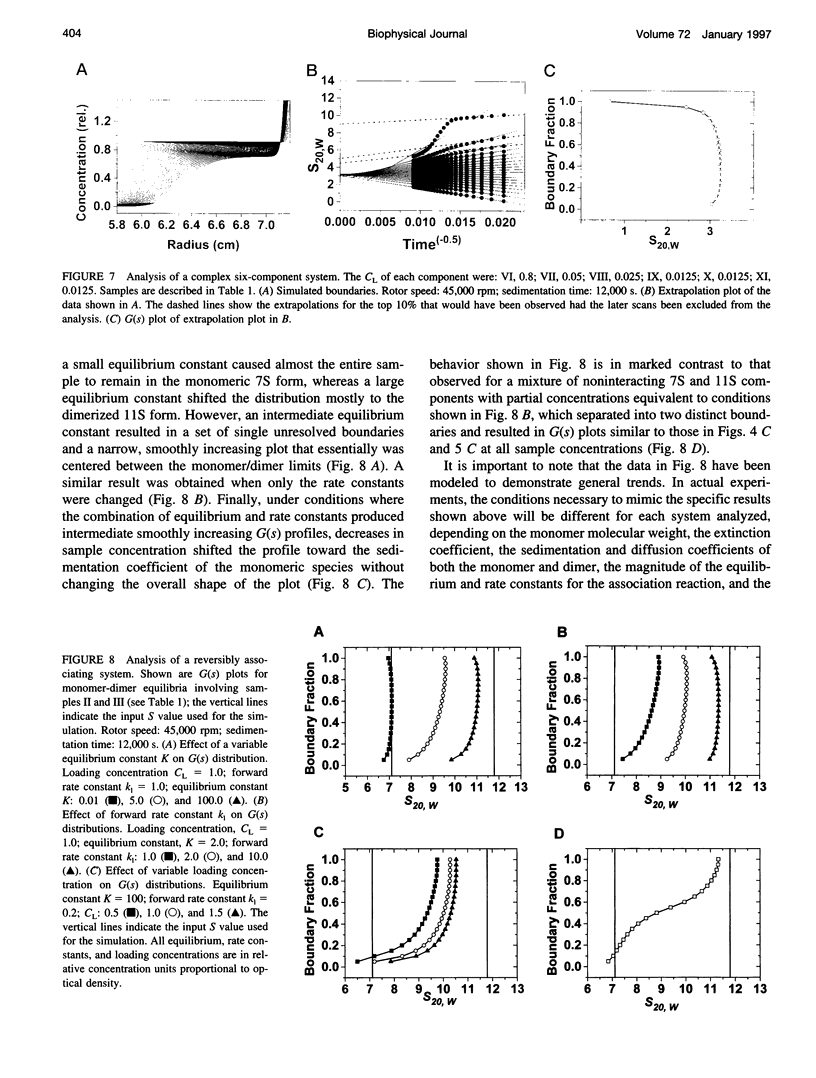
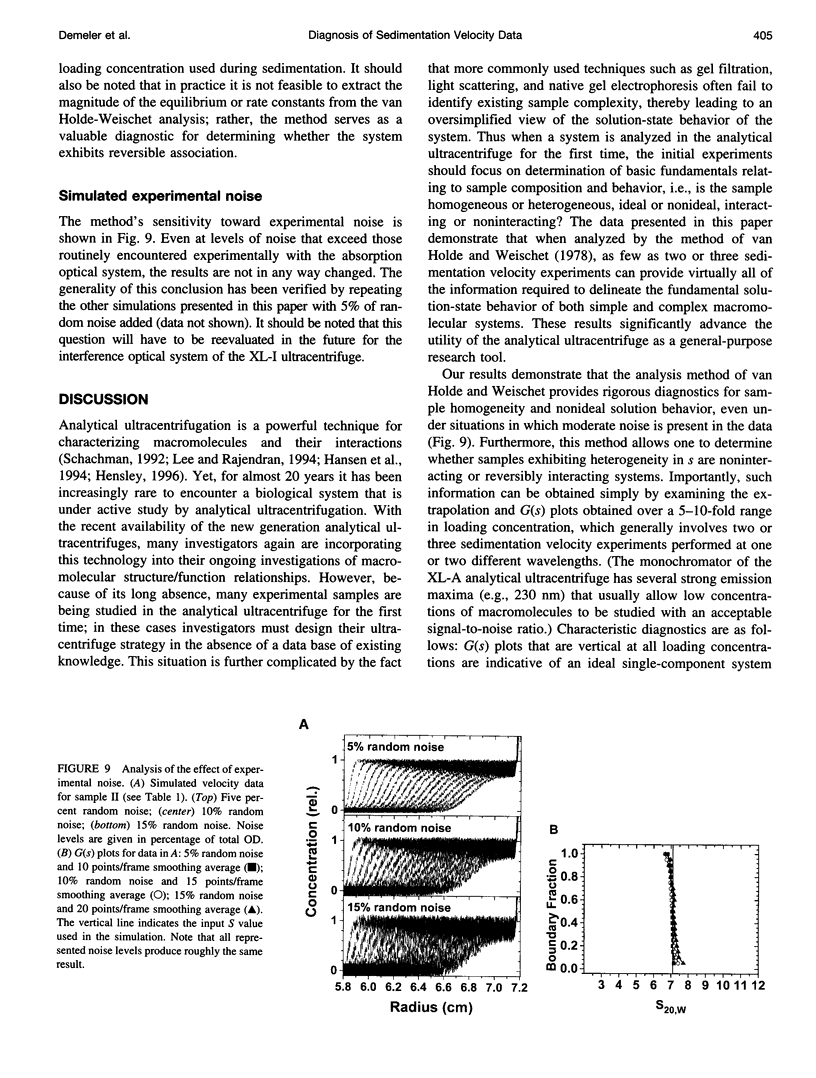
Abstract

Synthetic sedimentation velocity boundaries were generated using finite-element solutions to the original and modified forms of the Lamm equation. Situations modeled included ideal single- and multicomponent samples, concentration-dependent samples, noninteracting multicomponent samples, and reversibly self-associating samples. Synthetic boundaries subsequently were analyzed using the method of van Holde and Weischet, and results were compared against known input parameters. Results indicate that this analytical method provides rigorous diagnostics for virtually every type of sample complexity encountered experimentally. Accordingly, both the power and utility of sedimentation velocity experiments have been significantly expanded.

Full text

PDF
397

Images in this article

399FIGURE 1
on p.399
401FIGURE 2
on p.401
402FIGURE 3
on p.402
402FIGURE 4
on p.402
403FIGURE 5
on p.403
404FIGURE 7
on p.404
405FIGURE 9
on p.405

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Claverie J. M., Dreux H., Cohen R. Sedimentation of generalized systems of interacting particles. I. Solution of systems of complete Lamm equations. Biopolymers. 1975 Aug;14(8):1685–1700. doi: 10.1002/bip.1975.360140811. [DOI] [PubMed] [Google Scholar]
  2. Claverie J. M. Sedimentation of generalized systems of interacting particles. III. Concentration-dependent sedimentation and extension to other transport methods. Biopolymers. 1976 May;15(5):843–857. doi: 10.1002/bip.1976.360150504. [DOI] [PubMed] [Google Scholar]
  3. Correia J. J., Johnson M. L., Weiss G. H., Yphantis D. A. Numerical study of the Johnston-Ogston effect in two-component systems. Biophys Chem. 1976 Jul;5(1-2):255–264. doi: 10.1016/0301-4622(76)80038-5. [DOI] [PubMed] [Google Scholar]
  4. Eisenberg H. Sedimentation in the ultracentrifuge and diffusion of macromolecules carrying electrical charges. Biophys Chem. 1976 Jul;5(1-2):243–251. doi: 10.1016/0301-4622(76)80037-3. [DOI] [PubMed] [Google Scholar]
  5. Hansen J. C., Lebowitz J., Demeler B. Analytical ultracentrifugation of complex macromolecular systems. Biochemistry. 1994 Nov 15;33(45):13155–13163. doi: 10.1021/bi00249a001. [DOI] [PubMed] [Google Scholar]
  6. Hensley P. Defining the structure and stability of macromolecular assemblies in solution: the re-emergence of analytical ultracentrifugation as a practical tool. Structure. 1996 Apr 15;4(4):367–373. doi: 10.1016/s0969-2126(96)00042-1. [DOI] [PubMed] [Google Scholar]
  7. Johnson M. L., Correia J. J., Yphantis D. A., Halvorson H. R. Analysis of data from the analytical ultracentrifuge by nonlinear least-squares techniques. Biophys J. 1981 Dec;36(3):575–588. doi: 10.1016/S0006-3495(81)84753-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Schwarz P. M., Hansen J. C. Formation and stability of higher order chromatin structures. Contributions of the histone octamer. J Biol Chem. 1994 Jun 10;269(23):16284–16289. [PubMed] [Google Scholar]
  9. Todd G. P., Haschemeyer R. H. General solution to the inverse problem of the differential equation of the ultracentrifuge. Proc Natl Acad Sci U S A. 1981 Nov;78(11):6739–6743. doi: 10.1073/pnas.78.11.6739. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES