Magneto-ionic vortices: voltage-reconfigurable swirling-spin analog-memory nanomagnets

Abstract

Rapid progress in information technologies has spurred the need for innovative memory concepts, for which advanced data-processing methods and tailor-made materials are required. Here we introduce a previously unexplored nanoscale magnetic object: an analog magnetic vortex controlled by electric-field-induced ion motion, termed magneto-ionic vortex or “vortion”. This state arises from paramagnetic FeCoN through voltage gating and gradual N^3– ion extraction within patterned nanodots. Unlike traditional vortex states, vortions offer comprehensive analog adjustment of key properties such as magnetization amplitude, nucleation/annihilation fields, or coercivity using voltage as an energy-efficient tuning knob. This manipulation occurs post-synthesis, obviating the need for energy-demanding methods like laser pulses or spin-torque currents. By leveraging an overlooked aspect of N^3– magneto-ionics—planar ion migration within nanodots—precise control of the magnetic layer’s thickness is achieved, which enables reversible transitions among paramagnetic, single-domain, and vortion states, offering future prospects for analog computing, multi-state data storage, or brain-inspired devices.

Magneto-ionics are a promising approach for controlling magnetism via electric fields, but most studies have been limited to thin films, rather than the nanostructures that would form the basis of a magneto-ionic memory unit. Here, Spasojevic et al demonstrate magneto-ionic control over transitions among paramagnetic, single domain, and vortex states in an array of nanodots.

Introduction

With the advent of Big Data, energy resources spent on information technologies are growing exponentially¹. One of the reasons for this is that most memory systems utilize electric currents to write data, which dissipates power by Joule heating². Control of magnetic memories with electric fields instead of electric currents has emerged as a leading strategy to minimize this problem^3–6. Among the various mechanisms to tune magnetism with voltage (electrostatic charging, strain-mediated multiferroic coupling or electrochemical reactions^3,7), magneto-ionics, which involves the manipulation of magnetic properties through voltage-driven insertion/removal of ions, provides unprecedented performance for non-volatile control of coercivity, anisotropy, exchange bias or magnetization, ultimately causing conversion between magnetic and non-magnetic states^8–14. So far, most investigated magneto-ionic systems are continuous thin films utilizing different ion species (O^2–, N^3–, H⁺, Li⁺, etc.). Reports on magneto-ionic effects in nanoscale lithographed dots are scarce^15,16. From the fundamental viewpoint, in-situ measurements of voltage-driven ion motion in nanometer-sized structures might unveil changes in the magnetization reversal mechanisms, which may allow precise, analog control of magnetic bit properties that can be used to create novel neuromorphic functionalities.

At the nanoscale, unique magnetization switching mechanisms and topological spin configurations emerge, such as skyrmions or vortices. Magnetic vortices hold promise in applications such as multi-state data storage¹⁷, racetrack memories¹⁸, biomedicine¹⁹, spin-logics²⁰, or spin-torque nano-oscillators²¹, where the latter is relevant to microwave generation/detection²² and neuromorphic computing²³. Magnetic vortices compete with other spin configurations such as single-domain (SD), C- or S-states, or double-vortices^24,25. The ground state of the system is determined by the interplay between exchange and magnetostatic energy and is traditionally controlled by tuning the aspect ratio of as-grown nanostructures according to existing phase diagrams. This implies that altering the magnetization reversal mechanism and the magnetic properties of nanodots after sample growth is not straightforward. Post-synthesis manipulation of magnetic vortices has been accomplished, to some extent, by spin-torque effects²⁶, laser pulse excitation²⁷, or through the coupling with adjacent antiferromagnets²⁸, all requiring significant energy resources. Consequently, alternative approaches to controlling magnetism in nanoscale objects, by harnessing electric fields rather than relying on electrical currents or heating processes, are needed.

Voltages applied across piezoelectric substrates with magnetostrictive nanodots grown on top can trigger the creation and annihilation of magnetic vortices²⁹, a change of the vortex chirality/polarity³⁰, or a magnetization reorientation in SD nanodots³¹ via the Villari effect. However, strain-mediated coupling cannot induce an analog modulation of the magnetization amplitude, crucial for mimicking weights in artificial synapses,³² nor can it be used to precisely control the nucleation/annihilation fields of vortex states. Furthermore, strain-coupled devices suffer from long-term fatigue and eventual cracking that limit their useful lifetime. Moreover, the magnetic state of each nanodot is often unpredictably influenced by the local strain stemming from the complex ferroelectric domain structure of the substrate. Considering all the shortcomings of existing strategies, the analog modification of magnetic properties via voltage-induced migration of ions in nanometer-sized dots arises as an unparalleled alternative.

Here, we demonstrate the operation principle of an analog magnetic vortex controlled by electric-field-driven ion motion (“vortion” or magneto-ionic vortex). Such state is generated from paramagnetic FeCoN nanodots upon voltage-driven gradual extraction of N^3– ions. The characteristic properties of vortions (nucleation and annihilation fields, coercivity, or remanence) can be fully controlled with voltage. While these objects show some resemblance to conventional magnetic vortices, a unique feature of vortions is that the amplitude of their magnetization, akin to synaptic weight, can be dynamically reconfigured in an analog manner by adjusting the voltage actuation time. Additionally, voltage can induce a reversible transition among three distinct states via migration of N^3– ions – paramagnetic, single-domain and magneto-ionic vortex– which is not possible using conventional methods. Such control exploits a rather unique, so far overlooked, aspect of N^3– magneto-ionics: contrary to O^2– magneto-ionics (where voltage generates ferromagnetic clusters within a paramagnetic matrix), diffusion of N^3– ions results in the formation of a planar migration front, dividing the nanodot into sub-layers with dissimilar composition and magnetic features.

Results and discussion

Unraveling the magneto-ionic vortex: formation and control

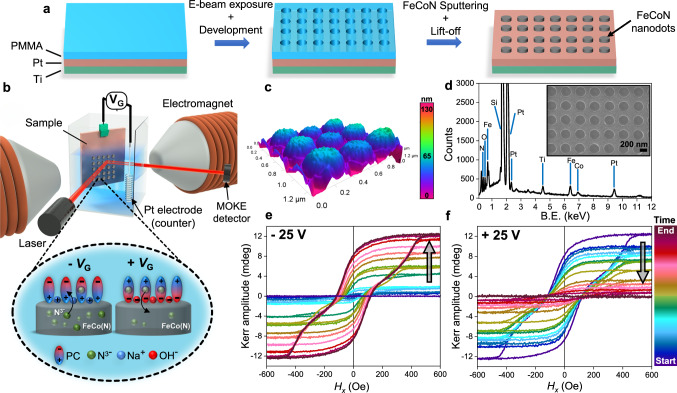
FeCoN nanodot arrays were prepared by electron beam lithography, followed by magnetron sputtering and lift-off, as depicted in Fig. 1a (see Section “Methods”). Atomic force microscopy (AFM) topography and transmission electron microscopy (TEM) images show that patterned nanodots have diameter of 280 nm and thickness around 35 nm (Fig. 1c and Supplementary Fig. 1). Energy dispersive X-ray analysis (EDX) reveals a Fe:Co atomic ratio of 65:35 (Fig. 1d). This composition was chosen since it shows the largest nitrogen magneto-ionic effects reported so far³³. To trigger ionic migration, we employed an electrolyte-gated setup in a capacitor configuration within a custom-made electrochemical cell (Fig. 1b) that allowed us to track real-time alterations of magnetic properties using magneto-optical Kerr effect (MOKE). Propylene carbonate (PC) with Na⁺- and OH⁻-solvated species was employed as an anhydrous polar liquid electrolyte. Its role is twofold: to act as a reservoir for N^3– ions, and to facilitate the creation of an electric double layer (EDL), which comprises a sub-nm-thick layer of solvated ions drawn to the interface between the gated layer and the electrolyte. This generates a strong electric field capable of efficiently transporting N^3– ions into and out of FeCoN, depending on the gate voltage (V_G) polarity⁶. Once in PC, N^3– ions are stabilized by PC solvation shells, possibly forming transient ion pairs with Na⁺ cations. The as-grown FeCoN nanodots are paramagnetic with virtually no Kerr amplitude (Fig. 1e, purple line, and Supplementary Fig. 2a). Upon application of V_G = –25 V, N^3– ions begin to migrate towards the PC, generating ferromagnetic phases within each FeCoN nanodot. After 6 min, an appreciable, narrow hysteresis loop emerges, characterized by a Kerr amplitude of 0.5 mdeg (Supplementary Fig. 2b). Interestingly, with increasing actuation time, not only does the Kerr amplitude increase, but the shape of hysteresis loops undergoes a transformation, from square-like (short actuation times) to constricted loops (longer actuation times) (Supplementary Fig. 2c, d), typical of vortex formation^24,34–36. When a voltage of opposite polarity is applied (V_G = +25 V), N^3– ions are reintroduced from the electrolyte into the FeCo(N) layer. This results in a decrease of the Kerr amplitude (Fig. 1f), accompanied by a change of hysteresis loops’ shape (from vortex-like to square-like) and, finally, recovery of the paramagnetic FeCoN state (Supplementary Fig. 2e–h). As a control, we measured the hysteresis loop of 35 nm thick FeCoN continuous film after negative voltage gating, following the same procedure, which displayed a square-like shape with no evidence of constriction (Supplementary Fig. 3).

Fig. 1. Device and set-up schematics for voltage-induced ferromagnetism in FeCoN nanodots.

a Schematic representation of FeCoN nanodots preparation by electron-beam lithography and sputtering. b Schematics of the electrochemical cell, custom-made in our lab, used for the in-situ measurements of voltage-induced magnetism within FeCoN nanodots by MOKE (see Section “Methods”). A zoomed-in panel depicts electric-double layer formation at the FeCoN/propylene carbonate (PC) electrolyte interface and N^3– migration out of and into the FeCoN layer when negative or positive gate voltage (V_G) is applied between working and counter electrode, respectively. c 3D topography of FeCoN nanodots measured by AFM in tapping mode. d EDX analysis of as-grown FeCoN nanodots. The inset shows an SEM image of the nanodots array. Evolution of hysteresis loops measured by MOKE during negative (e) and positive (f) voltage actuation of FeCoN nanodots. Starting from the paramagnetic state (purple curve in e), Kerr amplitude progressively increases over time. Simultaneously, the measured hysteresis loops undergo a transition in shape, evolving from square-like to constricted (see Supplementary Fig. 2). The opposite happens when positive voltage is applied, whereby the initial paramagnetic state can be reversibly restored.

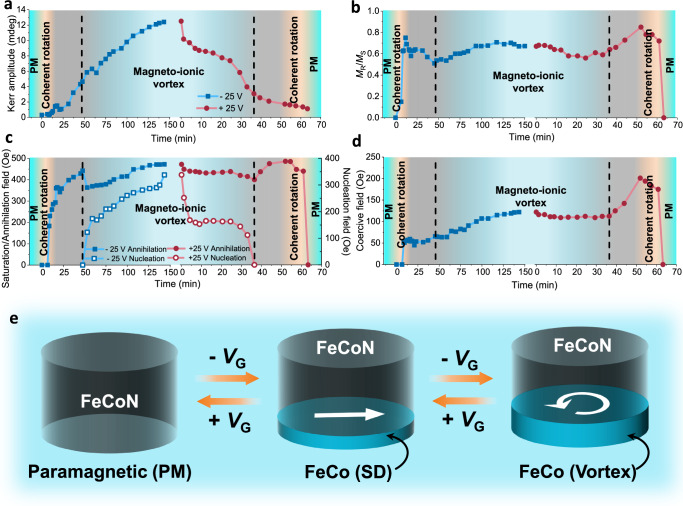
The dependance of the Kerr signal amplitude at saturation (A_Kerr), squareness ratio (i.e., remanence-to-saturation ratio, M_R/M_S), saturation field (annihilation for the vortex state) (H_S or H_A), vortex nucleation field (H_N) and coercivity (H_C) on time is plotted in Fig. 2. The blue curves illustrate the time evolution of specific parameters under – 25 V. In contrast, the red curves depict the change in the same parameters over time under + 25 V, providing information about the reversibility of magneto-ionic actuation. Given the finite spot size in MOKE measurements, it should be noted that the reported values of the measured parameters represent the average values obtained from several dots within the same region. As shown in Fig. 2a, A_Kerr progressively increases in the presence of a negative voltage, and diminishes when the voltage polarity is reversed, as expected. The M_R/M_S ratio (Fig. 2b) exhibits a non-monotonic behavior while applying –25 V. It first increases with time while the loops present no constriction (SD state) but, after 15 min, M_R/M_S starts to decrease for actuation times up to 50 min, after which a clear loop constriction is observed. Notably, this behavior follows the same trend upon the application of +25 V. The abrupt change in M_R/M_S at 50 min marks the onset in the emergence of a certain nucleation field and coincides with a sudden alteration in H_A characteristics, as illustrated in Fig. 2c. Once again, the behaviors of H_S (or H_A) and H_N follow a reversible and opposite trend when a positive voltage is applied. The concurrent alterations in the mentioned parameters align with the emergence of clear constriction in the hysteresis loops and therefore indicate a change in the magnetization reversal mechanism—from coherent rotation (orange region, with square-like loops) to vortex formation (blue region). The transition from coherent rotation to vortex states and vice versa proceeds gradually, as denoted by grey shadowed regions in Fig. 2a–d. Within these transient regimes, where SD-like and vortex-like states coexist, the hysteresis loops’ shape falls somewhere between the two states (Supplementary Fig. 2c, f). The black dotted lines in Fig. 2a–d delimitate the regions where vortions are stable for positive and negative voltage actuation, respectively.

Fig. 2. Magneto-ionic vortex (i.e., vortion) operation.

Evolution of hysteresis loop parameters and main reversal mechanisms with voltage actuation time such as Kerr amplitude measured at saturation (H_applied = 2000 Oe) (a), squareness ratio M_R/M_S (b), saturation/annihilation field (left axis) and nucleation field (right axis) (c) and coercivity (d). Blue lines (denoted by full or empty squares) and red lines (denoted by full or empty circles) depict evolution of a given parameter with time when negative or positive voltage is applied, respectively. For short actuation time, a thin ferromagnetic layer (highly or fully depleted in nitrogen) is formed, resulting in a low Kerr amplitude and square-like hysteresis loops. This indicates the presence of single domain (SD) state and magnetization reversal by coherent rotation (orange regions). Conversely, for extended actuation at –25 V, the ferromagnetic layer thickness increases gradually, which stabilizes the magneto-ionic vortex state and provides a means to fine-tune its magnetization amplitude and critical fields (blue regions). The grey regions indicate transient states, representing the transitional phases between the SD and vortex states, and vice versa. The black dotted vertical lines delimitate the regions where the magneto-ionic vortex state is fully stable. e Schematic representation of the transition between paramagnetic (PM), SD and magneto-ionic vortex states within the same FeCo(N) nanodot driven by N^3– ion migration when a gate voltage V_G is applied.

Remarkably, upon application of V_G = – 25 V, once in the vortion regime, both H_A and H_N clearly evolve with time, where increasing voltage actuation time dynamically impacts the stability of the vortex state. Specifically, when coming from positive saturation (descending branch of the hysteresis loops), extending the voltage actuation time results in the vortex state nucleating earlier and annihilating later. Thus, longer application of voltage leads to increased stability of the vortex state. Micromagnetic simulations and analytical calculations show that inter-dot dipolar interactions have a minimal impact on the annihilation field, reducing it by less than 6 % for the thickest generated magnetic phase (Supplementary Section II) and even less for thinner layers. This effect contrasts with the observed behavior of H_A over time (whereby H_A increases -instead of decreasing- with the layer thickness), shown in Fig. 2c, further supporting the conclusion that the increase in H_A stems from the enhanced stability of the vortex state.

Our observations are consistent with an increase in thickness of the formed ferromagnetic phase as depicted in Fig. 2e. Commencing with paramagnetic FeCoN, brief negative voltage actuation induces the formation of a thin ferromagnetic layer within FeCoN nanodots, giving rise to a SD state and magnetization reversal through coherent rotation. This layer could be FeCo alloy or (Fe,Co)₄N, both of which are ferromagnetic. With prolonged negative voltage application, the thickness of the ferromagnetic layer gradually increases, destabilizing the SD state and causing the nucleation of the vortex state²⁵. The progressive increase in the thickness of the ferromagnetic layer further stabilizes the vortex configuration (thereby increasing H_N and H_A), in agreement with the literature^35,37. Importantly, in our case, magneto-ionic actuation allows precise tuning of the magnetic phase thickness within the same sample. This allows accurate post-synthesis control over the magnetization reversal mechanism and enables analog modulation of magnetization along with the other characteristic parameters of the magneto-ionic vortex state. Several paramagnetic ⟷ single domain ⟷ vortion cycles are shown in the Supplementary Fig. 4.

We delved deeper into the impact of actuation time on the magnetization reversal mechanism by MFM imaging. Figure 3 displays two hysteresis loops obtained by MOKE after voltage treatments for varying durations, together with overlaid MFM phase images collected at different values of in-plane magnetic field. Results in panel a) were obtained for short actuation times, giving rise to magnetization reversal via coherent rotation (i.e., rotating dipolar contrast as a function of magnetic field). Conversely, for long-term actuation (Fig. 3b), one can observe magnetization reversal via vortex formation in agreement with the constriction observed in the hysteresis loop. Formation of the vortex is evidenced by a featureless MFM phase contrast, with a signal arising only from the discernible vortex cores (Fig. 3c)^38–40 that have magnetization perpendicular to the plane of nanodots. Direct evidence of vortex formation in long-term treated 280 nm dots was obtained through magnetic imaging at the Photoemission Electron Microscope (PEEM) endstation at the ALBA Synchrotron, using X-ray circular magnetic dichroism (XMCD) contrast (see Section “Methods”). Figure 3d–f shows XMCD-PEEM images at Co L₃ edge, where the characteristic bright-dark magnetic contrast observed in an array of six 280-nm nanodots after long-term negative voltage treatment (Fig. 3d) unequivocally demonstrates the formation of the magnetic vortex state. This is evidenced by the spins curling around the vortex core, as depicted in Fig. 3e for a single 280-nm nanodot. Additionally, we patterned another array of FeCoN nanodots, maintaining the same thickness but increasing their diameter to 1 µm and subjected them to the same voltage treatment. XMCD-PEEM image of a single 1 µm nanodot (Fig. 3f) further confirms the presence of the magnetic vortex state. As expected, no contrast was observed in the as-grown nanodots (Supplementary Fig. 8a). Moreover, we demonstrate that our procedure can be extrapolated to larger dots showing the same phenomenology and allowing observation of the magnetic states by other (non-synchrotron based) techniques, e.g. Kerr imaging (see Supplementary Figs. 5 and 6).

Fig. 3. MOKE hysteresis loops with MFM imaging for selected voltage-actuation times and XMCD-PEEM imaging.

a Hysteresis loop and MFM phase images of one of the disks measured after short-time voltage actuation (–25 V), corresponding to the formation of thin ferromagnetic layer. The shape of the hysteresis loop, together with the observed rotation of dipolar contrasts, shows that in such thin magnetic layers, magnetization reversal proceeds via coherent rotation. b Hysteresis loop and MFM phase images measured after long-time voltage actuation, corresponding to the formation of a thick ferromagnetic layer. In this case, the obtained results reveal that magnetization reversal occurs through formation of a swirling spin (i.e., vortion) state. c MFM phase image of three adjacent nanodots, measured near coercivity after long-term negative voltage treatment (i.e. 150 min at –25 V), where vortex cores can be envisaged, as indicated by dashed lines for one nanodot. XMCD-PEEM images recorded at the Co L₃ absorption edge and near coercivity for an array of six 280 nm FeCo(N) nanodots (d), single 280 nm FeCo(N) dot (e) and a single 1 µm FeCo(N) dot (f) after long-term voltage treatment at –25 V. Characteristic bright-dark magnetic contrast, observed for both dot diameters, demonstrates the presence of the magnetic vortex state, where the blue arrows represent the average spin direction in certain areas of the dot.

Figure 2d reveals that H_C, during –25 V gating, exhibits a minor peak precisely at the moment when the vortex state starts to form. An analogous behavior is evident in the opposite case scenario, albeit with significantly higher H_C values. Enhancement of H_C at the transition between SD and vortex states has been previously reported.⁴¹ Superimposed to this behavior is a steady increase of H_C, observed while going from SD to vortex state and vice versa, which is persistent over time. The increase of H_C under negative voltage is consistent with the formation of FeCo or (Fe,Co)₄N magnetic phases. As previously observed in FeCoN films, a reduction in nitrogen content (i.e., from FeCoN_x to FeCo) results in progressively higher magnetization and coercivity^42,43. The final coercivity values during positive gating (≈170 Oe) are substantially higher compared to initial values (≈50 Oe) when negative voltage is applied, indicating the presence of magnetic phases with dissimilar nitrogen content at the beginning and at the end of gating with negative and positive voltages, respectively.

Microstructural insights into the mechanisms of ion migration

To elucidate the ion migration mechanism in FeCoN nanodots, we conducted high-resolution TEM (HR-TEM), high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) and electron energy loss spectroscopy (EELS) compositional mapping on cross-sectional lamellae extracted from as-grown and – 25 V treated samples. EELS compositional maps for each sample state were collected in two distinct regions, as indicated by rectangles in HAADF-STEM images of the nanodot’s cross-sections (Fig. 4a, d), covering the entire nanodot and its interior. Additionally, for each state, we measured EELS compositional line profile across the nanodot (Fig. 4g, h). A uniform distribution of Fe, Co, and N ions within the dot is observed in the as-grown sample (Fig. 4b, c, g). Following the application of negative voltage, ions within the sample exhibit a distinct, altered distribution. Specifically, positively charged Fe ions migrate towards the bottom interface with Pt, where they accumulate (Fig. 4e, f, h, blue line). Upon treatment, the concentration of Co ions also slightly increases towards the bottom interface of the nanodot. Similar motion of Ni²⁺ ions upon voltage application has been recently reported in gated NiO films⁴⁴. A more intriguing aspect lies in the distinct behavior of negatively charged N^3– ions, exhibiting a counter-directional migration compared to transition metal ions, that following partial release into the electrolyte, also accumulate at the top interface of the FeCoN films. This generates a distinctive planar migration front which subdivides the FeCoN dot into two sub-layers with dissimilar nitrogen content: N-depleted or N-free (at the bottom) and N-rich (top) of the nanodot (Fig. 4f, h). This nitrogen accumulation phenomenon has been observed in systems characterized by relatively fast nitrogen magneto-ionic effects. When nitrogen diffuses faster than it dissolves, the EDL becomes saturated with N^3– ions, locally surpassing the solubility limit of nitrogen in PC. In this scenario, N^3– ions reach a point where they cannot be released further into the liquid, resulting in their accumulation at the upper part of the FeCoN nanodot^33,45. EELS maps allowed us to estimate the thickness of the magneto-ionically induced magnetic layer in this case to be ≈11–12 nm. Additional images of nitrogen EELS compositional mapping for different gating conditions are provided as Supplementary Fig. 7.

Fig. 4. HR-TEM and EELS compositional mappings.

a HAADF-STEM image of as-grown FeCoN nanodot. Red and orange rectangles indicate two areas where EELS compositional mapping was performed. EELS compositional maps, comprising the entire as-grown nanodot (Area 1, b) and closer examination of nanodot’s interior (Area 2, c), show uniform distribution of Fe, Co and N throughout both regions. d HAADF-STEM image of FeCoN nanodot treated with –25 V. EELS compositional maps performed in two areas (e, f) indicated in (d) show that upon negative voltage treatment Fe/Co ions and N^3– ions migrate in opposite directions, thereby creating a distinct planar migration front indicated by black dashed lines in (f). This planar front divides the nanodots into two sub-layers with distinct magnetic properties: ferromagnetic FeCo/(Fe,Co)₄N (i.e., nitrogen-depleted) at the bottom part and paramagnetic FeCoN (i.e., nitrogen-rich) in the upper part of the nanodot. g, h Normalized EELS compositional line profiles of as-grown and treated FeCoN dots, respectively, collected starting from the top of the nanodot. HR-TEM images of nanodot’s interior before (i) and after (j) voltage treatment (at –25 V), including the FFT of the areas marked by orange squares. Reflections marked by yellow and cyan circles in (i) correspond to the interplanar distances of 2.26 Å, 2.60 Å, respectively, and stem from (200) and (111) planes of $\mathrm{F}\overline{4}3\mathrm{m}$ (Fe,Co)N. After voltage treatment (j), new interplanar distances of 1.10 Å (green) and 2.15 Å (pink) emerge. Interplanar distance of 1.10 Å can be ascribed to (311) planes of face-centered cubic (fcc) $\mathrm{Fm}\overline{3}\mathrm{m}$ Co, (211) planes of body-centered cubic (bcc) $\mathrm{Im}\overline{3}\mathrm{m}$ Fe, or to (211) planes of simple cubic $\mathrm{Pm}\overline{3}\mathrm{m}$ FeCo alloy. Similarly, interplanar distance 2.15 Å can be related to (111) planes of fcc $\mathrm{Fm}\overline{3}\mathrm{m}$ Co, (110) planes of bcc $\mathrm{Im}\overline{3}\mathrm{m}$ Fe, (110) planes of $\mathrm{Pm}\overline{3}\mathrm{m}$ FeCo or (111) planes of $\mathrm{Pm}\overline{3}\mathrm{m}$ (Fe,Co)₄N.

Our observations underscore the critical significance of the formed nitrogen front in modulating the thickness of the induced ferromagnetic counterpart by adjusting the voltage actuation time. This phenomenon, absent in oxygen magneto-ionic systems such as CoO_x and FeO_x^12,16, plays a pivotal role in the transition from a SD to a vortion state. In most other systems, ion migration leads to the emergence of ferromagnetic clusters within a paramagnetic matrix, as opposed to the formation of distinct ferromagnetic thin bottom sub-layer alongside paramagnetic top sub-layer.

HR-TEM images of nanodot cross-sections and fast Fourier transforms (FFTs) of the areas enclosed within orange squares in Fig. 4i, j, were utilized to elucidate the nature of the phases before and after gating at –25 V, respectively. As-grown FeCoN nanodot has a nanocrystalline structure and exhibits two sets of discrete spots, corresponding to interplanar distances of 2.26 Å (yellow circles) and 2.60 Å (cyan circles), consistent with (200) and (111) planes of face-centered cubic (fcc) $\mathrm{F}\overline{4}3\mathrm{m}$ (Fe,Co)N, which is paramagnetic. FeCoN nanodots treated with –25 V show more amorphous structure with embedded nanocrystalline areas, especially visible at the bottom part of the film. The latter are characterized by the absence of the aforementioned (Fe,Co)N non-magnetic phase and by appearance of two new interplanar distances: 1.10 Å (green circles, which is consistent with planes from $\mathrm{Fm}\overline{3}\mathrm{m}$ Co, $\mathrm{Im}\overline{3}\mathrm{m}$ Fe or $\mathrm{Pm}\overline{3}\mathrm{m}$ FeCo), and 2.15 Å (pink circles, that matches planes from $\mathrm{Fm}\overline{3}\mathrm{m}$ Co, $\mathrm{Im}\overline{3}\mathrm{m}$ Fe, $\mathrm{Pm}\overline{3}\mathrm{m}$ FeCo or $\mathrm{Pm}\overline{3}\mathrm{m}$ (Fe,Co)₄N, all of them ferromagnetic). These findings agree with the aforementioned description of how ferromagnetic behavior emerges in the voltage-treated dots.

Micromagnetic modelling of magneto-ionic vortices

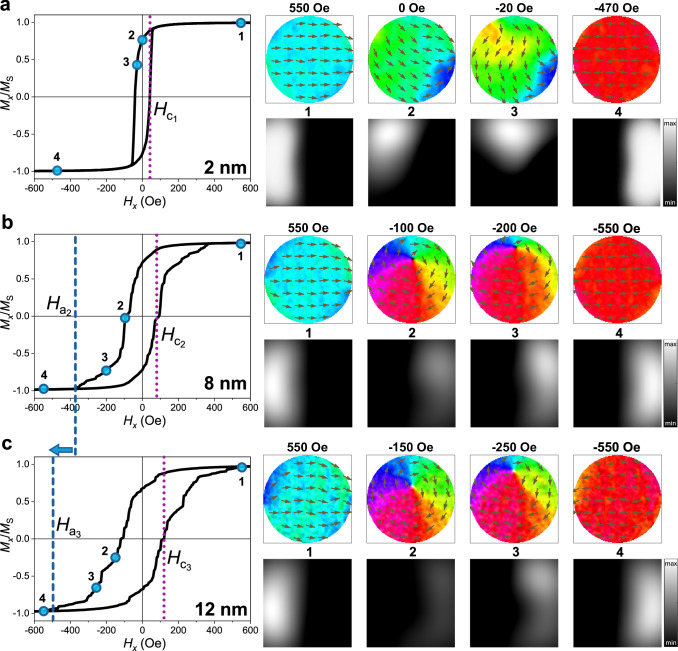
The observed evolution of magnetic properties upon gating was modelled using micromagnetic simulations. Figure 5 shows simulations of the magnetization reversal processes while applying – 25 V. As described in the “Methods” section, the thicknesses were chosen based on experimentally estimated values, and the magnitudes of M_S and K_u were tuned to obtain coercivities and saturation fields similar to experimental ones (Fig. 2). Importantly, an increase of both M_S and K_u with increasing thickness is needed to match the experimental loop characteristics (see Supplementary Figs. 9 and 10 for details). This is consistent with a progressive loss of N content in the nanodots (in our case caused by voltage), as reported in the literature for FeCoN⁴². For the thinnest disks (Fig. 5a) the reversal process occurs via quasi-coherent rotation (with minor curling prior to saturation) and the loop shape and H_C of 50 Oe agree well with the experimental hysteresis loop (Supplementary Fig. 2b). For intermediate and large thicknesses (Fig. 5b, c), vortex reversal is observed, also in agreement with the experimental results. Note that the concomitant increase of H_C and H_A with gating time is captured by the simulations. In this context, although vortions resemble conventional magnetic vortices, they exhibit unique characteristic of finite coercivity, which, along with the associated anisotropy, prevents the complete closure of experimentally measured hysteresis loops, consistent with micromagnetic simulations. The high-coercivity square hysteresis loop measured after long-time gating at +25 V (Supplementary Fig. 2g) was also modelled. For this, a high K_u was used compared to the value for 2 nm thick disks initially formed at –25 V. During the +25 V treatment, the nitrogen front will move from the top to the bottom of the disks, resulting in a thinner ferromagnetic layer, but with material parameters similar to those of the previously generated thickest dots. Besides the high anisotropy, we slightly decreased the inter-grain exchange coupling to 30 % to match the experimental value of H_C (Supplementary Fig. 11). This is plausible since nitrogen ions might preferentially diffuse along grain boundaries and, in addition, grains might become less interconnected at progressively smaller thicknesses.

Fig. 5. Micromagnetic simulations showing the reversal process of the magnetic disks upon application of –25 V.

Simulated hysteresis loops are shown for 280-nm diameter magnetic disks where the thicknesses and magnetic parameters were chosen to capture the reversal behavior of (a) a short-term voltage treatment (thickness 2 nm, M_S = 400 emu cm⁻³, K_u = 2.5$\times$10⁵ erg cm⁻³), (b) a mid-term voltage treatment (thickness 8 nm, M_S = 500 emu cm⁻³, K_u = 3.5$\times$10⁵ erg cm^-3), and (c) long-term voltage treatment (thickness 12 nm, M_S = 550 emu cm⁻³, K_u = 6.0$\times$10⁵ erg cm^-3). The hysteresis loops shown on the left are an average of 10 runs (see Supplementary Fig. 10 for details), and the images on the right show spin distributions (top) and calculated MFM images (bottom) at selected fields for a representative run. Blue and purple dashed lines mark the values of annihilation H_A and coercive fields H_C, respectively.

Outlook

We have shown that voltage can serve as an energy-efficient actuation method for tuning magnetization reversal mechanism and magnetic properties of FeCoN nanodots between paramagnetic, SD and magneto-ionic vortex states. Under the action of electric field, N^3– ions diffuse via planar front formation, enabling the thickness of formed magnetic counterpart to gradually increase. This migration front, not present in other magneto-ionic systems, not only allows control over the magnetization reversal mechanism but also provides the capability to adjust magnetization and critical fields on-demand. The analog tuning of the vortex state, as demonstrated here, offers unique advantages over alternative methods like strain-mediated actuation relying on ferroelectric substrates, spin-transfer torque effects, or coupling with adjacent antiferromagnets, where the magnetization amplitude is held constant. In this context, vortions hold the potential to introduce innovative concepts in neuromorphic computing. Specifically, if integrated within spin-transfer-torque nano-oscillators—employed to emulate neurons⁴⁶—the magneto-ionic vortex is poised to offer tunable magnetic synaptic weights through voltage-driven modulation of magnetization. Furthermore, alteration of magnetic anisotropy within the nanodots, as also demonstrated in this study, could impact the gyroscopic frequency of precessing vortex cores.⁴⁷ This, in turn, could influence the magnetization dynamics of neighboring oscillators, akin to the way in which spikes affect post-synaptic neurons, therefore further expanding the applicability of magneto-ionic vortices in neuromorphic spintronics systems and multi-state analog computing.

Methods

Sample preparation

FeCoN nanodots with a diameter of 280 nm and thickness of 35 nm were prepared by electron beam lithography (EBL) and subsequent magnetron sputtering. EBL was performed by using a Raith GmbH-150-TWO nanofabrication system. A double layer MMA/PMMA photoresist mask was deposited by spinning for 55 s at 1500 rpm and baked for 60 s at 180 °C on top of [100]-oriented Si substrates previously coated with Ti (20 nm)/Pt (50 nm) layers (deposited by sputtering). Photoresists were developed using 1:3 methyl isobutyl ketone/isopropanol (MIBK/IPA) for 60 s. After pattering, 35 nm of ternary nitride Fe_0.65Co_0.35N (FeCoN) was deposited by reactive magnetron co-sputtering at room temperature. An AJA International ATC 2400 sputtering system with a base pressure of around 8$\times$10⁻⁸ Torr was used. The target-to-substrate distance was kept at 11 cm. Reactive sputtering was done at a total pressure of 3$\times$10⁻³ Torr in an Ar/N₂ mixed atmosphere. During the sputtering, the Ar:N₂ flow ratio was set to 1:1 in order to produce nitrogen-rich nanodots exhibiting paramagnetic behaviour. Based on a previous study, the metallic Fe target was operated at a constant DC power of 50 W, while the Co target was channelled to a RF source with a power of 55 W³³. Finally, non-exposed photoresist was removed by a lift-off process in acetone using an ultrasonic bath, revealing FeCoN nanodots.

MOKE measurements

In-situ measurements of hysteresis loops during voltage actuation were acquired using a Magneto-Optical Kerr Effect (MOKE) magnetometer (NanoMOKE3, Durham Magneto Optics Ltd.) in a longitudinal geometry with the magnetic field applied in-plane. The system enables the application of time-varying magnetic fields to the sample, and the rotation of the polarization plane of the reflected laser beam, referred to as the Kerr signal, is measured as a function of the applied field and plotted in the form of the hysteresis loops. For in-situ measurements in a propylene carbonate (PC) liquid electrolyte, we affixed a custom-made quartz electrochemical cell onto the sample holder. The cell, which we designed specifically for the magneto-ionic measurements in liquid, housed the Si/Ti(20 nm)/Pt(50 nm)/FeCoN nanodots sample and featured electrical contacts to the bottom Pt layer (working electrode) and Pt wire (counter electrode) in a capacitor configuration. We applied a gate voltage (V_G) between the mentioned electrodes using an external Agilent B2902A power supply, while simultaneously measuring the magnetic response of the sample, induced by the migration of ions within the FeCoN nanodots. The spot size of MOKE is around 2 μm, which means that around 20 nanodots from the same region were sampled in each measurement.

Magneto-optic Kerr imaging

Kerr imaging was performed with a high-resolution microscope (Evico Magnetics) using an oil immersion objective lens. The magnetic field is applied in-plane by a rotatable electromagnet with split pole pieces to enhance the field uniformity. In this set-up, it is possible to perform the simultaneous acquisition of two perpendicular components of the magnetization, transversal (parallel to the applied field) and longitudinal (perpendicular to the applied field).

Magnetic force microscopy (MFM) measurements

Magnetic Force Microscopy (MFM) measurements were conducted on both as-grown and voltage-treated samples using the MFP-3D Origin+ Atomic Force Microscope from Asylum Research, Oxford Instruments. The measurements were carried out in two-pass mode, employing previously magnetized ASYMFM-R2 probes. For the second pass, we used a lift-height of 15 nm. Variable magnetic fields were applied in an in-plane geometry using the Variable Field Module provided by the same manufacturer.

Photoemission electron microscopy (PEEM)

Magnetic imaging of the sample was performed at the Photoemission Electron Microscope (PEEM) endstation at the ALBA Synchrotron, using X-ray circular magnetic dichroism (XMCD) contrast. More details about the PEEM endstation can be found in ref. ⁴⁸. The energy of the circular polarized X-rays was tuned to the Co-L₃ absorption edge around 778 eV. The PEEM uses electrons photoemitted by the X-ray beam to form an image of the sample surface. Pixel-wise subtraction (and division by the sum) of images for circular left- and right-handed polarized X-rays yield magnetic contrast images, XMCD-PEEM.

Electron microscopy

Scanning electron microscopy (SEM) imaging was performed using a Zeiss Merlin SEM microscope. High-resolution transmission electron microscopy (HR-TEM), high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM), and electron energy loss spectroscopy (EELS) were performed on a FEI TECNAI G2 F20 HRTEM/STEM microscope with a field emission gun operated at 200 kV. Cross-sectional lamellae of the samples were cut by focused ion beam after the deposition of Pt protective layers and were subsequently placed onto a Cu TEM grid.

Micromagnetic simulations

Micromagnetic simulations of the magnetization reversal process were conducted for disks with a diameter of 280 nm using MuMax3^49,50. Cells with d_x = d_y = 2.1875 nm and d_z = 2 nm (along the thickness direction) were used to simulate nanodots with thicknesses ranging from 2 to 12 nm. Grains were included⁵¹, approximately 5 nm in size, since the disks are polycrystalline, and the grains are needed to reproduce the wide experimental hysteresis loop shapes (see Supplementary Information section II for details). A random anisotropy direction was assigned to each grain, and the anisotropy value assigned to each grain was allowed to vary randomly in magnitude by 10 % from the chosen K_u value. The hysteresis loops shown in Fig. 5 are averaged over 10 runs, where a new set of randomized anisotropy parameters was chosen for each run to capture the effect of averaging over an array. The exchange constant was held fixed at 1.3 μerg cm⁻¹, and the exchange coupling between grains was reduced by 10 %. To reduce the run time, only the downward leg of the hysteresis loop was simulated. In all cases a constant M_S is used across the thickness, and it should be considered as an effective M_S that might stem from the phases with different N content. The thicknesses for the hysteresis loops shown in Fig. 5 were chosen to match experimentally estimated values of the magnetic layer thickness for selected voltage treatments, and then the M_S and K_u parameters were tuned to obtain hysteresis loop shapes that matched the experiment. The parameters used for the simulations shown in Fig. 5 are: (a) L = 2 nm, M_S = 400 emu cm⁻³, K_u = 2.5$\times$10⁵ erg cm⁻³ to represent the thinnest disks after a negative voltage treatment; (b) L = 8 nm, M_S = 500 emu cm⁻³, K_u = 3.5$\times$10⁵ erg cm⁻³ for an intermediate voltage treatment; and (c) L = 12 nm, M_S = 550 emu cm^-3, K_u = 6.0$\times$10⁵ erg cm⁻³ for the thickest disks. Note that the M_S and K_u values increase while increasing the thickness of the voltage-induced ferromagnetic disks, which is consistent with a progressive denitriding process of FeCoN^42,43. Magnetic force microscopy images were also calculated, where the MFM contrast was obtained by finding the gradient of the out-of-plane component of the stray magnetic field at a height of 50 nm above the magnetic disk. The calculated images were convolved with a Gaussian function with a width parameter of 50 nm to account for the finite width of the MFM tip. Additional simulations, including simulations conducted to determine the parameters needed to reproduce the experimental hysteresis loops after long-term positive voltage treatment and examine the effects of inter-dot interactions, are included as Supplementary Materials. The parameters L = 2 nm, M_S = 500 emu cm^-3 (slightly lower than the value for the thickest disks) and K_u = 6.0$\times$10⁵erg cm⁻³ (the same value used for the thickest disks) were used to represent the thinnest disks after a positive long-term voltage treatment. The exchange coupling between grains was set to 30 % of the underlying exchange value inside the grains.

Author contributions

J.S. conceived and supervised the study. I.S., A.P., and Z.M. prepared the samples, with the help of A.B. I.S. and J.S. performed in situ MOKE measurements during sample gating and analyzed the results. I.S. and J.S. performed HR-TEM, HAADF-STEM, and EELS measurements and analyzed the results. I.S. performed and analyzed the MFM measurements. K.S.B. conducted the micromagnetic simulations with the inputs from J.S. and I.S. A.M. performed Kerr imaging experiments with inputs from F.C and P.T. and I.S. M.F and S.R.G performed XMCD-PEEM measurements. I.S. wrote the manuscript with input from J.S. and K.S.B. All authors contributed to the discussions.

Peer review

Peer review information

Nature Communications thanks Dhritiman Bhattacharya, Shuai Ning and Cheng Song for their contribution to the peer review of this work. A peer review file is available.

Data availability

The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information files. Source data have been deposited in the Figshare database under the accession code: 10.6084/m9.figshare.25594794.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-025-57321-8.