Evaluating the long-term effects of combination antiretroviral therapy of HIV infection: a modeling study

Abstract

Current HIV/AIDS treatments effectively reduce viral loads to undetectable levels as measured by conventional clinical assays, but immune recovery remains highly variable among patients. To assess the long-term treatment efficacy, we propose a mathematical model that incorporates latently infected CD4$_{}^{+}$ T cells and the homeostatic proliferation of CD4$_{}^{+}$ T cells. We investigate the dynamics of this model both theoretically and numerically, demonstrating that homeostatic proliferation can induce bistability, which implies that steady-state CD4$_{}^{+}$ T cell count is sensitively affected by initial conditions. The model exhibits rich dynamics, including saddle node bifurcations, Hopf bifurcations, and saddle node bifurcations related to periodic orbits. The interplay between homeostatic proliferation and latent HIV infection significantly influences the model’s dynamic behavior. Additionally, we integrate combination antiretroviral therapy (cART) into the model and fit the revised model to clinical data on long-term CD4$_{}^{+}$ T cell counts before and after treatment. Quantitative analysis estimates the effects of long-term cART, revealing an increasing sensitivity of steady-state CD4$_{}^{+}$ T cell count to drug efficacy. Correlation analysis indicates that the heightened activation of latently infected cells helps enhance treatment efficacy. These findings underscore the critical roles of CD4$_{}^{+}$ T cell homeostatic proliferation and latently infected cell production in HIV persistence despite treatment, providing valuable insights for understanding disease progression and developing more effective therapies, potentially towards eradication.

Introduction

Human immunodeficiency virus (HIV) can lead to massive reductions in CD4$_{}^{+}$ T cell populations and generalized dysregulation of the immune system (Hill et al. 2018). Combination antiretroviral therapy (cART) is very effective in controlling HIV replication and preventing disease progression. With the expansion of cART, as of 2022, the AIDS-related deaths have been reduced by 69% since the peak in 2004 (UNAIDS 2023) and people in developed countries have greatly improved their health status and quality of life. However, except in rare cases, the virus is not completely eradicated from the body, resulting in a chronic state of continuous viral replication. A number of studies have been used to explain the sustained existence of viruses (Shu and Wang 2012; Reeves et al. 2018; Wang and Rong 2019; Rong et al. 2023).

The latently infected resting memory CD4$_{}^{+}$ T cells are considered a major barrier to HIV eradication during cART (Chomont et al. 2009). These cells, with a median half-life of 44 months (Chun et al. 1997; Finzi et al. 1997, 1999), harbor inactivated HIV proviral DNA that persists for long periods despite treatment (Mzingwane and Tiemessen 2017). When the latently infected cells are activated, they can be induced to produce infectious viruses (Siliciano et al. 2003), which could cause viral blip or viral rebound. Besides, clinical studies have displayed that other factors, such as homeostasis of the susceptible T cell population, may also play a critical role in providing additional opportunities for HIV infection by freely moving virions (Catalfamo et al. 2011; Moreno-Fernandez et al. 2012). However, the relationship between these factors and the recovery of immune function is unclear and needs further study.

Various within-host mathematical models considering these factors aim to understand the mechanism of dynamic changes in T cell and viral load. Perelson et al. (1997) proposed an extension of a basic viral dynamic model including activation of latently infected cells to explain the second-phase decline of viral load. Kim and Perelson (2006) used a model that incorporated the rate of latently infected cell activation decreasing with time on antiretroviral therapy. Wang et al. (2017) developed a multi-stage latent infection model to evaluate the influence of treatment intensification with raltegravir on the viral load and 2-LTR circle dynamics. Doekes et al. (2017) employed a within-host model to explore the role of latently infected CD4$_{}^{+}$ T cell reservoirs on the evolution of strains. Pankavich et al. (2020) developed a model that includes the homeostatic proliferation of CD4$_{}^{+}$ T cells and shows bistability between infectious and viral clearance equilibria, along with the emergence of a Hopf bifurcation within biologically relevant parameter ranges. Moreover, some studies have explored the mechanisms underlying the persistent viral load by considering the immune response. Wang and Wang (2024) proposed a delayed HIV infection model with nonmonotonic immune response, which exhibits bistability and stable periodic solution. Wang et al. (2024) also found that the virus would rebound if the antioxidant parameter fell below the post-treatment control threshold.

There are relatively few models, including the homeostatic proliferation of CD4$_{}^{+}$ T cells which are combined with clinical data in the long term (Hadjiandreou et al. 2007; Hernandez-Vargas and Middleton 2013; Loudon and Pankavich 2017). Besides, the models currently established mostly focus on either pre-cART or post-cART viral dynamics, without incorporating a combined model that integrates both states. To our knowledge, we first attempt to propose and fit the dynamics models to the long-term CD4$_{}^{+}$ T cells clinical data before and after cART, which can effectively capture the long-term trends of CD4$_{}^{+}$ T cells. Our main goal is to investigate the overall cART effects on long-term trajectories of CD4$_{}^{+}$ T cells and viruses.

This paper is organized as follows. In Sect. 2, we construct an HIV latent infection model considering homeostatic proliferation of CD4$_{}^{+}$ T cells, and obtain the basic reproduction number ${\mathcal{R}}_0$. In Sect. 3, we analyze the existence and stability of equilibria of the model. In Sect. 4, the existence of forward bifurcation, backward bifurcation and Hopf bifurcation is investigated respectively. In Sect. 5, various bifurcation diagrams and solution trajectories are given to show the model dynamics and explain some biological phenomena. In Sect. 6, we introduce the cART to the model, fit it to the CD4$_{}^{+}$ T cells clinical data, and perform sensitivity analysis and correlation analysis. In the last section, we provide a summary and discussion.

Model formulation

Mathematical model

To further study the impact of homeostatic proliferation of CD4$_{}^{+}$ T cells in the context of the latent stage of infected CD4$_{}^{+}$ T cells, we propose a new model including uninfected CD4$_{}^{+}$ T cells T(t), actively infected CD4$_{}^{+}$ T cells $T_I(t)$, latently infected CD4$_{}^{+}$ T cells $T_L(t)$ and viruses V(t) as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{dT(t)}{\mathit{dt}}& =\lambda +\frac{\rho }{\eta +V(t)}T(t)V(t)-k_{1}T(t)V(t)-d_{1}T(t),\hfill \\ \hfill \frac{d{T}_I(t)}{\mathit{dt}}& =\alpha k_{1}T(t)V(t)+\beta T_L(t)-d_2{T}_I(t),\hfill \\ \hfill \frac{d{T}_L(t)}{\mathit{dt}}& =(1-\alpha )k_{1}T(t)V(t)-\beta T_L(t)-d_3{T}_L(t),\hfill \\ \hfill \frac{dV(t)}{\mathit{dt}}& =k_2{T}_I(t)-d_{4}V(t)\hfill \end{array}\end{array}$$ 1

The definitions of the model parameters are as follows. $\lambda$ is the recruitment rate of uninfected CD4$_{}^{+}$ T cells. The term $\frac{\rho }{\eta +V}TV$ describes the homeostatic production of CD4$_{}^{+}$ T cells due to the presence of the virus and subsequent decline in uninfected CD4$_{}^{+}$ T cells, where $\rho$ is the maximum growth rate and $\eta$ is the half-velocity constant of growth. $k_1$ represents the infection of CD4$_{}^{+}$ T cells by virus. $\alpha$ $(0<\alpha <1)$ is the fraction of infected CD4$_{}^{+}$ T cells become active while the rest $(1-\alpha )$ remains latent. $\beta$ represents the activate rate of latently infected CD4$_{}^{+}$ T cells. Free virus is produced from the actively infected CD4$_{}^{+}$ T cells at the rate $k_2$. $d_1,d_2$ and $d_3$ are the death rates of uninfected CD4$_{}^{+}$ T cells, actively infected CD4$_{}^{+}$ T cells and latently infected CD4$_{}^{+}$ T cells, respectively. $d_4$ is the clearance rate of free virus particles. All parameters are positive constants (see Table 1 in detail).

Table 1.

Definition of the parameters and their values

Parameter and its description		Value	Source
$\lambda$	Recruitment rate of uninfected CD4$_{}^{+}$ T cells	10 mm$_{}^{-3}$day$_{}^{-1}$	Perelson et al. (1993)
$\rho$	Maximum growth rate	0.01 day$_{}^{-1}$	Pankavich et al. (2020)
$\eta$	Half-velocity constant of growth	300 copies mm$_{}^{-3}$	Pankavich et al. (2020)
$k_1$	Infection rate of uninfected CD4$_{}^{+}$ T cells by virus	0.00387 mm$_{}^3$day$_{}^{-1}$	Hadjiandreou et al. (2007)
$\alpha$	Fraction of infected CD4$_{}^{+}$ T cells become active	0.97	Hadjiandreou et al. (2007)
$\beta$	Activate rate of latently infected CD4$_{}^{+}$ T cells	0.0003 day$_{}^{-1}$	Dong and Ma (2012)
$k_2$	Production rate of virus	0.537 mm$_{}^3$day$_{}^{-1}$	Dong and Ma (2012)
$d_1$	Death rate of uninfected CD4$_{}^{+}$ T cells	0.01 day$_{}^{-1}$	Dong and Ma (2012)
$d_2$	Death rate of actively infected CD4$_{}^{+}$ T cells	0.28 day$_{}^{-1}$	Dong and Ma (2012)
$d_3$	Death rate of latently infected CD4$_{}^{+}$ T cells	0.05 day$_{}^{-1}$	Dong and Ma (2012)
$d_4$	Clearance rate of free virus particles	2.39 day$_{}^{-1}$	Dong and Ma (2012)

Positivity of solutions

To show that model (1) is biologically meaningful, it is essential to disclose that all the state variables are non-negative for all time $t>0$. For this purpose, we have the following results.

Lemma 2.1

Every solution of model (1) with positive initial conditions remains positive in ${\mathbb{R}}_4^{+}$ as $t>0$.

Proof

From model (1), it is easy to obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\mathit{dT}}{\mathit{dt}}& ={|}_{[T=0,T_I\ge 0,T_L\ge 0,V\ge 0]}=\lambda >0,\hfill \\ \hfill \frac{d{T}_I}{\mathit{dt}}& ={|}_{[T\ge 0,T_I=0,T_L\ge 0,V\ge 0]}=\alpha k_{1}TV+\beta T_L\ge 0,\hfill \\ \hfill \frac{d{T}_L}{\mathit{dt}}& ={|}_{[T\ge 0,T_I\ge 0,T_L=0,V\ge 0]}=(1-\alpha )k_{1}TV\ge 0,\hfill \\ \hfill \frac{\mathit{dV}}{\mathit{dt}}& ={|}_{[T\ge 0,T_I\ge 0,T_L\ge 0,V=0]}=k_2{T}_I\ge 0.\hfill \end{array}\end{array}$$

The above rates are all non-negative over the boundary planes of the non-negative cone of ${\mathbb{R}}_4$ (Perelson et al. 1993; Zhang et al. 2024). Therefore, all the solutions with positive initial conditions will remain in the positive region only. $\square$

Basic reproduction number

Obviously, the infection-free equilibrium of model (1) is $E_0=(\frac{\lambda }{d_1},0,0,0)$. We use the next generation matrix method (Van den Driessche and Watmough 2002) to obtain the basic reproduction number ${\mathcal{R}}_0$. Let us consider $X=(T_I,T_L,V)$, and model (1) is written as $\dot{X}=\mathcal{F}-\mathcal{V}$, where

$$\begin{array}{c}\hfill \mathcal{F}=\left(\begin{array}{c}\alpha k_{1}TV\\ (1-\alpha )k_{1}TV\\ 0\end{array}\right),\mathcal{V}=\left(\begin{array}{c}-\beta T_L+d_2{T}_I\\ \beta T_L+d_3{T}_L\\ -k_2{T}_I+d_{4}V\end{array}\right).\end{array}$$

Jacobian matrices $\mathbb{F}$ and $\mathbb{V}$ at $E_0=(\frac{\lambda }{d_1},0,0,0)$ of $\mathcal{F}$ and $\mathcal{V}$ are given by

$$\begin{array}{c}\hfill \mathbb{F}=\left(\begin{array}{ccc}0& 0& \frac{\alpha k_1\lambda }{d_1}\\ 0& 0& \frac{k_1\lambda \left(1,-,\alpha \right)}{d_1}\\ 0& 0& 0\\ \end{array}\right),\mathbb{V}=\left(\begin{array}{ccc}{d}_2& -\beta & 0\\ 0& \beta +d_3& 0\\ -k_2& 0& d_4\\ \end{array}\right).\end{array}$$

Then the next generation matrix is

$$\begin{array}{c}\hfill \mathbb{F}{\mathbb{V}}^{-1}=\left(\begin{array}{ccc}\frac{\alpha k_1{k}_2\lambda }{d_1{d}_2{d}_4}\hfill & \frac{\alpha \beta k_1{k}_2\lambda }{d_1{d}_2{d}_4\left(\beta ,+,d_3\right)}\hfill & \frac{\alpha k_1\lambda }{d_1{d}_4}\hfill \\ \frac{k_1{k}_2\lambda \left(1,-,\alpha \right)}{d_1{d}_2{d}_4}\hfill & \frac{\beta k_1{k}_2\lambda \left(1,-,\alpha \right)}{d_1{d}_2{d}_4\left(\beta ,+,d_3\right)}\hfill & \frac{k_1\lambda \left(1,-,\alpha \right)}{d_1{d}_4}\hfill \\ 0\hfill & 0\hfill & 0\hfill \end{array}\right).\end{array}$$

The basic reproduction number ${\mathcal{R}}_0$ is the spectral radius of $\mathbb{F}{\mathbb{V}}^{-1}$, that is,

$$\begin{array}{c}\hfill {\mathcal{R}}_0=\frac{k_1{k}_2\lambda (\beta +\alpha d_3)}{d_1{d}_2{d}_4(\beta +d_3)}.\end{array}$$

Existence and stability of equilibria

Existence of equilibria

To find the equilibria of model (1), we set

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \lambda +\frac{\rho }{\eta +V}TV-k_{1}TV-d_{1}T=0,\hfill \\ \hfill & \alpha k_{1}TV+\beta T_L-d_2{T}_I=0,\hfill \\ \hfill & (1-\alpha )k_{1}TV-\beta T_L-d_3{T}_L=0,\hfill \\ \hfill & k_2{T}_I-d_{4}V=0.\hfill \end{array}\right)\end{array}$$ 2

When $V=0$, it is easy to get that $T^0=\frac{\lambda }{d_1}$ and $T_I^0=T_L^0=0$, that is, the infection-free equilibrium $E_0(\frac{\lambda }{d_1},0,0,0)$ always exists.

If the infected equilibrium $E^{\ast }(T^{\ast },T_I^{\ast },T_L^{\ast },V^{\ast })$ exists, then all components $T^{\ast },T_I^{\ast },T_L^{\ast },V^{\ast }$ should satisfy the equation (2) and be positive. When $V^{\ast }>0$, from the last three equations of (2), by calculations, $T^{\ast },T_I^{\ast }$ and $T_L^{\ast }$ can be represented by $V^{\ast }$, that is,

$$\begin{array}{c}\hfill T^{\ast }=\frac{d_2{d}_4\left(\beta ,+,d_3\right)}{k_1{k}_2\left(\beta ,+,\alpha ,d_3\right)},T_I^{\ast }=\frac{d_4}{k_2}{V}^{\ast },T_L^{\ast }=\frac{d_2{d}_4\left(1,-,\alpha \right)}{k_2\left(\beta ,+,\alpha ,d_3\right)}{V}^{\ast }.\end{array}$$ 3

Note that the expression of $T^{\ast }$ is only related to some parameters and is irrelevant to $V^{\ast }$. Next, substituting (3) into the first equation of (2) gives

$$\begin{array}{c}\hfill \frac{A_{1}V_{}^{_{}^{\ast }2}+A_2{V}^{\ast }+A_3}{k_1{k}_2\left(\beta ,+,\alpha ,d_3\right)V^{\ast }+\eta k_1{k}_2\left(\beta ,+,\alpha ,d_3\right)}=0,\end{array}$$ 4

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill A_1& =-d_2{d}_4{k}_1\left(\beta ,+,d_3\right)<0,\hfill \\ \hfill A_2& =k_1{k}_2\lambda \left(\beta ,+,\alpha ,d_3\right)-d_1{d}_2{d}_4\left(\beta ,+,d_3\right)+d_2{d}_4\left(\beta ,+,d_3\right)\left(\rho ,-,\eta ,k_1\right)\hfill \\ \hfill & =d_2{d}_4\left(\beta ,+,d_3\right)\left[d_1,\left({\mathcal{R}}_0,-,1\right),+,\left(\rho ,-,\eta ,k_1\right)\right],\hfill \\ \hfill A_3& =\eta \left[k_1,k_2,\lambda ,\left(\beta ,+,\alpha ,d_3\right),-,d_1,d_2,d_4,\left(\beta ,+,d_3\right)\right]\hfill \\ \hfill & =\eta d_1{d}_2{d}_4\left(\beta ,+,d_3\right)\left({\mathcal{R}}_0,-,1\right).\hfill \end{array}\end{array}$$

Notice that all parameters are greater than 0 and $V^{\ast }$ is non-negative. Therefore, the product of the parameters and $V^{\ast }$, along with the product of the parameters themselves, is greater than 0. As a result, the denominator of (4) is always positive and $A_1<0$. Define $f(V^{\ast })=A_1(V_{}^{\ast })_{}^2+A_2{V}^{\ast }+A_3$ and $\Delta =A_2^2-4A_1{A}_3$, where $f(V^{\ast })$ is a parabola function that opens downward. So next we discuss the number of positive roots of $f(V^{\ast })=0$ for the following cases.

Case 1: $A_3<0$, corresponding to ${\mathcal{R}}_0<1$:

• when $A_2⩽0$, $f(V^{\ast })=0$ has no positive root;

• when $A_2>0$, $f(V^{\ast })=0$ has two positive roots $V_1^{\ast }=\frac{-A_2+\sqrt{\Delta }}{2A_1}$ and $V_2^{\ast }=\frac{-A_2-\sqrt{\Delta }}{2A_1}$ if $\Delta >0$; $f(V^{\ast })=0$ has one positive root $V_1^{\ast }=-\frac{A_2}{2A_1}$ if $\Delta =0$; and $f(V^{\ast })=0$ has no positive root if $\Delta <0$.

Case 2: $A_3=0$, corresponding to ${\mathcal{R}}_0=1$:

• when $A_2⩽0$, $f(V^{\ast })=0$ has no positive root;

• when $A_2>0$, $f(V^{\ast })=0$ has one positive root $V_1^{\ast }=-\frac{A_2}{A_1}$.

Case 3: $A_3>0$, corresponding to ${\mathcal{R}}_0>1$:

• $f(V^{\ast })=0$ always has one positive root $V_1^{\ast }=\frac{-A_2+\sqrt{\Delta }}{2A_1}.$

To sum up, we have the following proposition for the existence of equilibria of model (1).

Proposition 3.1

The infection-free equilibrium $E_0(\frac{\lambda }{d_1},0,0,0)$ of model (1) always exists, and the model has at most two infected equilibria $E_1^{\ast }$ (higher viral load) and $E_2^{\ast }$ (lower viral load). Moreover,

• if ${\mathcal{R}}_0=1$, model (1) has one infected equilibrium $E_1^{\ast }$ when $A_2>0$;

• if ${\mathcal{R}}_0>1$, model (1) always has one infected equilibrium $E_1^{\ast }$;

• if ${\mathcal{R}}_0<1$, model (1) has one infected equilibrium $E_1^{\ast }$ when $A_2>0$ and $\Delta =0$; model (1) has two infected equilibria $E_1^{\ast }$ and $E_2^{\ast }$ when $A_2>0$ and $\Delta >0$,

• In other cases, model (1) does not have infected equilibrium.

Stability of infection-free equilibrium

Theorem 3.1

The infection-free equilibrium $E_0$ of model (1) is locally asymptotically stable if ${\mathcal{R}}_0<1$, and unstable if ${\mathcal{R}}_0>1$.

Proof

The Jacobian matrix of model (1) at equilibrium $E_0=(\frac{\lambda }{d_1},0,0,0)$ is

$$\begin{array}{c}\hfill J_{E_0}=\left(\begin{array}{cccc}-d_1& 0& 0& \frac{\lambda \left(\rho ,-,k_1,\eta \right)}{d_1\eta }\\ 0& -d_2& \beta & \frac{\alpha k_1\lambda }{d_1}\\ 0& 0& -\beta -d_3& \frac{k_1\lambda \left(1,-,\alpha \right)}{d_1}\\ 0& k_2& 0& -d_4\\ \end{array}\right).\end{array}$$

Obviously, $-d_1$ is a negative eigenvalue of matrix $J_{E_0}$.

For the submatrix

$$\begin{array}{c}\hfill J=\left(\begin{array}{ccc}-d_2& \beta & \frac{\alpha k_1\lambda }{d_1}\\ 0& -\beta -d_3& \frac{k_1\lambda \left(1,-,\alpha \right)}{d_1}\\ k_2& 0& -d_4\\ \end{array}\right),\end{array}$$

the corresponding characteristic equation is

$$\begin{array}{c}\hfill r^3+a_1{r}^2+a_{2}r+a_3=0,\end{array}$$

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill a_1& =\beta +d_2+d_3+d_4,\hfill \\ \hfill a_2& =\frac{\beta d_1{d}_2+\beta d_1{d}_4+d_1{d}_2{d}_3+d_1{d}_2{d}_4+d_1{d}_3{d}_4-\alpha k_1{k}_2\lambda }{d_1},\hfill \\ \hfill a_3& =\frac{d_1{d}_2{d}_4\left(\beta ,+,d_3\right)-k_1{k}_2\lambda \left(\beta ,+,\alpha ,d_3\right)}{d_1}=d_2{d}_4\left(\beta ,+,d_3\right)\left(1,-,{\mathcal{R}}_0\right).\hfill \end{array}\end{array}$$

It is easy to observe that $H_1=a_1>0$ and the sign of $a_3$ is determined by the size of ${\mathcal{R}}_0$. By calculations, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill H_2& =a_1{a}_2-a_3=\frac{1}{d_1}[(\beta +d_2+d_3+d_4)\hfill \\ \hfill & (\beta d_1{d}_2+\beta d_1{d}_4+d_1{d}_2{d}_3+d_1{d}_2{d}_4+d_1{d}_3{d}_4-\alpha k_1{k}_2\lambda )\hfill \\ \hfill & +\beta k_1{k}_2\lambda -\beta d_1{d}_2{d}_4-d_1{d}_2{d}_3{d}_4+\alpha d_3{k}_1{k}_2\lambda ]\hfill \\ \hfill & =\frac{1}{d_1}[(\beta +d_2+d_3+d_4)(d_1{d}_2{d}_4-\alpha k_1{k}_2\lambda )\hfill \\ \hfill & +(\beta +d_2+d_3+d_4)(\beta d_1{d}_2+\beta d_1{d}_4+d_1{d}_2{d}_3+d_1{d}_3{d}_4)\hfill \\ \hfill & +\beta k_1{k}_2\lambda -\beta d_1{d}_2{d}_4-d_1{d}_2{d}_3{d}_4+\alpha d_3{k}_1{k}_2\lambda ]\hfill \\ \hfill & =\frac{1}{d_1}[(\beta +d_2+d_3+d_4)(d_1{d}_2{d}_4-\alpha k_1{k}_2\lambda )\hfill \\ \hfill & +(\beta +d_2+d_3)(\beta d_1{d}_2+\beta d_1{d}_4+d_1{d}_2{d}_3+d_1{d}_3{d}_4)\hfill \\ \hfill & +d_4(\beta d_1{d}_4+d_1{d}_3{d}_4)+\beta k_1{k}_2\lambda +\alpha d_3{k}_1{k}_2\lambda ].\hfill \end{array}\end{array}$$

Since

$$\begin{array}{c}\hfill {\mathcal{R}}_0=\frac{k_1{k}_2\lambda \left(\beta ,+,\alpha ,d_3\right)}{d_1{d}_2{d}_4\left(\beta ,+,d_3\right)}<1⟺k_1{k}_2\lambda <\frac{d_1{d}_2{d}_4\left(\beta ,+,d_3\right)}{\left(\beta ,+,\alpha ,d_3\right)},\end{array}$$

we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill d_1{d}_2{d}_4-\alpha k_1{k}_2\lambda & >d_1{d}_2{d}_4-\alpha \frac{d_1{d}_2{d}_4\left(\beta ,+,d_3\right)}{\left(\beta ,+,\alpha ,d_3\right)}\hfill \\ \hfill & =\frac{d_1{d}_2{d}_4\left(\beta ,+,\alpha ,d_3\right)-\alpha d_1{d}_2{d}_4\left(\beta ,+,d_3\right)}{\left(\beta ,+,\alpha ,d_3\right)}\hfill \\ \hfill & =\frac{\left(1,-,\alpha \right)\beta d_1{d}_2{d}_4}{\left(\beta ,+,\alpha ,d_3\right)}>0.\hfill \end{array}\end{array}$$

Therefore, $d_1{d}_2{d}_4-\alpha k_1{k}_2\lambda >0$ if ${\mathcal{R}}_0<1$, which implies that $H_2>0$ if ${\mathcal{R}}_0<1$.

By the well-known Routh–Hurwitz criterion (DeJesus and Kaufman 1987), it is obtained that the real parts of all eigenvalues of the submatrix J are negative if ${\mathcal{R}}_0<1$, and the real parts of all eigenvalues of J have at least one positive root if ${\mathcal{R}}_0>1$. Hence the above result is obtained. $\square$

Stability of infected equilibria

Theorem 3.2

The infected equilibrium $E_{}^{\ast }$ of model (1) is locally asymptotically stable provided that

$$\begin{array}{c}\hfill b_1{b}_2{b}_3-b_3^2-b_1^2{b}_4>0\end{array}$$

holds true, where $b_i(i=1,2,3,4)$ are given by (6).

Proof

The Jacobian matrix of model (1) at any infected equilibrium $E_{}^{\ast }=(T_{}^{\ast },T_I^{\ast },T_L^{\ast },V_{}^{\ast })$ is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill J_{E_{}^{\ast }}^{}& =\left(\begin{array}{cccc}\frac{\rho V_{}^{\ast }}{V_{}^{\ast }+\eta }-k_{1}V_{}^{\ast }-d_1\hfill & 0\hfill & 0\hfill & \frac{\rho \eta T_{}^{\ast }}{\left(V_{}^{\ast },+,\eta \right)_{}^2}-k_{1}T_{}^{\ast }\hfill \\ \alpha k_{1}V_{}^{\ast }\hfill & -d_2\hfill & \beta \hfill & \alpha k_{1}T_{}^{\ast }\hfill \\ k_1\left(1,-,\alpha \right)V_{}^{\ast }\hfill & 0\hfill & -\beta -d_3\hfill & k_1\left(1,-,\alpha \right)T_{}^{\ast }\hfill \\ 0\hfill & k_2\hfill & 0\hfill & -d_4\hfill \end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{cccc}-\frac{\lambda }{T_{}^{\ast }}\hfill & 0\hfill & 0\hfill & N\hfill \\ \alpha k_{1}V_{}^{\ast }\hfill & -d_2\hfill & \beta \hfill & \alpha k_{1}T_{}^{\ast }\hfill \\ k_1\left(1,-,\alpha \right)V_{}^{\ast }\hfill & 0\hfill & -\beta -d_3\hfill & k_1\left(1,-,\alpha \right)T_{}^{\ast }\hfill \\ 0\hfill & k_2\hfill & 0\hfill & -d_4\hfill \end{array}\right),\hfill \end{array}\end{array}$$

where $N=\frac{\rho \eta T_{}^{\ast }}{\left(V_{}^{\ast },+,\eta \right)_{}^2}-k_{1}T_{}^{\ast }$ and $\frac{\rho V_{}^{\ast }}{V_{}^{\ast }+\eta }-k_{1}V_{}^{\ast }-d_1=-\frac{\lambda }{T_{}^{\ast }}$.

Firstly, we prove that N is always negative for any $V_{}^{\ast }>0$. It is easy to obtain that

$$\begin{array}{c}\hfill \frac{\rho V_{}^{\ast }}{V_{}^{\ast }+\eta }-k_{1}V_{}^{\ast }-d_1<0\text{for any}V_{}^{\ast }>0,\end{array}$$

which is equivalent to

$$\begin{array}{c}\hfill V_{}^{\ast }+\eta >\frac{\rho V_{}^{\ast }}{k_{1}V_{}^{\ast }+d_1}\text{for any}V_{}^{\ast }>0.\end{array}$$

The arbitrariness of $V_{}^{\ast }$ implies that

$$\begin{array}{c}\hfill V_{}^{\ast }+\eta >max\left\{\frac{\rho V_{}^{\ast }}{k_{1}V_{}^{\ast }+d_1}\right\},\end{array}$$

that is $V_{}^{\ast }+\eta >\frac{\rho }{k_1}$. Furthermore, we have

$$\begin{array}{c}\hfill \left(V_{}^{\ast },+,\eta \right)_{}^2>\frac{\rho }{k_1}\left(V_{}^{\ast },+,\eta \right)>\frac{\rho \eta }{k_1},\end{array}$$

which is equivalent to

$$\begin{array}{c}\hfill \frac{\rho \eta }{\left(V_{}^{\ast },+,\eta \right)_{}^2}<k_1.\end{array}$$

Therefore, we conclude that $N<0$.

Next, by calculations, the corresponding characteristic equation of the matrix $J_{E^{\ast }}$ is given by

$$\begin{array}{c}\hfill r^4+b_1{r}^3+b_2{r}^2+b_{3}r+b_4=0,\end{array}$$ 5

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill b_1& =\frac{\lambda }{T_{}^{\ast }}+\beta +d_2+d_3+d_4,\hfill \\ \hfill b_2& =\frac{\lambda \left(\beta ,+,d_2,+,d_3,+,d_4\right)}{T_{}^{\ast }}+\beta d_2+\beta d_4+d_2{d}_3+d_2{d}_4+d_3{d}_4-\alpha k_1{k}_{2}T_{}^{\ast },\hfill \\ \hfill b_3& =\frac{\lambda \left(\beta ,d_2,+,\beta ,d_4,+,d_2,d_3,+,d_2,d_4,+,d_3,d_4,-,\alpha ,k_1,k_2,T_{}^{\ast }\right)}{T_{}^{\ast }}\hfill \\ \hfill & +d_2{d}_4\left(\beta ,+,d_3\right)-k_1{k}_{2}T_{}^{\ast }\left(\beta ,+,\alpha ,d_3\right)-\alpha k_1{k}_{2}NV_{}^{\ast }T_{}^{\ast },\hfill \\ \hfill b_4& =\frac{\lambda \left[d_2,d_4,\left(\beta ,+,d_3\right),-,k_1,k_2,T_{}^{\ast },\left(\beta ,+,\alpha ,d_3\right)\right]}{T_{}^{\ast }}-k_1{k}_{2}NV_{}^{\ast }\left(\beta ,+,\alpha ,d_3\right).\hfill \end{array}\end{array}$$ 6

From (3), we conclude that

$$\begin{array}{c}\hfill d_2{d}_4\left(\beta ,+,d_3\right)-k_1{k}_{2}T_{}^{\ast }\left(\beta ,+,\alpha ,d_3\right)=0\end{array}$$

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill d_2{d}_4-\alpha k_1{k}_{2}T_{}^{\ast }& =d_2{d}_4-\alpha k_1{k}_2·\frac{d_2{d}_4\left(\beta ,+,d_3\right)}{k_1{k}_2\left(\beta ,+,\alpha ,d_3\right)}\hfill \\ \hfill & =\frac{\beta d_2{d}_4\left(1,-,\alpha \right)}{\left(\beta ,+,\alpha ,d_3\right)}>0,\hfill \end{array}\end{array}$$

which implies that $b_i>0$ for $i=1,2,3,4$.

The well-known Routh–Hurwitz criterion (DeJesus and Kaufman 1987) shows that the real part of all characteristic roots of matrix $J_{E_{}^{\ast }}^{}$ is negative if and only if

$$\begin{array}{c}\hfill L_1=b_1>0,L_2=b_1{b}_2-b_3>0,L_3=b_1{b}_2{b}_3-b_3^2-b_1^2{b}_4>0\\ \hfill \text{and}{L}_4=L_3{b}_4>0.\end{array}$$

Since $L_3=b_3{L}_2-b_1^2{b}_4$, it is easy to see that if $L_3$ is greater than 0, then $L_2$ is greater than 0. And if $L_2$ is less than 0, $L_3$ must be less than 0. Hence the stability of the infected equilibrium $E^{\ast }$ of model (1) is determined by $L_3=b_1{b}_2{b}_3-b_3^2-b_1^2{b}_4$. $\square$

Bifurcation analysis

Forward and backward bifurcations at infection-free equilibrium

Lemma 4.1

(see Theorem 4.1 in Castillo-Chavez and Song 2004) Consider a general system of ODEs with a parameter $\varphi$:

$$\begin{array}{c}\hfill \frac{\mathit{dx}}{\mathit{dt}}=f(x,\varphi ),f:{\mathbb{R}}^n\times \mathbb{R}\to {\mathbb{R}}^n\text{and}f\in {\mathbb{C}}^2\left({\mathbb{R}}^n,\times ,\mathbb{R}\right).\end{array}$$ 7

Without loss of generality, it is assumed that 0 is an equilibrium for system (7) for all values of the parameter $\varphi$, that is

$$\begin{array}{c}\hfill f(\mathbf{0},\varphi )\equiv \mathbf{0}\text{for}\text{all}\varphi .\end{array}$$

Furthermore, assume

1. $A=D_{x}f(\mathbf{0},0)=\left(\frac{\partial f_i}{\partial x_j},(\mathbf{0},0)\right)$ is the linearization matrix of system (7) around the equilibrium 0 with $\varphi$ evaluated at 0. Zero is a simple eigenvalue of A and all other eigenvalues of A have negative real parts.

2. Matrix A has a nonnegative right eigenvector w and a left eigenvector v corresponding to the zero eigenvalue.

Let $f_k$ be the k-th component of f and

$$\begin{array}{cc}\hfill a& =\sum _{k,i,j=1}^n{v}_k{w}_i{w}_j\frac{{\partial }^2{f}_k}{\partial x_i\partial x_j}(\mathbf{0},0),\hfill \\ \hfill b& =\sum _{k,i=1}^n{v}_k{w}_i\frac{{\partial }^2{f}_k}{\partial x_i\partial \varphi }(\mathbf{0},0).\hfill \end{array}$$

The local dynamics of (7) around equilibrium 0 are totally determined by a and b as follows:

1. $a>0,b>0$. When $\varphi <0$ with $|\varphi |\ll 1$, equilibrium 0 is locally asymptotically stable, and there exists an unstable infected equilibrium; when $0<\varphi \ll 1$, 0 is unstable and there exists a negative and locally asymptotically stable equilibrium, which corresponds to the forward bifurcation at $\varphi =0$ for equilibrium 0.

2. $a<0,b>0$. When $\varphi$ changes from negative to positive, equilibrium 0 changes its stability from stable to unstable and a negative unstable equilibrium becomes positive and locally asymptotically stable, which corresponds to the backward bifurcation at $\varphi =0$ for equilibrium 0.

Remark 1

(see Remark 1 in Castillo-Chavez and Song 2004) The requirement that w is nonnegative is not necessary; that is, $w(j)>0$ whenever $\mathbf{x}(j)=0$, and w(j) does not need to be positive if $\mathbf{x}(j)>0$, where $\mathbf{x}(j)$ is the j-th component of the nonnegative equilibrium $\mathbf{x}$ of system (7).

To apply this method in our model (1), we first denote the system with defining by $T=x_1,T_I=x_2,T_L=x_3,V=x_4$ and rewrite the model (1) as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{d{x}_1}{\mathit{dt}}& =\lambda +\frac{\rho }{\eta +x_4}{x}_1{x}_4-k_1{x}_1{x}_4-d_1{x}_1\triangleq f_1,\hfill \\ \hfill \frac{d{x}_2}{\mathit{dt}}& =\alpha k_1{x}_1{x}_4+\beta x_3-d_2{x}_2\triangleq f_2,\hfill \\ \hfill \frac{d{x}_3}{\mathit{dt}}& =\left(1,-,\alpha \right)k_1{x}_1{x}_4-\beta x_3-d_3{x}_3\triangleq f_3,\hfill \\ \hfill \frac{d{x}_4}{\mathit{dt}}& =k_2{x}_2-d_4{x}_4\triangleq f_4.\hfill \end{array}\end{array}$$ 8

Next we investigate the direction of the bifurcation around infection-free equilibrium $E_0=\left(x_1^{\ast },,,x_2^{\ast },,,x_3^{\ast },,,x_4^{\ast }\right)$ where $x_1^{\ast }=\frac{\lambda }{d_1}$ and $x_2^{\ast }=x_3^{\ast }=x_4^{\ast }=0$. We know that ${\mathcal{R}}_0$ ($\alpha$ is proportional to ${\mathcal{R}}_0$) determines the local stability of $E_0$, that is, it determines the sign of real part of a characteristic root of $J_{E_0}$ (other characteristic roots have negative real parts). Therefore, we choose parameter $\alpha$ as the bifurcation parameter, where $\alpha _{}^{\ast }=\frac{d_1{d}_2{d}_4\left(\beta ,+,d_3\right)-\beta k_1{k}_2\lambda }{d_3{k}_1{k}_3\lambda }$ by direct computation from ${\mathcal{R}}_0=1$. When $\alpha ={\alpha }^{\ast }$, the Jacobian matrix of model (8) at equilibrium $E_0$ is

$$\begin{array}{c}\hfill J_{E_0}\left(\alpha _{}^{\ast }\right)=\left(\begin{array}{cccc}-d_1& 0& 0& \frac{\lambda \left(\rho ,-,k_1,\eta \right)}{d_1\eta }\\ 0& -d_2& \beta & \frac{k_1\lambda \alpha _{}^{\ast }}{d_1}\\ 0& 0& -\beta -d_3& \frac{k_1\lambda \left(1,-,\alpha _{}^{\ast }\right)}{d_1}\\ 0& k_2& 0& -d_4\\ \end{array}\right).\end{array}$$

The associated right and left eigenvectors corresponding to the zero eigenvalue are $w={\left(w_1,,,w_2,,,w_3,,,w_4\right)}^T$ and $v=\left(v_1,,,v_2,,,v_3,,,v_4\right)$ respectively, where

$$\begin{array}{c}\hfill \begin{array}{cc}& w_1=\frac{k_2\lambda \left(\rho ,-,\eta ,k_1\right)}{d_1^2{d}_4\eta }{w}_2,w_3=\frac{k_1{k}_2\lambda \left(1,-,\alpha \right)}{d_1{d}_4\left(\beta ,+,d_3\right)}{w}_2,\hfill \\ \hfill & w_4=\frac{k_2}{d_4}{w}_2,w_2>0\text{is free},\hfill \end{array}\end{array}$$

and

$$\begin{array}{c}\hfill v_1=0,v_3=\frac{\beta }{\beta +d_3}{v}_2,v_4=\frac{d_2}{k_2}{v}_2,v_2>0\text{is free}.\end{array}$$

Clearly, $v_i⩾0$ and $w_i⩾0$ when $2⩽i⩽4$. By applying Remark 1, the requirement that $w_1$ is nonnegative is not necessary. Algebraic calculations show that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill a& =2v_2{w}_1{w}_4\frac{{\partial }^2{f}_2}{\partial x_1\partial x_4}\left(E_0,,,\alpha _{}^{\ast }\right)+2v_3{w}_1{w}_4\frac{{\partial }^2{f}_3}{\partial x_1\partial x_4}\left(E_0,,,\alpha _{}^{\ast }\right)\hfill \\ \hfill & =2v_2{w}_1{w}_4·k_1\alpha _{}^{\ast }+2v_3{w}_1{w}_4·k_1\left(1,-,\alpha _{}^{\ast }\right)\hfill \\ \hfill & =2w_1{w}_4{k}_1\left[\alpha _{}^{\ast },v_2,+,\left(1,-,\alpha _{}^{\ast }\right),v_3\right]\hfill \end{array}\end{array}$$

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill b=& 2v_2\left(w_1,·,\frac{{\partial }^2{f}_2}{\partial x_1\partial \alpha },\left(E_0,,,\alpha _{}^{\ast }\right),+,w_4,·,\frac{{\partial }^2{f}_2}{\partial x_4\partial \alpha },\left(E_0,,,\alpha _{}^{\ast }\right)\right)\hfill \\ \hfill & +2v_3\left(w_1,·,\frac{{\partial }^2{f}_3}{\partial x_1\partial \alpha },\left(E_0,,,\alpha _{}^{\ast }\right),+,w_4,·,\frac{{\partial }^2{f}_3}{\partial x_4\partial \alpha },\left(E_0,,,\alpha _{}^{\ast }\right)\right)\hfill \\ \hfill & =2v_2\left(w_1,·,k_1,x_4^{\ast },+,w_4,·,k_1,x_1^{\ast }\right)+2v_3\left(-,w_1,·,k_1,x_4^{\ast },-,w_4,·,k_1,x_1^{\ast }\right)\hfill \\ \hfill & =2w_4{k}_{1}x_1^{\ast }\left(v_2,-,v_3\right)\hfill \\ \hfill & =\frac{2k_1\lambda d_3}{d_1\left(\beta ,+,d_3\right)}{w}_4{v}_2>0.\hfill \end{array}\end{array}$$

It is easy to see that the sign of a is determined by $w_1$, that is,

$$\begin{array}{c}\hfill \text{sign}\left[a\right]=\text{sign}\left[w_1\right]=\text{sign}\left[\rho ,-,\eta ,k_1\right].\end{array}$$

Therefore, we have $a>0$ when $\rho >\overline{\rho }\triangleq \eta k_1$, and obtain the following result for the direction of the bifurcation around infection-free equilibrium $E_0$.

Theorem 4.2

If $\rho <\overline{\rho }$, a forward bifurcation around infection-free equilibrium $E_0$ of model (1) occurs at $\alpha =\alpha _{}^{\ast }$, corresponding to ${\mathcal{R}}_0=1$, and the direction of the bifurcation is backward if $\rho >\overline{\rho }$.

Remark 2

Theorem 4.2 demonstrates that a large value of parameter $\rho$ leads to backward bifurcation in the model, potentially resulting in bistability of $E_0$ and $E_1^{\ast }$. Biologically, the mechanism of homeostatic proliferation of CD4$_{}^{+}$ T cells makes whether HIV infection can be cleared greatly depend on the initial conditions, which may be the potential reason why the HIV treatment scenario is so complicated.

Local Hopf bifurcation at infected equilibrium

In this subsection, we explore the existence of Hopf bifurcation at infected equilibrium $E^{\ast }=(T^{\ast },T_I^{\ast },T_L^{\ast },V^{\ast })$ when parameter $\rho$ is used as the bifurcation parameter. Assume that $\lambda =i\omega$, where $\omega \in {\mathbb{R}}^{+}$ is the root of the characteristic equation (5). Substituting it into (5) yields

$$\begin{array}{c}\hfill {\omega }^4-b_1{\omega }^{3}i-b_2{\omega }^2+b_3\omega i+b_4=0.\end{array}$$

Separating the real and imaginary parts, we have

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\omega }^4-b_2{\omega }^2+b_4=0,\hfill \\ -b_1{\omega }^3+b_3\omega =0,\hfill \end{array}\right)\end{array}$$

which is equivalent to

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{b}_3^2+b_1^2{b}_4-b_1{b}_2{b}_3=0,\hfill \\ {\omega }^2=\frac{b_3}{b_1}.\hfill \end{array}\right)\end{array}$$

Denote $\Theta \left(\rho \right)=b_3^2+b_1^2{b}_4-b_1{b}_2{b}_3=0$. Then both $\Theta \left(\rho \right)$ and $b_i(i=1,2,3,4)$ are functions of $\rho$. Obviously, a pair of pure imaginary roots $\lambda =\pm i\omega$ of the characteristic equation exists only if there exists $\rho >0$ such that $\Theta \left(\rho \right)=0$. Suppose that $\Theta \left(\rho \right)=0$ has at least one positive real root ${\rho }^{\ast }$. Next, we validate the transversality condition of Hopf bifurcation.

By differentiating $P(\lambda ;\rho )=0$ defined in (5) with respect to $\rho$, we have

$$\begin{array}{c}\hfill \frac{d\lambda }{d\rho }=-\frac{b_1^{\prime }{\lambda }^3+b_2^{\prime }{\lambda }^2+b_3^{\prime }\lambda +b_4^{\prime }}{4{\lambda }^3+3b_1{\lambda }^2+2b_2\lambda +b_3},\end{array}$$

where $b_i^{\prime }$ is the derivative of $b_i$ with respect to $\rho$. Furthermore, $P(i\omega ;{\rho }^{\ast })=0$ implies that

$$\begin{array}{c}\hfill {\left(\frac{d\lambda }{d\rho }\right|}_{\lambda =i\omega }=-\frac{-b_1^{\prime }{\omega }^{3}i-b_2^{\prime }{\omega }^2+b_3^{\prime }\omega i+b_4^{\prime }}{-4{\omega }^{3}i-3b_1{\omega }^2+2b_2\omega i+b_3}=-\frac{b_4^{\prime }-b_2^{\prime }{\omega }^2+\left(b_3^{\prime },\omega ,-,b_1^{\prime },{\omega }^3\right)i}{b_3-3b_1{\omega }^2+\left(2,b_2,\omega ,-,4,{\omega }^3\right)i}.\end{array}$$

By calculations, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \text{Re}\left({\left(\frac{d\lambda }{d\rho }\right|}_{\lambda =i\omega }\right)& =-\frac{\left[\left(b_4^{\prime },-,b_2^{\prime },{\omega }^2\right),\left(b_3,-,3,b_1,{\omega }^2\right),+,\left(b_3^{\prime },\omega ,-,b_1^{\prime },{\omega }^3\right),\left(2,b_2,\omega ,-,4,{\omega }^3\right)\right]}{{\left(b_3,-,3,b_1,{\omega }^2\right)}^2+{\left(2,b_2,\omega ,-,4,{\omega }^3\right)}^2}\hfill \\ \hfill & =\frac{b_1{\Theta }^{\prime }\left({\rho }^{\ast }\right)}{2\left[{\left(b_1,b_2,-,2,b_3\right)}^2,+,b_1^3,b_3\right]},\hfill \end{array}\end{array}$$

where

$$\begin{array}{c}\hfill {\Theta }^{\prime }\left(\rho \right)=b_1^{\prime }\left(2,b_1,b_4,-,b_2,b_3\right)-b_2^{\prime }{b}_1{b}_3+b_3^{\prime }\left(2,b_3,-,b_1,b_2\right)+b_4^{\prime }{b}_1^2.\end{array}$$

Therefore, we obtain that

$$\begin{array}{c}\hfill \text{sign}\left[{\left(\frac{d\lambda }{d\rho }\right|}_{\lambda =i\omega }\right]=\text{sign}\left[\left(\frac{d\Theta \left(\rho \right)}{d\rho }\right|_{\rho =\rho _{}^{\ast }}^{}\right].\end{array}$$

Based on the above discussion, we have the following result by applying the Hopf bifurcation theorem (Marsden and McCracken 1976).

Theorem 4.3

If there exists ${\rho }^{\ast }>0$ such that $\Theta \left({\rho }^{\ast }\right)=0$ and $\left(\frac{d\Theta \left(\rho \right)}{d\rho }\right|_{\rho =\rho _{}^{\ast }}^{}\ne 0$, then model (1) undergoes a Hopf bifurcation at infected equilibrium $E^{\ast }=(T^{\ast },T_I^{\ast },T_L^{\ast },V^{\ast })$ when $\rho ={\rho }^{\ast }$.

Rich dynamics of model (1)

In this section, we draw some bifurcation diagrams and solution trajectories by using MATCONT (Dhooge et al. 2003) in MATLAB to illustrate the rich and interesting dynamics. Parameter values not specifically stated are from Table 1.

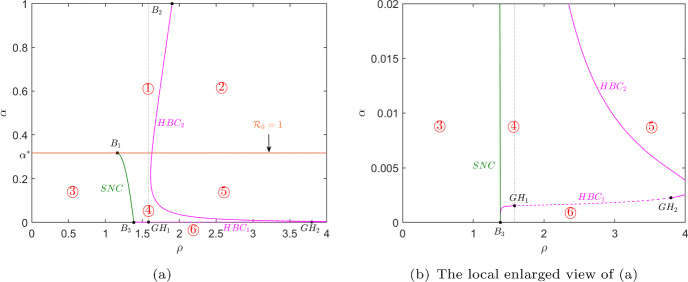
Figure 1 shows the dynamic behaviors of model (1) in $\left(\rho ,,,\alpha \right)$ plane, which is divided into six regions by the line $\alpha ={\alpha }^{\ast }=0.3179$ (orange line), saddle node bifurcation curve (green curve) and two Hopf bifurcation curves (magenta curves). When the values of parameters $\rho$ and $\alpha$ cross the saddle node bifurcation curve from region ③ to ④ or ⑤, two infected equilibria $E_1^{\ast }$ (higher virus load) and $E_2^{\ast }$ (lower virus load) appear. Besides, model (1) undergoes a Hopf bifurcation when $\rho$ and $\alpha$ cross the Hopf bifurcation curve. And Hopf bifurcation is supercritical when it crosses the solid magenta curve where a stable periodic orbit is produced, while it is subcritical when it passes through the dashed magenta curve where an unstable periodic orbit is appeared. The existence and corresponding local stability of equilibrium points of model (1) in each region of Fig. 1 are summarized in Table 2.

Fig. 1.

Saddle node bifurcation curve (green curve and marked SNC) and Hopf bifurcation curves (magenta curves and marked $HB{C}_i,i=1,2$) in $\left(\rho ,,,\alpha \right)$ plane, where the solid (dashed) magenta line represents the supercritical (subcritical) Hopf bifurcation. The orange line represents $\alpha ={\alpha }^{\ast }=0.3179$ corresponding to ${\mathcal{R}}_0=1$. The thresholds $B_1=\left(1.161,,,0.3179\right),B_2=\left(1.903,,,1\right),B_3=\left(1.384,,,0\right)$ are critical points and $G{H}_1=\left(1.584,,,0.001523\right),G{H}_2=\left(3.797,,,0.002257\right)$ are Generalized Hopf (Bautin) bifurcation points. All other parameter values except parameters $\rho$ and $\alpha$ are taken from Table 1

Table 2.

The existence and corresponding local stability of equilibrium points of model (1) in Fig. 1

Region	Stability
①	$E_0$ (unstable)	$E_1^{\ast }$ (stable)
②	$E_0$ (unstable)	$E_1^{\ast }$ (unstable)
③	$E_0$ (stable)	−
④	$E_0$ (stable)	$E_1^{\ast }$ (stable) and $E_2^{\ast }$ (unstable)
⑤	$E_0$ (stable)	$E_1^{\ast }$ (unstable) and $E_2^{\ast }$ (unstable)
⑥	$E_0$ (stable)	$E_1^{\ast }$ (unstable) and $E_2^{\ast }$ (unstable)

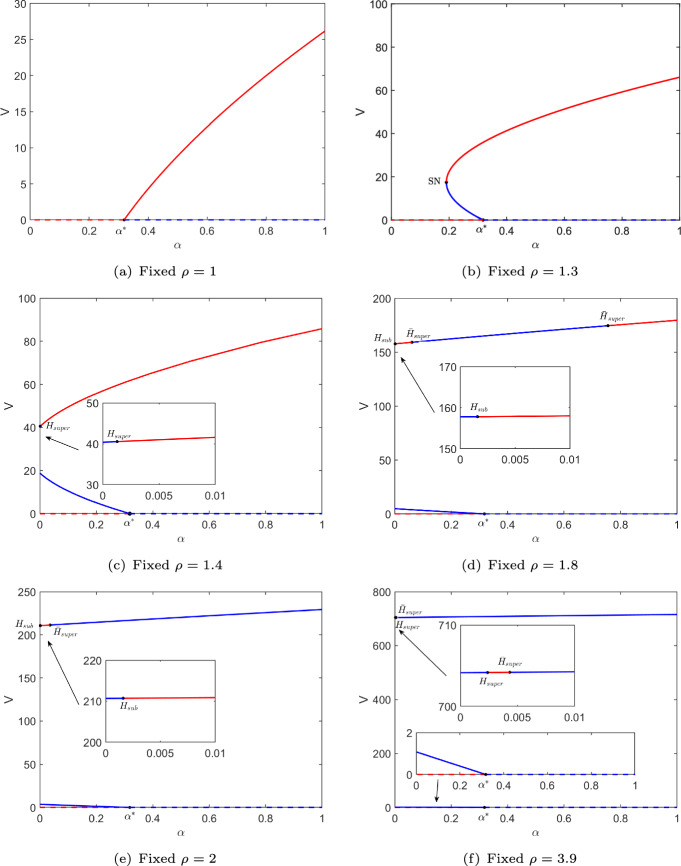
Furthermore, in Fig. 1, $\rho =1,1.3,1.4,1.8,2$ and 3.9 are fixed and then we draw the corresponding bifurcation diagrams of component V of equilibria of model (1) with respect to parameter $\alpha$, which is depicted in Fig. 2. Notation SN represents the saddle node bifurcation point and H expresses Hopf bifurcation point where the subscripts super and sub represent that the Hopf bifurcation is supercritical and subcritical, respectively. Figure 2a, b show the classic forward and backward bifurcations. Figure 2c shows a supercritical Hopf bifurcation point $H_{\mathit{super}}$ on the larger infected equilibrium $E_1^{\ast }$. Figure 2d shows three Hopf bifurcation points $H_{\mathit{sub}},{\overline{H}}_{\mathit{super}}$ and ${\overline{\overline{H}}}_{\mathit{super}}$. Figure 2e, f show two Hopf bifurcation points. The corresponding thresholds of all special points regarding parameter $\alpha$ are shown in Table 3.

Fig. 2.

Bifurcation diagrams of component V of equilibria of the model with respect to parameter $\alpha$ for different values of parameter $\rho$, where ${\alpha }^{\ast }=0.3179$ corresponding to ${\mathcal{R}}_0=1$. SN(on SNC) corresponds to saddle node bifurcation, H(on $HB{C}_1$), $\overline{H}$ and $\overline{\overline{H}}$(on $HB{C}_2$) express Hopf bifurcation where the subscripts super and sub represent that the Hopf bifurcation is supercritical and subcritical, respectively. The dashed and solid curves represent $E_0$ and $E^{\ast }$, where the red curve expresses stable equilibrium and the blue curve shows unstable one

Table 3.

The corresponding thresholds regarding parameter $\alpha$ in Fig. 2

	Threshold	First Lyapunov coefficient
Figure 2b	${\alpha }_{\mathit{SN}}=0.1907$	−
Figure 2c	${\alpha }_{H_{\mathit{super}}}=0.00128$	$-2.930474\times {10}^{-14}$
Figure 2d	${\alpha }_{H_{\mathit{sub}}}=0.001563$	$4.520355\times {10}^{-15}$
	${\alpha }_{{\overline{H}}_{\mathit{super}}}=0.06112$	$-3.495590\times {10}^{-11}$
	${\alpha }_{{\overline{\overline{H}}}_{\mathit{super}}}=0.7551$	$-2.182371\times {10}^{-8}$
Figure 2e	${\alpha }_{H_{\mathit{sub}}}=0.001595$	$7.722922\times {10}^{-15}$
	${\alpha }_{{\overline{H}}_{\mathit{super}}}=0.03641$	$-1.337931\times {10}^{-11}$
Figure 2f	${\alpha }_{H_{\mathit{super}}}=0.004319$	$-1.290048\times {10}^{-13}$
	${\alpha }_{{\overline{H}}_{\mathit{super}}}=0.002378$	$-4.973064\times {10}^{-15}$

By calculations, $\overline{\rho }=\eta k_1=1.161$ in Theorem 4.2. This implies that when $\alpha$ is used as the bifurcation parameter, the bifurcation direction at $\alpha ={\alpha }^{\ast }=0.3179$ near the infection-free equilibrium $E_0$ is forward if $\rho <\overline{\rho }=1.161$ and the direction is backward if $\rho >\overline{\rho }=1.161$, which accurately corresponds to the dynamics shown in Fig. 1 ($B_1=\left(1.161,,,0.3179\right)$) and Fig. 2.

Next, we explore the bifurcations of the periodic orbits. The Hopf bifurcation points $H_{\mathit{sub}}$ and ${\overline{H}}_{\mathit{super}}$ in Fig. 2e are used as initial points respectively, and then we continue to draw the bifurcation diagrams of the periodic orbits, which are depicted in Fig. 3a, b. It is observed from Fig. 2e that model (1) generates an unstable periodic orbit as parameter $\alpha$ increases near $H_{\mathit{sub}}$. Figure 3a further shows that the amplitude of this periodic orbit bifurcated from $H_{\mathit{sub}}$ increases as $\alpha$ increases until it undergoes the saddle node bifurcation at $\alpha ={\alpha }_{\mathit{SNC}}=0.001625$. Another stable periodic orbit appears and the amplitude increases as $\alpha$ decreases. Therefore, we choose $\alpha =0.00162$ to show the dynamics of model (1) in this case. Figure 3c, d show a larger stable periodic orbit (red) and a smaller unstable periodic orbit (blue), that is, the model has a stable infection-free equilibrium $E_0=(1000,0,0,0)$, a stable infected equilibrium $E_1^{\ast }=(42512,937.66,687979,210.68)$, a stable periodic solution and an unstable infected equilibrium $E_2^{\ast }=(42512,15.991,11732,3.5929)$ at the same time. They are generated by four different initial values $(500,1500,500,50),(30000,500,500000,100),(5000,500,410000,100)$ and (1300, 1200, 890000, 250), respectively. Figure 2e also shows that model (1) produces a stable periodic orbit as $\alpha$ increases near ${\overline{H}}_{\mathit{super}}$. Differently, we can see from Fig. 3b that the periodic orbit bifurcated from ${\overline{H}}_{\mathit{super}}$ undergoes a saddle node bifurcation at $\alpha ={\alpha }_{\overline{\mathit{HNC}}}=0.07035$, but another unstable periodic orbit appears when $\alpha =0.06842$. Therefore, we choose $\alpha =0.069$ to plot the phase diagram and solution trajectories of model (1), which can be seen in Figure ()e, d. It is observed from them that model (1) has a larger unstable periodic orbit and a smaller stable periodic orbit, that is, the model has a stable infection-free equilibrium $E_0=(1000,0,0,0)$, a stable periodic solution and two unstable infected equilibria $E_1^{\ast }=(4319.2,943.54,65589,212.00)$ and $E_2^{\ast }=(4319.2,12.506,869.37,2.8099)$ at the same time. They are generated by three different initial values (2000, 50, 2000, 50), (2300, 200, 240000, 150) and (11820, 1770, 38600, 350), respectively.

Fig. 3.

a, b Bifurcation diagrams of the periodic orbit generated by the Hopf bifurcation point $H_{\mathit{sub}}$ and ${\overline{H}}_{\mathit{super}}$ in Fig. 2e. c–f are the phase diagrams and solution trajectories of model (1) when $\alpha =0.00162$ in (a) and $\alpha =0.069$ in (b), respectively. The red and blue curves represent stable and unstable periodic orbits respectively

From Figs. 1 and 2, we can observe that parameters $\alpha$ and $\rho$ greatly affect the dynamics of model (1). When $\rho$ is small, if $\alpha$ is also small (region ③), the model (1) only has a unique stable infection-free equilibrium, indicating that the HIV infection will be eradicated. But if $\alpha$ is large (region ①), the model (1) has one stable infected equilibrium and the infection-free equilibrium is unstable, indicating that the infection will persist. When $\rho$ is large, if $\alpha$ is small (region ④ and ⑤), the model has very complex dynamics that makes the infection is unpredictable. If $\alpha$ is large (region ②the equilibria of the model (1) are unstable, but there exists at least a periodic solution, which will make the infection difficult to be controlled. To sum up, obviously, the smaller the $\rho$ is controlled, the better it is for controlling HIV infection. When $\rho$ is small, $\alpha$ should be controlled to be as small as possible. However, when $\rho$ is large, controlling $\alpha$ alone cannot effectively control HIV infection, and the changes in T cells are highly dependent on initial conditions. This may provide a new and meaningful perspective for HIV treatment strategies.

Model fitting to quantify the effects of cART

Model fitting and parameters estimation

In clinical practice, there are cases where patients delay initiation of therapy following an HIV diagnosis. However, the timing of treatment is crucial for restoring immune function and achieving rapid virus suppression (Dijkstra et al. 2021). When considering the effects of the cART and the timing of treatment, model (1) is extended into the following model (9) (Herz et al. 1996; Yang and Xiao 2010).

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\mathit{dT}}{\mathit{dt}}& =\lambda +\frac{\rho }{\eta +V}TV-{\overline{k}}_{1}TV-d_{1}T,\hfill \\ \hfill \frac{d{T}_I}{\mathit{dt}}& =\alpha {\overline{k}}_{1}TV+\beta T_L-d_2{T}_I,\hfill \\ \hfill \frac{d{T}_L}{\mathit{dt}}& =(1-\alpha ){\overline{k}}_{1}TV-\beta T_L-d_3{T}_L,\hfill \\ \hfill \frac{\mathit{dV}}{\mathit{dt}}& =k_2{T}_I-d_{4}V,\hfill \end{array}\end{array}$$ 9

where

$$\begin{array}{c}\hfill {\overline{k}}_1=\left\{\begin{array}{c}{k}_1,ift⩽t_{}^{\ast },\hfill \\ k_1\left(1,-,ϵ\right),ift>t_{}^{\ast }.\hfill \end{array}\right)\end{array}$$

The reverse transcriptase (RT) inhibitor blocks infection and hence reduces $k_1$ (Perelson and Nelson 1999; Huang 2010). Parameter $ϵ$ depicts the effectiveness of the RT inhibitor. If $ϵ$ = 1, the inhibition is 100% effective, whereas if $ϵ$ = 0, there is no inhibition. When $t=0$, the patient is first diagnosed, and $t=t^{\ast }$ is the time when treatment begins.

The data used to fit the model comes from 8 adult patients being treated with a three-drug regimen at the Second Hospital of Nanjing. Inclusion criteria were HIV-infected adults aged 18 years or older with available CD4$_{}^{+}$ T cell count records before and after treatment between January 2008 and December 2022, while exclusion criteria included patients with severe comorbidities, such as cancer or significant liver or kidney dysfunction. The three-drug regimen used by the patients consisted of two nucleoside reverse transcriptase inhibitors (NRTIs) and one non-nucleoside reverse transcriptase inhibitor (NNRTI). Baseline characteristics, such as age, gender, and route of infection, were recorded at the time of treatment. During the course of treatment, CD4$_{}^{+}$ T cell count was measured once or twice annually, using flow cytometry to ensure data accuracy. The median age of the patients at the time of treatment initiation was 35 years, and the median baseline CD4$_{}^{+}$ T cell count was 654 cells per $\mu$L. The Ethics Committee of the Second Hospital of Nanjing approved the study and waived the requirement for informed consent. Personal information of study participants was kept strictly confidential, and all information was used only for scientific research. The dynamic model (9) is fitted to CD4$_{}^{+}$ T cells data from patients by the using least squares method. To compare the best fits with different assumptions, the sum of squared residuals(SSR) is calculated. The estimation of parameters and numerical simulations are conducted by Matlab R2022a. For all patients, we estimate parameter values and calculate the mean and variance of them which are given in Table 4. We find a variation in the estimates of all individual parameters between patients. The coefficients of variation (CV) range from 1.9% to 130.8% for different parameters.

Table 4.

Parameter values of best fits of model (9) to eight treated patients

	1	2	3	4	5	6	7	8	Mean	SD	CV(%)
$\lambda$	5	9	13	13	20	10	33	16	15	9	57.8
$\rho$	0.010	0.067	0.038	0.0018	0.012	0.075	0.051	0.0092	0.033	0.029	86.7
$\eta$	570	227	226	300	453	495	284	443	375	132	35.2
$\beta$	0.0031	0.0019	0.0024	0.0064	0.00060	0.0015	0.0035	0.0022	0.0027	0.0018	65.3
$\alpha$	0.98	0.98	0.95	0.93	0.96	0.94	0.93	0.96	0.95	0.018	1.9
$k_1$	0.000061	0.000074	0.000029	0.000038	0.000053	0.000068	0.00045	0.000086	0.00011	0.00014	130.8
$k_2$	205.48	381.99	484.36	476.93	102.50	358.21	87.99	514.45	326.49	172.66	52.9
$d_1$	0.0083	0.011	0.017	0.012	0.010	0.026	0.037	0.027	0.019	0.010	55.7
$d_2$	0.37	0.70	0.65	1.02	0.42	0.33	0.86	0.73	0.64	0.25	38.7
$d_3$	0.00013	0.00018	0.00011	0.00054	0.00084	0.00063	0.00073	0.00075	0.00049	0.00030	61.6
$d_4$	11.38	16.80	10.59	14.93	8.20	11.92	25.24	22.34	15.17	5.98	39.4
T(0)	400	552	1467	1538	797	15	543	434	718	531	74.0
$T_I(0)$	270	70	43	35	176	89	351	301	167	126	75.4
$T_L(0)$	382	223	424	468	123	100	412	104	280	158	56.4
V(0)	11,147	88,018	3694	53,109	48,224	56,899	52,438	89,795	50,415	31048	61.6
$ϵ$	0.44	0.84	0.84	0.43	0.76	0.83	0.41	0.73	0.66	0.20	29.9
$ϵ_{}^{\ast }$	0.44	0.48	0.36	0.25	0.67	0.58	0.38	0.36	0.44	0.13	30.4

Note: Parameter units are the same as in Table 1

Figure 4 shows the dynamics of the uninfected CD4$_{}^{+}$ T cell population. There exists a discernible pattern in the change of CD4$_{}^{+}$ T cell count among patients from pre-treatment to post-treatment. As example, Fig. 4a presents the model fitting results for Patient01. After diagnosis, there is a rapid decrease of CD4$_{}^{+}$ T cells, followed by a slight recovery. Then the population achieves steady state in the absence of treatment. The simulation is consistent with the typical pattern (Simon and Ho 2003), where CD4$_{}^{+}$ T cell count drops after infection, climbs to a level after the virus has peaked, and then drops back to the eventual level attained in the asymptomatic stage. Upon starting treatment, CD4$_{}^{+}$ T cells experience a significant increase. Subsequently, the trend gradually stabilizes, reaching a dynamic equilibrium. The data provide support for the observed finding that robust CD4$_{}^{+}$ T cell responses to cART could sustain over several years (Nash et al. 2008).

Fig. 4.

Dynamics of CD4$_{}^{+}$ T cells $(m{m}^{-1})$ over the days. Simulation results are compared with clinical data. Blue and red points correspond to before and after treatment clinical data, while solid blue and red curves denote fitting results before and after treatment, respectively

Sensitivity analysis

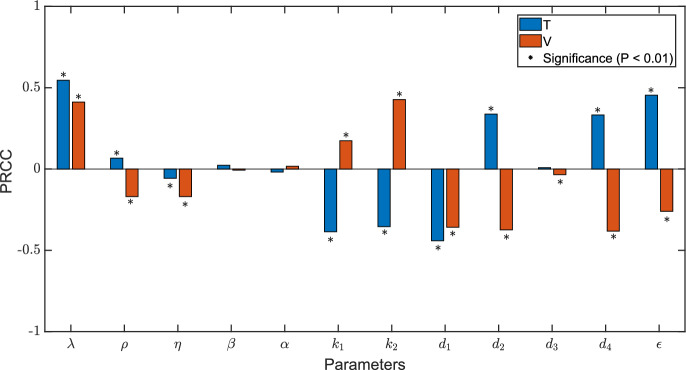
Sensitivity analysis is performed to find sensitive parameters influencing the changes in the number of CD4$_{}^{+}$ T cells and virus load using partial rank correlation coefficients (PRCCs) (Marino et al. 2008). Assuming that the input parameters are normally distributed, the expectations and standard deviations are the estimated values in Table 4. The values of components T and V of the stable infected equilibrium are the output values, respectively. In Table 5, the magnitude of the index determines the sensitivity and the sign of the index represents either a positive or negative correlation. The significance level is chosen as 0.05.

Table 5.

The PRCCs values on the outcome of components T and V of the stable infected equilibrium respectively

Parameter	PRCC for T	P value	PRCC for V	P value
$\lambda$	0.5452	0.0000*	0.4118	0.0000*
$\rho$	0.0666	0.0000*	0.3116	0.0000*
$\eta$	$-$0.0576	0.0000*	$-$0.1698	0.0000*
$\beta$	0.0225	0.0145	$-$0.0072	0.4315
$\alpha$	$-$0.0186	0.0431	0.0169	0.0663
$k_1$	$-$0.3861	0.0000*	0.1739	0.0000*
$k_2$	$-$0.3546	0.0000*	0.4268	0.0000*
$d_1$	$-$0.4415	0.0000*	$-$0.3578	0.0000*
$d_2$	0.3378	0.0000*	$-$0.3743	0.0000*
$d_3$	0.0083	0.3683	$-$0.0347	0.0002*
$d_4$	0.3322	0.0000*	$-$0.3817	0.0000*
$ϵ$	0.4541	0.0000*	$-$0.2603	0.0000*

The superscript “$\ast$” represents that the significance P$<0.01$

$_{}^1$All parameter values are derived from Table 4 (Mean values)

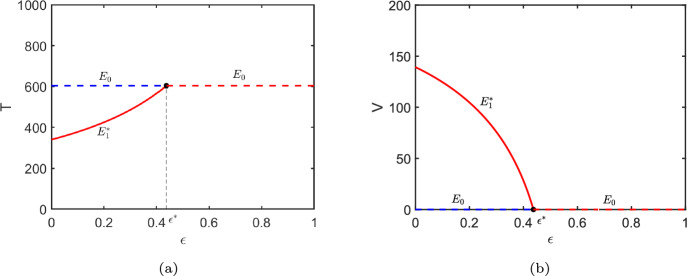
In Fig. 5, PRCCs suggest that $\lambda$, $ϵ$, and $d_1$ are the most significant parameters for CD4$_{}^{+}$ T cells. For viral load, the most sensitive parameters are $k_2$, $\lambda$, and $d_4$. It is observed that drug efficacy $ϵ$ is significantly sensitive to the number of variables T and V. Therefore, we further study how the steady-state of CD4$_{}^{+}$ T cells and viral load change as drug efficacy increases by using parameters from Patient01. Figure 6a shows that the number of CD4$_{}^{+}$ T cells in steady state is very sensitive to drug efficacy, particularly when CD4$_{}^{+}$ T cell count is relatively high as drug efficacy increases. From Fig. 6b it can also be found that there exists a threshold of drug efficacy ($ϵ_{}^{\ast }$) such that ${\mathcal{R}}_0=1$. When $ϵ\ge ϵ_{}^{\ast }$, the viral load could be completely eliminated in theory.

Fig. 5.

Sensitivity tests of uninfected CD4$_{}^{+}$ T cells (T) and viruses (V) to all parameters in model (9). The specific values of PRCCs could be observed from Table 5

Fig. 6.

Bifurcation diagrams of components T and V of the equilibria with respect to parameter $ϵ$. The threshold value ${ϵ}^{\ast }=0.437$ corresponds to ${\mathcal{R}}_0=1$. The dashed and solid curves represent $E_0$ and $E_1^{\ast }$ respectively, where the red curves express the stable equilibrium and the blue curves show the unstable one. Other parameter values are taken from Table 4 (Patient01)

Relation between parameters

We investigate the relationships between parameters using the Spearman rank correlation test. All P values are 2-sided with a significance level of 0.05. We find that the infection rate of uninfected CD4$_{}^{+}$ T cells by virus ($k_1$) is significantly positively correlated with the clearance rate of virus particles ($d_4$); $r=0.810,P=0.021$. The activate rate of latently infected CD4$_{}^{+}$ T cells ($\beta$) is significantly negatively correlated with threshold of drug efficacy ($ϵ_{}^{\ast }$); $r=-0.810,P=0.021$. Other correlations are summarized in Table 6.

Table 6.

The Spearman correlation coefficients between the parameters

	$\lambda$	$\rho$	$\eta$	$\beta$	$\alpha$	$k_1$	$k_2$	$d_1$	$d_2$	$d_3$	$d_4$	T(0)	$ϵ$	$ϵ_{}^{\ast }$
$\lambda$
$\rho$	$-$0.144
$\eta$	$-$0.252	$-$0.167
$\beta$	0.036	$-$0.476	$-$0.238
$\alpha$	$-$0.599	$-$0.119	0.286	$-$0.357
$k_1$	0.228	0.310	0.071	$-$0.048	0.000
$k_2$	$-$0.204	$-$0.357	$-$0.333	0.071	0.190	$-$0.262
$d_1$	0.563	0.214	$-$0.333	0.190	$-$0.643	0.524	0.167
$d_2$	0.479	$-$0.452	$-$0.571	0.643	$-$0.429	0.190	0.238	0.405
$d_3$	0.707	$-$0.095	0.310	$-$0.381	$-$0.238	0.452	$-$0.286	0.310	0.143
$d_4$	0.228	0.048	$-$0.262	0.405	$-$0.262	$0.{810}^{+}$	0.071	0.667	0.643	0.214
T(0)	0.299	$-$0.381	$-$0.643	0.286	$-$0.286	$-$0.595	0.238	$-$0.167	0.571	$-$0.143	$-$0.214
$ϵ$	$-$0.359	0.476	$-$0.310	$-$0.643	0.357	$-$0.357	0.405	$-$0.190	$-$0.500	$-$0.357	$-$0.476	0.071
$ϵ_{}^{\ast }$	$-$0.108	0.571	0.476	$-0.{810}^{+}$	0.310	0.238	$-$0.595	$-$0.333	$-$0.690	0.381	$-$0.310	$-$0.476	0.262	1.000

The superscript “$+$” denotes the significance P$<0.05$

Conclusion and discussion

In this article, we firstly construct a mathematical model considering HIV latency and the homeostatic proliferation of CD4$_{}^{+}$ T cells. The dynamics of the model are analyzed in detail. Secondly, we introduce the cART into the model (1), fit the model (9) to clinical data and estimate the parameters. Finally, we perform sensitivity analysis and correlation analysis to investigate the effects of cART and the biological mechanisms of HIV infection and persistence.

For model (1), we discuss the positivity of the solution, calculate ${\mathcal{R}}_0$ and investigate the existence and stability of equilibria. We theoretically and numerically show that bistability can be caused by a backward bifurcation in presence of HIV latency and the homeostatic proliferation of CD4$_{}^{+}$ T cells. Our results reveal that if the homeostatic proliferation of CD4$_{}^{+}$ T cells is insufficient, then backward bifurcation cannot occur. This means that when $\rho <\overline{\rho }$, the infected equilibrium does not exist as long as ${\mathcal{R}}_0<1$, and the virus will be eliminated. However, when $\rho >\overline{\rho }$, two infected equilibria exist even with ${\mathcal{R}}_0<1$. In this case, with a high initial viral load, the larger infected equilibrium tends to be locally asymptotically stable, preventing the virus from being eliminated. This highlights the critical impact of CD4$_{}^{+}$ T cell homeostatic proliferation on the complete eradication of the virus. We also theoretically prove the existence of Hopf bifurcation at the infected equilibrium. Numerical results show that when $\rho$ is small, $\alpha$ should be minimized to achieve HIV eradication. However, when $\rho$ is large, controlling $\alpha$ alone cannot effectively manage HIV infection, and the changes in CD4$_{}^{+}$ T cell counts are highly dependent on the initial conditions.

Next, we plot some one-parameter bifurcation diagrams with respect to parameter $\alpha$ when fixing different values of parameter $\rho$. Saddle node bifurcations, subcritical and supercritical Hopf bifurcations can be observed from Fig. 2. We also detect the saddle node bifurcations of the periodic orbits and find the coexistence of the periodic orbits in two cases, one is that the large periodic orbit is stable and the small one is unstable, and the other is the opposite (see Fig. 3). These findings suggest that the homeostatic proliferation of CD4$_{}^{+}$ T cells and the production of latently infected CD4$_{}^{+}$ T cells greatly affect the model dynamics, and play a critical role in HIV infection and persistence.

Furthermore, we incorporate cART into the model (1) and fit the modified model (9) to CD4$_{}^{+}$ T cells data from patients with available records both before and after treatment (Fig. 4). Despite the varying trajectories of CD4$_{}^{+}$ T cell counts in patients, model (9) provides good fits to the CD4$_{}^{+}$ T cells data. And the model (9) successfully duplicates the initial decrease and subsequent increase of healthy T cells during early infection before treatment (Clark et al. 1991). Upon starting cART, the parameter $ϵ$, representing overall drug efficacy, largely explains the recovery of CD4$_{}^{+}$ T cells. By ensuring consistency of parameters before and after treatment, our model enables to generate a more accurate assessment of the cumulative effect of antiviral therapy. The estimated parameters exhibit similarities with findings from prior research (Hill et al. 2018). Specifically, the values for parameters $\beta$ (Luo et al. 2012), $k_2$ (Huang et al. 2006), $d_2$ (Luo et al. 2012; Huang et al. 2010), $d_3$ (Hill et al. 2018), and $d_4$ (Markowitz et al. 2003) are consistent with the previously reported optimal estimates for these variables. Previous studies have estimated the range of drug efficacy to be between 0.67 and 0.88 (Luo et al. 2012) and 0.64 to 0.84 (Putter et al. 2002). However, in this article, the estimated range has shifted lower, from 0.40 to 0.84. One reason for this shift may be that prior studies have predominantly utilized patients data from short-term, precisely controlled clinical trial. In contrast, the data used in this study are derived from real-world settings, where patients have much longer medication cycles and may not adhere to their regimens as strictly as those in clinical trials, resulting in a generally lower overall drug efficacy.

We find that when the effectiveness of the cART approaches a critical threshold, the CD4$_{}^{+}$ T cells achieve maximum recovery. However, the current drug therapies for HIV-infected patients are not perfect effective. Iwami et al. (2015) investigated the dynamics of cell-to-cell and cell-free HIV-1 infections through experimental-mathematical investigation, suggesting that even a complete block of the cell-free infection would provide only a limited impact on HIV-1 spread. Fortunately, antiviral therapy can still greatly enhance the immune function of patients. Note that if the drug efficacy increases, then both the quantity of CD4$_{}^{+}$ T cells at steady-state and the rate of CD4$_{}^{+}$ T cells recovery rise gradually (Fig. 6). This implies that once treatment is initiated, it is highly necessary to enhance the efficacy of drug therapy by improving adherence, monitoring drug resistance and various strategies. Previous studies (Rong et al. 2007; Wang and Rong 2019) have confirmed that as drug efficacy increases, the viral load is suppressed to a lower level.

In addition, correlation analysis shows that the activate rate of latently infected CD4$_{}^{+}$ T cells ($\beta$) is significantly negatively correlated with threshold of drug efficacy ($ϵ_{}^{\ast }$). This suggests that a lower activation rate of latently infected CD4$_{}^{+}$ T cells in a patient requires a higher threshold of drug efficacy to effectively inhibit viral replication in long-term. This means that the higher the rate at which latently infected cells transition into actively infected cells, the more beneficial it is for clearing the virus through treatment. Currently, substantial efforts are being directed towards developing a class of drugs called latency-reversing agents (LRAs) that aim to activate HIV gene expression in latently infected cells, with the goal of eliminating the viral reservoir and eventually curing HIV infection. Our findings highlight the importance of the need for latently infected cell activation to optimize therapeutic efficacy. Consistent with previous studies (Archin et al. 2012; Elliott et al. 2014; Ke et al. 2015), it is to be expected that enhancing viral clearance would substantially improve the efficacy of LRAs, as evidenced by the findings presented in this study. Correlation analysis also reveals a significant positive correlation between the infection rate of uninfected CD4$_{}^{+}$ T cells by the virus and the virus clearance rate, indicating a highly dynamic balance between new cycles of infection and virus clearance.

Our proposed model appears to perform well in capturing the trajectories of CD4$_{}^{+}$ T cells observed under relatively complex clinical situations. However, some limitations exist for this study. Overall treatment effectiveness could be influenced by multiple factors. Various studies have explored viral dynamics models incorporating clinical factors such as drug adherence (Labbé and Verotta 2006; Huang et al. 2006), time-varying drug efficacy (Wu et al. 2005), drug resistance (Rong et al. 2007) and so on. The model we consider in this paper is a basic model with HIV latency. The homeostatic proliferation of CD4$_{}^{+}$ T cells is included to consider the variations in the initial CD4$_{}^{+}$ T cell count or the viral load. Besides, further studies need to be done to incorporate some other factors such as CTL immune response (Liu and Kong 2020; Wang and Li 2021), macrophages (Hadjiandreou et al. 2007; Hernandez-Vargas and Middleton 2013) into the dynamics models.

Data availability

The data that support the findings of this study are not openly available due to reasons of sensitivity and are available from the corresponding author upon reasonable request. Data are located in patient data repository of the Second Hospital of Nanjing.

Declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.