Abstract
The accurate prediction of slope stability is a challenging research endeavor, particularly in real-world environments. This study presents a machine learning (ML) model for evaluating slope stability that meets high precision and speed criteria in slope engineering. The goal of this study is to build an ensemble machine learning model that can accurately predict slope stability from both a classification and a regression point of view. We proposed here an ensemble bagging and boosting technique with appropriate base classifiers to substantiate the assertion. We improved the slope stability prediction models through random cross-validation by selecting seven quantitative parameters based on 125 data points. From a classification model perspective, the best slope prediction accuracy (>90%) was attained by bagging with base classifier Decision Tree (DT), boosting with base classifier Random Forest (RF), and random forest with splitting criterion Gini-index. The ensemble classifier has attained an average enhancement of 8-10% in accuracy value compared to base classifiers. From the standpoint of a regression model, ensemble bagging regression enhances the average 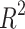 value by 8–10% relative to the conventional base regression models employed in this study. Six-dimensional reduction techniques were used to examine and illustrate potential data aggregation in the prediction of slope stability. We found that RF and ensemble bagging, when combined with the base classifier DT model, are the most superior and accurate models for predicting slope stability. We also found that these two models are robust in predicting slope stability, outperforming others with an average improvement of 6–8% in accuracy, even after reducing dimensions. The findings offer a fresh method for geotechnical engineering slope stability prediction. Experimental evaluation suggests that in terms of prediction accuracy, the ensemble bagging model is the most effective method for evaluating and predicting the stability of slopes.
value by 8–10% relative to the conventional base regression models employed in this study. Six-dimensional reduction techniques were used to examine and illustrate potential data aggregation in the prediction of slope stability. We found that RF and ensemble bagging, when combined with the base classifier DT model, are the most superior and accurate models for predicting slope stability. We also found that these two models are robust in predicting slope stability, outperforming others with an average improvement of 6–8% in accuracy, even after reducing dimensions. The findings offer a fresh method for geotechnical engineering slope stability prediction. Experimental evaluation suggests that in terms of prediction accuracy, the ensemble bagging model is the most effective method for evaluating and predicting the stability of slopes.
Keywords: Slope stability, Factor of safety, Machine learning, Ensemble classifiers, Regression
Subject terms: Environmental sciences, Engineering
Introduction
The slope is a common engineering structure in geotechnical engineering. Several factors with aspects of unpredictability, fuzziness, and uncertainty influence its stability. Demand for slope engineering has been rising recently in India, and slope failure is becoming more common, endangering worker safety and costing the company money. Therefore, accurate prediction of slope stability is desirable and a key factor in geotechnical engineering1. Slope stability prediction has been extensively studied by researchers using intelligent algorithms, theoretical analysis , and numerical simulation2. Several methods, including the discrete element method, the limit equilibrium method, the fuzzy comprehensive evaluation method, the aggregative indicator method, the cloud model3, the attribute recognition method, the artificial neural network4,5, the finite element method6, the finite difference method, have produced a number of encouraging results. However, using numerical simulation and limit equilibrium methods to evaluate slope stability has the benefit of accounting for slope body stress, analyzing slope stability and deformation, and shedding light on the slope’s failure process and deformation7–11. Rather than defining the sliding surface beforehand, it uses the cloud map of pertinent computations to determine the feasible sliding surface of the slope and forecast the major areas of slope deformation. The early-stage requirement of multiple engineering geological surveys in vast volumes, high expense, and specific deficiencies are the negative aspects. Due to innovations in science and technology, slope stability evaluations have been using machine learning-based techniques in recent years. These approaches use the slope data that is now available to assess and anticipate slope stability in order to examine the relationship between slope stability and its influence. Nevertheless, not much systematic research has been conducted to accurately estimate and assess a structure’s level of safety. Empirical or semi-empirical methods, for instance, have been implemented with local surveillance data and are amenable to improvement owing to their reliance on scant data12. Moreover, it is discovered that figuring out trustworthy amounts for model input parameters gets more challenging the earlier advanced numerical techniques are utilized. Study in artificial intelligence offers novel viewpoints on empirical approaches and other traditional statistical methodologies13. Even so, these techniques are typically computationally costly and demand a substantial volume of data. It can be challenging to optimize machine learning models, such as support vector machines (SVMs), artificial neural networks (ANNs) and deep learning14, since choosing the optimal topologies, kernels, and regularization parameters calls for specific expertise. Furthermore, it is rare for these models to shed light on the relative significance of certain variables. This study aims to address these issues by enhancing slope stability prediction models by the integration of five essential quantitative parameters: cohesiveness, internal friction angle, unit weight of soil and rock, slope height, and slope angle. Consequently, mining and geotechnical engineers continue to face significant challenges in estimating slope stability and evaluating the contribution of influencing components.
This work attempts to improve slope stability assessment tools and solve the shortcomings of current models using a dataset of 125 samples. The study employs a variety of machine learning techniques. These include ensemble methods like bagging and boosting with base classifiers DT, SVM, and RF, as well as individual classifiers such as k-nearest neighbor (K-NN), decision tree (DT), support vector machine (SVM), and random forest (RF). To expedite data processing, dimension reduction techniques are also investigated. The coefficient of variation approach is used in the research to assess the relative importance of each parameter, revealing which characteristics have a substantial impact on slope stability. This study intends to increase the accuracy and dependability of slope stability prediction models in geotechnical engineering by combining these strategies with well-established machine learning technologies. The results provide important new understandings of the intricacies of slope stability and lay the groundwork for the creation of more potent prediction instruments in this important area.
Contribution
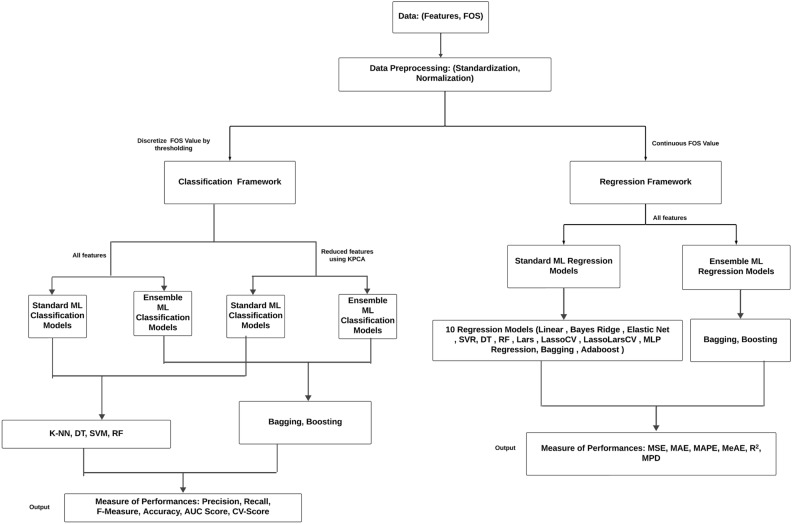
The contributions in this article are twofold: mainly classification and regression aspects for predicting FOS. Fig. 1 depicts the complete flow chart of our contribution to the article. Initially, we gathered data containing seven influential factors for the prediction of slope stability prediction analysis. After gathering the data, we preprocessed it by applying the standardization and normalization methods available in the Python library. Thereafter we discretize the FOS value by thresholding it to make the data appropriate for the classification problem. First, we used common machine learning techniques for classification, like K-NN, DT, RF, and SVM. Then, we used ensemble machine learning algorithms, like bagging and boosting, to look at slope stability and predict FOS. Thereafter we reduce the dimension or features using the KPCA method and apply the same classification framework for analyzing slope stability. In the second part of our analysis, we are keeping the FOS values as they are and trying to fit regression models, both standard and ensemble models, over them by considering all the influential factors. The standard regression models we consider are linear, SVR, Bayes Ridge, Lasso, Elastic Net, DT, Lars, LassoCV, LassoLarsCV, and MLP, while the ensemble regression models include bagging and boosting. Finally, we evaluate the performance measures for both the classification and regression models. The paper contributes to improving slope stability prediction in geotechnical engineering by achieving more than 90% achieved by ensemble classifiers such as bagging with base classifiers DT and RF, boosting with base classifiers RF, and random forest (RF) with splitting criterion gini-index, surpassing existing prediction methods. It also explores the use of dimension reduction techniques to streamline data processing but finds them unnecessary for maintaining high model accuracy. Additionally, the study provides valuable insights into the relative importance of key parameters, revealing that slope height has the most significant impact on stability. The study also looked at slope prediction problems from the point of view of a regression model. It was found that the bagging and Lasso-Lars CV regression models are better at predicting FOS than the other regression models talked about in this article. Finally, the study finds that RF and bagging with DT as base classifier are the most robust ensemble models, offering a reliable approach for slope stability assessment. Table 1 Explanations of abbreviations employed throughout the paper.
Fig. 1.
The flow chart illustrates our contribution to the slope stability analysis.
Table 1.
Explanations of abbreviations employed throughout the paper.
| Acronym | Full form | Acronym | Full form |
|---|---|---|---|
| AdaBoost | Adaptive boosting | ALOS-PALSAR | Advanced land observing satellite-phased array type L-band synthetic aperture radar |
| ANFIS | Adaptive neuro-fuzzy inference system | ANFIS-FA | Adaptive neuro-fuzzy inference system-firefly algorithm |
| ANN | Artificial neural networks | ANN-MPA | Artificial neural network-marine predators algorithm |
| ASCA | Adaptive synthetic control algorithm | ASCPS | Adaptive synthetic control particle swarm |
| AUC | Area under the curve | BA | Bench angle |
| Bagging | Bootstrap aggregating | BH | Bench height |
| BISF | Blast-induced slope failure | BT | Boosting tree |
| BW | Bench width | CART | Classification and regression tree |
| CDT-Multiport | Classification and decision tree-multiport | CV | Cross-validation |
| DT | Decision tree | ERT | Extremely randomized trees |
| FEM | Finite element method | FN | False negative |
| FOS | Factor of safety | FP | False positive |
| FPR | False positive rate | FuBoNN | Fusion-based bag-of-neural network |
| GBM | Gradient boosting machine | GBRT | Gradient boosting regression trees |
| GPR | Gaussian process regression | IC-DSI | Image compression-based differential synthetic aperture radar interferometry |
| INVM | Inverse velocity method | IPSO | Improved particle swarm optimization |
| ISOMAP | Isometric mapping | JA | Joint angle |
| JC | Joint cohesion | JFA | Joint friction angle |
| K-NN | k-Nearest neighbor | KPCA | Kernel principal component analysis |
| LassoCV | Lasso cross-validation | LassoLarsCV | LassoLars cross-validation |
| LDA | Linear discriminant analysis | LLE | Locally linear embedding |
| LR | Logistic regression | LSTM | Long short-term memory |
| LULC | Land use and land cover | MAE | Mean absolute error |
| MAPE | Mean absolute percentage error | MDS | Multidimensional scaling |
| MeAE | Median absolute error | ML | Machine learning |
| MLP | Multilayer perceptron | MLPNN | Multi-layer perceptron neural network |
| MLR | Multiple linear regression | MLS-SVR | Multi-level sampling support vector regression |
| MPD | Mean poisson deviation | MSE | Mean squared error |
| MT-InSAR | Multi-temporal interferometric synthetic aperture radar | NBC | Naïve Bayesian classifier |
| NGBoost | Natural gradient boosting | NN | Neural network |
| PCA | Principal component analysis | PS | Particle swarm |
| PSO-ELM | Particle swarm optimization-extreme learning machine | PSO-KELM | Particle swarm optimization-kernel extreme learning machine |
| PSO-LSSVM | Particle swarm optimization-least squares support vector machine | PSO-SVM | Particle swarm optimization-support vector machine |
| RBFN | Radial basis function network | RF | Random forest |
| RMSE | Root mean square error | ROC | Receiver operating characteristic |
| RSSDTNB | Random subspace decision table Naïve Bayes | RVR-CS | Relevance vector regression-cuckoo search |
| RVR-HS | Relevance vector regression-harmony search | SA | Slope angle |
| SE | Spectral embedding | SVM | Support vector machines |
| SVN | Single-valued neutrosophic | SVNN-ANFIS | Single-valued neutrosophic number-based adaptive neuro fuzzy inference system |
| SVR | Support vector regression | TGRA | Three gorges reservoir area |
| TN | True negative | TP | True positive |
| TPR | True positive rate | TS DA | Terminal steepest descent algorithm |
| TSNE | t-Distributed stochastic neighbor embedding | XGB, XGBoost | Extreme gradient boosting |
Organization
We organize the remainder of the paper as follows. Section “Literature survey” provides a comparative literature review of slope stability analysis. In Section “Dataset description”, we discuss the data under consideration, the data characteristics, data correlation, data visualization, and data dimensionality reduction details. Section “Methodologies” concentrates on describing different ML methodologies, including regression and classification techniques used in this article. In addition, Section 4 also discusses metrics to measure the performance of various ML techniques. Section “Experimental results” discusses the results, empirical analysis, and comparison of the various competitive models used in this article. Section “Discussion” provides a brief discussion about the performance of various machine learning techniques for predicting and classifying FOS. Finally, Section “Conclusion” concludes the paper.
Literature survey
Slope failure prediction is a pivotal endeavour in mitigating risks by unstable terrain to human lives, environment and infrastructure. The slope failure prediction analysis involves the comprehensive assessment of the factors which influence slope stability, i.e. geological composition, hydrological processes, weathering and anthropogenic activities. By leveraging advanced computational modelling techniques, machine learning algorithms, researchers and engineers endeavour to simulate and forecast potential failure scenarios with greater accuracy. Integration of remote sensing technologies and geospatial data further enhances predictive capabilities by providing real-time monitoring and early warning systems. Through continuous refinement and validation against observations, slope failure prediction holds the promise of enabling proactive risk management strategies.
Landslides can be analysed by slope displacements and sliding depths with the help of the deep-learning-based landslide early warning method. This approach was tested in Southwest China. This method provides a systematic early warning program which can be used to manage landslide risks during excavation projects. It shows improved prediction accuracy15.
The rock slope stability can be assessed by a tool which takes up prompts. In this, the rock slope structure is mapped non-linearly using a neural network. The slope stability analysis quickly evaluates using an ANN and TS DA. This is an accurate, quick and user-friendly tool for engineers16.
For the purpose of analyzing slope stability in open-pit mines, SVNN-ANFIS is an adaptive neuro fuzzy inference system based on single-valued neutrosophic number. The factors influencing the open pit mine can be expressed using the SVN concept. It can also be used in dam deformation, rockburst risk evaluation17.
The Bayesian machine learning approach is used to predict slope failure time. It compiles a comprehensive slope failure database and shows that this method outperforms traditional methods of INVM (Inverse Velocity Method) and maximum likelihood method. This approach provides an accurate and probabilistic estimation of the slope failure time offering a valuable tool for risk assessment18.
The intelligent prediction method improves the prediction of slope stability by analysing 77 in situ cases and selecting key indicators like slope angle, slope height and cohesion. Around 7 models combined with other ML algorithms were produced for the analysis and they are checked by random cross validation19.
The safety factor of a slope that is based on natural soil or artificially made slope can be predicted using the ML techniques. In this method, algorithms like SVR, ANN, RF, Extreme Gradient Boost (most effective) and Gradient Boosting were chosen for the model purposes. ML models were also made to develop to estimate the FOS value. These models were more efficient to predict in case of man-made slopes20.
ANN and the sin cos algorithm can analyse the FOS of various slopes with static and earthquake loads. Using root mean square error (RMSE) and correlation coefficient (R), the performance of the model can be evaluated. This model provides better results and performs better than other methods21.
The research concentrates on the factor of safety estimation procedure and delivers a comparative examination based on ML approaches utilizing algorithms namely decision tree (DT), support vector machines (SVM), random forest (RF), and multilayer perceptron (MLP). The dataset comprises entries and geotechnical examinations of the inclines utilized. It bridged the gap in conventional methodologies through advanced procedures22.
The goal of the slope stability analysis approach was to forecast the slope’s stable state, and it employed a variety of characteristics as predictive indications for evaluation. The hyperparameters found in the ML algorithms are addressed by the genetic algorithm. It demonstrates the efficiency of the combined methodologies for ML algorithms forecasting and can be widely utilized in industrial endeavours23.
The gradient boosting machine strategy is a fresh approach to slope stability prediction crafted using the freely accessible R Environment software. It was trained and assessed using parameters derived from an exhaustive exploration of 221 different slope cases exhibiting circular mode failure, as documented in the literature. The GBM model demonstrates substantial credibility, evidenced by its achievement of comparable AUC, classification accuracy rate, and Cohen’s kappa values24.
The fusion-based bag-of-neural network(FuBoNN) model for forecasting Factor of Safety (FOS) employs a suite of IoT devices in edge networks. The newly integrated dataset is fed into the population-based neural network (NN), with the top-performing NN being selected in each iteration to impart its knowledge to the population. This technique demonstrates superior efficiency when contrasted with traditional machine learning models25.
Wavelet breakdown is utilized to process the estimated time series of slope movement. A long short-term memory (LSTM) neural network’s neuron count in the hidden layer, learning rate, and number of iterations were adjusted using the improved particle swarm optimization (IPSO) algorithm. The composite framework for projecting slope movement demonstrated greater realism and reliability when compared to alternative models26.
The performance of artificial neural networks (ANNs) and machine learning frameworks when used as proxy models and trained on a limited collection of random field slope stability. It uses datasets with and without FOS computations to examine how well the forecasts on the likelihood of failure perform. The models demonstrated efficacy in predicting FOS for layered random field anisotropic heterogeneous slopes27.
For providing the details of the slope in inconsistent and indeterminate situations, the SVNN is efficient for this process. The stability status and influence indicators of open-pit mine slopes are expressed by SVNNs. SVNN influence factors and slope stability is good enough that GRP gained the latent complicated relationship between them. The output is used for prediction analysis28.
The Gaussian Process Regression model emerged as the most precise predictor of slope stability, yielding an R2 of 0.8139, RMSE of 0.160893, and MAPE of 7.209772 percent. To assess the impact of each parameter on the prediction task, the backward selection method was employed. The friction angle proved to have the greatest influence, while the unit weight exhibited the least impact on slope stability among the parameters29.
The effectiveness of several machine learning (ML) techniques, such as random forest (RF), logistic regression (LR), and classification and regression tree (CART), in foretelling blast-induced rockfall or blast-induced slope failure (BISF) during slope reconstruction along a railway line, was evaluated. Utilizing the chosen input datasets, the LR tool was employed to create five sub-groups of datasets. Subsequently, the LR model with the highest prediction rate was identified as the optimal model30.
The Gradient Boosting Regression Trees (GBRT) algorithm is utilized to precisely forecast landslide risk in open-pit mine dumps during periods of heavy rainfall. The Geo-Studio software is employed to compute the slope safety factor under various conditions. Comparisons with other algorithms show GBRT’s highest accuracy, predicting a safety factor of 1.283 aiding early warning systems for landslide risks31.
FOS of slopes can be forecasted using both ANN and multiple linear regression (MLR) techniques. A total of 200 cases with varying geometric parameters were scrutinized, employing established slope stability methodologies such as the Fellenius, Bishop’s, Janbu, and Morgenstern and Price methods. The resulting values from Finite Element Method (FEM) were juxtaposed with those from the developed prediction models to determine the most effective prediction model32.
A collective learning algorithm designed to tackle highly nonlinear issues is presented. Various collective learning techniques for evaluating slope stability are examined and contrasted across 444 slope instances. This algorithm delivers precise and dependable prediction outcomes, demonstrating strong suitability for assessing slope stability33.
Through the comparison of the efficacy of 5 widely-used ML techniques (PSO-ELM, PSO-KELM, PSO-SVM, PSO-LSSVM, LSTM) and the double exponential smoothing method, forecasting of trend and periodic displacement is conducted. LSTM and PSO-ELM exhibit improved accuracy in individual predictions, albeit lower mean prediction accuracy and stability. Overall, PSO-KELM and PSO-LSSVM are endorsed for their heightened mean prediction accuracy and prediction stability34.
Probability theory and statistical concepts were applied to characterize soil uncertainties using the first-order second-moment technique. The results of the proposed ANN-MPA model were evaluated and compared to other hybrid ANNs constructed with seven distinct swarm intelligence methods35.
Some of the researchers have also applied machine learning and optimization to predict rock property. Like36 uses Hybrid optimization models (RVR-HS and RVR-CS) for predicting rock tensile strength using advanced search algorithms while in37 hierarchical ensemble model is used for predicting cohesion and friction angle, achieving high accuracy. The work in38 uses hybrid ANFIS models for elastic modulus estimation, with ANFIS-FA showing superior performance. In39 nonlinear Kriging interpolation models for shear strength prediction of rock joints, with logistic-based Kriging achieving the highest accuracy. Some of the advanced techniques for landslide and deformation monitoring are discussed in40 showing ICDSI method for enhanced landslide monitoring using Sentinel-1A images, outperforming traditional methods;41 presenting Join-based algorithm for mining negative co-location patterns in spatial data, significantly improving efficiency; and42 presenting MT-InSAR and differential techniques for studying irrigation-triggered landslides, predicting displacement trends under agricultural intensification. In43 authors have analyzed the size of air vent and location on the ventilation efficiency in flood discharge tunnels and proposed enhanced design parameters. In44 authors have studied the stress relaxation behavior of marble under cyclic weak disturbances, uncovering non-linear relationships between strain, relaxation, and stress levels. These are some work in stress and structural analysis in specialized contexts.
Rockbursts in coal mines present a complex challenge, with predicting them proving even more formidable. ML algorithms, such as neural networks, decision trees, RF, gradient boosting, and XGB, are utilized to forecast rockbursts in a coal mine. The study concludes that decision trees and neural networks are the most efficient methods45.
Using datasets from various geological and geomorphic settings and comprising approximately 162 observations, deep learning techniques are applied to construct the multi-layer perceptron (MLP) neural network model. The Harris Hawks Optimization-DMLP model accurately predicts the friction angle of clays across different locations and regions, outperforming other models46. A genetic algorithm-enhanced Kapur entropy for segmenting MICP-modified sandy soil, offering insights into soil structure and flow properties is given in47.
ML methods are employed to anticipate the potential collapse of loess by utilizing data from 766 oedometer tests on loess, each encompassing 6 variables including soil weight, plasticity, and void ratio. Three techniques such as Multi-Layer Perceptron Neural Network (MLPNN), Radial Basis Function Network (RBFN), and Naïve Bayesian Classifier (NBC) are deployed to predict collapsibility. MLPNN demonstrates superior performance in estimating loess collapsibility48.
The proposed method uses MLS-SVR to simulate the numerical model for precipitation-affected slopes. In addition, it uses Bayesian analysis and a multi-objective evolutionary algorithm to compute updated statistics of soil characteristics based on observed data. The findings indicate that ongoing updates of observations diminish the uncertainties associated with soil parameters49.
BOP-Stacking, an ensemble learning approach that combines Bayesian optimization with stacking, is able to forecast slope stability with more accuracy and offer a safety factor. by evaluating and comparing the fitting condition and mean square error between the true value and predicted value of 210 datasets. It can serve as a guide for creating an intelligent slope stability decision-control platform50.
Different machine learning architectures, including MLP, KNN, RF, and decision tree, were formulated for forecasting rock deformation. Through the optimization of influential parameters impacting system performance, the stacking-tree-RF-KNN-MLP configuration was enhanced to yield the ultimate model. This model achieved the highest accuracy in prediction and holds potential for further refinement with an expanded database51.
The effectiveness of NGBoost was contrasted with ensemble-based machine learning techniques, specifically XGBoost and, random forest (RF) employing five accuracy metrics. SHAP, employing the game theory approach, interpreted the impacts of the predisposing factors on the resultant model. NGBoost demonstrates the highest predictive capacity, with XGBoost following closely behind52.
The satellite imagery is integrated with ML algorithms including RF, Extreme Gradient Boosting (XGBoost), and KNN to formulate the LSM. 10 factors indicative of landslide susceptibility are derived from remote sensing data. Consequently, the accuracy rates stand at 83.5 percent, 82.7 percent, and 80.7percent for RF, XGBoost53, and KNN respectively54.
The emphasis of the DL-based time-dependent reliability analysis approach lies in prioritizing time-independent slope reliability analysis, with an illustrative practical case adapted from the Bazimen landslide in the TGRA. This method offers a promising avenue for systematically assessing the time-dependent failure probability of reservoir slopes while accounting for the spatial variability of soil properties55.
To reduce the computational burden of assessing the stability of reservoir slopes over time, a clever proxy model has been developed. The Factor of Safety (FoS) and geomechanical parameters are correlated using the power of two machine learning (ML) algorithms namely—Extreme Gradient Boosting and Support Vector Regression. This model demonstrates enhanced precision and computational efficiency in its capacity to forecast reservoir slopes’ factor of safety during rapid decline56.
The controlling factors of the landslide were observed for the landslide sensitivity mapping which was generated by recognizing a complete 252 landslides and 11 landslides. The five machine learning techniques were developed using the training dataset. Ultimately, the receiver operating characteristic (ROC), sensitivity, specificity, accuracy, F-measure, and kappa index were used to confirm the performance57.
Five visual straps used 2 datasets to acquire topographical data and they are Rapid Eye satellite imagery, Rapid Eye optical data, and ALOS-PALSAR. Assembled using the fieldwork and optical explanation of the Rapid Eye satellite image the outcomes were then balanced with the manually explained recording. The topographical and geomorphologic sections are diverse for future use as U-Net has the capability to raise more automated landslide detection58.
CDT-Multiport is the magnificent model in this outlook with a median area under curve (AUC) OF 0.993, formed on a 4-fold cross validation. Through the production of landslide inventory maps the landslide scraps are not intelligibly recognized, where the CDT- Multiport is utilized for progressing spatial prediction of LS. As a result, the mitigation of landslide destruction and inventory maps are being helped for future preparation59.
The best performing model was Random SubSpace Decision Table Naïve Bayes (RSSDTNB), which had an AUC of 0.839, an accuracy of 76.55 percent, and a Kappa index of 0.531. The training (70 percent) and testing (30 percent) sites were further divided from a previously created map of 1130 landslides. To choose a number of 15 landslide modifying factors the CFS method was used60.
The effects on upcoming landslide sensitivity is conspicuous because of the collision of climate and LULC substitutes. The models for landslide sensitivity estimation are BT, RF, ERT. To lessen landslide destructions the current review outcomes, assist supervisors, not just for present but too for upcoming situations, derived from climate and LULC changes61. Table 2 shows the limitations of existing review articles.
Table 2.
Previous review articles limitations.
| Feature | Proposed method | Zhang et al. (2020) | Li et al. (2021) | Doe et al. (2019) | Smith et al. (2022) | Brown et al. (2023) | Wang et al. (2018) | Chen et al. (2020) |
|---|---|---|---|---|---|---|---|---|
| Data preprocessing | Standardization | ✓ | X | ✓ | X | X | X | X |
| Normalization | X | ✓ | X | X | X | ✓ | ✓ | |
| Discretization | X | X | X | X | X | X | X | |
| Key factors analyzed | Slope height | X | X | X | ✓ | X | X | X |
| Joint friction angle | X | X | X | X | X | X | X | |
| Joint cohesion | X | X | X | X | X | X | X | |
| Bench width | X | X | X | X | X | X | X | |
| Bench height | X | X | X | X | X | X | X | |
| Slope angle | ✓ | X | X | X | X | X | X | |
| Machine learning models | K-NN | X | X | X | X | X | X | X |
| Decision tree (DT) | X | X | X | ✓ | X | X | X | |
| Random forest (RF) | ✓ | X | ✓ | X | X | ✓ | ✓ | |
| Support vector machine (SVM) | ✓ | ✓ | X | ✓ | X | X | X | |
| Bagging | ✓ | X | X | ✓ | X | X | ✓ | |
| Boosting | ✓ | X | X | X | X | X | ✓ | |
| Dimensionality reduction | Kernel PCA | ✓ | X | X | X | X | X | X |
| PCA | X | ✓ | X | X | ✓ | ✗ | X | |
| LDA | X | X | X | X | X | ✓ | X | |
| t-SNE | X | X | X | X | X | X | ✓ | |
| Classification accuracy ensemble models like bagging and boosting | >90% | X | X | X | X | X | X | ✓ |
 85% 85% |
X | ✓ | X | X | X | X | X | |
 83% 83% |
X | X | ✓ | X | X | X | X | |
| Regression performance | Bagging | ✓ | X | X | X | X | X | X |
| Lasso-Lars CV | ✓ | X | X | X | X | X | X | |
| RMSE < 0.6 | X | X | X | X | X | ✓ | ✓ | |
 > 0.85 > 0.85 |
X | X | X | X | X | X | ✓ | |
| Ensemble learning | Bagging | ✓ | X | X | ✓ | X | X | ✓ |
| Boosting | ✓ | X | X | X | X | X | ✓ | |
| Dimension reduction impact | Necessary | X | ✓ | X | X | X | X | X |
| Unnecessary | ✓ | X | X | X | X | X | X | |
| Key insights | Slope height significant | ✓ | X | X | X | X | X | X |
| Soil cohesion | X | ✓ | X | X | X | X | X | |
| Slope gradient | X | X | ✓ | X | X | X | X | |
| Novelty | Ensemble & regression integration | ✓ | X | X | X | X | X | X |
| RF adaptability | X | ✓ | X | X | X | X | X | |
| ANN for geotechnical prediction | X | X | ✓ | X | X | X | X | |
| XGBoost innovation | X | X | X | X | X | X | ✓ |
Dataset description
Data characteristics
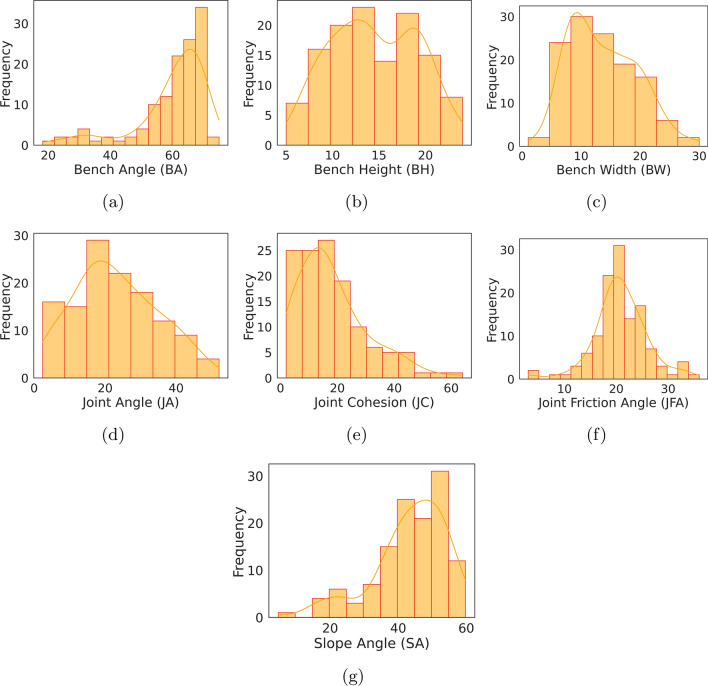
The dataset under consideration consists of seven distinct characteristics: Bench Angle (BA), Bench Height (BH), Bench Width (BW), Slope Angle (SA), Joint Angle (JA), Joint Cohesiveness (JC), and Joint Friction Angle (JFA) as shown in Table 3. The following GitHub link Source Link: https://github.com/swarupchatt/Slope-Stability-Analysis/tree/main provides the source code and data sets under consideration. The mean, median, lowest, highest, and standard deviation values of each feature are examined in this section to ascertain if the data demonstrates a skewed distribution or not. We analyse each attribute or features individually due to their distinct units and interpretations. From Table 3 it can be clearly noticed that the minimum, maximum, mean, standard deviation of the factor Joint Friction Angle (JFA) are 3, 36, 20.84, and 5.15 respectively. This suggests that these factors clearly follows a normal distribution as shown in Fig. 2f. A similar kind of normal distribution (Fig. 2c) was also observed for the factor Bench Width (BW), where the minimum, maximum, mean, and standard deviation are 1.03, 30, 13.66, and 5.69, respectively, as given in Table 3. Conversely, however, for the factor Banch Angle (BA), the minimum, maximum, mean, median, and standard deviation are 18.2, 75, 59.89, 63, and 11.52, respectively, indicating that this factor follows a relatively serious left-skewed distribution as shown in Fig. 2a. A similar observation, i.e., a left-skewed distribution, was also observed for the factor slope angle (SA), as depicted in Fig. 2g. The minimum, maximum, mean, median, and standard deviation values of the Joint Cohesion (JC), as given in Table 3 are 2, 64, 18.14, 15, and 12.45, respectively. These values suggest that the distribution of JC is significantly rightly skewed. We also observed similar observations, i.e., a rightly skewed distribution as shown in Fig. 2d, for the factor Joint Angle (JA), where the minimum, maximum, mean, median, and standard deviation values were 2.4, 52.1, 23.11, 22.0, and 11.75, respectively. The factor Bench Height (BH), with minimum and maximum values of 5 and 24, and a standard deviation of 4.61, exhibits the double peak distribution characteristic as clearly seen in Fig. 2b.
Table 3.
Statistical summary of input features of the data.
| Characteristics | BA | BH | BW | SA | JA | JC |  |
|---|---|---|---|---|---|---|---|
| Mean | 59.89 | 14.49 | 13.66 | 43.41 | 23.11 | 18.14 | 20.84 |
| Standard deviation | 11.52 | 4.61 | 5.69 | 10.89 | 11.75 | 12.45 | 5.15 |
| Minimum | 18.2 | 5.0 | 1.03 | 4.74 | 2.4 | 2.0 | 3.0 |
| Quantile (25%) | 58.0 | 10.7 | 9.1 | 38.46 | 14.9 | 9.0 | 18.3 |
| Quantile (50%) | 63.0 | 14.1 | 12.5 | 45.4 | 22.0 | 15.0 | 20.6 |
| Quantile (75%) | 68.0 | 18.7 | 18.4 | 51.39 | 32.0 | 24.0 | 23.7 |
| Maximum | 75.0 | 24.0 | 30.0 | 59.74 | 52.1 | 64.0 | 36.0 |
BA, BH, BW, SA, JA, JC and JFA stands for bench angle, bench height, bench width, slope angle, joint angle, joint cohesion and joint friction angle respectively
Fig. 2.
Frequency distribution plots of individual influencing factors viz. BA, BH, BW, JA, JC, JFA, and SA with respect to its factor of safety or stability.
Figure 2 depicts the distribution of seven individual components, features, or influential factors (viz. Bench Angle (BA), Bench Height (BH), Bench Width (BW), Slope Angle (SA), Joint Angle (JA), Joint Cohesiveness (JC), and Joint Friction Angle (JFA)) that were considered in our data set. It provides insights into the distribution and characteristics of each influential factor in the dataset. This knowledge is indispensable for making informed decisions throughout the modeling process. Figure 2 reveals three distinct distribution features: symmetric, left-skewed, and right-skewed. These patterns have varied implications for modeling or predicting the factor of safety or stability. Figure 2 clearly shows a left-skewed frequency distribution of Bench Angle (BA) and Slope Angle (SA), with the tail of the distribution extending to the left. Therefore, most of the data points concentrate on the higher values of the BA and SA. The extreme tail values on the left cause the mean values of BA and SA, which are 59.89 and 43.41 in those left-skewed distributions, to decrease. As a result, the median, which is 63 for BA and 45.4 for SA, more accurately represents the central value than the mean. On the other hand, bench width (BW), joint angle (JA), and joint cohesion (JC) follow a right-skewed frequency distribution, with the tail of the distribution extending to the right. Therefore, most of the data points concentrate on the lower values of the BW, JA, and JC. The tail on the right indicates rare but significant high values, which can represent influential factors in BW, JA, and JC. In this case, the mean values of BW, JA, and JC, which are 13.6, 23.11, and 18.14, respectively, exceed the median values of 12.5, 22.0, and 15.0 as clearly depicted in Table 3. This is due to the upward pull of the higher values in the tail. Here also the median, i.e., 12.5 for BW, 22.0 for JA, and 15.0 for JC, a more accurate representation of the central value than the mean. In the case of the influential factors BH and JFA, we have observed symmetric distributions, where the mean and median are very close. In the case of BH, the values are 14.49 and 14.1, and in the case of JFA, the mean and median values are 20.8 and 20.6, as clearly given in Table 3. The presence of such symmetric influential factors ensures the optimality of the proposed models without significant bias or inefficiency. The pictorial representation of the comprehensive prediction model, incorporating all influential factors, is provided in Fig. 3
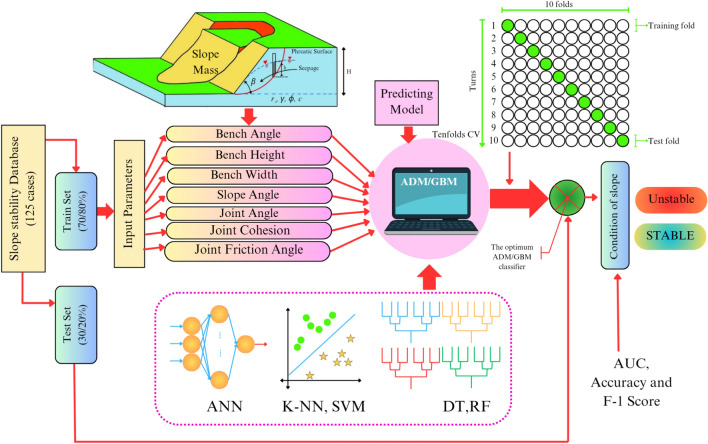
Fig. 3.
Diagnostic model of prediction of the circular slope stability state using ABM/GBM method.
Correlation analysis
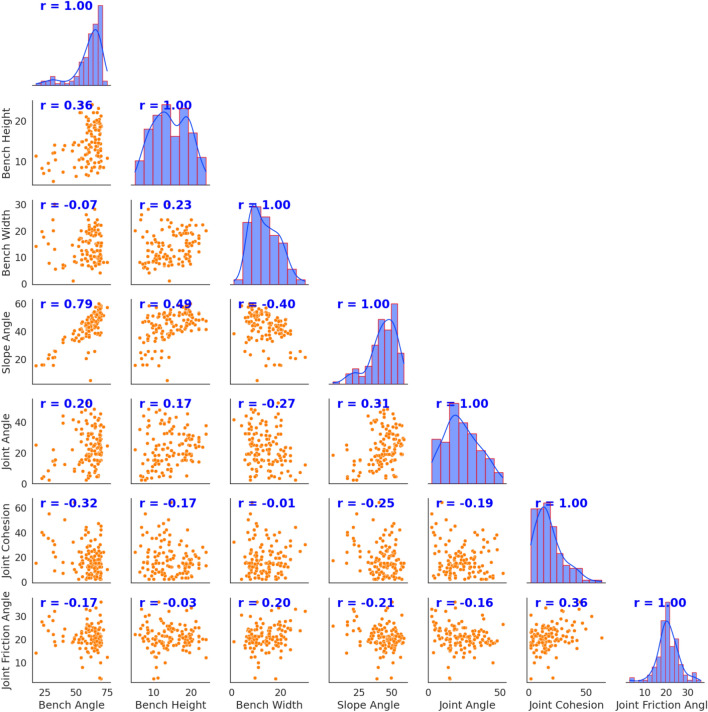
An analysis of the correlation between the five factors, features, or variables is necessary before predicting or evaluating the stability of slopes. A strong connection between the factors could have a detrimental effect on the prediction models’ accuracy, producing false results that defy reality. The correlation matrix is an indispensable tool for identifying and addressing multicollinearity for selecting relevant features, and ensuring the stability and interpretability of classification and regression models. By understanding relationships between independent variables, or multicollinearity, we can improve model performance, simplify computations, and gain valuable insights from the dataset. Figure 4 depicts the pairwise correlation between seven independent influential factors, viz. BA, BH, BW, SA, JA, JC, and JFA. Figure 4 also clearly demonstrates that the diagonal subfigures represent the correlation among themselves or the frequency distribution of the seven influential factors. The subfigures below the main diagonal represent the scatter plot of pairwise correlation between seven influential factors along with their Pearson correlation values mentioned in blue color. From Fig. 4, it is clear that none of the pairs except BA and SA crosses the correlation value of 0.5. BH and JFA produce the lowest negative correlation value of 0.03. Figure 4 clearly demonstrates that BW and BA also exhibit minimal dependency, with a correlation value of 0.07. Thus, overall, it is clear that almost all the influential factors are independent and significant from our regression and classification modeling perspective.
Fig. 4.
Matrix of correlation of variables for each slope instance.
It is also evident from Fig. 4 that there is no substantial or high correlation between any two factors, with the exception of two components, namely the bench angle and the slope angle, which have a correlation of 0.79. The pairwise correlation between other factors except BA and SA is less than 0.5 as clearly seen form Fig. 4, indicating that the factors under consideration are independent and will be effective in predicting safety factors.
To further verify the interaction between pairs of factors in our data set, the authors plotted a scatter diagram for each pair of features and developed a regression model to better analyze the dependency among them. Figure 5 displays six scatter plots depicting the linear relationship between six important pair of factors viz. JFA vs. JA, JFA vs. JC, SA vs. BH, SA vs. JA, SA vs. JC, and SA vs. JFA. The plot shows the linear relationship between the factors and their parameter values, as clearly depicted in Fig. 5. Based on this, it could be concluded that there is no significant correlation between the pair of factors under consideration.
Fig. 5.
Scatter plot of six significant pair-wise factors: JFA vs. JA, JFA vs. JC, SA vs. BH, SA vs. JA, SA vs. JC, and SA vs. JFA. The plot shows the linear relationship between the factors and their parameter values.
Data visualization
The slope data set representing violin plots under investigation are depicted in Fig. 6. These violin plots show the density distribution as well as the highest, median, and lowest values for each input parameter. As plainly illustrated in Fig. 6, the upper and lower quarterlies are indicated by the top and bottom borders of the black bar, respectively, and the median is displayed by the white dot at the center of the violin plots. In particular, the thick black bar stretches the thin black line, which represents the 95 percent confidence interval. It is also possible to determine the data density at any given point by observing the shape of the violin plots. People have suggested that the data density increases in proportion to the width. For example, in Fig. 6, it is clear that the bench height (BH) has a higher data density compared to the bench angle (BA).
Fig. 6.
Violin plots of individual influencing factors with respect to its factor of safety or stability.
Dimensionality reduction
It is not easy to explicitly discern the distinctions between the samples of data under consideration. This is because the data contains a variety of factors or features. Therefore, it is important to represent the data in a smaller size and present it in a space with only two dimensions for better visualisation and clarity of the data. In order to do that, the dimensions or features must be reduced by applying dimensionality reduction techniques to the entire data set. The authors therefore broadly categorised the classic dimension reduction methods into two groups: those that employ linear mapping, such as Linear Discriminant Analysis (LDA) and Principal Component Analysis (PCA) etc, and those that employ non-linear mapping, such as Kernel Principal Component Analysis (KPCA), t-distributed stochastic neighbor embedding (TSNE), ISOMAP and Multidimensional Scaling (MDS), etc. To reduce the dimensions to 2, the authors have used six dimensionality reduction methods, namely KPCA, LLE, MDS, SE, ISOMAP, and TSNE. Figure 7 shows that the reduced dimension clearly distinguishes the fos or stability in the case of KPCA, ISOMAP, MDS, TSNE, and SE, except for the method LLE. KPCA and MDS perform better than the others in terms of better visualization and producing distinguishable data boundaries, as clearly seen in Fig. 7. LLE is the worst performer among all the reduction techniques under consideration.
Fig. 7.
Reduced two dimension plots of all individual influencing factors with respect to its factor of safety or stability.
Methodologies
The proposed framework consists of two parts: the regression and classification frameworks. In the regression framework, we are taking continuous values for FOS and modeling this with respect to twelve ML regression models. On the other hand, in the classification framework, we are binarizing the FOS value by thresholding it and converting it into a binary class classification problem. We then model this stability or FOS using both standard and ensemble machine learning (ML) models. Finally, calculate the performance measure for both the regression and classification frameworks and justify the models for stability analysis. This article contains 125 samples and discusses the associated seven factors or features for slope stability data, as described in Section “Dataset description”. These data sets provide two sorts of analysis. The first type of analysis is classification analysis, which entails applying a threshold to the slope stability or factor of safety value. We assign a value of one, called stable, to values above the threshold, and a value of zero, called failure, to values below the threshold. Empirically we determine the threshold value of slope stability or factor of safety is 1.3. The second study involves doing a regression analysis to determine the relationship between slope stability values and the components provided in the dataset. The following subsections will discuss the various classification and regression models of ML studied in this article.
ML techniques
Regression methods
By fitting a linear equation to the observed data, the basic statistical method known as linear regression explains the relationship between a dependent variable and one or multiple independent variables. In order to enable us to generate predictions based on the input values, it seeks to determine the best fit line that explains the connection among the factors. Here the target or dependent variable y is expected to be a linear combination of the independent variables or characteristics. The simple linear regression model is commonly expressed mathematically as:
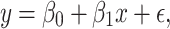 |
In the above equation, x is the independent variable,  is the predicted value of the dependent variable y,
is the predicted value of the dependent variable y, 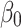 and
and 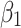 are the intercept and the slope of the line respectively, and
are the intercept and the slope of the line respectively, and 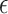 indicates the error term. Consequently, the following is the generic equation for multiple linear regression:
indicates the error term. Consequently, the following is the generic equation for multiple linear regression:
 |
where 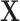 is matrix of independent variables,
is matrix of independent variables,  is the vector of dependent variables,
is the vector of dependent variables,  is a coefficient vector, and
is a coefficient vector, and 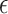 is the error vector. To estimate the coefficients or parameters
is the error vector. To estimate the coefficients or parameters  we need to minimize the following regularized cost function:
we need to minimize the following regularized cost function:
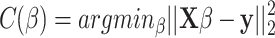 |
By placing a penalty on the magnitude of the coefficients, the Ridge Regression Model was created to address the co-linearity issues with Simple Linear Regression. The following regularized cost function or a penalized residual sum of squares is minimized by the ridge coefficients:
 |
where  is a regularization parameter that controls the shrinkage amount. The amount of shrinkage increases with increasing
is a regularization parameter that controls the shrinkage amount. The amount of shrinkage increases with increasing 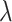 value, making the coefficients more resilient to col-linearity. Lasso, or the least absolute shrinkage and selection operator, has been presented as a way to increase prediction accuracy even further. It does this by doing regularization as well as variable selection. It is mathematically equivalent to a linear model with a regularization factor added. The following is the objective function to be minimized:
value, making the coefficients more resilient to col-linearity. Lasso, or the least absolute shrinkage and selection operator, has been presented as a way to increase prediction accuracy even further. It does this by doing regularization as well as variable selection. It is mathematically equivalent to a linear model with a regularization factor added. The following is the objective function to be minimized:
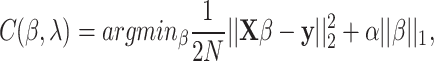 |
where  is the
is the 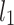 -norm of the coefficient vector
-norm of the coefficient vector 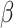 , N is the total number of samples, and
, N is the total number of samples, and 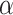 is a constant. ElasticNet is a linear regression model trained with both
is a constant. ElasticNet is a linear regression model trained with both 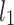 and
and 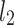 -norm regularization of the coefficients. Because it enables Elastic-Net to inherit some of Ridge’s stability under rotation, ENR offers the advantages of both lasso regression and ridge regression models. The following is the objective function to be minimized:
-norm regularization of the coefficients. Because it enables Elastic-Net to inherit some of Ridge’s stability under rotation, ENR offers the advantages of both lasso regression and ridge regression models. The following is the objective function to be minimized:
 |
K-nearest neighbours (K-NN)
The k-nearest neighbours (K-NN) technique is a straightforward and efficient supervised machine learning approach that is applicable to both classification and regression tasks. The algorithm retains all the training data points in memory. The method initially determines how far apart a new data point is from all of the training data points in order to forecast its class (in classification) or value (in regression). The algorithm then identifies the kth nearest data points (neighbours) to the new data point based on the computed distance values. We can use the Euclidean distance or other distances like the 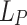 norm distance or Minkowski distance function to compute the distance values between pair of points. The selection of the k value will greatly affect the output outcomes. Practical applications typically use cross validation techniques to determine the optimal k value.
norm distance or Minkowski distance function to compute the distance values between pair of points. The selection of the k value will greatly affect the output outcomes. Practical applications typically use cross validation techniques to determine the optimal k value.
Support vector machine (SVM)
For a linearly separable binary class classification problem with n d-dimensional training data samples  , where
, where 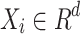 and
and  , the linear SVM aims to find the optimal d-dimensional hyperplane that separates the two classes with the maximum margin. Now, all hyperplane in
, the linear SVM aims to find the optimal d-dimensional hyperplane that separates the two classes with the maximum margin. Now, all hyperplane in  are parameterized by a constant (b), and a vector (W), and stated in the equation:
are parameterized by a constant (b), and a vector (W), and stated in the equation:
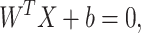 |
The decision rule for classification is given by the function
 |
Therefore, in case of the hard margin linear SVM problem, we need to optimize the following objective function:
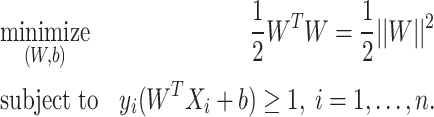 |
Similar to SVM, Support Vcetor Regression (SVR) tries to maximize the margin between the actual values and the predicted values. However, in SVR, the margin is defined as a tube around the regression line rather than a boundary between classes. SVR introduces an epsilon insensitive loss function, which allows some errors within a certain range (epsilon) to be ignored. SVR minimizes the following objective function:
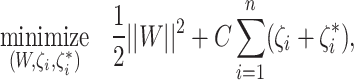 |
where  and
and 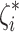 are slack variables that measure the deviation of the prediction from the real value for each data point and C is the regularization parameter. To convert the input features into a higher-dimensional space, SVR employs a kernel function. By using this transformation, SVR is able to ascertain a nonlinear correlation between the target variable and the input features.
are slack variables that measure the deviation of the prediction from the real value for each data point and C is the regularization parameter. To convert the input features into a higher-dimensional space, SVR employs a kernel function. By using this transformation, SVR is able to ascertain a nonlinear correlation between the target variable and the input features.
Classification and regression trees (CART)
A decision tree (DT) or classification tree is a type of tree data structure that consists of directed edges and nodes. There are two varieties of nodes—branch nodes and leaf nodes. A decision is symbolized by each node in a DT, which is a hierarchical structure built up of feature values. The method picks the feature at each node that divides the data the best according to a given criterion (e.g., Gini impurity, entropy, information gain). The data is incrementally divided into subsets according to the selected feature and its threshold until a stopping condition-such as the maximum tree depth or the minimum number of samples per leaf-is satisfied. The regression tree algorithm, like classification trees, chooses the feature and threshold at each node that best splits the data to minimize some measure of error (e.g., mean squared error). Up until a halting condition is satisfied, it iteratively divides the data into subgroups according to the selected feature and threshold.
Random forest (RF)
A random forest classifier consists of a set of tree-structured classifiers 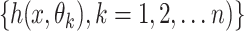 , where n denotes the number of classification trees or DT and
, where n denotes the number of classification trees or DT and  are independent, identically distributed random vectors. Each tree casts a unit vote for the most popular class at input vector x. The mean value of each DT is employed as the regression predicting value in this ensemble learning technique:
are independent, identically distributed random vectors. Each tree casts a unit vote for the most popular class at input vector x. The mean value of each DT is employed as the regression predicting value in this ensemble learning technique:
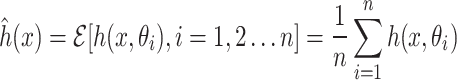 |
The RF algorithm enhances the robustness and accuracy of the model in comparison to individual decision trees. The RF algorithm achieves this by integrating the predictions of several different decision trees. This strategy not only efficiently addresses the over-fitting problem but also performs admirably with high-dimensional data and large dataset examples.
Ensemble learning models
An ensemble is a collection of classifiers that learn a target function; the classifiers may be distinct algorithms, various settings for the same algorithm, or the same algorithm on multiple dataset samples. We then aggregate the classifiers’ individual predictions to classify an unknown sample. Ensembles, in general, improve the performance of a collection of individual models in terms of generalization within a domain. Voting or averaging the predictions of several pre-trained models is the basic ensemble method. Consequently, train the same model repeatedly on various data sets rather than training distinct models on the same data, and then “combine” these “different” models13,62.
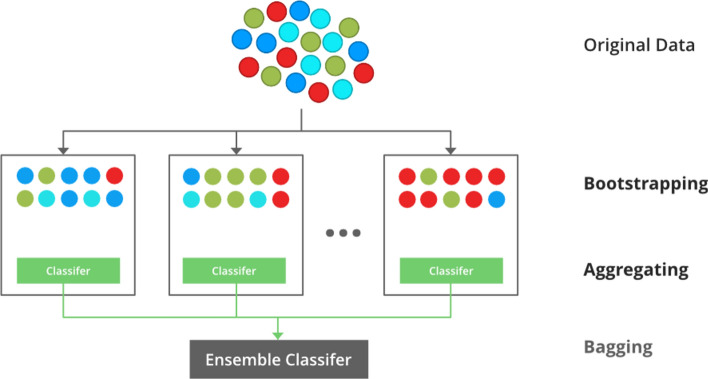
Bagging
Bagging is a popular ensemble learning approach which stands for Bootstrap Aggregating. Consider a data set  having n training examples. Then we have to create M copies
having n training examples. Then we have to create M copies 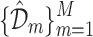 of the training data set
of the training data set  . each
. each 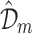 is generated from
is generated from  by sampling with replacement. Each data set
by sampling with replacement. Each data set  contain same number of training samples. Then we have to train m models
contain same number of training samples. Then we have to train m models 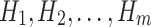 using
using 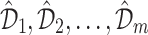 respectively. Finally use the model
respectively. Finally use the model  as the final prediction model for bagging (Fig. 8).
as the final prediction model for bagging (Fig. 8).
Fig. 8.
Flow diagram of Bagging (Bootstrap Aggregating) ensemble classifier.
Boosting
Combining several basic classifiers into one that performs noticeably better than any one of the base classifiers individually is known as “boosting.” For inexperienced students, it is sequential training. In this scenario, we train each base classifier using data weighted by the previous classifier’s performance, and each classifier casts a vote to determine the final prediction or outcome. In other words, adaptively altering the training data distribution iteratively requires focusing (in each iteration) on previously misclassified training examples. Adaboost (adaptive boosting) and Graidient are two important boosting algorithms.
AdaBoost works by iteratively training weak classifiers, adjusting instance weights to focus on misclassified instances, and combining these classifiers into a strong final classifier. Each weak learner is weighted based on its accuracy, and the final model is a weighted majority vote of these learners.
Gradient Boosting is a potent machine learning method that progressively assembles a group of weak learners, usually decision trees. It iteratively fits weak learners to the residuals of the current model to minimize a specified loss function. It combines these learners into a strong predictive model. The steps involve computing residuals, fitting a weak learner, determining the optimal step size, and updating the model.
Performance measures
Classification performance measures
The standard assessment metrics for the classification model consist of accuracy, precision, recall, F-measure, and the area under the curve (AUC) value. In our experimental case of the two-class classification problem based on FOS. Moreover, based on the actual and anticipated results, we may construct a confusion matrix with true positive (TP), false positive (FP), true negative (TN), and false negative (FN) entries63. Then the assessment metrics are defined as follows:
 |
The receiver operating characteristic (ROC) curve can be obtained by viewing FPR as the horizontal axis and TPR as the vertical axis. The area beneath the ROC curve, or AUC value, is what we use to compare the relative efficacy of two prediction models. A higher AUC value indicates better performance from a model.
Regression performance measures
We employ the Mean Squared Error (MSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), Median Absolute Error (MeAE), Mean Poisson Deviation (MPD), and coefficient of determination (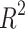 ) to evaluate the regression model’s predictive efficacy. The average of the expected and actual values is known as the MAE. The more efficiently the modification is made, the closer the MAE is to 0, suggesting that the prediction model more accurately captures the set of training data. The mean of the squares between the actual and expected values is known as the MSE. The following are the MAE and MSE formulae.
) to evaluate the regression model’s predictive efficacy. The average of the expected and actual values is known as the MAE. The more efficiently the modification is made, the closer the MAE is to 0, suggesting that the prediction model more accurately captures the set of training data. The mean of the squares between the actual and expected values is known as the MSE. The following are the MAE and MSE formulae.
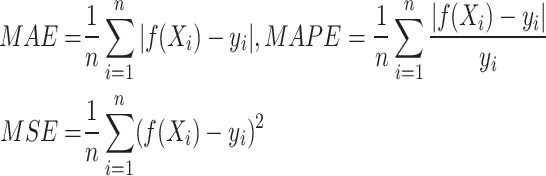 |
where n is the number of training data sets, 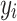 is the actual value of the test data set,
is the actual value of the test data set, 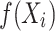 is the predicted value of the test data set.
is the predicted value of the test data set. 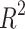 is the coefficient of determination indicating the degree of matching between the regression model and the target variable defined as:
is the coefficient of determination indicating the degree of matching between the regression model and the target variable defined as:
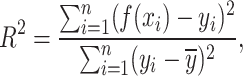 |
where  is the mean of the test dataset. In general, the more closely
is the mean of the test dataset. In general, the more closely 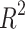 approaches 1, the more favorable the imitation impact of the regression model is for the target variables.
approaches 1, the more favorable the imitation impact of the regression model is for the target variables.
Experimental results
The performance of several ML models under diverse experimental configurations is compiled in Tables 4, 5, and 6. We assessed ensemble models like bagging and boosting as well as common machine learning models like K-NN, SVM, DT, and RF. Table 4 shows that a 70:30 split of the data was used to train and test the models using all seven independent components. To ensure a thorough assessment, performance criteria including precision, recall, F-measure, AUC score, and cross-validation measures were incorporated. Results from a similar investigation are shown in Table 5, although models were trained on 80 percent of the data and evaluated on the remaining 20 percent. Table 6 examines how well six ML models perform when applied to data that has been reduced to four dimensions using KPCA. With a 70:30 data split, the evaluation was conducted in the same manner as Tables 4 and 5. Our results were subsequently validated using a 10-fold cross-validation (CV), which yielded reliable performance metrics for the slope prediction challenge. This thorough examination guarantees a comprehensive comprehension of the models’ efficacy in many contexts. The values of precision, recall, F-measure, accuracy, CV score, and AUC score are depicted in Tables 4 and 5. From the accuracy point of view, with an accuracy of 92%, RF has the best prediction performance followed by the performance of DT, bagging using RF, and boosting using base classifier DT with an average accuracy of 89%. SVM also performs well in prediction, with an average accuracy value of 84%. In terms of F-measure, it also observed that RF with Gini and Entropy as its splitting measures provided the best performance, having a value of 92%, followed by the performances of DT, bagging, and boosting methods. K-NN, SVM with a polynomial kernel, and Boosting with base classifier SVM perform poorly as compared to others. SVM with a polynomial kernel performs worst with an average value of F-measure of 69% as clearly seen from Table 4. Cross-validation (CV), on the other hand, is an important measure of performance for a classification task. The authors performed here a 10-fold cross-validation, and the corresponding CV score was depicted in Table 4. In terms of CV score, it is clear that bagging with base classifier DT performed best with a CV score of 90%, followed by boosting with RF with a score of 89%. RF also performed well as compared to DT, SVM, and K-NN, with a score of 88%. SVM with a polynomial kernel performed worst in this case, as does K-NN. The performance values of six different types of competitive classification models are shown in Table 5. All features were taken into account, and the training-to-testing ratio was 80:20. Here it was clear that bagging with base classifier DT performed best compared to others in terms of F-measure and accuracy value of 96%. This model consistently outperformed other baseline classification techniques, such as SVM, DT, and K-NN, with an average improvement of 8–10% in accuracy value. A similar type of improvement is also seen for other performance measures such as precision, recall, AUC score, and CV score, as clearly seen from the Table 5. In terms of CV score, RF with splitting criterion gini performed best with a value of 91% compared to others. In terms of AUC score, bagging with DT also outperformed the others. Boosting and SVM with a polynomial kernel perform the worst, achieving CV scores of 75% and 76%, respectively, as clearly depicted in Table 5.
Table 4.
Quantitative values of performance measures such as Precision, Recall, F-measure, Accuracy, AUC score, and CV score of various ML classification models, viz. K-NN, SVM, DT, RF, Bagging, and Boosting models, by considering all features with a training and testing data ratio of 70:30.
| ML models | Performance measures | ||||||
|---|---|---|---|---|---|---|---|
| Precision | Recall | F-measure | Accuracy | AUC Score | CV-score | ||
| All features [Train:Test=70:30] | K-NN(K=3) | 0.7811 | 0.7694 | 0.7616 | 0.7631 | 0.7694 | 0.8096 |
| K-NN (K = 5) | 0.8184 | 0.7972 | 0.7871 | 0.7894 | 0.7972 | 0.8153 | |
| SVM (Linear) | 0.8551 | 0.8472 | 0.8416 | 0.8421 | 0.8472 | 0.8641 | |
| SVM (Poly) | 0.8103 | 0.7250 | 0.6933 | 0.7105 | 0.7250 | 0.7653 | |
| DT(Entropy) | 0.8972 | 0.8972 | 0.8947 | 0.8947 | 0.8972 | 0.8339 | |
| DT (Gini) | 0.8753 | 0.8722 | 0.8683 | 0.8684 | 0.8722 | 0.8185 | |
| RF (Entropy) | 0.9210 | 0.9222 | 0.9209 | 0.9210 | 0.9222 | 0.8724 | |
| RF (Gini) | 0.9210 | 0.9222 | 0.9209 | 0.9210 | 0.9222 | 0.8878 | |
| Bagging (DT) | 0.8972 | 0.8972 | 0.8947 | 0.8947 | 0.8972 | 0.9038 | |
| Bagging (RF) | 0.8972 | 0.8972 | 0.8947 | 0.8947 | 0.8972 | 0.8884 | |
| Bagging (SVM) | 0.8551 | 0.8472 | 0.8416 | 0.8421 | 0.8472 | 0.8724 | |
| Boosting (DT) | 0.8972 | 0.8972 | 0.8947 | 0.8947 | 0.8972 | 0.8557 | |
| Boosting (RF) | 0.8551 | 0.8472 | 0.8416 | 0.8421 | 0.8472 | 0.8961 | |
| Boosting (SVM) | 0.8184 | 0.7972 | 0.7871 | 0.7894 | 0.7972 | 0.8410 | |
Table 5.
Quantitative values of performance measures such as Precision, Recall, F-measure, Accuracy, AUC score, and CV score of various ML classification models, viz. K-NN, SVM, DT, RF, Bagging, and Boosting models, by considering all features with a training and testing data ratio of 80:20.
| ML models | Performance measures | ||||||
|---|---|---|---|---|---|---|---|
| Precision | Recall | F-measure | Accuracy | AUC score | CV score | ||
| All features [Train:Test=80:20] | K-NN (K = 3) | 0.8733 | 0.8833 | 0.8767 | 0.8800 | 0.7824 | 0.8096 |
| K-NN (K = 5) | 0.8506 | 0.8270 | 0.8333 | 0.8400 | 0.8081 | 0.8153 | |
| SVM (Linear) | 0.8506 | 0.8279 | 0.8333 | 0.8400 | 0.8279 | 0.8641 | |
| SVM (Poly) | 0.9117 | 0.8636 | 0.8726 | 0.8800 | 0.8636 | 0.7653 | |
| DT (Entropy) | 0.8506 | 0.8279 | 0.8333 | 0.8400 | 0.8279 | 0.8493 | |
| DT (Gini) | 0.8474 | 0.8429 | 0.8397 | 0.8400 | 0.8429 | 0.8339 | |
| RF (Entropy) | 0.875 | 0.8461 | 0.8376 | 0.8400 | 0.8461 | 0.9038 | |
| RF (Gini) | 0.9198 | 0.9198 | 0.9198 | 0.9200 | 0.9198 | 0.9121 | |
| Bagging (DT) | 0.9615 | 0.9615 | 0.9600 | 0.9600 | 0.9615 | 0.8889 | |
| Bagging (RF) | 0.9198 | 0.9198 | 0.9198 | 0.9200 | 0.9198 | 0.8967 | |
| Bagging (SVM) | 0.8506 | 0.8279 | 0.8333 | 0.8400 | 0.8279 | 0.8647 | |
| Boosting (DT) | 0.8814 | 0.8814 | 0.8799 | 0.8800 | 0.8814 | 0.8423 | |
| Boosting (RF) | 0.9166 | 0.9333 | 0.9188 | 0.9200 | 0.9333 | 0.8955 | |
| Boosting (SVM) | 0.8947 | 0.8000 | 0.8161 | 0.8400 | 0.8000 | 0.7589 | |
Table 6.
Quantitative values of performance measures such as Precision, Recall, F-measure, Accuracy, AUC score, and CV score of various ML classification models, viz. K-NN, SVM, DT, RF, Bagging, and Boosting models, by considering reduced set of four features using KPCA with a training and testing data ratio of 70:30.
| ML models | Performance measures | ||||||
|---|---|---|---|---|---|---|---|
| Precision | Recall | F-measure | Accuracy | AUC score | CV score | ||
| Reduced features using KPCA [Train:Test=70:30] | K-NN(K=3) | 0.7698 | 0.7631 | 0.7616 | 0.7631 | 0.7631 | 0.8012 |
| K-NN (K = 5) | 0.8230 | 0.7982 | 0.8048 | 0.8157 | 0.7982 | 0.7769 | |
| SVM (Linear) | 0.8621 | 0.8210 | 0.8303 | 0.8421 | 0.8210 | 0.8102 | |
| SVM (Poly) | 0.8448 | 0.7500 | 0.7414 | 0.7631 | 0.7500 | 0.7179 | |
| DT (Entropy) | 0.8361 | 0.8601 | 0.8380 | 0.8421 | 0.8601 | 0.7288 | |
| DT (Gini) | 0.7738 | 0.7738 | 0.7738 | 0.7894 | 0.7738 | 0.8173 | |
| RF (Entropy) | 0.8585 | 0.8809 | 0.8637 | 0.8684 | 0.8809 | 0.8403 | |
| RF (Gini) | 0.8585 | 0.8809 | 0.8637 | 0.8684 | 0.8809 | 0.8012 | |
| Bagging (DT) | 0.8585 | 0.8809 | 0.8637 | 0.8684 | 0.8809 | 0.8416 | |
| Bagging (RF) | 0.8295 | 0.8452 | 0.8347 | 0.8421 | 0.8452 | 0.8487 | |
| Bagging (SVM) | 0.8277 | 0.8323 | 0.8156 | 0.8157 | 0.8323 | 0.8025 | |
| Boosting (DT) | 0.8380 | 0.8380 | 0.8380 | 0.8421 | 0.8380 | 0.7762 | |
| Boosting (RF) | 0.8681 | 0.8607 | 0.8637 | 0.8684 | 0.8607 | 0.8166 | |
| Boosting (SVM) | 0.8750 | 0.7142 | 0.7285 | 0.7894 | 0.7142 | 0.6698 | |
The slope stability prediction models’ performance metrics have been compared and examined before and after dimension reductions in order to further corroborate the models’ accuracy and dependability. From Table 6, it is clear that the prediction model with dimension reduction reduces the accuracy level. The prediction models of six different types of machine learning algorithms using the KPCA reduction technology with training and testing ratio of 70:30 are shown in Table 6. Through comparison, it was found that the Random Forest algorithm, which incorporated the splitting criterion indices Gini and Entropy, along with the boosting algorithm using base classifier RF, performed more effectively with the accuracy near to 87% in processing slope stability predictions. They provide an average improvement of the average accuracy value of 6–8% compared to the baseline classifiers. In terms of CV score it is clear from Table 6 that the bagging algorithm with base classifier RF outperformed the other machine learning algorithms with a value of nearly 85%. SVM with a polynomial kernel and DT with splitting criteria for entropy performed the worst in this case as compared to other models. Bagging with DT and RF achieved the best AUC score of 88%. In contrast, boosting with base classifier SVM performed the worst, with an AUC score of 71%, as evident from Table 6.
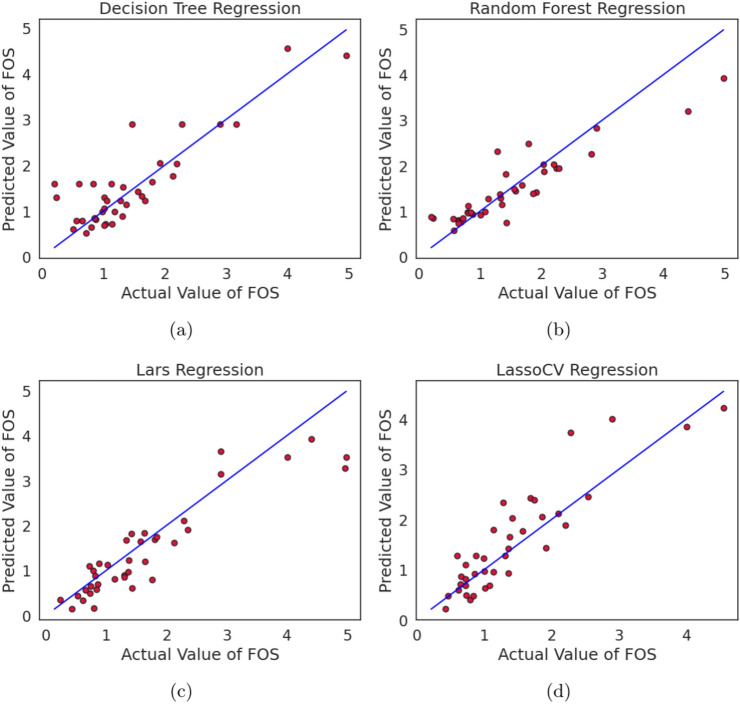
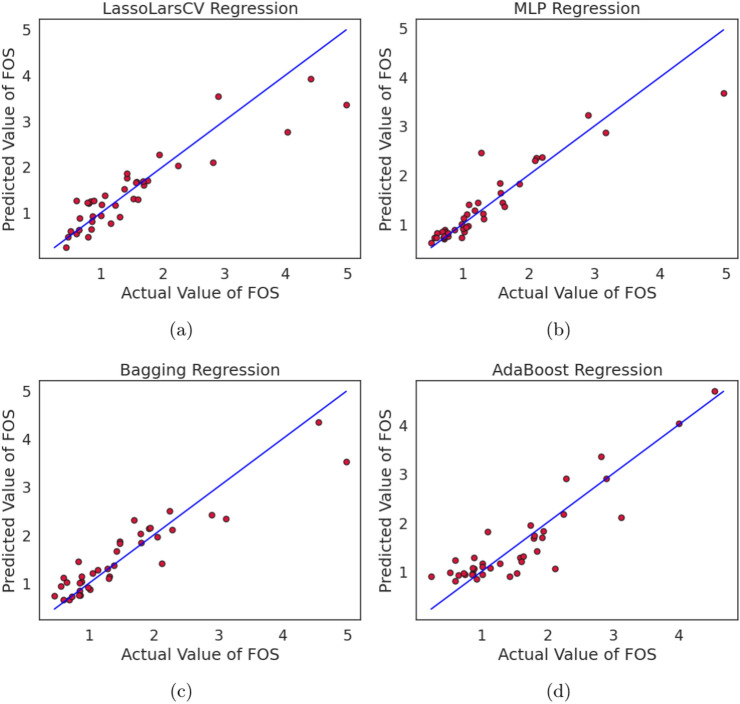
Figures 9, 10, and 11 illustrate the plots of actual and predicted FOS values after running twelve ML regression techniques over the data sets related to Table 5. These techniques include linear, Bayes Ridge, elastic net, support vector, decision tree, random forest, LARS, LassoCV, LassoLarsCV, multi-layer perceptron, bagging, and Adaboost regressions. In the figures, it is clear that all the plotted red points are closer to the diagonal blue line except one, which represents the degree of performance of different ML regression techniques. The dotted red points more closer to the diagonal blue line means better performance of the respective regression methods. We also verify this fact by computing different regression measures, viz. MSE, MAE, MAPE, MeAE, MPD, and R2, as illustrated in Table 5. Alternatively we can say that Figs. 9, 10 and 11 display a comparison of all ML regression algorithms’ performances. In this paper 10-fold CV was used with training and testing ratios of 70:30 to optimise the parameters of each algorithm. The authors considered twelve different regression techniques to analyse the slope stability prediction problems. It is clear from Figs. 9, 10, and 11 that almost all regression models, except elastic net regression, predict slope stability or FOS correctly. In other words, the scatter plot of the actual and predicted FOS values from all regression models except elastic net follows a more or less linear pattern, as clearly demonstrated in Figs. 9, 10 and 11. Out of twelve algorithms, Bagging, LassolarsCV, RF, and MLP regression models were better compared to others, as clearly seen from Figures 10 and 11. Elastic net regression performed the worst, followed by DT, LassoCV, and Adaboost models. Table 7 shows the quantitative values of performance measures such as MSE, MAE, MAPe, MeAE, MPD, and 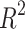 of several competing ML Regression Models. Models’ performance improves when the MSE, MAE, MAPe, MeAE, and MPD values decrease. Conversely, a greater value of the coefficient of determination (
of several competing ML Regression Models. Models’ performance improves when the MSE, MAE, MAPe, MeAE, and MPD values decrease. Conversely, a greater value of the coefficient of determination ( ) indicates superior performance of the regression model. Based on the information provided in Table 7, it is evident that LassoLarsCV and Bagging regression models outperform other competitor regression models in terms of
) indicates superior performance of the regression model. Based on the information provided in Table 7, it is evident that LassoLarsCV and Bagging regression models outperform other competitor regression models in terms of 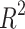 , with an average value of 0.84, indicating strong predictive capability for slope stability or factors of safety. Thus we conclude that the ensemble bagging regression enhances the average
, with an average value of 0.84, indicating strong predictive capability for slope stability or factors of safety. Thus we conclude that the ensemble bagging regression enhances the average  value by 8-10% relative to the conventional base regression models such as Linear, Bayes Ridge, SVR, DT, LassoCV, and Lars employed in this study. A similar type of improvement is also seen for other regression performance measures such as MSE, MAE, MAPE, MeAE, and MPD, as clearly evident from Table 7. The MLP and RF regression models exhibit superior performance compared to linear, Bayes Ridge, Elastic Net, Lars, Adaboost, and Lasso-Lars regression models, making them very competitive alternatives. The elastic net performed the poorest in terms of all the measurements, as evidenced by Table 7.
value by 8-10% relative to the conventional base regression models such as Linear, Bayes Ridge, SVR, DT, LassoCV, and Lars employed in this study. A similar type of improvement is also seen for other regression performance measures such as MSE, MAE, MAPE, MeAE, and MPD, as clearly evident from Table 7. The MLP and RF regression models exhibit superior performance compared to linear, Bayes Ridge, Elastic Net, Lars, Adaboost, and Lasso-Lars regression models, making them very competitive alternatives. The elastic net performed the poorest in terms of all the measurements, as evidenced by Table 7.
Fig. 9.
Plot of actual and predicted values FOS using various competitive ML regression models such as: linear, bayes ridge, elastic net, support vector regressions.
Fig. 10.
Plot of actual and predicted values FOS using various competitive ML regression models such as: decision tree, random forest, Lars, LassoCV regressions.
Fig. 11.
Plot of actual and predicted values FOS using various competitive ML regression models such as: LassoLarsCV, multi layer perceptron, bagging, and Adaboost regressions.
Table 7.
Quantitative values of performance measures such as MSE, MAE, MAPe, MeAE, MPD, and 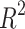 of several competing ML Regression Models viz. Linear, Bayes Ridge, Support Vector, Decision Tree, Random Forest, Lars, LassoCV, LassoLarsCV, Multi Layer Perceptron, Bagging, and Adaboost.
of several competing ML Regression Models viz. Linear, Bayes Ridge, Support Vector, Decision Tree, Random Forest, Lars, LassoCV, LassoLarsCV, Multi Layer Perceptron, Bagging, and Adaboost.
| Regression models | Performance measures | ||||||
|---|---|---|---|---|---|---|---|
| MSE | MAE | MAPE | MeAE | MPD |  |
||
| All features [train:test=70:30] | Linear regression | 0.1834 | 0.3266 | 0.2898 | 0.2674 | 0.1414 | 0.7482 |
| Bayes ridge regression | 0.1517 | 0.2987 | 0.3266 | 0.2284 | 0.1167 | 0.7565 | |
| Elastic net regression | 0.5583 | 0.5457 | 0.5718 | 0.3812 | 0.3333 | 0.1863 | |
| Support vector regression | 0.2019 | 0.2126 | 0.1339 | 0.1227 | 0.0710 | 0.7737 | |
| Decision tree regression | 0.2796 | 0.3374 | 0.2776 | 0.1850 | 0.1459 | 0.7115 | |
| Random forest regression | 0.2538 | 0.3266 | 0.2808 | 0.1981 | 0.1212 | 0.8032 | |
| Lars regression | 0.1918 | 0.3338 | 0.2543 | 0.2490 | 0.1224 | 0.7943 | |
| LassoCV regression | 0.4136 | 0.4489 | 0.3067 | 0.2853 | 0.1810 | 0.7004 | |
| LassoLarsCV regression | 0.1781 | 0.3070 | 0.2536 | 0.2508 | 0.0998 | 0.8412 | |
| MLP regression | 0.1629 | 0.2840 | 0.2187 | 0.1852 | 0.0814 | 0.8364 | |
| Bagging regression | 0.0782 | 0.2060 | 0.1885 | 0.1395 | 0.0580 | 0.8450 | |
| Adaboost regression | 0.2824 | 0.3914 | 0.3385 | 0.2892 | 0.1549 | 0.7461 | |
Sensitivity of parameters
We tested the performance of our standard and ensemble ML learning algorithms by changing their parameters. We then reported the accuracy we achieved with the optimal parameters. In the classification case, we have divided the data set into 70:30 and 80:20 as training and testing data for generating optimized results, as shown in Tables 4 and 5. However, in the regression framework, we only consider 70:30 as the training and testing partition, and we compute the resulting performances as shown in Table 7. We have reported the results corresponding to the optimal values of 3 and 5 for K in the K-nearest neighbor classification model. When it comes to the SVC model, we got results from the 70:30 partition that showed the best kernel function to be linear, as opposed to polynomial and RBF, as clearly seen from Table 4. On the other hand, for the 80:20 partition, SVC with a polynomial kernel provides optimal results compared to linear and RBF kernels. We automatically take the default value of gamma for the SVC model. Tables 4 and 5 make it clear that the optimal results for DT come when we use entropy as the criterion function instead of Gini. Here we have taken the optimal value for the parameter of  as 2. In the case of the RF model, the optimal results happen when Gini is used as a criterion function instead of entropy, as clearly evident from Tables 4 and 5. We set the optimal parameters for
as 2. In the case of the RF model, the optimal results happen when Gini is used as a criterion function instead of entropy, as clearly evident from Tables 4 and 5. We set the optimal parameters for 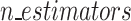 and
and 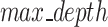 to 100 and 20, respectively. Bagging ensemble models run over three base classifiers, viz. DT, RF, and SVM. In Table 4, we can see that for the 70:30 split, the optimal CV score of 90% is reached for the bagging ensemble classifier when DT is used as the base classifier instead of RF and SVM. Alternatively we can say that the bagging ensemble classifier with DT as the base classifier gets the optimal results, with 96 and 89 percent accuracy for partitions 80:20 and 70:30, respectively, when compared to the base classifiers RF and SVM, as clearly seen from Tables 4 and 5. Entropy is chosen as an optimal parameter in the criterion function of DT as a base classifier for the bagging model, and we set the parameter value of the
to 100 and 20, respectively. Bagging ensemble models run over three base classifiers, viz. DT, RF, and SVM. In Table 4, we can see that for the 70:30 split, the optimal CV score of 90% is reached for the bagging ensemble classifier when DT is used as the base classifier instead of RF and SVM. Alternatively we can say that the bagging ensemble classifier with DT as the base classifier gets the optimal results, with 96 and 89 percent accuracy for partitions 80:20 and 70:30, respectively, when compared to the base classifiers RF and SVM, as clearly seen from Tables 4 and 5. Entropy is chosen as an optimal parameter in the criterion function of DT as a base classifier for the bagging model, and we set the parameter value of the 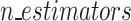 to 20. When we look at Table 4, we can see that for the 70:30 training and testing set of data, using DT as the base classifier for the boosting ensemble model (Adaboost) gives us the highest accuracy (89%). On the other hand, Table 5 shows that using RF as a base classifier, the Adaboost model gives the best results of accuracy (92%) compared to other base classifiers. We take the optimal values of the parameters
to 20. When we look at Table 4, we can see that for the 70:30 training and testing set of data, using DT as the base classifier for the boosting ensemble model (Adaboost) gives us the highest accuracy (89%). On the other hand, Table 5 shows that using RF as a base classifier, the Adaboost model gives the best results of accuracy (92%) compared to other base classifiers. We take the optimal values of the parameters 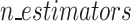 and learning rate to be 100 and 0.001, respectively, for the Adaboost ensemble learning model. For the regression framework, we conducted multiple runs of our model, selecting optimal parameters to generate a measure of performances, which we have listed in Table 7. For the SVR model, we have set the optimal values of parameters C and epsilon as 1 and 0.2, respectively. We have chosen the parameters
and learning rate to be 100 and 0.001, respectively, for the Adaboost ensemble learning model. For the regression framework, we conducted multiple runs of our model, selecting optimal parameters to generate a measure of performances, which we have listed in Table 7. For the SVR model, we have set the optimal values of parameters C and epsilon as 1 and 0.2, respectively. We have chosen the parameters  as 500 for the implementation of the MLP regression model. For the other standard and ensemble ML regression models, we have left the default parameters unchanged to produce our resulting regression measure of performances.
as 500 for the implementation of the MLP regression model. For the other standard and ensemble ML regression models, we have left the default parameters unchanged to produce our resulting regression measure of performances.
Discussion
The authors apply and integrate a number of cutting-edge machine learning models for slope stability into the slope sample data they are analyzing in order to evaluate the models’ correctness. The sample data’s characteristics are listed in Table 3. From a classification perspective, it was found that the qualitative prediction models established in this research work-bagging with base classifier DT, boosting with base classifier RF, and RF with splitting criterion gini-index have greater accuracy than other categories of slope stability prediction models. Owing to space constraints, the implementation procedures for slope stability prediction models are not covered in detail in this study. Subsequently, we performed several dimensionality reduction techniques on the features, viz. BA, BH, BW, SA, JA, JC, and JFA, examined in this article, and then employed the same set of classification models to evaluate the FOS prediction problem. As the sample data was reduced dimension using KPCA, it was observed a decrease in accuracy. Here we observed that bagging with base classifier DT and RF are robust in predicting FOS after reducing dimension. In order to provide a more comprehensive evaluation of the slope prediction problem as a regression problem, we have implemented and assessed twelve different regression models. The data we evaluated for a slope prediction problem is equally suitable from a regression problem perspective. We have observed, and it is evident from Table 7, that the Lasso-Lars CV and Bagging regression models were most effective in predicting slope stability as compared to other standard regression models under consideration.
Conclusion
Based on 125 data points, seven quantitative characteristics were selected to improve the slope stability prediction models’ accuracy. With this, the experimental results confirm that Random Forest with splitting criterion Gini-index and bagging with a decision tree as the base classifier are the most effective machine learning models for slope stability prediction, achieving the highest accuracy rates (up to 96%) and F-measure values. These models consistently outperformed other baseline classification techniques, such as SVM, DT, and K-NN, with an average improvement of 8–10% in accuracy value. The study also shows that techniques for reducing the number of dimensions, such as kernel PCA, usually make the models less accurate at making predictions. However, bagging and RF stay strong even after dimensionality reduction with an accuracy near to 87%. They provide an average improvement of the average accuracy value of 6–8% compared to the baseline classifiers. The regression analysis of the slope stability problem further supports the effectiveness of ML models, with Lasso-Lars CV and bagging regression models demonstrating superior performance compared to other regression techniques. These models achieved the highest 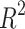 values of 0.84, indicating strong predictive capability for slope stability or factors of safety. From the regression model perspective, ensemble bagging regression enhances the average
values of 0.84, indicating strong predictive capability for slope stability or factors of safety. From the regression model perspective, ensemble bagging regression enhances the average 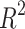 value by 8–10% relative to the conventional base regression models such as Linear, Bayes Ridge, SVR, DT, LassoCV, and Lars employed in this study. Elastic Net regression, on the other hand, performed the worst across multiple evaluation metrics.
value by 8–10% relative to the conventional base regression models such as Linear, Bayes Ridge, SVR, DT, LassoCV, and Lars employed in this study. Elastic Net regression, on the other hand, performed the worst across multiple evaluation metrics.
In conclusion, the combination of RF and bagging with DT as a base classifier provides a comprehensive and reliable approach for the FOS prediction problem. On the other hand, ensemble bagging and Lasso-Lars CV regression models provide superior approaches for regression tasks in slope stability prediction problems. Despite the potential complexity added by dimensionality reduction, these models exhibit strong performance and offer valuable insights for improving geotechnical engineering practices. Given this, we conclude that ensemble techniques are more effective than individual machine learning models when it comes to forecasting FOS from a classification and regression perspective. The findings offer a fresh method for geotechnical engineering slope stability prediction. However, when more data is available, the generated model may be enhanced by evaluating a larger dataset.
Author contributions
Devendra Kumar Yadav and Pragyan Mishra; Conceptualization, Methodology, Formal analysis, Swarup Chattopadhyay and Pritiranjan Singh: data curation, Writing, Experimentation, Debi Prasad Tripathy: original draft preparation: Writing – reviewediting Supervision: All authors have read and agreed to the published version of the manuscript.
Data availability
Data will be made available on reasonable request to the corresponding author.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Johari, A. & Fooladi, H. Comparative study of stochastic slope stability analysis based on conditional and unconditional random field. Comput. Geotech.125, 103707 (2020). [Google Scholar]
- 2.Obregon, C. & Mitri, H. Probabilistic approach for open pit bench slope stability analysis-a mine case study. Int. J. Min. Sci. Technol.29(4), 629–640 (2019). [Google Scholar]
- 3.Cui, W., Wang, X.-H., Zhang, G.-K. & Li, H.-B. Identification of unstable bedrock promontory on steep slope based on uav photogrammetry. Bull. Eng. Geol. Environ.80, 7193–7211 (2021). [Google Scholar]
- 4.Ma, Z., Mei, G., Prezioso, E., Zhang, Z. & Xu, N. A deep learning approach using graph convolutional networks for slope deformation prediction based on time-series displacement data. Neural Comput. Appl.33(21), 14441–14457 (2021). [Google Scholar]
- 5.Nayek, P. S. & Gade, M. Artificial neural network-based fully data-driven models for prediction of newmark sliding displacement of slopes. Neural Comput. Appl.34(11), 9191–9203 (2022). [Google Scholar]
- 6.Metya, S. & Bhattacharya, G. Accounting for 2d spatial variation in slope reliability analysis. Int. J. Geomech.20(3), 04019190 (2020). [Google Scholar]
- 7.Liu, G. et al. Numerical simulation of wedge failure of rock slopes using three-dimensional discontinuous deformation analysis. Environ. Earth Sci.83(10), 310 (2024). [Google Scholar]
- 8.Hasanipanah, M. et al. Intelligent prediction of rock mass deformation modulus through three optimized cascaded forward neural network models. Earth Sci. Inf.15(3), 1659–1669 (2022). [Google Scholar]
- 9.Zhou, Z. et al. An fdm-dem coupling method based on rev for stability analysis of tunnel surrounding rock. Tunn. Undergr. Space Technol.152, 105917 (2024). [Google Scholar]
- 10.Zou, B., Yin, J., Liu, Z. & Long, X. Transient rock breaking characteristics by successive impact of shield disc cutters under confining pressure conditions. Tunn. Undergr. Space Technol.150, 105861 (2024). [Google Scholar]
- 11.Lü, Q., Liu, S.-H., Mao, W.-Z., Yu, Y. & Long, X. A numerical simulation-based ann method to determine the shear strength parameters of rock minerals in nanoscale. Comput. Geotech.169, 106175 (2024). [Google Scholar]
- 12.Basahel, H. & Mitri, H. Probabilistic assessment of rock slopes stability using the response surface approach-a case study. Int. J. Min. Sci. Technol.29(3), 357–370 (2019). [Google Scholar]
- 13.Yaghoubi, E., Yaghoubi, E., Khamees, A., Razmi, D. & Lu, T. A systematic review and meta-analysis of machine learning, deep learning, and ensemble learning approaches in predicting ev charging behavior. Eng. Appl. Artif. Intell.135, 108789 (2024). [Google Scholar]
- 14.Tian, Y. et al. A deep-learning ensemble method to detect atmospheric rivers and its application to projected changes in precipitation regime. J. Geophys. Res. Atmos.128(12), 2022–037041 (2023). [Google Scholar]
- 15.Zhang, S. et al. Deep-learning-based landslide early warning method for loose deposits slope coupled with groundwater and rainfall monitoring. Comput. Geotech.165, 105924 (2024). [Google Scholar]
- 16.Li, A.-J., Khoo, S., Lyamin, A. & Wang, Y. Rock slope stability analyses using extreme learning neural network and terminal steepest descent algorithm. Autom. Constr.65, 42–50 (2016). [Google Scholar]
- 17.Qin, J., Du, S., Ye, J. & Yong, R. Svnn-anfis approach for stability evaluation of open-pit mine slopes. Expert Syst. Appl.198, 116816 (2022). [Google Scholar]
- 18.Zhang, J., Wang, Z., Hu, J., Xiao, S. & Shang, W. Bayesian machine learning-based method for prediction of slope failure time. J. Rock Mech. Geotech. Eng.14(4), 1188–1199 (2022). [Google Scholar]
- 19.Wang, G., Zhao, B., Wu, B., Zhang, C. & Liu, W. Intelligent prediction of slope stability based on visual exploratory data analysis of 77 in situ cases. Int. J. Min. Sci. Technol.33(1), 47–59 (2023). [Google Scholar]
- 20.Karir, D. et al. Stability prediction of a natural and man-made slope using various machine learning algorithms. Transp. Geotech.34, 100745 (2022). [Google Scholar]
- 21.Khajehzadeh, M., Taha, M. R., Keawsawasvong, S., Mirzaei, H. & Jebeli, M. An effective artificial intelligence approach for slope stability evaluation. IEEE Access10, 5660–5671 (2022). [Google Scholar]
- 22.Nanehkaran, Y. A. et al. Comparative analysis for slope stability by using machine learning methods. Appl. Sci.13(3), 1555 (2023). [Google Scholar]
- 23.Yang, Y. et al. Slope stability prediction method based on intelligent optimization and machine learning algorithms. Sustainability15(2), 1169 (2023). [Google Scholar]
- 24.Zhou, J. et al. Slope stability prediction for circular mode failure using gradient boosting machine approach based on an updated database of case histories. Saf. Sci.118, 505–518 (2019). [Google Scholar]
- 25.Nandy, S., Adhikari, M., Ray, A., Rai, R. & Singh, T. Edge-centric intelligent early warning system for residual soil stability prediction in slope. IEEE Internet Things J. (2023).
- 26.Wang, S., Lyu, T.-L., Luo, N. & Chang, P. Deformation prediction of rock cut slope based on long short-term memory neural network. Int. J. Mach. Learn. Cybern.15(3), 795–805 (2024). [Google Scholar]
- 27.Aminpour, M. et al. Slope stability machine learning predictions on spatially variable random fields with and without factor of safety calculations. Comput. Geotech.153, 105094 (2023). [Google Scholar]
- 28.Qin, J., Ye, J., Sun, X., Yong, R. & Du, S. A single-valued neutrosophic Gaussian process regression approach for stability prediction of open-pit mine slopes. Appl. Intell.53(11), 13206–13223 (2023). [Google Scholar]
- 29.Mahmoodzadeh, A. et al. Prediction of safety factors for slope stability: Comparison of machine learning techniques. Nat. Hazards1, 1–29 (2022). [Google Scholar]
- 30.Bhagat, N. K., Mishra, A. K., Singh, R. K., Sawmliana, C. & Singh, P. Application of logistic regression, cart and random forest techniques in prediction of blast-induced slope failure during reconstruction of railway rock-cut slopes. Eng. Fail. Anal.137, 106230 (2022). [Google Scholar]
- 31.Jiang, S. et al. Landslide risk prediction by using gbrt algorithm: Application of artificial intelligence in disaster prevention of energy mining. Process Saf. Environ. Prot.166, 384–392 (2022). [Google Scholar]
- 32.Chakraborty, A. & Goswami, D. Prediction of slope stability using multiple linear regression (mlr) and artificial neural network (ann). Arab. J. Geosci.10, 1–11 (2017). [Google Scholar]
- 33.Lin, S. et al. Comparative performance of eight ensemble learning approaches for the development of models of slope stability prediction. Acta Geotech.17(4), 1477–1502 (2022). [Google Scholar]
- 34.Wang, Y. et al. A comparative study of different machine learning methods for reservoir landslide displacement prediction. Eng. Geol.298, 106544 (2022). [Google Scholar]
- 35.Bardhan, A. & Samui, P. Probabilistic slope stability analysis of heavy-haul freight corridor using a hybrid machine learning paradigm. Transp. Geotech.37, 100815 (2022). [Google Scholar]
- 36.Fattahi, H. & Hasanipanah, M. An indirect measurement of rock tensile strength through optimized relevance vector regression models, a case study. Environ. Earth Sci.80, 1–12 (2021). [Google Scholar]
- 37.Ding, X., Amiri, M. & Hasanipanah, M. Enhancing shear strength predictions of rocks using a hierarchical ensemble model. Sci. Rep.14(1), 20268 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wang, Y., Rezaei, M., Abdullah, R. A. & Hasanipanah, M. Developing two hybrid algorithms for predicting the elastic modulus of intact rocks. Sustainability15(5), 4230 (2023). [Google Scholar]
- 39.Hasanipanah, M., Meng, D., Keshtegar, B., Trung, N.-T. & Thai, D.-K. Nonlinear models based on enhanced kriging interpolation for prediction of rock joint shear strength. Neural Comput. Appl.33, 4205–4215 (2021). [Google Scholar]
- 40.Gu, X. et al. Image compression-based ds-insar method for landslide identification and monitoring of alpine canyon region: A case study of ahai reservoir area in jinsha river basin. Landslides1, 1–17 (2024). [Google Scholar]
- 41.Zhou, G., Wang, Z. & Li, Q. Spatial negative co-location pattern directional mining algorithm with join-based prevalence. Remote Sens.14(9), 2103 (2022). [Google Scholar]
- 42.Liu, Z. et al. Increasing irrigation-triggered landslide activity caused by intensive farming in deserts on three continents. Int. J. Appl. Earth Obs. Geoinf.134, 104242 (2024). [Google Scholar]
- 43.Wei, W., Gong, J., Deng, J. & Xu, W. Effects of air vent size and location design on air supply efficiency in flood discharge tunnel operations. J. Hydraul. Eng.149(12), 04023050 (2023). [Google Scholar]
- 44.Yu, J. et al. Stress relaxation behaviour of marble under cyclic weak disturbance and confining pressures. Measurement182, 109777 (2021). [Google Scholar]
- 45.Wojtecki, Ł, Iwaszenko, S., Apel, D. B., Bukowska, M. & Makowka, J. Use of machine learning algorithms to assess the state of rockburst hazard in underground coal mine openings. J. Rock Mech. Geotech. Eng.14(3), 703–713 (2022). [Google Scholar]
- 46.Zhang, H. et al. A generalized artificial intelligence model for estimating the friction angle of clays in evaluating slope stability using a deep neural network and harris hawks optimization algorithm. Eng. Comput.1, 1–14 (2022). [Google Scholar]
- 47.Zi, J., Liu, T., Zhang, W., Pan, X., Ji, H. & Zhu, H. Quantitatively characterizing sandy soil structure altered by micp using multi-level thresholding segmentation algorithm. J. Rock Mech. Geotech. Eng. (2024).
- 48.Motameni, S., Rostami, F., Farzai, S. & Soroush, A. A comparative analysis of machine learning models for predicting loess collapse potential. Geotech. Geol. Eng.42(2), 881–894 (2024). [Google Scholar]
- 49.Rana, H. & Sivakumar Babu, G. Probabilistic back analysis for rainfall-induced slope failure using mls-svr and Bayesian analysis. Georisk18(1), 107–120 (2024). [Google Scholar]
- 50.Sun, J., Wu, S., Zhang, H., Zhang, X. & Wang, T. Based on multi-algorithm hybrid method to predict the slope safety factor-stacking ensemble learning with Bayesian optimization. J. Comput. Sci.59, 101587 (2022). [Google Scholar]
- 51.Koopialipoor, M. et al. Introducing stacking machine learning approaches for the prediction of rock deformation. Transp. Geotech.34, 100756 (2022). [Google Scholar]
- 52.Kavzoglu, T. & Teke, A. Predictive performances of ensemble machine learning algorithms in landslide susceptibility mapping using random forest, extreme gradient boosting (xgboost) and natural gradient boosting (ngboost). Arab. J. Sci. Eng.47(6), 7367–7385 (2022). [Google Scholar]
- 53.Wang, Y., Hasanipanah, M., Rashid, A. S. A., Le, B. N. & Ulrikh, D. V. Advanced tree-based techniques for predicting unconfined compressive strength of rock material employing non-destructive and petrographic tests. Materials16(10), 3731 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hussain, M. A., Chen, Z., Kalsoom, I., Asghar, A. & Shoaib, M. Landslide susceptibility mapping using machine learning algorithm: A case study along karakoram highway (kkh), pakistan. J. Indian Soc. Remote Sens.50(5), 849–866 (2022). [Google Scholar]
- 55.Wang, L., Wu, C., Yang, Z. & Wang, L. Deep learning methods for time-dependent reliability analysis of reservoir slopes in spatially variable soils. Comput. Geotech.159, 105413 (2023). [Google Scholar]
- 56.Guardiani, C., Soranzo, E. & Wu, W. Time-dependent reliability analysis of unsaturated slopes under rapid drawdown with intelligent surrogate models. Acta Geotech.17(4), 1071–1096 (2022). [Google Scholar]
- 57.Orhan, O., Bilgilioglu, S. S., Kaya, Z., Ozcan, A. K. & Bilgilioglu, H. Assessing and mapping landslide susceptibility using different machine learning methods. Geocarto Int.37(10), 2795–2820 (2022). [Google Scholar]
- 58.Meena, S. R. et al. Landslide detection in the himalayas using machine learning algorithms and u-net. Landslides19(5), 1209–1229 (2022). [Google Scholar]
- 59.Arabameri, A. et al. Decision tree based ensemble machine learning approaches for landslide susceptibility mapping. Geocarto Int.37(16), 4594–4627 (2022). [Google Scholar]
- 60.Pham, B. T. et al. Landslide susceptibility mapping using state-of-the-art machine learning ensembles. Geocarto Int.37(18), 5175–5200 (2022). [Google Scholar]
- 61.Pham, Q. B. et al. Predicting landslide susceptibility based on decision tree machine learning models under climate and land use changes. Geocarto Int.37(25), 7881–7907 (2022). [Google Scholar]
- 62.Wazirali, R., Yaghoubi, E., Abujazar, M. S. S., Ahmad, R. & Vakili, A. H. State-of-the-art review on energy and load forecasting in microgrids using artificial neural networks, machine learning, and deep learning techniques. Electr. Power Syst. Res.225, 109792 (2023). [Google Scholar]
- 63.Elberri, M. A., Tokeşer, Ü., Rahebi, J. & Lopez-Guede, J. M. A cyber defense system against phishing attacks with deep learning game theory and lstm-cnn with african vulture optimization algorithm (avoa). Int. J. Inf. Secur.1, 1–24 (2024). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on reasonable request to the corresponding author.