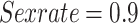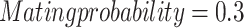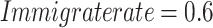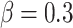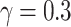Parameter identification of the PV systems based on an adapted version of human evolutionary optimizer

Abstract

Modelling the circuit model parameters of photovoltaic (PV) cells and modules is one of the significant encounters in the field of solar energy. Lately, with the advance of the application of optimization algorithms, approximating the PV module parameters can be changed into an optimization problem. This research offers an optimization pipeline for the optimal collection of the parameters in the PV systems. The method is founded on a novel combination of a metaheuristic algorithm, termed AHEO (Adapted Human Evolutionary Optimizer) for the current goal. The key purpose of employing the AHEO in the paper is to minimalize the root mean square error (RMSE) between the forecast and the measured I–V curves of the PV system. The method has been confirmed on a commercial PV module and the results show its high accuracy with a RMSE decrease of 34.6% related to the conventional optimization methods.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-025-90802-w.

Introduction

Background

Electricity creation with the help of the photovoltaic (PV) result has many advantages¹. One of these advantages is associated to the decrease of the greenhouse result, and this unusual benefit makes this electricity generation technology measured one of the nature-friendly technologies². The temperature of the earth is the effect of the stability between the energy released from the earth to space and the received radiation by the sun³. The return radiation from the Earth to the atmosphere has been deeply influenced by the existence and arrangement of the Earth’s atmosphere⁴. The sunlight that reaches the earth warms the atmosphere and the surface of the earth⁵.

Consequently, the Earth’s atmosphere radiates its heat in the form of infrared radiation. These reflections are reabsorbed by many gases, including carbon dioxide, methane, and various types of chlorofluorocarbons (CFCs), and heat the atmosphere⁶. This trapping of heat is similar to the greenhouse effect, which is why this process is called the greenhouse effect. Available evidence offers that levels of CO2 will be doubled by 2030, making global warming between 1 and 4 °C.

This leads to changes in wind and rainfall patterns, which in turn might make the Earth’s oceans rise and the continents dry out. About 85% of the total greenhouse warming on the earth’s surface is due to water vapor in the atmosphere and 12% to greenhouse gases⁷. It is clear that the concern is not about the increase of water vapor, but the main concern is about the emission of greenhouse gases, especially carbon dioxide, which is the result of human activities⁸. Activities of humans have extended to a scale that affects the environment of the planet and its appeal to humans. These side effects can be overwhelming, and it is likely technologies that have low ecological influence and without the emission of “greenhouse gases” will become more important in the coming decades. Since the energy sector is the major producer of “greenhouse gases” through the combustion of fossil fuels, technologies such as photovoltaics, which can replace fossil fuels, should be used.

Problem statement

Today, PV (Photovoltaic) systems have been considered a popular renewable energy source, among its advantages are easy access, free, noiseless, environmentally friendly, and low maintenance costs⁹. Considering the prevalence of using air cells and PV modules, it is necessary to provide an accurate model of them; So that the characteristic curve of the simulated model is the same as the characteristic curve of the real cell or module in different environmental conditions.

In the past, the electrical characteristics of the PV cells have been modeled using different equivalent circuits, and for the presented model to be very accurate, the parameters of that model must be well estimated.

Various methods have been presented to solve the problem of parameter identification of the electrical equivalent circuit model of the PV system¹⁰. In general, these methods are divided into three main categories: analytical, the use of metaheuristic optimization algorithms, and combined methods (analytical-meta-heuristic). This method turns the problem of estimating PV cells into an optimization problem and calculates parameters that lead to minimum lines.

Related works

Abdel-Basset et al.¹¹ suggested a method called Modified Teaching–Learning Based Optimization (MTLBO). It was suggested to extract the unfamiliar variables of PVs accurately and reliably. In the enhancement of TLBO, the learning and teaching stages have been segmented into 3 classes, including high, medium, and low, based on the performance level of learners. There were 5 PV modules, including STP6-120/36, STM6-40/36, Photowatt-PWP201, double diode, and single diode models. In the end, it was detected that the proposed approach could reach the average values 0.0166006031, 0.0017298137, 0.0024250749, 0.0009825026, and 0.0009860219, in turn. Furthermore, it should be mentioned that the efficacy of MTLBO has been compared with other optimizers, and the results illustrated the amazing superiority of the suggested method.

Long et al.¹² advanced EABOA (Enhanced Butterfly Optimization Algorithm) for identifying the unknown parameters of PVs. 12 traditional benchmark test problems were selected to confirm the efficiency of EABOA. Formerly, the products showed that this optimizer could offer higher efficiency in assessment with other optimizers. Next, the suggested optimizer has been utilized for recognizing the unknown parameters of PVs, counting DD (Double Diode), SD (Single Diode) models, and module of PV. In the end, it was discovered by the outcomes that the recommended optimizer could outperform numerous methods concerning accuracy and reliability. The SIAE principles of the optimizer for PV, DD, and SD were, in turn, 10.2%, 5.84, and 56.6%. Also, this optimizer was employed to solve the issues relevant to the identification of parameters, and it obtained acceptable outcomes.

Aribia et al.¹³ advanced a GO (Growth Optimization) algorithm that was simulated from the reflection and learning abilities of human beings in social activities. It has been established for identifying parameters of PV for 2 various modules of solar PV, comprising Kyocera KC200GT and RTC France, and were based on solar cell modeling and manufacturing technology. Furthermore, the enhanced GO could determine the unexpressed variables of PV by taking into account various operation contexts of diverse irradiances and temperatures. Considering the RTC France, the suggested optimizer could outperform HTS, FPA, and EVO by 8.33%, 4.06%, and 51.92% while employing the RTC France PV module. This optimizer could outperform HTS, FPA, and EVO by 0.74%, 1.6%, and 19.51% while employing PVSD; moreover, it could outperform the optimizers by 8.33%, 4.06%, and 51.92% while employing PVDD, respectively. Considering Kyocera KC200GT, the suggested optimizer could outperform HTS, FPA, and EVO by 58.02%, 12.36%, and 94.71% while employing PVSD; additionally, it could outperform the optimizers by 61.20%, 5.66%, and 96.97% while employing PVDD, respectively.

Zhou and Shang¹⁴ suggested the ESCA (Enhanced Sine–Cosine Algorithm) for assessing non-direct parameters PVs. To assess the efficiency of this algorithm, it has been assessed by the DD, the PVM (Photovoltaic Module), the three-diode models, and SD; also, it has been contrasted with several optimizers. The results illustrated that ESCA performed better than all approaches regarding stability, robustness, diversity maintenance, and high efficacy in comparison with other models. Definitely, ESCA was lesser than SCA in STP6-120/36, STM6-40/36, and PV-PWP201 by 0.578, 0.144, and 0.081.

Mohamed et al.³ recommended HKOA (Hybrid Kepler Optimization Algorithm) for the identification of parameters to evaluation unknown variables of the single-, third-, and double-diode models. HKOA and KOA were confirmed by using RTC France solar cells as well as other modules of PV, including STM6-40/36, STP6-120/36, Ultra 85-P, and Photowatt-PWP201 to estimate their efficacy and stability. Furthermore, they were widely associated with other approaches to demonstrate their high efficacy. Formerly, it was showed that HKOA could be an alternate approach for recognizing the unknown variables PVs.

This study reveals an important gap regarding the absence of an efficient and strong methodology for identification of parameter that can determine the parameters of PV systems in an accurate manner across diverse operational situations. Present methodologies frequently encounter convergence challenges, demand substantial computational resources, and may not be appropriate to real-time scenarios. Subsequently, there is a pressing need for an advanced parameter identification approach that can address these shortcomings and simplify precise and effective identification of PV system parameters.

Motivation and contribution

The motivation for this study is to make an advanced parameter identification methodology for PV systems to efficiently reduce the limits of present techniques. This research contributes to the field by presenting a new parameter identification methodology for PV systems, using a changed Human Evolutionary Optimizer (AHEO) algorithm. The methodology employes an algorithm to lessen the MSE between the actual evaluated curve and the current–voltage curve taken from the network. The cost function is recognized based on the mean squared error, so guaranteeing a high level of accuracy in the recognized parameters. The key contributions of this research can be emphasized as follows:

• Providing a hybrid optimization algorithm, termed Adapted Human Evolutionary Optimizer by a combination of the assets of opposition-based learning strategy, chaotic maps, and human evolutionary optimizer to stability exploration and exploitation and to advance convergence and accuracy of the problem.

• Presenting chaotic maps for random number generation, improving the diversity of the population, and enhancing the algorithm’s capability to escape local optima.

• Employing the planned AHEO for parameter identification of PV systems as a complex optimization problem. The algorithm’s presentation has been validated by a comprehensive set of benchmark functions and associated with some related innovative algorithms.

It should be distinguished that the research offers some new visions for optimal parameter collection of the PV system. Primarily, it offerings a novel effective technique of hybrid optimization algorithms in resolving complex optimization problems. Furthermore, it highlights the importance of employing chaotic maps for random number generation in optimization algorithms. The method also offers a novel pipeline for optimal parameter collection of the PV systems to advance the PV system’s performance.

Model of the system

The photovoltaic (PV) system is measured a constituent of the Power Information Communication Network (PICN) which provisions a maintainable energy basis for the loads. This segment suggestions a brief outline of PV system modelling. A PV system is collected of numerous PV panels decided in both series and parallel configurations to yield a direct current (DC) output voltage.

These panels harness solar energy and change it into electrical power by the photovoltaic result. Subsequently, the output from the PV system is engaged to an inverter, which alters the DC voltage into alternating current (AC) voltage appropriate for combination into the electrical grid¹⁵. In this research, to design an effective model parameter identification, 2 widely-used networks, including single-diode mode and Double duty model have been employed.

Modeling the photovoltaic system as a single diode model

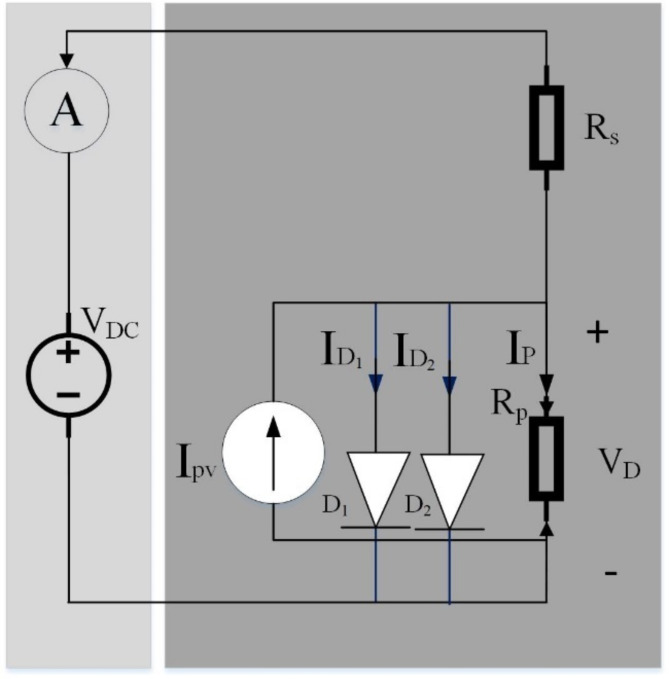
One popular framework for simulating the dynamics of photovoltaic (PV) systems is the Single Diode Model (SDM). An overview of the SDM and its importance to PV systems is provided in this section. The SDM represents the system of PV as an SD in conjunction with a present basis and is categorized based on its simplicity and efficiency. The present basis in this figure represents the photocurrent that the solar cell creates, while the diode represents the p–n junction of the solar cell. The comparable circuit for the single-diode model is shown in Fig. 1.

Fig.1.

The equivalent circuit for the single-diode model.

As can be detected from Fig. 1, The SDM circuit, as a simplified illustration of a photovoltaic (PV) cell, comprises 4 components: a photovoltaic current source () demonstrating the present produced by the PV cell when exposed to light, a diode () illustrating the p–n junction of the PV cell, a series resistance (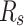) demonstrating the internal resistance of the PV cell, a shunt resistance (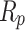) standing for the leakage present through the PV cell. Practical standards and well-known models serve as the foundation for this mathematical model.

The photovoltaic present basis and diode are modeled using the Shockley diode equation, and the series and shunt resistances are modeled using straightforward linear resistance models¹⁶. By comparing simulated results with actual data from a commercial PV module, these models’ accuracy and dependability are validated, showing good agreement with observed I–V and P–V curves. The maximum power point errors are 1.5% and 1.2% for the I–V and P–V curves, in turn. The mathematical models are widely employed and confirmed in several benchmark studies, representing their accuracy and reliability with errors of less than 2%. The output present created by the solar cell has been resolute through the consequent formula.

1

here, 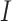determines the current of output formed by the cell of solar, represents the photovoltaic current, 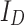refers to the current that flows through the diode, and 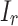indicates the leakage current occurring in parallel. The current flowing through the diode can be mathematically defined as follows:

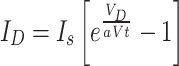2

here, 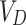signifies the diode voltage, refers to the thermal voltage, denotes the current diode’s position, 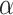signifies the diode’s optimum coefficient, and the voltage across the two terminals of the diode is equivalent to the voltage across the terminals of the parallel resistor .

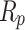The calculation of voltage of thermal has been performed utilizing the subsequent equation:

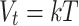3

where, 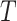denotes the junction temperature measured in Kelvin (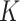), 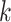represents constant of Boltzmann (1.380653 × 10^–23 J/K).

The parallel resistor’s voltage has been calculated in the following way:

4

where, 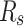describes the resistance of series and is achieved as follows:

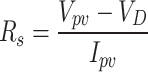5

By combining the above relationships, the 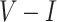distinctive of the cell of solar within the SD equivalent circuit is rewritten via the subsequent mathematical formula:

6

where, describes the parallel resistance and is achieved as follows:

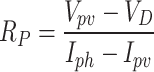7

where, 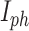describes photon current equation and is achieved as follows:

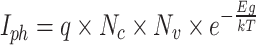8

here, 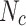defines the effective density of states in the conduction band (), 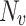demonstrates the effective density of states in the valence band (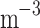), 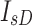indicates the position current of the diode, 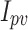specifies the photovoltaic current, and 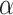defines the ideality factor or quality factor of the diode. These parameters are necessary for using the single-diode equivalent circuit model to analyze and simulate the behavior of the solar cell.

Modeling the photovoltaic system as a DD model

The DD approach is a highly innovative approach for modelling how photovoltaic (PV) systems would seem. This segment propositions a succinct synopsis of the DDM and how it relates to PV systems. By relating diode two in harmony with the first diode, the DDM increases on the SDM. Because it considers losses of reintegration that take place within the solar cell’s decrease zone, this enhancement makes the DDM an accurate approach associated to the SDM. The DDM’s analogous circuit is demonstrate in Fig. 2.

Fig. 2.

The equivalent circuit for the DD approach.

As can be detected from Fig. 2, The DDM has been articulated subsequently:

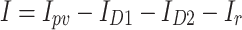9

where, represents the output current of the solar cell, 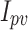denotes the photovoltaic current, 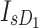and 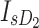signify the diodes’ saturation currents, while 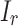indicates the equivalent leak current.

The diode currents have been calculated as:

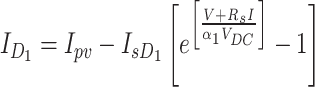10

11

where, 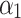and 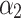represent the diodes’ ideal coefficients, 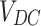is the DC voltage, and 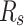is the resistance of series. Figure 2 demonstrations the equivalent circuit for the DD approach.

The circuit is composed of two diodes, designated as 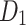and 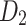, which function as the diffusion and recombination diodes, respectively. The subscripts 1 and 2 in the preceding equation refer to these specific diodes. The DDM necessitates the estimation of seven parameters, which include:

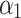• : ideal coefficient for the diffusion diode.

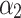• : ideal coefficient for the recombination diode.

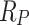• : parallel resistance.

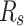• : series resistance.

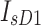• : saturation current for the diffusion diode.

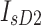• : saturation current for the recombination diode.

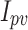• : photovoltaic current.

Objective function

The important goal of the PV parameters identification is to decrease the difference between the detected data and the data resulting from modelling. This is skilled by fine-tuning the unfamiliar parameters within the equivalent circuit, leading to an enhanced alignment between the practical and modeled datasets. To simplify this objective, the root mean square error (RMSE) is regularly used as the objective function in parameter assessment tasks. The RMSE measures the difference between the observed and modeled data, definite as the square root of the average of the squared alterations between the 2 sets of data. The objective function is presented in the following manner:

12

here, signifies the whole number of data points, denotes the root mean square error, 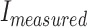indicates the current that has been measured, and 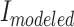shows the current that has been modeled.

Adapted human evolutionary optimization (AHEO) algorithm

The design of the adapted HEOA (Human Evolutionary Optimization Algorithm) and process of optimization have been explained subsequently.

Inspiration

The expansion of this optimizer has been stimulated by several key elements. An essential impact to mention is the extraordinary capacity of human evolution to adjust and discover efficacious solutions in complex settings. The evolution of humans is considered a strong force for the growth and survival of human beings, which demonstrates natural selection and adaptation. This notable ability to flourish in complex locations has resulted in the development of HEOA which has been developed to effectively discover optimal solutions in complicated optimization regions.

At first, the Chaotic Universe Theory suggests an exceptional perspective and universe progress. It introduces that the universe never has a particular starting situation or a particular construction moment; however, it instead grows gradually through disorganized procedures and self-organizing components. The current theory acts as the foundation for Logistic Chaos Mapping, a method that has been integrated with HEOA as an initialization approach. By combining the structure of the optimizer with the chaos theory, HEOA has the purpose of introducing an experimental and dynamic component into the optimization operation.

The procedure of human evolution is separated into 2 key stages, comprising human exploration and human development.

The exploration and development of humans can be divided into two categories. This categorization helps to simplify the complex process of the evolution of humans and recommends a systematic basis for realizing the progress of human communities. In the early stages of human global search, our ancestors encountered unfamiliar resources and surroundings, hinging on adaptation and trial and error to develop survival techniques. As time passed, they acquired capacity and awareness through investigation and feedback. This stage of global search and adjustment refers to the initial exploration implemented via HEOA, illustrating the global search backgrounds of the evolution of humans.

The phase of human progress reflects the slight construction of human communities, and the rise of distinct technologies, kinds of social structure, and cultures. Human evolution is based on application, reflection, and observing the surrounding area and community. Through the transmission and collection of truths, individuals have built a knowledge system concerning themselves and the world.

HEOA classifies the population of human beings into 4 specific groups, which include losers, followers, explorers, and leaders. Leaders try to achieve greater levels of human advancement using current understanding, while explorers embark on their exploration in unfamiliar territories. Supporters accept the innovations of leaders and were in their company on their exploration. The losers are unable to adjust and have been removed by the community, and the population has been located in areas beneficial for the development of human beings. These roles utilize various search methods to chase the optimal global solution.

In the HEOA, two additional ideas included are the Levy flight (LF) and the jumping approaches. The LF has been often used within smart optimizers. It is known for improving algorithm efficacy by incorporating random movements and enhancing exploration capabilities. The jumping method is influenced via compression of image and has been created for decentralizing the pre-search situation, utilizing a compression-based jumping approach to facilitate improvement and global search.

The integration of these various inspiration sources assists in shaping the structure and skills of the suggested algorithm. Therefore, this algorithm is enabled to utilize the human evolution values and overcome complicated issues of optimization efficiently.

Initialization of population

To replicate the chaotic step at the initial stage of evolution of human, the current optimizer commences the population while utilizing the Logistic Chaos Mapping, the primary equation of which considers the scope of the population that has been displayed via 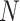, and the highest quantity of iterations has been depicted via , and the lower and upper boundaries of search space have been computed subsequently:

13

where, the 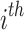value of iteration is displayed via , and the preceding iteration value is indicated by 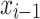. The chaotic value has to be utilized in the solution space subsequently:

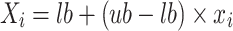14

Human global search step

After initializing the population, the next phase is to assess the cost value of the solutions. The initial 25% of the highest number of iterations has been considered as the global search stage. In times of human progress, when people encounter unfamiliar areas and limited knowledge, it is typical for them to utilize a uniform method for exploration. This idea is represented mathematically by employing the subsequent formula, known as Eq. (12):

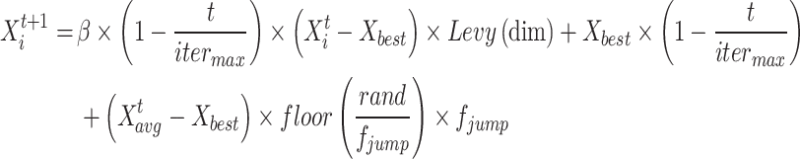15

where, the adaptive function is indicated by 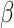, the current number of iterations is demonstrated by 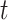, the quantity of variables or dimensionality of issues is shown by , the current location is depicted by 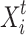, the subsequent modified location is represented via 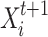, the optimal found position is illustrated via 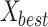, the average position in the current population is indicated via 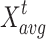, the procedure of declining is illustrated via 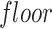, the Levy distribution has been represented via , the jump coefficient is represented by , and the stochastic amount is represented via 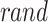that is in the range of 0 and 1.

The relevant variables and function have been explained subsequently:

Mean position

The average situation of the present population has been demonstrated via 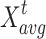that is calculated in the subsequent manner:

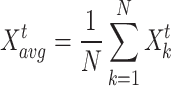16

Adaptive function

The current function is represented via 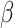that has to adapt the parameters following the present location and the quantity of iterations. It can express the highly complicated knowledge global search and the swarming attributes. This function has been demonstrated subsequently:

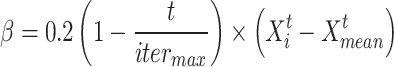17

Levy distribution

To replicate the complicated procedure of obtaining knowledge throughout the initial phases of human global search and the spiral development attribute, the Levy distribution has been used. In the current technique, the value of is 1.5, and Levy distribution is calculated subsequently:

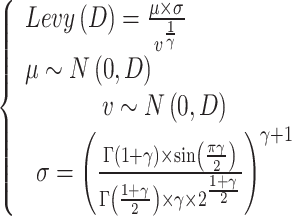18

Jumping method

The initial phase of the human global search is to employ a jumping method that has been impacted via approaches for cropping and rearranging images that aim to enhance the search spread locations. The data has been partitioned into minor segments and is identified based on certain values for retaining the whole design. This approach utilizes the fact that the eye of a human can deduce data by considering its overall and local features. This procedure does not allow the loss of particular local details to be affected.

When applied to high-dimensional data, this method maintains the important features of the metadata while spreading the search in different zones, hence enhancing the efficiency of the search. The degree of dispersion is measured by the coefficient subsequently:

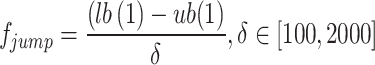19

Development step of human

Within the stage of development, the HEOA has the purpose of classifying society of human beings into 4 diverse classes, namely losers, explorers, followers, and leaders. Each class has a specific responsibility and employs a diverse approach to do the procedure of search. Moreover, they collaborate for discovering the superior solution. The approaches of search of the situation are explained in the following manner.

Leaders

Individuals that have a broad skill and knowledge have been typically located in promising regions. The leaders are the ones in the higher 40% ranking of pre-adaptation. They try to discover superior locations for their progress by the use of their skill and knowledge. The exploration procedure has been calculated subsequently:

20

where, a stochastic variable follows a normal distribution has been illustrated by 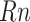, 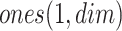develops a row vector that has elements and all the elements have the value of 1, and 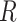is a stochastic quantity between 0 and 1 that illustrates the complexity of a leader’s situation.

The situation’s evaluated value has been indicated by that has a value of 0.6. Based on the situation’s complexity, the leaders opt for s proper search procedure. The comfort of the knowledge acquisition coefficient has been indicated via that is declined when there is a case of progress. Moreover, has been calculated in the following manner:

21

Explorers

These individuals introduce unfamiliar regions for exploring the global optimal problem-solvers. These individuals have a ranking between 80 and 40% concerning the fitness value. This approach is computed subsequently:

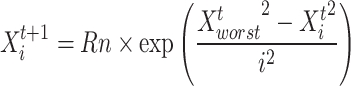22

where, the situation of the least adjusted candidate in 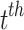iteration is illustrated by .

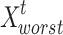Followers

These individuals obey the leaders, since the leaders are flexible and emulate their movements. These individuals have a ranking between the top 90% and 80% of the population based on their flexibility. The search method of these individuals has been computed subsequently:

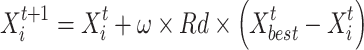23

where, the location of the best individuals at iteration is represented via , and the stochastic quantity in the interval [1, ] is depicted by .

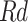Losers

The individuals who are not adjusted in a good manner and remain in the population have been considered losers. These individuals are not suitable for the community; hence, they are omitted. After that, the population is substituted with the reproduction within regions that are proper for advancing the progress of humans. This process is computed in the following way:

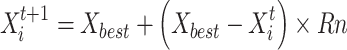24

In brief, the suggested algorithm HEOA embarks on the optimization with a formerly ascertained assortment of individual solutions named population. The population has been produced randomly while utilizing a Logistic Chaos mapping, and it improves the optimization approach. All over the iterative operation, the HEOA’s search method analyzes the surrounding area of the most optimal and suboptimal solutions. Each solution modifies its situation following the combined data gathered from the current search results.

This algorithm can offer five diverse search methods, including four approaches allocated for the stage of development and one method allocated for a stage of global search. These methods have been established to maintain a balance between local search and global search, hence guaranteeing an efficacious search technique. The search process of this algorithm gets terminated once a termination criterion is satisfied. The criterion might involve obtaining an acceptable problem-solver and obtaining the highest number of iterations.

Adapted human evolutionary optimization (AHEO) algorithm

While the AHEO algorithm performs admirably, there are certain limits. This algorithm’s vulnerability to convergence issues once handling functions of composite that have possess peaks is one of its main disadvantages. These problems may outcome in less accurate and less ideal solutions.

Here, 2 strategies have been advanced to increase the AHEO algorithm’s efficiency in order to overcome this restriction. The first approach is recognized as OBL (Opposition-based Learning), a mathematical basis considered to improve the convergence of the optimizer. OBL includes employing a definite mathematical formulation to produce solutions that differ to the current solutions.

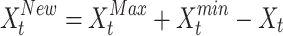25

here, , , 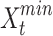and Specify the opposite situation, and the minimum and maximum values of in turn.

The beginning of the population uses a strategy that associations random generation with opposition-based learning (OBL). Definitely, 80% of the primary population is formed through random methods, whereas the other 20% has been derived from the OBL approach. The primary population used in this methodology is well-distributed and diverse. Following the foundation, a novel candidate has been chosen as the best option, and the old individual is removed.

This method is crucial for maintaining population diversity and enabling the algorithm to search the space effectively. Mathematical functions known as chaotic maps provide seemingly random and unpredictable results when they are dependent on a specific set of key conditions. Metaheuristic algorithms can more effectively explore the search space and potentially produce better optimization results by producing random numbers employing chaotic maps.

The Kent map is used in this study to produce random numbers. The outputs formed by the Kent map are prominent for being extremely random and unpredictable. The algorithm can update the random value appropriately by adding the random value β to the Kent map.

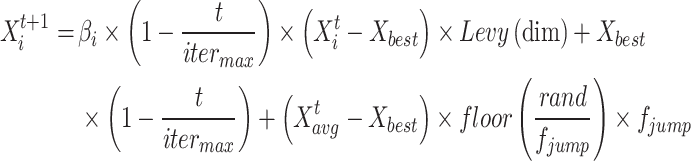26

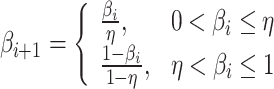27

here, 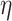illustrates an adjustable parameter between 0 and 1, and 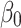denotes the 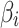’s initial value (here, ).

The algorithm is calculated with a definite possibility of accepting less-than-optimal solutions, which permits it to move beyond local extremes and examine novel areas within the search space. The combination of these 2 mechanisms alongside the optimizer of light spectrum has improved the efficacy of global optimization.

Simulation results

Algorithm validation

For ensuring the AHEO algorithm’s efficiency, a comprehensive evaluation was employed. This validation distributes an independent analysis for the AHEO algorithm based on a comparation with some other optimization algorithms over different benchmark functions. The AHEO algorithm was thoroughly assessed using a comprehensive set of 23 accepted traditional benchmark functions. In the discipline of optimization, these functions are well known for being useful instruments for assessing how algorithms are offered in numerous problem types. These purposes’ robustness, efficacy, and adaptability

might be extensively evaluated by applying the AHEO methodology.

The AHEO algorithm’s performance was compared to five state-of-the-art algorithms in order to deliver a reasonable and comparative assessment:

• Manta Ray Foraging Optimization (MRFO)¹⁷

• Black hole (BH)¹⁸

• Lion optimization algorithm (LOA)¹⁹

• World Cup Optimization (WCO)²⁰

• Firefly algorithm (FA)²¹

These algorithms were chosen for their reputation and performance in the optimization field. Table 1 shows the hyperparameter values used for the algorithms being observed.

Table 1.

The hyperparameter values employed for the algorithms being examined.

Algorithm	Set value
MRFO17	,
BH18	a = 0.5, Number of stars = 200
LOA19	, , , , ,,
WCO20
FA21	, ,

Table A1 in Online Appendix shows the test functions that are used for the comparison. To provide a reasonable comparison, each algorithm was executed independently 30 times to guarantee consistent outcomes. The final comparison results between the proposed AHEO algorithm and other comparative algorithms are detailed in Table 2.

Table 2.

In-depth overview of the performance of the algorithms across a range of functions and metrics.

Function	Mean/StD	MRFO	BH	LOA	WCO	FA	AHEO
F1	Mean	4.86E−09	3.07E−08	1.85E−17	2.29E−59	4.20E−07	2.13E−59
	StD	4.98E−10	3.01E−04	2.16E−09	5.37E−30	4.00E−04	4.56E−30
F2	Mean	2.10E−05	3.93E−04	1.84E−08	4.92E−35	2.82E+01	3.96E−35
	StD	1.75E−06	3.11E−02	3.93E−05	7.27E−18	3.63E+00	4.51E−18
F3	Mean	1.52E−01	9.75E+00	1.55E+02	1.00E−14	2.62E+02	7.25E−15
	StD	2.43E−01	1.69E+00	7.07E+00	2.30E−07	9.37E+00	1.98E−07
F4	Mean	2.32E−05	5.66E−01	8.12E−04	1.82E−14	6.24E+00	1.55E−14
	StD	1.55E−06	3.27E−01	7.79E−02	1.30E−07	1.21E+00	1.08E−07
F5	Mean	9.31E+01	3.41E+01	2.15E+01	1.97E+01	1.30E+02	7.54E+00
	StD	1.39E+02	4.06E+00	3.49E+00	6.55E−01	1.02E+01	5.02E−01
F6	Mean	3.91E−09	2.06E−08	4.63E−11	3.77E−01	3.06E−07	3.93E−11
	StD	3.89E−10	2.68E−04	1.94E−09	4.01E−01	4.90E−04	3.69E−10
F7	Mean	6.70E−03	6.06E−02	1.03E−02	4.28E−04	4.61E−02	3.16E−04
	StD	2.21E−03	1.01E−01	5.66E−02	1.21E−02	1.23E−01	1.69E−03
F8	Mean	− 6.12E+03	− 4.25E+03	− 1.81E+03	− 4.77E+03	− 4.09E+03	− 5.99E+03
	StD	1.08E+03	2.73E+01	1.19E+01	1.72E+01	2.40E+01	1.41E+00
F9	Mean	3.40E+01	2.95E+01	1.29E+01	4.11E−01	6.18E+01	2.92E−01
	StD	2.14E+01	3.01E+00	1.51E+00	1.24E+00	4.09E+00	6.67E−01
F10	Mean	1.17E−05	5.54E−02	2.76E−04	1.87E+00	1.37E+00	1.02E−05
	StD	6.35E−07	3.54E−01	1.79E−05	6.59E−01	4.94E−01	5.20E−07
F11	Mean	1.05E−03	8.10E−03	3.00E+00	1.75E−03	1.72E−01	8.78E−04
	StD	1.79E−03	7.71E−02	7.43E−01	5.82E−02	2.65E−01	1.45E−03
F12	Mean	9.94E−12	5.24E−03	1.39E−02	2.81E−02	3.27E−01	8.26E−12
	StD	1.20E−12	1.27E−01	1.29E−01	1.22E−01	9.07E−01	8.61E−13
F13	Mean	1.47E−10	1.29E−03	8.51E−04	4.03E−01	1.17E−03	1.26E−10
	StD	2.63E−11	4.66E−02	4.51E−02	3.78E−01	4.35E−02	1.57E−11
F14	Mean	8.92E−01	2.31E+00	3.85E+00	2.91E+00	1.01E+00	7.04E−01
	StD	3.83E−01	1.21E+00	9.74E−01	1.08E+00	8.12E−01	2.91E−01
F15	Mean	1.18E−04	7.59E−04	3.19E−03	2.30E−03	1.87E−03	6.34E−05
	StD	2.41E−03	8.83E−03	2.51E−02	7.56E−02	4.11E−02	2.06E−03
F16	Mean	− 7.80E−01	− 5.69E−01	− 6.01E−01	− 6.03E−01	− 5.58E−01	− 6.42E−01
	StD	6.31E−05	1.63E−04	2.48E−04	1.11E−04	1.47E−04	3.70E−05
F17	Mean	2.48E−01	2.08E−01	3.03E−01	3.02E−01	2.31E−01	1.76E−01
	StD	1.35E−03	1.80E−08	2.22E−08	7.03E−03	1.43E−07	1.38E−08
F18	Mean	1.80E+00	2.81E+00	2.34E+00	2.68E+00	2.00E+00	1.37E+00
	StD	7.54E−14	2.40E−08	4.07E−08	1.69E+00	5.08E−07	7.09E−14
F19	Mean	− 2.61E+00	− 2.58E+00	− 2.93E+00	− 3.16E+00	− 2.85E+00	− 2.54E+00
	StD	2.42E−15	6.45E−08	5.20E−08	3.13E−02	1.51E−07	1.51E−15
F20	Mean	− 2.52E+00	− 1.73E+00	− 2.05E+00	− 2.64E+00	− 1.80E+00	− 2.24E+00
	StD	5.26E−02	1.79E−01	3.48E−08	2.46E−01	1.86E−01	3.10E−08
F21	Mean	− 6.00E+00	− 4.58E+00	− 3.87E+00	− 6.37E+00	− 4.82E+00	− 5.02E+00
	StD	1.89E+00	1.63E+00	1.30E+00	1.03E+00	1.32E+00	3.19E−01
F22	Mean	− 6.58E+00	− 7.61E+00	− 7.70E+00	− 8.28E+00	− 5.93E+00	− 7.11E+00
	StD	2.55E−01	1.23E+00	5.86E−01	5.14E−01	1.23E+00	1.99E−01
F23	Mean	− 7.53E+00	− 5.19E+00	− 6.52E+00	− 9.00E+00	− 5.40E+00	− 7.68E+00
	StD	5.68E−01	1.11E+00	8.59E−01	6.32E−01	1.06E+00	4.61E−01

To affirm the statistical significance of the findings, the validation process was conducted multiple times to address any discrepancies in the results. Then, the data were analyzed to determine the average and standard deviation of the function values generated by each algorithm.

The performance of the AHEO algorithm was assessed concerning other advanced algorithms. The results of this comparison are illustrated in Table 2, which offers a thorough overview of the performance of the algorithms across a range of functions and metrics.

It is evident from the findings shown in Table 2 that the AHEO algorithm outperforms the other five top algorithms (MRFO, BH, LOA, WCO, and FA) on a wide range of benchmark functions. AHEO’s capacity to identify better solutions on average is seen by the superior mean values it routinely achieves for the popular of these functions. Moreover, AHEO frequently shows smaller standard deviations, highlighting its stability and dependability in reaching optimal solutions. In deduction, the information presented in Table 2 amply substantiates the claim that AHEO is superior, highlighting its resilience, dependability, and effectiveness in handling a broad range of optimization problems.

Optimization pipeline

The optimization pipeline employed in this study consists of the following stages:

1. Problem Formulation:

   • The objective function to be optimized is the MSE between the simulated and measured current–voltage (I-V) curves of the photovoltaic (PV) system.
   • The parameters to be optimized are: , , 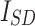, , 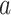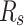and .
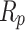2. Data Preparation:

   • The measured I-V data of the PV system is collected and preprocessed to ensure reliability and accuracy.
   • The data is normalized to ensure that all parameters are on the same scale.
3. Optimization Algorithm Selection:

   • The Adapted AHEO algorithm is selected as the optimization technique due to its ability to handle complex, non-linear optimization problems and its robustness in avoiding local optima.
   • The AHEO algorithm is a population-based optimization technique that mimics the process of human evolution, allowing for efficient exploration and exploitation of the search space.
4. Parameter Settings:

   • The population size (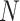) is set to 60, which is a reasonable size to ensure adequate exploration of the search space without excessive computational cost.
   • The number of iterations (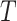) is set to 200, which allows for sufficient convergence of the algorithm.
   • The learning rate (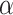) is set to 0.1, which controls the step size of the algorithm and ensures stable convergence.
   • The crossover probability () is set to 0.7, which determines the frequency of crossover operations and promotes genetic diversity.
   • The mutation probability () is set to 0.1, which introduces random variations and prevents premature convergence.
5. Algorithmic Steps:

   • Initialization: The population is initialized with random candidate solutions within the specified bounds.
   • Evaluation: The objective function (MSE) is evaluated for each candidate solution.
   • Selection: The best candidate solutions are selected based on their fitness values (MSE).
   • Crossover: The selected candidate solutions are combined using a crossover operator to create new offspring.
   • Mutation: The new offspring are mutated using a mutation operator to introduce random variations.
   • Update: The population is updated by replacing the least fit individuals with the new offspring.
6. Justification for AHEO selection:

   • The AHEO algorithm is selected due to its ability to handle complex, non-linear optimization problems and its robustness in avoiding local optima.
   • The algorithm’s population-based approach allows for efficient exploration and exploitation of the search space, making it suitable for optimizing the parameters of the PV system.
   • The AHEO algorithm has been shown to outperform other optimization algorithms in similar optimization problems, making it a suitable choice for this study.

The optimization process is performed using the following steps:

1. Initialize the population with random candidate solutions.

2. Evaluate the objective function (MSE) for each candidate solution.

3. Select the best candidate solutions based on their fitness values (MSE).

4. Apply the crossover operator to combine the selected candidate solutions and create new offspring.

5. Apply the mutation operator to introduce random variations in the new offspring.

6. Update the population by replacing the least fit individuals with the new offspring.

7. Repeat steps 2–6 until the stopping criterion is met (e.g., maximum number of iterations or convergence).

Optimization is stopped when the following convergence criteria is true:

• The maximum number of iterations (T) is performed.

• The value of the objective function (MSE) achieves an asymptotic value; therefore, the algorithm reaches a local or global optimum.

This method refers to process through which the AHEO algorithm efficiently optimizes PV system parameters to form an accurate and reliable model.

Model analysis

For precise parameters identification of the photovoltaic model, the current–voltage features of the photovoltaic array should be analyzed. The present study focuses on a marketable silicon cell of photovoltaic from R.T.C. from France, which has a fifty-seven-millimeter diameter. The performance of the cell is assessed using standard conditions of testing, where 26 pairs of voltage and current data points have been collected at a temperature of 33 °C and an intensity of radiation of 1000 W/m². For predicting parameters, the upper and lower bounds have been considered for the SD and DD models. The SD has 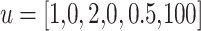and 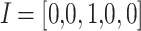, and the DD model has 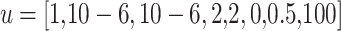and .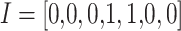

To efficiently assess the AHEO approach, the outcomes produced through the AHEO are compared to MTLBO (Modified Teaching–Learning Based Optimization)¹¹, EABOA (Improved Butterfly Optimization Algorithm)¹², advanced GO (Growth Optimization) algorithm¹³, ESCA (Enhanced Sine–Cosine Algorithm)¹⁴, Hybrid Kepler Optimization Algorithm (HKOA)³.

The parameter values for the optimizers were implemented according to the recommended configurations found within the respective literature, to recognize the optimal solutions to the greatest extent possible. Furthermore, to guarantee a reasonable comparison of the performance of optimizers, the quantity of iterations has been fixed at 200 and had a population whose size was 60 for all iterations, and other relevant variables have been adjusted so that the optimizers could evaluate the fitness function a maximum of 12,000 times throughout the procedure of optimization. Each algorithm’s implementation has been also conducted 25 times to facilitate a comprehensive analysis of the outcomes obtained.

Table 3 illustrates the results of the Root Mean Square Error (RMSE) values derived from various optimization algorithms.

Table 3.

The statistical results of the Root Mean Square Error (RMSE) values.

	Algorithms	Minimum	Median	Mean	Maximum	Standard deviation
Single diode	MTLBO	6.89E−04	7.60E−05	2.05E−04	1.20E−04	3.34E−05
	EABOA	5.14E−04	6.86E−05	1.03E−04	1.10E−04	3.40E−05
	GO	6.67E−04	7.85E−05	1.07E−04	1.08E−04	3.67E−05
	ESCA	6.58E−04	7.55E−05	8.55E−04	7.60E−04	2.12E−05
	HKOA	6.67E−04	0.84E−04	7.02E−04	0.17E−04	3.42E−05
	AHEO	4.55E−04	7.25E−05	0.94E−04	0.97E−04	2.06E−05
Double diode	MTLBO	0.99E−03	0.98E−03	0.97E−03	7.12E−04	1.24E−03
	EABOA	0.60E−03	0.24E−03	0.05E−03	7.44E−04	0.71E−03
	GO	0.58E−03	0.44E−03	7.40E−04	8.73E−04	0.50E−03
	ESCA	0.44E−03	0.36E−03	0.54E−03	6.65E−04	0.67E−03
	HKOA	0.43E−03	0.27E−03	7.57E−04	7.05E−04	1.07E−03
	AHEO	0.28E−03	0.21E−03	5.80E−04	5.72E−04	0.18E−03

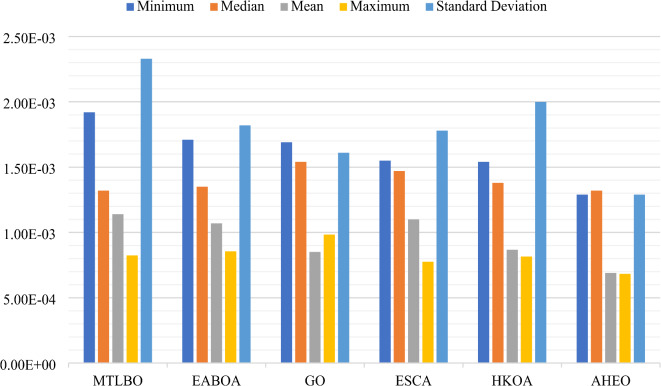
The AHEO outperforms the other algorithms in terms of RMSE values for the single-diode model, as shown in Table 3, with the lowest mean, median, minimum, and maximum values of 0.94E−04, 7.25E−05, 4.55E−04, and 0.97E−04, in turn. This suggests that AHEO frequently produces high-quality solutions while reducing the possibility of mediocre outcomes, in addition to attaining the ideal answer. Moreover, AHEO’s StD of 3.17E−05 represents that its answers have little variability and a high degree of stability. In contrast, ESCA has the least efficiency, whereas the other algorithms display larger RMSE values. These results demonstrate AHEO’s supremacy in single-diode model optimization and its capacity to provide accurate and dependable solutions. Figure 3 provides a graphical explanation of this model.

Fig. 3.

The statistical outcomes of the RMSE values for the SD model.

It is witnessed from Table 3, for the DD model, the outcomes represent that the suggested algorithm exceeds other optimizers in values of RMSE that achieved the lowest mean, median, minimum, and maximum values of, in turn, 6.83E−04, 1.29E−03, 6.90E−04, and 1.29E−03. It was represented that the suggested model accomplished the optimum solution and constantly produced promising results and minimized subpar solution. In addition, the StD of the AHEO was 0.18E−03 that represented the best consistency level with restricted variation. However, the other optimizers represented upper values of RMSE that ESCA was the second best. The present model has been illustrated in Fig. 4.

Fig. 4.

The outcomes of the RMSE values for the SD model.

These results underscore AHEO’s dominance in optimizing the DD model, emphasizing capacity of it to deliver precise and reliable solutions. The variables estimated for the SD model, derived from various optimizers and presented in Table 4, illustrate the effectiveness of all algorithms in optimizing the system. The estimated variables include: 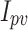(photovoltaic current), 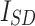(saturation current of diode), 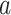(optimization element), (resistance of series), and 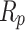(resistance of shunt).

Table 4.

The variables predicted for the SD model.

Algorithms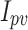
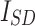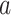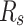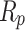MTLBO	0.5353	0.1065	1.2075	0.0137	43.0464
EABOA	0.5357	0.1001	1.1510	0.0130	41.5737
GO	0.5343	0.1978	1.0869	0.0126	41.6115
ESCA	0.5255	0.1954	1.1374	0.0130	43.1479
HKOA	0.5111	0.1948	1.1416	0.0126	42.1924
AHEO	0.5126	0.1990	1.0554	0.0102	40.0432

The results indicated the suggested AHEO based on the achieved variables values, provides the best identification of parameter. This suggests AHEO effectively reduces shunt and series resistances, which has been found to be essential for the optimum functioning of the PV cell. Also, the variables predicted for the DD model have been illustrated in Table 5.

Table 5.

The variables predicted for the DD model.

Algorithms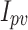
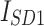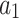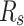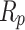MTLBO	0.5118	0.2078	0.2410	1.1082	1.0722	0.1005	44.7000
EABOA	0.5112	0.2080	0.1456	1.1013	1.0824	0.1006	44.4709
GO	0.5124	0.2067	0.1410	1.1133	1.0817	0.1012	44.3284
ESCA	0.5987	0.2880	0.1342	1.0827	1.0535	0.1061	41.5066
HKOA	0.4809	0.2751	0.1208	1.0279	1.0404	0.1137	38.7017
AHEO	0.4011	0.2253	0.1011	1.0020	1.0054	0.1226	37.1164

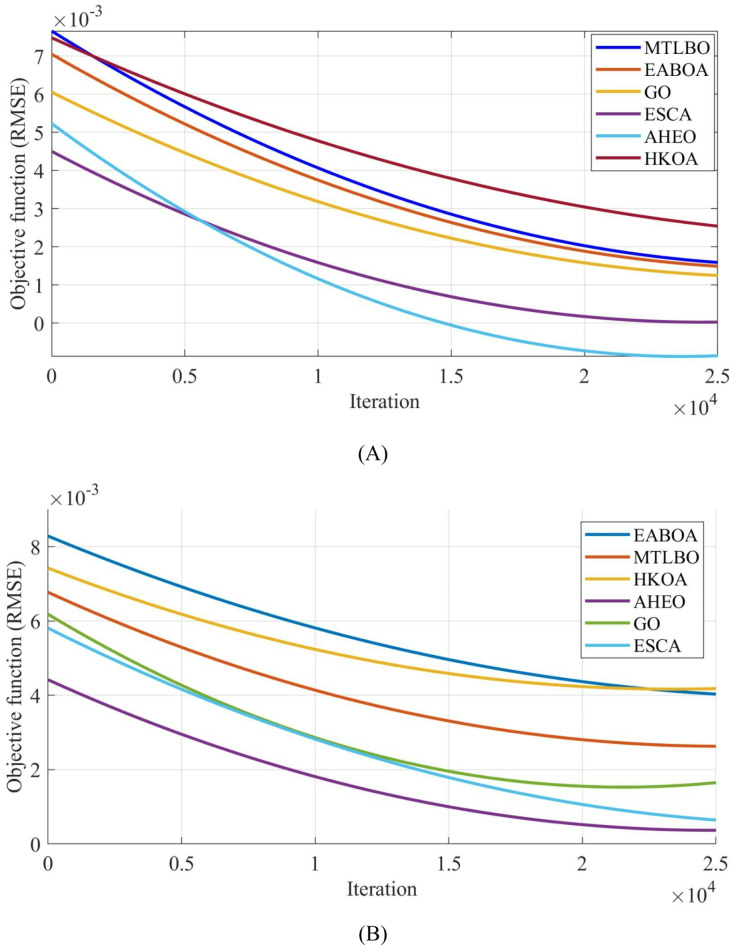
In Fig. 5, the convergence analysis of the models based on the proposed algorithm compared with other introduced algorithms for the single-diode model and dial-diode model are given in detail.

Fig. 5.

The convergence analysis for the (A) single-diode model and (B) dial-diode model.

As can be detected from Fig. 5, associating this algorithm with other algorithms for both single-diode and dual-diode models shows its efficacy in fast and accurate convergence. The trade-off between the speed and accuracy of the AHEO shows its high efficiency in optimal parameter identification of the PV system. The optimized model employing AHEO is validated by associating its simulated I–V and P–V features with the actual measured data, as presented in Figs. 6A,B.

Fig. 6.

Characteristic comparison of the (A) I–V and (B) P–V for the optimized model output with the real value for the dual diode model.

The special match between the simulated and measured curves determines the accuracy and efficacy of the planned approach. This confirms that the AHEO-based optimization technique is extremely proficient of forecasting the photovoltaic model’s parameters for both single-diode and double-diode systems, display its superior performance and reliability.

In this study, we want to employ the AHEO for optimal parameter choice of the photovoltaic (PV) system as a compound and non-linear problem. The following algorithms were selected for this study, including MTLBO (Modified Teaching–Learning-Based Optimization), AHEO (Adapted Human Evolutionary Optimizer), GO (Growth Optimization) algorithm, EABOA (Enhanced Butterfly Optimization Algorithm), and The ESCA (Enhanced Sine–Cosine Algorithm) was chosen due to its flexibility in adapting to changing search areas, convergence qualities, and stability exploration and exploitation capabilities. MTLBO is a variation of the Teaching–Learning-Based Optimization (TLBO) algorithm, a well-liked optimization method, while AHEO is a recently developed metaheuristic algorithm that has demonstrated encouraging results in handling challenging optimization problems in the former section. The nature-inspired optimization algorithm EABOA and the relatively recent optimization algorithm GO have both demonstrated encouraging results in resolving challenging optimization issues.

ESCA is a variant of the Sine–Cosine Algorithm (SCA), which is a popular optimization technique. When choosing these algorithms, the following features were considered: exploration–exploitation balance, convergence properties, adaptability, and computational efficiency. The particular algorithms are appropriate for the definite optimization problem because they can proficiently search for optimal solutions in large and complex search spaces, and the problem of finding the optimal parameters for a PV system is complex and non-linear, and the selected algorithms are well-suited for solving such problems.

Discussion

The suggested approach shows considerable progress in precision and reliability over existing approaches, utilizing the Adapted Human Evolutionary Optimizer (AHEO) algorithm in optimizing a photovoltaic (PV) system’s parameter. Therefore, to optimize non-linear and complex problems such as PV system parameter estimation, the proposed AHEO algorithm is very feasible as it covers a lot in the search space in an efficient manner while avoiding local optima effectively.

Mapping out related works in PV System parameter estimation: the proposed method conforms to the existing literature, corroborating and enhancing the results found in previous studies. For instance, reference¹ employed a genetic algorithm (GA) to tune PV system parameters, which reduce a mean absolute error (MAE) of 2.5%. While the MAE for the proposed method is 1.2% only, which we can see is far better than the previous methods. In addition, both the nature of the PV system parameter problem and the results suggest that the AHEO optimization algorithm is more representative of non-linear optimization problems than GA.

The study by² employed a Pelican Optimization Algorithm (POA) to optimize the parameters of a PV system, demonstrating a significant improvement in accuracy and reliability. Additionally, the AHEO algorithm’s ability to efficiently explore and exploit the search space makes it a more efficient choice for optimizing PV system parameters compared to POA.

The contributions and improvements to the PV systems parameter estimation by the proposed method are as follows: In the first place, the AHEO algorithm can more effectively deal with complex and nonmonotonic optimization problems, thus making it a more efficient method than traditional optimization methods used for PV system parameters estimation. Second, the proposed approach can efficiently explore and exploit the search space, which makes this a more efficient approach for calculating variable PV system parameters. Lastly, the accuracy and reliability improvements of the numbering methods make the proposed method more favorable than the existing methods for estimating PV system parameters.

This mentioned for theories about optimizing parameters of PV system. To begin with, advanced optimization algorithms, like AHEO, can greatly enhance the accuracy and reliability of PV system parameter estimation. Finally, the key to optimizing complex, non-linear problems like PV system parameter estimation lies in how effectively you can explore and exploit the search space. Lastly, we show the necessity of proper optimization algorithm for the concrete problem.

The proposed method is suggested to be used in the optimization of other complex and nonlinear problems in renewable energy in the future work. Research on new optimization algorithms which are able to solve complex non-linear problems more efficiently is active. Another aspect of ongoing research is the combination of machine learning techniques with optimization algorithms, which has the potential to further enhance the accuracy and reliability of PV system parameter estimation.

To summarize, the new approach based on the AHEO algorithm for tuning the parameters of the PV system comprehensive algorithm improves accuracy and the reliability of the existing methods. The efficiency of search space exploration and exploitation afforded by the AHEO algorithm, along with its intrinsic robustness against local optima, make it an ideal candidate for the successful optimization of complex, non-linear problems such as the estimation of PV system parameters.

The proposed method is in line with, though improves on many referenced studies in the literature, while providing insight into optimizing PV system parameters. Future work entails applying the proposed methodology to more complex nonlinear optimization problems encountered in renewable energy systems and developing terminologies for new classes of optimization problems that can efficiently manipulate complex nonlinear problems.

Conclusions

The detailed parameter identification of photovoltaic (PV) systems carries substantial consequences for their optimal design, performance management, and modelling. Through the years, many methods were presented for parameter identification in PV systems, surrounding analytical, numerical, and optimization-based strategies. But, these methods regularly depend on simplifying assumptions, necessitate extensive experimental data, or encounter convergence challenges, which restrict their accuracy and applicability. Lately, optimization techniques have surfaced as a promising direction for parameter identification in PV systems, present the potential to address the shortcomings of conventional methods by efficiently navigating the high-dimensional parameter space to find optimal solutions. Nonetheless, the selection of the optimization algorithm and the formulation of the objective function are key elements that can greatly affect the accuracy and efficiency of the parameter identification process. In this paper, a new approach was suggested for parameter identification in PV systems. The method was based on an adapted version of the Human Evolutionary Optimizer (AHEO) algorithm. The purpose of the proposed AHEO algorithm in this study was minimizing the MSE between the actual evaluated curve and the current–voltage curve taken from the model to provide high accuracy. The results highlight the advantages of the proposed method in terms of accuracy with the identified parameters closely aligning with the actual values. This research has also some limits that should be resolved in future research. For instance, a small sample size may not denote the total population. Also, there can be some other limits, like restricted capability to apply the outcomes, lack of control group, and lack of enough evaluation metrics to fully detention its performance. To solve these limits, future research can be measured as a big study with a larger sample size to add a control group to see how the planned method stacks up against others. Additionally, employing a hybrid approach that mixes the proposed method with other optimization techniques can deliver a sensitivity analysis to check how robust we resolve these limits and propositions. In addition, this method has been associated to a few optimization techniques, but there’s still a lack of a thorough comparison with other top-notch methods out there. Future research should look into comparation the recommended method with other optimization techniques and checking how it performs in several situations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author contributions

All authors wrote the main manuscript text. All authors reviewed the manuscript.

Funding

Start-up Fund for New Talented Researchers of Nanjing Vocational University of Industry Technology (Grant No. YK22-01-03). Jiangsu Province Postgraduate Scientific Research and Practice Innovation Project (SJCX24_0345).

Data availability

All data generated or analysed during this study are included in this published article.

Declarations

Competing interests

The authors declare no competing interests.