Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2025 Feb 12;129(8):2108–2116. doi: 10.1021/acs.jpca.4c08065

Using Conformational Sampling to Model Spectral and Structural Changes of Molecules at Elevated Pressures

Felix Zeller †, Philipp Pracht ‡, Tim Neudecker †,§,∥,*
PMCID: PMC11874042  PMID: 39937466

Abstract

graphic file with name jp4c08065_0008.jpg

Conformational sampling is nowadays a standard routine in computational chemistry. Within this work, we present a method to perform conformational sampling for systems exposed to elevated pressures within the CREST program, allowing us to model pressure-induced changes of molecular ensembles and structural parameters. For this purpose, we extend the molecular Hamiltonian with the PV (pressure times volume) term, using the solvent-accessible volume. The volume computation is performed within the new standalone library libpvol. A first application shows good agreement with experimental data and provides a reasonable explanation for severe pressure-induced structural and spectroscopic changes of the molecules dichloroethane and tetra(4-methoxyphenyl)ethylene.

Introduction

High-pressure chemistry, that is, chemistry occurring at pressures in the gigapascal (GPa) scale, offers a multitude of interesting phenomena. A nonexhaustive list contains effects such as phase transitions1−3 and crystal structure changes,4−6 amorphizations,7,8 changes in reaction behavior and kinetics,9,10 reversible changes in color,11 and the pressure-induced switching of the spin state of transition metal complexes.12,13 Experimentally, hydrostatic pressures up to several hundred gigapascals, as in planetary interiors,14 can be created using the diamond anvil cell.15−17

The experimental analysis of high-pressure phenomena can be combined with a plethora of theoretical models. Molecular dynamics (MD) simulations with a barostat can be used to simulate the behavior of amorphous materials, solutions, and biomolecules under high pressures.18−28 Pressure-induced crystal structure changes are routinely investigated using the plane-wave density functional theory (DFT) with the stress theorem.29−38 In both approaches, increasing pressure leads to shorter interatomic distances and thus higher electrostatic repulsion terms. Additionally, several models have been developed to approximate high-pressure effects in single-molecule calculations.39−44 Those usually lead to the potential energy surface (PES) being changed by an external pressure potential, which we therefore call the “pressure-modified” PES.

In recent years, the use of plane-wave DFT-based crystal structure search algorithms, the analogue of conformer sampling for periodic systems, led to an increasing accuracy in modeling high-pressure crystal structures.4,45−47 High-pressure MD simulations have been extensively used to model the pressure-induced denaturation process of proteins in the low GPa regime and show a high impact of pressure on the conformational ensemble.26,28,48,49

For single molecules at zero or ambient pressure, several sampling algorithms, e.g., based on MD50,51 or Monte Carlo techniques,52,53 have been developed to efficiently find the conformational ensemble on the PES.54 The iterative metadynamics-genetic crossing (iMTD-GC) algorithm forms the heart of the CREST55−57 program and offers an efficient and accurate way to find conformational ensembles of molecules and small molecular clusters, by using metadynamics together with Grimme’s extended tight-binding (xTB) methods.58 One of the many examples of the importance of conformational sampling includes trifluoro-pentanol dimers, where the correct description of the conformational ensemble was crucial to reproduce the experimental rotational spectrum.59

Within this publication, we aim to transfer the successes of high-pressure crystal structure search algorithms to single molecules. We hope this allows for a better understanding of high-pressure effects in solutions and amorphous materials and access to the fully developed toolkit of spectroscopic simulation techniques provided by modern quantum chemistry. For this purpose, we present a new library libpvol extending the CREST program, by adding the PV (pressure times volume) term to the electronic energy, allowing us to search the pressure-modified PES of single molecules for novel conformations and changes in the molecular conformational ensemble. We then use our approach to investigate the pressure dependence of the composition of molecular ensembles using the examples of the gauche/trans isomerization of dichloroethane (DCE) and the piezochromism of tetra(4-methoxyphenyl)ethylene (TMOE).

The rest of this paper is structured as follows. First, we discuss the details of the volume calculation and the implementation into the CREST program. Afterward, we will present the results of the chosen example applications.

Methods

Theory

To incorporate the effects of a pressure P into conformational sampling algorithms, the electronic energy Eel is extended with the PV term, and thus, the molecular enthalpy H is considered

graphic file with name jp4c08065_m001.jpg 1

where P is a constant user-defined pressure and Vmol is the solvent-accessible volume (SAV) of the molecule, which is obtained by the overlap of spheres around each atom having the solvent-accessible radius rSA consisting of the van der Waals (vdW) radius rvdW extended with a probe radius rprobe

graphic file with name jp4c08065_m002.jpg 2

The evaluation of the SAV of proteins and other biomolecules is of longstanding interest, and consequently, numerous algorithms have been developed.60Vmol is routinely calculated by numerical grid integration of the solvent-accessible surface area (SASA), as is done for example in the XP-PCM.44

graphic file with name jp4c08065_m003.jpg 3

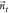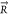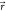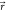Here, t is a discretization point of the surface, Inline graphic is its normal vector, Inline graphic is its spatial position, at is its area element, and Nd is the number of discretization points. The discretization of the SASA is a standard procedure in continuum-based solvation models and can be achieved in several ways.61−66 In this work, a volume exclusion function H({Inline graphic}, Inline graphic) is used on a Lebedev–Laikov grid to discretize the SASA,67 as introduced by Im et al.63 This procedure is also used in the recently presented analytical linearized Poisson–Boltzmann implicit solvation model.68H({Inline graphic}, Inline graphic) implements a simple switching function that leads to a smooth SASA with an analytical gradient while being computationally efficient enough for seamless integration with semiempirical methods and other low-cost potentials. The volume exclusion function depends on the nuclear coordinates {Inline graphic} and takes the form of a product of atomic volume functions

graphic file with name jp4c08065_m011.jpg 4

Using the substitution x = 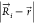Inline graphic, Hi(x) is given as

graphic file with name jp4c08065_m013.jpg 5

Here, rSAi is the solvent-accessible radius (eq 2) of atom i and w defines the switching region. w is chosen to be 0.3 Å, as recommended by Im et al.63 Each discretization point t belonging to an atom j is assigned an area at based on its position

graphic file with name jp4c08065_m014.jpg 6

where wa and wr are the angular and radial integration weights, respectively.

The volume gradient is obtained by derivation of eq 3 with respect to the atomic positions

graphic file with name jp4c08065_m015.jpg 7

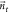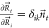Note that the normal vectors Inline graphic are independent of the atomic positions and the grid point coordinates Inline graphic and only depend on one atomic position k, resulting in Inline graphic. This leads to the following simpler expression for the volume gradient

graphic file with name jp4c08065_m019.jpg 8

where the second summation runs over all discretization points Nd(i) associated with the atom i. Thus, the only additional quantity to compute is the derivative of the areas with regard to the atomic coordinates, which is implemented following the method of Im et al.63

In initial implementations, we attempted to use our extended hydrostatic compression force field (X-HCFF) model to conduct conformational sampling at elevated pressures.57 In the X-HCFF model, forces 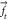Inline graphic are summed for each grid point t of the discretized vdW surface and added to the gradient of the associated atom i. The forces take the form42

graphic file with name jp4c08065_m021.jpg 9

Unfortunately, the X-HCFF gradient does not fulfill the necessary condition of integrability, and it is not possible to define a clean energy term for it. However, inspecting eq 1, one can see that the X-HCFF gradient is equal to the second term in eq 8 times P. Thus, one can use the X-HCFF gradient as an approximation to the PVmol gradient by assuming

graphic file with name jp4c08065_m022.jpg 10

Using the X-HCFF gradient has the advantage that the derivatives of the area segments do not have to be computed, significantly reducing computation time. The validity of this approximation was tested by comparing the pressure-independent parts of X-HCFF and PV gradients for a test set containing the proteinogenic amino acids, where the X-HCFF gradients deviated by about 10–20% from the PV gradients. The coordinates, gradients, and gradient norms of the test set are provided in the SI. We generally advise using the analytical PV gradient; however, when dense integration grids are used, the computation of the PV term can become a computational bottleneck, where the usage of the X-HCFF gradient may save significant amounts of computation time.

Implementation Details

The PV term described above is implemented in the standalone library libpvol, which is interfaced with the CREST program. This design allows for integration of the PV term into CREST via a modular calculator interface introduced in version 3.0.57 The libpvol library, similar in concept to the tblite package,69 is dedicated to the calculation of energy and gradient contributions. These contributions can be accessed through an interface object, enabling libpvol to be utilized in conjunction with any quantum mechanical software by extending the molecular Hamiltonian with an additional PV term.

The upcoming CREST version 3.1 includes integration of the PV functionalities by default. The libpvol library itself is written in Fortran, but Python and C++ wrappers are provided for ease of use, along with an interface to the atomic simulation environment (ASE).70 This flexible design ensures that libpvol can integrate with a variety of computational chemistry workflows.

Details on the use of wrappers and interfaces with libpvol can be found in its documentation.71 To allow refinement with quantum chemical accuracy and calculation of vibrational spectra at high pressure, we also implemented the PV computation into the Q-Chem software package. The implementation will be part of the Q-Chem 6.2.2 update.72 To enable fast frequency calculations, a seminumerical method was used, where the numerical Hessian of the PV gradient term is added to the analytical Hessian of the electronic energy.

Figure 1 shows the structure of libpvol. In a first step, the interface has to be initialized with the calculation parameters. The most important parameters are the number of discretization points per atom, the set of vdW radii to use, and the probe radius rprobe. Currently, the pairwise D3-cutoff radii for H–Pu and the Bondi set for H–Ar are implemented as possible sets of vdW radii.73−75 For the probe radius, a default value of 1.5 Å was chosen, which is approximately the radius of a water molecule. It should be noted that the added probe radius directly affects the SAV and consequently the energies added to conformers at a given pressure. We urge the user to employ conservative estimates of the probe radius.

Figure 1.

Figure 1

Open in a new tab

Schematic workflow for a pressure calculation with libpvol.

After initialization, the PV term and its gradient can be computed. This requires only a molecular geometry as input. The evaluation of eqs 3–8 is implemented as a loop over discretization points t, which allows for efficient parallelization and memory usage. libpvol is available via GitHub.71

A PV calculation in CREST can be requested via the new TOML input format76 as shown in Listing 1 below.graphic file with name jp4c08065_0009.jpg

Results

In the following, we present two applications of our workflow—the gauche/trans conformational ensemble of DCE and the spectroscopic darkening of TMOE at high pressure—and compare them with experimental data. The first application shows that one can model pressure effects on reaction equilibria and structural parameters reasonably well using a simple model such as the PV term. The second example demonstrates that new chemical insights can be gained via high-pressure conformational sampling.

Gauche/Trans Isomerization of DCE

As a first example application, DCE was investigated, which, as commonly known, has two conformers: gauche and trans (Figure 2). The influence of pressure onto the equilibrium has been experimentally investigated by high-pressure infrared spectroscopy and ultrasound experiments.77−80 These studies coherently suggest the gauche conformer to become the predominant conformer of DCE at elevated pressures and presented reaction volumes ΔVg/t between −0.7 and −5.9 cm3/mol, depending on the examined pressure range and the type of the experiment.

Figure 2.

Figure 2

Open in a new tab

Conformations of DCE.

High-pressure conformational searches for DCE were performed using GFN2-xTB with the default probe radius of 1.5 Å at pressures between 0 and 6 GPa, otherwise using the default iMTD-GC workflow of CREST as described in detail in ref (55). Regardless of the input conformation, the conformational search correctly found solely the gauche and trans isomers at all investigated pressures. To obtain the molecular ensemble with a higher accuracy, the conformational search was refined with DFT geometry optimizations using the Q-Chem program package and the B3LYP-D3BJ/def2-QZVP81−85 level of theory with Becke–Johnson damping and the PV expanded Hamiltonian. The resulting gauche/trans isomerization enthalpies before and after refinement are shown in Figure 3. It can be seen that the DFT computations do not change the qualitative results but mostly will grant more accurate conformational energies. However, the effect here is rather marginal, as GFN2-xTB seems to describe the energy difference between the gauche and trans conformers rather well. In agreement with experiments, the gauche conformer becomes favored at elevated pressures. Assuming entropic effects to be negligible, ΔVg/t can be approximated as the slope of the DFT plot to be −2.1 cm3/mol, which is in good agreement with the experimental data. It should be noted that the calculated reaction enthalpies do not depend on pressure in a strictly linear way, as eq 1 suggests. This behavior is caused by the dihedral angle between the two chlorine atoms slowly decreasing from 66.5° to 59.5°, allowing for an additional reduction in volume.

Figure 3.

Figure 3

Open in a new tab

Enthalpy of isomerization from the trans to the gauche conformer of DCE between 0 and 6 GPa calculated at the B3LYP-D3BJ/def2-QZVP level of theory. The slope of the linear regression is interpreted as reaction volume ΔVg/t.

It is important to note that when using small numbers of integration grid points, we found varying numbers of additional conformers. This behavior can be understood considering the PES cut along the Cl–C–C–Cl dihedral angle depicted in Figure 4. The low number of integration points leads to a large numerical error in the volume, causing the PES to become noisy and allowing for “artifact minima”. We generally found the numerical error to sufficiently decrease when more than 1000 points per atom are used. We thus set the default value to 1202 within libpvol and strongly advise against the use of fewer integration points.

Figure 4.

Figure 4

Open in a new tab

Normalized PES of DCE at 5 GPa cut along the Cl–C–C–Cl dihedral angle for differently dense integration grids.

High-Pressure Spectra of TMOE

TMOE is a propeller-shaped molecule consisting of four methoxyphenyl groups attached to a central ethene unit, as shown in Figure 5a. The spectroscopic behavior of TMOE was investigated by Wu et al. using high-pressure Raman and fluorescence spectroscopies up to 2.6 GPa.86 The molecule shows severe reductions in the spectral fluorescence and Raman intensities under elevated pressures. While the fluorescence intensities decline linearly, the Raman peaks are nearly unaffected up to 0.8 GPa and then start to quickly decline until they almost completely vanish at 1.7 GPa. Interestingly, the process was nearly completely reversible upon the relief of pressure. Based on constrained DFT optimizations and Raman simulations, Wu et al. suspected that the changes in the Raman spectrum are related to a change in the dihedral angle between the central ethylene unit and the phenyl groups, where an increase of the angle lowered the Raman intensities.

Figure 5.

Figure 5

Open in a new tab

Predominant conformations of TMOE and their respective volumes in the absence of pressure (a), at 2.5 GPa (b), and at 4 GPa (c), obtained via conformation search. The respective Cartesian coordinates can be found in the SI.

To investigate this behavior, conformation analysis was performed, using the default iMTD-GC workflow of CREST as described in detail in ref (55), at pressures between 0 and 4 GPa, using GFN2-xTB. To account for the experiments being carried out in the solid state, the probe radius was reduced to a more conservative value of 1.0 Å, resembling the closest distance to find a neighboring hydrogen atom. To get more reliable relative energies, the obtained ensembles were then refined with geometry optimizations at the B3LYP-D3BJ/cc-pVDZ81−84,87−90 level of theory and the PV term. In the absence of pressure, the ensemble of TMOE was found to consist of four propeller-shaped conformers (see Figure 5a), which only deviate in the orientations of the methoxy groups. Up to 2 GPa, the ensemble of TMOE is mostly unaffected by the pressure with similar Boltzmann weights and we found only small deviations in the orientation of the phenyl groups. However, at pressures above 2 GPa, the number of found conformers started to grow significantly, including a sandwich conformation (Figure 5c), which becomes the energetically favored conformation at pressures above 3.5 GPa. The number of found conformers spikes at 2.5 GPa with eight conformers having a Boltzmann weight larger than 1% and declines again at higher pressures. In the pressure range between 2 and 3.5 GPa, the ensemble is dominated by an intermediate conformer, where two phenyl units take the propeller and two take the sandwich form (Figure 5b). The isomerization to the sandwich conformer results in reduction in the molecular volume by about 10%, making it the only thermally accessible conformer at 4 GPa with a Boltzmann weight larger than 98%. The relative energies and Boltzmann weights of all conformers at the discussed pressures are provided in the SI. The absence of imaginary modes within frequency calculations confirmed that the new conformations are indeed minima on the pressure-modified PES. Also, we emphasize that a pressure-free geometry optimization of the sandwich conformer will restore the propeller shape, showing that external pressure can indeed be a contributing factor and lead to novel and unexpected conformations. However, contradicting the explanation of Wu et al., the dihedral angles between ethylene and the phenyl groups did not change significantly. As in the case of DCE, the refinement does not change the qualitative results of the original conformational sampling using GFN2-xTB. However, here, the aforementioned changes in the conformational ensemble appear at lower pressures from 1.5 GPa onward and the sandwich conformation becomes the most stable isomer at 2.75 GPa.

For further analysis, the Boltzmann-weighted Raman and UV/vis spectra for each TMOE ensemble were computed, which are shown in Figures 6 and 7, respectively. The Raman spectrum of TMOE exhibits two main features, an intense sharp peak at about 1130 cm–1 caused by the vibration of the carbon bond connecting the central ethylene unit and the phenyl rings and a broad split peak centered at approximately 1600 cm–1.86 These features are reproduced reasonably well by the calculated spectra, with a sharp peak at 1162 cm–1 and three neighboring peaks at 1606, 1636, and 1664 cm–1. For pressures up to 2 GPa, the peaks are found to be slightly red-shifted, but the peak intensities remain nearly unchanged. Upon isomerization to the intermediate and sandwich conformers, the peak intensities strongly decrease, and the splitting between the phenyl vibration modes increases. While our calculations do not suggest that the Raman spectrum becomes completely dark at elevated pressures as observed in the experiment, they show a strong decrease of the Raman intensities.

Figure 6.

Figure 6

Open in a new tab

Boltzmann-weighted Raman spectra of TMOE ensembles in the region of the most intense peaks at pressures between 2 and 4 GPa. The intensities are scaled to the most intense peak of the pressure-free spectrum. For better visibility, the intensities in the left plot are scaled by a factor of 3. The spectra were calculated at the B3LYP-D3BJ/cc-pVDZ87−91 level of theory. The line spectrum was calculated from frequencies and oscillator strengths using Lorentzian functions with a broadening parameter of 1.0 cm–1. Information on the number of found conformers and respective Boltzmann weights can be found in the SI.

Figure 7.

Figure 7

Open in a new tab

Boltzmann-weighted UV/vis spectra of TMOE ensembles at pressures between 0 and 4 GPa. The intensities are scaled to the most intense absorption at 0 GPa. The spectra were calculated at the CAM-B3LYP-D3BJ/aug-cc-pVTZ84,87−91 level of theory. The line spectrum was approximated using Gaussian functions with an exponential prefactor of 5.0 nm2. Information on the number of found conformers and respective Boltzmann weights can be found in the SI.

The experimental UV/vis spectrum of TMOE shows three absorption maxima at 230, 260, and 330 nm.86 The absorption spectra were simulated using time-dependent density functional theory (TD-DFT)92 using the CAM-B3LYP-D3BJ/aug-cc-pVTZ87−91 level of theory. Our excited-state calculations for the pressure-free ensemble show absorption maxima at 243 and 320 nm as shown in Figure 7. While the calculations do not reproduce the split UV maxima, they otherwise agree reasonably well with the experimental absorption spectrum.86 The presence of pressures up to 2 GPa already has an influence on the visible spectrum by causing a slight red shift and a decrease in the absorption intensity of the absorption maximum in the visible region. Analogous to the experiment, lower pressures already reduce the absorption intensities, while the Raman intensities remain nearly unaffected. At higher pressures, TMOE will isomerize to the sandwich conformation, which leads to the visible absorption spectrum of TMOE to darken nearly completely. Considering that an excitation wavelength of 365 nm was used in the experimental fluorescence spectra, the simulated absorption spectra explain the behavior in fluorescence experiments. The isomerization to the sandwich conformation leads to a strong reduction of absorption intensity around the used excitation wavelength and consequently will also strongly reduce the intensity in the fluorescence spectrum.

In conclusion, the high-pressure conformation analysis of TMOE provides a good qualitative explanation for its spectral darkening at high pressures. However, our results suggest that the pressures leading to this effect are overestimated by a factor of 2. We found the reversible spectral darkening to be caused by the isomerization from a propeller-shaped conformer to a sandwich-shaped conformer that is only stable at elevated pressures. Furthermore, the UV/vis spectra seem to be far more susceptible to small reorientations of the phenyl units, which explains a continuous darkening up to pressures of 1 GPa. Many conformations found at higher pressures are not stable in the absence of the same, clearly demonstrating the effects of directly including the pressure into the conformation sampling.

Conclusions and Outlook

Within this article, we presented a method to include pressure effects in conformational sampling calculations. For this purpose, the molecular Hamiltonian is extended to the enthalpy by adding the PV (pressure times volume) term. Here, the pressure is kept constant and the volume is computed by integration of the SASA within a new standalone library libpvol, which is interfaced with the CREST conformational sampling program. We then used our implementation to model the gauche/trans isomerization of DCE and the spectral darkening of TMOE under elevated pressures. The results of the high-pressure conformational sampling agreed well with the experimental results for DCE. For TMOE, we provide a reasonable explanation for its spectral darkening, that is, it isomerizes to a new sandwich conformation that is only stable at elevated pressures.

We hope that our work will contribute to a better modeling of the influence of pressure on reactions in the GPa regime and help design novel molecules that change their spectroscopic properties when exposed to elevated pressures. In the future, we will work on the transfer of our approach to small molecular clusters and solvent shells. We also plan to postprocess our semiempirical results with more sophisticated single-molecule pressure models such as Gaussians on surface tesserae simulate hydrostatic pressure (GOSTSHYP).39

Acknowledgments

P.P. gratefully acknowledges the Stiftung Stipendien-Fonds des Verbands der Chemischen Industrie (VCI) for a Liebig fellowship. The authors thank Christoph Bannwarth for the motivation to pursue research on high-pressure conformational sampling.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.4c08065.

  • Test set to compare pressure-independent parts of X-HCFF and PV gradients (coordinates of test molecules are given in Å, gradients and norms in Bohr2); Cartesian coordinates of conformers in figure; relative energies in kJ/mol; and Boltzmann weights of conformers for weighted spectra of TMOE at each presented pressure (ZIP)

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry Aspecial issue “Quantum Chemistry Software for Molecules and Materials”.

Supplementary Material

jp4c08065_si_001.zip (76.2KB, zip)

References

  1. McMahon M. I.; Nelmes R. J. High-pressure structures and phase transformations in elemental metals. Chem. Soc. Rev. 2006, 35, 943. 10.1039/b517777b. [DOI] [PubMed] [Google Scholar]
  2. Manjón F. J.; Errandonea D. Pressure-induced structural phase transitions in materials and earth sciences. physica status solidi (b) 2009, 246, 9–31. 10.1002/pssb.200844238. [DOI] [Google Scholar]
  3. Levitas V. I. High pressure phase transformations revisited. J. Phys.: Condens. Matter 2018, 30, 163001 10.1088/1361-648X/aab4b0. [DOI] [PubMed] [Google Scholar]
  4. Rychkov D. A. A Short Review of Current Computational Concepts for High-Pressure Phase Transition Studies in Molecular Crystals. Crystals 2020, 10, 81. 10.3390/cryst10020081. [DOI] [Google Scholar]
  5. Errandonea D.; Pellicer-Porres J.; Manjón F. J.; Segura A.; Ferrer-Roca C.; Kumar R. S.; Tschauner O.; López-Solano J.; Rodríguez-Hernández P.; Radescu S.; et al. Determination of the high-pressure crystal structure of BaWO4 and PbWO4. Phys. Rev. B 2006, 73, 224103 10.1103/PhysRevB.73.224103. [DOI] [Google Scholar]
  6. Degtyareva O. Crystal structure of simple metals at high pressures. High Pressure Research 2010, 30, 343–371. 10.1080/08957959.2010.508877. [DOI] [Google Scholar]
  7. Arora A. Pressure-induced amorphization versus decomposition. Solid State Commun. 2000, 115, 665–668. 10.1016/S0038-1098(00)00253-2. [DOI] [Google Scholar]
  8. Sharma S. M.; Sikka S. Pressure induced amorphization of materials. Prog. Mater. Sci. 1996, 40, 1–77. 10.1016/0079-6425(95)00006-2. [DOI] [Google Scholar]
  9. Jenner G. Role of the Medium in High Pressure Organic Reactions. A Review. Mini-Reviews in Organic Chemistry 2004, 1, 9–26. 10.2174/1570193043489015. [DOI] [Google Scholar]
  10. Matsumoto K.; Hamana H.; Iida H. Compendium of Cycloaddition Reactions under High Pressure. Helv. Chim. Acta 2005, 88, 2033–2234. 10.1002/hlca.200590156. [DOI] [Google Scholar]
  11. Liang J.; Ju C.-W.; Zheng W.; Wagner M.; Qiu Z.; Weil T. Helical Molecular Springs under High Pressure. ChemRxiv 2022, 10.26434/chemrxiv-2021-w3r3j. [DOI] [Google Scholar]
  12. Bouldi N.; Mannini M.; Retegan M.; Miller R. G.; Cahier B.; Sainctavit P.; Guihéry N.; Mallah T.; Cabaret D.; Gouéré D.; et al. XAS and XMCD Reveal a Cobalt(II) Imide Undergoes High-Pressure-Induced Spin Crossover. J. Phys. Chem. C 2022, 126, 5784–5792. 10.1021/acs.jpcc.2c00614. [DOI] [Google Scholar]
  13. Kershaw Cook L. J.; Thorp-Greenwood F. L.; Comyn T. P.; Cespedes O.; Chastanet G.; Halcrow M. A. Unexpected Spin-Crossover and a Low-Pressure Phase Change in an Iron(II)/Dipyrazolylpyridine Complex Exhibiting a High-Spin Jahn–Teller Distortion. Inorg. Chem. 2015, 54, 6319–6330. 10.1021/acs.inorgchem.5b00614. [DOI] [PubMed] [Google Scholar]
  14. Li B.; Ji C.; Yang W.; Wang J.; Yang K.; Xu R.; Liu W.; Cai Z.; Chen J.; Kwang Mao H. Diamond anvil cell behavior up to 4 Mbar. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, 1713–1717. 10.1073/pnas.1721425115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Weir C. E.; Lippincott E. R.; Van Valkenburg A.; Bunting E. N. Infrared studies in the 1- to 15-micron region to 30,000 atm. Journal of Research of the National Bureau of Standards Section A: Physics and Chemistry 1959, 63A, 55. 10.6028/jres.063A.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Katrusiak A. Lab in a DAC – high-pressure crystal chemistry in a diamond-anvil cell. Acta Crystallographica Section B Structural Science, Crystal Engineering and Materials 2019, 75, 918–926. 10.1107/S2052520619013246. [DOI] [PubMed] [Google Scholar]
  17. Mao H.-K.; Chen X.-J.; Ding Y.; Li B.; Wang L. Solids, liquids, and gases under high pressure. Rev. Mod. Phys. 2018, 90, 015007 10.1103/RevModPhys.90.015007. [DOI] [Google Scholar]
  18. Nosé S.; Klein M. Constant pressure molecular dynamics for molecular systems. Mol. Phys. 1983, 50, 1055–1076. 10.1080/00268978300102851. [DOI] [Google Scholar]
  19. Parrinello M.; Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
  20. Hoover W. G. Constant-pressure equations of motion. Phys. Rev. A 1986, 34, 2499–2500. 10.1103/PhysRevA.34.2499. [DOI] [PubMed] [Google Scholar]
  21. Wentzcovitch R. M. Invariant molecular-dynamics approach to structural phase transitions. Phys. Rev. B 1991, 44, 2358–2361. 10.1103/PhysRevB.44.2358. [DOI] [PubMed] [Google Scholar]
  22. Moog M.; Pietrucci F.; Saitta A. M. Carbon Dioxide under Earth Mantle Conditions: From a Molecular Liquid through a Reactive Fluid to Polymeric Regimes. J. Phys. Chem. A 2021, 125, 5863–5869. 10.1021/acs.jpca.1c01026. [DOI] [PubMed] [Google Scholar]
  23. Spooner J.; Wiebe H.; Boon N.; Deglint E.; Edwards E.; Yanciw B.; Patton B.; Thiele L.; Dance P.; Weinberg N. Molecular dynamics calculation of molecular volumes and volumes of activation. Phys. Chem. Chem. Phys. 2012, 14, 2264. 10.1039/c2cp22949h. [DOI] [PubMed] [Google Scholar]
  24. Shanavas K. V.; Garg N.; Sharma S. M. Classical molecular dynamics simulations of behavior of GeO2 under high pressures and at high temperatures. Phys. Rev. B 2006, 73, 094120 10.1103/PhysRevB.73.094120. [DOI] [Google Scholar]
  25. Horbach J. Molecular dynamics computer simulation of amorphous silica under high pressure. J. Phys.: Condens. Matter 2008, 20, 244118 10.1088/0953-8984/20/24/244118. [DOI] [Google Scholar]
  26. Paci E. High pressure simulations of biomolecules. Biochimica et Biophysica Acta (BBA) -Protein Structure and Molecular Enzymology 2002, 1595, 185–200. 10.1016/S0167-4838(01)00343-0. [DOI] [PubMed] [Google Scholar]
  27. Adjaoud O.; Steinle-Neumann G.; Jahn S. Mg2SiO4 liquid under high pressure from molecular dynamics. Chem. Geol. 2008, 256, 185–192. 10.1016/j.chemgeo.2008.06.031. [DOI] [Google Scholar]
  28. Sarupria S.; Ghosh T.; García A. E.; Garde S. Studying pressure denaturation of a protein by molecular dynamics simulations. Proteins: Struct., Funct., Bioinf. 2010, 78, 1641–1651. 10.1002/prot.22680. [DOI] [PubMed] [Google Scholar]
  29. Nielsen O. H.; Martin R. M. First-Principles Calculation of Stress. Phys. Rev. Lett. 1983, 50, 697–700. 10.1103/PhysRevLett.50.697. [DOI] [Google Scholar]
  30. Nielsen O. H.; Martin R. M. Stresses in semiconductors: Ab initio calculations on Si, Ge, and GaAs. Phys. Rev. B 1985, 32, 3792–3805. 10.1103/PhysRevB.32.3792. [DOI] [PubMed] [Google Scholar]
  31. Nielsen O. H.; Martin R. M. Quantum-mechanical theory of stress and force. Phys. Rev. B 1985, 32, 3780–3791. 10.1103/PhysRevB.32.3780. [DOI] [PubMed] [Google Scholar]
  32. Huang L.; Han Y.; Liu J.; He X.; Li J. Ab Initio Prediction of the Phase Transition for Solid Ammonia at High Pressures. Sci. Rep. 2020, 10, 7546. 10.1038/s41598-020-64030-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Guńka P. A.; Olejniczak A.; Fanetti S.; Bini R.; Collings I. E.; Svitlyk V.; Dziubek K. F. Crystal Structure and Non-Hydrostatic Stress-Induced Phase Transition of Urotropine Under High Pressure. Chem.—Eur. J. 2021, 27, 1094–1102. 10.1002/chem.202003928. [DOI] [PubMed] [Google Scholar]
  34. Liu H.; Wang F.; Gong X. DFT studies on 7-nitrotetrazolo [1,5]furazano[4,5-b]pyridine 1-oxide: Crystal structure, detonation properties, sensitivity and effect of hydrostatic compression. Structural Chemistry 2014, 25, 239–249. 10.1007/s11224-013-0279-0. [DOI] [Google Scholar]
  35. Mishra A. K.; Murli C.; Pandey K. K.; Sakuntala T.; Poswal H. K.; Verma A. K. Competing Interactions: Evolution of Inter and Intramolecular Hydrogen Bonds in Salicylic Acid at High Pressures. J. Phys. Chem. B 2020, 124, 373–379. 10.1021/acs.jpcb.9b10432. [DOI] [PubMed] [Google Scholar]
  36. Barnes B. C.; Brennan J. K.; Byrd E. F. C.; Izvekov S.; Larentzos J. P.; Rice B. M. In Computational Approaches for Chemistry Under Extreme Conditions, Goldman N., Ed.; Challenges and Advances in Computational Chemistry and Physics; Springer International Publishing: Cham, 2019; Vol. 28, pp 229–282. [Google Scholar]
  37. Hoja J.; Reilly A. M.; Tkatchenko A. First-principles modeling of molecular crystals: structures and stabilities, temperature and pressure. WIREs Comput. Mol. Sci. 2017, 7, e1294 10.1002/wcms.1294. [DOI] [Google Scholar]
  38. Zurek E.; Grochala W. Predicting crystal structures and properties of matter under extreme conditions via quantum mechanics: the pressure is on. Phys. Chem. Chem. Phys. 2015, 17, 2917–2934. 10.1039/C4CP04445B. [DOI] [PubMed] [Google Scholar]
  39. Scheurer M.; Dreuw A.; Epifanovsky E.; Head-Gordon M.; Stauch T. Modeling Molecules under Pressure with Gaussian Potentials. J. Chem. Theory Comput. 2021, 17, 583–597. 10.1021/acs.jctc.0c01212. [DOI] [PubMed] [Google Scholar]
  40. Cammi R.; Verdolino V.; Mennucci B.; Tomasi J. Towards the elaboration of a QM method to describe molecular solutes under the effect of a very high pressure. Chem. Phys. 2008, 344, 135–141. 10.1016/j.chemphys.2007.12.010. [DOI] [Google Scholar]
  41. Cammi R. In The Quantum Chemical Study of Chemical Reactions at Extreme High Pressure by Means of the Extreme-Pressure Polarizable Continuum Model, Dixon D. A., Ed.; Annual Reports in Computational Chemistry; Elsevier, 2017; Vol. 13, pp 117–135. [Google Scholar]
  42. Stauch T. A mechanochemical model for the simulation of molecules and molecular crystals under hydrostatic pressure. J. Chem. Phys. 2020, 153, 134503 10.1063/5.0024671. [DOI] [PubMed] [Google Scholar]
  43. Subramanian G.; Mathew N.; Leiding J. A generalized force-modified potential energy surface for mechanochemical simulations. J. Chem. Phys. 2015, 143, 134109 10.1063/1.4932103. [DOI] [PubMed] [Google Scholar]
  44. Cammi R.; Chen B. Studying and exploring potential energy surfaces of compressed molecules: A fresh theory from the extreme pressure polarizable continuum model. J. Chem. Phys. 2022, 157, 114101 10.1063/5.0104269. [DOI] [PubMed] [Google Scholar]
  45. Roberts J.; Zurek E. Computational materials discovery. J. Chem. Phys. 2022, 156, 210401 10.1063/5.0096008. [DOI] [PubMed] [Google Scholar]
  46. Wang Y.; Ma Y. Perspective: Crystal structure prediction at high pressures. J. Chem. Phys. 2014, 140, 040901 10.1063/1.4861966. [DOI] [PubMed] [Google Scholar]
  47. Pickard C. J.; Needs R. J. Ab initio random structure searching. J. Phys.: Condens. Matter 2011, 23, 053201 10.1088/0953-8984/23/5/053201. [DOI] [PubMed] [Google Scholar]
  48. Hata H.; Nishiyama M.; Kitao A. Molecular dynamics simulation of proteins under high pressure: Structure, function and thermodynamics. Biochimica et Biophysica Acta - General Subjects 2020, 1864, 129395 10.1016/j.bbagen.2019.07.004. [DOI] [PubMed] [Google Scholar]
  49. Okumura H. Temperature and pressure denaturation of chignol Folding and unfolding simulation by multibaric-multithermal molecular dynamics method. Proteins: Struct., Funct., Bioinf. 2012, 80, 2397–2416. 10.1002/prot.24125. [DOI] [PubMed] [Google Scholar]
  50. Vymětal J.; Vondrášek J. Metadynamics As a Tool for Mapping the Conformational and Free-Energy Space of Peptides — The Alanine Dipeptide Case Study. J. Phys. Chem. B 2010, 114, 5632–5642. 10.1021/jp100950w. [DOI] [PubMed] [Google Scholar]
  51. Leone V.; Marinelli F.; Carloni P.; Parrinello M. Targeting biomolecular flexibility with metadynamics. Curr. Opin. Struct. Biol. 2010, 20, 148–154. 10.1016/j.sbi.2010.01.011. [DOI] [PubMed] [Google Scholar]
  52. Wales D. J.; Doye J. P. K. Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. J. Phys. Chem. A 1997, 101, 5111–5116. 10.1021/jp970984n. [DOI] [Google Scholar]
  53. Wales D. J.; Scheraga H. A. Global Optimization of Clusters, Crystals, and Biomolecules. Science 1999, 285, 1368–1372. 10.1126/science.285.5432.1368. [DOI] [PubMed] [Google Scholar]
  54. Hawkins P. C. D. Conformation Generation: The State of the Art. J. Chem. Inf. Model. 2017, 57, 1747–1756. 10.1021/acs.jcim.7b00221. [DOI] [PubMed] [Google Scholar]
  55. Pracht P.; Bohle F.; Grimme S. Automated exploration of the low-energy chemical space with fast quantum chemical methods. Phys. Chem. Chem. Phys. 2020, 22, 7169–7192. 10.1039/C9CP06869D. [DOI] [PubMed] [Google Scholar]
  56. Pracht P.; Grimme S. Calculation of absolute molecular entropies and heat capacities made simple. Chemical Science 2021, 12, 6551–6568. 10.1039/D1SC00621E. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Pracht P.; Grimme S.; Bannwarth C.; Bohle F.; Ehlert S.; Feldmann G.; Gorges J.; Müller M.; Neudecker T.; Plett C.; et al. CREST—A program for the exploration of low-energy molecular chemical space. J. Chem. Phys. 2024, 160, 114110 10.1063/5.0197592. [DOI] [PubMed] [Google Scholar]
  58. Bannwarth C.; Caldeweyher E.; Ehlert S.; Hansen A.; Pracht P.; Seibert J.; Spicher S.; Grimme S. Extended tight-binding quantum chemistry methods. WIREs Comput. Mol. Sci. 2021, 11, e1493 10.1002/wcms.1493. [DOI] [Google Scholar]
  59. Mort A. N.; Xie F.; Hazrah A. S.; Xu Y. Rotational spectroscopy of hydrogen-bonded binary trifluoro-propanol conformers: conformational diversity, preference and abundances in a jet expansion. Phys. Chem. Chem. Phys. 2023, 25, 16264–16272. 10.1039/D3CP01035J. [DOI] [PubMed] [Google Scholar]
  60. Ali S.; Hassan M.; Islam A.; Ahmad F. A Review of Methods Available to Estimate Solvent-Accessible Surface Areas of Soluble Proteins in the Folded and Unfolded States. Current Protein & Peptide Science 2014, 15, 456–476. 10.2174/1389203715666140327114232. [DOI] [PubMed] [Google Scholar]
  61. Scalmani G.; Frisch M. J. Continuous surface charge polarizable continuum models of solvation. I. General formalism. J. Chem. Phys. 2010, 132, 114110 10.1063/1.3359469. [DOI] [PubMed] [Google Scholar]
  62. York D. M.; Karplus M. A Smooth Solvation Potential Based on the Conductor-Like Screening Model. J. Phys. Chem. A 1999, 103, 11060–11079. 10.1021/jp992097l. [DOI] [Google Scholar]
  63. Im W.; Lee M. S.; Brooks C. L. Generalized Born Model with a Simple Smoothing Function. J. Comput. Chem. 2003, 24, 1691–1702. 10.1002/jcc.10321. [DOI] [PubMed] [Google Scholar]
  64. Lange A. W.; Herbert J. M. Polarizable Continuum Reaction-Field Solvation Models Affording Smooth Potential Energy Surfaces. J. Phys. Chem. Lett. 2010, 1, 556–561. 10.1021/jz900282c. [DOI] [Google Scholar]
  65. Lee M. S.; Feig M.; Salsbury F. R.; Brooks C. L. New analytic approximation to the standard molecular volume definition and its application to generalized born calculations. J. Comput. Chem. 2003, 24, 1821–1821. 10.1002/jcc.10367. [DOI] [PubMed] [Google Scholar]
  66. Pascual-Ahuir J. L.; Silla E. GEPOL: An improved description of molecular surfaces. I. Building the spherical surface set. J. Comput. Chem. 1990, 11, 1047–1060. 10.1002/jcc.540110907. [DOI] [Google Scholar]
  67. Lebedev V. I.; Laikov D. N. A quadrature formula for the sphere of the 131st algebraic order of accuracy. Doklady Math. 1999, 477–481. [Google Scholar]
  68. Ehlert S.; Stahn M.; Spicher S.; Grimme S. Robust and Efficient Implicit Solvation Model for Fast Semiempirical Methods. J. Chem. Theory Comput. 2021, 17, 4250–4261. 10.1021/acs.jctc.1c00471. [DOI] [PubMed] [Google Scholar]
  69. tblite - A light-weight tight-binding framework. https://github.com/tblite/tblite, January 29, 2025.
  70. Larsen A. H.; Mortensen J. J.; Blomqvist J.; Castelli I. E.; Christensen R.; Dułak M.; Friis J.; Groves M. N.; Hammer B.; Hargus C.; et al. The atomic simulation environment—a Python library for working with atoms. J. Phys.: Condens. Matter 2017, 29, 273002 10.1088/1361-648X/aa680e. [DOI] [PubMed] [Google Scholar]
  71. libpvol - Implementation of a PV Hamiltonian contribution. https://github.com/neudecker-group/libpvol, January 29, 2025.
  72. Epifanovsky E.; Gilbert A. T. B.; Feng X.; Lee J.; Mao Y.; Mardirossian N.; Pokhilko P.; White A. F.; Coons M. P.; Dempwolff A. L.; et al. Software for the frontiers of quantum chemistry: An overview of developments in the Q-Chem 5 package. J. Chem. Phys. 2021, 155, 084801 10.1063/5.0055522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  74. Rowland R. S.; Taylor R. Intermolecular nonbonded contact distances in organic crystal structures: Comparison with distances expected from van der Waals Radii. J. Phys. Chem. 1996, 100, 7384–7391. 10.1021/jp953141+. [DOI] [Google Scholar]
  75. Bondi A. van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. 10.1021/j100785a001. [DOI] [Google Scholar]
  76. toml-f - TOML parser implementation for data serialization and deserialization in Fortran. https://github.com/toml-f/toml-f, January 29, 2025.
  77. McClain B. L.; Ben-Amotz D. Global Quantitation of Solvent Effects on the Isomerization Thermodynamics of 1,2-Dichloroethane and trans −1,2-Dichlorocyclohexane. J. Phys. Chem. B 2002, 106, 7882–7888. 10.1021/jp0140973. [DOI] [Google Scholar]
  78. Ikawa S.; Whalley E. Effect of pressure on molecular conformations. V. The internal rotation angle of 1,2-dichloroethane by infrared spectroscopy. J. Chem. Phys. 1984, 81, 1620–1625. 10.1063/1.447876. [DOI] [Google Scholar]
  79. Taniguchi Y.; Takaya H.; Wong P. T. T.; Whalley E. Effect of pressure on molecular conformations. II. T r a n s – g a u c h e equilibrium of 1,2-dichloroethane and 1,2-dibromoethane. J. Chem. Phys. 1981, 75, 4815–4822. 10.1063/1.441908. [DOI] [Google Scholar]
  80. Seki W.; Choi P.-K.; Takagi K. Ultrasonic relaxation and the volume difference between the rotational isomers in 1,2-dichloroethane. Chem. Phys. Lett. 1983, 98, 518–521. 10.1016/0009-2614(83)80101-8. [DOI] [Google Scholar]
  81. Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  82. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  83. Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
  84. Grimme S. Density functional theory with London dispersion corrections. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 211–228. 10.1002/wcms.30. [DOI] [Google Scholar]
  85. Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  86. Wu J.; Tang J.; Wang H.; Qi Q.; Fang X.; Liu Y.; Xu S.; Zhang S. X.-A.; Zhang H.; Xu W. Reversible Piezofluorochromic Property and Intrinsic Structure Changes of Tetra(4-methoxyphenyl)ethylene under High Pressure. J. Phys. Chem. A 2015, 119, 9218–9224. 10.1021/acs.jpca.5b02362. [DOI] [PubMed] [Google Scholar]
  87. Wilson A. K.; Woon D. E.; Peterson K. A.; Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. IX. The atoms gallium through krypton. J. Chem. Phys. 1999, 110, 7667–7676. 10.1063/1.478678. [DOI] [Google Scholar]
  88. Woon D. E.; Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. 10.1063/1.464303. [DOI] [Google Scholar]
  89. Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  90. Balabanov N. B.; Peterson K. A. Systematically convergent basis sets for transition metals. I. All-electron correlation consistent basis sets for the 3d elements Sc-Zn. J. Chem. Phys. 2005, 123, 064107 10.1063/1.1998907. [DOI] [PubMed] [Google Scholar]
  91. Yanai T.; Tew D. P.; Handy N. C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  92. Bauernschmitt R.; Ahlrichs R. Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory. Chem. Phys. Lett. 1996, 256, 454–464. 10.1016/0009-2614(96)00440-X. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp4c08065_si_001.zip (76.2KB, zip)

Articles from The Journal of Physical Chemistry. a are provided here courtesy of American Chemical Society

RESOURCES