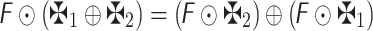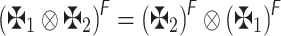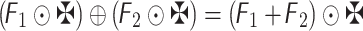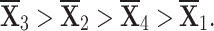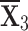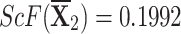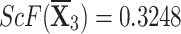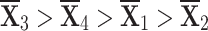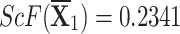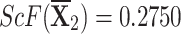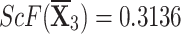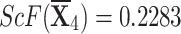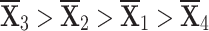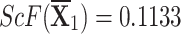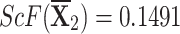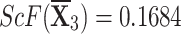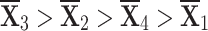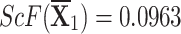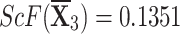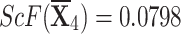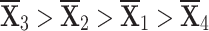Abstract
The q-rung picture fuzzy sets act as a proficient and extensive extension of q-rung orthopair fuzzy sets and picture fuzzy sets within fuzzy set theory. The parameter q and the three real-valued membership functions enable us to perform better than existing approaches in describing mysterious data. Here, we built aggregation operators for the q-RPLFS framework using the Schweizer and Sklar (SS) operations. We introduced and analyzed several kinds of aggregation operators in detail, including the q-rung picture linguistic SS weighted averaging operator (q-RPLSSAO) and the q-rung picture linguistic SS geometric operator (q-RPLSSGO). The q-RPLFS framework for solving MADM problems contains SS t-norms and t-conorms, allowing the generated operators to make the information aggregation technique more flexible than existing ones. Additionally, we described a numerical example to support the applicability and advantages of the suggested approach. To confirm the accuracy and feasibility of the suggested approaches, comparison results with the current methods are also provided.
Keywords: Q-rung orthopair fuzzy sets, Q-rung picture linguistic fuzzy sets, Power aggregation operators, Schweizer and Sklar (SS) norms, MADM
Subject terms: Applied mathematics, Computational science
Introduction
A decision maker can use the MADM technique to analyze and select from a predetermined set of options depending on their values and preferences. When making decisions, we don’t select from as many options as we can; instead, we pick the one that best suits our needs, demands, etc. Zadeh1established the fuzzy set (FS) theory with the goal of enhancing the adaptability of the assessments that aid in the method of decision-making (DM)2,3. The idea has been very successful in the fields of computing, engineering, and business studies4–9. Owing to flaws in FS, particularly the reality that it only includes a partial membership (MemD), Atanassov10proposed the idea of an intuitionistic FS, which is distinguished by both a nonmembership (Non-MemD) and a MemD. Picture FS originated by Cuong11 as an extended version of IFS. Because it permits refusal, which are commonly included in expert judgments along with comfort and displeasure levels, Picture FS prevails over IFS. The elements that symbolize MemD, Neutral-MemD, and Non-MemD for each Picture FS are triplets 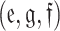 ; these elements must meet the prerequisite
; these elements must meet the prerequisite  . The element’s connected Indeterminacy Deg. is then
. The element’s connected Indeterminacy Deg. is then  . Yager12 developed the concept of Pythagorean FS, which substitutes the more broad constraint
. Yager12 developed the concept of Pythagorean FS, which substitutes the more broad constraint 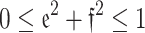 for the requirement
for the requirement  of IFS. Yager13 introduced the q-rung orthopair FS, which generalized the constraint of orthopair membership degrees (MemDs) to
of IFS. Yager13 introduced the q-rung orthopair FS, which generalized the constraint of orthopair membership degrees (MemDs) to 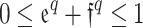 . This further restricted the term of ambiguity. Gundogdu and Kahraman14created an improved representation called the spherical FS in order to reinforce the concept of Picture FS15. The restriction in Picture FS is replaced by
. This further restricted the term of ambiguity. Gundogdu and Kahraman14created an improved representation called the spherical FS in order to reinforce the concept of Picture FS15. The restriction in Picture FS is replaced by 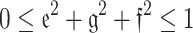 in SFS. The idea of q-RPFS, which is simply constrained by the rule
in SFS. The idea of q-RPFS, which is simply constrained by the rule 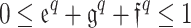 , was originally proposed by Li et al.16. A q-RPFS is more useful in decision-making (DM) situations than a Picture FS or a Spherical FS since, when q=1, it reduces to Picture FS or 1-RPFS; for q=2, it falls to Spherical FS or 2-RPFS; for q=3, it falls to 3-RPFS; and for q=4, it turns into 4-RPFS. q-RPFS meets
, was originally proposed by Li et al.16. A q-RPFS is more useful in decision-making (DM) situations than a Picture FS or a Spherical FS since, when q=1, it reduces to Picture FS or 1-RPFS; for q=2, it falls to Spherical FS or 2-RPFS; for q=3, it falls to 3-RPFS; and for q=4, it turns into 4-RPFS. q-RPFS meets 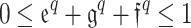 , wherein
, wherein  . The additional problem is that, in certain cases, decision-makers are happier with qualitative choices than quantitative ones because they are pressed for time or possess relevant experience. The linguistic factors proposed by Zadeh17are effective tools for modeling these situations. Wang and Li18have noted that linguistic factors are limited in their ability to convey the qualitative preferences of decision-makers. They are not capable of accounting for MemD or Non-MemD of a component concerning a specific idea. They then put up the idea of an intuitionistic linguistic FS. Additional extensions include picture FLS of Liu and Zhang19 and interval-valued Pythagorean FLS of Du et al.20. Thus, this research combines linguistic factors with q-RPFSs to put forward the idea of q-RPLS.
. The additional problem is that, in certain cases, decision-makers are happier with qualitative choices than quantitative ones because they are pressed for time or possess relevant experience. The linguistic factors proposed by Zadeh17are effective tools for modeling these situations. Wang and Li18have noted that linguistic factors are limited in their ability to convey the qualitative preferences of decision-makers. They are not capable of accounting for MemD or Non-MemD of a component concerning a specific idea. They then put up the idea of an intuitionistic linguistic FS. Additional extensions include picture FLS of Liu and Zhang19 and interval-valued Pythagorean FLS of Du et al.20. Thus, this research combines linguistic factors with q-RPFSs to put forward the idea of q-RPLS.
The aggregation operator study is centered on two primary domains. The operational norms come foremost. Since algebraic operational rules are a specific instance of Archimedean norms, they are now employed by the majority of aggregation operators that employ q-RPLFS. SS norms meet the standards of Archimedean norms21. However, because SS operations include a controllable parameter, they are far more adaptable compared to other current methods. Because of their capacity to react to particular requirements, individuals are able to draw predictions that are both ebullient and miserable, which helps those who make decisions balance risk effectively. Because of their versatility, SS norms have drawn the interest of numerous scholars.
Motivation
The motivation for this work is that we first worked on the generalized q-ROPFS environment with linguistic terms that convey the situation in a broader sense than previous frames. When evaluating a worker, a manager may state, “very competent (0.8), not incompetent (0.7), with certain reservations (0.5)” to provide a more precise estimation of efficiency, then we need to use a q-RPLF set. On the other hand, due to the parameter 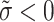 , aggregation operators that employ SS operations such as q-RPLSSWA and q-RPLSSWG, are preferable. We may examine how altering the parameter
, aggregation operators that employ SS operations such as q-RPLSSWA and q-RPLSSWG, are preferable. We may examine how altering the parameter  can increase reliability. Compared to present operators, these potential operators offer greater versatility in situations in life.
can increase reliability. Compared to present operators, these potential operators offer greater versatility in situations in life.
We have talked about the remaining portions below:
In section “Preliminaries”, we elaborated some preliminaries regarding q-RPFS as well as an introduction and review of the literature.
In section "Deployment of generalized operations and q-rung picture linguisticSchweizer and Sklar aggregation operators", we developed some generalized aggregation operators relying on SS operations.
In section "Method for Tackling the MADM Problem", we discussed the methodology and in section “Application”, we mentioned application of our proposed aggregation operators.
In section “Sensitivity Analysis”, we did sensitivity analysis and in section “Comparison analysis”, we covered a comparison of our suggested operators via existing ones and the validation test and discussion were also described.
We had predicted our conclusion and future directions in section “Conclusions”.
Preliminaries
Here, we outline fundamental ideas to show the innovation of our theory. We discuss some significant studies on fuzzy sets (FSs) in the subsequent chapter. We examine a variety of fuzzy sets (FSs) including interval-valued FSs, intuitionistic FSs, Pythagorean FSs, picture FSs, q-rung picture FSs, q-rung picture linguistic FSs, and many others. We look additionally at the operations and scoring functions (ScF) and accuracy functions (AcF) defined for all kinds of FS. Moreover, to further develop generalized aggregation operators, we offer norm and co-norm functions.
Definition 1
22 A q-rung orthopair FS (as depicted in figure 1) on  is expressed as below:
is expressed as below:
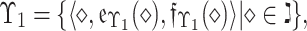 |
1 |
wherein  represents the MemD of
represents the MemD of 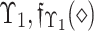 represents the Non-MemD of
represents the Non-MemD of  and
and 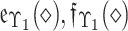 fulfill the condition:
fulfill the condition: 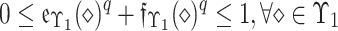 . The indeterminacy Deg. of
. The indeterminacy Deg. of  in
in  is:
is:
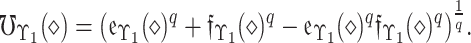 |
Fig. 1.

q-rung orthopair fuzzy set.
Definition 2
23 A picture FS on  is expressed as below:
is expressed as below:
 |
2 |
wherein 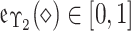 known as the MemD of
known as the MemD of 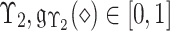 known as Neural-MemD of
known as Neural-MemD of  and
and 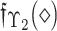 known as Non-MemD of
known as Non-MemD of  and
and  . The indeterminacy Deg. of
. The indeterminacy Deg. of  in
in 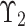 is:
is:
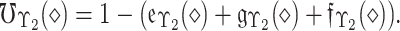 |
Definition 3
24 A q-rung picture FS (as illustrated in figure 2) on  is expressed as bellow:
is expressed as bellow:
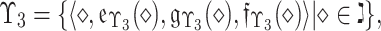 |
3 |
wherein  known as MemD of
known as MemD of 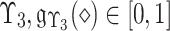 known as Neutral-MemD of
known as Neutral-MemD of 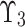 and
and  known as Non-MemD of
known as Non-MemD of 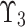 and
and 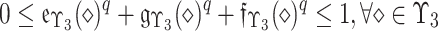 . The indeterminacy Deg. of
. The indeterminacy Deg. of  in
in 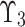 is:
is:
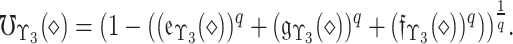 |
Fig. 2.

q-rung picture fuzzy set.
Definition 4
25 Suppose 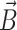 is a continuous linguistic term set of
is a continuous linguistic term set of 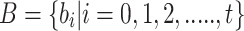 , then a q-rung picture linguistic FS on
, then a q-rung picture linguistic FS on  is expressed as bellow:
is expressed as bellow:
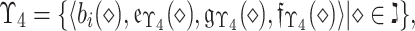 |
4 |
wherein  known as MemD of
known as MemD of 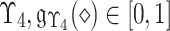 known as Neutral-MemD of
known as Neutral-MemD of  and
and 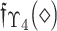 known as Non-MemD of
known as Non-MemD of 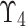 and
and  and
and 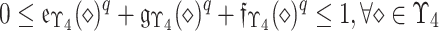 . The indeterminacy Deg. of
. The indeterminacy Deg. of  in
in 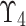 is:
is:
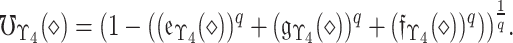 |
For more simplicity, 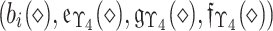 is referred as q-rung picture linguistic fuzzy number (q-RPLFN) and is represented as
is referred as q-rung picture linguistic fuzzy number (q-RPLFN) and is represented as 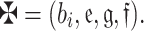
Linguistic Scale Function (LSF)
It’s widely recognized that whenever fuzzy numbers interact with linguistic ideas straight away, operations can’t be performed easily. Investigating and describing novel linguistic scale functions for linguistic modeling is essential to establish the operations of q-RPLFNs. The newly developed linguistic scale function will give linguistic terms distinct linguistic values based on the context to facilitate the versatile display of linguistics and make more efficient use of information. It might be an increase or decrease in the absolute divergence between consecutive linguistic subscripts in linguistic evaluation scales where the linguistic subscripts grow. In practice, the linguistic scale function that is stated below is better. This is due to the flexibility of this function, which can produce more predictable outcomes based on various semantic interpretations. The element 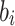 in B has a strictly monotonically increasing conjunction with its subscript i.
in B has a strictly monotonically increasing conjunction with its subscript i.
The LSF26 is a mapping 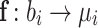 wherein
wherein 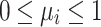 and
and 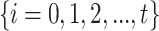 such that
such that 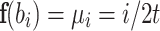 .
.
When the decision-makers use the linguistic phrase 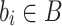 , their choices are expressed in the symbol
, their choices are expressed in the symbol 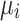 .
.
The aforementioned function is continuous and increases monotonically, implying that there is a one-to-one function due to monotonicity and the existence of 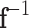 .
.
Definition 5
16,27 Suppose that 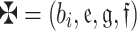 is a q-RPLFN, then the ScF for
is a q-RPLFN, then the ScF for  is demonstrated as:
is demonstrated as:
 |
5 |
Definition 6
16,27 Suppose  is a q-RPLFN, then the AcF for
is a q-RPLFN, then the AcF for  is demonstrated as:
is demonstrated as:
 |
6 |
Definition 7
16,27 Consider 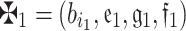 and
and 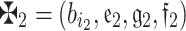 are any two q-RPLFNs,
are any two q-RPLFNs,  and
and  are score functions of
are score functions of  and
and  correspondingly,
correspondingly,  and
and  are the accuracy functions of
are the accuracy functions of 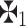 and
and 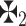 raccordingly.
raccordingly.
If
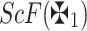 >
> 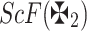 , then
, then  >
> 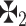
- If
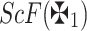 =
=  , then
, then - If
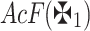 >
> 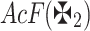 , then
, then 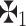 >
> 
- If
 =
=  , then
, then  =
= 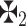
Yager28 pioneered the power average operator, permitting input values to support each other in the aggregation level via SS t-norms and t-conorms-based procedures.
Definition 8
29 Consider  is an array of q-RPLFNs. Then, the Power Average operator (PA) is stated as
is an array of q-RPLFNs. Then, the Power Average operator (PA) is stated as
 |
7 |
wherein  and
and  for
for 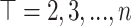 .
.
Utilizing the PA operator and geometric mean, Xu and Yager30 developed the PG operator.
Definition 9
29 Consider 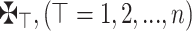 is an array of q-RPLFNs. Then, The (PG) Power Geometric operator is stated as
is an array of q-RPLFNs. Then, The (PG) Power Geometric operator is stated as
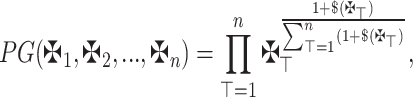 |
8 |
wherein the concept provides the previously described meaning.
Norm and Co-norm
A quick explanation of the relevant ideas and the background information on norm and co-norm is provided in the following part.
Definition 10
25 A function  , where
, where 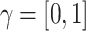 is known as t-norm if
is known as t-norm if
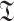 is associative, continuous, and monotonic.
is associative, continuous, and monotonic. .
.
Definition 11
25 A function 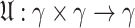 , where
, where  is known as t-conorm if
is known as t-conorm if
 is associative, continuous, and monotonic.
is associative, continuous, and monotonic.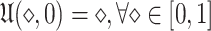 .
.
We then describe two distinct kinds of t-norms and t-conorms as follows.
Definition 12
29 The Schwaizer and Sklar triangular norm may be demonstrated as
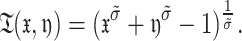 |
Similarly, the Schweizer and Sklar triangular conorm can be stated as
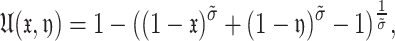 |
wherein  and
and  .
.
Deployment of generalized operations and q-rung picture linguistic Schweizer and Sklar aggregation operators
In this section, we define the generalized operations for q-rung picture linguistic FNs by using the combination of a q-rung picture FS and a linguistic FS. we prove some properties of derived operations. Additionally, we derive generalized operators by employing the notion of generalized operations.
Generalized operations
This subsection advances the current q-RP linguistic operational rules to a more generic form, based on Schweizer and Sklar (SS) norms.
Definition 13
Assume that  ,
,  , and
, and 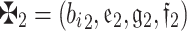 are any q-RPLFNs and
are any q-RPLFNs and 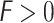 and
and 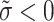 , then
, then
- Additive operation:

- Multiplication operation:
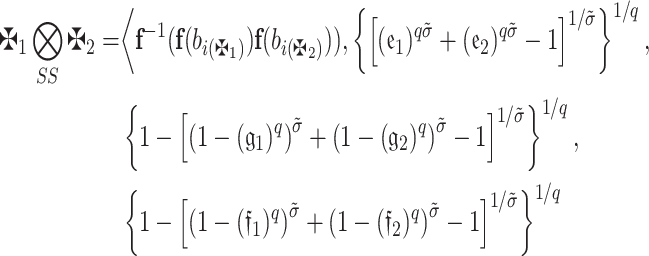
- Scalar-multiplication operation:
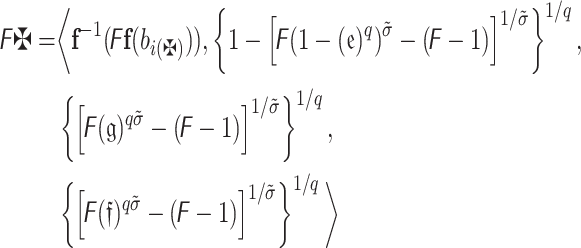
- Power operation:

Theorem 1
Consider that 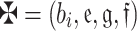 ,
,  , and
, and 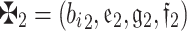 be any three q-RPLFNs and
be any three q-RPLFNs and 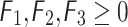 are three scalars, then the below-mentioned properties hold.
are three scalars, then the below-mentioned properties hold.
Proof
It is trivial to be proved. 
q-rung picture linguistic Schweizer and Sklar weighted averaging operator
Definition 14
29 Assume that 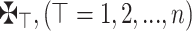 is an array of q-RPLFNs and
is an array of q-RPLFNs and 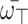 is WV lies within 0 and 1 and whose sum equals 1. Then, q-RPLSSWAO is a mapping
is WV lies within 0 and 1 and whose sum equals 1. Then, q-RPLSSWAO is a mapping 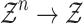 so that
so that
 |
9 |
wherein 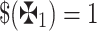 and
and 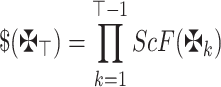 for
for 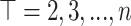 .
.
Theorem 2
Assume that  for
for  is an array of q-RPLFNs and
is an array of q-RPLFNs and 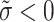 . Also, assume that
. Also, assume that 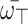 is WV lies within 0 and 1 and whose sum equals 1. Then the aggregation utilizing the q-RPLSSWA operator which relies on SS operations is still a q-RPLFN and fulfills
is WV lies within 0 and 1 and whose sum equals 1. Then the aggregation utilizing the q-RPLSSWA operator which relies on SS operations is still a q-RPLFN and fulfills
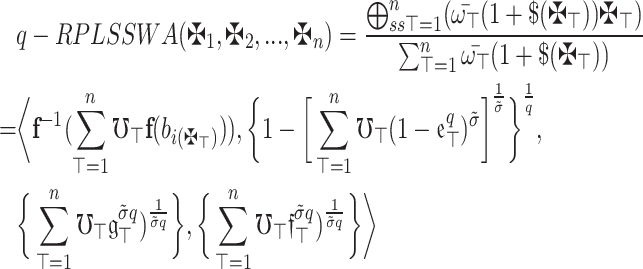 |
10 |
where 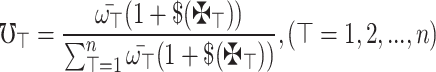
Proof
We will initially make the following outcome.
For any  ,
,
 |
11 |
The preceding equation will be proven by mathematical induction. Take  ,
,
 |
For  = 2, the outcome is valid. Consequently, for
= 2, the outcome is valid. Consequently, for 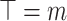 , it will be true.
, it will be true.
 |
Now, consider 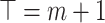 . Then by definition 13.
. Then by definition 13.
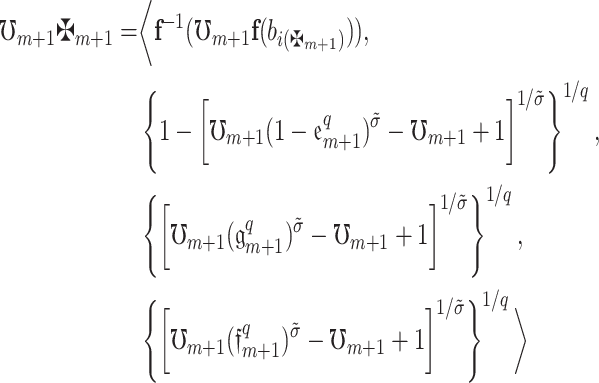 |
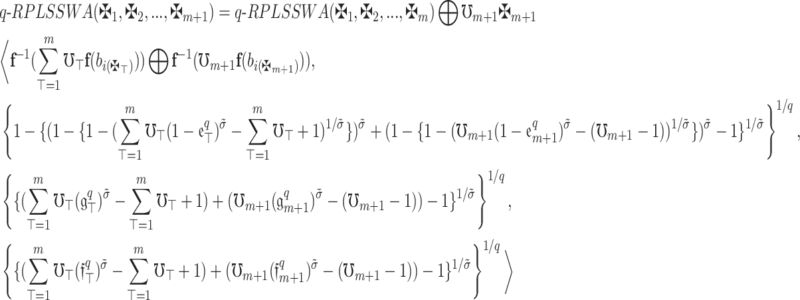 |
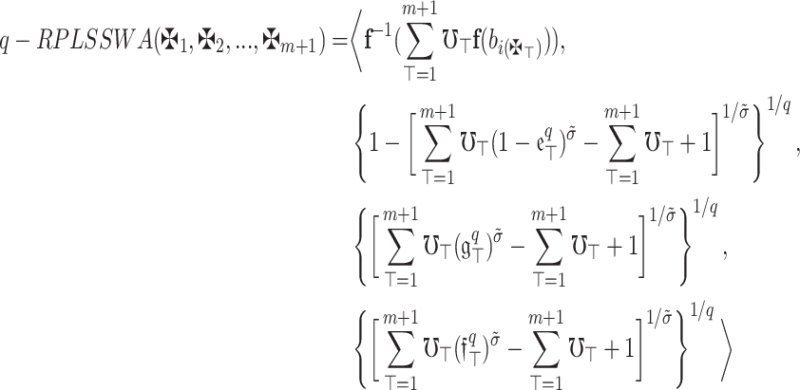 |
For  , the conclusion is thus valid.
, the conclusion is thus valid.
The assertion is valid for any value of  , so long as
, so long as  and
and  are satisfied.
are satisfied.
Thus, the theorem has been proved. 
The following introduces the intriguing properties of the recommended aggregation operators, such as idempotency, monotonicity, boundedness, and symmetry:
Theorem 3
(Idempotency) Consider  be an array of q-RPLFNs. Also, assume that
be an array of q-RPLFNs. Also, assume that 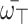 is WV lies within 0 and 1 and whose sum equals 1. If
is WV lies within 0 and 1 and whose sum equals 1. If 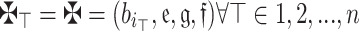 ,then:
,then:
 |
12 |
Proof
Here,
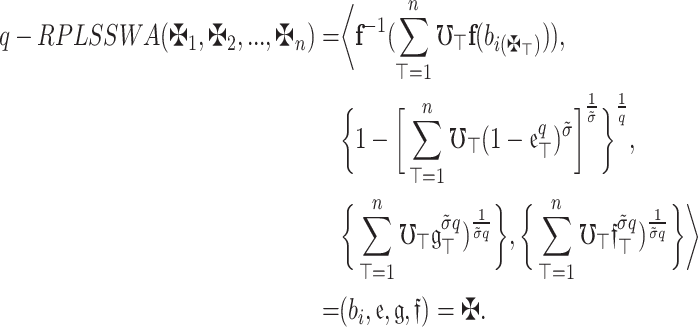 |
Hence, the outcome is so shown. 
Theorem 4
(Monotonicity) Assume that 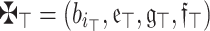 and
and 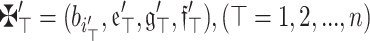 are an array of q-RPLFNs. Also, assume that
are an array of q-RPLFNs. Also, assume that 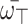 is WV lies within 0 and 1 and whose sum equals 1. If
is WV lies within 0 and 1 and whose sum equals 1. If  then:
then:
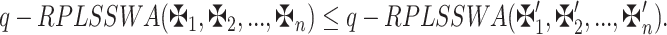 |
13 |
Proof
Here,
 |
and
 |
Because 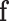 tends to increase monotonically, therefore
tends to increase monotonically, therefore  .
.
Since 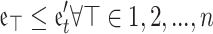 ,
,
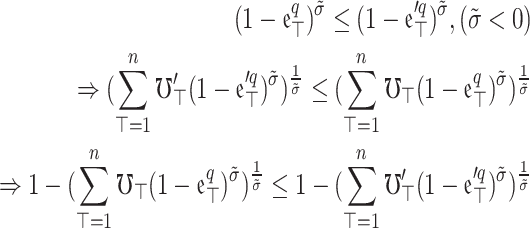 |
In an analogous way, if 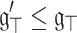 , it may be expressed as
, it may be expressed as
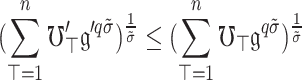 |
Further, if 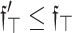 , it may be expressed as
, it may be expressed as
 |
This means
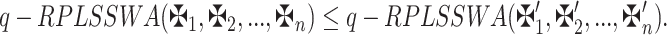 |
Thus, the proof is finished. 
Theorem 5
(Boundedness) Consider 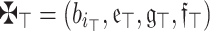 is an array of q-RPLFNs. Also, assume that
is an array of q-RPLFNs. Also, assume that 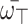 is WV lies within 0 and 1 and whose sum equals 1, then
is WV lies within 0 and 1 and whose sum equals 1, then
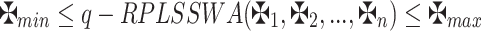 |
where 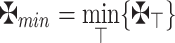 and
and  .
.
Proof
Considering that
 |
Consequently, based on the above Theorems 3and 4.
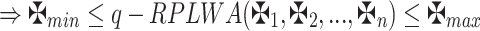 |
Theorem 6
(Symmetry) Assume that 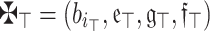 is an array of q-RPLFNs. If
is an array of q-RPLFNs. If 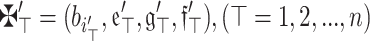 is any permutation of
is any permutation of 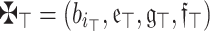 , following this, we possess:
, following this, we possess:
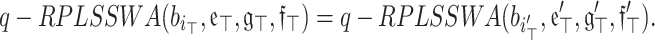 |
14 |
Proof
It’s easy to see how. Thus, it is skipped. 
Remark 7
Whenever  =0, then a specific version of the
=0, then a specific version of the 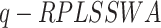 operator occurs. In this instance,
operator occurs. In this instance,
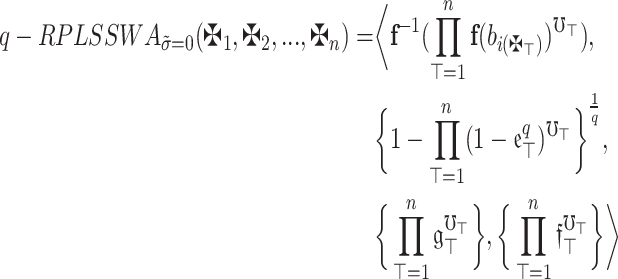 |
wherein  .
.
q-Rung Picture Linguistic Schweizer and Sklar Weighted Geometric Operator
Definition 15
29 Assume that 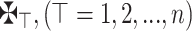 is an array of q-RPLFNs and
is an array of q-RPLFNs and 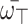 is WV lies within 0 and 1 and whose sum equals 1. Then, q-RPLSSWGO is a mapping
is WV lies within 0 and 1 and whose sum equals 1. Then, q-RPLSSWGO is a mapping  so that
so that
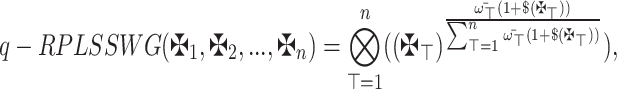 |
15 |
wherein  and
and 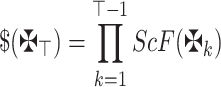 for
for  .
.
Theorem 8
Assume that  for
for  is an array of q-RPLFNs and
is an array of q-RPLFNs and 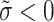 . Also, assume that
. Also, assume that 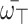 is WV lies within 0 and 1 and whose sum equals 1. Then the aggregation utilizing the q-RPLSSWG operator which relies on SS operations is still a q-RPLFN and fulfills
is WV lies within 0 and 1 and whose sum equals 1. Then the aggregation utilizing the q-RPLSSWG operator which relies on SS operations is still a q-RPLFN and fulfills
 |
16 |
where 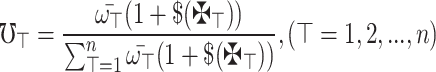
Proof
This theorem is proved in the similar manner as Theorem 2. We skip out since it is easy to demonstrate. 
Similar to the q-RPLSSWA operator, the q-RPLSSWG operator exhibits a few intriguing characteristics, which are listed below (without evidence):
Theorem 9
(Idempotency) Consider 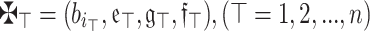 be an array of q-RPLFNs. Also, assume that
be an array of q-RPLFNs. Also, assume that 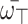 is WV lies within 0 and 1 and whose sum equals 1. If
is WV lies within 0 and 1 and whose sum equals 1. If 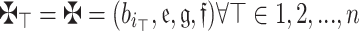 ,then:
,then:
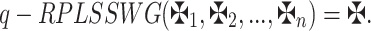 |
17 |
Theorem 10
(Monotonicity) Assume that 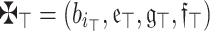 and
and 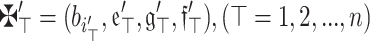 are an array of q-RPLFNs. Also, assume that
are an array of q-RPLFNs. Also, assume that  is WV lies within 0 and 1 and whose sum equals 1. If
is WV lies within 0 and 1 and whose sum equals 1. If 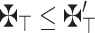 then:
then:
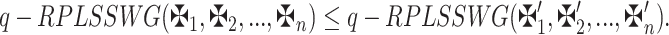 |
18 |
Theorem 11
(Boundedness) Consider  is an array of q-RPLFNs. Also, assume that
is an array of q-RPLFNs. Also, assume that 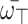 is WV lies within 0 and 1 and whose sum equals 1, then
is WV lies within 0 and 1 and whose sum equals 1, then
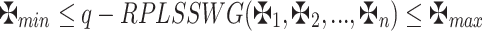 |
where 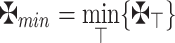 and
and 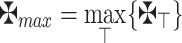 .
.
Theorem 12
(Symmetry) Assume that 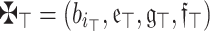 is an array of q-RPLNs. If
is an array of q-RPLNs. If  is any permutation of
is any permutation of 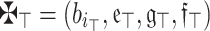 , following this, we possess:
, following this, we possess:
 |
19 |
Method for tackling the MADM problem
Assume that we have 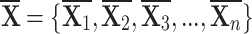 is any finite array of n alternatives. We have finite set of m attributes like
is any finite array of n alternatives. We have finite set of m attributes like 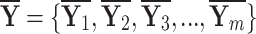 . They will gather the information in the form of q-RPLFNs so that
. They will gather the information in the form of q-RPLFNs so that 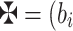 ,
, Wherein,
Wherein, 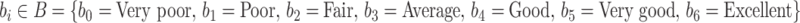 and the prerequisite for the quantitative portion of
and the prerequisite for the quantitative portion of  is
is  .
.
-
Step 1
Data collection:
Collect the evaluation data from the decision-makers via matrix
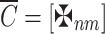 as
as 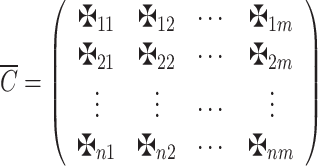
-
Step 2
Normalization:
In this stage, the decision-matrix DM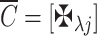 is changed to become the normalized-matrix NM
is changed to become the normalized-matrix NM 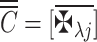 with the subsequent setup:
with the subsequent setup:
wherein for any q-RPLNs,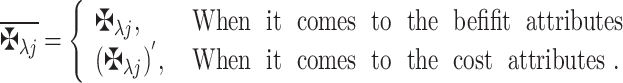
20 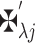 is referred to as
is referred to as 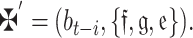
21 -
Step 3
Aggregation:
Aggregate the q-RPLFNs (j=1,2,3,...,m) for all alternative
(j=1,2,3,...,m) for all alternative  into the specific choice value
into the specific choice value  with the known WV
with the known WV 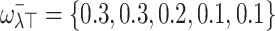 whose sum equals 1, utilizing the developed q-RPLSSWA (or q-RPLSSWG) operators.
whose sum equals 1, utilizing the developed q-RPLSSWA (or q-RPLSSWG) operators.
where
22 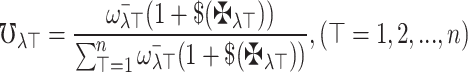 Or,
Or,
where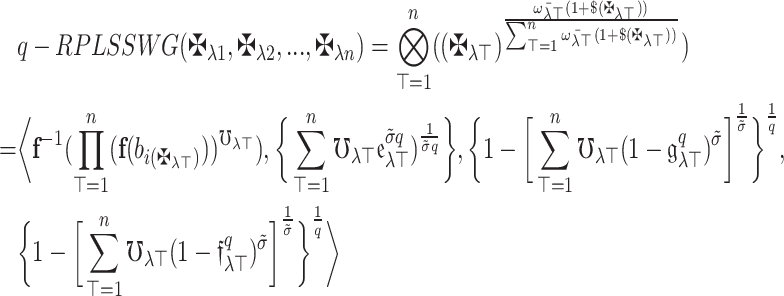
23 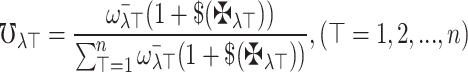
-
Step 4
Evaluate the score values: We evaluated the score values
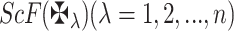 corresponding to all q-RPLNs by utilizing the equation 5 (When score values are equal then we use accuracy function as in equation 6).
corresponding to all q-RPLNs by utilizing the equation 5 (When score values are equal then we use accuracy function as in equation 6). -
Step 5
Ranking: Sort all of the alternatives
 to select the best one in accordance with the above getting score values
to select the best one in accordance with the above getting score values  (or accuracy values).
(or accuracy values).
To navigate the entire procedure clearly, we offer the flowchart that is shown in figure 3.
Fig. 3.
Flowchart of suggested methodology.
Application
This section emphasizes how the built model relates to the MADM issue in the q-rung picture linguistic framework.
A depiction of selecting a smart home security system is used in this section to have a look at the results and practical aspects of the proposed strategy. The progressed technique is not only confined to the smart home security system selection problem and can be implemented to highlight different decision-making troubles.
Many security solutions are brought into existence with the help of technology in order to cope with the demand for home safety. Investing in smart home security systems has gained much significance in the present era of modern living by facilitating mankind with plenty of ease along peace of mind. Without physical availability, our homes can be checked remotely, alerts can be recorded and that is how the safety of our beloved relations and possessions can be guaranteed.
The landlord wants to buy a smart home security system and is willing to get information about the system that functions amazingly from other choices that can be seen in the market. He/she goes to his/her friends and asks for suggestions as they are experts in choosing security systems (see figure 4). It can be observed that the majority of the security systems are evaluated depending on the following criteria: cost  , reliability
, reliability  , user-friendliness
, user-friendliness  , features
, features 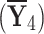 , and customer support
, and customer support 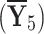 . Then, he/she decides to go with any of the following four best-selling systems but gets puzzled about which one to purchase: System A
. Then, he/she decides to go with any of the following four best-selling systems but gets puzzled about which one to purchase: System A 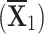 , System B
, System B 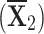 , System C
, System C  , and System D
, and System D  .
.
Fig. 4.

Security systems for home.
Without any ambiguity, it can be seen that the selection way of smart home security systems is a MADM (Multi-Attribute Decision Making) problem including five criteria  and four alternatives
and four alternatives 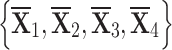 and expert
and expert 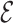 . Later, the progressed analysis can be considered to search for the solution of our choice.
. Later, the progressed analysis can be considered to search for the solution of our choice.
-
Step 1
: Data Collection (as illustrated in Table 1).
-
Step 2
: Normalize the above q-RPLFNs utilizing the suggested methodology as depicted in Table 2.
-
Step 3
: First, we employed the known weights
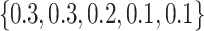 to assess the matrix
to assess the matrix  . Next, we utilized the aggregation operators (q-RPLSSWA and q-RPLSSWG) associated with
. Next, we utilized the aggregation operators (q-RPLSSWA and q-RPLSSWG) associated with  that we originally had in the preceding phase.We acquired the subsequent outcomes for
that we originally had in the preceding phase.We acquired the subsequent outcomes for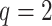 and the parameter
and the parameter 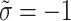 :
:
and then,
-
q-RPLSSWA:
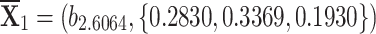 ,
, 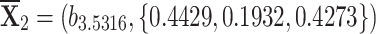 ,
,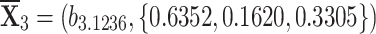 , and
, and 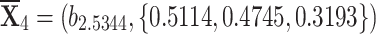
-
q-RPLSSWG:
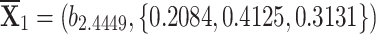 ,
,  ,
,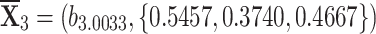 , and
, and 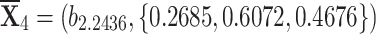
-
-
Step 4We evaluate the score values for each choice in this stage.
-
q-RPLSSWA:
 ,
, 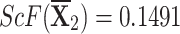 ,
,  , and
, and 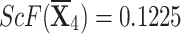 .
. -
q-RPLSSWG:
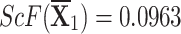 ,
, 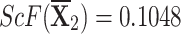 ,
, 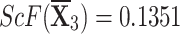 , and
, and  .
.
-
- Step 5
Table 1.
q-RPL decision-matrix taken by  .
.
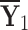
|
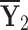
|
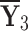
|
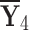
|
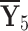
|
|
|---|---|---|---|---|---|
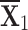
|
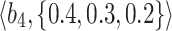
|
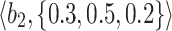
|
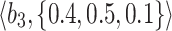
|
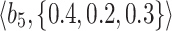
|

|
|
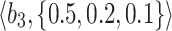
|
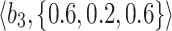
|

|
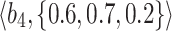
|
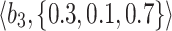
|

|
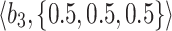
|
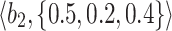
|
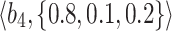
|
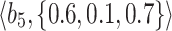
|

|
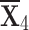
|

|
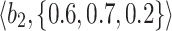
|
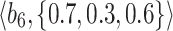
|
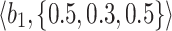
|
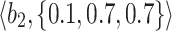
|
Table 2.
Normalized-Matrix.

|
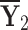
|
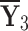
|
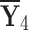
|
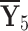
|
|
|---|---|---|---|---|---|
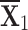
|
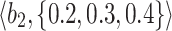
|

|
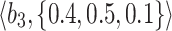
|
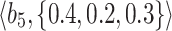
|
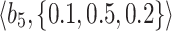
|
|
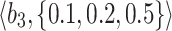
|

|

|
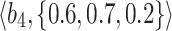
|

|
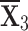
|
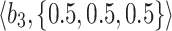
|

|
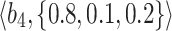
|
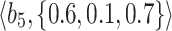
|
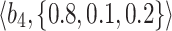
|
|
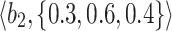
|
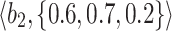
|

|
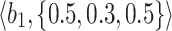
|
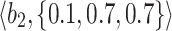
|
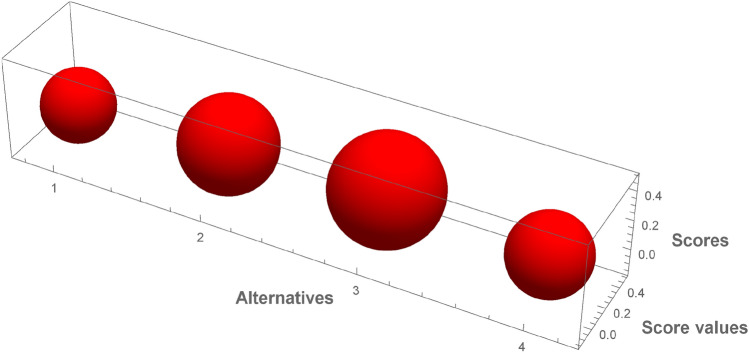
Fig. 5.
Graphical interpretation of score values for  by employing q-RPLSSWAO.
by employing q-RPLSSWAO.
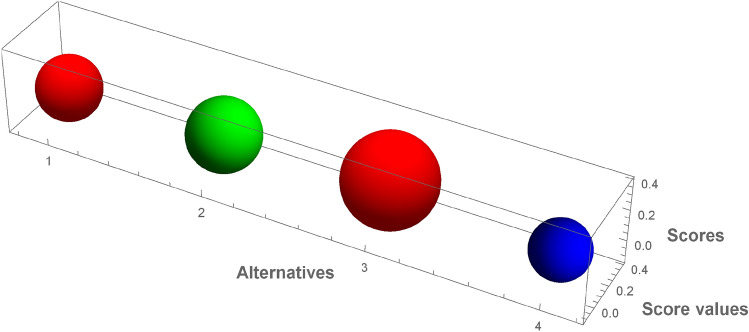
Fig. 6.
Graphical interpretation of score values for  by employing q-RPLSSWGO.
by employing q-RPLSSWGO.
Sensitivity analysis
The financial simulation termed sensitivity analysis is employed to examine what variations in input elements affect track-related factors. Predictions obtained through this method depend upon key variables, such as the sensitivity of a parameter (represented as 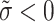 ) to specific weights. Both of the sequences constructed by the q-RPLSSWA and q-RPLSSWG operators have options that vary in some respect, but
) to specific weights. Both of the sequences constructed by the q-RPLSSWA and q-RPLSSWG operators have options that vary in some respect, but 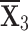 remains the optimal choice. The reduction of ambiguity in mathematical simulations, such as changes in the source values, is made possible by sensitivity analysis. When used in conjunction with ambiguity examination, it is commonly used to improve the reliability of evaluation and modeling that rely on assertions about input fidelity. Sensitivity analysis is a useful tool for forecasting, computing, and identifying areas in cycles that require editing or modification. Note that previous occurrences do not necessarily predict future ones, so relying solely on past information may lead to wrong predictions.
remains the optimal choice. The reduction of ambiguity in mathematical simulations, such as changes in the source values, is made possible by sensitivity analysis. When used in conjunction with ambiguity examination, it is commonly used to improve the reliability of evaluation and modeling that rely on assertions about input fidelity. Sensitivity analysis is a useful tool for forecasting, computing, and identifying areas in cycles that require editing or modification. Note that previous occurrences do not necessarily predict future ones, so relying solely on past information may lead to wrong predictions.
Parametric sensitivity
In this subsection, we study sensitivity employing 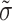 -q-RPLSSWA and
-q-RPLSSWA and 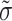 -q-RPLSSWG operators (wherein q=2) from afterward portions. We look at how altering
-q-RPLSSWG operators (wherein q=2) from afterward portions. We look at how altering 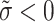 impacts the ordering of alternatives. As
impacts the ordering of alternatives. As  drops, alternative scores diminish while the top choice,
drops, alternative scores diminish while the top choice, 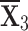 , keeps stable.
, keeps stable.
Sensitivity for 
-
q-RPLSSWA:
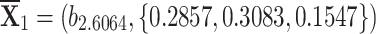 ,
, 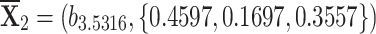 ,
, , and
, and 
-
q-RPLSSWG:
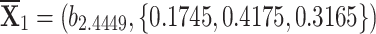 ,
, 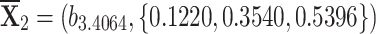 ,
,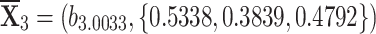 , and
, and 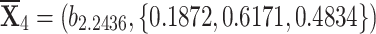
We evaluate the score values for each choice.
-
q-RPLSSWA:
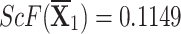 ,
, 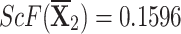 ,
, 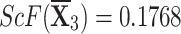 , and
, and 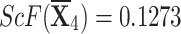 .
. -
q-RPLSSWG:
 ,
,  ,
, 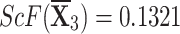 , and
, and  .
.
Ranking the choices using score values yields the following result:
- q-RPLSSWA:
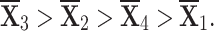
- q-RPLSSWG:

With the greatest score value out of all the options, 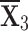 is deemed to be the optimal choice (see figures 7 and 8).
is deemed to be the optimal choice (see figures 7 and 8).
Fig. 7.
Graphical interpretation of score values for 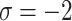 by employing q-RPLSSWAO.
by employing q-RPLSSWAO.
Fig. 8.
Graphical interpretation of score values for 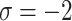 by employing q-RPLSSWGO.
by employing q-RPLSSWGO.
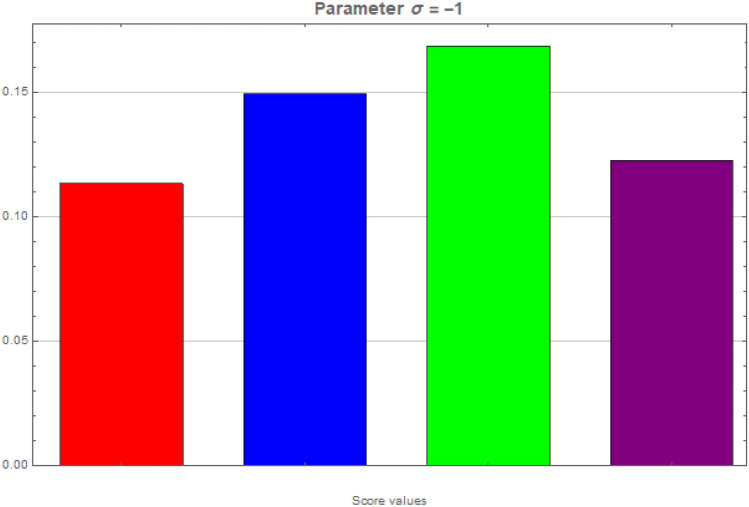
Sensitivity for 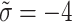
-
q-RPLSSWA:
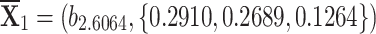 ,
,  ,
,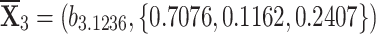 , and
, and 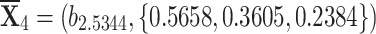
-
q-RPLSSWG:
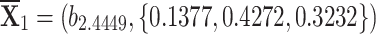 ,
, 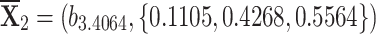 ,
, , and
, and 
We evaluate the score values for each choice.
-
q-RPLSSWA:
 ,
,  ,
, 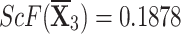 , and
, and  .
. -
q-RPLSSWG:
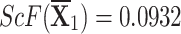 ,
, 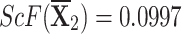 ,
, 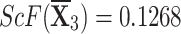 , and
, and  .
.
Ranking the choices using score values yields the following result:
- q-RPLSSWA:
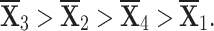
- q-RPLSSWG:
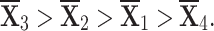
With the greatest score value out of all the options, 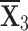 is deemed to be the optimal choice (see figures 9 and 10).
is deemed to be the optimal choice (see figures 9 and 10).
Fig. 9.
Graphical interpretation of score values for 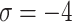 by employing q-RPLSSWAO.
by employing q-RPLSSWAO.
Fig. 10.
Graphical interpretation of score values for 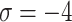 by employing q-RPLSSWGO.
by employing q-RPLSSWGO.
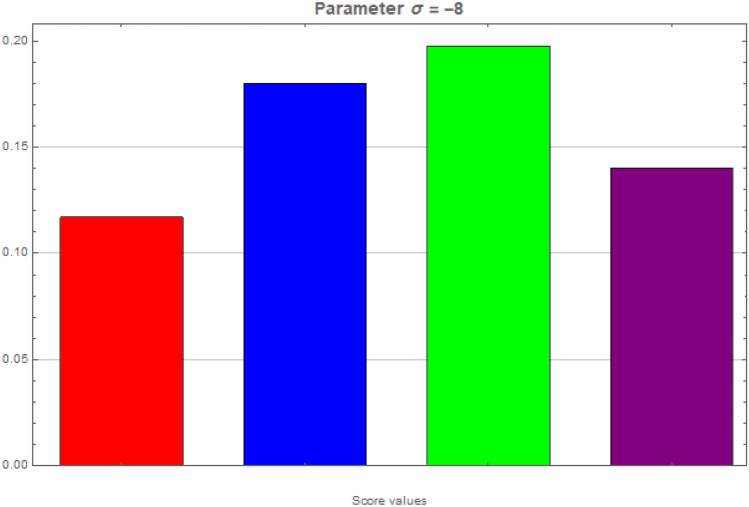
Sensitivity for 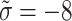
-
q-RPLSSWA:
 ,
, 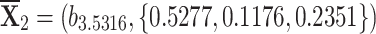 ,
, , and
, and 
-
q-RPLSSWG:
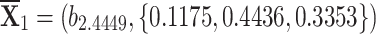 ,
, 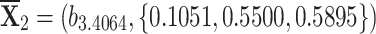 ,
,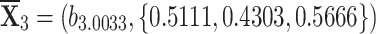 , and
, and 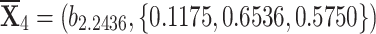
We evaluate the score values for each choice.
-
q-RPLSSWA:
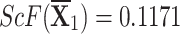 ,
,  ,
,  , and
, and 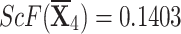 .
. -
q-RPLSSWG:
 ,
,  ,
, 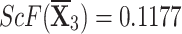 , and
, and  .
.
Ranking the choices using score values yields the following result:
- q-RPLSSWA:

- q-RPLSSWG:
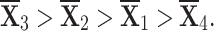
With the greatest score value out of all the options, 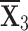 is deemed to be the optimal choice (see figures 11 and 12).
is deemed to be the optimal choice (see figures 11 and 12).
Fig. 11.
Graphical interpretation of score values for  by employing q-RPLSSWAO.
by employing q-RPLSSWAO.
Fig. 12.
Graphical interpretation of score values for 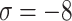 by employing q-RPLSSWGO.
by employing q-RPLSSWGO.
Sensitivity via weights
A quick strategy for decision-making, particularly in MADM, is sensitivity analysis on attribute weights. It modifies the results of different weights given to assessed attributes. Most often, attributes are assigned varying weights depending on the user’s preferences, level of experience, or other factors. The analysis entails changing the weights and assessing the impact on the ultimate decision-making step. Our major goal is to determine the important characteristics and comprehend how changing weights impact judgments. By choosing the best home security systems, homeowners, security professionals, and policymakers may improve their home security tactics and make efficient use of available resources thanks to this research. Sensitivity analysis, illustrated in tables [3] and [4], is essential for analyzing decision-making situations and assessing how adaptable they are to alterations to attribute weights.
Table 3.
Sensitivity of q-RPLSSWA operator via weights.
| WV | ScF(q-RPLNs) | Ranking |
|---|---|---|
| {0.3,0.3,0.2,0.1,0.1} |
 , , 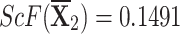 , ,  , and , and 
|
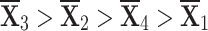 |
| {0.4237,0.2119,0.2024,0.1215,0.0405} |
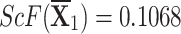 , , 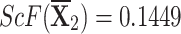 , , 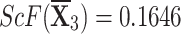 , and , and 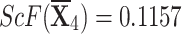
|
 |
| {0.4759,0.2873,0.1586,0.0391,0.0391} |
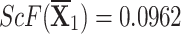 , , 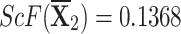 , , 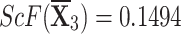 , and , and 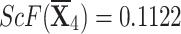
|
 |
Table 4.
Sensitivity of q-RPLSSWG operator via weights.
| WV | ScF(q-RPLNs) | Ranking |
|---|---|---|
| {0.3,0.3,0.2,0.1,0.1} |
 , , 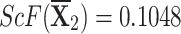 , ,  , and , and 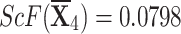
|
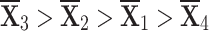
|
| {0.4237,0.2119,0.2024,0.1215,0.0405} |
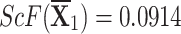 , ,  , , 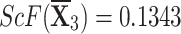 , and , and 
|
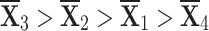
|
| {0.4759,0.2873,0.1586,0.0391,0.0391} |
 , ,  , ,  , and , and 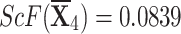
|
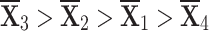
|
Thus, 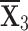 is the most suitable choice, and the figures [13] and [14] show that the alternate weight allocation causes a slight change in the categorization of choices.
is the most suitable choice, and the figures [13] and [14] show that the alternate weight allocation causes a slight change in the categorization of choices.
Fig. 13.
Graphical interpretation of q-RPLSSWA operator via weights.
Fig. 14.
Graphical interpretation of q-RPLSSWG operator via weights.
Comparison analysis
Through a comprehensive comparative analysis, we are able to illustrate the advantages and merits of our suggested methodologies eloquently. We discover that our suggested operators are significantly more versatile when contrasted with the current ones. When contrasted with the q-Rung picture linguistic number weighted aggregation operator (q-RPLNWAA) and q-Rung picture linguistic number weighted geometric aggregation operator (q-RPLNWGA) proposed by Ali et al.25, we attain superior choices, displayed in Table 5, employing q identically equal to 2. Our operators yield identical superior options with a little bit of alteration as those in Table 5. While 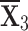 is still the best option, our suggested operators offer more precision by adjusting the parameter
is still the best option, our suggested operators offer more precision by adjusting the parameter  (see figure 15). On the other hand, because this parameter is missing, the operators presented by Ali et al. provide fewer assurances and dependability. By employing the parameter
(see figure 15). On the other hand, because this parameter is missing, the operators presented by Ali et al. provide fewer assurances and dependability. By employing the parameter 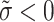 , our SS operations-based aggregation operators offer simplicity and increased accuracy in spite of identical environments. Given that q-RPLFS is the most advanced structure, current fuzzy aggregation techniques frequently attempt to handle the complexity of the underlying data. This highlights the limited reach of current aggregation techniques. Thus, compared to current measurements, our proposed method is more suitable for addressing decision-making issues.
, our SS operations-based aggregation operators offer simplicity and increased accuracy in spite of identical environments. Given that q-RPLFS is the most advanced structure, current fuzzy aggregation techniques frequently attempt to handle the complexity of the underlying data. This highlights the limited reach of current aggregation techniques. Thus, compared to current measurements, our proposed method is more suitable for addressing decision-making issues.
Table 5.
Comparison with existing operators.
Fig. 15.
Comparison with existing operators.
Validation
The suggested operators, q-RPLSSWAO and q-RPLSSWGO, have a strong +ve correlation with one another, suggesting that the ranks they provide are extremely comparable. Furthermore, q-RPLSSWGO and q-RPLNWGAO show a perfect correlation, indicating that their ranking behaviors are also the same. This information can help to improve the decision-making models and comprehend how the various operators compare with regard to ranking outcomes (see Table 6).
Table 6.
Spearman’s rank correlation coefficient.
| q-RPLNWAAO | q-RPLNWGAO | q-RPLSSWAO | q-RPLSSWGO | |
|---|---|---|---|---|
| q-RPLNWAAO | 1.0 | 0.2 | 0.4 | 0.2 |
| q-RPLNWGAO | 0.2 | 1.0 | 0.8 | 1.0 |
| q-RPLSSWAO | 0.4 | 0.8 | 1.0 | 0.8 |
| q-RPLSSWGO | 0.2 | 1.0 | 0.8 | 1.0 |
Discussion
SS norms in conjunction with power aggregation procedures, via parameter  , are used to construct the q-RPLSSWA and q-RPLSSWG operators. These methods tend to have flaws but also become uncommon, particularly in dynamic fuzzy cases. Their tendency to degrade productivity when engaging with huge data sets limits their use in real-world scenarios related to big-data handling. Also, the process of selecting suitable settings for these operators is laborious and typically involves trial and error, contributing an aspect of subjectivity that can limit their ease of use. Furthermore, even if these operators provide a sophisticated framework for decision-making in the face of inconsistencies, it is important to carefully assess their effectiveness in a variety of cases because they may not align exactly with the decisions made by different decision-makers.
, are used to construct the q-RPLSSWA and q-RPLSSWG operators. These methods tend to have flaws but also become uncommon, particularly in dynamic fuzzy cases. Their tendency to degrade productivity when engaging with huge data sets limits their use in real-world scenarios related to big-data handling. Also, the process of selecting suitable settings for these operators is laborious and typically involves trial and error, contributing an aspect of subjectivity that can limit their ease of use. Furthermore, even if these operators provide a sophisticated framework for decision-making in the face of inconsistencies, it is important to carefully assess their effectiveness in a variety of cases because they may not align exactly with the decisions made by different decision-makers.
Conclusions
In the current work, different aggregation operators founded on the constructed SS operational rules are discovered and addressed through a q-rung picture fuzzy linguistic framework. This also depicts that the majority of the present q-RPL aggregation operators are exceptional scenarios. Furthermore, some traits of the suggested operators that are needed, are established. A MADM strategy dependent on the proposed operators is developed to label the MADM problems with Unknown Weight vector (WV) data. Summing up, the approach’s flexibility and practical advantages are labeled by an exemplary instance, and the results show that the methodology may facilitate the decision-makers with more choices than the previous options. Comparison and sensitive examination are also being completed in order to mark the greatness and stability of the progressed approach.
Future work
Future paths in the field of analysis where additional MADM problems could be labeled by adapting the model presented in this thesis. The issues could include choosing a supplier, choosing a project, marketing, and a range of other scientific and technological issues. Thus, the subsequent tracks might be used to search the produced examination:
Suggested aggregation operators can be generalized to q-rung picture linguistic FSs or some other complex background to classify the substitutes.
Real-life decision-making is getting more harder, illustrating the significance of the inclusion of different DMs with changing knowledge structures and priorities. Our future analysis will concentrate on how to apply the propound technique to a wide-spread range of group decision-making.
The established aggregation operators can be used in different MADM algorithms like WASPAS, TODIM, VIKOR31, and ELECTRE in order to make their efficiency much better.
Analysts may also probe the focused PMSMS operators by putting the prioritization terms alongside the operators that are elaborated in this thesis for the increment in the working algorithms.
Data availability
The datasets used and analyzed during the current study are available from the corresponding author on reasonable request.
Declarations
Conflicts of Interest
All authors declare no conflict of interest.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Zadeh, L. A. Fuzzy sets. Information and control8(3), 338–353 (1965). [Google Scholar]
- 2.Jana, C., Garg, H., Pal, M., Sarkar, B. & Wei, G. Mabac framework for logarithmic bipolar fuzzy multiple attribute group decision-making for supplier selection. Complex & Intelligent Systems10(1), 273–288 (2024). [Google Scholar]
- 3.Jana, C., Simic, V., Pal, M., Sarkar, B. & Pamucar, D. Hybrid multi-criteria decision-making method with a bipolar fuzzy approach and its applications to economic condition analysis. Engineering Applications of Artificial Intelligence132, 107837 (2024). [Google Scholar]
- 4.Chen, S.-M. “A fuzzy reasoning approach for rule-based systems based on fuzzy logics,’’ IEEE Transactions on Systems, Man, and Cybernetics. Part B (Cybernetics)26(5), 769–778 (1996). [DOI] [PubMed] [Google Scholar]
- 5.Chen, S.-M. & Chen, S.-W. Fuzzy forecasting based on two-factors second-order fuzzy-trend logical relationship groups and the probabilities of trends of fuzzy logical relationships. IEEE transactions on cybernetics45(3), 391–403 (2014). [DOI] [PubMed] [Google Scholar]
- 6.Chen, S.-M. & Huang, C.-M. Generating weighted fuzzy rules from relational database systems for estimating null values using genetic algorithms. IEEE Transactions on Fuzzy Systems11(4), 495–506 (2003). [Google Scholar]
- 7.Chen, S.-M. & Niou, S.-J. Fuzzy multiple attributes group decision-making based on fuzzy preference relations. Expert Systems with Applications38(4), 3865–3872 (2011). [Google Scholar]
- 8.Chen, S.-M. & Jong, W.-T. “Fuzzy query translation for relational database systems,’’ IEEE Transactions on Systems, Man, and Cybernetics. Part B (Cybernetics)27(4), 714–721 (1997). [DOI] [PubMed] [Google Scholar]
- 9.Manoj, T., Leena, J. & Soney, R. B. Knowledge representation using fuzzy petri nets-revisited. IEEE transactions on knowledge and data engineering10(4), 666–667 (1998). [Google Scholar]
- 10.Atanassov, K. T. & Atanassov, K. T. Intuitionistic fuzzy sets. Springer (1999).
- 11.Cuong, B. C. & Kreinovich, V. Picture fuzzy sets. Journal of computer science and cybernetics30(4), 409–420 (2014). [Google Scholar]
- 12.Yager, R. R. “Pythagorean fuzzy subsets,” in 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS), pp. 57–61, IEEE (2013).
- 13.Yager, R. R. Generalized orthopair fuzzy sets. IEEE transactions on fuzzy systems25(5), 1222–1230 (2016). [Google Scholar]
- 14.Kutlu Gündoğdu, F. & Kahraman, C. Spherical fuzzy sets and spherical fuzzy topsis method. Journal of intelligent & fuzzy systems36(1), 337–352 (2019). [Google Scholar]
- 15.Jana, C., Pal, M., Balas, V. E., & Yager, R. R. Picture Fuzzy Logic and Its Applications in Decision Making Problems. Elsevier (2023).
- 16.Li, L., Zhang, R., Wang, J., Shang, X. & Bai, K. A novel approach to multi-attribute group decision-making with q-rung picture linguistic information. Symmetry10(5), 172 (2018). [Google Scholar]
- 17.Zadeh, L. A. The concept of a linguistic variable and its application to approximate reasoning-ii. Information sciences8(4), 301–357 (1975). [Google Scholar]
- 18.Wang, S. & Liu, J. Extension of the todim method to intuitionistic linguistic multiple attribute decision making. Symmetry9(6), 95 (2017). [Google Scholar]
- 19.Liu, P. & Zhang, X. A novel picture fuzzy linguistic aggregation operator and its application to group decision-making. Cognitive Computation10(2), 242–259 (2018). [Google Scholar]
- 20.Du, Y., Hou, F., Zafar, W., Yu, Q. & Zhai, Y. A novel method for multiattribute decision making with interval-valued pythagorean fuzzy linguistic information. International Journal of Intelligent Systems32(10), 1085–1112 (2017). [Google Scholar]
- 21.Klement, E. P., Mesiar, R., & Pap, E. Triangular norms, vol. 8. Springer Science & Business Media (2013).
- 22.Akram, M., Alsulami, S., Karaaslan, F. & Khan, A. q-rung orthopair fuzzy graphs under hamacher operators. Journal of Intelligent & Fuzzy Systems40(1), 1367–1390 (2021). [Google Scholar]
- 23.Dutta, P. & Ganju, S. Some aspects of picture fuzzy set. Transactions of A. Razmadze Mathematical Institute172(2), 164–175 (2018). [Google Scholar]
- 24.Pinar, A. & Boran, F. E. A novel distance measure on q-rung picture fuzzy sets and its application to decision making and classification problems. Artificial Intelligence Review55(2), 1317–1350 (2022). [Google Scholar]
- 25.Ali, J., Naeem, M. & Mahmood, W. Generalized q-rung picture linguistic aggregation operators and their application in decision making. Journal of Intelligent & Fuzzy Systems44(3), 4419–4443 (2023). [Google Scholar]
- 26.Wang, J.-Q., Wu, J.-T., Wang, J., Zhang, H.-Y. & Chen, X.-H. Interval-valued hesitant fuzzy linguistic sets and their applications in multi-criteria decision-making problems. Information sciences288, 55–72 (2014). [Google Scholar]
- 27.Wang, H., Ju, Y. & Liu, P. Multi-attribute group decision-making methods based on q-rung orthopair fuzzy linguistic sets. International Journal of Intelligent Systems34(6), 1129–1157 (2019). [Google Scholar]
- 28.Yager, R. R. The power average operator. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans31(6), 724–731 (2001). [Google Scholar]
- 29.Chunsong, B., Khalid, U., Binyamin, M. A., & Ali, J. “Revolutionizing diabetes care with innovative decision-making using cubic intuitionistic fuzzy schweizer and sklar power aggregation operators,” Heliyon (2024). [DOI] [PMC free article] [PubMed]
- 30.Xu, Z. & Yager, R. R. Power-geometric operators and their use in group decision making. IEEE Transactions on Fuzzy Systems18(1), 94–105 (2009). [Google Scholar]
- 31.Shit, C. & Ghorai, G. Charging method selection of a public charging station using an interval-valued picture fuzzy bidirectional projection based on vikor method with unknown attribute weights. Information16(2), 94 (2025). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and analyzed during the current study are available from the corresponding author on reasonable request.