Abstract
Optical coherence tomography (OCT) is a non-invasive, high-resolution imaging technology that provides cross-sectional images of tissues. Dense acquisition of A-scans along the fast axis is required to obtain high digital resolution images. However, the dense acquisition will increase the acquisition time, causing the discomfort of patients. In addition, the longer acquisition time may lead to motion artifacts, thereby reducing imaging quality. In this work, we proposed a hybrid attention structure preserving network (HASPN) to achieve super-resolution of under-sampled OCT images to speed up the acquisition. It utilized adaptive dilated convolution-based channel attention (ADCCA) and enhanced spatial attention (ESA) to better capture the channel and spatial information of the feature. Moreover, convolutional neural networks (CNNs) exhibit a higher sensitivity of low-frequency than high-frequency information, which may lead to a limited performance on reconstructing fine structures. To address this problem, we introduced an additional branch, i.e., textures & details branch, using high-frequency decomposition images to better super-resolve retinal structures. The superiority of our method was demonstrated by qualitative and quantitative comparisons with mainstream methods. Furthermore, HASPN was applied to three out-of-distribution datasets, validating its strong generalization capability.
Keywords: Optical coherence tomography, Super-resolution, Attention mechanism
Subject terms: Biomedical engineering, Electrical and electronic engineering
Introduction
Optical coherence tomography (OCT) is a non-invasive optical imaging technique1. Due to its cellular-level imaging resolution, it has been widely used in ophthalmology, dermatology, and cardiology2–4. OCT’s high-resolution imaging capability allows for detailed visualization of retinal structures, enabling early detection and monitoring of various retinal conditions, such as age-related macular degeneration (AMD)5, diabetic retinopathy6, and glaucoma7. The ability to capture cross-sectional images of the retina in vivo has revolutionized the field of ophthalmology, providing clinicians with critical information that influences diagnosis and treatment plans.
Typically, dense acquisition is required to capture fine microstructures of the sample. However, conducting dense acquisition, especially over a large field of view, will decrease the imaging speed and thereby cause the discomfort of patients. Moreover, the longer acquisition time is likely to exacerbate eye motion, introducing artifacts into the image8. Down-sampling is the easiest way to speed up the acquisition, however, at the sacrifice of the resolution.
To improve the digital resolution of under-sampled images, various conventional methods have been proposed. Fang et al. proposed a sparsity-based framework that simultaneously performed interpolation and denoising to reconstruct OCT images efficiently9. Abbasi et al. introduced a non-local weighted sparse representation (NWSR) method, which integrates sparse representations of multiple noisy and denoised patches to improve image quality10. Wang et al. proposed to utilize compressive sensing (CS) and digital filters to enhance the down-sampled OCT angiography images11. The study demonstrated that the vascular structures could be well reconstructed through CS with a sampling rate on B-scans at 70%, suggesting that CS could significantly accelerate acquisition in the OCT system. However, the traditional methods tend to perform poorly at high scale factors. Specifically, these methods have difficulty in reconstructing OCT images with high accuracy and may lead to artifacts at high scale factors. Hence, they cannot be applied in some scenarios where low scan density is required.
In recent years, deep learning methods have been popular among various medical image processing tasks12–14. Huang et al. utilized a generative adversarial network (GAN) to super-resolve OCT images while reducing the noise, introducing deep learning into OCT super-resolution for the first time15. Qiu et al. proposed a novel semi-supervised method using UNet and DBPN to achieve simultaneous super-resolution and denoising16. However, these deep-learning-based super-resolution networks ignore the fact that convolutional neural network (CNN) is more sensitive to low-frequency information17, potentially limiting the performance on reconstructing fine-grained structures in OCT images. With the success of transformers in the field of computer vision18, many researchers have successfully applied transformers to OCT super-resolution19. Yao et al. proposed the PSCAT20 composed of window self-attention21 and CBAM22 to achieve denoising and super-resolution simultaneously. Lu et al. presented a pyramid long-range transformer TESR23 to reconstruct under-sampled OCT images. Furthermore, the transformer was integrated with the CNN to leverage their complementary strengths, i.e., global dependency and local dependency, for OCT super-resolution24.
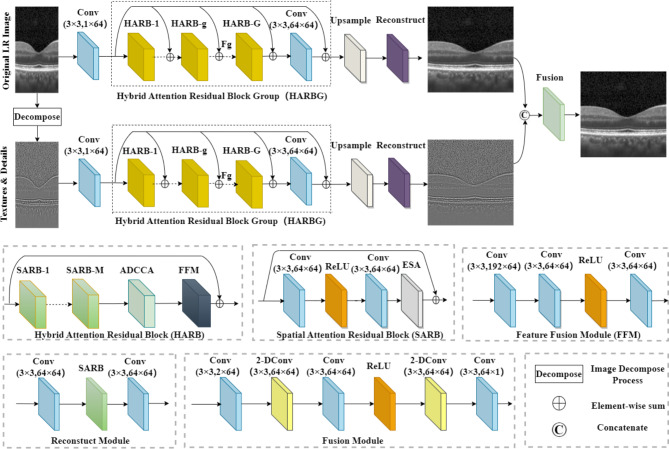
To obtain high digital resolution images within a short acquisition time, we proposed a novel OCT super-resolution model named hybrid attention structure preserving network (HASPN). HASPN has two branches. One branch was used to primarily restore the low-frequency features of images. The another branch could enhance the perceptual quality of the output by learning the high-frequency features of decomposed images. The low-frequency and high-frequency features from the two branches were concatenated over channels to fuse the information. Additionally, the hybrid attention mechanism was introduced to enhance the network’s capacity to learn spatial and channel information, improving the reconstruction capability. Next, we utilized the public retinal OCT image dataset OCT2017 to test HASPN at different sampling rates. Compared with the current mainstream methods, HASPN achieved the best results at 4x and 8x SR. Moreover, we investigated the impact of network depths and widths on performance and conducted ablation studies to validate the effectiveness of our key components and hybrid loss. Finally, the experiment demonstrated that our proposed HASPN exhibited strong generalization capabilities for diabetic macular edema (DME), choroidal neovascularization (CNV), and drusen in early AMD which was unseen during training.
Methods
Data preparation
In this paper, we utilized the retinal OCT image dataset OCT201725. The original dataset contains 84,495 images in total, covering normal and abnormal retinal images. From the subset of normal retinal images, 1,300 images were selected for the training set, 200 images for the validation set, and 100 images for the testing set.
Considering the limited GPU resources, the images were randomly cropped into 256 × 256 as the high-resolution (HR) ground truth. To generate low-resolution (LR) images, we under-sampled the columns of the ground truth, obtaining 2x, 4x, and 8x images. Subsequently, the LR-HR image pairs were obtained. In addition, 100 OCT images of DME, CNV, and DRUSEN from the OCT2017 dataset were utilized to create corresponding sub-datasets for validating the network’s generalization capability.
Image decomposition
Unsharp masking (USM) is commonly employed in image processing to enhance high-frequency details26. To be specific, The original image is subtracted by its blurred version to generate a residual image. This residual image is then added back to the original image to enhance edges and details. Its specific steps are as follows:
 |
1 |
 |
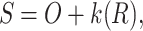2 |
where 
, 
, 
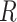represent the original image, the blurred image, and the residual image (high-frequency image). 
is the scaling coefficient used to adjust the degree of sharpening, while 
is the sharpened image.
Xu et al. demonstrated that CNN exhibited a greater sensitivity to low-frequency information than high-frequency information17. However, high-frequency information is essential for reconstructing fine details. To address this problem, we proposed an approach inspired by USM that involved decomposing images into a residual image enriched with high-frequency content. This residual image was subsequently input into an additional branch to enhance the reconstruction of high-frequency features. Specifically, a Gaussian filter with a kernel size of 5 × 5 and a kernel standard deviation of 1.5 in the X direction was applied to blur the image. Then, the high-frequency image could be obtained by subtraction. Both LR and HR images were decomposed to generate the corresponding high-frequency images. Different from the Eq. 2, we utilized a textures & details CNN branch to enhance edges and details. The outputs of the original branch and the textures & details branch will then be concatenated and fused to generate the final image.
Hybrid attention mechanism
Previous studies have proven the effectiveness of attention mechanisms in super-resolution tasks27. It can enable the network to focus on important features, thereby enhancing the quality of reconstruction. As shown in Fig. 1, we designed a hybrid attention mechanism, i.e., intra-block and inter-block attention. First, we integrated an enhanced spatial attention (ESA)28 in the spatial attention residual block (SARB). Initially, a 1 × 1 convolutional layer was performed to reduce the channel dimension, thereby decreasing the computational complexity of the ESA module. And then, a 3 × 3 convolutional layer with a stride of 2 was utilized to reduce the resolution of the feature map by half. Next, a 7 × 7 max pooling with a stride of 3 was used to achieve downsampling and enlarge the receptive field. Subsequently, a 3 × 3 convolutional layer was used for feature extraction. Bilinear interpolation and 1 × 1 Conv were utilized to recover the spatial and channel dimensions, respectively. Finally, the input of ESA was dotted with the attention score matrix. Different from the conventional ESA, we did not use Conv Group (two Conv(3 × 3)-ReLU and one Conv(3 × 3)) to extract features. We experimentally found that using a 3 × 3 convolution for feature extraction was better than using the Conv Group in the original ESA. Specifically, utilizing 3 × 3 Conv for feature extraction yielded a notable enhancement in PSNR, demonstrating an increase of 1.87dB, as well as an improvement in SSIM, which exhibited a rise of 0.017, in comparison to the use of Conv Group. That means adopting a single 3 × 3 convolutional layer not only significantly reduces the model’s computational complexity but also achieves better performance. As shown in Fig. 2, the output feature map of ESA displays more distinct retinal layers compared to the original one. It demonstrates that ESA enables the network to focus on specific spatial regions, leading to a better performance.
Fig. 1.
Hybrid attention mechanism in HASPN. (a) Modified ESA, where Conv-N represents a NxN convolutional layer. (b) ADCCA, where N-DConv (kxk, ixo) denotes a kxk convolutional layer with a dilation factor of N, input channel of i, and output channel of o.
Fig. 2.
Visualization of feature maps. (a) The input feature map of ESA. (b) The output feature map of ESA.
Secondly, to further enhance the ability of the network to distinguish the importance of different channels, adaptive dilated convolution-based channel attention (ADCCA) was incorporated every M SARBs (as shown in Fig. 3). ADCCA exploits kernels of different sizes and different dilated factors (1, 3, 5) to enrich the receptive field of convolution, thereby capturing information of various scales. Similar to SENet29, ADCCA first performs a squeeze operation using max pooling to reduce the resolution of the feature maps by half. Then, it follows with an excitation step, which involves dilated Conv-ReLU-dilated Conv (DC-ReLU-DC) operations with different dilated factors. Subsequently, a global pooling is used to decrease the resolution of feature maps to 1 × 1 to obtain the attention of each channel.
Fig. 3.
Framework of the proposed HASPN.
Super resolution network framework
Inspired by the TDPN30, we proposed a novel network named HASPN as shown in Fig. 3. The network contained two parallel branches: one branch was responsible for restoring the coarse image, while the other branch focused on the restoration of fine textures and details. In addition, we implemented a dual-branch weight-sharing strategy. This approach not only increases the connection between dual branches but also significantly reduces the number of parameters. The outputs of the two branches were finally integrated through a fusion module to generate super-resolution images.
Each branch consisted of three parts: shallow feature extraction, deep feature extraction, and upsampling reconstruction. In the shallow feature extraction stage, a 3 × 3 convolutional layer was used to extract the shallow features of the network. These features were then fed to each hybrid attention residual block group (HARBG) module through the skip connections from the shared source to help the network better focus on high-frequency features. Deep feature extraction consisted of multiple hybrid attention residual block (HARB) units and a 3 × 3 convolutional layer. Each HARB unit consisted of M SARBs, an ADCCA, and a feature fusion module (FFM). ESA was introduced into SARB to allow the network focus on some important spatial features, significantly enhancing the perceptual quality of reconstructed images in super-resolution. After processed by multiple SARB units, multi-scale information was extracted by ADCCA which adaptively used convolutions of various sizes and different dilation factors. In addition, it made the network focus more on key feature channels effectively. Finally, FFM was used to merge feature maps at various scales in ADCCA.
Bilinear interpolation was utilized as the horizontal upsampling method. The reconstruction module contained a 3 × 3 Conv, a SARB, and another 3 × 3 Conv. Finally, the coarse image reconstructed by the original LR image branch and the high-frequency image reconstructed by the textures & details branch were concatenated over channel and fused together. The fusion module has a similar structure to the FFM, with one key difference: it incorporates a 2-DConv between every two convolutional layers. This modification enables the fusion module to capture a larger receptive field and integrate a wider range of contextual information within both branches. As a result, the reconstructed images have richer details and more accurate structures.
Evaluation metrics
To evaluate the performance of the proposed method, two image quality metrics are introduced: peak signal-to-noise ratio (PSNR)31, structural similarity index metric (SSIM)32. PSNR is a commonly used metric to measure the quality of image reconstruction. It evaluates the similarity between the reconstructed image and the original image at the pixel intensity level. It is defined as follows:
 |
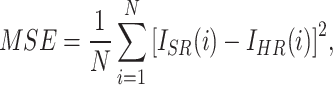3 |
 |
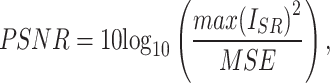4 |
where i and N represent the index of the pixels and the total number of pixels in an image, respectively.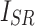 
represents the image reconstructed by the network, and 
is the ground truth image.
SSIM focuses on the perceptual structure of the image and assesses the similarity of images in terms of luminance, contrast, and structure. The definition of SSIM is given by:
 |
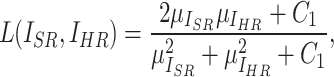5 |
 |
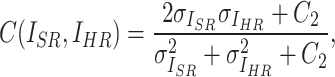6 |
 |
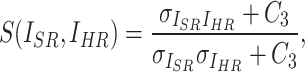7 |
where 
, 
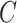, and 
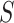represent luminance, contrast, and structure, respectively. 
, 
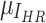denote the means of 
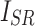and 
, respectively. While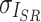 
, 
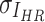are the variances of 
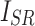and 
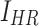, respectively. 
indicates the covariance between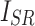 
and 
. SSIM is the product of these three components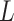 
, 
, and 
. When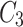 
is set to 
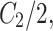the final SSIM is expressed as follows:
 |
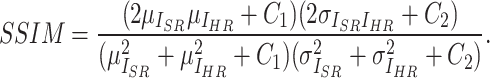8 |
Loss function
To pursue a high PSNR while preserving more accurate retinal structures, our loss function was defined as:
 |
9 |
where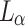 
, 
, and 
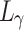represent the losses between the reconstructed coarse image 
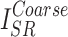and 
, the reconstructed high-frequency image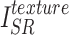 
and the high-frequency image of the ground truth 
, as well as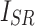 
and 
, respectively.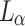 
, 
, and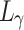 
were the same function as follows:
 |
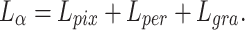10 |
Lim et al. found that while minimizing the L2 norm can maximize the PSNR value, using the L1 norm can lead to a better network convergence33. Consequently, the L1 norm was employed to measure the pixel error between the output and the ground truth.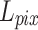 
was defined as follows:
 |
11 |
where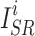 
and 
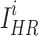represent the i-th SR image and the i-th HR image in a batch, respectively.
However, only using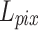 
may not achieve a good perceptual performance. Hence, a perceptual loss34 was included to enhance the visual similarity of the output images to HR images. Specifically, it utilized a pre-trained VGG19 network35 to extract high-level information from the L-th layer, and employed the L2 norm to measure the error of the extracted features. 
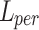was defined as follows:
 |
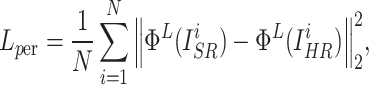12 |
where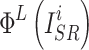 
and 
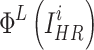represent the features of the i-th SR image extracted by the L-th layer and the features of the i-th HR image extracted by the L-th layer in a batch, respectively.
To avoid the smoothing effect caused by minimizing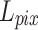 
, the gradient loss was used to penalize the gradient of images. 
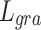was defined as follows:
 |
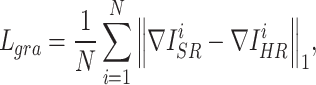13 |
where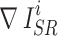 
and 
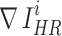represent the gradient operator of the i-th SR image and the gradient operator of the i-th HR image in a batch, respectively. We used the Sobel gradient operator (first-order derivatives) because it could enhance regions of rapid intensity change (edges) while being less affected by minor intensity variations (noise), in contrast to the Laplacian operator (second-order derivatives). 
was defined as follows, where ∗ denotes the convolution operation:
 |
14 |
 |
15 |
 |
16 |
Implementation details
During training, the hyperparameters G and M for HASPN were set to 20 and 5, respectively. All the networks were optimized using the Adam optimizer with β1 = 0.9 and β2 = 0.999, with an initial learning rate of 1e-4. The learning rate for each layer across all networks decayed by 50% every 20 epochs. The batch size for each network were 2. All models were trained for 200 epochs to ensure their convergences.
The entire process was implemented within the PyTorch 2.1.0 framework, compatible with Python version 3.10, on a Tesla A100 GPU with 40GB of memory.
Results and discussion
To demonstrate the superiority of our proposed network HASPN, it was qualitatively compared with several prevailing methods, including Bicubic, SRCNN36, FSRCNN37, EDSR33, RDN38, RCAN39, SRGAN40, ESRGAN41, RFANet28, RVSRNet42, TDPN30, SwinIR43, ESRT44.
As shown in Fig. 4 (pair_72), the outer segment (OS) of the Bicubic reconstructed image exhibited discontinuity. Due to the inherent characteristics of interpolation methods, many ringing artifacts existed at the edges of the external limiting membrane (ELM) and the retinal pigment epithelium (RPE). The ELM in the FSRCNN reconstructed image was excessively blurred and affected by artifacts when deconvolution was used as the upsampling method45. These artifacts significantly affected the final quality of the images. Surprisingly, compared to the results of Bicubic and FSRCNN, the ELM reconstructed by SRCNN displayed higher contrast and sharpness. However, the RPE layers in these reconstructed images were severely distorted compared to the HR image. EDSR, RDN, and RCAN employed a wide-channel residual block, dense residual connections, and channel attention in their network designs, respectively, to enhance the network’s ability to learn features. This led to better visual performance than Bicubic, SRCNN, and FSRCNN. Additionally, EDSR, RDN, and RCAN achieved results comparable to those of GAN-based methods (SRGAN, ESRGAN) and RFANet. Furthermore, TDPN reconstructed clearer retinal structures than aforementioned methods except for our model. Conversely, it is worth noting that TDPN and RVSRNet failed to reconstruct the tiny granular structures observed in the RPE layer. While SwinIR and ESRT effectively reconstructed fine-grained structures in the RPE layer, they failed to reconstruct the ELM with high contrast and introduced artifacts in the OS. In comparison, our model HASPN could reconstruct these subtle structures better, and the restored ELM exhibited higher contrast than that of other methods. Moreover, the OS reconstructed by HASPN was more continuous.
Fig. 4.
Visual comparisons of HASPN with prevailing models at 8x SR.
For pair_67, the internal limiting membrane (ILM) reconstructed by Bicubic, SRGAN, and RFANet exhibited a ladder-like structure. For the reconstruction of the central fovea (denoted by the green arrow), most methods, except for FSRCNN, SwinIR, ESRT and HASPN, showed large differences with the HR image. RDN and ESRGAN failed to accurately reconstruct the inner nuclear layer (INL). Although the differences between TDPN and the HR image in the reconstruction of the INL were smaller, the reconstructed ILM and the central fovea remained slightly blurred. SwinIR and ESRT also did not perform well in reconstructing the INL, resulting in blurred edges in the reconstructed images. In contrast, our model HASPN shown excellent performance in restoring these structures. It not only completely reconstructed the INL but also had the best visual similarity to the HR image in the ILM. These results demonstrate the superiority of HASPN in reconstructing fine structures in retinal images.
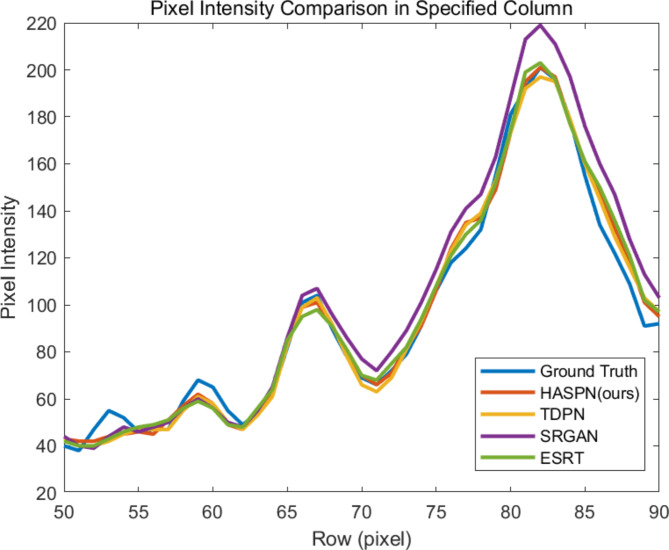
Next, to further reflect the performance of our method, we compared HASPN with TDPN, SRGAN (ranked second in terms of PSNR), and ESRT (ranked second in terms of SSIM) by plotting the profile of the selected A-line (indicated by the dashed orange line in HR(8x): pair_72 of Fig. 4). The comparisons were shown in Fig. 5. The peak observed in Fig. 5, specifically in rows 65 to 70, corresponds to the inner/outer segment junction (IS/OS junction) depicted in Fig. 4. It was evident that the structures reconstructed by HASPN and TDPN closely aligned with the ground truth, whereas a notable discrepancy existed between the reconstructions produced by ESRT and the ground truth. Notably, the outer segment (OS), represented by rows 70 to 75, reconstructed by HASPN nearly coincided with the ground truth, in contrast to the slight gaps observed in the OS reconstructions generated by TDPN and ESRT. This underscores the superiority of HASPN in preserving the integrity of retinal layers at the pixel level. Additionally, within the retinal pigment epithelium (RPE) layer, represented by rows 80 to 85, the reconstruction results of TDPN, ESRT, and HASPN closely approximate the ground truth. However, the results obtained from SRGAN exhibited a significant deviation from the ground truth, which may be attributed to the method’s tendency to produce excessively smooth edges during the reconstruction process.
Fig. 5.
Profile of the orange dashed line in HR(8x): pair_72 of Fig. 4.
In Table 1, we quantitatively compared HASPN with other prevailing methods using model complexity metrics (FLOPs, Param, Average Latency) and image quality metrics (PSNR, SSIM). The results indicated that ESRGAN and RFANet attained the highest and second-highest performance at 2x SR, respectively. Although HASPN did not achieve the highest PSNR at 2x SR, its SSIM was only slightly lower than that of ESRGAN. Notably, FSRCNN demonstrated performance that was second only to HASPN while maintaining the smallest model complexity. However, its visual quality was inferior to several other prevailing methods. Moreover, SRGAN and ESRT attained the second highest PSNR and the second highest SSIM at 8x SR, respectively. Our proposed HASPN yielded the best results compared to other methods at both 4x and 8x SR. However, its substantial FLOPs and relatively high latency may limit its applicability in clinical settings. In the future, we will explore techniques to decrease its computational burden.
Table 1.
Quantitative comparisons of 2x, 4x, and 8x SR.
| Model | upscale | FLOPs[G]↓ | Param[M]↓ | Average Latency[S]↓ | PSNR↑ | SSIM↑ |
|---|---|---|---|---|---|---|
| Bicubic | 2x | - | - | 0.052014 | 31.73 | 0.8410 |
| SRCNN | 2x | 15.0158 | 0.057281 | 0.000371 | 33.62 | 0.8877 |
| FSCRNN | 2x | 0.662979 | 0.010289 | 0.000487 | 33.66 | 0.8884 |
| EDSR | 2x | 2591.4 | 39.5402 | 0.087134 | 33.59 | 0.8871 |
| RDN | 2x | 1444.9 | 22.0472 | 0.089945 | 33.67 | 0.8897 |
| RCAN | 2x | 999.595 | 15.3685 | 0.060812 | 32.55 | 0.8667 |
| SRGAN | 2x | 32.5143 | 0.491911 | 0.002044 | 32.42 | 0.8620 |
| ERSGAN | 2x | 1098 | 16.6385 | 0.066602 | 33.73 | 0.8913 |
| RFANet | 2x | 642.309 | 6.4015 | 0.061185 | 33.69 | 0.8898 |
| RVSRNet | 2x | 422.278 | 6.4421 | 0.022905 | 32.18 | 0.8486 |
| TDPN | 2x | 1900 | 0.564972 | 0.096445 | 31.36 | 0.8761 |
| SwinIR | 2x | 48.0272 | 0.762889 | 0.040426 | 33.54 | 0.8861 |
| ESRT | 2x | 43.1854 | 0.639061 | 0.061485 | 33.49 | 0.8862 |
| HASPN | 2x | 1940.5 | 0.579052 | 0.108374 | 32.65 | 0.8881 |
| Bicubic | 4x | - | - | 0.042997 | 27.68 | 0.6633 |
| SRCNN | 4x | 7.5079 | 0.057281 | 0.000172 | 29.44 | 0.7102 |
| FSCRNN | 4x | 0.397546 | 0.012305 | 0.000474 | 30.11 | 0.7637 |
| EDSR | 4x | 1373.2 | 40.7204 | 0.044873 | 29.95 | 0.7593 |
| RDN | 4x | 727.313 | 22.1211 | 0.042283 | 29.92 | 0.7589 |
| RCAN | 4x | 504.671 | 15.4423 | 0.052618 | 30.01 | 0.7507 |
| SRGAN | 4x | 21.433 | 0.565767 | 0.001517 | 29.68 | 0.7402 |
| ERSGAN | 4x | 565.921 | 16.6551 | 0.036978 | 29.74 | 0.7557 |
| RFANet | 4x | 325.959 | 6.4753 | 0.063954 | 29.97 | 0.7604 |
| RVSRNet | 4x | 211.139 | 6.4421 | 0.010950 | 29.11 | 0.6939 |
| TDPN | 4x | 1037.6 | 0.564972 | 0.058766 | 30.06 | 0.7629 |
| SwinIR | 4x | 28.8874 | 0.836745 | 0.088075 | 29.96 | 0.7607 |
| ESRT | 4x | 24.0506 | 0.676053 | 0.036188 | 29.95 | 0.7611 |
| HASPN | 4x | 1060.1 | 0.579052 | 0.107809 | 30.14 | 0.7650 |
| Bicubic | 8x | - | - | 0.041999 | 25.74 | 0.5686 |
| SRCNN | 8x | 3.7539 | 0.057281 | 0.000168 | 27.79 | 0.6276 |
| FSCRNN | 8x | 0.264832 | 0.016337 | 0.000450 | 28.25 | 0.6733 |
| EDSR | 8x | 764.072 | 41.9005 | 0.026542 | 28.29 | 0.6538 |
| RDN | 8x | 368.531 | 22.1949 | 0.021923 | 28.27 | 0.6541 |
| RCAN | 8x | 257.21 | 15.5162 | 0.059235 | 28.14 | 0.6421` |
| SRGAN | 8x | 15.8923 | 0.639623 | 0.001417 | 28.35 | 0.6624 |
| ERSGAN | 8x | 452.247 | 16.6884 | 0.052569 | 28.34 | 0.6645 |
| RFANet | 8x | 167.715 | 6.5492 | 0.062491 | 28.04 | 0.6392 |
| RVSRNet | 8x | 105.57 | 6.4421 | 0.005082 | 27.94 | 0.6232 |
| TDPN | 8x | 693.935 | 0.564972 | 0.070226 | 27.64 | 0.6482 |
| SwinIR | 8x | 19.3175 | 0.910601 | 0.049893 | 28.30 | 0.6739 |
| ESRT | 8x | 14.4833 | 0.713045 | 0.018722 | 28.28 | 0.6742 |
| HASPN | 8x | 709.793 | 0.579052 | 0.105395 | 28.55 | 0.6786 |
The upward arrow (↑) and the downward arrow (↓) indicate that higher and lower values yield better performance, respectively. The best and second best results were highlighted in bold and italics, respectively.
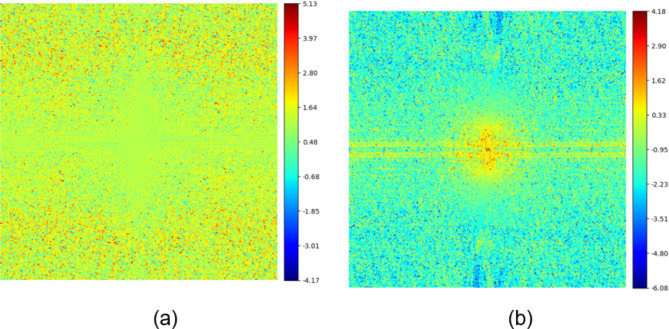
To validate the role of two branches in enhancing low-frequency and high-frequency features respectively, we visualized the spectral amplitude difference map between the final SR image and the original branch reconstructed image, as well as that between the final SR image and the textures & details branch reconstructed image. As shown in Fig. 6, the final SR image contains more high-frequency components than the original branch reconstructed image, while it contains more low-frequency components than the textures & details branch reconstructed image. This demonstrates that the textures & details branch compensates for the shortcoming of the original branch in extracting high-frequency features, thereby enhancing the overall network performance.
Fig. 6.
Spectral amplitude difference maps. (a) Difference map between the final SR image and the original branch reconstructed image. (b) Difference map between the final SR image and the textures & details branch reconstructed image.
Subsequently, we systematically reduced the quantities of HARB (G), SARB (M), and channel (C) to investigate the impact of different network depths and widths on performance. As presented in Table 2, an increase in the numbers of G, M, and C corresponded with an enhancement in model performance. This finding demonstrates that expanding the depth and width of the network can significantly improve its capabilities in feature extraction and representation. Notably, the model attained its peak PSNR and SSIM values at 4x SR when G, M, and C were set to 20, 5, and 64, respectively. Furthermore, it was observed that G contributed substantially to improvements in both PSNR and SSIM at lower values (8 and 16). Conversely, at smaller values of M (2 and 4), the enhancement in SSIM was relatively limited, and when C was modest (16 and 32), the increase in PSNR was marginal.
Table 2.
Quantitative comparisons of HASPN architectures with different widths and depths at 4x SR. G, M, C represent the number of HARB, SARB, and channel in each layer, respectively.
| G | M | C | PSNR↑ | SSIM↑ |
|---|---|---|---|---|
| 20 | 5 | 64 | 30.14 | 0.7650 |
| 16 | 5 | 64 | 29.57 | 0.7564 |
| 8 | 5 | 64 | 28.66 | 0.7474 |
| 20 | 4 | 64 | 29.83 | 0.7546 |
| 20 | 2 | 64 | 29.17 | 0.7536 |
| 20 | 5 | 32 | 29.12 | 0.7352 |
| 20 | 5 | 16 | 29.08 | 0.7287 |
To demonstrate the effectiveness of the proposed key components, we performed ablations on ESA, ADCCA, and the textures & details branch, respectively. As shown in Table 3, the PSNR and SSIM values of the images super-resolved by Model 1 were not particularly remarkable. However, with the integration of both ADCCA and ESA, the performance of our model significantly improved. When all key components were integrated, our model displayed the best performance. Furthermore, we ablated our hybrid loss function to validate the effectiveness of its different components. As shown in Table 4, the model achieved the best performance when pixel, perceptual, and gradient losses were used, proving the role of hybrid loss in enhancing the performance of the model.
Table 3.
Comparisons of ablating different key components on 8x SR.
| Model | ESA | ADCCA | Tex branch | PSNR↑ | SSIM↑ |
|---|---|---|---|---|---|
| 1 | × | × | × | 28.01 | 0.6359 |
| 2 | √ | × | × | 28.11 | 0.6404 |
| 3 | × | √ | × | 28.23 | 0.6492 |
| 4 | √ | √ | × | 28.26 | 0.6540 |
| 5 | √ | √ | √ | 28.55 | 0.6786 |
Table 4.
Comparisons of ablating different components of the loss function on 8x SR.
| Loss | Pix | Per | Gra | PSNR↑ | SSIM↑ |
|---|---|---|---|---|---|
| 1 | √ | × | × | 28.18 | 0.6645 |
| 2 | × | √ | × | 25.68 | 0.4913 |
| 3 | × | × | √ | 28.17 | 0.6756 |
| 4 | √ | √ | √ | 28.55 | 0.6786 |
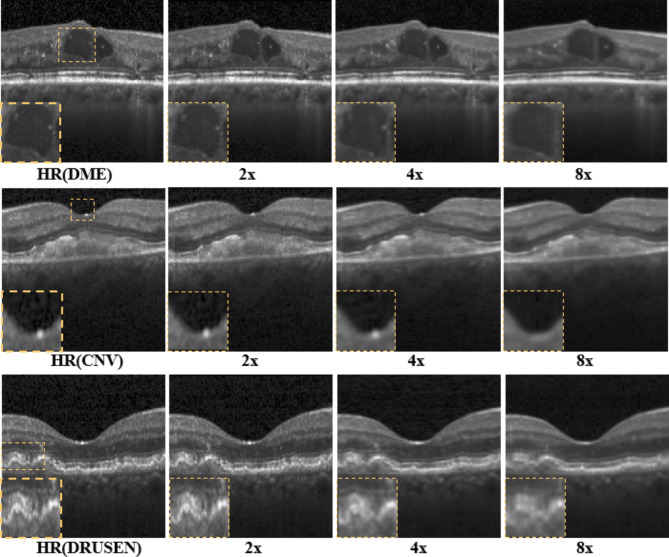
Last, we tested the generalization capability of our proposed model trained with the normal retinal dataset using DME, CNV, and DRUSEN sub-datasets as mentioned in the “Data preparation” section. As illustrated in Fig. 7, HASPN can effectively reconstruct retinal layer structures at 2x, 4x, and 8x SR. When the upscaling factor was 2x, the reconstructed image closely resembled the HR image. However, when performing super-resolution at 8x, certain structures were not adequately reconstructed (indicated by the dashed orange rectangle). Aside from these intricate details, our method can reconstruct most of the retinal layer structures. Consequently, it can be inferred that HASPN possesses an excellent generalization ability, indicating its potential for clinical applications.
Fig. 7.
Generalization performance of the proposed network on diabetic macular edema (DME), choroidal neovascularization (CNV), and multiple drusen in early AMD.
Conclusions
In this work, we proposed a novel hybrid attention structure preserving network (HASPN) to speed up the acquisition while obtaining high digital resolution images comparable to those by dense acquisition. HASPN displays a superior lateral super-resolution reconstruction performance compared to many mainstream super-resolution methods on the public OCT retinal dataset OCT2017. Through qualitative and quantitative analyses, we demonstrated that HASPN achieved the best results at 4x and 8x SR while effectively preserving the structural information of OCT under-sampled images and restoring more details. Furthermore, we not only investigated the impact of depths and widths on the performance of the network but also conducted ablation studies to demonstrate the effectiveness of our key components and hybrid loss. Finally, we validated that HASPN had an excellent generalization capability and could be applied to reconstruct cross-domain OCT images. Our future research will explore self-supervised methods for reconstructing under-sampled OCT images. Additionally, we will consider applying HASPN to other medical imaging modalities, such as magnetic resonance imaging and computed tomography, to expand its use in medical research and applications.
Acknowledgements
This work was supported by Hebei Provincial Social Science Foundation Project (No. HB20TQ003).
Author contributions
Zezhao Guo designed the methods, conducted the experiments and wrote the manuscript. Zhanfang Zhao reviewed the manuscript.
Data availability
The code of this work will be available at https://github.com/ZacharyG666/HASPN-for-OCT.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Huang, D. et al. Optical coherence tomography. Science254(5035), 1178–1181 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.van Velthoven, M. E., Faber, D. J., Verbraak, F. D., van Leeuwen, T. G. & de Smet, M. D. Recent developments in optical coherence tomography for imaging the retina. Prog. Retin. Eye Res.26(1), 57–77 (2007). [DOI] [PubMed] [Google Scholar]
- 3.Shin, E.-S. et al. OCT-defined morphological characteristics of coronary artery spasm sites in vasospastic angina. J JACC: Cardiovasc. Imaging8(9), 1059–1067 (2015). [DOI] [PubMed] [Google Scholar]
- 4.Baran, U., Choi, W. J. & Wang, R. K. Potential use of OCT-based microangiography in clinical dermatology. Skin Res. Technol.22(2), 238–246 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Regatieri, C. V., Branchini, L. & Duker, J. S. The role of spectral-domain OCT in the diagnosis and management of neovascular age-related macular degeneration. Ophthalmic Surg. Lasers Imaging Retina42(4), S56–S66 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ghazal, M., Al Khalil, Y., Alhalabi, M., Fraiwan, L., & El-Baz, A. Early detection of diabetics using retinal OCT images. In Diabetes and Retinopathy, 173–204 (Elsevier, 2020).
- 7.Bussel, I. I., Wollstein, G. & Schuman, J. S. OCT for glaucoma diagnosis, screening and detection of glaucoma progression. Br. J. Ophthalmol.98(Suppl 2), ii15–ii19 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Xu, J., Ishikawa, H., Wollstein, G. & Schuman, J. S. 3D OCT eye movement correction based on particle filtering. 53–56. [DOI] [PMC free article] [PubMed]
- 9.Fang, L. et al. Fast acquisition and reconstruction of optical coherence tomography images via sparse representation. IEEE Trans. Med. Imaging32(11), 2034–2049 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Abbasi, A., Monadjemi, A., Fang, L. & Rabbani, H. Optical coherence tomography retinal image reconstruction via nonlocal weighted sparse representation. J. Biomed. Opt.23(3), 036011–036011 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Wang, L., Chen, Z., Zhu, Z., Yu, X. & Mo, J. Compressive-sensing swept-source optical coherence tomography angiography with reduced noise. J. Biophotonics15(8), e202200087 (2022). [DOI] [PubMed] [Google Scholar]
- 12.Mei, S., Fan, F., Thies, M., Gu, M., Wagner, F., Aust, O., Erceg, I., Mirzaei, Z., Neag, G. & Sun, Y. Reference-free multi-modality volume registration of X-ray microscopy and light-sheet fluorescence microscopy. arXiv preprint arXiv:2404.14807 (2024).
- 13.Wang, L., Sahel, J. A. & Pi, S. Sub2Full: Split spectrum to boost optical coherence tomography despeckling without clean data. Optics Lett.49(11), 3062–3065 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hyun, C. M., Kim, H. P., Lee, S. M., Lee, S. & Seo, J. K. Deep learning for undersampled MRI reconstruction. Phys. Med. Biol.63(13), 135007 (2018). [DOI] [PubMed] [Google Scholar]
- 15.Huang, Y. et al. Simultaneous denoising and super-resolution of optical coherence tomography images based on generative adversarial network. Optics Express27(9), 12289–12307 (2019). [DOI] [PubMed] [Google Scholar]
- 16.Qiu, B. et al. N2NSR-OCT: Simultaneous denoising and super-resolution in optical coherence tomography images using semisupervised deep learning. J. Biophotonics14(1), e202000282 (2021). [DOI] [PubMed] [Google Scholar]
- 17.Xu, K., Qin, M., Sun, F., Wang, Y., Chen, Y.-K. & Ren, F. Learning in the frequency domain. 1740–1749.
- 18.Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer, M., Heigold, G. & Gelly, S. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929 (2020).
- 19.Wang, L., Wang, B., Chhablani, J., Sahel, JA., Pi, S. Freqformer: Frequency-Domain Transformer for 3-D Visualization and Quantification of Human Retinal Circulation. Electrical Engineering and Systems Science (2024).
- 20.Yao, B. et al. PSCAT: A lightweight transformer for simultaneous denoising and super-resolution of OCT images. Biomed. Optics Express15(5), 2958–2976 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., Lin, S. & Guo B. Swin transformer: Hierarchical vision transformer using shifted windows, 10012–10022.
- 22.Woo, S., Park, J., Lee, J.-Y. & Kweon, I. S. Cbam: Convolutional block attention module, 3–19.
- 23.Lu, Y. et al. Super-resolution reconstruction of OCT images based on pyramid long-range transformer. Chin. J. Lasers50(15), 1507107 (2023). [Google Scholar]
- 24.Huang, W. et al. Deep local-to-global feature learning for medical image super-resolution. Comput. Med. Imaging Graph.115, 102374 (2024). [DOI] [PubMed] [Google Scholar]
- 25.Retinal OCT Images (optical coherence tomography). Kaggle, Vol. https://www.kaggle.com/paultimothymooneyIkermany2018 (2017).
- 26.Ramponi, G., Strobel, N. K., Mitra, S. K. & Yu, T.-H. Nonlinear unsharp masking methods for image contrast enhancement. J. Electron. Imaging5(3), 353–366 (1996). [Google Scholar]
- 27.Zhu, H., Xie, C., Fei, Y. & Tao, H. Attention mechanisms in CNN-based single image super-resolution: A brief review and a new perspective. Electronics10(10), 1187 (2021). [Google Scholar]
- 28.Liu, J., Zhang, W., Tang, Y., Tang, J. & Wu, G. Residual feature aggregation network for image super-resolution, 2359–2368.
- 29.Hu, J., Shen, L. & Sun, G. Squeeze-and-excitation networks, 7132–7141. [DOI] [PubMed]
- 30.Cai, Q. et al. TDPN: Texture and detail-preserving network for single image super-resolution. IEEE Trans. Image Process.31, 2375–2389 (2022). [DOI] [PubMed] [Google Scholar]
- 31.Wang, Z., Chen, J. & Hoi, S. C. Deep learning for image super-resolution: A survey. IEEE Trans. Pattern Anal. Mach. Intell.43(10), 3365–3387 (2020). [DOI] [PubMed] [Google Scholar]
- 32.Wang, Z., Bovik, A. C., Sheikh, H. R. & Simoncelli, E. P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process.13(4), 600–612 (2004). [DOI] [PubMed] [Google Scholar]
- 33.Lim, B., Son, S., Kim, H., Nah, S. & Mu Lee, K. Enhanced deep residual networks for single image super-resolution, 136–144.
- 34.Johnson, J., Alahi, A. & Fei-Fei L. Perceptual losses for real-time style transfer and super-resolution, 694–711.
- 35.Simonyan, K. & Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556 (2014).
- 36.Dong, C., Loy, C. C., He, K. & Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell.38(2), 295–307 (2015). [DOI] [PubMed] [Google Scholar]
- 37.Dong, C., Loy, C. C. & Tang, X. Accelerating the super-resolution convolutional neural network, 391–407.
- 38.Zhang, Y., Tian, Y., Kong, Y., Zhong, B. & Fu, Y. Residual dense network for image super-resolution, 2472–2481. [DOI] [PubMed]
- 39.Zhang, Y., Li, K., Li, K., Wang, L., Zhong, B. & Fu, Y. Image super-resolution using very deep residual channel attention networks, 286–301.
- 40.Ledig, C., Theis, L., Huszár, F., Caballero, J., Cunningham, A., Acosta, A., Aitken, A., Tejani, A., Totz, J. & Wang, Z. Photo-realistic single image super-resolution using a generative adversarial network, 4681–4690.
- 41.Wang, X., Yu, K., Wu, S., Gu, J., Liu, Y., Dong, C., Qiao, Y. & Change Loy, C. Esrgan: Enhanced super-resolution generative adversarial networks.
- 42.Wang, L. et al. Axial super-resolution optical coherence tomography via complex-valued network. Phys. Med. Biol.68(23), 235016 (2023). [DOI] [PubMed] [Google Scholar]
- 43.Liang, J., Cao, J., Sun, G., Zhang, K., Van Gool, L. & Timofte, R. Swinir: Image restoration using swin transformer, 1833–1844.
- 44.Lu, Z., Li, J., Liu, H., Huang, C., Zhang, L. & Zeng, T. Transformer for single image super-resolution, 457–466.
- 45.Odena, A., Dumoulin, V. & Olah, C. Deconvolution and checkerboard artifacts. Distill1(10), e3 (2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The code of this work will be available at https://github.com/ZacharyG666/HASPN-for-OCT.