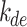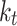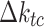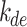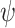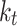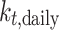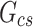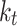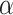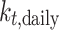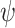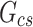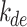Application of explainable machine learning for estimating direct and diffuse components of solar irradiance

Abstract

The inclusion of diffuse horizontal irradiance (DHI) and direct normal irradiance (DNI) is crucial in the context of solar energy applications. However, most solar irradiance instruments primarily prioritize the measurement of global horizontal irradiance (GHI) due to the high cost associated with devices used to measure DNI and DHI. Hence, numerous prior works have investigated various solar decomposition models aimed at computing direct and diffuse irradiance from GHI. The present study introduces a novel separation approach for direct and diffuse irradiance, employing machine learning algorithms and utilizing data with a temporal resolution of 1 min. Three machine learning models utilizing the gradient boost technique are suggested and trained using data collected from 10 stations across the world with different climate conditions. The machine learning model called CatBoost outperforms all the solar decomposition models at every station. It achieves the lowest root mean squared error (RMSE) of 8.73% when calculating DNI. The concept of explainable machine learning is further explored through the utilization of shapley additive explanations (SHAP), which allows for the assessment of the significance and interaction of the input parameters. In summary, the results of this study reveal that humidity is an important parameter for the estimation of DNI and DHI.

Introduction

Solar energy applications indeed rely on precise solar irradiance data, including global horizontal irradiance (GHI), direct normal irradiance (DNI), and diffuse horizontal irradiance (DHI). These specific irradiance measurements are crucial for assessing the availability and potential of solar energy resources, enabling efficient design and operation of solar power systems, and optimizing their performance. GHI measures the total solar radiation received on a horizontal surface, capturing both direct and diffuse radiation. DNI quantifies the intensity of solar radiation directly from the sun, while DHI represents the diffused solar radiation received from the sky, scattered by atmospheric particles and clouds. Collectively, these data points are essential for various aspects of solar energy planning, from site selection and system design to energy yield predictions and operational monitoring.

GHI is a vital resource of solar energy information that enables a higher production of photovoltaic (PV) power across all sky conditions^1,2. Furthermore, GHI is beneficial for predicting the energy production of PV systems and reducing the potential power fluctuations in electric grid injections³. DNI is an essential component of global irradiance, especially under clear sky conditions, and it represents a solar resource that may be exploited by several types of concentrating solar technology^4–8. It also provides essential data for predicting solar radiation entering vehicles, which affects thermal comfort and influences energy requirements for cooling or heating the cabin⁹. DHI is important because it is applied in energy and building applications^10–15. It plays a significant role in passive solar heating by estimating the amount of diffuse radiation that enters through windows, affecting indoor temperatures¹³. The prevailing issue lies in the fact that most solar irradiance measurements prioritize GHI due to the considerable cost associated with instruments capable of measuring DNI and DHI. Specifically, the deployment of a pyrheliometer for DNI measurement and a pyranometer equipped with a shadow-ball device for DHI measurement necessitates regular maintenance and calibration. This is primarily attributed to their installation of sun-tracking systems that continuously adjust their positioning following the movement of the sun across the sky.

To address this issue, in the past century, researchers have developed solar radiation decomposition models to separate DNI and DHI from GHI data, addressing a critical issue in solar energy estimation^16,17. Numerous studies have been conducted to compare these decomposition models across various locations^18,19. However, it has been observed that the accuracy of these separation models is highly dependent on local atmospheric conditions²⁰. Surprisingly, even the latest decomposition models, which incorporate more input variables, do not consistently improve performance. For instance, Han et al.²¹ demonstrated that the Erbs model²², which requires only the clearness index as input, outperforms the Engerer model¹⁷, which utilizes multiple input variables to estimate DHI using satellite data. This result is unsurprising since most decomposition models are empirically constructed and customized to suit particular geographical regions. As a result, determining the optimal decomposition model for estimating DNI and DHI remains a challenging task, given the variability in atmospheric conditions from one location to another.

In recent times, the application of machine learning for estimating DHI and DNI has gained popularity due to their potential to establish more robust empirical relationships compared to traditional solar decomposition models^23–26. While many machine learning-based solar irradiance estimation models have demonstrated high performance, most of these algorithms are regarded as black boxes, lacking transparency and interpretability for human understanding. As a result, various studies employ different sets of input parameters for machine learning models, often without a systematic consideration of the most significant variables. For instance, in the work of Aler et al.²³, an exploration of 24 potential input parameters is conducted within the framework of the original 140 separation models. However, through the application of a gradient boosting model, only 14 input parameters are identified as relevant. In contrast, Oh et al.²⁷ achieved more accurate estimates of DNI using an artificial neural network (ANN) with just eight selected input parameters, outperforming Aler’s model. This highlights the importance of judiciously selecting significant input parameters for both the estimation of DNI and DHI and for ensuring computational efficiency.

To address the existing research gap, this study aims to develop a highly accurate estimation model for sub-hourly DNI and DHI. This model is constructed through a combination of machine learning models and shapley additive explanation (SHAP) methods. This approach not only enables the automated and dependable capture of complex and non-linear interactions among multiple input factors but also offers a quantitative interpretation of the resulting machine learning model. Moreover, the existing solar decomposition models are constructed with diverse input parameters, making explainable machine learning invaluable for examining the impact of each input parameter and selecting the significant input parameters. To achieve these objectives, we gathered solar radiation data from 10 diverse locations around the world, allowing us to assess the performance of both decomposition and machine learning models across varying climatic conditions. The analysis incorporates a range of input parameters, including measured and calculated data, to elucidate their relationships and impacts on the target parameter. In conclusion, this study identifies key input parameters essential for both efficiency analysis and the more accurate estimation of DNI and DHI, surpassing the capabilities of existing solar decomposition models.

The remainder of this paper is structured into five sections. Section “Data collection and preprocessing” provides a detailed description of the data utilized in this study. Section “Methodology” outlines the methodology. Subsequently, section “Results and discussion” thoroughly examines and discusses all the obtained results. Finally, in section “Conclusions”, we summarize the noteworthy findings and draw conclusions from this research.

Data collection and preprocessing

Solar irradiance measurements are obtained from 10 locations worldwide through the Baseline Surface Radiation Network (BSRN)²⁸. Table 1 presents information on each station, including the site name, latitude, longitude, elevation, data period, and climatic type.

Table 1.

Information of data sourced from 10 stations includes climate type information, namely arid (AR), high albedo (HA), temperate (TM), and tropical (TR).

Nos.	Code	Site name	Latitude (°)	Longitude (°)	Elevation (m)	Period	Climate
1	ALE	Alert	82.4900	− 62.4200	127.0	2011–2013	HA
2	BER	Bermuda	32.3008	− 64.7660	8.0	2009–2011	TM
3	CAB	Cabauw	51.9711	4.9267	0.0	2019–2021	TM
4	CNR	Cener	42.8160	− 1.6010	471.0	2011–2013	TM
5	DAR	Darwin	− 12.4250	130.8910	30.0	2011–2013	TR
6	FLO	Florianopolis	− 27.6047	− 48.5227	11.0	2017–2019	TM
7	GOB	Gobabeb	− 23.5614	15.0420	407.0	2019–2021	AR
8	MAN	Momote	− 2.0580	147.4250	6.0	2010–2012	TR
9	PTR	Petrolina	− 9.0680	− 40.3190	387.0	2015–2017	TR
10	REG	Regina	50.2050	− 104.7130	578.0	2008–2010	TM

The dataset used in this study comprises 3 years of data collected from each location. This dataset, obtained from the BSRN, not only includes solar irradiance data but also encompasses additional meteorological parameters such as air temperature, humidity, and atmospheric pressure. To develop and evaluate our proposed machine learning model, we need to partition the data into training, validation, and testing datasets. In our approach, the first 2 years of data from each location are designated for training and validation purposes, while the last year of data from each station is used for model performance evaluation. To ensure a fair comparison with the decomposition model, which is also part of this study, we allocated only the last year of data for each station for use in the solar decomposition model. One crucial aspect of this study is the handling of missing data, as it significantly impacts the results. Table 2 provides comprehensive information regarding the occurrence of missing data. Notably, some stations have missing data exceeding 20%, particularly in the case of diffuse irradiance. However, it is essential to emphasize that most stations offer nearly complete data records. Therefore, we decided not to address or impute the missing data, considering the high variability of solar irradiance data at sub-hourly intervals. Attempting to fill in these missing values could potentially introduce biases and inaccuracies into our analysis, a risk we aim to avoid in our research.

Table 2.

Missing data details for each station.

Data	ALE (%)	BER (%)	CAB (%)	CNR (%)	DAR (%)	FLO (%)	GOB (%)	MAN (%)	PTR (%)	REG (%)
Training and validation (2 years)
GHI (W/m2)	1.1	8.9	0.3	0.3	3.2	1.5	0.1	1.2	7.2	0.1
DNI (W/m2)	6.5	10.2	0.2	0.3	1.9	20.0	0.1	2.8	20.4	0.0
DHI (W/m2)	2.7	44.4	0.2	0.3	0.1	20.4	0.0	0.1	21.6	0.0
Temperature (°C)	0.7	18.0	0.1	0.3	0.0	1.8	0.0	0.8	4.4	0.0
Humidity (%)	2.1	22.4	0.1	0.3	0.0	23.6	0.0	3.5	4.4	0.0
Pressure (hPa)	5.3	7.7	0.1	0.3	0.0	1.2	0.0	3.5	5.6	0.0
Testing (1 year)
GHI (W/m2)	2.8	2.2	0.5	0.7	18.8	7.7	0.2	1.1	24.1	4.9
DNI (W/m2)	6.2	1.9	1.2	0.7	1.9	6.7	0.1	3.1	8.5	1.0
DHI (W/m2)	8.2	4.1	1.4	0.7	0.1	14.8	0.0	0.4	32.7	1.0
Temperature (°C)	1.8	0.0	0.3	0.7	0.0	2.7	0.0	0.1	0.0	1.0
Humidity (%)	2.3	0.0	0.3	0.7	0.0	0.0	0.0	0.1	0.0	13.9
Pressure (hPa)	13.8	0.0	0.3	0.7	0.0	0.0	0.0	0.1	24.1	8.5

All input parameters are selected and analyzed at a resolution of 1 min. Measured solar irradiance and weather data, including temperature, humidity, and pressure, are collected from the BSRN. Parameters such as apparent solar time (AST), solar zenith angle, solar azimuth angle, and extraterrestrial irradiance are calculated as input variables, and other parameters such as turbidity are estimated using monthly linke turbidity data from PVLib²⁹. It is essential to note that DNI and DHI are not employed as input variables in the machine learning model, but rather serve as the primary objectives of our estimation framework.

The objective of this research is to estimate DNI and DHI utilizing GHI and other relevant parameters. Therefore, it is imperative to ensure the quality and reliability of the solar irradiance data used in this study. To achieve this, a rigorous set of quality control (QC) procedures and explicit standards is employed. Data QC involves the application of techniques and processes to assess whether the data meets both overarching quality objectives and specific quality criteria³⁰. A comprehensive set of QC procedures, aligned with the recommendations of the BSRN³¹, is outlined in Table 3, ensuring that the data used in our research adheres to stringent quality standards.

Table 3.

QC procedure for solar irradiance data.

Category	Limit
Physically possible limit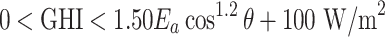
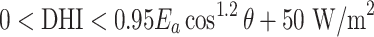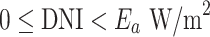Closure comparison
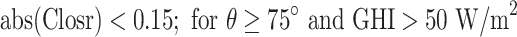Diffuse fraction comparison

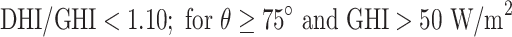The QC procedures applied in this study draw inspiration from the physically possible limit tests, closure comparison, and diffuse fraction comparison recommended by the BSRN. is solar zenith angle, is the extraterrestrial irradiance on a plane normal to the sun, and 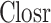is the difference between estimated GHI (using measured DNI and DHI) and measured GHI (calculated by 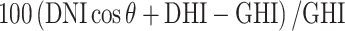). In addition, we incorporated a condition requiring a solar zenith angle of less than 85° to eliminate data points associated with low solar elevation, which could introduce significant errors into solar radiation models³². As a result of these rigorous quality control measures, data points that do not meet the specified criteria are removed, resulting in a dataset containing 3 million data points for training and validation and 1.57 million for testing. It is worth noting that all data analysis, calculations for decomposition models, and machine learning tasks are carried out using the Python programming tool on a computer equipped with a 32 GB RAM operating system and an Intel core i7-10700 K CPU running at 3.80 GHz.

Methodology

Figure 1 illustrates the step-by-step process employed for estimating DNI and DHI, commencing from data preparation and extending to model evaluation. In the data preparation phase, a set of nine input parameters is carefully chosen for the machine learning models. Subsequently, the data is partitioned into training, validation, and testing subsets. Three machine learning models, specifically based on the gradient boosting model, are chosen to carry out the estimation of DNI and DHI. The next step involves leveraging explainable machine learning techniques, particularly SHAP values, to scrutinize and identify the significant input parameters that exert a notable impact on the estimation outcomes. Following this, the trained machine learning model undergoes testing across various stations. To assess the effectiveness of the proposed model, a comparative analysis is conducted against several existing solar decomposition models, employing evaluation metrics for a comprehensive understanding of model performance.

Fig. 1.

Flow chart of the proposed separation model used in this study to estimate direct and diffuse irradiance.

Solar radiation decomposition model

Solar decomposition models are primarily developed empirically, relying on historical data and meteorological parameters to unravel the complex dynamics of solar radiation. The models can be broadly categorized into two types: those starting from the use of a single variable, such as the clearness index, and those employing multiple variables, encompassing parameters like clear sky irradiance, solar elevation angle, AST, and more. While most solar decomposition models have traditionally been built using hourly data, only a limited number of models originate from minute-resolution data. Minute-level decomposition models offer a distinct advantage by capturing rapid fluctuations in atmospheric conditions, thus providing more accurate estimations of DNI and DHI, which are essential for assessing the efficiency and performance of solar energy systems. To ensure precision in this research, we exclusively employ decomposition models developed using minute-level data. Furthermore, we utilize the latest decomposition models, highlighting the importance of staying up to date with advancements in the field. The solar decomposition models selected incorporate input variables outlined in Table 4.

Table 4.

Input variables of the solar decomposition model.

Solar decomposition model	Input variables
ENGERER217	, , AST, ,
ENGERER433	, , AST, ,
EVERY34	, , AST, ,
STARKE235	, , AST, , ,
STARKE336	, , AST, , , ,
YANG437	, , AST, , ,

Solar decomposition models first determine the parameter diffuse fraction, 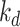, which is then transformed into DHI, . Then, DNI is computed using the solar irradiance equation, . Additionally, in the ENGERER2, ENGERER4, STARKE2, STARKE3, and YANG4 models, clear sky irradiance, 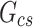, is required to calculate other parameters such as portion of diffuse fraction, 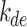and difference between clearness index,. In this particular scenario, the Ineichen clear sky model³⁸ is used, because it simplicity and only requires a few input variables. All solar decomposition models incorporate the clearness index, , as a fundamental parameter. Additionally, some models make use of other parameters, including solar elevation angle, , and three-point moving of clearness index, .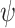

Machine learning

In this study, we proposed machine learning models that utilize boosting methods, including extreme gradient boosting (XGB), light gradient-boosting machine (LightGBM), and categorical boosting (CatBoost). Boosting is a machine learning strategy that involves the ensemble or combination of numerous simple models, resulting in improved performance compared to an individual model³⁹. The functioning of this process involves the iterative training of a sequence of weak learners, such as decision trees or linear models. Each learner is specifically designed to address the areas where previous learners encountered the most difficulties. A concise overview of the three models is presented in the next section.

XGBoost

XGBoost is an optimized and scalable implementation of gradient boosting, which is a powerful ensemble learning technique, encompassing various objective functions for tasks like regression and classification⁴⁰. This highly efficient algorithm operates within the gradient tree boosting framework, where it transforms weak classifiers into robust ones by continuously splitting variables and constructing multiple regression trees. XGBoost utilizes a combination of loss functions and regularization terms to fine-tune the model, enabling it to capture intricate data relationships and yield remarkably accurate predictions. Notably, it offers features like parallel processing and GPU acceleration, significantly expediting the model training process, which has made it a favored choice among data scientists and machine learning professionals. An essential strength of XGBoost is its adeptness at efficiently managing complex, high-dimensional data, featuring automated feature selection and the provision of feature importance scores, facilitating both data understanding and feature selection. Furthermore, it incorporates built-in regularization techniques to curb overfitting, thereby enhancing its model stability.

LightGBM

LightGBM is a gradient boosting framework known for its speed and efficiency when compared to other boosting algorithms. It excels in processing large datasets quickly, conserving memory resources, delivering high prediction accuracy, and supporting parallel and GPU learning⁴¹. LightGBM incorporates two innovative concepts, namely gradient-based one-side sampling (GOSS) and exclusive feature bundling (EFB), which contribute to its exceptional performance. GOSS is a novel sampling method that leverages the idea that data instances with larger gradients provide more information gain. As a result, it selectively retains instances with significant gradients while randomly discarding instances with smaller gradients during the down sampling process. This approach leads to a more precise estimation of information gain without the need for a large dataset. To address the sparsity often found in high-dimensional data, EFB is introduced as an almost lossless technique for reducing feature dimension. EFB identifies mutually exclusive features that can be combined into denser features, effectively reducing the number of operations performed on zero feature values⁴². The utilization of the advanced methodologies, GOSS and EFB, in combination, enhances the capability of LightGBM to provide very precise estimations by means of a more efficient and simplified training procedure.

CatBoost

CatBoost is a gradient boosting algorithm developed by Yandex with a primary focus on accommodating categorical features⁴³. It was introduced in April 2017 as an alternative to boost the performance of gradient boosting machines (GBM) such as XGBoost and LightGBM. The algorithm possesses the capability to effectively process categorical features without necessitating human preprocessing, rendering it a significant asset for real-world datasets that frequently contain category variables. The CatBoost algorithm employs an ordered boosting methodology to construct a collection of decision trees. Additionally, it integrates multiple regularization algorithms to mitigate overfitting and enhance generalization. An outstanding characteristic of CatBoost is its proficient handling of missing values. The process of training is facilitated by the automatic population of missing values, hence minimizing the requirement for data imputation. Additionally, CatBoost is renowned for its strong resilience and typically necessitates less adjustment of hyperparameters in comparison to alternative gradient boosting algorithms.

Input parameters

The selection of input parameters is guided by the variables utilized in existing solar decomposition models. Figure 2 illustrates the extraction of specific input parameters from each equation of the solar decomposition models. The chosen input parameters include GHI, turbidity, extraterrestrial irradiance, solar zenith angle, and AST. Additionally, weather-related parameters such as humidity, temperature, and pressure are incorporated due to their availability at each station. Furthermore, the inclusion of a broader set of parameters is motivated by their consistent availability across stations. The study aims to discover important input parameters, and this comprehensive method enables a detailed investigation of how each parameter affects the estimation results. Therefore, a broader range of parameters facilitates a more intricate comprehension of the interrelationships among multiple variables and their impact on the outcomes of the estimation process.

Fig. 2.

Process of selection input parameters.

Machine learning explainability

Most existing machine learning algorithms, especially for solar irradiance estimation using machine learning models focus on improving accuracy rather than explainability. Most current machine learning models are commonly perceived as black boxes, as they provide output in the form of target values without revealing the underlying knowledge or processes involved in generating such outputs. Therefore, this work aims to employ the explainable machine learning technique known as SHAP to comprehensively comprehend, place confidence in, and critically evaluate the results generated by the estimation model. The SHAP approach is presented by Lundberg⁴⁴ as a means to comprehend and evaluate the predictions generated by intricate machine learning models. This methodology offers a means to allocate the contribution of each characteristic to a specific estimation, hence facilitating the explication of the model output in a more comprehensible and interpretable manner. A brief mathematical background of the SHAP method is given below:

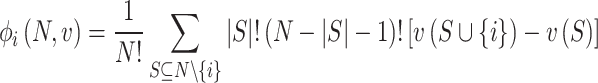1

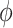is the shapley value for a specific feature, 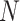is the set containing all the features, is a subset of the features, 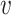is the value function, 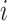is an element of .

Evaluation metric

The accuracy of the estimation models, including the decomposition and machine learning models, is assessed using root–mean–square error (RMSE) and mean bias error (MBE). As the current data are obtained from multiple locations, the relative metrics such as relative root–mean–square error (rRMSE) and relative root–mean bias error (rMBE) are more insightful in assessing the models, as they exhibit the percentage difference. In addition, coefficient of determination 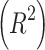is used to evaluate the fit of the model. The value quantifies the proportion of variance in the observed data that is explained by the model.

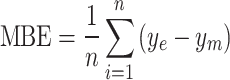2

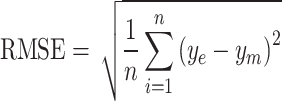3

4

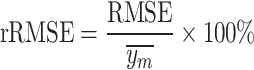5

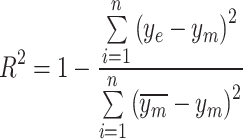6

where 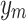, , 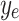, represent the actual output, estimated output, mean value of actual output, and the number of samples, respectively.

Results and discussion

To identify the significant input parameters for the estimation model, the initial step involves training machine learning models using the complete set of input parameters. These models are built using data collected from all stations and subsequently analyzed using SHAP values. This analysis is conducted to discern the influence and impact of each individual parameter on the estimation model. On the other hand, the importance of this experiment lies in the selection of the optimal number of input variables, as overfitting can potentially be induced by using too many input variables⁴⁵.

To improve the accuracy and prevent overfitting of the proposed machine learning models, the optimal hyperparameters are identified. In this study, GridSearchCV function is used for tuning hyperparameters that combine the grid search and k-fold cross-validation approaches. This algorithm evaluates the performance of the model using various combinations of hyperparameters. It measures the model score during the training phase and determines the optimal hyperparameter combination for the machine learning models. The algorithm examines each of the provided hyperparameter combinations and selects the one with the highest performance. This optimal combination is then employed to build the actual model and estimate the objective variables. fivefold cross-validation is also used during grid optimization for training investigation. The training set is divided into five folds, with one-fold used for validation and the remaining folds used for training in each training iteration. The details of the selected hyperparameters for each model are listed in Table 5.

Table 5.

Information of the optimized hyperparameters.

Model	Optimized hyperparameters
XGBoost	learning_rate = 0.1; max_depth = 10; subsample = 1; colsample_bytree = 0.6; min_child_weight = 1; reg_alpha = 0.1; reg_lambda = 0.1;
LightGBM	learning_rate = 0.1; max_depth = 10; subsample = 1; colsample_bytree = 0.6; reg_alpha = 0.1; reg_lambda = 0.1; min_child_weight = 1
CatBoost	learning_rate = 0.1; depth = 10; subsample = 1; colsample_bylevel = 0.8;

SHAP analysis

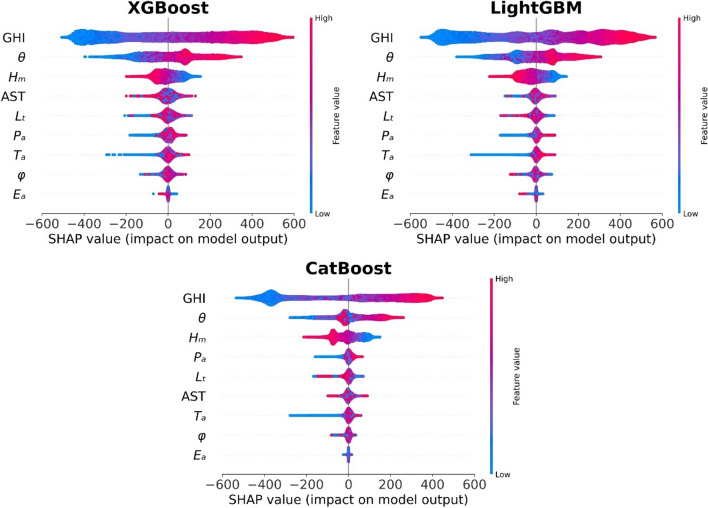
The SHAP technique is capable of determining the overall significance of features by combining the individual explanations. The feature importance plot demonstrates positive outcomes in comparison to alternative methods for determining feature importance. Figure 3 provides a detailed summary plot, offering a comprehensive view of the model performance on the testing dataset. This summary figure combines feature importance and feature effect. The features are ordered in decreasing importance, following a top-to-bottom arrangement along the vertical axis, consistent with the feature importance plot. In this summary plot, each feature line represents a case history, and a single dot is used to represent each case history across all feature lines. The horizontal axis displays the SHAP value associated with each point. Points located to the right of zero on the SHAP value scale indicate a positive impact, suggesting good results for the estimation. Conversely, points located to the left of zero indicate a negative impact, implying a reduction in the model accuracy. Each point is assigned a color based on its corresponding feature values, as indicated by the color bar on the right-hand side. The density of SHAP values along the vertical axis is represented by the overlapping of points in certain areas for each feature. The findings from these figures show that specific factors have a positive impact on the estimation of DNI. These factors include high GHI, high solar zenith angle, low relative humidity, high temperature, and high pressure. In contrast, low GHI, low solar zenith angle, high relative humidity, low temperature, and low pressure have a negative impact on DNI estimation.

Fig. 3.

Contribution of different input variables: (a) XGBoost; (b) LightGBM; (c) CatBoost.

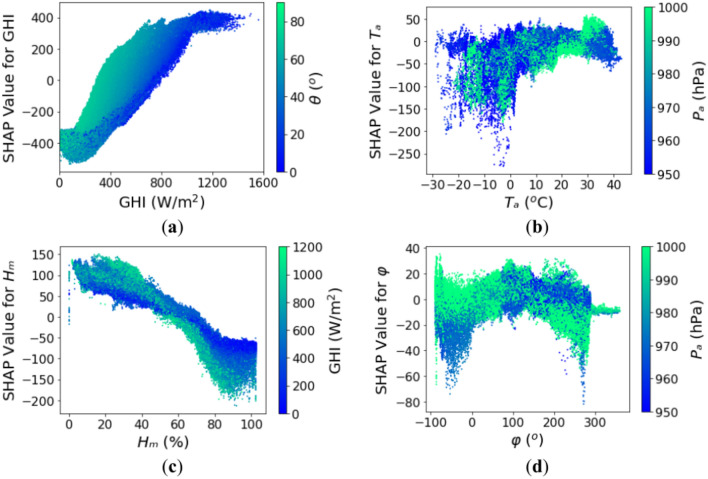
To enhance comprehension, the interactions between two input variables for the CatBoost model, as determined by the SHAP values, are presented. The CatBoost model is chosen due to its training and validation results showing the least variance, indicating a lower probability of overfitting. These interactions are visualized by coloring each data point according to the values of the interacting input variables in the dependence plot. Figure 4 provides a clear representation of these interactions, with a color bar on the right side of each plot indicating the interacting input variables. In this color bar, blue and green represent lower and higher values of the interacting input variables, respectively. Figure 4a illustrates the interaction pattern between GHI and the solar zenith angle on the estimation of DNI. The results show that high GHI combined with a low solar zenith angle positively impacts DNI estimation, reflecting the conditions of direct sunlight with minimal atmospheric scattering. Conversely, low GHI coupled with a high solar zenith angle negatively affects DNI estimation. This trend reflects the impact of the increased path length through the atmosphere at higher zenith angles, leading to significant attenuation of direct solar radiation. Figure 4b showcases the interaction between ambient temperature and atmospheric pressure on DNI estimation. Low temperatures negatively influence the estimation, regardless of atmospheric pressure, likely due to cloud formation or reduced solar intensity in colder environments. In contrast, moderate to high temperatures combined with higher atmospheric pressure positively affect DNI estimation, as such conditions typically correspond to clear skies and stable atmospheric conditions that enhance direct solar radiation. The interaction between GHI and relative humidity is demonstrated in Fig. 4c. High GHI with low relative humidity positively influences DNI estimation, indicating clear-sky conditions with minimal water vapor interference. However, as relative humidity increases beyond 50%, the positive impact diminishes. High GHI coupled with high relative humidity negatively impacts DNI estimation, possibly due to the scattering and absorption effects of water vapor or cloud presence, which reduce the direct component of solar irradiance. Figure 4d highlights the interaction between the solar azimuth angle and atmospheric pressure on DNI estimation. When the azimuth angle lies within − 100° to 100°, representing the sun’s position closer to the southern horizon (in the northern hemisphere), and is combined with high atmospheric pressure, it positively impacts DNI estimation. This is likely due to the stable, clear-sky conditions associated with high pressure. Conversely, azimuth angles beyond this range (100–300°) combined with high atmospheric pressure negatively affect DNI estimation, possibly due to increased atmospheric scattering and lower direct irradiance at these positions.

Fig. 4.

Interaction of input components: (a) GHI – Solar zenith angle; (b) Temperature – Atmospheric pressure; (c) Relative Humidity – GHI; (d) Solar azimuth angle – Atmospheric pressure.

Once the ranking of input parameters is determined through the SHAP values, the subsequent step involves training machine learning models using varying numbers of input parameters. Results of machine learning models for estimating DNI using multiple input variables are presented in Fig. 5. It shows that as the number of input variables increases, there is a noticeable enhancement in the accuracy of all machine learning models. Although the XGBoost model outperforms the others when using all input variables, it exhibits a significant discrepancy in accuracy between the training and validation datasets, with an rRMSE difference of 1.8%. In contrast, the LightGBM and CatBoost models show much smaller differences in rRMSE between the training and validation datasets, with only 0.8% and 0.1% variations, respectively.

Fig. 5.

rRMSE of training and validation data of machine learning models using data from 10 stations.

The comparison between using 8 input parameters and 9 input parameters reveals a marginal improvement in the rRMSE value. The modest 1% improvement suggests that extraterrestrial irradiance has minimal impact on the model performance. This aligns with the findings from the SHAP values, which consistently indicate that extraterrestrial irradiance has the smallest impact across all machine learning models. As a consequence, we opted to comprise each machine learning model with a mere eight input parameters, omitting the extraterrestrial irradiance parameter.

Results for each station

The results of both machine learning and solar radiation decomposition models for estimating DNI are presented in Table 6. This table displays the performance of these models at twelve different locations, using five solar radiation decomposition models, and assesses their accuracy in terms of rMBE and rRMSE. The test dataset utilized for evaluation includes data from the last year for each station. Interestingly, while the CatBoost machine learning model initially demonstrated lower accuracy during training when trained using datasets from all stations, its performance improved significantly when tested individually for each station. Specifically, the CatBoost model consistently showed the lowest rRMSE for each location, surpassing the performance of both the solar radiation decomposition models and other machine learning models. This improvement in performance for the CatBoost model when tested at individual stations may be attributed to the small difference in error between the training and validation results when using data from all stations. This small difference in error suggests a reduced probability of overfitting occurring within the CatBoost model. The accuracy of the solar radiation decomposition models varied by location due to the unique characteristics of each site. For DNI estimation, the ALE station has the highest error in terms of rRMSE for the decomposition model, whereas the machine learning models demonstrate an improvement in accuracy of over 4%. Conversely, at the GOB station, which has the lowest error in the decomposition model, machine learning models still perform better, with an accuracy improvement of more than 2%.

Table 6.

rRMSE (%) and rMBE (%) of DNI estimation using decomposition and machine learning models for 10 locations.

DNI	rRMSE	rMBE	rRMSE	rMBE	rRMSE	rMBE	rRMSE	rMBE	rRMSE	rMBE
	ALE		BER		CAB		CNR		DAR
Mean (W/m2)	331.58		379.93		268.07		392.43		523.52
ENGERER2	36.78	13.63	28.29	1.90	36.29	7.42	26.61	− 6.57	21.35	− 6.28
ENGERER4	41.07	18.13	32.46	11.01	38.27	10.15	25.83	1.52	23.21	− 3.14
EVERY	56.63	36.58	45.95	23.82	50.99	18.04	33.71	11.85	29.32	4.22
STARKE2	56.38	37.20	39.43	21.22	44.35	17.78	29.03	10.14	24.38	4.58
STARKE3	50.83	30.32	35.17	13.60	43.14	15.70	26.62	3.28	24.00	1.56
YANG4	35.33	12.01	27.62	3.68	34.26	7.59	23.58	− 2.88	18.11	− 2.45
XGBoost	41.39	− 10.71	27.49	2.64	32.94	− 2.80	23.25	− 1.27	17.47	− 4.05
LightGBM	35.62	− 9.99	26.45	1.55	31.60	− 2.13	21.94	− 0.36	16.37	− 3.75
CatBoost	30.60	− 7.63	24.85	2.62	28.44	− 1.57	20.29	− 0.71	15.06	− 3.26

	FLO		GOB		MAN		PTR		REG
Mean (W/m2)	359.7		803.18		357.49		431.49		416.5
ENGERER2	26.76	− 3.19	14.76	− 8.82	29.61	− 3.24	26.10	− 7.00	29.43	3.33
ENGERER4	28.39	1.59	12.42	− 6.88	30.60	3.88	25.92	5.10	31.87	9.15
EVERY	37.17	14.78	11.67	2.65	40.46	12.55	37.22	17.59	43.64	23.47
STARKE2	33.69	14.44	10.28	0.13	35.28	11.88	30.21	13.33	38.76	20.21
STARKE3	30.66	8.63	10.43	− 0.03	33.47	6.62	27.38	6.40	35.65	15.30
YANG4	26.23	− 1.26	10.21	− 5.33	29.14	− 1.38	25.34	− 2.46	30.11	5.90
XGBoost	29.96	− 5.35	9.46	− 2.69	28.30	− 6.17	25.88	1.41	25.61	− 4.49
LightGBM	27.61	− 4.73	8.61	− 2.29	26.37	− 6.16	23.93	0.91	23.02	− 3.96
CatBoost	23.79	− 2.96	7.75	− 2.25	24.69	− 4.84	21.89	1.62	21.12	− 3.23

Table 7 provides a similar comparison, but it focuses on estimating DHI. In this scenario, DHI is indirectly estimated using a machine learning approach, but it is calculated using a solar irradiance equation, 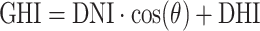. GHI is measured data, DNI is estimated value using machine learning model, and is solar zenith angle from the calculation. Similar to the DNI estimation, the CatBoost model also demonstrates the best performance for DHI estimation. The GOB station has the highest error in terms of rRMSE for the decomposition model, whereas CatBoost shows an accuracy improvement of over 11%. The location with the lowest decomposition error, which is the CAB station, indicates that DHI estimation using machine learning continues to improve with an accuracy increase of more than 5%.

Table 7.

Same as Table 6 but for DHI.

DHI	rRMSE	rMBE	rRMSE	rMBE	rRMSE	rMBE	rRMSE	rMBE	rRMSE	rMBE
	ALE		BER		CAB		CNR		DAR
Mean (W/m2)	167.55		228.19		192.56		177.03		205.35
ENGERER2	32.73	− 11.42	33.46	− 2.24	31.94	− 5.92	37.66	7.41	39.21	9.78
ENGERER4	36.65	− 15.38	37.65	− 12.58	33.89	− 8.46	38.00	− 3.62	41.52	2.99
EVERY	50.16	− 31.55	53.32	− 28.10	45.74	− 16.04	50.22	− 19.32	54.33	− 13.12
STARKE2	49.86	− 31.87	46.33	− 24.59	39.52	− 15.11	43.69	− 16.85	45.54	− 11.80
STARKE3	44.96	− 25.93	41.10	− 16.17	38.40	− 13.50	39.11	− 7.18	43.87	− 6.38
YANG4	30.76	− 9.69	34.18	− 6.38	31.07	− 6.56	35.56	2.43	37.63	4.89
XGBoost	34.27	8.57	35.44	− 4.30	27.84	0.31	35.44	− 2.50	34.52	4.02
LightGBM	29.80	7.92	34.07	− 2.86	26.76	− 0.32	34.23	− 3.83	32.08	3.36
CatBoost	26.25	5.85	31.34	− 4.26	24.43	− 0.76	31.32	− 3.28	29.78	2.38

	FLO		GOB		MAN		PTR		REG
Mean (W/m2)	203.35		120.4		235.59		230.27		190.69
ENGERER2	33.67	2.79	77.35	47.98	34.64	3.35	36.89	11.83	38.78	0.60
ENGERER4	36.56	− 3.13	63.49	38.03	35.52	− 4.90	35.06	− 4.38	40.54	− 7.21
EVERY	49.52	− 20.21	53.30	− 10.10	47.34	− 16.11	50.59	− 22.74	55.80	− 27.41
STARKE2	44.83	− 19.05	49.52	3.90	41.20	− 14.45	40.72	− 16.38	48.81	− 22.54
STARKE3	40.36	− 11.98	49.39	4.22	38.69	− 8.49	37.10	− 6.95	45.34	− 16.23
YANG4	34.14	− 1.14	66.51	31.95	32.56	2.13	34.15	8.15	35.74	− 3.49
XGBoost	37.61	4.52	45.44	10.86	32.52	4.44	38.08	− 1.53	34.35	7.74
LightGBM	34.88	3.67	41.70	8.82	30.23	4.45	34.21	− 0.89	31.15	7.03
CatBoost	30.39	1.35	37.78	8.52	28.39	2.96	31.05	− 1.85	28.62	6.15

Detailed comparison at another location

To validate the accuracy of machine learning models, data from locations different from those used for model training is provided. In this case, data for the year 2020, including solar irradiance and weather data, are gathered from Kookmin University (KMU) station in Seoul, South Korea. The measurements of solar radiation are conducted using a range of devices from EKO Instruments, a Japanese manufacturer. These devices encompass a pyranometer, pyrheliometer, sun tracker, and tracking ball. The pyranometers and pyrheliometer employed in this study are classified as class A sensors and have undergone calibration according to ISO 9060:2018 standards. The MS-80 type pyranometers, utilized for measuring GHI and DHI, possess sensitivities of 10.18 μVm²/W and 10.44 μVm²/W, respectively. The MS-57 type pyrheliometer is characterized by a sensitivity of 7.68 μVm²/W. Each of these sensors is designed to operate within a temperature range of − 40 to 80 °C and can measure irradiances within the range of 0–4000 W/m². Furthermore, QC procedures have been applied to the collected solar irradiance data. The outcomes of these QC procedures are presented in Fig. 6, which displays the GHI, DHI, and DNI values after applying the limit points established during the quality control process.

Fig. 6.

Solar irradiance measurements from KMU station after quality control. The green points represent the filtered data, and the red points represent the limits.

Machine learning models trained on global data are applied to the KMU station and compared with the results of a solar decomposition model presented in Table 8. The results reveal that all machine learning models surpassed the performance of solar decomposition models, with the CatBoost model demonstrating the lowest error in terms of rRMSE for both DNI and DHI at 24.65% and 25.23%, respectively. Additionally, the model demonstrates favorable results for rMBE with values of 5.12% and − 1.45% for DNI and DHI, respectively.

Table 8.

rRMSE and rMBE of DNI and DHI estimation using decomposition and machine learning models at KMU station.

	XGBoost	LightGBM	CatBoost	ENGERER2	ENGERER4	EVERY	STARKE 2	STARKE4	YANG4
DNI
RMSE (W/m2)	89.89	85.52	78.71	93.12	104.59	104.69	106.10	102.31	82.77
rRMSE (%)	28.15	26.78	24.65	29.16	32.75	32.78	33.22	32.04	25.92
MBE (W/m2)	19.19	9.96	16.35	25.73	38.90	16.75	− 48.27	− 53.39	25.16
RMBE (%)	6.01	3.12	5.12	8.06	12.18	5.25	− 15.12	− 16.72	7.88
DHI
RMSE (W/m2)	57.46	53.17	49.41	60.49	68.64	68.47	69.78	68.13	51.84
rRMSE (%)	29.34	27.15	25.23	30.89	35.05	34.96	35.63	34.79	26.47
MBE (W/m2)	− 1.61	2.68	− 2.84	− 11.51	− 20.75	− 8.57	35.73	39.39	− 10.91
RMBE (%)	− 0.82	1.37	− 1.45	− 5.88	− 10.59	− 4.37	18.24	20.11	− 5.57

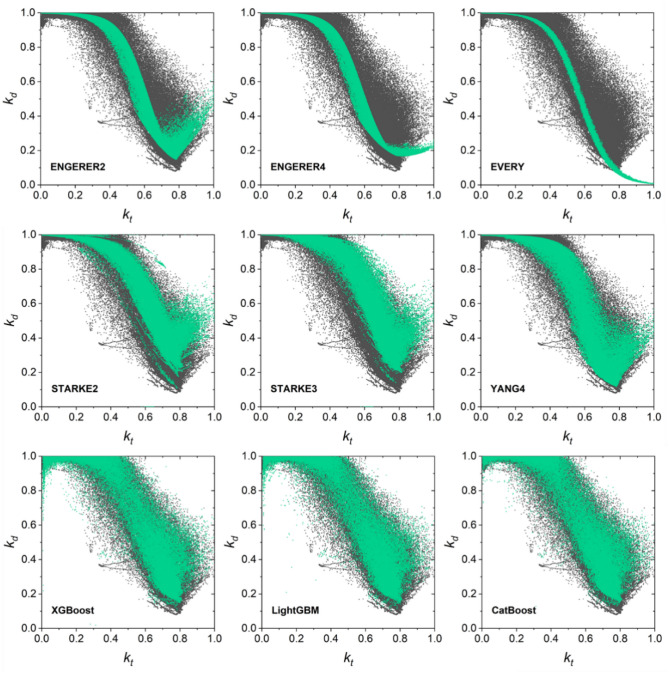
To further investigate the variations in the models, the diffuse fraction and clearness index are examined and are displayed in Fig. 7. The results obtained from the application of the solar radiation decomposition model indicated that the diffuse fraction distribution is unable to adequately describe the observed patterns in the measurement data. However, the machine learning models excelled in performance because they are able to address the limitations of the solar radiation decomposition models. Additionally, the machine learning models exhibited superior capabilities and provided broader coverage in this context.

Fig. 7.

Plots of clearness index and diffuse fraction that show the comparison of estimation results and measurement data. Gray points represent the measurement data and green points indicate the estimated diffuse fraction.

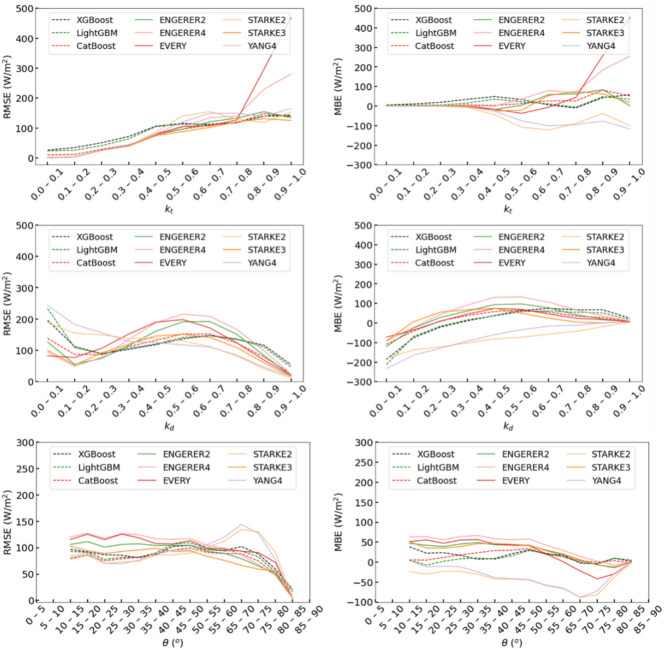
To enhance comprehension of the plot depicting clearness index and diffuse fraction, Fig. 8 illustrates the RMSE and MBE for the estimation of DNI across variations in clearness index, diffuse fraction, and solar zenith angle. Notably, solar decomposition models exhibit superior performance over machine learning models only when the clearness index is below 0.5. Concerning diffuse fraction, the YANG4 and STARKE2 models outperform machine learning models in the high diffuse fraction range from 0.6 to 1. However, in terms of MBE, machine learning models demonstrate better performance, with their plot lines closely approaching zero compared to other solar decomposition models. Regarding solar zenith angle, machine learning models compete with the YANG4 and STARKE2 models for angles less than 50°; however, machine learning models outperform these models at higher solar zenith angles.

Fig. 8.

RMSE and MBE for estimating DNI using the variance of , , and .

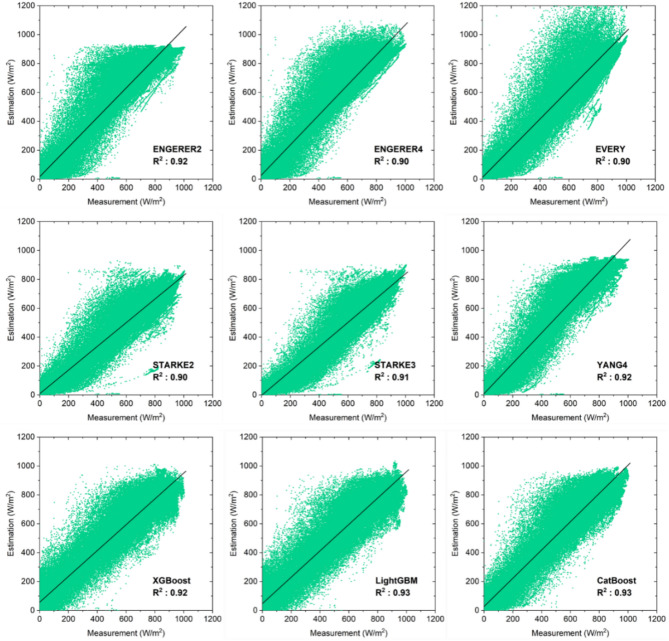
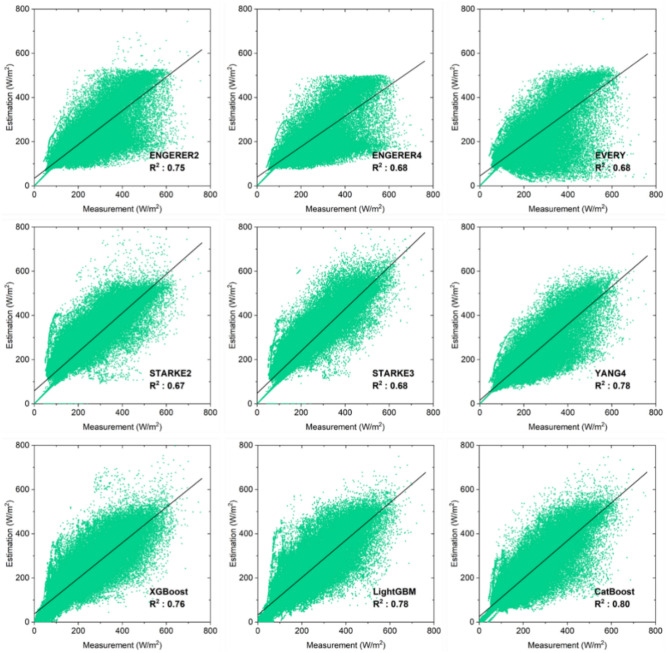
The scatterplots of the estimated versus measured data utilizing all the models to estimate DHI and DNI are depicted in Figs. 9 and 10. As observed, the scatterplots of all the machine learning models are much more appealing than the decomposition model, which is further substantiated by the higher R² of the machine learning model. Using the decomposition model to estimate DNI and DHI, the YANG4 model yielded higher R² values of 0.92 and 0.78, respectively. When comparing all the models, the CatBoost model achieved the best results, with R² values of 0.93 and 0.80, respectively.

Fig. 9.

Scatterplots of measured and estimated DNI using solar decomposition and machine learning models at the KMU site.

Fig. 10.

Same as Fig. 9 but for DHI.

Conclusions

To assess the performance of machine learning and solar decomposition models, solar irradiance data are collected from 10 global stations. The results indicate that machine learning models employing boosting algorithms like XGBoost, LightGBM, and CatBoost consistently outperform solar decomposition models in estimating DNI and DHI. In the validation dataset, XGBoost demonstrates superior performance, but during testing at each station, CatBoost consistently outperforms all models. This is not surprising since CatBoost displayed consistent performance in both training and validation, with a minimal 0.1% difference in rRMSE, suggesting a low risk of overfitting. The CatBoost model achieved the best results in estimating DNI and DHI with errors of 7.45% and 24.43%, respectively. Additionally, the CatBoost model consistently outperformed other models across all locations. Notably, when applied to data from the KMU station, which is not part of the training dataset, the CatBoost model improves solar radiation estimations for both DNI and DHI.

The interpretability of machine learning models is essential to identify significant input parameters and their contributions. In this study, SHAP is proposed to analyze all input parameters in machine learning models. SHAP values also provide insights into the impact of each feature value on the estimation results. This transparency is not only crucial for accessing the information contained within machine learning models, but it also serves as a valuable reference for enhancing the performance of future model separations. While most solar decomposition models rely on the clearness index to separate DNI and DHI from GHI, SHAP analysis reveals that humidity plays a substantial role in enhancing estimation results. According to the SHAP values obtained from the CatBoost model, humidity has an impact more than four times larger than other parameters such as pressure, turbidity, AST, temperature, and solar azimuth angle.

While the results are promising, there is a trade-off between model accuracy and interpretability. SHAP, while offering valuable insights into feature contributions, introduces a computational burden due to the need for multiple model evaluations. This can be a significant issue, especially when dealing with large datasets or complex models, limiting scalability. However, the strength of SHAP lies in its ability to provide transparency, helping to explain the decision-making process of the model. This transparency is crucial for building trust and guiding the development of future models. To address the computational challenges, one possible solution is to optimize the SHAP calculation by using more efficient sampling methods or approximations, like TreeSHAP for tree-based models. Additionally, future work could explore the balance between interpretability and model complexity by testing different model architectures that maximize both computational efficiency and accuracy, ensuring they remain practical for real-world applications.

List of symbols

Extraterrestrial irradiance, W/m²

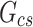
Clear-sky irradiance, W/m²

Relative humidity, %

Clear-sky index

Diffuse fraction

Portion of diffuse fraction

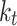
Clearness index

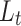
Linke turbidity

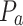
Pressure, hPa

Temperature, °C

Greek symbols

Solar zenith angle, °

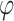
Solar azimuth angle, °

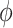
Shapley value

Solar elevation angle, °

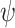
Three-point moving of clearness index

Abbreviations

AST

Apparent solar time

DHI

Diffuse horizontal irradiance, W/m²

DNI

Direct normal irradiance, W/m²

GHI

Global horizontal irradiance, W/m²

MBE

Mean bias error

QC

Quality control

rMBE

Relative mean bias error

RMSE

Root-mean-square error

rRMSE

Relative root-mean-square error

SHAP

Shapley additive explanations

Author contributions

R.R. conceptualized idea, developed methods, and wrote a draft of manuscript. R.R. and H.L. analyzed results and revised the manuscript. H.L. acquired funds and supervised.

Data availability

The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Declarations

Competing interests

The authors declare no competing interests.