Geographic routing in social networks

Abstract

We live in a “small world,” where two arbitrary people are likely connected by a short chain of intermediate friends. With scant information about a target individual, people can successively forward a message along such a chain. Experimental studies have verified this property in real social networks, and theoretical models have been advanced to explain it. However, existing theoretical models have not been shown to capture behavior in real-world social networks. Here, we introduce a richer model relating geography and social-network friendship, in which the probability of befriending a particular person is inversely proportional to the number of closer people. In a large social network, we show that one-third of the friendships are independent of geography and the remainder exhibit the proposed relationship. Further, we prove analytically that short chains can be discovered in every network exhibiting the relationship.

Anecdotal evidence that we live in a “small world,” where arbitrary pairs of people are connected through extremely short chains of intermediary friends, is ubiquitous. Sociological experiments, beginning with the seminal work of Milgram and his coworkers (1–3) and Killworth and Bernard (4), have shown that a source person can transmit a message to a target through only a small number of intermediate friends, using only scant information about the target's geography and occupation; in other words, social networks are navigable small worlds. On average, the successful messages passed from source to target through six intermediaries; from this experiment came the popular notion of “six degrees of separation.”

As part of the recent surge of interest in networks, there has been active research exploring strategies for navigating synthetic and small-scale social networks (5–12), including routing through common membership in groups, popularity, and geographic proximity, the property on which we focus. In both the experiments by Milgram and coworkers (1–3) and a more recent e-mail-based replication (13), one sees the message geographically “zeroing in” on the target step by step as it is passed on. Furthermore, subjects report that geography and occupation are by far the two most important dimensions in choosing the next step in the chain (4), and geography tends to predominate in early steps (13). These reports lead to an intriguing question: what is the connection between friendship and geography, and to what extent can this connection explain the navigability of large-scale real-world social networks? Of course, adding nongeographic dimensions to routing strategies, especially once the chain has arrived at a point geographically close to the target, can make routing more efficient, sometimes considerably (2, 8, 9, 14). However, geography appears to be the single most valuable dimension for routing, and we are thus interested in understanding how powerful geography alone may be.

Here, we present a study that combines measurements of the role of geography in a large social network with theoretical modeling of path discovery, using the measurements to validate and inform the theoretical results. First, a simulation-based study on a 500,000-person online social network reveals that routing through geographic information alone allows people to discover short paths to a target city. Second, through empirical investigation of the relationship between geography and friendship in this network, we discover that ≈70% of friendships are derived from geographical processes, but existing models that predict the probability of friendship solely on the basis of geographic distance are too weak to explain these friendships, rendering previous theoretical results inapplicable. [The proportion of links in a network that are between two entities separated by a particular geographic distance has been studied in a number of different contexts: the infrastructure of the Internet (15–17), small-scale e-mail networks within a company (9, 14), transportation networks (17), and wireless-radio networks (18).] Finally, we propose a density-aware model of friendship formation called rank-based friendship, relating the probability that a person befriends a particular candidate to the inverse of the number of closer candidates. We are able to rigorously prove that the presence of rank-based friendship for any population density implies that the resulting network will contain discoverable short paths to small destination regions. Rank-based friendship is then shown by measurement to be present in the large social network. Thus, we observe that a large online social network exhibits short paths under a simple geographical routing model, and we identify rank-based friendship as an important social-network property whose presence in the network implies the existence of short paths under geographic routing.

The social network that we consider comprises the 1,312,454 bloggers in the LiveJournal online community (www.livejournal.com), in February 2004. A blog, abbreviated from “web log,” is an online diary, often updated daily, typically containing reports on the user's personal life, reactions to world events, and commentary on other blogs. In the LiveJournal system, each blogger also explicitly provides a profile, including his or her geographic location, topical interests, and a list of other bloggers whom he or she considers to be a friend. Of these 1.3 million bloggers, there are 495,836 in the continental United States who list a hometown and state that we find in the United States Geological Survey Geographic Names Information System (ref. 19; http://geonames.usgs.gov) and are thus able to map to a longitude and latitude; the resolution of our geographic data is limited to the level of towns and cities. Thus, our discussion of routing is from the perspective of reaching the home town or city of the destination individual. That is, we study the problem of “global” routing, in which the goal is to direct a message to the target's city; once the proper locality has been reached, a “local” routing problem must then be solved to move the message from the correct city down to the correct person. There is evidence that geographic concerns predominate in the early stages of real-world message passing to solve the global-routing problem before the target individual is found by using a wide set of potential nongeographic factors, like interests or profession (1, 13).

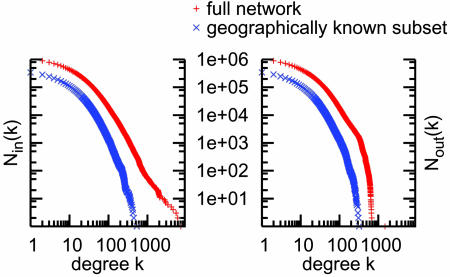
The LiveJournal social network is defined as the ≈500,000 LiveJournal users with locations in the United States in their profiles, with the “u is a friend of v” relationship defined by the explicit appearance of blogger u in the list of friends in the profile of blogger u. Let d(u, v) denote the geographic distance between two people u and v. There are 3,959,440 friendship links in this directed network, an average of about eight friends per user. (Although u can be listed as a friend of v without v being listed as a friend of u, we find that 80% of friendships are reciprocal.) This network exhibits many of the same important structural features observed in other social networks (20, 21). For example, 384,507 people (77.6%) form a giant component in which any two people u and v are connected by chains of friends leading from the coefficient of the network; that is, the proportion of the time that u and v are themselves friends if they have a common friend w is 0.2; this high clustering coefficient is characteristic of social networks (22). Fig. 1 shows the degree distribution, the fraction of the population with at least k friends for every k, both for the entire 1,312,454-person network and the 495,836 locatable people in the United States. The in-degree log/log plot is more linear than the out-degree plot, but both appear far more parabolic than linear; these curves provide some evidence supporting a log-normal degree distribution in social networks, instead of a power-law distribution (23–25).

Fig. 1.

In-degree (Left) and out-degree (Right) distributions in LiveJournal. For each k, the number N_in(k) of LiveJournal users who are listed as a friend of at least k users and the number N_out(k) of people who list at least k friends are shown, both for all 1,300,000 users and the 500,000 users who list locatable hometowns in the United States.

Geographic Routing

We perform a simulated version of the message-forwarding experiment in the LiveJournal social network, using only geographic information to choose the next message holder in a chain. This simulation may be viewed as a thought experiment, with two goals. First, we seek to determine whether individuals using purely geographic information in a simple way can succeed in discovering short paths to a destination city. Second, we seek to analyze the applicability of existing theoretical models that explain the presence or absence of short discoverable paths in networks (8, 10–12). Our simulation should not be viewed as a replication of real-world experiments studying human behavior (1, 13), but rather as an investigation into what would be possible for people participating in a message-passing experiment in such a network. Our approach, using a large-scale network of real-world friendships but simulating the forwarding of messages, allows us to investigate the performance of simple routing schemes without suffering from a reliance on the voluntary participation of the people in the network. (Further, in real-world experiments, dropout rates may depend on chain length, possibly biasing results toward shorter estimates of chain length.) Our detailed information on the location of every friend of every participant then allows us to analyze in detail the underlying geographic basis of friendship in explaining these results.

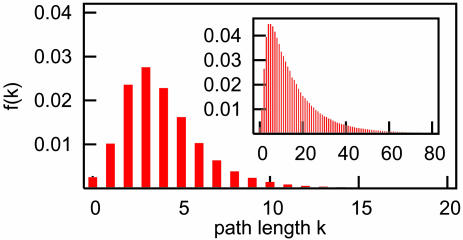
In our simulation, messages are forwarded by using the geographically greedy routing algorithm geogreedy (10): if a person u currently holds the message and wants to eventually reach a target t, then she considers her set of friends and chooses as the next step in the chain the friend in this set who is geographically closest to t. If u is closer to the target than all of her friends, then she gives up, and the chain terminates. When sources and targets are chosen randomly, we find that the chain successfully reaches the city of the target in ≈13% of the trials, with a mean completed-chain length of slightly more than four (Fig. 2). Recall that our data set does not contain intracity geographic information, so we do not attempt to reach the target itself; we instead focus on global routing in these simulated experiments. For a target t chosen uniformly at random from the network, the average population of t's city is 1,306 and always under 8,000; we therefore study the success of geography in narrowing the search from 500,000 users across the United States to the on-average 1,300 residents in a particular city.

Fig. 2.

Results of geogreedy on LiveJournal. In each of 500,000 trials, a source s and target t are chosen randomly; at each step, the message is forwarded from the current message-holder u to the friend v of u geographically closest to t.If d(v, t) > d(u, t), then the chain is considered to have failed. The fraction f(k) of pairs in which the chain reaches t's city in exactly k steps is shown (12.78% chains completed; median 4, μ = 4.12, σ = 2.54 for completed chains). (Inset) For 80.16% completed, median 12, μ = 16.74, σ = 17.84; if d(v, t) > d(u, t) then u picks a random person in the same city as u to pass the message to, and the chain fails only if there is no such person available.

A success rate of 13% with an average length of just over four in this simulated experiment shows a surface similarity to Milgram's original experiment (1), where 18% of chains were completed to the destination individual, with an average length of just under six. Our experiment, however, routes messages only to the destination city and does not suffer from problems of voluntary participation, which may explain why our completion rate is significantly higher than that of Dodds et al. (13). On the other hand, our simulated participants have a much narrower choice of actions, as they are restricted to friends whom they have explicitly listed in their profile and can forward only to the friend geographically closest to the target. Overall, we conclude that, even under restrictive forwarding conditions, geographic information is sufficient to perform global routing in a significant fraction of cases. This simulated experiment may be taken as a lower bound on the presence of short discoverable paths, because only the on-average eight friends explicitly listed in each LiveJournal profile are candidates for forwarding. By way of comparison, we modify the routing algorithm: an individual u who has no friend geographically closer to the target instead forwards the message to a person selected at random from u's city. Under this modification, chains complete 80% of the time, with median length 12 and mean length 16.74 (see Fig. 2). The completion rate is not 100% because a chain may still fail by landing at a location in which no inhabitant has a friend closer to the target. This modified experiment may be taken as an upper bound on completion rate, when the simulated individuals doggedly continue forwarding the message as long as any closer friend or collocated individual exists.

The Geographic Basis of Friendship

Thus, geographically greedy routing in the LiveJournal social network under a restrictive model allowed 13% of paths to reach their destination city in just over four steps, which is comparable to (or higher than) the end-to-end completion rates of earlier experiments on real human subjects (1, 13). Because such a restrictive global-routing scheme enjoys a high success rate, a question naturally arises: is there some special structure relating friendship and geography that might explain this finding?

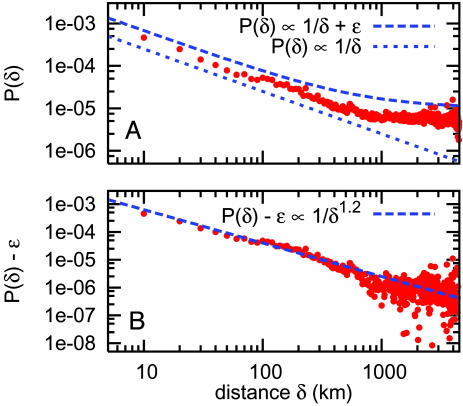
In Fig. 3A, we examine the relationship between friendship and geographic distance in the LiveJournal network. For each distance δ,let P(δ) denote the proportion of pairs u,v separated by distance d(u, v) = δ who are friends. As δ increases, we observe that P(δ) decreases, indicating that geographic proximity indeed increases the probability of friendship. [We note that this relationship holds even in the virtual LiveJournal community; at first blush, geographic location might have very little to do with the identity of a person's online friends, but Fig. 3A verifies that geography remains crucial in online friendship. Although it has been suggested that the impact of distance is marginalized by communications technology (26), a large body of research shows that proximity remains a critical factor in effective collaboration and that the negative impacts of distance on productivity are only partially mitigated by technology (27).] However, for distances larger than ≈1,000 km, the δ-versus- P(δ) curve approximately flattens to a constant probability of friendship between people, regardless of the geographic distance between them.

Fig. 3.

The relationship between friendship probability and geographic distance. (A) For each distance δ, the proportion P(δ) of friendships among all pairs u, v of LiveJournal users with d(u, v) = δ is shown. Distances are rounded down to multiples of 10 km. The number of pairs u, v with d(u, v) = δ is estimated by computing the distance between 10,000 randomly chosen pairs of people in the network. The curved line corresponding to P(δ) ∝ ε + 1/δ in A models the fact that some LiveJournal friendships are independent of geography: for distances larger than ≈1,000 km, the background friendship probability ε begins to dominate geography-based friendships. (B) The same data are plotted, correcting for the background friendship probability: we plot distance δ versus P(δ) – 5.0 × 10^–6.

The shape of Fig. 3A can be explained by postulating a background probability ε of friendship that is independent of geography, so that the probability that two people who are separated by distance δ are friends is modeled as for a function f(δ) that varies as the distance δ changes. That is, we model friendship creation by the union of two distinct processes, one comprising all geography-dependent mechanisms (like meeting in a shared workplace) and one comprising all nongeographic processes (like meeting online through a shared interest). A model for geographic friendships should reflect a decrease in the probability f(δ) of geographic friendship as the distance δ increases. Such a model will still account for some friendships between distant people, so we cannot simply equate geographic friendships with “nearby” friendships. Fig. 3A shows that P(δ) flattens to P(δ) ≈ 5.0 × 10^–6 for large distances δ; the background friendship probability ε dominates f(δ) for large separations δ. We thus estimate ε as 5.0 × 10^–6. We can use this value to estimate the proportion of friendships in the LiveJournal network that are formed by geographic and nongeographic processes. The probability of a nongeographic friendship between u and v is ε, so on average u will have 495,836 · ε ≈2.5 nongeographic friends. An average person in the LiveJournal network has eight friends, so ≈5.5 of an average person's eight friends (69% of her friends) are formed by geographic processes. This statistic is aggregated across the entire network: no particular friendship can be tagged as geographic or nongeographic by this analysis; friendship between distant people is simply more likely (but not guaranteed) to be generated by the nongeographic process. However, this analysis does allow us to estimate that about two-thirds of LiveJournal friendships are geographic in nature.

Because nongeographic friendships are by definition independent of geography, we can remove them from our plot to see only the geographic friendships. Fig. 3B shows the plot of geographic distance δ versus the geographic-friendship probability f(δ) = P(δ) – ε. The plot shows that f(δ) decreases smoothly as δ increases. Our computed value of ε implies that just over two-thirds of the friendships in the network are generated by geographic processes. Of course, the average person's 2.5 nongeographic friends may represent the realization of other deep and complex mechanisms, and they may themselves explain small-world phenomena and other fundamental properties of social networks. Here, though, we use only the average person's 5.5 geographic links to give a sufficient explanation of the navigable small-world phenomenon.

A natural starting point in modeling geographic friendships is the recent work of Kleinberg (10–12) and Watts and coworkers (8, 22). Watts et al. (8) present a model to explain searchability in social networks based on assignments of individuals to locations in multiple hierarchical dimensions; two individuals are socially similar if they are nearby in any dimension. They give examples of geography and occupation as dimensions, so their model may be viewed as an enclosing framework for our geography-specific results. However, the generality of their framework does not specifically treat geographic aspects, and it leaves two open areas that we address. First, although interests or occupations might be naturally hierarchical, geography is far more naturally expressed in 2D Euclidean space, embedding geographic proximity into a tree hierarchy is not possible without significant distortion (28). Second, although they provide a detailed simulation-based evaluation in terms of the number of hierarchical dimensions and a homophily parameter, their work does not include a theoretical analysis of the model as the network size grows, nor does it include a direct empirical comparison to a real social network. Our work seeks to build on their lead in these aspects.

Watts and Strogatz (22) give a compelling model of social networks, simultaneously accounting for the presence of short connecting chains and the high clustering coefficients of real social networks, but the goal of their model was to explain the existence of short paths rather than to give an explanation of social-network navigability. A major step toward explaining navigability was taken by Kleinberg (10–12). He modeled social networks by a k-dimensional grid of people, where each person knows his immediate geographic neighbors in every cardinal direction, and the probability of a long-distance link from u to v is proportional to 1/d(u, v)α, for some constant α ≥ 0. Kleinberg showed that short paths can be discovered in these networks if α = k; more surprisingly, he proved that this is the only value of α for which these networks are navigable. (The shortest paths that can be discovered in a network with α ≠ k are exponentially longer than the discoverable paths in networks with α = k.) Kleinberg (12) has subsequently generalized his model and results to an abstract characterization of group structures in social networks, and a number of researchers have presented extensions and improved analyses of these models (29–34).

If the LiveJournal data confirm this relationship between friendship probability and geographic distance, i.e., if the probability f[d(u, v)] of geographic friendship between u and v is roughly proportional to 1/d(u, v)², as the Earth's surface is 2D, then the finding of short paths by geogreedy will be explained. Fig. 3B explores this conjecture, showing the best fit for geographic-friendship probability as a function of geographic distance. However, the geographic-friendship probability between two people separated by distance δ is best modeled as f(δ) = 1/δα for α ≈ 1; Kleinberg's results (12), and those of all extensions to his model, in fact show that this exponent cannot result in a navigable social network based on a 2D mesh. Yet the LiveJournal network is clearly navigable, as shown in our simulation of geogreedy.

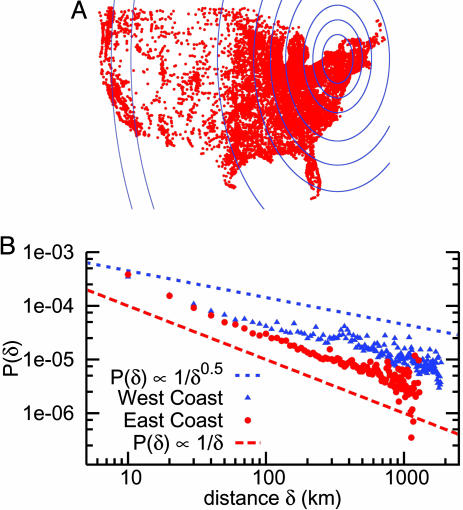
This seeming contradiction is explained by a large variance in population density across the LiveJournal network, which is thus ill-approximated by the uniform 2D mesh of Kleinberg's model. Fig. 4 explores population patterns in more detail. Fig. 4A shows concentric circles representing bands of equal population around Ithaca, NY. Under uniform population density, the width of each band should shrink as the distance from Ithaca increases. In the LiveJournal data set, however, the distance between annuli actually gets larger instead of smaller. Furthermore, purely distance-based predictions imply that the probability of a friendship at a given distance should be constant for different people in the network. Fig. 4B explores this concern, showing a distinction in friendship probability as a function of distance for residents of the East and West coasts. Thus a geographic model of friendship must be based on more than distance alone, as no accurate uniform description of friendship as a function of distance applies throughout the network.

Fig. 4.

Evidence of the nonuniformity of the LiveJournal population. (A) A dot is shown for every distinct United States location home to at least one LiveJournal user. The population of each successive displayed circle (all centered on Ithaca, NY) increases by 50,000 people. Note that the gap between the 350,000- and 400,000-person circles encompasses almost the entire Western United States. (B) We show the relationship between friendship probability and geographic distance, as in Fig. 3, restricted to people living on the West Coast (California, Oregon, and Washington) and the East Coast (from Virginia to Maine), respectively.

To summarize, we have shown that any model of friendship that is based solely on the distance between people is insufficient to explain the geographic nature of friendships in the LiveJournal network. The model of Watts et al. (8) naturally captures individuals' geographic similarity by approximating their Euclidean distance by their distance in some hierarchy, assigning friendship probability based on a function of this distance as long as geography remains the most proximate coordinate. Thus current models do not take into account the organization of people into cities of arbitrary location and population, and they cannot explain the success of the simulated message-passing experiment. We therefore seek a network model that reconciles the linkage patterns in real-world networks with the success of geogreedy on these networks. Such a model must be based on something beyond distance alone.

Population Networks and Rank-Based Friendship

We explore the idea that a simple model of the probability of friendship that combines distance and density may apply uniformly over the network. Consider a person u and a person v who lives 500 m away from u. In rural Iowa, say, u and v are probably next-door neighbors and very likely know each other; in Manhattan, there may be 10,000 people who live closer to u than v does, and the two are unlikely to have ever even met. This discrepancy suggests why geographic distance alone is insufficient as the basis for a geographical model. Instead, our model uses rank as the key geographic notion: when examining a friend v of u, the relevant quantity is the number of people who live closer to u than v does. Formally, we define the rank of v with respect to u as

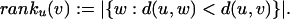Under the rank-based friendship model, we model the probability that u and v are geographic friends by

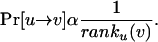Under this model, the probability of a link from u to v depends only on the number of people within distance d(u, v) of u and not on the geographic distance itself; thus the nonuniformity of LiveJournal population density fits naturally into this framework. Although either distance- or rank-based models may be appropriate in some contexts, we will show that (i) analytically, rank-based friendship implies that geogreedy will find short paths in any social network; and (ii) empirically, the LiveJournal network exhibits rank-based friendship.

We model a geographic n-person social network as follows. Consider a 2D N as a model of the 2D surface of the Earth. The grid divides the Earth's surface into small squares; we may take N to represent 1°-by-1° squares centered at the intersection of integral lines of longitude and latitude, for example. At every point (x, y) ∈ N, we have a population p(x, y) denoting the number of people who live in the square centered at (x, y), with ∑_x,y p(x, y) = n and p(x, y) > 0. The condition that p(x, y) > 0 is imposed to guarantee that a routing algorithm can always make some progress toward any target at every step of the chain. We refer to the combination of the grid N and the population p as a population network. Building on the navigable small-world model of Kleinberg (11, 10), we model linkage in population networks as follows. Each person u in the network has an arbitrarily chosen neighbor in each of the four adjacent grid points: north, east, south, and west. In addition to these four neighbors, person u has a long-range link to a fifth person chosen according to rank-based friendship, that is, the probability that u chooses v as her long-range link is inversely proportional to rank_u(v).

The notion of adding links with probability inversely proportional to the number of closer candidates is implicit in Kleinberg's work on his group-structure model (12), which is based on people's membership in groups like organizations or neighborhoods. This model, a generalization of his grid-based model (10, 11), introduces a long-range link between u and v with probability inversely proportional to the size of the smallest group containing both u and v. When the groups satisfy two key properties, a member of a group g must always belong to a subgroup of g that is not too much smaller than g, and every collection of small groups with a common member must have a relatively small union, Kleinberg has proven that the resulting network is a navigable small world. He suggests defining a set of geographic groups by “centering” groups of various geographic radii at each person in the network. This model is similar to rank-based friendship, in that friendships between people separated by a fixed distance are less likely in regions of high population density, and in a uniform-population setting the models approximately match both each other and Kleinberg's grid-based model. The models differ in that groups not centered at u do not play a role in determining u's friends in rank-based friendship. The first key property above also does not hold in the LiveJournal network: the population of the group of radius 100 km around a person u living 100 km north of Las Vegas will be massively larger than the population of any 99-km group containing u.

One important feature of rank-based friendship (and the group-structure model) is that it is independent of the dimensionality of the space in which people live. For example, in the 2D grid with uniform population density, we have that |{w: d(u, w) ≤ δ}| ∝ δ², so Pr[u → v] ∝ d(u, v)^–2, as required by Kleinberg's grid-based model, that is, the rank satisfies rank_u(v) ≈ d(u, v)². In the LiveJournal data set, we observe that rank and distance have a nearly linear relationship. The relationship between geographic distance and rank, in fact, in some sense measures the effective dimensionality of the network. Define the fractional dimension of (the set of geographic locations of the people in) a network as the exponent α of the best-fit function rank_u(v) = c·d(u, v)^α, averaged over all u and v. [This notion is similar to that of Yook et al. (15), but is distinct from the scaling of neighborhood size (17, 35, 36), which measures the relationship between graph distance and rank and is unrelated to geographic location.] The LiveJournal social network has fractional dimension ≈0.8, immediately explaining why we do not observe the inverse-square relationship between distance and friendship probability that one would expect in a navigable uniform 2D space.

Rank-based friendship results in a fundamental theoretical property that holds in every population network. Consider an n-person population network with arbitrary population densities, and suppose that individuals in the network choose their friends according to rank-based friendship. We show analytically that the expected length of the chain of friends found by geogreedy from any source s to the city of a randomly chosen target person t is short, that is, grows as a polynomial of the logarithm of population size.

Theorem. Let N be an arbitrary k-dimensional grid of locations, and let P be an arbitrary n-person population on N with rank-based friendship. For an arbitrary source person s and a target person t chosen uniformly at random from P, let ρ denote the path from s to the city of t found by geogreedy. Then the expected length of ρ is at most c·log³n, for a constant c independent of n, N, s, and P but dependent on k.

Proof outline: (Full details of the proof are in ref. 37.) Consider a message traveling from source person s to target person t by using geogreedy. We claim that if t is chosen uniformly at random from P, then the expected number of steps before the message reaches a person within distance d(s, t)/2 of t is at most c·log²n. After the distance to t is halved logn times, the message will have arrived at its destination. Thus the expected number of steps to reach t is at most c·log³n. To prove the claim, we show that the probability that a person forwards the message to someone within the small d(s, t)/2-radius neighborhood around t is at least 1/logn times the relative densities of the small neighborhood around t compared with a larger neighborhood containing both s and t. By taking expectations over t and appropriately approximating the densities of these neighborhoods, we show that the expected number of steps before the message reaches the small neighborhood around t is at most c·log²n.

There is significant evidence from real-world message-passing experiments that an effective routing strategy typically begins by making long geography-based hops as the message leaves the source and ends by making hops based on attributes other than geography (1, 13). Thus there is a transition from geography-based to nongeography-based routing at some point in the process. We can extend our theorem to show that short paths are constructible by using geogreedy through any level of resolution in which rank-based friendship holds.

Geographic Linking in the LiveJournal Social Network

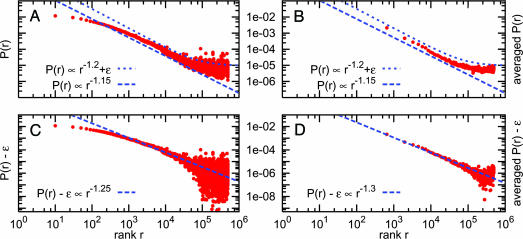
We return to the LiveJournal social network to show that rank-based friendship holds in a real network. The relationship between rank_v(u) and the probability that u is a friend of v shows an approximately inverse linear fit for ranks up to ≈100,000 (Fig. 5A). Because the LiveJournal data contain geographic information limited to the level of towns and cities, our data do not have sufficient resolution to distinguish between all pairs of ranks. (Specifically, an average person in the network lives in a city of population 1,306.) Thus in Fig. 5B we show the same data, where the probabilities are averaged over a range of 1,306 ranks. (Because of the logarithmic scale of the rank axis, the sliding window may appear to apply broad smoothing; however, smoothing by a window of size 1,300 causes a point to be influenced by <0.3% of the closest points on the curve.) This experiment validates that the LiveJournal social network does exhibit rank-based friendship, which thus yields a sufficient explanation for the experimentally observed navigability properties.

Fig. 5.

The relationship between friendship probability and rank. The probability P(r) of a link from a randomly chosen source u to the rth closest node to u, that is, the node v such that rank_u(v) = r, in the LiveJournal network, averaged over 10,000 independent source samples. A link from u to one of the nodes S_δ = {v:d(u, v) = δ}, where the people in S_δ are all tied for rank r + 1,..., r +|S_δ|, is counted as a (1/|S_δ|) fraction of a link for each of these ranks. As before, the value of ε represents the background probability of a friendship independent of geography. (A) Data for every 20th rank are shown. Because we do not have fine-grained geographic data, on average the ranks r through r + 1,305 all represent people in the same city; thus we have little data to distinguish among these ranks. (B) The data are averaged into buckets of size 1,306: for each displayed rank r, the average probability of a friendship over ranks {r – 652,..., r + 653} is shown. (C and D) The same data are replotted (unaveraged and averaged, respectively), correcting for the background friendship probability: we plot the rank r versus P(r) – 5.0 × 10^–6.

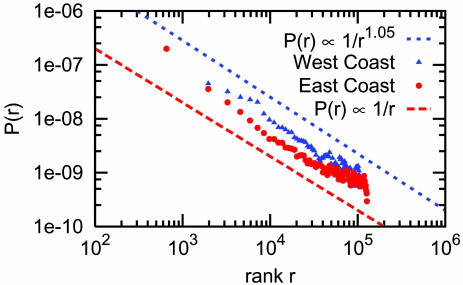
Fig. 6 displays the same data as in Fig. 5B, restricted to the East and West coasts. The slopes of the lines for the two coasts are nearly the same, and they are much closer together than the distance/friendship-probability slopes shown in Fig. 4B, confirming that probabilities based on ranks are a more accurate representation than distance-based probabilities.

Fig. 6.

The relationship between friendship probability and rank, as in Fig. 5, restricted to the West and East coasts and averaged over a range of 1,306 ranks.

In summary, the LiveJournal social network displays a surprising and variable relationship between geographic distance and probability of friendship, which is inconsistent with earlier theoretical models. Further, the network evinces short paths discoverable by using geography alone, even though existing models predict the opposite. We present rank-based friendship, a core mechanism for geographically biased friendship formation that may be embedded into a wide variety of broader models. Rank-based friendship is unique in simultaneously providing two desirable properties: (i) it matches our experimental observations regarding the relationship between geography and friendship; and (ii) it admits a mathematical proof that networks exhibiting rank-based friendship will contain discoverable short paths. As a validation of this theorem, the LiveJournal network exhibits rank-based friendship and does indeed contain discoverable short paths. Thus, we nominate rank-based friendship as a mechanism that has been empirically observed in real networks and theoretically guarantees small-world properties.

In fact, rank-based friendship explains geographic routing to a destination city; our data do not allow conclusions about routing within a city. Watts et al. (8) suggest that multiple independent dimensions play a role in message routing, and our results confirm this viewpoint: on average about one-third of LiveJournal friendships are independent of geography and may derive from other dimensions, like occupation and interests. These edges may play a role in local routing within the destination city and may also supplement the geographic links in global routing to the city; characterizing these geography-independent friendships is an interesting area for future work.

We have shown that the natural mechanisms of friendship formation result in rank-based friendship: people in aggregate have formed relationships with almost exactly the connection between friendship and rank that is required to produce a navigable small world. In a lamentably imperfect world, it is remarkable that people form friendships so close to the perfect distribution for navigating their social structures.