Fractal intermediates in the self-assembly of silicatein filaments

Abstract

Silicateins are proteins with catalytic, structure-directing activity that are responsible for silica biosynthesis in certain sponges; they are the constituents of macroscopic protein filaments that are found occluded within the silica needles made by Tethya aurantia. Self-assembly of the silicatein monomers and oligomers is shown to form fibrous structures by a mechanism that is fundamentally different from any previously described filament-assembly process. This assembly proceeds through the formation of diffusion-limited, fractally patterned aggregates on the path to filament formation. The driving force for this self-assembly is suggested to be entropic, mediated by the interaction of hydrophobic patches on the surfaces of the silicatein subunits that are not found on highly homologous congeners that do not form filaments. Our results are consistent with a model in which silicatein monomers associate into oligomers that are stabilized by intermolecular disulfide bonds. These oligomeric units assemble into a fractal network that subsequently condenses and organizes into a filamentous structure. These results represent a potentially general mechanism for protein fiber self-assembly.

There is considerable interest in the mechanisms governing the supramolecular assembly of proteins in biological systems (1–6). This interest stems from the dual desire to understand the fundamental mechanisms and harness them for use in technological applications (7–10). A recently discovered family of proteins, called silicateins, are interesting candidates for use in nanobiotechnology because of their dual roles as structural and enzymatic proteins that catalyze and structurally direct the formation of silica, silsesquioxanes, and metal oxide semiconductors (11–16). Thus, silicateins offer the potential for controlled site-directed assembly of nanofibers, which could serve as templates for the enzymatic formation of inorganic materials for use in semiconductor and optoelectronic devices.

Silicatein proteins govern the enzymatic and structurally controlled synthesis of silica in marine demosponges. Typically, silicateins are axial protein filaments (2 μm × 2 mm) that are occluded within, and run the entire length of, the silica spicules (20 μm × 2 mm) that constitute 75% of the dry weight of the sponge Tethya aurantia (11, 12). The filament is composed of three related proteins (silicatein α, β, and γ in an apparent ratio of 12:6:1), constituting ≈95% of the mass of the filament (11). Preliminary x-ray fiber-diffraction experiments reveal a crystalline order in the filament, although the arrangement of proteins has not been determined because of the complexity of the diffraction pattern (17). In vitro, the silicatein filament is capable of catalyzing the hydrolysis and polycondensation of silicon alkoxides and certain molecular precursors of metal oxides to yield a coating of the filament with silica, titanium dioxide, or gallium oxide (depending on the precursor that is used) (12, 15, 16). Also, in certain cases, the resulting inorganic material has crystalline order and consists of a polymorph that is not normally formed at ambient temperature and pH, suggesting a templating activity of the silicatein filament that may depend on the crystalline structure of the filament.

Although existing in the native form as an insoluble filament with a highly organized substructure (17–19), the silicateins exhibit strong structural homology to a family of monomeric, secreted “catalytic triad” proteases, with highest similarity to cathepsin L (11). The active site residues are in equivalent positions in the silicateins and cathepsin L, although the nucleophile in the active site of silicatein is a serine, rather than a cysteine as in cathepsin L. This finding suggested a hydrolytic activity in the mechanism of action of the silicateins (11, 12, 14). This suggestion was confirmed experimentally with the observations that (i) silicatein catalyzes the hydrolysis leading to the subsequent polycondensation of various molecular precursors of silica, organically substituted silsesquioxanes, and metal oxides (11, 12, 15, 16); and (ii) site-directed mutagenesis of the catalytic triad reduced this activity (20). The homology to cathepsin L also raises an interesting evolutionary question: What amino acid sequence changes in a soluble protein could result in the ability for the controlled assembly of a filamentous structure? This relationship affords a unique opportunity to investigate the relationship between primary amino acid sequence and the ability to form fibrous structures.

The mechanisms that govern fiber formation in biological proteins are entropy-driven (21) and can be divided broadly into two groups. In the first category, monomers with inherently high aspect ratios align in parallel to form larger assemblies, akin to liquid crystalline phases (e.g., collagen; refs. 22–24). In the second category, globular proteins assemble into helical protofilaments that subsequently aggregate to form larger filamentous structures [such as actin (25–27) and tubulin (28, 29)]. Here, we show that the in vitro self-assembly of the silicatein proteins yields fibrous structures in a mechanism that is fundamentally different from the two previously described mechanisms. Specifically, silicatein self-assembly proceeds through the formation of diffusion-limited fractally patterned aggregates on the path to filament formation. This progression of assembly is distinct from previously described assembly processes, and it represents a previously uncharacterized mechanism for protein fiber self-assembly.

Materials and Methods

Hydropathy Plots and Modeling. Hydropathy calculations for silicatein α (GenBank accession no. AAC23951), silicatein β (GenBank accession no. AAF21819), cathepsin L [Protein Data Bank (PDB) ID code 1ICF], and cathepsin K (PDB ID code 7PCK) were performed by protscale [ExPASy (Expert Protein Analysis System), Swiss Institute of Bioinformatics, Basel; available at: http://us.expasy.org/tools/protscale.html] by using the Kyte–Doolittle amino acid scale (30) with a window size of 9 and a linear weight-variation model. Energy minimized structures were based on the structure of cathepsin L (PDB ID code 1ICF) by using the insight ii modeling program (Accelerys, San Diego).

Silicatein Protein Preparation. Spicules were isolated from the marine sponge T. aurantia as described in ref. 11. Filaments were prepared by demineralization with a buffered hydrofluoric acid (HF) solution. Specifically, 2.5 g of spicules were combined with 200 ml of 2.5 M HF/5 M NH₄F (pH 5), with constant agitation on an orbital shaking platform until all silica had been removed from the filaments (≈2 h). Silicatein filaments were isolated by centrifugation and washed three times with 200 ml of 25 mM Tris·HCl (pH 6.8) at 4°C. Silicatein oligomers were prepared by the addition of 25 mM Tris·HCl (pH 9.1) and incubated at 4°C for 30 min, by which point the solution had cleared appreciably. Monodisperse oligomers were isolated by passage through a 0.2-μm Anotop 10 filter (Whatman) to remove any remaining large protein aggregates and to break up weakly interacting species by shearing.

Light Scattering. Dynamic light scattering (DLS) analyses were performed in glass scintillation vials, cleaned, and freed of dust with a minimum of 3-ml volumes by using a quasielastic-light-scattering DLS detector with a miniDAWN as the laser source (Wyatt Technologies, Santa Barbara, CA). Dilute oligomer solutions (40 μg/ml in 25 mM Tris·HCl, pH 9.1) were interrogated with a laser with wavelength of 690 nm at 4°C, with temperature being monitored by an internal detector. Data were collected at a detector 90° relative to the incident light and averaged over 5 s. Data were analyzed by using astra v software (Wyatt Technologies); analyses of distributions used the regularization template based on the dynals computational algorithm (Alango, Tirat Carmel, Israel).

Turbidity Assays. Turbidity assays were performed in 96-well polystyrene plates with a SpectraMax microplate reader (Molecular Devices) read at 600 nm. One hundred microliters of filtered oligomers was added to 100 μl of 0.1 M Na-phosphate buffer and 50 μl of salt solution of various concentrations. The turbidity of the solution was monitored at 600 nm at 30 min and 2 h.

Electron Microscopy. Oligomers were filtered through a 0.22-μm poly(vinylidene difluoride) filter (Millipore) and incubated at 4°C (pH 9). Protein concentration was 0.4 mg/ml (17 μM). At 0, 15, 30, and 60 min, a 2-μl aliquot was removed and placed on a copper transmission electron microscopy (TEM) grid coated with Formvar (Ted Pella, Redding, CA). The protein was allowed to adsorb to the grid for 2 min and the solvent then wicked off by using Whatman 1 filter paper. Uranyl acetate (Sigma; 5 μl of a 2% solution) was applied and allowed to incubate for 2 min and wicked off. The grid was then washed with Milli-Q water and allowed to dry in air overnight. Images were collected on a JEM-1230 TEM (JEOL) operated at 80 kV, and digital images were recorded with an Advantage charge-coupled device (CCD) camera system (AMT, Danvers, MA).

Fractal Dimension. The fractal dimensions of the structures seen during the time course of assembly were calculated by using the image j image-manipulation program (National Institutes of Health, Bethesda). TEM digital images were converted to a 16-bit binary format, and the fractal dimension was calculated by using the box-counting algorithm with box values of 2, 4, 8, 16, 32, 64, 128, 256, and 512 (31). In this algorithm, grids with varying numbers of boxes were overlaid on the image, and the number of nonempty boxes was counted. Data were plotted as the log of the number of boxes vs. the log of the number of boxes that were nonempty. Linear regression of the resulting line determined the slope, which corresponds to the fractal dimension D, by using prism (GraphPad, San Diego).

Results

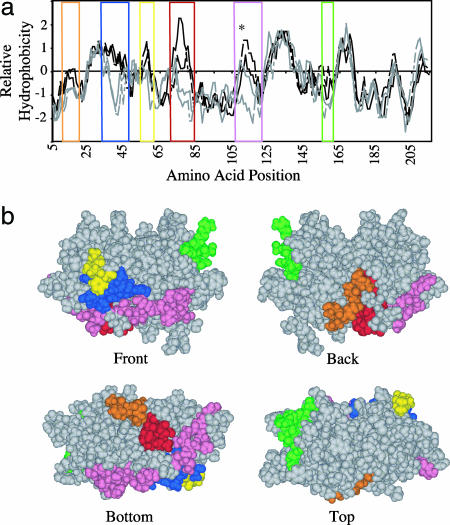
Mapping of Potential Intermolecular Interactions Based on Homology Modeling. The overall sequence similarity between silicatein α and cathepsin L is 65%, with 50% sequence identity (11). Silicatein β shares a 67% identity with silicatein α and 42% identity with cathepsin K. Conservation of the position of the six cysteine residues that form the three intramolecular disulfide bonds in the cathepsin and conservation (with one minor substitution) of the active-site residues combined with the high sequence identity indicate that the three-dimensional structures are very similar. Comparison of the hydrophobicity of the four related proteins (Fig. 1a) reveals five regions that differ appreciably between the soluble cathepsins and the insoluble silicatein, identifying hydrophobic regions that may be important in the formation and stabilization of the silicatein filament (32, 33). By using the structure of cathepsin L as a template, an energy-minimized three-dimensional model of silicatein α was constructed. Superimposition of those unique hydrophobic patches on the model of silicatein α shows that these regions are present on the solvent-accessible surface of the silicatein α monomer (Fig. 1b).

Fig. 1.

Identification of probable sites of subunit–subunit interactions for self-assembly. (a) Hydropathy analysis. Five regions where the hydrophobicity differs between filament forming silicateins (black) and the soluble cathepsins (gray) were identified. The asterisk marks the position at which cathepsin L is glycosylated (51), which lowers the hydrophobicity in that region. Amino acid positions are color-coded as follows: orange, 10–16; blue, 31–42; yellow, 59–61; red, 72–80; pink, 105–123; and green, 151–159. (b) Superimposition of the color-coded regions on a model of silicatein α derived from the crystal structure of cathepsin L shows they are present on the solvent-accessible surface of silicatein.

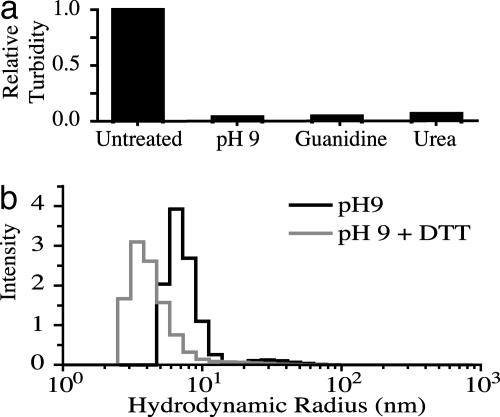
Filament Disassembly into Oligomeric Units. Exposure of native filaments isolated from spicules to high concentrations of guanidine or urea, or to pH 9 buffer, results in a decrease in the turbidity of the initial suspension because of the dissolution of the filaments (Fig. 2a). This observation suggests that noncovalent forces, rather than covalent bonds or cross-links such as those present in other filamentous proteins such as collagen and elastin, are responsible for the structural integrity of the filament. Raising the pH to 9 increases the net negative charge of the silicateins (pI ≈ 5.1; ref. 11), apparently causing electrostatic repulsion that results in filament dissolution; this effect is likely to result from the deprotonation of solvent-accessible tyrosine residue hydroxyl groups (pK_a 9.11) and the deprotonation of lysines (pK_a 8.95) to generate neutral amine species. DLS was used to characterize the species resulting from the dissolution of the silicatein filament under basic conditions. DLS allows measurement of the diffusion coefficient of a particle through intensity fluctuations of light scattering, which can be related to the hydrodynamic radius. DLS analysis of a diluted solution of disaggregated filaments reveals the presence of one major population possessing an average radius of hydration of 7.0 nm (Fig. 2b), which is considerably greater than the ≈2.3 nm that would be expected for a monomer of molecular mass of 23 kDa (32). This finding suggests that the filament dissolved to yield a population of oligomers, rather than silicatein monomers. At low protein concentrations, the size distribution does not change over the span of several hours (data not shown), suggesting that the oligomers are stable intermediates and not a result of nonspecific aggregation. When the reducing agent DTT is added, the average radius of hydration shifts to a lower average of 4.0 nm (Fig. 2b). This value, although larger than expected for a silicatein monomer, could correspond to a partially unfolded silicatein monomer resulting from the breakage of intermolecular disulfide bonds as well as the intramolecular disulfide bonds that hold the molecule in a compact geometry. This result indicates that the oligomers are composed of silicatein monomers held together by intermolecular disulfide bonds.

Fig. 2.

Dissolution of the silicatein filaments. (a) Turbidity measurements taken at 600 nm of filaments before and after addition of agents that disrupt the filament structure. (b) Weight-averaged distribution of light-scattering data with and without DTT, respectively. The data show that one major population exists with an average radius of hydration of 7.0 nm in the absence of DTT and one major population exists with an average radius of hydration of 4.0 nm in the presence of DTT.

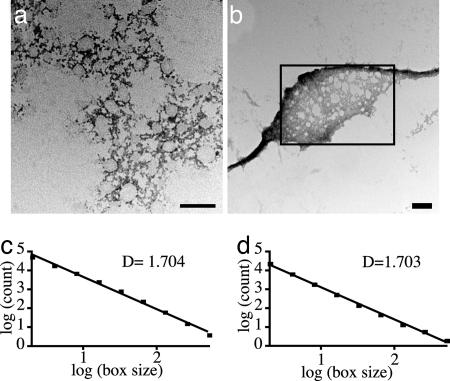
Silicatein Oligomers Self-Assemble into Filaments. Because covalent bonds are not crucial for the stability of the oligomer–oligomer interactions that contribute to the filament structure (disaggregation to the oligomers being promoted by chaotropic agents and by exposure to pH 9), it remained to be determined whether the information required to define the filamentous structure was fully specified in the silicatein oligomers alone. The self-assembly reactions were initiated by filtering to remove any large aggregates and by shearing to disrupt any weakly interacting species, thus shifting the equilibrium toward assembly. After filtering, the oligomers were incubated at pH 9 and 4°C without stirring; aliquots were removed from the solution as a function of time and adsorbed onto a TEM grid. Subsequent EM revealed that the silicatein oligomers self-assemble into filaments as a function of time. TEM snapshots of the assembly process are shown in Fig. 3. After 15 min, the oligomers are shown as 13- to 17-nm spheres that are visualized by negative staining with uranyl acetate (Fig. 3a). These observations agree well with results from DLS. After 30 min, assembly yields the complicated network shown in Fig. 3b. This intermediate state contains clusters of proteins that hierarchically assemble into structures with increasing morphological complexity that is defined both by the protein clusters and the systematic vacancies. After 1 h, the network is shown to have organized and condensed to form fibers of 70–100 nm in width that vary in length from a few micrometers to several hundreds of micrometers (Fig. 3c). The dimensions of these self-assembled filaments formed in vitro are smaller than those of the native filaments isolated from silica spicules produced in vivo (2 mm in length by 1 μm in diameter). However, we note that the in vitro assembly process that we have observed occurs without the structural confinement or environmental control exerted by the membrane enclosure that surrounds the assembling filaments in vivo (33).

Fig. 3.

Transmission electron micrographs of structural intermediates in the self-assembly process at 15 (a), 30 (b), and 60 (c) min. (Scale bars, 100 nm.)

Intermediate Structures Are Fractal. The intermediate structures shown in Fig. 3b appear to be chaotic, and the path leading to the assembly of a fibrous structure is not obvious. However, because the assembly eventually proceeds to an organized, highly condensed structure (perhaps related to the fibers formed in vivo that exhibit crystalline order; refs. 17 and 18), the structural information or assembly rules for its formation are apparently included within the complex network intermediate. Although the pattern of the intermediate seems to be random, it is reminiscent of the fractal patterns of aggregates that were first described in the diffusion-limited aggregation (DLA) of inorganic colloids (34–37). Fractals in biological systems typically are defined as structures or patterns (such as the branching of trees) that can be represented mathematically by fractal sets (38). Determining the mathematically defined fractal dimension of patterns such as these offers a measure of the complexity and self-scaling (or “self-similarity” over multiple scales of dimension) of the structure. A common way to calculate the fractal dimension D is to use the box-counting method, in which grids with a varying number of boxes are superimposed on an image of the pattern of interest (31). If a structure is fractal (i.e., self-similar over multiple scales of dimension), the log of the number of boxes that are filled plotted against the log of the total number of boxes yields a straight line. Linear-regression analysis gives a slope that corresponds to the fractal dimension. Euclidian shapes have fractal dimensions that are integers (a line has D = 1, a plane has D = 2, etc.), whereas fractal structures have nonintegral values of D. By using the box-counting method, it was determined that the intermediate structures shown in Fig. 4a possess a fractal dimension of 1.7 (Fig. 4c). This D value gives a quantitative measure of the self-similarity of the structures and their increasing complexity with length scale, and it is in close agreement with the theoretical value for structures formed during a DLA process (35). This result suggests that the formation of the fractal intermediate that we have observed may be the result of DLA, but it does not give insight into how the assembly process further progresses into filament formation. However, because the fractal dimension of a noncondensed area of the reconstituted filament is also 1.7 (Fig. 4 b and d), there is quantitative evidence that these structures are related, and the fractal structure represents a true intermediate in the path to filament formation.

Fig. 4.

Transmission electron micrographs of fractal structures and the calculation of fractal dimension by using the box-counting method. (a and c) The 30-min intermediate. (b and d) The 60-min time point, showing a fractal network flanked by filamentous structures. Fractal dimension was calculated only for the area in the rectangle. (Scale bar, 100 nm.)

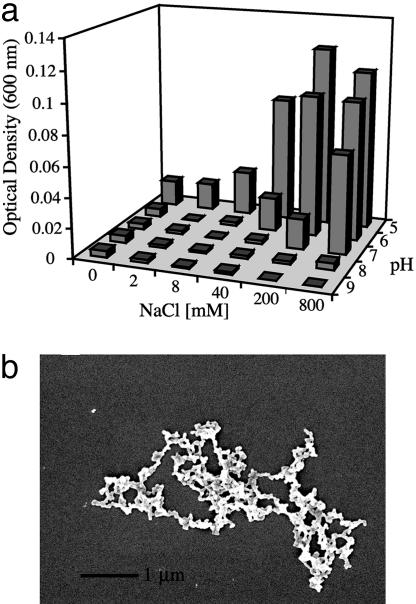
Increasing Salt and Lowering pH Change the Morphology of Aggregation. Changing the conditions of assembly alters the morphology of the structures that form. When the pH of the oligomer solution is brought to the pI of silicatein (pH 5), increasing aggregation is observed with an increasing salt concentration (Fig. 5a). However, the morphology of the product resulting from self-assembly at low-pH conditions differs from that of the in vitro self-assembly process at pH 9. At the lower pH and with high salt, monodisperse spheres of 70–80 nm aggregate to form chain-like networks that exhibit a fractal dimension of 1.4 (Fig. 5b), which is significantly lower than the structures produced at higher pH with no salt. These networks of spheres do not subsequently form filamentous structures, but they represent an endpoint pattern that is similar to that observed in the aggregation of inorganic colloids. This result suggests that the terminal pattern formed at low pH and high salt is the result of less specific protein–protein interactions that lead to structures that are not biologically relevant.

Fig. 5.

Salt and pH dependence of aggregation of silicatein oligomers. (a) OD₆₀₀ of oligomers as a function of salt and pH conditions. (b) Scanning electron micrograph of the morphology of the product generated under low-pH, high-salt conditions.

Discussion

The homologous relationship between the silicateins and cathepsin L (a soluble secreted protease, for which the complete atomic structure is known to the 2.5-Å level; ref. 39) offers insight into the intermolecular interactions that may be responsible for the supramolecular assembly of the silicatein proteins into filamentous structures. Therefore, differences in the amino acid sequences between cathepsin L and the silicateins are hypothesized to account for the ability of the silicateins to form filament structures. The most striking of these sequence differences is the presence of four hydrophobic patches that are spaced at geometrically distinct areas on the solvent-accessible surface of the silicateins. Although supramolecular assembly requires many covalent and noncovalent interactions to work in concert, we postulate that, unlike the case of the soluble monomeric cathepsins, hydrophobic regions on the surfaces of the silicatein subunits are essential for the intermolecular interactions that specify filament formation (40, 41).

The silicatein intermediate structures that are formed from spontaneous assembly possess qualitative and quantitative similarities to structures that are formed in the DLA of inorganic colloids (such as gold and silica; refs. 34–36). The process of DLA occurs in a dilute solution or suspension in which particles diffuse by Brownian motion and a random walk process until they contact and adhere to another particle. This process occurs multiple times to form clusters; as a result of steric constraints, a diffusing particle is more likely to adhere to the outer edges of a growing cluster than to the interior. This shielding of the interior of the cluster leads to the formation of branched or dendritic structures that are fractal (38). The complexity of the system can be related to the fractal dimension D, which is calculated by using the box-counting method (see Materials and Methods). The structures resulting from DLA have morphological similarities and fractal dimensions (D = 1.7) that are consistent with those of the silicatein intermediates. However, the structures produced by DLA of inorganic colloids are static endpoints; they do not progress into a more ordered structure. The resulting morphology is random because there are no structural requirements for orientation of interacting subunits, because the surface of the colloidal particles can be considered isotropic. In contrast, silicatein oligomers have a well defined three-dimensional structure with an anisotropic surface; thus, certain interactions will be favored over others. Also, the complexity of the self-assembled intermediate structures is likely to additionally reflect the presence of the three different silicatein subunits (silicatein α, β, and γ); these subunits may interact in geometrically constrained orientations, conferring further specificity on the assembly process and ultimately specifying the formation of the highly organized filament structure. Therefore, although the fractal structures of both the silicateins and inorganic colloids may be formed by the same process (DLA), we suggest that the fractal nature and unique specific geometry of the silicatein intermediate have a crucial role in the subsequent condensation and organization of the fractal structure into a filament.

Seemingly disordered protein-based structures are capable of transforming to extremely well ordered ones [e.g., secretory granules in mussel byssus thread (40) and in the silk-secretory glands of orb spiders (41)]. However, these conversions typically are driven by chemical or other environmental changes, including proteolytic processing, covalent modification, pH changes, or mechanical shear forces that induce alignment. In contrast, the silicatein oligomers from the native filament self-assemble in vitro into a filamentous structure, without spatial constraints or extreme changes in the reaction environment, demonstrating that all of the information needed for assembly is contained within the primary sequence of silicatein. Also, exogenous energy sources are not required for the assembly, in contrast to the assembly of actin or microtubules (which involve ATP or GTP hydrolysis, respectively).

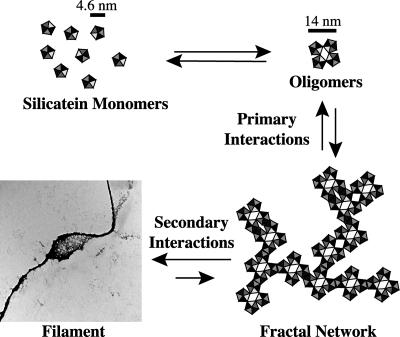
The route of self-assembly of the silicatein oligomers transitions progressively from an isotropic state to a seemingly chaotic, fractal state and, last, to an ordered structure. Because a filamentous structure is ultimately formed, there must be structural information and assembly rules in the fractal intermediate state. Our results are consistent with the model presented in Fig. 6. We propose that the silicatein monomers associate to form oligomers by means of hydrophobic interactions that are stabilized by intersubunit disulfide bonds (Fig. 2). (Note that it is these oligomers that we have observed as the primary products of dissagregation of the biogenic silicatein filaments upon treatment with elevated pH. These oligomers could be dissociated only to the monomeric subunits by treatment with disulfide reducing agents.) The resulting oligomers associate with each other by means of hydrophobic interactions; the specificity of these interactions (because of complementarities of shape, surface hydrophobicity, and possibly charge) results in the formation of fractal intermediate structures. As soon as these fractal intermediates are formed, weak secondary interactions (which may include hydrophobic, ionic, and/or van der Waals interactions) dominate because of the close proximity of the interacting protein surfaces, leading to further stereospecific condensation and organization of the fractal network into a filament.

Fig. 6.

Model of fractal assembly. Silicatein monomers associate into oligomers via disulfide bonds. The oligomers form fractal networks by DLA. As soon as the fractal network is formed, the close proximity and reduction in degrees of freedom drives the condensation and organization into a filament.

The filament-assembly process can be altered dramatically by changes in assembly conditions. When assembly proceeds at high pH, the large negative charge of silicatein causes electrostatic repulsion between the oligomers that slows the assembly process, allowing the specific interactions between the oligomers to direct the formation of an ordered filamentous structure. In contrast, at pH 5 (the isoelectric point of silicatein), high-salt concentrations screen the charges that otherwise would contribute to the specificity of interactions, thus allowing nonspecific hydrophobic interactions to dominate. The final morphology of the aggregates produced under these conditions more closely resembles the aggregation of inorganic colloids produced from random interactions between particles.

The fractal assembly process of the silicatein proteins on their path to filament formation is unique and distinct from the processes observed in the formation of other biomolecular fibers. Although many biological systems have been characterized with the calculation of fractal dimension, including ganglion cells (42), β-amyloid aggregates (43), and trabecular bone (44), the fractal state was not in these cases related to any assembly mechanism. Although the assembly of collagen has been modeled computationally by using rules for DLA (45, 46), no fractal intermediates have been observed experimentally. Interest in exploiting fractal geometry to manufacture complex patterns out of biological materials has led to the development of design principles for constructing DNA fractal structures (47, 48), as well as recent intriguing reports (49, 50) of fractal structures that are composed of engineered peptides. However, the fractal structures formed did not proceed to further organize into a more compact structure.

It is not yet known whether the fractal assembly process that we have observed in vitro recapitulates the in vivo assembly process that occurs inside a membrane-enclosed space of unknown composition within a cell. The fact that the reconstituted filaments have a smaller diameter than the native filaments does not preclude an in vivo fractal assembly. The differences in dimensions can be attributed to the spatial and chemical control governing the assembly process in vivo and to the cleavage of the silicatein propeptide (analogous to that of procollagen) that we suggest may assist in the correct folding of silicatein as well as prevent ectopic fibril formation. Also, it is unknown whether the crystallographic order that is exhibited in the native filaments occurs also in the in vitro system.

Conclusion

The spontaneous organization of filaments by fractal intermediates could be a general mechanism of self-assembly in both natural and engineered systems. The two-step system (fractal-intermediate assembly, followed by condensation) offers opportunities to engineer the stabilization of intermediates while exploiting fractal geometry to make a wide variety of complex structures. Computational modeling in conjunction with high-resolution atomic force microscopy studies could help us to understand more about the structural requirements of fractal assembly of anisotropic protein subunits, which would be useful for identifying assembly rules that could be applied to the development of biomimetics.